1 Introduction

Transient liquid phase (TLP) bonding has emerged as a suitable technique for the repair or joining of advanced materials, which are difficult to repair or join using conventional welding methods, due to their very high proneness to hot cracking during welding.[1,2] TLP bonding involves the use of an interlayer containing melting point depressant (MPD) elements such as phosphorus, silicon, and boron. The interlayer is melted between the conjoining base materials and the diffusion of MPD elements into the base materials results in isothermal solidification. In TLP bonding, the processed components do not undergo plastic deformation; hence, their mechanical properties are often identical to those of the base materials.[3,4,5,6] An in-depth understanding of the underlying mechanisms of TLP bonding process is important for its commercial exploitation; therefore, several modeling and experimental efforts have been made.[7,8,9,10,11,12,13,14,15] Existing theoretical models, for simplicity, assume one-dimensional (1D) migration of the solid–liquid interfaces during the joining of components by TLP bonding. Under this assumption, the solid–liquid interfaces are considered to be planar; hence, the modeling of the TLP bonding process is considered a symmetrical problem and as a result, only one solid–liquid interface is required to be modeled. However, many practical cases of TLP bonding involve two-dimensional (2D) or three-dimensional (3D) migration of the solid–liquid interfaces. Examples of these practical cases include the joining of components with curved surfaces, the lap joint of a solid cylindrical part to a hollow cylindrical part, and the joining of a solid spherical part to a hollow spherical part as depicted in Figure 1. In these practical cases, the solid–liquid interfaces are non-planar and the modeling problem cannot be considered as symmetrical; hence, two solid–liquid interfaces which are concurrently undergoing 2D or 3D migration must be modeled simultaneously. This situation cannot be handled by existing theoretical models. Moreover, most of the models available in the literature also assume constant diffusivity whereas in reality, diffusivity can vary significantly not only with concentration but also with time.[15,16,17,18] Therefore, the goal of this work is to develop a new numerical model for simulating TLP bonding involving two solid–liquid interfaces that concurrently undergo 2D or 3D migration while also incorporating diffusion coefficient that can change both with concentration and time and use the new model to gain a better understanding of the kinetics of TLP bonding process.

Fig. 1
figure 1

Schematic illustration of (a) the joining of a solid spherical part to a hollow one and (b) the lap joint of a solid cylindrical part to a hollow one

Full size image

2 Model Development

To study TLP bonding involving multidimensional (2D or 3D) migration of two solid–liquid interfaces, a hybrid explicit–fully implicit finite difference method is used to develop a numerical model which conserves solute. The model assumes an initial condition of thermal equilibrium at the bonding temperature and handles both the dissolution and isothermal solidification stages of the TLP bonding process without the existence of temperature gradient throughout the process. In spite of their stability, Crank-Nicolson and the fully implicit methods usually require simplification by several assumptions when used to solve non-linear differential equations. Explicit approaches avoid such assumptions and generally produce more accurate results; however, they require the use of small time steps for stability.[15] Since the use of small time steps leads to reduced computational efficiency, a hybrid explicit–fully implicit method is used to harness the stability and accuracy features of the fully implicit and explicit approaches, respectively. An explicit approach is employed in solving the diffusion equation in the solid phases while a fully implicit approach is used to solve the diffusion equation in the liquid phase. Furthermore, the TLP bonding process is typified by a consistent change in the thickness of the solid and liquid phases. To account for these dimensional changes, an aspect regarded as the most challenging in TLP bonding process modeling,[16] the space variable is transformed in each phase by the Murray–Landis space transformation.[19]

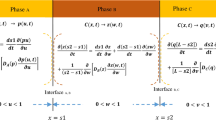
Multidimensional solid–liquid interface migration joint system in the form of the joining of a hollow cylindrical substrate to a solid cylindrical substrate (2D) or a hollow spherical substrate to a solid spherical substrate (3D) as depicted in Figure 1 is considered in this work. Schematic illustration of the numerical modeling scheme based on the Murray–Landis transformation is shown in Figure 2.

Fig. 2
figure 2

Schematic illustration of the numerical modeling scheme for a joint system involving 2D or 3D migration of two solid–liquid interfaces

Full size image

The variables \(u\), \(v\), and \(w\) are concentrations which are functions of the radial position \(r\) and time \(t\) within phase A, B, and C, respectively; \(l\), \(m\), and \(n\) represent the number of nodes in phase A, B, and C, respectively; \(f\), \(g,\) and \(h\) represent the local transformed coordinates in phase A, B, and C, respectively; \({C}_{\text{AB}}\), \({C}_{\text{BA}}\), \({C}_{\text{AC}}\), and \({C}_{\text{CA}}\) are the equilibrium solute concentrations at the interfaces; \(R\) is the half-width of the system; \({I}_{1}\) and \({I}_{2}\) are the instantaneous positions of the liquid/outside solid, and inside solid/liquid interfaces, respectively; the width of phase A is the initial liquid width; width of phase B is the radial thickness of the outside substrate; and width of phase C is the radius of the inside substrate.

As a diffusion-controlled process, the TLP bonding process is based on Fick’s laws as governing equations.

$$\frac{\partial v(r,t)}{\partial t}=\frac{\partial }{\partial r}\left({D}_{\text{B}}\left(v\left(r,t\right)\right)\frac{\partial v(r,t)}{\partial r}\right), {I}_{1}\le r\le R$$
(1)
$$\frac{\partial u(r,t)}{\partial t}=\frac{\partial }{\partial r}\left({D}_{\text{A}}\left(u\left(r,t\right)\right)\frac{\partial u(r,t)}{\partial r}\right), {I}_{2}\le r\le {I}_{1}$$
(2)
$$\frac{\partial w(r,t)}{\partial t}=\frac{\partial }{\partial r}\left({D}_{\text{C}}\left(w\left(r,t\right)\right)\frac{\partial w(r,t)}{\partial r}\right), 0\le r\le {I}_{2}$$
(3)
$${\left.{D}_{\text{A}}\left(u\left(r,t\right)\right)\frac{\partial u(r,t)}{\partial r}\right|}_{{{I}_{1}}^{-}}-{\left.{D}_{\text{B}}\left(v\left(r,t\right)\right)\frac{\partial v\left(r,t\right)}{\partial r}\right|}_{{{I}_{1}}^{+}}=\left[{C}_{\text{BA}}-{C}_{\text{AB}}\right]\frac{{\text{d}}{I}_{1}}{dt}, r={I}_{1}$$
(4)
$${\left.{D}_{\text{C}}\left(w\left(r,t\right)\right)\frac{\partial w(r,t)}{\partial r}\right|}_{{{I}_{2}}^{-}}-{\left.{D}_{\text{A}}\left(u\left(r,t\right)\right)\frac{\partial u\left(r,t\right)}{\partial r}\right|}_{{{I}_{2}}^{+}}=\left[{C}_{\text{AC}}-{C}_{\text{CA}}\right]\frac{{\text{d}}{I}_{2}}{{\text{d}}t}, r={I}_{2}$$
(5)

Equations [1] through [3] describe diffusion in phase B (outside solid), phase A (liquid), and phase C (inside solid), respectively. The moving boundary condition at the liquid/outside solid interface is described by Eq. [4] while the moving boundary condition at the inside solid/liquid interface is described by Eq. [5]. \({D}_{\text{A}}\left(u\left(r,t\right)\right)\), \({D}_{\text{B}}\left(v\left(r,t\right)\right)\), and \({D}_{\text{C}}\left(w\left(r,t\right)\right)\) are diffusivities, which are functions of concentration in phase A, B, and C, respectively.

Multidimensional interface migration is taken into account by the introduction of a parameter, \(\gamma \) which takes the value, 1 in 2D interface migration (cylindrical) systems and 2 in 3D interface migration (spherical) systems.[20] Putting \(\gamma \) as 0 reduces the model to the simplified case of 1D interface migration. Equations [1] through [3] are therefore rewritten as:

$$ r^{\gamma } \frac{{\partial v\left( {r,t} \right)}}{\partial t} = \frac{\partial }{\partial r}\left( {r^{\gamma } D_{{\text{B}}} \left( {v\left( {r,t} \right)} \right)\frac{{\partial v\left( {r,t} \right)}}{\partial r}} \right), I_{1} \le r \le R $$
(6)
$$ r^{\gamma } \frac{{\partial u\left( {r,t} \right)}}{\partial t} = \frac{\partial }{\partial r}\left( {r^{\gamma } D_{{\text{A}}} \left( {u\left( {r,t} \right)} \right)\frac{{\partial u\left( {r,t} \right)}}{\partial r}} \right), I_{2} \le r \le I_{1} $$
(7)
$$ r^{\gamma } \frac{{\partial w\left( {r,t} \right)}}{\partial t} = \frac{\partial }{\partial r}\left( {r^{\gamma } D_{{\text{C}}} \left( {w\left( {r,t} \right)} \right)\frac{{\partial w\left( {r,t} \right)}}{\partial r}} \right), 0 \le r \le I_{2} $$
(8)

The radial position, \(r\), in each phase (Eqs. [6] through [8]) can be expressed in terms of the Murray–Landis transformed positional variables, \(f\), \(g\), and \(h\) as follows.

$$ r = \left\{ {\begin{array}{*{20}l} {g\left( {R - I_{1} } \right) + I_{1} ,} \hfill & {I_{1} \le r \le R} \hfill \\ {f\left( {I_{1} - I_{2} } \right) + I_{2} ,} \hfill & {I_{2} \le r \le I_{1} } \hfill \\ {hI_{2} ,} \hfill & {0 \le r \le I_{2} } \hfill \\ \end{array} } \right. $$
(9)

The mass transfer equations [6] through [8] are modified using Eq. [9] to give:

$$ \left[ {g\left( {R - I_{1} } \right) + I_{1} } \right]^{\gamma } \left[ {\frac{\partial v}{{\partial t}} - \frac{{\left( {1 - g} \right)}}{{R - I_{1} }}\dot{I}_{1} \frac{\partial v}{{\partial g}}} \right] = \frac{\partial }{\partial g}\left\{ {\frac{{\left[ {g\left( {R - I_{1} } \right) + I_{1} } \right]^{\gamma } }}{{\left( {R - I_{1} } \right)^{2} }}D_{{\text{B}}} \left( {v\left( {r,t} \right)} \right)\frac{\partial v}{{\partial g}}} \right\},\quad 0 \le g \le 1 $$
(10)
$$ \left[ {f\left( {I_{1} - I_{2} } \right) + I_{2} } \right]^{\gamma } \left\{ {\frac{\partial u}{{\partial t}} - \frac{{\left[ {f\dot{I}_{1} + \left( {1 - f} \right)\dot{I}_{2} } \right]}}{{I_{1} - I_{2} }}\frac{\partial u}{{\partial f}}} \right\} = \frac{\partial }{\partial f}\left\{ {\frac{{\left[ {f\left( {I_{1} - I_{2} } \right) + I_{2} } \right]^{\gamma } }}{{\left( {I_{1} - I_{2} } \right)^{2} }}D_{{\text{A}}} \left( {u\left( {r,t} \right)} \right)\frac{\partial u}{{\partial f}}} \right\},\quad 0 \le f \le 1 $$
(11)
$$ \left( {hI_{2} } \right)^{\gamma } \left[ {\frac{\partial w}{{\partial t}} - \frac{h}{{I_{2} }}\dot{I}_{2} \frac{\partial w}{{\partial h}}} \right] = \frac{\partial }{\partial h}\left[ {\frac{{\left( {hI_{2} } \right)^{\gamma } }}{{I_{2}^{2} }}D_{{\text{C}}} \left( {w\left( {r,t} \right)} \right)\frac{\partial w}{{\partial h}}} \right],\quad 0 \le h \le 1 $$
(12)

The Eqs. (10–12) are modified into divergent forms which describe the physical requirements of the system.

$$ \frac{\partial }{\partial t}\left\{ {v\left( {R - I_{1} } \right)\left[ {g\left( {R - I_{1} } \right) + I_{1} } \right]^{\gamma } } \right\} = \frac{\partial }{\partial g}\left\{ {v\left( {1 - g} \right)\dot{I}_{1} \left[ {g\left( {R - I_{1} } \right) + I_{1} } \right]^{\gamma } } \right\} + \frac{\partial }{\partial g}\left\{ {\frac{{\left[ {g\left( {R - I_{1} } \right) + I_{1} } \right]^{\gamma } }}{{R - I_{1} }}D_{{\text{B}}} \left( {v\left( {r,t} \right)} \right)\frac{\partial v}{{\partial g}}} \right\},\quad 0 \le g \le 1 $$
(13)
$$ \frac{\partial }{\partial t}\left\{ {u\left( {I_{1} - I_{2} } \right)\left[ {f\left( {I_{1} - I_{2} } \right) + I_{2} } \right]^{\gamma } } \right\} = \frac{\partial }{\partial f}\left\{ {u\left[ {f\dot{I}_{1} + \left( {1 - f} \right)\dot{I}_{2} } \right]\left[ {f\left( {I_{1} - I_{2} } \right) + I_{2} } \right]^{\gamma } } \right\} + \frac{\partial }{\partial f}\left\{ {\frac{{\left[ {f\left( {I_{1} - I_{2} } \right) + I_{2} } \right]^{\gamma } }}{{I_{1} - I_{2} }}D_{{\text{A}}} \left( {u\left( {r,t} \right)} \right)\frac{\partial u}{{\partial f}}} \right\},\,\quad 0 \le f \le 1 $$
(14)
$$ \frac{\partial }{\partial t}\left[ {wI_{2} \left( {hI_{2} } \right)^{\gamma } } \right] = \frac{\partial }{\partial h}\left[ {wh\dot{I}_{2} \left( {hI_{2} } \right)^{\gamma } } \right] + \frac{\partial }{\partial h}\left[ {\frac{{\left( {hI_{2} } \right)^{\gamma } }}{{I_{2} }}D_{{\text{C}}} \left( {w\left( {r,t} \right)} \right)\frac{\partial w}{{\partial h}}} \right],\quad 0 \le h \le 1 $$
(15)

To obtain a finite difference scheme for phase C, which is discretized in \(n\) points, Eq. [15] is integrated with respect to space from \(h_{{i - \frac{1}{2}}}\) to \(h_{{i + \frac{1}{2}}}\), and with respect to time from a time, \(t^{j}\) to a future time \(t^{j + 1}\). Intermediate space nodes between nodes \(i - 1\), \(i\), and \(i + 1\) are represented by \(i - \frac{1}{2}\) and \(i + \frac{1}{2}\); \(j\) and \(j + 1\) represent the current and future times; dt is the time step; \(c\) corresponds to the radial position in phase C; \(j + \beta\) represents a time between \(j\) and \(j + 1\) after a fraction \(\beta\) of time step dt has elapsed. Diffusion in phase C is described by the resulting equation.

$$ \begin{gathered} \frac{1}{\gamma + 1}\left\{ {w_{i}^{j + 1} \left[ {\left( {c_{{i + \frac{1}{2}}}^{j + 1} } \right)^{\gamma + 1} - \left( {c_{{i - \frac{1}{2}}}^{j + 1} } \right)^{\gamma + 1} } \right] - w_{i}^{j} \left[ {\left( {c_{{i + \frac{1}{2}}}^{j} } \right)^{\gamma + 1} - \left( {c_{{i - \frac{1}{2}}}^{j} } \right)^{\gamma + 1} } \right]} \right\} \hfill \\ = \left( {c_{{i + \frac{1}{2}}}^{j + \beta } } \right)^{\gamma } \left[ {w_{{i + \frac{1}{2}}}^{j + \beta } dI_{2}^{j + \beta } h_{{i + \frac{1}{2}}} + \frac{{{\text{d}}t\left( {D_{{\text{C}}} } \right)_{{i + \frac{1}{2}}}^{j + \beta } }}{{I_{2}^{j + \beta } }}\left. {\frac{\partial w}{{\partial h}}} \right|_{{i + \frac{1}{2}}}^{j + \beta } } \right] \hfill \\ - \left( {c_{{i - \frac{1}{2}}}^{j + \beta } } \right)^{\gamma } \left[ {w_{{i - \frac{1}{2}}}^{j + \beta } {\text{d}}I_{2}^{j + \beta } h_{{i - \frac{1}{2}}} + \frac{{{\text{d}}t\left( {D_{{\text{C}}} } \right)_{{i - \frac{1}{2}}}^{j + \beta } }}{{I_{2}^{j + \beta } }}\left. {\frac{\partial w}{{\partial h}}} \right|_{{i - \frac{1}{2}}}^{j + \beta } } \right],\quad {\text{for}} = \, 1, \ldots n \hfill \\ \end{gathered} $$
(16)

where \({c}_{i\pm \frac{1}{2}}^{j}={h}_{i\pm \frac{1}{2}}.{{I}_{2}}^{j}\)

Finite difference schemes are obtained in similar fashion for phases A and B where \(a\) and \(b\) correspond to radial positions in phase A and B, respectively. Diffusion in phase A is described by:

$$ \begin{gathered} \frac{1}{\gamma + 1}\left\{ {u_{i}^{j + 1} \left[ {\left( {a_{{i + \frac{1}{2}}}^{j + 1} } \right)^{\gamma + 1} - \left( {a_{{i - \frac{1}{2}}}^{j + 1} } \right)^{\gamma + 1} } \right] - u_{i}^{j} \left[ {\left( {a_{{i + \frac{1}{2}}}^{j} } \right)^{\gamma + 1} - \left( {a_{{i - \frac{1}{2}}}^{j} } \right)^{\gamma + 1} } \right]} \right\} \hfill \\ = \left( {a_{{i + \frac{1}{2}}}^{j + \beta } } \right)^{\gamma } \left\{ {u_{{i + \frac{1}{2}}}^{j + \beta } \left[ {f_{{i + \frac{1}{2}}} {\text{d}}I_{1}^{j + \beta } + \left( {1 - f_{{i + \frac{1}{2}}} } \right){\text{d}}I_{2}^{j + \beta } } \right] + \frac{{{\text{d}}t\left( {D_{A} } \right)_{{i + \frac{1}{2}}}^{j + \beta } }}{{I_{1}^{j + \beta } - I_{2}^{j + \beta } }}\left. {\frac{\partial u}{{\partial f}}} \right|_{{i + \frac{1}{2}}}^{j + \beta } } \right\} \hfill \\ - \left( {a_{{i - \frac{1}{2}}}^{j + \beta } } \right)^{\gamma } \left\{ {u_{{i - \frac{1}{2}}}^{j + \beta } \left[ {f_{{i - \frac{1}{2}}} {\text{d}}I_{1}^{j + \beta } + \left( {1 - f_{{i - \frac{1}{2}}} } \right){\text{d}}I_{2}^{j + \beta } } \right] + \frac{{{\text{d}}t\left( {D_{A} } \right)_{{i - \frac{1}{2}}}^{j + \beta } }}{{I_{1}^{j + \beta } - I_{2}^{j + \beta } }}\left. {\frac{\partial u}{{\partial f}}} \right|_{{i - \frac{1}{2}}}^{j + \beta } } \right\},\quad {\text{ for}} = \, 1, \ldots l \hfill \\ \end{gathered} $$
(17)

where \({a}_{i\pm \frac{1}{2}}^{j}={f}_{i\pm \frac{1}{2}}\left({{I}_{1}}^{j}-{{I}_{2}}^{j}\right)+{{I}_{2}}^{j}\)

Diffusion in phase B is described by:

$$ \begin{gathered} \frac{1}{\gamma + 1}\left\{ {v_{i}^{j + 1} \left[ {\left( {b_{{i + \frac{1}{2}}}^{j + 1} } \right)^{\gamma + 1} - \left( {b_{{i - \frac{1}{2}}}^{j + 1} } \right)^{\gamma + 1} } \right] - v_{i}^{j} \left[ {\left( {b_{{i + \frac{1}{2}}}^{j} } \right)^{\gamma + 1} - \left( {b_{{i - \frac{1}{2}}}^{j} } \right)^{\gamma + 1} } \right]} \right\} = \left( {b_{{i + \frac{1}{2}}}^{j + \beta } } \right)^{\gamma } \left[ {v_{{i + \frac{1}{2}}}^{j + \beta } {\text{d}}I_{1}^{j + \beta } \left( {1 - g_{{i + \frac{1}{2}}} } \right) + \frac{{{\text{d}}t\left( {D_{B} } \right)_{{i + \frac{1}{2}}}^{j + \beta } }}{{R - I_{1}^{j + \beta } }}\left. {\frac{\partial v}{{\partial g}}} \right|_{{i + \frac{1}{2}}}^{j + \beta } } \right] \hfill \\ - \left( {b_{{i - \frac{1}{2}}}^{j + \beta } } \right)^{\gamma } \left[ {v_{{i - \frac{1}{2}}}^{j + \beta } {\text{d}}I_{1}^{j + \beta } \left( {1 - g_{{i - \frac{1}{2}}} } \right) + \frac{{{\text{d}}t\left( {D_{{\text{B}}} } \right)_{{i - \frac{1}{2}}}^{j + \beta } }}{{R - I_{1}^{j + \beta } }}\left. {\frac{\partial v}{{\partial g}}} \right|_{{i - \frac{1}{2}}}^{j + \beta } } \right],\quad {\text{ for}} = \, 1, \ldots m \hfill \\ \end{gathered} $$
(18)

where \({b}_{i\pm \frac{1}{2}}^{j}={g}_{i\pm \frac{1}{2}}\left(R-{{I}_{1}}^{j}\right)+{{I}_{1}}^{j}\)

Equation [17] is now modified using the fully implicit finite difference approach to obtain a simplified equation for future concentrations in the liquid phase A. This is achieved by putting \(\beta =1\) into Eq. [17] to obtain:

$$ \begin{gathered} \frac{1}{\gamma + 1}\left\{ {u_{i}^{j + 1} \left[ {\left( {a_{{i + \frac{1}{2}}}^{j + 1} } \right)^{\gamma + 1} - \left( {a_{{i - \frac{1}{2}}}^{j + 1} } \right)^{\gamma + 1} } \right] - u_{i}^{j} \left[ {\left( {a_{{i + \frac{1}{2}}}^{j} } \right)^{\gamma + 1} - \left( {a_{{i - \frac{1}{2}}}^{j} } \right)^{\gamma + 1} } \right]} \right\} \hfill \\ = \left( {a_{{i + \frac{1}{2}}}^{j + 1} } \right)^{\gamma } \left\{ {u_{{i + \frac{1}{2}}}^{j + 1} \left[ {f_{{i + \frac{1}{2}}} \left( {I_{1}^{j + 1} - I_{1}^{j} } \right) + \left( {1 - f_{{i + \frac{1}{2}}} } \right)\left( {I_{2}^{j + 1} - I_{2}^{j} } \right)} \right] + \frac{{{\text{d}}t\left( {D_{{\text{A}}} } \right)_{{i + \frac{1}{2}}}^{j + 1} }}{{I_{1}^{j + 1} - I_{2}^{j + 1} }}\frac{{u_{i + 1}^{j + 1} - u_{i}^{j + 1} }}{{f_{i + 1} - f_{i} }}} \right\} \hfill \\ - \left( {a_{{i - \frac{1}{2}}}^{j + 1} } \right)^{\gamma } \left\{ {u_{{i - \frac{1}{2}}}^{j + 1} \left[ {f_{{i - \frac{1}{2}}} \left( {I_{1}^{j + 1} - I_{1}^{j} } \right) + \left( {1 - f_{{i - \frac{1}{2}}} } \right)\left( {I_{2}^{j + 1} - I_{2}^{j} } \right)} \right] + \frac{{{\text{d}}t\left( {D_{{\text{A}}} } \right)_{{i - \frac{1}{2}}}^{j + 1} }}{{I_{1}^{j + 1} - I_{2}^{j + 1} }}\frac{{u_{i}^{j + 1} - u_{i - 1}^{j + 1} }}{{f_{i} - f_{i - 1} }}} \right\},\quad {\text{for}} = \, 1, \ldots l \hfill \\ \end{gathered} $$
(19)

Explicit finite difference approach is employed to obtain simplified equations for future concentrations in phases B and C. This is achieved by putting \(\beta =0\) in Eqs. [16] and [18] to obtain the following:

$$ \begin{gathered} \frac{1}{\gamma + 1}\left[ {\left( {b_{{i + \frac{1}{2}}}^{j + 1} } \right)^{\gamma + 1} - \left( {b_{{i - \frac{1}{2}}}^{j + 1} } \right)^{\gamma + 1} } \right]v_{i}^{j + 1} = \frac{{v_{i}^{j} }}{\gamma + 1}\left[ {\left( {b_{{i + \frac{1}{2}}}^{j} } \right)^{\gamma + 1} - \left( {b_{{i - \frac{1}{2}}}^{j} } \right)^{\gamma + 1} } \right] \hfill \\ + \left( {b_{{i + \frac{1}{2}}}^{j} } \right)^{\gamma } \left[ {v_{{i + \frac{1}{2}}}^{j} \left( {I_{1}^{j + 1} - I_{1}^{j} } \right)\left( {1 - g_{{i + \frac{1}{2}}} } \right) + \frac{{{\text{d}}t\left( {D_{{\text{B}}} } \right)_{{i + \frac{1}{2}}}^{j} }}{{R - I_{1}^{j} }}\frac{{v_{i + 1}^{j} - v_{i}^{j} }}{{g_{i + 1} - g_{i} }}} \right] \hfill \\ - \left( {b_{{i - \frac{1}{2}}}^{j} } \right)^{\gamma } \left[ {v_{{i - \frac{1}{2}}}^{j} \left( {I_{1}^{j + 1} - I_{1}^{j} } \right)\left( {1 - g_{{i - \frac{1}{2}}} } \right) + \frac{{{\text{d}}t\left( {D_{{\text{B}}} } \right)_{{i - \frac{1}{2}}}^{j} }}{{R - I_{1}^{j} }}\frac{{v_{i}^{j} - v_{i - 1}^{j} }}{{g_{i} - g_{i - 1} }}} \right],\quad {\text{ for}} = \, 1, \ldots m \hfill \\ \end{gathered} $$
(20)
$$ \begin{gathered} \frac{1}{\gamma + 1}\left[ {\left( {c_{{i + \frac{1}{2}}}^{j + 1} } \right)^{\gamma + 1} - \left( {c_{{i - \frac{1}{2}}}^{j + 1} } \right)^{\gamma + 1} } \right]w_{i}^{j + 1} = \frac{{w_{i}^{j} }}{\gamma + 1}\left[ {\left( {c_{{i + \frac{1}{2}}}^{j} } \right)^{\gamma + 1} - \left( {c_{{i - \frac{1}{2}}}^{j} } \right)^{\gamma + 1} } \right] + \left( {c_{{i + \frac{1}{2}}}^{j} } \right)^{\gamma } \hfill \\ \left[ {w_{{i + \frac{1}{2}}}^{j} \left( {I_{2}^{j + 1} - I_{2}^{j} } \right)h_{{i + \frac{1}{2}}} + \frac{{{\text{d}}t\left( {D_{{\text{C}}} } \right)_{{i + \frac{1}{2}}}^{j} }}{{I_{2}^{j} }}\frac{{w_{i + 1}^{j} - w_{i}^{j} }}{{h_{i + 1} - h_{i} }}} \right] - \left( {c_{{i - \frac{1}{2}}}^{j} } \right)^{\gamma } \left[ {w_{{i - \frac{1}{2}}}^{j} \left( {I_{2}^{j + 1} - I_{2}^{j} } \right)h_{{i - \frac{1}{2}}} + \frac{{{\text{d}}t\left( {D_{{\text{C}}} } \right)_{{i - \frac{1}{2}}}^{j} }}{{I_{2}^{j} }}\frac{{w_{i}^{j} - w_{i - 1}^{j} }}{{h_{i} - h_{i - 1} }}} \right],\quad {\text{for}} = \, 1, \ldots n \hfill \\ \end{gathered} $$
(21)

Equations [19] through [21] are used to compute the future concentrations at each node in phase A, B, and C, respectively. To generate a finite difference scheme for the interfaces, boundary conditions which enforce local equilibrium, are applied to Eqs. [16] through [18]. The two outer boundaries of the system (\(h=0\) and \(g=1\)) are subject to zero-flux condition since no transfer of solute is allowed beyond the system. Also, the interfacial concentrations are equal to the respective solidus and liquidus concentrations. The boundary conditions are mathematically written as follows:

$${\left.\frac{\partial w}{\partial h}\right|}_{h=0}={\left.\frac{\partial v}{\partial g}\right|}_{g=1}=0, \forall t$$
(22)
$$w\left(h,t\right)=\left\{\begin{array}{c}w\left(h,t\right), 0\le h<1\\ {C}_{CA}, h=1\end{array}\right., t\ge 0$$
(23)
$$u\left(f,t\right)=\left\{\begin{array}{c}{C}_{AC}, f=0\\ u\left(f,t\right), 0<f<1\\ {C}_{AB}, f=1\end{array}, t\ge 0\right.$$
(24)
$$v\left(g,t\right)=\left\{\begin{array}{c}{C}_{BA}, g=0\\ v\left(g,t\right), 0<g\le 1\end{array}\right., t\ge 0$$
(25)

To obtain the scheme for the liquid/outside solid interface, Eqs. [24] and [25] are applied as conditions to Eqs. [17] and [18]. The two resulting expressions are equated to obtain the moving boundary equation, from which the position of the liquid/outside solid interface at any time \({t}^{j+1}\) can be approximated as follows.

$${{I}_{1}}^{j+1}={{I}_{1}}^{j}+\frac{\left[{\left({b}_{1\frac{1}{2}}^{j+1}\right)}^{\gamma } \frac{{\text{d}}t{\left({D}_{\text{B}}\right)}_{1\frac{1}{2}}^{j+1}}{R-{{I}_{1}}^{j+1}} \frac{{v}_{2}^{j+1}-{C}_{\text{BA}}}{{g}_{2}} - {\left({a}_{l-\frac{1}{2}}^{j+1}\right)}^{\gamma } \frac{{\text{d}}t{\left({D}_{\text{A}}\right)}_{l-\frac{1}{2}}^{j+1}}{{{I}_{1}}^{j+1}-{{I}_{2}}^{j+1}} \frac{{C}_{\text{AB}}-{u}_{l-1}^{j+1}}{1-{f}_{l-1}}\right]}{{C}_{\text{AB}}\left[{\left({{I}_{1}}^{j+1}\right)}^{\gamma }-{\left({a}_{l-\frac{1}{2}}^{j+1}\right)}^{\gamma }{f}_{l-\frac{1}{2}}\right] + {\left({a}_{l-\frac{1}{2}}^{j+1}\right)}^{\gamma }{u}_{l-\frac{1}{2}}^{j+1}{f}_{l-\frac{1}{2}}- {\left({b}_{1\frac{1}{2}}^{j+1}\right)}^{\gamma }{v}_{1\frac{1}{2}}^{j+1}\left({1-g}_{1\frac{1}{2}}\right) - {C}_{\text{BA}}\left[{\left({{I}_{1}}^{j+1}\right)}^{\gamma }-{\left({b}_{1\frac{1}{2}}^{j+1}\right)}^{\gamma }\left({1-g}_{1\frac{1}{2}}\right)\right]}$$
(26)

The scheme for the inside solid/liquid interface is obtained by applying Eqs. [23] and [24] to Eqs. [16] and [17]. Following a similar procedure, the instantaneous position of the inside solid/liquid interface is given as:

$${{I}_{2}}^{j+1}={{I}_{2}}^{j}+\frac{\left[{\left({a}_{1\frac{1}{2}}^{j+1}\right)}^{\gamma } \frac{{\text{d}}t{\left({D}_{\text{A}}\right)}_{1\frac{1}{2}}^{j+1}}{{{I}_{1}}^{j+1}-{{I}_{2}}^{j+1}} \frac{{u}_{2}^{j+1}-{C}_{\text{AC}}}{{f}_{2}} - {\left({c}_{n-\frac{1}{2}}^{j+1}\right)}^{\gamma } \frac{{\text{d}}t{\left({D}_{\text{C}}\right)}_{n-\frac{1}{2}}^{j+1}}{{{I}_{2}}^{j+1}} \frac{{C}_{\text{CA}}-{w}_{n-1}^{j+1}}{1-{h}_{n-1}}\right]}{{C}_{\text{CA}}\left[{\left({{I}_{2}}^{j+1}\right)}^{\gamma }-{\left({c}_{n-\frac{1}{2}}^{j+1}\right)}^{\gamma }{h}_{n-\frac{1}{2}}\right] + {\left({c}_{n-\frac{1}{2}}^{j+1}\right)}^{\gamma }{w}_{n-\frac{1}{2}}^{j+1}{h}_{n-\frac{1}{2}}- {\left({a}_{1\frac{1}{2}}^{j+1}\right)}^{\gamma }{u}_{1\frac{1}{2}}^{j+1}\left({1-f}_{1\frac{1}{2}}\right) - {C}_{\text{AC}}\left[{\left({{I}_{2}}^{j+1}\right)}^{\gamma }-{\left({a}_{1\frac{1}{2}}^{j+1}\right)}^{\gamma }\left({1-f}_{1\frac{1}{2}}\right)\right]}$$
(27)

The mass transfer equations [19] through [21] in phase A, B, and C and the interface equations [26] and [27] are simultaneously solved to simulate TLP bonding in a joint system involving 2D or 3D migration of two solid–liquid interfaces. To simulate the condition of constant diffusivity, which is generally assumed in literature, the diffusivities throughout phase A, B, and C are kept at constant values \(D_{{\text{A}}}\), \(D_{{\text{B}}}\), and \(D_{{\text{C}}}\), respectively.

Even though models in the literature mostly assume constant diffusivity for simplicity, in reality, diffusivity can vary with concentration.[16,17,18] It has also been reported in literature that not only can diffusivity be concentration-dependent, but also the concentration dependency of diffusivity can significantly vary with time.[15,21] The overall diffusivity when diffusivity varies with both concentration and time can be expressed as the product of time-dependent diffusivity and concentration-dependent diffusivity which are represented by exponential functions.[16,22] Diffusivity is generally known not to vary significantly within the liquid phase; however, diffusivity can be significantly dependent on concentration in the solid phase.[15] Hence, the cases of concentration-dependent diffusivity, and concentration and time-dependent diffusivity are investigated in this work by incorporating exponential equations [28] and [29], and [30] and [31], respectively, in the solid phases B and C.

$$ \left( {D_{{\text{B}}} } \right)_{{i \pm \frac{1}{2}}}^{j + 1} = D_{{0{\text{B}}}} \exp \left( {K_{1} . v_{{i \pm \frac{1}{2}}}^{j + 1} } \right) $$
(28)
$$ \left( {D_{{\text{C}}} } \right)_{{i \pm \frac{1}{2}}}^{j + 1} = D_{{0{\text{C}}}} \exp \left( {K_{1} . w_{{i \pm \frac{1}{2}}}^{j + 1} } \right) $$
(29)
$$ \left( {D_{{\text{B}}} } \right)_{{i \pm \frac{1}{2}}}^{j + 1} = D_{{0{\text{B}}}} \exp \left( {K_{1} .v_{{i \pm \frac{1}{2}}}^{j + 1} } \right) \exp \left( {{\raise0.7ex\hbox{$t$} \!\mathord{\left/ {\vphantom {t {K_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${K_{2} }$}}} \right) $$
(30)
$$ \left( {D_{{\text{C}}} } \right)_{{i \pm \frac{1}{2}}}^{j + 1} = D_{{0{\text{C}}}} \exp \left( {K_{1} .w_{{i \pm \frac{1}{2}}}^{j + 1} } \right) \exp \left( {{\raise0.7ex\hbox{$t$} \!\mathord{\left/ {\vphantom {t {K_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${K_{2} }$}}} \right) $$
(31)

where \(D_{{0{\text{B}}}}\) and \(D_{{0{\text{C}}}}\) are taken as the constant diffusivities \(D_{{\text{B}}}\) and \(D_{{\text{C}}}\), respectively; \(K_{1}\) is a constant associated with the concentration dependency function; and \(K_{2}\) is a constant integer associated with the time dependency function. The Eqs. [28] and [29] are substituted into the mass transfer and interface equations when the modeling is performed under the condition of concentration-dependent diffusivity, \(D\left( C \right)\). The Eqs. [30] and [31] are substituted into the mass transfer and interface equations when the modeling is performed under the condition of concentration and time-dependent diffusivity, \(D\left( {C,t} \right)\). Simulations are done using input parameters available in the Reference 11 for the bonding of Ni substrates using Ni-P filler alloy (\(D_{{\text{A}}} = 500 \mu {\text{m}}^{2} \,{\text{s}}^{ - 1}\), \(D_{{\text{B}}} = D_{{\text{C}}} = 18 \,\mu {\text{m}}^{2} \,{\text{s}}^{ - 1}\), \(C_{{{\text{AB}}}} = C_{{{\text{AC}}}} = 10.223 \,{\text{at}}.\,{\text{pct}}\), and \(C_{{{\text{BA}}}} = C_{{{\text{CA}}}} = 0.166\, {\text{at}}.\,{\text{pct}}\), and \({\text{d}}t = 0.1 \,{\text{seconds}}\)). While the solid phases B and C have initial concentration and thickness of \(0 \,{\text{at}}.\,{\text{pct}}\) and 1 cm, respectively, the initial concentration and thickness of liquid phase A are \(19\,{\text{ at}}.\,{\text{pct}}\) and \(25\, \mu {\text{m}}\), respectively.[11]

3 Results and Discussion

3.1 TLP Bonding Involving 2D or 3D Interface Migration Under Constant Diffusivity

In this section, the results of modeling and simulation performed under the condition of constant diffusivity are presented. The developed numerical model is applicable for simulating the joining of two substrates of the same material and the kinetics of isothermal solidification, \(\Phi\), measured by the plot of isothermal solidification width against the square-root of time is investigated. A joint system is made up of two converging individual portions as can be deduced from Figure 2. The first portion consists of the inside solid (inside substrate) and a part of the liquid, separated by the inside solid/liquid interface and this portion will be referred to as the inside solid portion. The second portion consists of the outside solid (outside substrate) and a part of the liquid, separated by the liquid/outside solid interface and will be referred to as the outside solid portion. The developed model is firstly used to simulate the generally assumed case of 1D interface migration in the joint system depicted in Figure 2 and the behavior of isothermal solidification kinetics in the two portions of the system is shown in Figure 3. It is found that the behavior of isothermal solidification kinetics in the two portions of the joint system is exactly the same throughout the process. Also, the behavior in each portion of the joint system is such that the kinetics, \(\Phi\), maintains a single constant parameter (the slope of the graph) throughout the process. Although this is widely reported in the literature for the generally assumed case of 1D interface migration, many practical applications involve the cases of 2D and 3D interface migration which are usually not considered.

Fig. 3
figure 3

Isothermal solidification kinetics behavior in the joint system assuming 1D migration of the interface

Full size image

The developed numerical model is used to investigate the behavior of isothermal solidification kinetics in the two portions of a joint system involving 2D interface migration, and the result which presents interesting information is shown in Figure 4.

Fig. 4
figure 4

Isothermal solidification kinetics in the joint system with 2D interface migration showing the evolving increase with time and decrease with time in the outside solid and inside solid portions, respectively

Full size image

It is found that contrary to the case of 1D interface migration, the kinetics behavior in the two portions is similar only at the initial stage after which there is a transition to a condition where the kinetics in the two portions behaves differently. In the newly evolving condition, the kinetics, \(\Phi\), increases with time in the outside solid portion and reduces with time in the inside solid portion of the joint system. This is in contrast to the 1D case where the kinetics in both portions can be represented by a single constant parameter. The evolving distinction in the kinetics behaviors of the two portions manifest as an asymmetric solidification behavior such that the extents of isothermal solidification on the two substrates which are initially comparable now become different. In this later stage where asymmetric solidification behavior exists, the extent of isothermal solidification on the outside substrate (outside solid portion) is larger than that on the inside substrate (inside solid portion) as shown by the data points presented in Figure 5 (some data points skipped to aid visibility). This is in contrast to the 1D case where the extents of isothermal solidification on the two substrates are comparable throughout the process as can be deduced from Figure 3.

Fig. 5
figure 5

Scatter plot showing transition from symmetric solidification behavior to asymmetric solidification behavior in the 2D migration case

Full size image

The isothermal solidification kinetics of the TLP bonding process is analytically expressed as \(\Phi = 2K\sqrt D\) where \(D\) is diffusivity, and \(K\) is a function of the equilibrium concentrations at the interface and the initial solute concentration in the substrate.[7,9] Accordingly, when two components of the same material are joined under exactly the same bonding conditions (e.g., temperature), it is generally expected that the behavior of the kinetics of isothermal solidification on each component should be the same throughout the process. Hence, the unique transition to asymmetric solidification behavior, in which isothermal solidification on one component exhibits faster kinetics compared to the other, as observed in the 2D migration case defies expectation and necessitates further investigation. In this work, it is found that contrary to the 1D case, solute diffusion is accompanied by changes in curvature in a system where the interface migrates in 2D. In the outside solid portion, curvature reduces along the direction of solute diffusion and this implies that solute is consistently transported across the liquid/outside solid interface from regions of smaller area into regions of larger area. This alters the trend of solute redistribution around the liquid/outside solid interface in such a way that the interface kinetics and ultimately the kinetics of the process in the outside solid portion is increased as can be deduced from Eq. [4]. On the other hand, increase in curvature along the direction of solute diffusion implies that solute is consistently transported across the inside solid/liquid interface from regions of larger area into regions of smaller area, resulting in reduced kinetics in the inside solid portion as can be deduced from Eq. [5]. Even though the same materials and bonding conditions exist in the two portions, the effects of curvature become increasingly significant as the process progresses. As a result of this, the behavior of the solidification kinetics in each of the two portions becomes increasingly distinct. This distinction is what manifests outwardly as the asymmetric solidification behavior where the extent of isothermal solidification becomes larger on the outside substrate than on the inside substrate as the process progresses. It should be emphasized that this distinction is neither due to \(K\) nor \(D\) but the curvature-induced disparity in the rates of solidification in the two portions. This explanation also applies to the case of 3D interface migration where the same trend as in the 2D case exists in a more pronounced manner as can be deduced from Figure 6.

Fig. 6
figure 6

Isothermal solidification kinetics behavior compared in the 1D, 2D, and 3D cases

Full size image

Hence, contrary to what is generally reported in the literature, during TLP bonding involving 2D or 3D migration of solid–liquid interface, not only \(K\) and \(D\) determine the kinetics of the process but also a third factor – curvature. This is mathematically expressed by Eq. [32].

$$ \Phi_{{2{\text{D}}/3{\text{D}}}} = 2K\sigma \sqrt D $$
(32)

where \(\sigma\) is the curvature factor whose values in each of the two portions will depend on the type and degree of curvature at the migrating solid–liquid interfaces, i.e., whether curvature is increasing or reducing along the direction of solute diffusion. It should be noted that \(\sigma\) changes as the curvatures of the migrating interfaces change in the two portions of the system; hence, \(\Phi_{{2{\text{D}}/3{\text{D}}}}\) is not constant. In the outside solid portion, curvature factor increases with time so kinetics, \(\Phi_{{2{\text{D}}/3{\text{D}}}}\), increases with time. In the inside solid portion, curvature factor reduces with time and so kinetics, \(\Phi_{{2{\text{D}}/3{\text{D}}}}\), reduces with time.

3.2 TLP Bonding Involving 2D or 3D Interface Migration Under Variable Diffusivity

In this section, the effect of variable diffusivities on the kinetics of TLP joining involving 2D interface migration is investigated. As in the previous section, this is achieved by using the developed numerical model to determine the kinetics behavior in the 2D case. The 2D case is first considered under the condition of concentration-dependent diffusivity,\( D\left( C \right)\) (\(K_{1} = 1\)). As shown in Figure 7, the behavior of the kinetics in each of the two portions of the joint system under \(D\left( C \right)\) condition is found to be similar to that of the constant diffusivity case. Under \(D\left( C \right)\) condition, there is a transition from symmetric solidification behavior to the asymmetric solidification behavior in which the extent of isothermal solidification on the outside substrate (outside solid) is larger than that on the inside substrate (inside solid). Also, it is found that the kinetics which increases with time in the outside solid portion and reduces with time in the inside solid portion cannot be represented by a single constant parameter in either portion of the joint as in the constant diffusivity condition. This striking similarity of the kinetics behavior under the \(D\left( C \right)\) condition to that under the constant diffusivity condition is due to the fact that although diffusivity depends on concentration, the equilibrium condition at the interfaces keeps the diffusivities at the interfaces unchanged throughout the process. This result is in agreement with results from analytical[8] and numerical[15] work done on the 1D case in the literature where concentration-dependent diffusivity is reported not to alter isothermal solidification kinetics behavior.

Fig. 7
figure 7

Isothermal solidification kinetics in the joint system with 2D interface migration under concentration-dependent diffusivity condition using Eqs. [28] and [29] where \(K_{1} = 1\) vs constant diffusivity condition

Full size image

Apart from diffusivity depending on concentration, it has also been reported in the literature that diffusivity can reduce with time.[22,23] This second type of variable diffusivity—\(D\left( {C,t} \right)\) (\(K_{1} = 1\), \(K_{2} = - 1.5 \times 10^{5}\))—is simulated for the joint system involving 2D interface migration and the result is presented in Figure 8.

Fig. 8
figure 8

Isothermal solidification kinetics in the joint system with 2D interface migration under concentration and time-dependent diffusivity using Eqs. [30] and [31] where \(K_{1} = 1\) and \(K_{2} = - 1.5 \times 10^{5}\) vs constant diffusivity condition

Full size image

Similar to the conditions of constant diffusivity and concentration-dependent diffusivity, the result shows the unique transition to asymmetric solidification behavior where the extent of isothermal solidification on the outside substrate (outside solid) becomes consistently larger than that on the inside substrate (inside solid) as the process progresses. However, under this condition of \(D\left( {C,t} \right)\) where diffusivity reduces with time, the kinetics behavior exhibits some uniqueness. The diffusivities at the interfaces which would normally remain unchanged throughout the process even under \(D\left( C \right)\) due to the equilibrium condition at the interfaces, now reduce as the process progresses. This consistent reduction of diffusivity aggravates the curvature-induced reduction in process kinetics in the inside solid portion (Figure 8). On the other hand, in the outside solid portion, the consistently reducing diffusivity can either alleviate the curvature-induced increase in kinetics or completely override it depending on the level of \(D\left( {C,t} \right)\). The latter scenario results in a solidification kinetics behavior in the outside solid portion which is similar to that of the inside solid portion in that the kinetics reduces rather than increases with time (Figure 8). Conversely, a condition of \(D\left( {C,t} \right)\) (\(K_{1} = 1\), \(K_{2} = 1.5 \times 10^{5}\)) where diffusivity increases with time can result in a case where the isothermal solidification kinetics behavior of both the inside and outside solid portions increases rather than reduces with time as shown in Figure 9. Figure 10 shows results for the concentration and time dependency condition with other values of \(K_{1}\) and \(K_{2}\) where diffusivity increases with time (b and d) or reduces with time (a and c). This new concept which is peculiar to the condition of \(D\left( {C,t} \right)\) where diffusivity either reduces or increases with time is very informative as it can be used as a criterion for determining if diffusivity changes with both concentration and time in a system.

Fig. 9
figure 9

Isothermal solidification kinetics in the joint system with 2D interface migration under concentration and time-dependent diffusivity using Eqs. [30] and [31] where \(K_{1} = 1\) and \(K_{2} = 1.5 \times 10^{5}\) vs constant diffusivity condition

Full size image
Fig. 10
figure 10

Isothermal solidification kinetics in the joint system with 2D interface migration under concentration and time-dependent diffusivity where (a)\(K_{1} = - 1.5\),\(K_{2} = - 1.5 \times 10^{5}\), (b)\( K_{1} = 1.5\), \(K_{2} = 5 \times 10^{4}\), (c)\( K_{1} = - 2\), \(K_{2} = - 1.5 \times 10^{5}\), and (d)\( K_{1} = 1.5\), \(K_{2} = 1.5 \times 10^{5}\).

Full size image

3.3 Experimental Verification

The developed model provides major predictions about the TLP bonding process involving two solid–liquid interfaces that concurrently undergo 2D migration. The model predicts a transition from symmetric solidification behavior to asymmetric solidification behavior such that the extents of isothermal solidification on the two substrates which are comparable at the initial stages of the process become different as the process progresses. Additionally, the model predicts that in this latter stage during which the asymmetric solidification behavior occurs, the substrate in which curvature reduces along the direction of solute diffusion (outside substrate) will exhibit the larger extent of isothermal solidification. This feature predicted by the new model does not occur when the solid–liquid interfaces migrate in 1D, but it is found to be common to all the simulated cases of 2D interface migration regardless of whether the diffusivity is constant, concentration-dependent, or concentration and time-dependent. Even though the existence of temperature gradient or material dissimilarity can also induce asymmetric solidification behavior, it should be noted that the present model features the joining of similar materials and a situation where there is no temperature gradient; hence, the asymmetric solidification behavior reported in this work is solely due to the curvature-induced disparity in solidification rates. This key behavior has never been previously reported elsewhere in the literature and hence requires experimental verification.

To perform the experimental verification, TLP bonding in a cylindrical (2D) joint system of IN738 superalloy substrates using Nicrobraz 150 filler alloy powder was done. Circular slots of inner radius 0.5 mm and depth 5 mm were machined into a 20 × 20 × 8 mm IN738 superalloy plate using 1.5875 mm 4-flute cobalt windmill cutters. This arrangement is equivalent to the joining of a 1 mm solid cylinder to a 4.2 mm hollow cylinder as depicted in Figure 11.

Fig. 11
figure 11

Schematics of IN738 2D joint specimen with dimensions in mm

Full size image

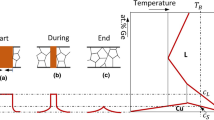
Specimens were cut out by electro-discharge machining (EDM). The faying surfaces of the specimens were cleaned with acetone in an ultrasonic bath for 25 minutes to ensure surface integrity. The gap in each specimen was then filled with Nicrobraz 150 filler alloy powder and a ceramic stop-off applied along the rim of the slots to prevent liquid spills during the TLP bonding process. The specimens were held in a ceramic-coated jig and processed at ~ 10−6 Torr and 1100 °C with a heating ramp rate of 12 °C/min for holding times ranging between 4 and 75 hours, in a tube vacuum furnace that is equipped with a special controller that maintains three specific uniform temperature zones. In order to avoid the occurrence of temperature gradient across the samples, the three zones are set and maintained at the bonding temperature, and samples are placed at the center of the middle uniform temperature zone. TLP-bonded samples were sectioned and prepared following typical metallographic procedures for analysis by optical microscopy. Using optical microscope-equipped CLEMEX vision image analyzer, the widths of the isothermal solidification zones (ISZ) are determined through an average of 20 repeated measurements taken along the radial direction, from the micrograph of each bonded sample as shown in Figure 12. Figure 13 shows the plots of the ISZ width against the square-root of time in the outside solid and the inside solid portions of the TLP-bonded samples.

Fig. 12
figure 12

A typical micrograph of the TLP-bonded joint region showing the isothermal solidification zones on the outside solid, ISZ (out) and the inside solid, ISZ (in) of the joint

Full size image
Fig. 13
figure 13

Plot of isothermal solidification zone (ISZ) width against square-root of time during isothermal solidification in a cylindrical TLP joint system of IN738 substrates using Nicrobraz 150 filler alloy

Full size image

Figure 13 shows statistically comparable solidification widths around the two substrates at the initial stages of the process, followed by the asymmetric solidification behavior where the ISZ widths become clearly different. The asymmetric solidification behavior is evident in the experimental data as predicted by the numerical model developed in this work. Moreover, it can be seen that during the later stages where asymmetric solidification behavior occurs, the outside substrate exhibits the larger of the two ISZ widths which concurs with the model prediction. The results provide experimental verification of the model key predictions and validate the newly developed numerical model. Overall, this work shows for the first time that when two solid–liquid interfaces move in 2D or 3D during TLP bonding, the isothermal solidification process transits from symmetrical to asymmetrical solidification behavior, which could affect the microstructure and properties of the joint.

4 Summary and Conclusions

A new numerical model has been developed for TLP bonding involving two solid–liquid interfaces that concurrently undergo two-dimensional (2D) or three-dimensional (3D) migration in contrast to previous models in the literature where the two solid–liquid interfaces are assumed to undergo one-dimensional (1D) migration. The developed model incorporates variable diffusivity and conserves solute by using a unique hybrid explicit–fully implicit approach and an adaptable space discretization based on Murray–Landis transformation, respectively. The key predictions of the model are experimentally verified. The following are the key conclusions.

  1. 1.

    In contrast to what occurs in the case of 1D migration, the isothermal solidification process during TLP bonding involving two solid–liquid interfaces that concurrently undergo 2D or 3D migration exhibits a transition from symmetric to asymmetric solidification behavior. This behavior has not been previously reported in the literature.

  2. 2.

    The asymmetric solidification occurs such that the extent of the isothermal solidification is consistently larger on the solid substrate where the solid–liquid interfacial curvature reduces along the direction of solute diffusion.

  3. 3.

    The transition from symmetric to asymmetric solidification behavior indicates that the isothermal solidification kinetics cannot be represented by a single constant parameter, as is the case during 1D migration of the solid–liquid interface.

  4. 4.

    This work shows that aside from diffusivity, equilibrium concentrations at the solid–liquid interface, and initial substrate composition, the isothermal solidification kinetics during 2D or 3D migration of the solid–liquid interface is also controlled by the type and degree of curvature at the migrating solid–liquid interfaces.