1 Introduction

The formation of proeutectoid-ferrite from metastable austenite is an important transformation in steel, and there has been a plethora of both experimental and theoretical studies on this transformation in order to understand its mechanism as well as predict the microstructural evolution. Most of the earlier theoretical models are based on the local equilibrium approach[1,2,3,4] where the concentrations across the interface are assumed to be same as those obtained by the equality of chemical potentials. This assumption is actually valid for very slow transformation. As the velocity increases, solute gets trapped behind the advancing front which is known as ‘solute trapping’. Phenomena like solute trapping, massive transformation, etc. have established the theory of interface-controlled transformation.[5] Therefore, a more general approach for modeling phase transformation has been introduced in the concept of ‘mixed-mode’ transformation[6,7,8] which lies between two extremes: one extreme is diffusional transformation where the solute does not get trapped as quasi-equilibrium prevails in the interface, and the second extreme is interface-controlled transformation. A ‘mixed-mode’ of transformation is basically a mixture of both modes of transformation in the sense that the composition at the parent side of the interface lies between the equilibrium and the initial compositions.[7,8]

In the late stage of transformation, wide diffusion layers around growing nuclei impinge on each other. This phenomenon is known as ‘soft-impingement’, and it significantly affects both nucleation and growth.[9,10,11,12] The progress of growth under soft-impingement results in a change in the composition of the bulk parent phase far away from the nuclei. The major limitation for formulation of growth models under soft-impingement is the lack of knowledge on the exact nature of diffusion layers. However, some workers assume a linear diffusion field around the nuclei and model the transformation of growth under soft-impingement to formulate the parabolic growth coefficient and the transformed volume fraction.[13,14,15,16,17] However, a linear diffusion layer is clearly an oversimplified assumption. Chen proposes a polynomial function of degree n, to describe the diffusion layer as shown in Figure 1(a), having the following form[18]:

$$\begin{aligned} c_{\gamma }(x)=c_i+(c_{\gamma }^{*}-c_i)\left( 1-\frac{x-x_0}{L}\right) ^{n-1} \end{aligned}$$
(1)

The analysis suggests that a quadratic expression for the diffusion layer is more appropriate than the linear one, although a detailed comparison with experimental data is yet to be carried out to establish the exact nature of the diffusion layers.

Fig. 1
figure 1

(a) Schematic of diffusion layer. \(c_i\) is the bulk concentration of austenite, \(c_{\gamma }^{*}\) is the peak concentration at the austenite side of the interface, \(c_{\alpha }^{eq}\) is the equilibrium concentration of ferrite, L is the diffusion length, \(c_{\gamma }(x)\) is the concentration in austenite in the diffusion layer with x is the distance measured from the origin and \(x_0\) is the length of the transformed ferrite. (b) Schematic of hexagonal austenitic grain geometry chosen in the present work. The simulation domain is marked by A

Full size image

The phase-field model has gained considerable attention for its ability to simulate realistic evolution of the microstructure during phase transformation.[19,20,21,22,23] The model is based on thermodynamic principles, and the fact that it does not require the interface to be tracked in every timestep has made it hugely popular.[24,25,26] Also, in an alloy phase-field model, the flux conservation is automatically satisfied and no prior assumption is required for modeling the diffusion layer and its interaction.[21,28,29] Due to the limitations of local equilibrium-based models, the phase-field model has been formulated to simulate the mixed-mode of transformation.[30,31,32] Moreover, the anomalous jump in chemical potential leading to undesired dependency on the interface length is removed by introducing a simple diffusivity interpolation.[21,27,28,30,33] In the present work, we use the phase-field model for mixed-mode and study the interactions of diffusion layers and its effect on growth of ferrite in austenite.

2 Methods

2.1 Sharp Interface Relationships for Mixed-Mode of Transformation

We briefly discuss the ‘Case 2’ class of transformation of austenite (\(\gamma \)) to ferrite (\(\alpha \)) as explained in Reference 30. In this class of transformation, solute carbon atoms can diffuse much faster than solvent iron atoms. Therefore, during the transformation, carbon atoms can redistribute themselves close to equilibrium, but less mobile Fe atoms cannot. The redistribution of Fe atoms away from the equilibrium results in the following inequality of diffusion potentials:

$$\begin{aligned} \left. \frac{\partial f_{\alpha }}{\partial c_{\alpha }}\right| _{c_{\alpha }=c_{\alpha }^{*}}=\left. \frac{\partial f_{\gamma }}{\partial c_{\gamma }}\right| _{c_{\gamma }=c_{\gamma }^{*}}+K \end{aligned}$$
(2)

\(c_{\alpha }^{*}\) and \(c_{\gamma }^{*}\) are the solute carbon concentrations at the ferrite and austenite sides of the interface, \(f_{\alpha }\) and \(f_{\gamma }\) are the free energy densities of ‘\(\alpha \)’ and ‘\(\gamma \)’ phases, respectively, and \(K=\mu _{Fe}^{\gamma }(c_{\gamma }^{*},T)-\mu _{Fe}^{\alpha }(c_{\alpha }^{*},T)\). Furthermore, the diffusivity of carbon in ferrite is about two orders higher than that in austenite. Therefore, carbon diffusion in ferrite allows the homogeneous distributution of solute so that the ferrite-side carbon concentration can be assumed to be equal to the equilibrium composition i.e. \(c_{\alpha }^{*} \approx c_{\alpha }^{eq}\).[8,34] These assumptions result in the following relationship in one dimension:

$$\begin{aligned} \frac{c_{\gamma }^{*}}{c_{\gamma }^{eq}}=1-(1-k_{eq}){\bar{\beta }} V \end{aligned}$$
(3)

where \({\bar{\beta }}=1/c_{\gamma }^{eq}(1-k_{eq})MRT\) is a kinetic coefficient, V is the transformation velocity, M is the mobility of the \(\gamma -\alpha \) interface and \(k_{eq}\) is the equilibrium partition coefficient. If \(V \rightarrow 0\), \(c_{\gamma }^{*} \rightarrow c_{\gamma }^{eq}\), which captures the local equilibrium mode of transformations. Otherwise, for any \(V>0\), \(c_{\gamma }^{*} < c_{\gamma }^{eq}\). The flux–balance relationship for this model becomes:

$$\begin{aligned} -\left. D_{\gamma }\frac{\partial c_{\gamma }}{\partial x}\right| _{\gamma }=V(c_{\gamma }^{*} -c_{\alpha }^{eq}) \end{aligned}$$
(4)

This model does not consider any diffusion within the ferrite, and the flux in austenite is entirely due to the rejection of carbon from the ferrite.

2.2 The Phase-Field Model

The phase-field model essentially considers a diffuse interface having a very small, but finite volume, along which the phase-field variable \(\phi \) changes from unity in ferrite to zero in austenite. The global free energy functional \({\cal {{F}}}(\phi ,c,T)\) can be written as the following

$$\begin{aligned} {\cal {{F}}}=\int \left\{ \frac{\epsilon ^{2}}{{2}} (\nabla \phi )^2+ f(\phi ,c,T)+ \omega g(\phi )\right\} {\rm d}v \end{aligned}$$
(5)

where \(\epsilon \) is the gradient energy constant which introduces the penalty in energy due to the interface; \(g(\phi )=\phi ^2(1-\phi )^2\) is the double-well potential and T is the temperature of the interface. Since the present study considers isothermal transformation, the temperature remains the same in the whole domain. \(f(\phi ,c,T)\) is the homogeneous part of the free energy (i.e. without an interface) representing free energy density of the phases, given as

$$\begin{aligned} f(\phi ,c,T)=h(\phi )f_{\alpha }(c_{\alpha },T)+\left\{ 1-h(\phi )\right\} f_{\gamma }(c_{\gamma },T)) \end{aligned}$$
(6)

\(h(\phi )\) is an interpolating function with \(h(\phi )=1\) when \(\phi =1\) and \(h(\phi )=0\) when \(\phi =0\). Using the same interpolation function, the solute carbon concentration (c) can be written as

$$\begin{aligned} c=h(\phi )c_{\alpha }^{eq}+[1-h(\phi )]c_{\gamma } \end{aligned}$$
(7)

The interface is considered to be a mixture of ferrite with a constant composition of \(c_{\alpha }^{eq}\) and austenite with the composition of \(c_{\gamma }(x)\). The present model assumes the inequality of the diffusion potential as given in Eq. [2].

$$\begin{aligned} \left. \frac{\partial f_{\alpha }}{\partial c_{\alpha }}\right| _{c_{\alpha }=c_{\alpha }^{eq}}=\frac{\partial f_{\gamma }}{\partial c_{\gamma }}+K \end{aligned}$$
(8)

The relationship in Eq. [2] is actually applicable for the austenite and ferrite sides of the interface. It has been shown by using matched asymptotic analysis that the leading order \(c_{\gamma }\) is constant in the present model.[30] Therefore, the relationship in Eq. [2] can be extended within the interface as given in Eq. [8]. The constant K in this equation defines the jump in potential across the interface which is dependent on the interface velocity, and this jump results in the concentration at the phase boundary as given in Eq. [3], when the interface-controlled transformation prevails. Even though K does not enter into the governing equations, it determines \(c_{\gamma }^{*}\) by fixing the mobilities for the interface-controlled transformation.[30]

The evolution of the phase-field ensuring the phenomenological minimization of free energy functional \(\cal {F}\) results in the following relationship:

$$\begin{aligned} \frac{1}{M_{\phi }}\frac{\partial \phi }{\partial t}=\epsilon ^2\nabla ^2\phi -h'(\phi )\left\{ f_{\alpha }(c_{\alpha }^{eq})-f_{\gamma }(c_{\gamma })\right\} -\left\{ 1-h(\phi )\right\} \frac{\partial f_{\gamma }}{\partial c_{\gamma }}\frac{\partial c_{\gamma }}{\partial \phi }-\omega g'(\phi ) \end{aligned}$$
(9)

Since K in Eq. [8] is not known beforehand, differentiating Eq. [7] with respect to \(\phi \) and considering \(c_{\gamma }\) to be a function of c and \(\phi \), the following relationship can be obtained[35]:

$$\begin{aligned} \frac{\partial c_{\gamma }}{\partial \phi }=\frac{(c_{\gamma }-c_{\alpha }^{eq}) h'(\phi )}{1-h(\phi )} \end{aligned}$$
(10)

From Eqs. [9] and [10], the evolution equation of the phase-field can be derived as follows:

$$\begin{aligned} \frac{1}{M_{\phi }}\frac{\partial \phi }{\partial t}= \epsilon ^2\nabla ^2\phi - h'(\phi )\left[f_{\alpha }-f_{\gamma }+\frac{\partial f_{\gamma }}{\partial c_{\gamma }}(c_{\gamma }-c_{\alpha })\right]- \omega g'(\phi ) \end{aligned}$$
(11)

Similarly, the diffusion equation based on the phenomenological equation for solute flux and chemical potential can be written as

$$\begin{aligned} \frac{\partial c}{\partial t}=\nabla M_c \nabla \frac{\partial f}{\partial c}=\nabla \cdot D \nabla c+ \nabla \cdot D\frac{f_{c\phi }}{f_{cc}}\nabla \phi \end{aligned}$$
(12)

where \(f_{c\phi }=\partial ^2f/\partial c \partial \phi \) and \(f_{cc}=\partial ^2f/\partial c^2\), diffusivity \(D=M_cf_{cc}\) and \(M_c\) is the mobility. Using the relationships in Eqs. [6] and [7], the following relationship for diffusion potentials can be derived:

$$\begin{aligned} \frac{\partial f}{\partial c}=\frac{\partial f_{\gamma }}{\partial c_{\gamma }} \end{aligned}$$
(13)

This relationship indicates that, as \(c_{\alpha }\) is constant, the diffusion is strictly limited to \(c_{\gamma }\). A straightforward manipulation with the relationship in Eq. [13] results in the following relationships:

$$\begin{aligned}&f_{cc}=\frac{\partial ^2 f_{\gamma }}{\partial c_{\gamma }^2}\frac{\partial c_{\gamma }}{\partial c}\nonumber \\&f_{c\phi }=\frac{\partial ^2 f_{\gamma }}{\partial c_{\gamma }^2}\frac{\partial c_{\gamma }}{\partial \phi } \end{aligned}$$
(14)

Using Eqs. [12] and [14], the diffusion equation can be finally obtained as:

$$\begin{aligned} {\frac{\partial c}{\partial t}=\nabla \cdot D \nabla c+\nabla \cdot D h'(\phi )(c_{\gamma }-c_{\alpha }^{eq}) \nabla \phi } \end{aligned}$$
(15)

Solving the governing Eqs. [11] and [15], along with Eq. [7], simulates the growth of ferrite from austenite under mixed-mode transformation.

Using matched asymptotic analysis, it has been shown that the sharp interface relationships in Eqs. [3] and [4] are recovered for thin interface limit.[30] The same analysis also results in the correlation of the phase-field and the sharp interface mobility as given below:

$$\begin{aligned} M_{\phi }=c_{\gamma }^{eq}(1-k_{eq})^2d_0MRT/W^2\omega \end{aligned}$$
(16)

where \(d_0=\gamma T_M/\triangle H_M {\bar{m}} c_{\gamma }^{eq}(1-k_{eq})\) is the capillary length, \({\bar{ m}}=RT^2(1-k_{eq})/\triangle H_M\) is the slope of the line demarcating the austenite-ferrite and austenite phases in the phase diagram. \(T_M\) is the temperature where the free energies of pure ‘\(\alpha \)’ and ‘\(\gamma \)’ phases are equal, and \( \Delta H_M\) is the latent heat released at \(T_M\). The gradient energy constant \(\epsilon \) and barrier \(\omega \) are related to the interface length W and the interfacial energy \(\gamma \) which are the input parameters for the present model.

$$\begin{aligned} W=\epsilon /\sqrt{\omega }&\qquad ; \qquad \gamma =\frac{ \epsilon \sqrt{ \omega }}{3\sqrt{2}} \end{aligned}$$
(17)

2.3 Quantitative Phase-Field Model

We briefly explain the technique for quantitative phase-field simulation so that numerical simulations are independent of input interface lengths, as discussed in Reference 30, with a matched asymptotic analysis. Since, \(c_{\alpha }\) is constant in the present model, the diffusion Eq. [15] can be converted into the following form

$$\begin{aligned} {\frac{\partial c}{\partial t}=\nabla D\cdot \left\{ 1- h(\phi )\right\} \nabla c_{\gamma }} \end{aligned}$$
(18)

Considering the one-dimensional form and the front moving with a steady velocity, V, the following relationship can be obtained :

$$\begin{aligned} -V\frac{dc}{dx}=\frac{d}{dx}D(\phi )\left\{ 1-h(\phi )\right\} \frac{{\rm d}c_{\gamma }}{{\rm d}x} \end{aligned}$$
(19)

Using the relationship in Eq. [7] and integrating from the origin of the interface to either side, \(c_{\gamma }\) at the two sides of the interface can be shown to be the following[30]:

$$\begin{aligned} \ln (c_{\gamma }-c_{\alpha }^{eq})|_0^{+\infty }=-V\int _0^{+\infty }\frac{{\rm d}x}{D(\phi )} \end{aligned}$$
(20)
$$\begin{aligned} \ln (c_{\gamma }-c_{\alpha }^{eq})|_0^{-\infty }=-V\int _0^{-\infty }\frac{{\rm d}x}{D(\phi )} \end{aligned}$$
(21)

If the diffusivity profile \(D(\phi )\) is symmetric around the origin located at \(\phi =0.5\), chemical potentials become equal on both sides of the interface, and this equality is necessary for implementing the local equilibrium condition. Failure of this equality leads to an anomalous chemical potential jump which scales with the interface length, and leads to an undesirable dependency of the solution on the interface length. In order to remove this anomaly, the diffusivity profile must satisfy the following equality:

$$\begin{aligned} {\int _{0}}^{x \rightarrow +\delta }\left\{ 1-\frac{D_{\gamma }}{D(\phi _0)}\right\} {\rm d}x=\int _0^{x \rightarrow -\delta }\left\{ \frac{D_{\gamma }}{D(\phi _0)}-\frac{D_{\gamma }}{D_{\alpha }}\right\} {\rm d}x \end{aligned}$$
(22)

The present model assumes an inherent jump in chemical potential. If the symmetry relationship in Eq. [22] is not satisfied, there will be an additional jump in chemical potential which will not only produce the dependency of the solution on the interface length but also modify the actual jump in chemical potential intended in the present study. In order to satisfy this equality, the following diffusivity interpolation has been adopted:

$$\begin{aligned} \ln D(\phi _0)= h(\phi _0)^{\bar{n}}\ln D_{\alpha }+\left\{ 1-h(\phi _0)^{\bar{n}}\right\} \ln D_{\gamma } \end{aligned}$$
(23)

where \({\bar{n}}\) is an adjustable parameter which allows the symmetry relationship in Eq. [23] to satisfy. Performing simulations with different input interface lengths, it has been shown that this technique of diffusivity interpolation indeed removes the undesired dependency of the simulations on interface length in one dimension.[30] In Appendix B, it has been shown that the diffusivity interpolation in Eq. [23] also removes the dependency on the input interface length in two dimensions.

2.4 Free Energy Density

Free density functions of the phases are important parameters for the simulation. The present study adopts the free energy density functions from the relevant thermodynamic database.[36] However, this database considers site ratio instead of mole fraction as the concentration variable. Therefore, the free energy density functions are constructed in the following form:

$$\begin{aligned} f_{\theta }=A_{\theta }+B_{\theta }c_{\theta }+RT\left\{ c_{\theta } \ln c_{\theta }+(1-c_{\theta })\ln (1-c_{\theta })\right\} \end{aligned}$$
(24)

where ‘\(\theta \)’ represents the phases ‘\(\alpha \)’ and ‘\(\gamma \)’ . The details of evaluation of the constants A and B for the phases are given elsewhere.[30] Using the constructed free energy density functions, \(c_{\alpha }^{eq}\) and \(c_{\gamma }^{eq}\) at different temperatures are calculated. From these calculations, the slope \({\bar{m}}\) and then the capillary length \(d_0\) are determined. During the evaluation of \(d_0\), \(\triangle S_T\) (instead of \(\triangle S_M\), the entropy change at \(T=T_M\)) is used, as it is usually assumed that \(\triangle S_M \approx \triangle S_T\) where \(\triangle S_T\) is the change in entropy at the transformation temperature. The effect of the alloying element is introduced by magnetic and nonmagnetic Zener parameters.[37]

2.5 Simulation Methodology

In the present work, we study the transformation of austenite to ferrite under mixed-mode in one dimension. The simulation domain is based on Bradley’s work, in which the grain size of ASTM No 1 to 2 has been adopted.[38] Assuming hexagonal austenitic grain, the distance between opposite vertices represents the grain size of 216 \(\mu \)m which is ASTM grain size no 1.5.[13] Furthermore, we apply the site saturation approach of nucleation in all the corners of the hexagon.[39,40,41,42] We also assume that the dominant overlapping of the diffusion layers takes place between the nearest neighboring nuclei only. Therefore, the simulation domain becomes any side of the hexagon with the dimension of 125 \(\mu \)m as shown in Figure 1(b).[13] In the present simulation, we neglect \(x_0\) in the domain as \(x_0\) is very small as compared to the whole domain. The transformations of austenite to ferrite have been studied in two compositions of steel:

  • Alloy B: 0.23 pct C, 0.002 pct Mn, 0.003 pct Si, 0.001 pct P, 0.005 pct S, 0.001 pct O, 0.001 pct N, balance Fe.

  • Alloy C: 0.42 pct C, 0.002 pct Mn, 0.004 pct Si, 0.001 pct P, 0.004 pct S, 0.001 pct O, 0.001 pct N, balance Fe.

Austenite to ferrite transformation in Alloy B is simulated for isothermal transformation temperatures of 1048 K and 1088 K (775 °C and 815 °C), and for alloy C, the transformation temperature is 1048 K (775 \(^{\circ }\)C). In the present simulation, elaborate initial \(\phi \) and c, based on the leading order terms, obtained from the matched asymptotic analysis, are implemented. The details of the construction of the initial \(\phi \) and c are discussed elsewhere.[30] In the present work, at the two ends of the one-dimensional domain, nuclei and identical initial \(\phi \) and c distributions are applied. Using the initial phase-field distribution, the values of the exponent \({\bar{n}}\) in Eq. [23] are evaluated in order to satisfy Eq. [22]. In the present work, dual meshing is adopted, i.e., spatial resolutions: \(\Delta x_{\phi }=10^{-7}\)m (for phase-field) and \(\Delta x_c=10^{-8}\)m (for diffusion equations) are different, but both the meshes are coincident on the same simulation domain. The interim values of the phase-field in the numerical domain of diffusion are calculated by a cubic spline. In a similar way, dual time-stepping is applied. Therefore, the present work uses fine spatial and temporal resolutions for the diffusion equation for better numerical solution which ensures conservation of solutes. On the other hand, the phase-field equation is allowed to be solved in coarser mesh, and the anomalous effect of using a high interface length is removed by using appropriate diffusivity interpolation. In Appendix A, the conservation property of the dual mesh and dual time-stepping scheme is discussed in detail. Altogether, the numerical solution of the present work can be considered to be fairly accurate. All the related data used in the present simulation are given in t Table I. The effect of alloying effect is negligible, and therefore the present simulation can be considered to be the transformation in a binary Fe-C system. We assume that the effect of the high diffusivity of the grain boundary having a very small thickness is limited to a negligibly small region surrounding the grain boundary (which is actually along the side of the hexagon), but, in the region slightly away from the grain boundary in a direction perpendicular to it, volume diffusivity dominates the growth.

Table I Parameters for the Present Simulation
Full size table

3 Results and Discussion

3.1 Soft-Impingement

In Figures 2(a) through (c), the simulated concentration profiles for the transformation temperatures of 1048 K and 1088 K (775 \(^{\circ }\)C and 815 \(^{\circ }\)C) in alloys B and C are shown. Since the solubility of carbon in ferrite is much lower than that in austenite, the excess carbon is rejected and piled up ahead of the interface in austenite to form a wide diffusion layer. These concentration profiles are very similar to that shown in the schematic Figure (1(a)). Diffusion layers in macroscale can actually be observed to be much longer at a finer micron level (as shown in the inset figures of Figure 2(a) through (c). In macroscale, the diffusion layers neither overlap nor show any characteristic of soft-impingement, whereas a progressive buildup of solute concentration can be observed in bulk (exactly midway between the ferrites) at the microlevel. Such a behavior indicates that phase-field simulation predicts a much more complicated functional form of diffusion layers as compared to theoretical models.

The numerical study of soft-impingement in the present work is primarily based on L and \(c_i\). The diffusion length L in the numerical domain is measured by the distance from the position of \(c_{\gamma }^{*}\) until the concentration gradually decreases along the diffusion layer to \(c_i\) as shown in Figure 1(a). In the present work, \(c_i\) represents the concentration of the midpoint of the simulation domain. According to theory, \(c_i\) gradually increases with time during soft-impingement, and the progressive increase in \(c_i\) during the transformation of austenite to ferrite, as shown in Figure 2(a) through (c) (and also corroborated by Figure 3(a) through (c), is in qualitative agreement with the theory. Based on the accumulation of carbon in the bulk austenite for the same duration of transformation, the degree of soft-impingement appears to be highest for the highest transformation temperature of 1088 K (815 \(^{\circ }\)C). Therefore, it appears that the diffusivity of the parent phase has a strong influence on soft-impingement. In contrast, almost similar levels of increase in \(c_i\) can be observed for alloys B and C for the same transformation temperature of 1048 K (775 \(^{\circ }\)C), and, therefore, accumulation of solute due to soft-impingement does not appear to be strongly dependent on supersaturation.

Fig. 2
figure 2

The concentration profile at different time intervals for (a) \(T=1048\) K (775 \(^{\circ }\)C) in Alloy B, (b) \(T=1088\) K (815 \(^{\circ }\)C) in Alloy B, and (c) \(T=1048\) K (775 \(^{\circ }\)C) in Alloy C . In all the cases, the soft-impingement is evident

Full size image
Fig. 3
figure 3

The variation of the diffusion length with time for different transformation temperatures and compositions. In all the cases, the diffusion length gradually decreases in average sense. Also, the bulk concentration of austenite (i.e. carbon concentration of the center of the domain) is plotted and its gradual rise is an indication of soft-impingement. (a) T = 1048 K (775 °C) in Alloy B, (b) T = 1088 K (815 °C) in Alloy B, and (c) T = 1048 K (775 °C) in Alloy C

Full size image

In Figures 3(a) through (c), we show the simultaneous variation of L and \(c_i\) for the transformation temperatures of 1048 K and 1088 K (775 \(^{\circ }\)C and 815 \(^{\circ }\)C) in alloys B and C. In all the simulations, it is observed that L on an average decreases while \(c_i\) increases with time. Chen has shown that L increases until soft-impingement and then decreases during transformation.[18] The present simulation is therefore consistent with the current theory. However, the present work also shows that the diffusion length periodically increases followed by a sharp decrease. This observation is related to the very mechanism of soft-impingement and current theory cannot explain this behavior. In theory, the ends of two diffusion layers during the transformation approach each other and meet at the center point of the domain. Meeting at the center point is considered to be the onset of soft-impingement. After soft-impingement, both the colliding ends of the diffusion layers are fixed at the center of domains while the other free ends move towards each other, resulting in an overall and continuous decrease in L. However, the present work has revealed that the ends of the diffusion layers are actually extended much further than that can be conceived in the macrolevel and these ends quickly meet each other causing instantaneous soft-impingement. In the present simulation, the increase in L indicates the swift movement of the two end points of the diffusion layers towards each other. However, the remaining portions of the diffusion layers lag far behind the ends. The ends of the diffusion layers meet each other when L increases to a maximum value, and a cycle of soft-impingement is complete after the increased level of concentration becomes uniform in and around the meeting point. The next ends of the diffusion layer lags far behind and the diffusion length decreases until the ends advance for the next cycle of soft-impingement. This situation is elucidated with an observation from the simulation for the transformation temperature of 1048 K (775 \(^{\circ }\)C) in alloy B in Figure 4(a) and by a schematic in Figure 4(b), although the same observation has been made with the other alloy and transformation temperature. It is worth mentioning that the steps in the concentration profile in Figure 4(a) are actually numerical artifacts (they form because of discretization and truncation error while storing the values), but the mechanism of soft-impingement described is not affected by these numerical features. The schematic presented in Figure 4(b) describes the same mechanism without involving this numerical artifact. In Figure 4(a), at 24 seconds, one end of the diffusion layer moves towards the other end and the length therefore increases at 25 seconds. Eventually, these two ends meet and the diffusion length is at a maximum. In Figure 4(b), \(L_2\) represents the maximum diffusion length followed by the completion of one cycle of soft-impingement. At this stage, the remaining part of the diffusion layer lags far behind and the diffusion length drops sharply to \(L_3\). Furthermore, it can be observed that L after the completion of the soft-impingement cycle at 26 seconds is slightly shorter than that at 24 seconds. Considering the significant movement of the transformation front in the mean 2 seconds, a net decrease in diffusion length is easily conceivable.

Fig. 4
figure 4

(a) The diffusion lengths (L) for alloy B at 1048 K (775 \(^{\circ }\)C) between 24 and 26 seconds. L at 26 seconds is smaller than that at 24 seconds. and the diffusion length gradually decreases. (b) The mechanism of discontinuous accumulation of solute during soft-impingement. \(L_2\) is the largest diffusion length

Full size image

3.2 Interface Velocity

Figure 5(a) through (c) describes the variation of interface velocity and concurrent peak concentration \(c_{\gamma }^{*}\) for all the transformation temperatures and compositions. The observed periodic acceleration and deceleration in all the cases are related to the mechanism of transformation. The transformation of austenite with f.c.c crystal structure into ferrite with b.c.c crystal structure derives the driving force which results in instantaneous acceleration. Since the advance of the \(\gamma -\alpha \) transformation front is also associated with the accumulation of rejected solute carbon from the ferrite, the transformation slows down. Removal of some of the accumulated carbon by diffusion in austenite away from the transformation front restores the driving force and brings back the acceleration. The periodic acceleration and deceleration can be observed to coincide with the periodic drop and increase in \(c_{\gamma }^{*}\), respectively, for all the simulations to support the mechanism outlined here.[30] The periodic acceleration and deceleration are also evidenced experimentally and attributed to strain energy.[43] The influence of strain energy in austenite to allotriomorphic ferrite is emphasised in some works,[41,42] but the present work does not consider the strain energy and yet simulates the periodic acceleration and deceleration. Therefore, this observation does not appear to be related to strain energy. Furthermore, it can be observed that, for the transformation temperature of 1048 K (775 \(^{\circ }\)C) in both the alloys, the amplitude of the interface velocity is approximately in the range of 1.1 to 1.8 \(\times 10^{-9}\) m/s, whereas for the transformation temperature of 1088 K (815 \(^{\circ }\)C), the amplitude is nearly twice that (\(4 \times 10^{-9}\) m/s). Therefore, the amplitude of periodic acceleration and deceleration appears to be strongly dependent on the diffusivity of bulk austenite.

Fig. 5
figure 5

The variations of peak concentration and the concurrent transformation velocity for all the transformation temperatures and compositions. Both the variations are periodic with identical periods. (a) T = 1048 K (775 °C) in Alloy B, (b) T = 1088 K (815 °C) in Alloy B, and (c) T = 1048 K (775 °C) in Alloy C

Full size image
Fig. 6
figure 6

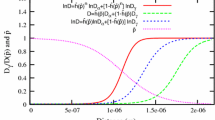
Comparison of peak concentrations obtained from simulation for T = 1048 K (775 \(^{\circ }\)C) in alloy B with those predicted by theory for overlapping[18] and non-overlapping[6] diffusion fields. The peak concentration can be observed to be lower than the equilibrium concentration \(c_{\gamma }^{eq}\)

Full size image

The present work reveals that average \(c_{\gamma }^{*}\) in all the simulations increases with time despite its periodicity as shown in Figure 5(a) through (c). In an earlier work, isolated ferrite has been shown to grow with constant average interface velocity and \(c_{\gamma }^{*}\), despite periodicity under the same mixed-mode of transformation.[30] Therefore, the increase in average \(c_{\gamma }^{*}\) in the present work is attributed to soft-impingement, and this increase is consistent with the corresponding decrease in interface velocity in the average sense. According to Zwaag and his coworkers, the peak concentration under the mixed-mode of transformation is[6]:

$$\begin{aligned} c_{\gamma }^{*}=\frac{Zc_i+\triangle c_i(c_{\alpha }^{eq}+c_{\gamma }^{eq})+\sqrt{Zc_i+\triangle c_0 (c_{\alpha }^{eq}+c_{\gamma }^{eq})^2-(Z+2\triangle c_i)(Zc_i^2+2\triangle c_ic_{\alpha }^{eq}c_{\gamma }^{eq})}}{Z+2\triangle c_i} \end{aligned}$$
(25)

where \(Z=D_{\gamma }(n-1)/M\chi n x_0\), \(\triangle c_i=c_i-c_{\alpha }^{eq}\) and \(\chi \) is a thermodynamic parameter dependent on temperature.[6,18] Here, n is the degree of the polynomial used to construct the diffusion layer, as in Eq. [1], M is the phase mobility, and Z and z are the parameters which decide whether the transformation is diffusion-controlled (when \(Z=0\)) or interface-controlled (when \(Z \rightarrow \infty \)), respectively. In the present simulation \(c_i=c_i(t)\) in Eq. [25], even though this expression has not been derived for overlapping of diffusion fields. Chen considers the soft-impingement and modifies the expression in Eq. [25].[18]

$$\begin{aligned} c_{\gamma }^{*}=\frac{(c_{\alpha }^{eq}+c_{\gamma }^{eq}-z+\sqrt{(c_{\alpha }^{eq}+c_{\gamma }^{eq}-z)^2-4(c_{\alpha }^{eq}c_{\gamma }^{eq}-z\frac{Xc_i-x_0c_{\alpha }^{eq}}{X-x_0})}}{2} \end{aligned}$$
(26)

where \(z=D_{\gamma }n/M\chi (X-x_0)\). In the present work, we compare \(c_{\gamma }^{*}\) obtained from the simulation for the transformation temperature of 1048 K (775 \(^{\circ }\)C) in alloy B with those predicted by the expressions in Eqs. [25] and [26] as shown in Figure 6. The value of \(x_0\) is calculated from the mass balance and \(\chi =110\) J/at.fr. The change in L\(=X-x_0\) and \(x_0\) with time in Eq. [26] during the transformation results in negligible variation of \(c_{\gamma }^{*}\) with time. On the other hand, the variation of \(c_{\gamma }^{*}\) with time can probably be the best explained by the non-overlapping diffusion fields as in Eq. [25] for \(n=3\). Such a disparity between theory and simulation arises due to a difference in the nature of overlapping assumed in theory and that observed in the simulation. In theory, the buildup of solute carbon in and around the meeting point at X is continuous, and the diffusion layer is assumed to be linear during the soft-impingement. In comparison, the soft-impingement simulated in the present work is not continuous, and there is a well defined gap between two consecutive meetings of the ends of the diffusion layers leading to a buildup of carbon in and around X. Also, the slope of the diffusion layer is never constant throughout its length. The near-agreement of simulated and theoretical \(c_{\gamma }^{*}\) for non-overlapping diffusion fields also suggests that the phase-field simulations performed are consistent with the theory of mixed-mode transformation.

3.3 Growth Coefficient

It is common practice to describe the migration of an interface with a suitable growth law, having the form of \(S={\bar{\alpha }} {t}^{m}\) where S is the distance traversed by the interface in time t , \({\bar{\alpha }}\) is a growth coefficient and m is the growth exponent. For diffusional transformation, \(m=1/2\) and the growth of isolated ferrite under mixed mode of transformation has been shown to have \(m=1\).[30] In Figure 7, we plot the interface migration for all the transformation temperatures and alloys as a function of time with respect to a position obtained after 5 seconds in all the simulations. It can be observed that, initially, the interface migrates with a constant interface velocity (though actually the interface periodically accelerates and decelerates, but that variation does not appreciably change the slope of the curve). In the same plot, the calculated interface positions are extrapolated based on the linear relationship (i.e. \(m=1\)), and the average velocity determined in the initial stage of the transformations. The later stage of transformation shows considerable deviation from linearity. In Figure 8, the variation of the growth exponent m with time has been shown for all the simulations. It can be observed that, at the beginning, all the transformations follow a growth law with approximately \(m=1\). As the transformation progresses, m gradually decreases from unity for all the transformations. There is some experimental evidence which shows that the growth exponent of austenite to proeutectoid ferrite transformation is well above 1/2 but below 1.[38] The present simulation is therefore consistent with the experimental observation. The extent of the decrease in the exponent m for the same duration of the transformation is the highest for the transformation temperature of 1048 K (775 \(^{\circ }\)C) in alloy C, which has the lowest supersaturation. But no general relationship between the supersaturation and the drop in the exponent m has been concluded in the present work for higher supersaturation. The change in growth exponent is considered to be associated with the change in mechanism of the transformation. The consistent decrease in m during the progress of the transformation suggests a change in the nature of the growth which can be attributed to soft-impingement.

Fig. 7
figure 7

The deviation of interface migration from the linear growth for all the transformations simulated

Full size image
Fig. 8
figure 8

The variation of growth exponent with time. As the transformation progresses, the exponent gradually decreases from unity

Full size image
Fig. 9
figure 9

The variation of parabolic growth coefficient with time. The theoretical and experimentally determined growth coefficients are also shown for the same transformation temperatures and compositions

Full size image

Since the interface movement follows a growth law with an exponent less than unity, we have fitted a parabolic growth law and evaluated the parabolic growth coefficient. In Figure 9, parabolic growth coefficients from simulations are plotted. According to the theory, the growth coefficient should decrease with time due to soft-impingement.[14] In contrast, the present work shows an increase in parabolic growth coefficient for all the transformations with time. The nature of the variation of the growth coefficients with time suggests that all the curves approach asymptotically to steady values. In the same plot, growth coefficients estimated experimentally from the thickening of proeutectoid ferrite under the assumption of volume diffusion-controlled transformation are plotted along with the same predicted by an expression proposed by Zener for diffusional transformation[1]:

$$\begin{aligned} {\bar{\alpha }} \exp \left( \frac{\bar{\alpha }^2}{4D_{\gamma }}\right) erfc\left( \frac{{\bar{\alpha }}}{2\sqrt{D_{\gamma }}}\right) =\left( \frac{c_{\gamma }^{eq}-c_i}{c_{\gamma }^{eq}-c_{\alpha }^{eq}}\right) \end{aligned}$$
(27)

Comparing the growth coefficients obtained from simulations at 30 seconds with the experimental values, the deviation can be estimated to be 258 pct for T = 1048 K (775 \(^{\circ }\)C), Alloy C, 186 pct for T = 1088 K (815 \(^{\circ }\)C), Alloy B, and 1.16 pct for T = 1048 K (775 \(^{\circ }\)C), Alloy B, while the error percentages for theoretical predictions are 230, 208 and 101 pct, respectively. Taking cognizance of the fact that the parabolic growth coefficients are approaching a steady value asymptotically in the present simulation, these errors will not change drastically for simulations with longer runtimes. Both the theory and the present model can be observed to overestimate the growth coefficient, but the present model predicts better growth behavior of austenite to ferrite transformation in terms of error. Also, for the highest supersaturation (T = 1048 K (775 \(^{\circ }\)C), Alloy B), the predicted growth coefficient is remarkably close to the experimental observations and, as the supersaturation increases, the simulated growth behavior becomes closer to that observed in the experiments.

4 Conclusion

In the present work, the transformation of austenite to ferrite has been studied with a phase-field model based on a mixed-mode of growth. In order to achieve a better accuracy, a novel numerical strategy has been applied. The present work predicts a discontinuous nature of accumulation of the solute in bulk austenite due to soft-impingement in and around the meeting points of the diffusion layers, as opposed to the continuous accumulation in theory. In fact, using a realistic simulation domain, it has been shown that the soft-impingement occurs in the early stage of the transformation when the diffusion layers are far apart in the macroscale, while the accumulation of solute continues due to soft-impingement in the micron scale. The present analysis suggests modeling the diffusion layer with a polynomial of a much higher degree than one. The mixed-mode phase-field model predicts periodic rises and drops in \(c_{\gamma }^{*}\) concurrent with periodic deceleration and acceleration, while the average interface velocity consistently decreases with time with corresponding increases in the average \(c_{\gamma }^{*}\) which also conforms with theory. During the growth of ferrite, the growth exponent m gradually decreases from unity with time, which is attributed to the incumbent mechanism of soft-impingement. The simulated interface migration results in parabolic growth coefficients which are reasonably close to the experimental observation. The present model has been found to be more accurate for higher supersaturation.

The simulations are performed in one dimension without considering the possible contribution of grain boundary diffusion, which is several orders higher than the volume diffusivity employed in the present work. It will be an interesting study in the future to simulate the growth kinetics in real three-dimensional austenitic geometry with grain boundary diffusion, incorporating the contribution of crystalline defects in multicomponent alloys. In the present work, the simulations have been performed for 35 seconds, in which the late stage of transformation has not been attempted to capture. It should be extended for an even longer run so that the diffusion layers in macroscale start to overlap. The evolution of growth exponents and parabolic growth coefficients should be investigated for longer runs. Also, the effect of spacing between the ferrite layers and thickness on soft-impingement should be investigated. More detailed numerical and experimental studies on the discontinuous nature of the accumulation of solute carbon in and around the meeting point of diffusion layers, and the periodic acceleration and deceleration of the austenite-ferrite transformation front, should be performed for better understanding of this transformation, although such investigations are beyond the scope of the present work.