Discovering patterns in time-varying graphs: a triclustering approach

Abstract

This paper introduces a novel technique to track structures in time varying graphs. The method uses a maximum a posteriori approach for adjusting a three-dimensional co-clustering of the source vertices, the destination vertices and the time, to the data under study, in a way that does not require any hyper-parameter tuning. The three dimensions are simultaneously segmented in order to build clusters of source vertices, destination vertices and time segments where the edge distributions across clusters of vertices follow the same evolution over the time segments. The main novelty of this approach lies in that the time segments are directly inferred from the evolution of the edge distribution between the vertices, thus not requiring the user to make any a priori quantization. Experiments conducted on artificial data illustrate the good behavior of the technique, and a study of a real-life data set shows the potential of the proposed approach for exploratory data analysis.

1 Introduction

In real world problems, interactions between entities are generally evolving through time. This is the case for instance in transportation networks (roads, train, etc) or communication networks (mobile phone, web, etc). Understanding the corresponding time evolving interaction graphs implies both to discover structures in those graphs and to track the evolution of those structures through time. In a subway network for example, entities are the stations and interactions are the passenger journeys from an origin to a destination station at a given start time. Understanding the evolving distribution of journeys over time is of great help for network planners, for instance to schedule trains efficiently.

Early works on the structure of the interactions in graphs dates back to the 1950s in the context of social networks analysis: Nadel (1957) proposes to group the actors that play similar roles within the network. The clustering of vertices—that models the actors—has been extensively studied. The vast literature on graph partitioning is surveyed in such as the one of Schaeffer (2007), Goldenberg et al. (2009) and Fortunato (2010), among others.

The analysis of time-varying/time-evolving/dynamic graphs is quite recent (Casteigts et al. 2012). Hopcroft et al (2004) have been first interested in the evolution of the vertices clustering. In their approach, a time-varying graph is modeled by a sequence of static graphs in which the clusters are retrieved using an agglomerative hierarchical clustering, where the similarity between the clusters is a cosine (Li and Jain 1998). Then, the evolution of the clusters across the snapshots is investigated. In more recent works, Palla et al. (2007) adapt their own clique percolation method (Palla et al. 2005) to time-evolving graphs by exploiting the overlap of the clusters at t and $t+1$ to study their evolution through time. Xing et al. (2010) use a probabilistic approach to study the evolution of the membership of each vertex to the clusters. As for Sun et al. (2007), they have introduced an information-theoretic based approach named Graphscope. It is a two-stage method dedicated to simple bipartite graphs that tracks structures within time-varying graphs. First, a partition of the snapshots is retrieved and evaluated using a minimum description length (MDL) framework (Grünwald 2007), then an agglomerative process is used to determine the temporal segmentation. As discussed by Lang (2009), the partitioning results may be sensitive to the coding schemes: in particular, coding schemes like those used by Sun et al. (2007) have no guarantee of robustness w.r.t. random graphs.

The approaches introduced above focus on a specific way of introducing time evolution into interaction analysis: they study a sequence of static interaction graphs. This is generally done via a quantization of the time which turns temporal interaction with possibly continuous time stamps into said sequence of graphs. The quantization is mainly ad hoc, generally based on “expert” or “natural” discrete time scales (such as hourly graphs or daily graphs) which lead to snapshots of the temporal interaction structure. Then the clusters of vertices are detected separately from the time quantization step hiding potential dependencies between those two aspects, as well as possible intricate temporal patterns. Fortunato (2010) has raised these problems and considers more suitable the approaches that track the clusters of vertices and the temporal structure in one unique step.

Co-clustering is a way to address this requirement. This technique aims at simultaneously partitioning the variables describing the occurrences in a data set (Hartigan 1972). Co-clustering has been applied to gene expressions problems (Van Mechelen et al. 2004) and has been widely used in documents classification (Dhillon et al. 2003), among other applications. An example of the application of co-clustering to graphs is given by Rege et al. (2006) in the case of static graphs. In this type of approaches, the graph is represented by its adjacency matrix: the rows and the columns correspond to the vertices and the values in the cells quantify the edge intensities between two vertices. The simultaneous partitioning of rows and columns coincide with the clusters of vertices. One advantage of co-clustering is that it is able to deal with nominal and numerical variables (Bekkerman et al. 2005; Nadif and Govaert 2010). Thus, co-clustering approaches for static graphs can be adapted to time-evolving graphs by introducing a third variable with temporal information. Such an approach was explored in Zhao and Zaki (2005) in order to study the temporal evolution of micro-array data. While the algorithm defined in this paper, TriCluster, uses the three-mode representation idea it aims at finding patterns rather than at clustering the three dimensions together. Therefore it shares only its data representation paradigm with the approach presented in the present paper. A closer technique is presented by Schepers et al. (2006) who introduce a three-mode partitioning approach. They define a three dimensional block model, that is optimized by minimizing a least squares loss function. To that end, the performances of several algorithms are investigated. The results shows that partitioning simultaneously all the three dimension provides better results than dealing with them independently. Moreover, Schepers et al. (2006) point out the difficulty of optimizing their global criterion and discuss the benefits of a multistart procedure. This is also treated in the present paper.

In this paper, we propose an approach for time-varying graphs built upon the MODL approach of Boullé (2011). Our method groups vertices based on similarity between connectivity patterns at the cluster level. In addition, it partitions the time interval into time segments during which connectivity patterns between the clusters are stationary. This corresponds to a triclustering structure which is optimized jointly in our method, without introducing any user chosen hyper-parameter (in particular, the number of clusters is chosen automatically). This approach is resilient to noise and reliable in the sense that no co-clustering structure is detected in case of uniform random graphs (e.g. Erdős and Rényi 1959) and that no time segmentation is retrieved in case of stationary graphs. In addition, the true underlying distribution is asymptotically estimated.

The rest of the paper is organized as follows. Section 2 introduces the type of temporal interaction data our model can handle. A combinatorial generative model for such data is described in Sect. 3. Section 4 presents our maximum a posteriori (MAP) strategy for estimating the parameters of this model from a temporal data set. Section 5 investigates the behavior of the method using artificial data. Finally, the method is applied on a real-life data set in order to show its effectiveness on a practical case in Sect. 6. Finally, Sect. 7 gives a summary and suggests future work.

2 Temporal interaction data and time-varying graph

In this paper, we study interactions between entities that take place during a certain period of time. We assume given two finite sets S and D which are respectively the set of sources (entities from which interactions start) and the set of destinations (entities to which interactions are destined). Each interaction is a triple $(s,d,t)\in S\times D\times \mathbb {R}$ where t is the instant at which the interaction takes place (in general t is called the time stamp of the interaction). In this paper a temporal interaction data set is a finite set $E\subset S\times D\times \mathbb {R}$ made of $m$ interaction triples, $(s_n,d_n,t_n)_{1\le n\le m}$.

Time stamps are assumed to be measured with enough precision to ensure that each of the $t_n$ is unique among the $(t_j)_{1\le j\le m}$ and thus the third variable of a temporal interaction data set could be seen as a continuous variable. However, to avoid contrast related effects and to simplify data modeling, we use a rank based transformation: each $t_n$ is replaced by its rank in $(t_j)_{1\le j\le m}$, leading to an integer valued variable.

As pointed about in the introduction, interaction data are frequently represented in graph forms. Taking into account the temporal aspect of interactions has led to the introduction of several notions of time-varying (or dynamic, or evolving) graphs. A unifying framework is proposed in Casteigts et al. (2012) and can be specialized to address different temporal notions. In this framework, a temporal interaction data set E as defined above corresponds to a time-varying graph given by the triple $\mathcal {G} = (V,F,\rho )$, where $V=S\cup D$ is the set of vertices of the graph, $F=\{(s,d)\in S\times D | \exists t\in \mathbb {R}, (s,d,t)\in E\}$ is the projection of E on $S\times D$ (giving the edges of the graph) and where the presence function $\rho$ from $F\times \mathbb {R}$ to $\{0,1\}$ is given by

$$\begin{aligned} \rho (s,d,t)=\left\{ \begin{array}{cl} 1&{}\quad \text {if } (s,d,t)\in E,\\ 0&{}\quad \text {if }(s,d,t)\not \in E. \end{array} \right. \end{aligned}$$

(1)

Thus, $E=(s_n,d_n,t_n)_{1\le n\le m}$ can be seen a particular case of time-varying graph, a fact that will prove useful in order to define a generative model for such temporal interaction data. In this context the pair of terms “entity” and “vertex”, as well as the pair of terms “edge” and “interaction”, are interchangeable. Nevertheless, we will standardize on the graph related terminology (vertex and edge) to avoid confusion.

Notice that the temporal interaction data notion used here is quite general as it can lead to simple directed graphs (where $S=D$ in general), but also to bipartite graphs (when $S\cap D=\emptyset$). In addition, temporal interaction data and thus time-varying graphs are inherently multigraphs (using the graph theory term): provided they have different time stamps, two edges can have exactly the same source and destination vertices, allowing this way multiple interactions to take place between the same actors at different moments. In addition, undirected graphs can also be studied under this general paradigm.

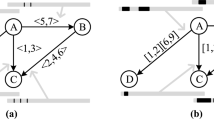
Notice also that while we use interchangeably the terms “temporal graph”, “time-evolving graph” and ”time-varying graph”, the first one is more accurate than the others in the sense that we are studying a (multi)graph with temporal information rather than e.g. a time series of graphs. Indeed each time stamp is attached to one interaction rather than to a full graph. However, we use also the terms “time-evolving graph” because we look for time intervals in which the interaction pattern is stationary leading to a time series of such fixed interaction patterns which can be seen as a time-evolving graph (but at a coarser grain). By interaction pattern we mean here a high level structure in a static graph, as seen in e.g. stochastic block models (Nowicki and Snijders 2001): for instance, in some situations, one might partition the vertices into clusters such that the graph contains a small number of edges between members of different clusters and a high number of edges between members of the same cluster (this is a modular structure as looked for by community detection algorithms see e.g. Fortunato 2010). Figure 1 gives an example of four such patterns.

Fig. 1

Sample of graphs for four time values. $n=50$ vertices, $m=10^6$ edges, $k=5$ clusters, $\epsilon =10^{-2}$

3 A generative model for temporal interaction data

We propose in this paper a probabilistic modeling (Murphy 2012) of temporal interaction data: we introduce a probabilistic model that can generate data that resemble the observed data. The present section describes the model in details while Sect. 4 explains how to fit the model to a given data by estimating its parameters.

The model is inspired by the graph view of the data. As in a static graph data analysis, we aim at producing a form of block model in which source entities/vertices and destination entities/vertices are partitioned into homogeneous classes (in terms of connectivity patterns). Therefore, the model is based on a partition of the source set S and on a partition of the destination set D. Time is handled via a piecewise stationary assumption. The model uses a partition of the time stamp ranks, $\{1,\ldots ,m\}$, into consecutive subsequences (which correspond to time intervals). Each subsequence is associated to a specific block model.

The initial view of the data as a three dimensional data set allows one to interpret the block models as a triclustering. Indeed, each source vertex, each destination vertex and each time stamp belongs to a cluster of the corresponding set (respectively S, D and $\mathbb {R}$). In addition, clusters of time stamps respect the natural ordering of time (as they are consecutive subsequences).

As described below, the model is based on a combinatorial view of temporal interaction data rather than on the continuous parameter based model used in classical block models. It is based on the MODL approach of Boullé (2011) which addresses density estimation via this type of combinatorial model.

3.1 Notations and definitions

In order to define our generative model, we need first to introduce some notations and vocabulary. Given a set A, |A| is the cardinality of A. As explained in Sect. 2, time stamps are transformed into ranks. Thus the set of time stamps is $\{1, 2, \ldots , \nu \}$ where $\nu$ is the number of edges/interactions.¹ A partition of $\{1, 2, \ldots , \nu \}$ respects its ordering if and only if given any pair of distinct classes of the partition, $c_1$ and $c_2$, all the elements of $c_i$ are smaller than all the elements of $c_j$ either for $i=1$ and $j=2$ or for $i=2$ and $j=1$. Obviously, classes of a partition that respects the order of $\{1, 2, \ldots , \nu \}$ are consecutive subsequences of $\{1, 2, \ldots , \nu \}$. We call any such consecutive subsequence an interval because it represents a time interval in the original data set. For instance the subsequence $\{1, 2, 3\}$ represents the time interval ranging from the oldest time stamp in the data set (the first one) to the third one in the data set.

Given three sets A, B and C and three partitions $P_A$, $P_B$ and $P_C$ of those sets, a tricluster is the Cartesian product of a class of each partition, that is $a\times b\times c$ with $a\in P_A$, $b\in P_B$ and $c\in P_c$. It is a subset of $A\times B\times C$ by construction, and the set of all triclusters generated by $P_A$, $P_B$ and $P_C$ forms a partition of $A\times B\times C$, called a triclustering.

For instance if $A=\{x, y, z\}$, $B=\{1, 2, 3, 4\}$ and $C=\{\alpha , \beta \}$, elements of $A\times B\times C$ are the triplets $(x, 1, \alpha )$, $(z, 3, \beta )$, etc. A way to build a very structured clustering, called a triclustering, of $A\times B\times C$ consists in building three clusterings: one for A, e.g. $A=\{x, z\}\cup \{y\}$, one for B, e.g. $B=\{1, 2\}\cup \{3, 4\}$ and one for C, e.g. $C=\{\alpha \}\cup \{\beta \}$. Then the clustering of $A\times B\times C$ if made of the Cartesian products of the clusters of A, B and C. One of such cluster is $\{x, z\}\times \{1, 2\}\times \{\alpha \}$ which contains the following triplet:

$$\begin{aligned} \{(x, 1, \alpha ), (x, 2, \alpha ), (z, 1, \alpha ), (z, 2, \alpha )\}. \end{aligned}$$

Other clusters of this clustering are $\{x, z\}\times \{3, 4\}\times \{\beta \}$, etc.

3.2 Model parameters

As explained above, our generative model is based on a triclustering. The partitions of the source and destination vertices are considered as parameters of the model, together with a series of other parameters described below. We list here all the parameters, but consistency constraints on the model prevent those parameters to be chosen arbitrarily. The constraints and our choice of free parameters are explained in the next subsection.

In the end, all parameters will have been estimated on the basis of the data.

Given a set of source vertices S, a set of destination vertices D, the model uses the following parameters:

• 1. $\nu$, the number of edges to generate;

• 2. $\mathbf {C}^S=(c^S_1,\ldots ,c^S_{k_S})$, the partition of the source vertices into $k_S$ clusters;

• 3. $\mathbf {C}^D=(c^D_1,\ldots ,c^D_{k_D})$, the partition of the destination vertices into $k_D$ clusters;

• 4. $\mathbf {C}^T=(c^T_1,\ldots ,c^T_{k_T})$, the partition of the time stamp ranks $\{1,\ldots ,\nu \}$ into $k_T$ clusters. This partition must respect the order of the ranks (clusters are intervals/consecutive subsequences);

• 5. $\varvec{\mu }=\{\mu _{ijl}\}_{1 \le i \le k_S, 1 \le j \le k_D, 1 \le l \le k_T}$, the number of edges that will be generated by the tricluster indexed by (i, j, l). More precisely, for each tricluster $c^S_i\times c^D_j\times c^T_l$ the model will generate $\mu _{ijl}$ edges with sources in $c^S_i$, destinations in $c^D_j$ and time stamps in $c^T_l$;

• 6. $\varvec{\delta }^S=\{\delta ^S_{s}\}_{s \in S}$, the out-degree of each source vertex s. In other words, $\delta ^S_s$ is the number of edges generated by the model for which the source vertex is s;

• 7. $\varvec{\delta }^D=\{\delta ^D_{d}\}_{d\in D}$, the in-degree of each destination vertex. In other words, $\delta ^D_d$ is the number of edges generated by the model for which the destination vertex is d.

Notice that $\mathbf {C}^S$, $\mathbf {C}^D$ and $\mathbf {C}^T$ build a triclustering of the set $S\times D\times \{1,\ldots ,\nu \}$. Each tricluster consists here in a cluster of source vertices, a cluster of destination vertices and an interval of time stamp ranks.

3.3 Constrained and free parameters

The parameters described in the previous subsection have to satisfy some constraints. The most obvious one links $\varvec{\mu }$ to $\nu$ by

$$\begin{aligned} \nu =\sum _{1 \le i \le k_S, 1 \le j \le k_D, 1 \le l \le k_T}\mu _{ijl}. \end{aligned}$$

(2)

To introduce the other constraints, we will use classical marginal count notations applied to the three dimensional array $\varvec{\mu }$, that is

$$\begin{aligned} \mu _{{i}..}&=\sum _{1 \le j \le k_D, 1 \le l \le k_T}\mu _{ijl},\end{aligned}$$

(3)

$$\begin{aligned} \mu _{.{j}.}&=\sum _{1 \le i \le k_S, 1 \le l \le k_T}\mu _{ijl},\end{aligned}$$

(4)

$$\begin{aligned} \mu _{..{l}}&=\sum _{1 \le i \le k_S, 1 \le j \le k_D}\mu _{ijl}. \end{aligned}$$

(5)

In theses notations, a dot . indicates that a sum is made over all possible values of the corresponding index.

Degrees must be consistent with edges produced by each cluster. We have therefore

$$\begin{aligned} \forall i \in \{1,\ldots ,k_S\}, \quad \sum _{s\in c^S_i}\delta ^S_{s}=\mu _{{i}..}, \end{aligned}$$

(6)

and

$$\begin{aligned} \forall j \in \{1,\ldots ,k_D\}, \quad \sum _{d\in c^D_j}\delta ^D_{d}=\mu _{.{j}.}. \end{aligned}$$

(7)

Indeed, all the edges that have a source in e.g. $c^S_i$ must have been generated by triclusters of the form $c^S_i\times c^D\times c^T$ where $c^D$ and $c^T$ are arbitrary clusters of destination vertices and time stamps, respectively. The left hand part of the equation counts those edges by summing the degrees in $c^S_i$ while the right hand part counts them by summing the edge counts in the triclusters.

There is a much stronger link between $\mathbf {C}^T$ and $\varvec{\mu }$. As for the other clusters, marginal consistency is needed and therefore we have

$$\begin{aligned} \forall l\in \{1,\ldots ,k_T\}, \left| c^T_l\right| =\mu _{..{l}}. \end{aligned}$$

(8)

The consistency equation is simpler than in the case of source/destination clusters because the time stamp ranks are unique and there is no “degree” attached to them.

In addition, as $\mathbf {C}^T$ respects the order of $\{1,\ldots ,\nu \}$, its classes can be reordered such that $c^T_1$ contains the smallest ranks, $c^T_2$ the second smallest ranks, etc. Then as the classes are consecutive subsequences, the only possible partition is given by

$$\begin{aligned} \mathbf {C}^T=\left( \left\{ 1,\ldots ,\mu _{..{1}}\right\} ,\left\{ \mu _{..{1}}+1,\ldots ,\mu _{..{1}}+\mu _{..{2}}\right\} ,\ldots ,\left\{ \sum _{l=1}^{k_t-1}\mu _{..{l}}+1,\ldots ,\nu \right\} \right) . \end{aligned}$$

(9)

In practical terms, this means that up to a renumbering of its classes, there is a unique partition $\mathbf {C}^T$ of the time stamp ranks that respects their order and that is compatible with a given $\varvec{\mu }$. Then $\mathbf {C}^T$ can be seen as a bound parameter. Notice that we could on the contrary leave $\mathbf {C}^T$ free and then obtain constraints on $\varvec{\mu }$. This would be more complex to handle in terms of the prior distribution on the parameters.

In the rest of the paper, we denote $\mathcal {M}$ a complete list of values for the free parameters of the model, that is $\mathcal {M}=(\nu ,\mathbf {C}^S,\mathbf {C}^D,\varvec{\mu },\varvec{\delta }^S,\varvec{\delta }^D)$. We assume implicitly that $\mathcal {M}$ fulfills the constraints outlined above. In addition, even when we use this choice of free parameters, a value of $\mathcal {M}$ will be called a triclustering. In particular, $\mathbf {C}^T$ will always denote the time stamp partition uniquely defined by $\mathcal {M}$. We will also always denote $k_S$, $k_D$ and $k_T$ the number of clusters in each of the three partitions.

An example: to illustrate the parameter space, a simple example is described below. The source set is $S=\{1,\ldots ,6\}$ and the destination set is $D=\{a, b, \ldots , h\}$. We fix $\nu =50$ and thus the time stamp ranks form the set $\{1,\ldots , 50\}$. We choose three source clusters

$$\begin{aligned} \mathbf {C}^S=\{\{1, 2, 3\}, \{4, 5\}, \{6\}\}, \end{aligned}$$

two destination clusters

$$\begin{aligned} \mathbf {C}^D=\{\{a, b, c, d, e\},\{f, g, h\}\}, \end{aligned}$$

and three time clusters (unspecified yet as they will be consequences of $\varvec{\mu }$). A possible choice for $\varvec{\mu }$ is given by the following tables

$$\begin{aligned} \begin{array}{c|c|c|} &{}c^D_1&{} c^D_2\\ \hline c^S_1 &{}5 &{} 1\\ \hline c^S_2 &{}2 &{} 0\\ \hline c^S_3 &{}4 &{} 0 \\ \hline &{} c^T_1&{} \\ \end{array} \quad \begin{array}{c|c|c} &{}c^D_1&{}c^D_2\\ \hline c^S_1 &{}2 &{} 2\\ \hline c^S_2 &{}2 &{} 5 \\ \hline c^S_3 &{}5 &{} 5\\ \hline &{} c^T_2 &{} \\ \end{array} \quad \begin{array}{c|c|c} &{}c^D_1&{}c^D_2\\ \hline c^S_1 &{}0 &{}0\\ \hline c^S_2 &{}1 &{}0\\ \hline c^S_3 &{}1 &{}15\\ \hline &{} c^T_3&{} \\ \end{array} \end{aligned}$$

There is one table per time stamp interval and in each table the rows correspond to the three source clusters while the columns correspond to the two destination clusters. For instance $\mu _{111}=5$. Notice that the sum of all the numbers in the table cells equals $\nu =50$, as imposed by the constraints.

Marginal counts induced by $\varvec{\mu }$ are then

$$\begin{aligned} \begin{array}{l|ccc} i&{}1&{}2&{}3\\ \hline \mu _{{i}..}&{}10&{}10&{}30 \end{array} \quad \quad \begin{array}{l|cc} j&{}1&{}2\\ \hline \mu _{.{j}.}&{}22&{}28 \end{array} \quad \quad \begin{array}{l|ccc} l&{}1&{}2&{}3\\ \hline \mu _{..{l}}&{}12&{}21&{}17 \end{array} \end{aligned}$$

They are compatible, for instance, with the following out degrees $\varvec{\delta }^S$

$$\begin{aligned} \begin{array}{l|*{3}{c}|*{2}{c}|c} s&{} 1 &{} 2 &{} 3 &{} 4 &{} 5 &{} 6 \\ \hline \delta ^S_s &{}3 &{} 6 &{} 1 &{} 2 &{} 8 &{} 30 \end{array} \end{aligned}$$

and in degrees $\varvec{\delta }^D$

$$\begin{aligned} \begin{array}{l|*{5}{c}|*{3}{c}} d&{} a &{} b &{} c &{} d &{} e &{} f &{} g &{} h \\ \hline \delta ^D_d &{}3 &{} 6 &{} 2 &{} 6 &{} 5 &{} 13 &{} 8 &{} 7 \end{array} \end{aligned}$$

As explained above, the only possible time stamp rank partition is then

$$\begin{aligned} \mathbf {C}^T=\{\{1,\ldots ,12\},\{13,\ldots ,33\},\{34,\ldots ,50\}\}. \end{aligned}$$

3.4 Data generating mechanism in the proposed model

Given the parameters $\mathcal {M}$, a temporal data set $E=(s_n,d_n,t_n)_{1\le n\le \nu }$ is generated by a hierarchical distribution build upon uniform distributions.

• 1. The $\nu$ edges are generated by first choosing which one of $k_S \times k_D \times k_T$ triclusters is responsible for generating each of the edges. This is done by assigning each of the $\nu$ edges to a tricluster under the constraints given by the assignment $\varvec{\mu }$. All compatible mappings from edges to triclusters are considered equiprobable. Then a given mapping $E_{map}$ has a probability of one divided by the number of compatible mappings, that is:

  $$\begin{aligned} P(E_{map}|\mathcal {M})=\dfrac{ \prod _{i=1}^{k_S} \prod _{j=1}^{k_D} \prod _{l=1}^{k_T} \mu _{ijl}!}{\nu !}. \end{aligned}$$

  (10)

• 2. In two independent second steps, edges are mapped to source vertices and destination vertices. Indeed, each source cluster $C^S_i$ is responsible for generating $\mu _{{i}..}$ edges under the assignment constraints specified by the degrees of the source vertices (and similarly for destination vertices). As in the previous step, all mappings from the edges assigned to a cluster to its vertices that are compatible with the assignment are considered equiprobable. In addition, mappings are independent from cluster to cluster. Then a given source mapping $S_{map}$ and a destination mapping $D_{map}$ have the following probabilities:

  $$\begin{aligned} P(S_{map}|\mathcal {M})=\dfrac{ \prod _{s\in S}\delta ^S_s!}{ \prod _{i=1}^{k_S}\mu _{{i}..}!},\quad P(D_{map}|\mathcal {M})=\dfrac{ \prod _{d \in D}\delta ^D_d!}{\prod _{j=1}^{k_D}\mu _{.{j}.}!}. \end{aligned}$$

  (11)

• 3. Based on the previous steps, each edge has now a source vertex and a destination vertex. Its time stamp is obtained in a similar but simpler marginal procedure. Indeed inside a time interval, we simply order the edges in an arbitrary way, using a uniform probability on all possible orders. Orders are also independent from one interval to another. Then a given time ordering of the edges $T_{order}$ has a probability:

  $$\begin{aligned} P(T_{order}|\mathcal {M})=\dfrac{1}{ \prod _{l=1}^{k_T} \mu _{..{l}}!}. \end{aligned}$$

  (12)

An example (continued): using the parameter list given as an example in the previous subsection, we can generate a temporal data set. As a first step, we assign the 50 edges to the 18 triclusters (in fact only to the 13 triclusters with non zero values in $\varvec{\mu }$). To simplify the example, we choose the assignment in which edges are generated from 1 to 50 by the first available tricluster in the lexicographic order on the indexing triple (i, j, l). This means that edges 1 to 5 are generated by the tricluster (1, 1, 1), that is $c^S_1\times c^D_1\times c^T_1$, then edges 6 and 7 are generated by tricluster $c^S_1\times c^D_1\times c^T_2$, then edge 8 by tricluster $c^S_1\times c^D_2\times c^T_1$ (we skip $c^S_1\times c^D_1\times c^T_3$ because $\mu _{113}=0$), etc. This is summarized in the following tables:

$$\begin{aligned} \begin{array}{c|c|c|} &{}c^D_1&{}c^D_2\\ \hline c^S_1 &{}\{1, \ldots , 5\} &{} \{8\}\\ \hline c^S_2 &{}\{11, 12\} &{} \emptyset \\ \hline c^S_3 &{}\{21, \ldots , 24\} &{} \emptyset \\ \hline &{} c^T_1 &{} \\ \end{array} \quad \begin{array}{c|c|c|} &{}c^D_1&{}c^D_2\\ \hline c^S_1 &{}\{6, 7\} &{} \{9, 10\}\\ \hline c^S_2 &{}\{13, 14\} &{} \{16, \ldots , 20\} \\ \hline c^S_3 &{}\{25, \ldots , 29\} &{} \{31, \ldots , 35\}\\ \hline &{} c^T_2 &{} \\ \end{array} \quad \begin{array}{c|c|c|} &{}c^D_1&{}c^D_2\\ \hline c^S_1 &{}\emptyset &{}\emptyset \\ \hline c^S_2 &{}\{15\} &{}\emptyset \\ \hline c^S_3 &{}\{30\} &{}\{36, \ldots , 50\}\\ \hline &{} c^T_3 &{}\\ \end{array} \end{aligned}$$

The edges are assigned variable per variable. For instance vertices in $c^S_1$ are the source vertex for the following edges

$$\begin{aligned} \{1, \ldots , 5\} \cup \{8\} \cup \{6, 7\} \cup \{9, 10\}=\{1, \ldots , 10 \}. \end{aligned}$$

Using the degree constraints $\delta ^S_1, \delta ^S_2$ and $\delta ^S_3$, one possible assignment is

$$\begin{aligned} \begin{array}{r|*{10}{c|}} \text {edge} &{} 1 &{} 2 &{} 3 &{} 4 &{} 5 &{} 6 &{} 7 &{} 8 &{} 9 &{} 10\\ \hline \text {source}&{} 2 &{} 2 &{} 1 &{} 2 &{} 1 &{} 3 &{} 2 &{} 1 &{} 2 &{} 2 \end{array} \end{aligned}$$

Similarly, vertices in $c^D_1$ are the destination vertex for the following edges

$$\begin{aligned} \{1, \ldots , 5\} \cup \{6, 7\} \cup \{11, 12\} \cup \{13, 14\} \cup \{15\} \cup \{21, \ldots , 24\} \cup \{25, \ldots , 29\} \cup \{30\}, \end{aligned}$$

which can be obtained using the following assignment

$$\begin{aligned} \begin{array}{r|*{22}{c|}} \text {edge} &{} 1 &{} 2 &{} 3 &{} 4 &{} 5 &{} 6 &{} 7 &{} 11 &{} 12 &{} 13 &{} 14 &{} 15 &{} 21 &{} 22 &{} 23 &{} 24 &{} 25 &{} 26 &{} 27 &{} 28 &{} 29 &{} 30 \\ \hline \text {destination}&{} d &{} d &{} e &{} a &{} b &{} a &{} b &{} e &{} d &{} d &{} b &{} b &{} b &{} d &{} a &{} e &{} c &{} d &{} e &{} e &{} b &{} c \end{array} \end{aligned}$$

Finally, time stamp ranks are assigned in a similar way. For instance time stamp ranks from $\{1, \ldots , 12 \}$ are assigned to edges

$$\begin{aligned} \{1, \ldots , 5\} \cup \{8\} \cup \{11, 12\} \cup \{21, \ldots , 24\}, \end{aligned}$$

for instance by

$$\begin{aligned} \begin{array}{r|*{12}{c|}} \text {edge} &{} 1 &{} 2 &{} 3 &{} 4 &{} 5 &{} 8 &{} 11 &{} 12 &{} 21 &{} 22&{}23&{}24 \\ \hline \text {time stamp rank}&{} 5 &{} 7 &{} 10 &{} 4 &{} 8 &{} 2 &{} 9 &{} 6 &{} 1 &{} 3 &{} 12 &{} 11 \end{array} \end{aligned}$$

At the end of this process, a full temporal data set is generated. In our working example, the first five edges are

$$\begin{aligned} \begin{array}{c|ccc} \text {edge}&{}\text {source}&{}\text {destination}&{}\text {time stamp rank}\\ \hline 1&{}2&{}d&{}5\\ 2&{}2&{}d&{}7\\ 3&{}1&{}e&{}10\\ 4&{}2&{}a&{}4\\ 5&{}1&{}b&{}8 \end{array} \end{aligned}$$

3.5 Likelihood function

Because of the combinatorial nature of the proposed model, the likelihood function has a peculiar form. Let $E=(s_n,d_n,t_n)_{1\le n\le m}$ be a temporal data set. The likelihood function $\mathcal {L}(\mathcal {M}|E)$ takes a non zero value if and only if $\mathcal {M}$ and E are compatible according to the following definition.

Definition 1

A temporal data set $E=(s_n,d_n,t_n)_{1\le n\le m}$ and a parameter list $\mathcal {M}=(\nu ,\mathbf {C}^S,\mathbf {C}^D,\varvec{\mu },\varvec{\delta }^S,\varvec{\delta }^D)$ are compatible if and only if:

• 1. $m=\nu$;

• 2. for all $s\in S$, $\delta ^S_s=|\{n\in \{1,\ldots ,m\}|s_n=s\}|$;

• 3. for all $d\in D$, $\delta ^D_d=|\{n\in \{1,\ldots ,m\}|d_n=d\}|$;

• 4. for all $i\in \{1,\ldots ,k_S\}$, $j\in \{1,\ldots ,k_D\}$ and $l\in \{1,\ldots ,k_T\}$.

  $$\begin{aligned} \varvec{\mu }_{ijl}=\left| \left\{ \{n\in \{1,\ldots ,m\}|s_n\in c^S_i, d_n\in c^D_j, t_n\in c^T_l\right\} \right| . \end{aligned}$$

  (13)

Based on this definition, the likelihood function is equal to zero when $\mathcal {M}$ and E are not compatible and is given by the following formula when they are compatible

$$\begin{aligned} \mathcal {L}(\mathcal {M}|E)=\dfrac{ \left( \prod _{i=1}^{k_S} \prod _{j=1}^{k_D} \prod _{l=1}^{k_T} \mu _{ijl}!\right) \left( \prod _{s\in S}\delta ^S_s!\right) \left( \prod _{d \in D}\delta ^D_d!\right) }{\nu ! \left( \prod _{i=1}^{k_S}\mu _{{i}..}!\right) \left( \prod _{j=1}^{k_D}\mu _{.{j}.}!\right) \left( \prod _{l=1}^{k_T}\mu _{..{l}}!\right) }. \end{aligned}$$

(14)

Notice that while the formula is expressed in terms of the parameters $\mathcal {M}$ only, it depends obviously on the characteristics of the data set E, via the compatibility constraints between $\mathcal {M}$ and E.

One of the interesting properties of the likelihood function is that it increases when the block structure associated to the triclustering “sharpens” in the following sense: the likelihood increases when the number of empty triclusters ($\mu _{ijl}=0$) increases.

4 Parameter estimation

In order to adjust the parameters $\mathcal {M}$ of our model to a temporal data set E, we use a MAP approach where the estimator for the parameters is given by $\mathcal {M}^{*}={\hbox {argmax}}_{\mathcal {M}}P(\mathcal {M}) P(E|\mathcal {M})$. Together with a non informative prior distribution on the parameters, this enables us to adjust all the parameters of the model without introducing any user chosen hyper-parameter. In addition, the chosen prior distribution penalizes complex models to limit the risk of overfitting.

The model is designed in such a way that when the number of edges in $\mathcal {M}$ is $\nu$, then all temporal data sets generated have exactly $\nu$ edges. In an estimation context, we fix therefore directly $\nu =m$ where $m$ is the observed number of edges. This can be seen as fixing $\nu$ to its MAP estimate as the likelihood of $\mathcal {M}$ given E is zero when $\nu \ne m$. For the rest of the parameters, we specify a non informative prior distribution as follows.

4.1 Prior distribution on the parameters

The prior is built hierarchically and uniformly at each stage in order to be uninformative. This is done as follows:

• 1. For source and destination partitions, a maximal number of clusters is drawn uniformly at random between 1 and the cardinality of the set to cluster (for instance |S| for the set of source vertices). For the time stamps partition, the number of clusters is drawn in the same way. We obtain this way $k_S^{\max }$, $k_D^{\max }$ and $k_T$ with the associated probability distribution:

  $$\begin{aligned} p(k_S^{\max }) = \dfrac{1}{|S|}, \quad p(k_D^{\max }) = \dfrac{1}{|D|} , \quad p(k_T) = \dfrac{1}{m}. \end{aligned}$$

  (15)

  The case with one single cluster corresponds to the null triclustering, where there is no significant pattern within the graph. The other extreme case corresponds to the most refined triclustering where each vertex plays a role that is significantly specific to be clustered alone: the triclustering has as many clusters as vertices (on both source and destination). In social networks analysis, both extreme clustering structures are consistent with the notion of regular equivalence introduced in the works of White and Reitz (1983) and Borgatti (1988).

  The case with one time segment corresponds to a stationary graph over time. The one with as many time segments as edges is an extremely fine-grained quantization: as time is a continuous variable, this case is allowed in our approach. It can appear when the connectivity patterns are gradually changing over time in a very smooth way, see Sect. 5 for an example.

  Notice that this prior is given for the sake of mathematical soundness, but in practice, it has no effect on the MAP criterion as it does not depend on the actual values $k_S^{\max }$, $k_D^{\max }$ and $k_T$, but only on fixed quantities |S|, |D| and $\nu$ (the latter been fixed in the MAP context).

• 2. Given the maximal number of clusters, partitions are equiprobable among the partitions with at most the specified maximal number of clusters, that is

  $$\begin{aligned} p(\mathbf {C}^S| k^{\max }_S) = \dfrac{1}{B(|S|,k_S^{\max })} , \quad p(\mathbf {C}^D| k^{\max }_D) = \dfrac{1}{B(|D|,k_D^{\max })}, \end{aligned}$$

  (16)

  where $B(|S|,k^{\max }_S)=\sum _{k=1}^{k^{\max }_S} S(|S|,k)$ is the sum of Stirling numbers of the second kind, i.e the number of ways of partitioning |S| elements into k non-empty subsets.

  At this step, the prior does not favor any particular structure in the partition of vertices beside their number of clusters (partitions will low number of clusters are favored over partitions with a high number of clusters). It depends indeed only on $k^{\max }_S$ and $k^{\max }_D$ not on the actual partitions.

  This is quite different from e.g. Kemp and Tenenbaum (2006) where a Dirichlet process is used as a prior on the number of clusters and on the distribution of vertices on the clusters. Such a prior favors a structure with a few populated clusters and several smaller clusters and penalizes balanced clustering models. Our approach overcomes this issue owing to the choice of its prior (see also below).

• 3. For a triclustering with $k_S$ source, $k_D$ destination clusters and $k_T$ time segments, assignments of the $m$ edges on the $k_S \times k_D \times k_T$ triclusters are equiprobable. It is known that the number of such assignments (i.e. the $k_S\times k_D\times K_T$ numbers $\varvec{\mu }$ which sum to $m$) is $\left( {\begin{array}{c}m+k_Sk_Dk_T-1\\ k_Sk_Dk_T-1\end{array}}\right)$, leading to

  $$\begin{aligned} p(\varvec{\mu }|k_S,k_D,k_T) = \frac{1}{\genfrac(){0.0pt}0{m+k_Sk_Dk_T-1}{k_Sk_Dk_T-1}}. \end{aligned}$$

  (17)

  Notice that this prior penalizes a high number of triclusters. As the numbers of vertex clusters are already penalized before (via the number of partitions), this has mostly an effect on the number of time intervals $k_T$.

• 4. Similarly, for each source cluster $c^S_i$, the out-degrees of the vertices are chosen uniformly at random among the degree lists that sums to $\mu _{{i}..}$, as requested by the constraints (this holds also for destination clusters), which leads to

  $$\begin{aligned} p(\{\delta ^S_{s}\}_{s\in c^S_i} | \varvec{\mu }, \mathbf {C}^S) = \dfrac{1}{\genfrac(){0.0pt}0{\mu _{{i}..} + |c^S_i| -1}{|c^S_i| -1}}, \end{aligned}$$

  (18)

  and similarly to

  $$\begin{aligned} p(\{\delta ^D_{d}\}_{d\in c^D_j} | \varvec{\mu }, \mathbf {C}^D) = \dfrac{1}{\genfrac(){0.0pt}0{\mu _{.{j}.} + |c^D_j| -1}{|c^D_j| -1}}. \end{aligned}$$

  (19)

  For a given assignment $\varvec{\mu }$, this prior penalizes large clusters (in terms of degree, i.e. high values of $|c^S_i|$ or $|c^D_j|$), or in other words, it favors balanced partitions (with clusters of the same sizes, again in terms of degree). For given partitions, the prior penalizes high marginal counts, in particular in large (degree) clusters.

Overall, the prior is rather flat, as it is uniform at each level of the hierarchy of the parameters. It does not make strong assumptions and let the data speak for themselves, as the prior terms vanish rapidly compared to the likelihood terms. Notice that other prior distribution could be considered, especially if expert knowledge is available.

4.2 The MODL criterion

The product of the prior distribution above and of likelihood term obtained in the previous section results in a posterior probability, the negative log of which is used to build the criterion presented in Definition 2.

Definition 2

(MODL Criterion) According to the MAP approach, the best adjustment of the model and the temporal data set E is obtained when triclustering $\mathcal {M}$ is compatible with E (according to Definition 1) and minimizes the following criterion:

$$\begin{aligned}&c(\mathcal {M}) = \log |S| + \log |D| + \log m+ \log B(|S|,k_S) + \log B(|D|,k_D) \nonumber \\&\quad +\log \displaystyle \left( {\begin{array}{c}m+k_Sk_Dk_T-1\\ k_Sk_Dk_T - 1\end{array}}\right) + \displaystyle \sum _{i=1}^{k_S} \log \left( {\begin{array}{c}\mu _{{i}..} + |c^S_{i}| -1\\ |c^S_{i}| -1\end{array}}\right) + \displaystyle \sum _{j=1}^{k_D} \log \left( {\begin{array}{c}\mu _{.{j}.} + |c^D_j| -1\\ |c^D_j| -1\end{array}}\right) \nonumber \\&\quad +\log m! - \displaystyle \sum _{i=1}^{k_S}\sum _{j=1}^{k_D} \sum _{l=1}^{k_T} \log \mu _{ijl}! + \displaystyle \sum _{l=1}^{k_T} \log \mu _{..{l}}! \nonumber \\&\quad + \displaystyle \sum _{i=1}^{k_S} \log \mu _{{i}..}! - \displaystyle \sum _{s \in S} \log \delta ^S_s! + \displaystyle \sum _{j=1}^{k_D} \log \mu _{.{j}.}! - \displaystyle \sum _{d \in D} \log \delta ^D_d!. \end{aligned}$$

(20)

It is important to note that the quality criterion is defined only for parameters that are compatible with the data set E. This explains why only m appears directly in the criterion: the actual characteristics of the data set influence indirectly the value of the criterion (for a given set of parameters) via the compatibility equations from Definition 1. In particular, the degrees $\varvec{\delta }^S$ and $\varvec{\delta }^D$ are fixed, and each triclustering $\mathbf {C}^S$, $\mathbf {C}^D$ and $\mathbf {C}^T$ leads to a unique compatible $\varvec{\mu }$. In this sense, the MODL criterion is really a triclustering quality criterion.

In addition, the evaluation criterion of Definition 20 relies on counting the number of possibilities for the model parameters and for the data given the model. As negative log of probability amounts to a Shannon–Fano coding length (Shannon 1948), the criterion can be interpreted in terms of description length. The two first lines of the criterion correspond to the description length of the triclustering $-\log P(\mathcal {M})$ (prior probability) and the two last lines to the description length of the data given the triclustering $-\log P(E|\mathcal {M})$ (likelihood). Minimizing the sum of these two terms therefore has a natural interpretation in terms of a crude MDL principle (Grünwald 2007). Triclustering fitting well the data get low negative log likelihood terms, but too detailed triclusterings are penalized by the prior terms, mainly the partition terms which grow with the size of the partitions and the assignment parameters terms which grow with the number of triclusters.

4.3 Optimization strategy

The criterion $c(\mathcal {M})$ provides an exact analytic formula for the posterior probability of the parameters $\mathcal {M}$, but the parameter space to explore is extremely large. That is why the design of sophisticated optimization algorithms is both necessary and meaningful. Such algorithms are described by Boullé (2011).

Interestingly while the assignment based representation allows one to define a simple non informative prior on the parameters, it is not a realistic representation for exploring the parameter space. Indeed there is no natural and simple operator to move from one compatible assignment $\varvec{\mu }$ to another one. On the contrary, working directly with the three partitions $\mathbf {C}^S$, $\mathbf {C}^D$ and $\mathbf {C}^T$, and getting $\varvec{\mu }$ from the data (under the compatibility constraints) is much more natural.

The criterion is indeed minimized using a greedy bottom-up merge heuristic. It starts from the finest model, i.e the one with one cluster per vertex and one interval per time stamp. Then merges of source clusters, of destination clusters and of adjacent time intervals are evaluated and performed so that the criterion decreases. This process is reiterated until there is no more improvement, as detailed in Algorithm 1.

The greedy heuristic may lead to computational issues and a naive straightforward implementation would be barely usable because of a too high algorithmic complexity. By exploiting both the sparseness of the temporal data set and the additive nature of the criterion, one can reduce the memory complexity to O(m) and the time complexity to $O(m\sqrt{m}\log m)$. The optimized version of the greedy heuristic is time efficient, but it may fall into a local optimum. This problem is tackled using the variable neighborhood search (VNS) meta-heuristic (Hansen and Mladenovic 2001), which mainly benefits from multiple runs of the algorithms with different random initial solutions to better explore the space of models. The optimized version of the greedy heuristic as well as the meta-heuristics are described in details in Boullé (2011).

4.4 Simplifying the triclustering structure

When very large temporal data sets are studied, i.e. when $m$ becomes large compared to |S| and |D|, the number of clusters of vertices and of time stamps in the best triclustering may be too large for an easy interpretation. This problem has been raised by White et al. (1976), who suggest an agglomerative method as an exploratory analysis tool in the context of social networks analysis. We describe in this section a greedy aggregating procedure that reduces this complexity in a principled way, using only one user chosen parameter.

The method we propose in this paper consists in merging successively the clusters and the time segments in the least costly way until the triclustering structure is simple enough for an easy interpretation. Starting from a locally optimal set of parameters according to the criterion detailed in Eq. (20), clusters of source vertices, of destination vertices or time stamp ranks are merged sequentially (in such way that time stamp partitions always respect the order of the time stamps). At each step, the two clusters to merge are the ones that induce the smallest increase of the value of the criterion. This post-treatment is equivalent to an agglomerative hierarchical clustering where the dissimilarity measure between two clusters is the variation of the criterion due to this merge, as in the following definition.

Definition 3

Let $\mathcal {M}$ be a triclustering and let $c_1$ and $c_2$ be two clusters of $\mathcal {M}$ on the same variable (that is two source clusters, or two destination clusters or two consecutive time stamp clusters).

The MODL dissimilarity between $c_1$ and $c_2$ is given by

$$\begin{aligned} \Delta _{ MODL }(c_1,c_2)=c(\mathcal {M}_{\text {merge } c_1 \text { and }c_2})- c(\mathcal {M}), \end{aligned}$$

(21)

where $\mathcal {M}_{\text{ merge } c_1 \text { and }c_2}$ is the triclustering obtained from $\mathcal {M}$ by merging $c_1$ and $c_2$ into a single cluster.

Appendix 1 provides some interpretations of this dissimilarity.

To handle the coarsening of a triclustering in practice, a measure of informativeness of the triclustering is computed at each agglomerative step of Algorithm 1. It corresponds to the percentage of informativity the triclustering has kept after a merge, compared to a null model.

Definition 4

(Informativity of a triclustering) The null triclustering $\mathcal {M}_{\emptyset }$ has a single cluster of source vertices and a single cluster of destination vertices and one time segment. It corresponds to a stationary graph with no underlying structure. Given the best triclustering $\mathcal {M}^*$ obtained by optimizing the criterion defined in Definition 1, the informativity of a triclustering $\mathcal {M}$ is:

$$\begin{aligned} \tau (\mathcal {M})=\dfrac{c(\mathcal {M})-c(\mathcal {M}_{\emptyset })}{c(\mathcal {M}^*)-c(\mathcal {M}_{\emptyset })}. \end{aligned}$$

(22)

By definition, $0 \le \tau (\mathcal {M}) \le 1$ for all triclusterings more probable than the null triclustering. In addition, $\tau (\mathcal {M}_{\emptyset }) = 0$ and $\tau (\mathcal {M}^*) = 1$.

The informativity is chosen (or monitored) by the analyst in order to stop the merging process. This is the only user chosen parameter of our method. Notice in particular that the merging process chooses automatically which variable to coarsen: the user do not need to decide whether to reduce the number of clusters on e.g. the source vertices versus the time stamps.

In practice, the coarsening can be seen as a modification of Algorithm 1. Rather than accepting a merge only if the quality criterion is increased, the algorithm selects the best merge in term of the quality of the obtained triclustering (in the inner for loop) and proceeds this way until the triclustering is reduced to only one cluster or the informativity drops below a user chosen value (in the outer while loop).

5 Experiments on artificial data sets

Experiments have been conducted on artificial data in order to investigate the properties of our approach. To that end, we generate artificial graphs with known underlying time evolving structures [see Guigourès et al. (2012) for complementary experiments on a graph with unbalanced clusters].

5.1 Data sets

Experiments are conducted on temporal graphs in which the edge structure changes through time from a quasi-co-clique pattern where edges are concentrated between different clusters to a quasi-clique pattern where edges are concentrated inside clusters.

More precisely, we consider given a source vertex set S and a target vertex set D, both partitioned into k balanced clusters, respectively $(A^S_i)_{1\le i\le k}$ and $(A^D_j)_{1\le j\le k}$. The time interval is arbitrarily fixed to [0, 1]. On this interval, a function ${\varTheta }$ is defined with values in the set of squared $k\times k$ matrices by:

$$\begin{aligned} {\varTheta }(t) = \left\{ \begin{array}{ll} \theta _{ii}(t) = \frac{0.9t + 0.1(1-t)}{k}, \\ \theta _{ij}(t) = \frac{0.1t + 0.9(1-t)}{k(k-1)} \text { when } i \ne j. \end{array} \right. \end{aligned}$$

(23)

The term $\theta _{ij}(t)$ can be seen as a connection probability between a source vertex in cluster $A^S_i$ and a destination vertex in $A^D_j$ (this is slightly more complex, as explained below). In particular, when $t=0$, connections will seldom appear inside diagonal clusters, while they will concentrate on the diagonal when $t=1$ (see Fig. 1).

Given k and m a number of edges to generate, a temporal graph is obtained by building each edge $e_l=(s_l, d_l, t_l)$ according to the following procedure:

• 1. $t_l$ is chosen uniformly at random in [0, 1];

• 2. the clusters indexes $(u_l,v_l)$ are chosen according to the categorical distribution on all the pairs $(i,j)_{1\le i\le k, 1\le j\le k}$ specified by ${\varTheta }(t_l)$ (that is $P(u_l=i, v_l=j)=\theta _{ij}(t_l)$);

• 3. $s_l$ is chosen uniformly at random in $A^S_{u_l}$ and $d_l$ is chosen uniformly at random in $A^D_{v_l}$.

Notice that this procedure is different from what is done in stochastic block models (Nowicki and Snijders 2001) and related models as it aims at mimicking repeated interactions. The procedure is also quite different from the generative approach detailed in Sect. 3 and does not favor our model.

Two additional methods are also used to make the data more complex. The first one consists in randomly reallocating the three variables (source vertex, destination vertex and time stamp) for a randomly selected subset of edges. The reallocation is made uniformly at random independently on each variable. The percentage of reallocated edges measures the difficulty of the task. The second complexity increasing method (applied independently) consists in shuffling the time stamps to remove the temporal structure from the interaction graph. Finally, we use also Erdős–Rényi random graphs with time stamps chosen uniformly at random in [0, 1] to study the robustness of the method.

5.2 Results

We report results with $k=5$ clusters, 50 source vertices and 50 destination vertices. Edge number varies from 2 to $2^{20}$ (considering all powers of 2). For a given number of edges, we generate 20 different graphs. On 10 of them, we applied the reallocation procedure described above for 50 % of the edges.

Fig. 2

Results for graphs with a temporal structure and two levels of noise (no noise and 50 % of reallocated edges). Violin plots (Hintze and Nelson 1998) combine a box plot and a density estimator, leading here to a better view of the variability of the results than e.g. standard deviation bars. The figure represents via violin plots the number clusters (a) and time segmented (b) detected by the proposed approach as a function of the number of edges (yellow no noise, violet 50 % noise) (color figure online)

5.2.1 Temporal graphs

The Fig. 2a, b display respectively the average number of clusters of vertices and the average number of time segments selected by the MODL approach, in graphs in which the structure is preserved either completely (no noise) or partly (50 % of reallocated edges). Bars show the standard deviation of the number of clusters/segments. They are generally non visible as the results are very stable excepted during the transition between the low number of edges to the high number of edges.

For a small number of edges (below $2^{10}$), the method does not discover any structure in the data in the sense that the (locally) optimal triclustering has only one cluster for each variable. The number of edges is too small for the method to find reliable patterns: the gain in likelihood does not compensate the reduction in a posteriori probability induced by the complexity of the triclustering itself. Between $2^{11}$ and $2^{12}$, data are numerous enough to detect clusters but too few to support the detection of the true underlying structure (the results are somewhat unstable at this point and the actual number of clusters discovered by the method varies between each generated graph). Finally, beyond $2^{12}$ edges, we have enough edges to retrieve the true structure. More precisely, the number of clusters of source and destination vertices reaches the true number of clusters and their content agree, while the number of time segments increases with the number of edges. This shows the good asymptotic behavior of the method: it retrieves the true actor patterns and exploits the growing number of data to better approximate the smooth temporal evolution of the connectivity structure. Indeed ${\varTheta }(t)$ is a $C^\infty$ function with bounded (constant) first derivatives and is therefore smooth, with no brutal changes.

Notice finally that the behavior of the method is qualitatively similar on the noisy patterns as on the noiseless ones, but that the convergence to the true structure and the growth of the number of temporal clusters are slower in the noisy case, as expected.

5.2.2 Stationary graphs

When the temporal structure is destroyed by the time stamp shuffling, the method does not partition the time stamps, leaving them in a unique cluster, regardless of the number of edges. Given enough edges ($2^{13}$ without noise and $2^{15}$ with $50~\%$ noise), vertex clusters are recovered perfectly. This shows the efficiency of the regularization induced by the prior distribution on the parameters. As in the case of the temporal graph, disturbing the structure via reallocating edges postpone the detection of the clusters to a larger number of edges.

5.2.3 Random graphs

When applied to Erdős–Rényi random graphs with no structure (neither actor clustering, nor temporal evolution), the method selects as the locally optimal triclustering the one with only one cluster on each dimension, as expected for a non overfitting method.

6 Experiments on a real-life data set

Experiments on a real-life data set have been conducted in order to illustrate the usefulness of the method on a practical case.

6.1 The London cycles data set

The data set is a record of all the cycle hires in the Barclays cycle stations of London between May 31, 2011 and February 4, 2012. The data are available on the website of TFL.² The data set consists in 488 stations and $m=4{.}8$ million journeys. It is modelled as a graph with the departure stations as source vertices, the destination stations as destination vertices and the journeys as edges, with time stamps corresponding to the hire time with minute precision. In this data set $S=D$ (with $|S|=488$) as every station is the departure station and the arrival station of some journeys.

6.2 Most refined triclustering

By applying the proposed method³ to this data set, we obtain 296 clusters of source stations, 281 clusters of destination stations and 5 time stamp clusters. Most of the clusters consist in a unique station, leading to a very fine-grained clustering on the geographical/spatial point of view. This is not the result of some form of overfitting: due to the very large number of bicycle hires compared to the number of stations, the distributions of edges coming from/to the vertices are characteristic enough to distinguish the stations, in particular because many journeys are locally distributed around a source station. On the contrary, and perhaps surprisingly, the temporal dynamic is quite simple as only 5 time stamp clusters are identified. We label them as follows: the morning (from 7.06 AM to 9.27 AM), the day (from 9.28 AM to 3.25 PM), the evening (from 3.26 PM to 6.16 PM), the night (from 6.17 PM to 4.12 AM) and the dawn (from 4.13 AM to 7.05 AM).

6.3 Simplified triclustering

We apply the exploratory post-processing described in Sect. 4.4 in order to study a simplified triclustering. Clusters of stations are successively merged until obtaining 20 clusters of both departure and destination stations while the number of time stamp clusters remains unchanged. By applying this post-processing technique, 70 % of the informativity of the most refined triclustering is retained (see Definition 4). Notice that the merging algorithm is not constrained to avoid merging time intervals and/or to balance departure and destination clusters. On the contrary, each merging step is chosen optimally between all the possible merges on each of the three variables available at this stage. This shows that while the temporal structure is simple, it is very significant on a statistical point of view.

While the data set does not contain explicit geographic information, a detailed analysis of the clusters reveals that the clustered stations are in general geographically correlated. This is a natural phenomenon in a bike share system where short journeys are favored both by the pricing structure and because of the physical effort needed to travel from one point to another. A notable exception is observed for the cycle stations in front of Waterloo and King’s Cross train stations (white discs on Fig. 3) that have been grouped together while they are quite distant. This specific pattern is detailed and interpreted in Sect. 6.4, using an appropriate visualization method.

Fig. 3

Clusters of source stations: each station is represented by a symbol whose shape and level of gray is specific to the corresponding source cluster

Fig. 4

Destination cluster contributions to the mutual information between the source cluster ’Waterloo/King’s Cross’ (stations drawn using stars) and all the destination clusters. Within a destination cluster, all stations share the same color whose intensity is proportional to the contribution of the cluster to the mutual information. Positive contributions are represented in red, negative in blue. The present figure shows mainly positive or null contributions (no blue circles) (color figure online)

The triclusterings obtained by our method are not constrained to yield identical results on S and D even if $S=D$ (which is the case here). This would be an important limitation as it would constraint an actor to have the same role as a source than as a destination. In the bike share data set, we obtain comparable but not identical clustering structures on the set of source and destination vertices. The main notable difference lies on the segmentation of the financial district of London: one single destination cluster covers the area while it is split into two source clusters (the two types of gray squares on Fig. 3 form the source clusters, while most red discs on the right hand side of Fig. 4 form the destination cluster).

6.4 Detailed visualization

The triclustering obtained with our method can help understanding the corresponding temporal data set, in particular when it is used to build specialized visual representations, as illustrate below.

In order to better understand the partition of the stations, we investigate the distribution of journeys originating from (resp. terminating to) the clusters. To that end, we study the contribution to the mutual information of each pair of source/destination stations. We first define more formally the distributions under study. We denote $\mathbb {P}^S_C$ the probability distribution on $\{1,\ldots ,k_S\}$ given by

$$\begin{aligned} \mathbb {P}^S_C(\{i\})=\frac{\mu _{{i}..}}{m}. \end{aligned}$$

(24)

It corresponds to the empirical distribution of the clusters in the data set. Similarly, we denote $\mathbb {P}^D_C$ the probability distribution on $\{1,\ldots ,k_D\}$ given by

$$\begin{aligned} \mathbb {P}^D_C(\{j\})=\frac{\mu _{.{j}.}}{m}. \end{aligned}$$

(25)

Finally, the joint distribution $\mathbb {P}^{S,D}_C$ on $\{1,\ldots ,k_S\}\times \{1,\ldots ,k_d\}$ is given by

$$\begin{aligned} \mathbb {P}^{S,D}_C(\{(i, j)\})=\frac{\sum _{l=1}^{k_T}\mu _{ijl}}{m}. \end{aligned}$$

(26)

To measure the dependencies between the source and destination vertices at the cluster level, we use the mutual information (Cover and Thomas 2006) between the cluster distribution, that is

$$\begin{aligned} MI_C^{S,D}=\sum _{i=1}^{k_S}\sum _{j=1}^{k_D}\mathbb {P}^{S,D}_C(\{(i, j)\})\log \frac{\mathbb {P}^{S,D}_C(\{(i, j\})}{\mathbb {P}^S_C(\{i\})\mathbb {P}^D_C(\{j\})}. \end{aligned}$$

(27)

Mutual information is necessarily positive and its normalized version (NMI) is commonly used as a quality measure in the co-clustering problems (Strehl and Ghosh 2003). Here, we only focus on the contribution to mutual information of a pair of source/destination clusters. This value can be either positive or negative according to whether the observed joint probability of journeys $\mathbb {P}^{S,D}_C(\{(i, j\})$ is above or below the expected probability $\mathbb {P}^S_C(\{i\})\mathbb {P}^D_C(\{j\})$ in case of independence. Such a measure quantifies whether there is a lack or an excess of journeys between two clusters of stations in comparison with the expected number.

For instance, Fig. 4 shows an excess of journeys from the Waterloo and King’s Cross train stations to the central areas of London. Both train stations being major intercity railroad stations, we can assume that people there have the same behavior and all converge to the same points in London: the business districts. This convergence pattern explains why distant cycle stations can be grouped in the same cluster.

In this first analysis, the time variable is not taken into account. It can be integrated into a visualization by considering for instance the dependency between the time stamp clusters on one hand and pairs of source and destination clusters on the other hand. We first define $\mathbb {P}^T_C$ the probability distribution on $\{1,\ldots ,k_T\}$ by

$$\begin{aligned} \mathbb {P}^T_C(\{l\})=\frac{\mu _{..{l}}}{m}. \end{aligned}$$

(28)

The full joint distribution on the clusters is given by the probability distribution $\mathbb {P}^{S,D,T}_C$ on $\{1,\ldots ,k_S\}\times \{1,\ldots ,k_D\}\times \{1,\ldots ,k_T\}$ given by

$$\begin{aligned} \mathbb {P}^{S,D,T}_C(\{(i, j, l)\})=\frac{\mu _{ijl}}{m}. \end{aligned}$$

(29)

Then we display the individual contributions to the mutual information between pairs of source/destination clusters and time clusters:

$$\begin{aligned} MI_C^{(S,D),T}= \sum _{i=1}^{k_S}\sum _{j=1}^{k_D}\sum _{l=1}^{k_T}\mathbb {P}^{S,D,T}_C(\{(i, j, l)\})\log \frac{\mathbb {P}^{S,D,T}_C(\{(i, j, l\})}{\mathbb {P}^{S,D}_C(\{(i, j)\})\mathbb {P}^T_C(\{l\})}. \end{aligned}$$

(30)

Similarly to the previous measure, this one aims at showing the pairs of clusters between which there is an excess of traffic compared to the usual daily traffic between these stations and the usual traffic at this period in London. For example, for the source cluster Waterloo/King’s Cross, the traffic is higher than expected on mornings to the destination clusters located in the center of London (see Fig. 5). By contrast there is a lack of evening journeys (see Fig. 6). These results are not really surprising because we can assume that in the mornings, people use the cycles as a mean of transport to their office rather than as a leisure activity.

Fig. 5

Each station is colored according to the contribution of its destination cluster and of the source cluster Waterloo/King’s Cross (stations drawn using stars) to the mutual information between the source/destination pairs and the time segments. As in Fig. 4, color intensity measures the absolute value of the contribution, while the sign is encoded by the hue (red for positive and blue for negative). In the present figure, the time segment is the morning one, with mainly positive or null contributions (no blue circles) (color figure online)

Fig. 6

Mutual information contribution for the evening time segment. See Fig. 5 for details. The present figure shows mainly negative or null contributions (no red circles) (color figure online)

7 Conclusion

This paper introduces a new approach for discovering patterns in time evolving graphs, a type of data in which interactions between actors are time stamped. The proposed approach, based on the MODL methodology, operates by grouping in clusters source vertices, destination vertices and time stamps in the same procedure. Time stamps clusters are constrained to respect their ordering, leading to the construction of time intervals. The proposed method is related to co-clustering in that we consider the graph as a set of edges described by three variables: source vertices, destination vertices and time. All of them are simultaneously partitioned in order to build time interval on which the interactions between actors can be summarized at the cluster level. This approach is particularly interesting because it does not require any data preprocessing, such as an aggregation of time stamps or a selection of significant edges. Moreover the evolving structure of the graph is tracked in one unique step, making the approach more reliable to study the temporal graphs. Its good properties have been assessed with experiments on artificial data sets. The method is reliable because it is resilient to noise and asymptotically finds the true underlying distribution. It is also suitable in practical cases as illustrated by the study on the cycles renting system of London. In future works, such a method could be extended to co-clustering in k-dimensions, adding labels to the vertices or another temporal feature, such as the day of week or the duration of an interaction for example. This would allow us for instance to model the cycles renting system in more details by taking into account both the departure time and the arrival time of a bike ride. A more ambitious goal would be to allow more complex clustering structures. Indeed in this paper, vertex clusters are time independent, while it would make sense to allow some time dependencies to the clustering. In our framework, a possibility would be to retain more clusters during a some time intervals and less during others, when the structure is simplified. In other words, two clusters of vertices could be merged on interval $[t_1,t_2]$ but kept separated during interval $[t_2,t_3]$. This would allow tracking the complexity of interaction patterns in a non uniform way through time, rather in the implicitly uniform way we handle them in the current method.

Appendix 1: Interpretations of the dissimilarity between two clusters

Interestingly, the dissimilarity given in Definition 3 receives several interpretations. It corresponds to a loss of coding length (when the MODL criterion is interpreted as a description length), a loss of posterior probability of the triclustering given the data (see Proposition 1), and asymptotically to a divergence between probability distributions associated to the clusters (see Proposition 2).

Proposition 1

The exponential of the dissimilarity between two clusters, $c_1$ and $c_2$, gives the inverse ratio between the probability of the simplified triclustering given the data set and the probability of the original triclustering given the data set:

$$\begin{aligned} P(\mathcal {M}|E)=e^{\Delta _{ MODL }(c_1,c_2)} P(\mathcal {M}_{\text{ merge } c_1 \text { and }c_2}|E). \end{aligned}$$

(31)

Asymptotically—i.e when the number of edges tends to infinity - the dissimilarity between two clusters is proportional to a generalized Jensen–Shannon divergence between two distributions that characterize the clusters in the triclustering structure. To simplify the discussion, we give only the definition and result for the case of source clusters, but this can be generalized to the two other cases.

Definition 5

Let $\mathcal {M}$ be a triclustering. For all $i\in \{1,\ldots ,k_S\}$ we denote

$$\begin{aligned} \mathbb {P}^S_i=\left( \frac{\mu _{ijl}}{\mu _{{i}..}}\right) _{1\le j\le k_D, 1\le l\le k_T}. \end{aligned}$$

(32)

The matrix $\mathbb {P}^S_i$ can be interpreted as a probability distribution over $\{1, \ldots , k_D\}\times \{1, \ldots , k_T\}$. It characterizes $c^S_i$ as a cluster of source vertices as seen from clusters of destination vertices and of time stamps.

We denote $\mathbb {P}^S$ the associated marginal probability distribution obtained by

$$\begin{aligned} \mathbb {P}^S=\left( \frac{\sum _{i=1}^{k_S}\mu _{ijl}}{\sum _{i=1}^{k_S}\mu _{{i}..}}\right) _{1\le j\le k_D, 1\le l\le k_T}. \end{aligned}$$

(33)

Obviously, we have

$$\begin{aligned} \mathbb {P}^S=\sum _{i=1}^{k_S}\pi _i\mathbb {P}^S_i, \end{aligned}$$

(34)

where

$$\begin{aligned} \pi _i=\frac{\mu _{{i}..}}{\sum _{k=1}^{k_S}\mu _{{k}..}}. \end{aligned}$$

(35)

Proposition 2

Let $\mathcal {M}$ be a triclustering and let $c^S_i$ and $c^S_k$ be two source clusters. Then

$$\begin{aligned} \dfrac{\Delta _{ MODL }(c^S_i,c^S_k)}{\nu }\underset{\nu \rightarrow +\infty }{\longrightarrow } (\pi _i+\pi _k) JS^{\alpha _i,\alpha _k} (\mathbb {P}^S_i,\mathbb {P}^S_k), \end{aligned}$$

(36)

with

$$\begin{aligned} JS^{\alpha _i,\alpha _k} (\mathbb {P}^S_i,\mathbb {P}^S_k)=\alpha _i KL(\mathbb {P}^S_i || \alpha _i \mathbb {P}^S_i + \alpha _k \mathbb {P}^S_k) + \alpha _k KL(\mathbb {P}^S_k || \alpha _i \mathbb {P}^S_i + \alpha _k \mathbb {P}^S_k), \end{aligned}$$

(37)

and where $\alpha _i$ and $\alpha _k$ are the normalized mixture coefficients such as $\alpha _i = \frac{\pi _i}{\pi _i+\pi _k}$ and $\alpha _k = \frac{\pi _k}{\pi _i+\pi _k}$.

Proof

JS is the generalized Jensen–Shannon Divergence (Lin 1991) and KL, the Kullback–Leibler Divergence. The full proof is left out for brevity and relies on the Stirling approximation: $\log n!= n \log (n) - n + O(\log n)$, when the difference between the criterion value after and before the merge is computed. $\square$

The Jensen–Shannon divergence has some interesting properties: it is a symmetric and non-negative divergence measure between two probability distributions. In addition, the Jensen–Shannon divergence of two identical distributions is equal to zero. While this divergence is not a metric, as it is not sub-additive, it has nevertheless the minimal properties needed to be used as a dissimilarity measure within an agglomerative process in the context of co-clustering (Slonim and Tishby 1999).