Introduction

System uncertainties arising from errors in system modeling, variation of system parameters and unmodelled physical phenomena such as unstructured friction, are inevitable and produce an extra difficulty in the process of controller design[1, 2].

Various control techniques have been evolved to mitigate the effects of uncertainties for decades and have recently reattracted notable attentions from both industry and academic investigation. Among these methods, robust and adaptive methods provide appealing and efficient approaches to handle the control analysis and synthesis of uncertain and ill-defined complex nonlinear systems.

In the adaptive approach, the controller learns the parameter uncertainties and gets tuned with the parameter variations. Hence adaptive method can be used for a wide range of system uncertainties. Since the controller parameters should be updated with the uncertainty variations, this method is a time consuming approach[2].

In the past decades, robust control of uncertain nonlinear dynamics has undergone rapid developments and there have been developed a lot of robust control methods such as linear-quadratic-Gaussian (LQG), loop transfer recovery (LTR), H ∞ control, sliding mode control and etc. In contrast to adaptive controllers, a robust controller has a fixed structure which yields an acceptable performance for a restricted range of uncertainties. A robust controller does not need the exact functional nature of the model[3], however it requires some knowledge about bounding functions on the largest possible size of the uncertainties[1].

A systematic framework for tackling a robust output regulation problem for general uncertain nonlinear systems was given in [4–6]. It was evolved from the proposed approach in [1] and deals with a local robust output regulation problem through an output feedback control. In [7], a constant bound for parametric uncertainties is assumed. Different uncertainty bounds have been considered for designing robust robot controllers[8–16]. Unstructured uncertainty bound has been usually considered as a constant[8, 9] or as a function of state variables[10–16].

Actuator dynamics contemplate as a significant component of the entire robot dynamics, particularly in the cases of high-velocity maneuver and highly varying loads[17]. Contemplating the actuators into the dynamic equations engenders the system dynamics to be described by a set of third-order differential equations and complicates the controller design and its stability analysis[18]. Control of rigid robots including actuator dynamics is still an open forum in the literature[19–25].

The main subject of this paper is to deal with trajectory tracking of electrically driven robotic systems considering uncertainties in both mechanical and electrical subsystems. The overall controller is designed through a backstepping approach.

The main contribution of this paper can be addressed as:

  1. 1)

    Relaxing the restrictive assumption made on the largest possible size of the system uncertainties. In [16], we have developed a robust controller for robotic systems. The proposed method like many conventional methods is suffering from the restricted range of applications due to the bound made on the system uncertainties (especially the inertia matrix). This restriction will be removed through the deployment of the new method.

  2. 2)

    The presented method improves the performance of the system in tracking any given desired trajectories such that it results in global asymptotic stability of the system.

  3. 3)

    In the majority of the previous researches, the actuator dynamics is neglected, while in this study actuators dynamics as well as their uncertainties are taken into account in the development of the controller.

The remainder of this paper is organized as follows. In Section 2, dynamical model of electrically driven robots and its properties are presented. In Section 3, the controller is designed. Section 4 analyzes the stability of the proposed model. In Section 5, the proposed controller will be extended to constrained robotic systems. The numerical and experimental results for two different case studies; a two link serial manipulator and a four-bar linkage, are presented in Section 6. Section 7 concludes the analysis.

Dynamic modeling of robotic systems

In this section, initially we present the governing dynamic equations of an n-link manipulator. Then two useful properties related to these equations are summarized.

Equations of motion

Based on the Euler-Lagrange formulation, the motion equations of an n-link rigid manipulator can be represented as

$$M^{\prime}(q)\ddot q + C^{\prime}(q,\dot q)\dot q + g^{\prime}(q) + J_f^{{\rm{\prime T}}}{\tau _d} + f^{\prime}(\dot q) = \tau $$
(1)

where q ∈ Rn is the generalized coordinates (joint positions), τ ∈ Rn is the actuating torques vector, M′(q) ∈ Rn×n is the inertia matrix, \(C^{\prime}(q,\dot q)\dot q \in {{\bf{R}}^n}\) represents the centripetal and coriolis torques, g′(q) ∈ Rn is the vector of gravitational torques, \(f^{\prime}(\dot q) \in {{\bf{R}}^n}\) represents friction terms, τ d ∈ Rn represents unknown bounded constant disturbance vector represented in the Cartesian workspace and J′ f ∈ Rn×n is the Jacobian matrix calculated by

$$J_f^{\prime} = {{\partial {r_f}} \over {\partial q}}$$
(2)

where r f is the foot point of τ d , and it is assumed to be uncertain.

The brushed direct current (BDC) motors dynamics can be modeled as

$${L_m}\dot I + {R_m}I + {K_{em}}\dot q = v$$
(3)

where I ∈ Rn is the vector of the armatures current, v ∈ Rn is the vector of armatures voltage, L m ∈ Rn×n is the actuators inductance matrix, R m ∈ Rn×n is the actuators resistance matrix and K em ∈ Rn×n is the motors back emf coefficient matrix.

The correlation between motors current and torque is defined by

$$\tau = {K_{Tm}}I$$
(4)

where K Tm ∈ Rn×n is the motors electromechanical coefficients. Note that R m , L m , K em and K Tm are all diagonal and positive definite constant matrices.

Rewriting (1) with a new notation, one obtains

$$M(q)\ddot q + C(q,\dot q)\dot q + g(q) + J_f^{\rm{T}}{\tau _d} + f(\dot q) = I$$
(5)

where

$$\matrix{{M(q) = K_{Tm}^{- 1}M^{\prime}(q)} \hfill \cr {C(q,\dot q) = K_{Tm}^{- 1}C^{\prime}(q,\dot q)} \hfill \cr {g(q) = K_{Tm}^{- 1}g^{\prime}(q),\quad f(\dot q) = K_{Tm}^{- 1}f^{\prime}(\dot q)} \hfill \cr {{J_f} = J_f^{\prime}(q)K_{Tm}^{- {\rm{T}}}.} \hfill \cr}$$
(6)

  • Definition 1. For an arbitrary positive definite or negative definite symmetric matrix such as B, throughout this paper, by B m and B M the authors mean the minimum and maximum eigenvalues of that matrix. Hence, for any arbitrary vector x, we can state,

    $${B_m}{\left\Vert x \right\Vert ^2} \leq {x^{\rm{T}}}Bx \leq {B_M}{\left\Vert x \right\Vert ^2}.$$
    (7)

Note that ∥·∥ represents the 2 induced norm for matrices and Euclidean norm for vectors.

Properties of the equation of motion

Structure of the equations of motion expressed by (5) benefits from the following properties which will be used in the development of the control law.

  • Property 1. The inertia matrix M(q)is known to be positive definite and symmetric.

  • Property 2. A suitable definition of \(C(q,\dot q)\) makes the matrix \({\textstyle{1 \over 2}}\dot M - C\) skew symmetric. In particular, the elements of \(C(q,\dot q)\) may be defined as

    $$C(ij)(q,\dot q) = {1 \over 2}\left[ {{{\dot q}^{\rm{T}}}{{\partial {M_{ij}}} \over {\partial q}} + \sum\limits_{k = 1}^n {\left({{{\partial {M_{ik}}} \over {\partial {q_j}}} - {{\partial {M_{jk}}} \over {\partial {q_i}}}} \right){{\dot q}_k}}} \right].$$
    (8)

Therefore (9) holds for any arbitrary vector x ∈ Rn:

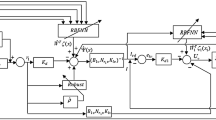
$${x^{\rm{T}}}\left[ {{1 \over 2}\dot M - C(q,\dot q)} \right]\;\;x = 0.$$
(9)

Controller design

Here initially the control law is proposed, and then it is substituted into the robot dynamic equation represented by (5) in order to obtain the final closed-loop error dynamics. This closed loop dynamics is then used in the Lyapunov analysis to show that this control law is appropriate to push the robotic system to track the desired trajectory.

Error dynamics

Introducing the desired joint positions and velocities by q d and \({\dot q_d}\), and defining the modified error by

$$r = \Lambda e + \dot e$$
(10)

where e = q − q d , \(\dot e = \dot q - {\dot q_d}\) and Λ = diag {λ1, ⋯,λn}, λ i > 0. Equation (5) can be written as

$$\matrix{{M\dot r = M(\Lambda \dot e - {{\ddot q}_d}) - C(q,\dot q)(r - \Lambda e + {{\dot q}_d}) -} \hfill \cr {\quad \quad g(q) - f(\dot q) - J_f^{\rm{T}}{\tau _d} + I.} \hfill \cr}$$
(11)

Since the robot equation is linear in parameters[26], we can define the right side of (11) in the regression form as

$$\matrix{{{Y_1}(q,\dot q,t){\Phi _1} = M(\Lambda \dot e - {{\ddot q}_d}) - g(q) - f(\dot q) -} \hfill \cr {\quad \quad \quad \quad \quad \quad C(q,\dot q)(- \Lambda e + {{\dot q}_d}) - J_f^{\rm{T}}{\tau _d}} \hfill \cr}$$
(12)

where Y1(·) ∈ Rn×m is the robot regressor matrix, Φ1 ∈ Rm represents uncertain mechanical parameters, is a constant vector, and m is the number of uncertain parameters.

Hence, (11) can be written as

$$M\dot r = {Y_1}(q,\dot q,t){\Phi _1} - C(q,\dot q)r + I.$$
(13)

Trajectory tracking control

A backstepping-like approach is used to design the controller for the system modeled by (5).

In the first step using the mechanical subsystem dynamics, a desired current signal I d is calculated such that the trajectory tracking control is performed. Then in the second step, in order to enforce I tracks its desired values, I d , the required voltage input, is determined using the electrical subsystem dynamics.

Let us define the desired current calculated by

$${I_d} = - {K_v}r - {Y_1}(\cdot){\bar \Phi _1} + {u_1}$$
(14)

where K v ∈ Rn×n is a positive definite symmetric gain matrix, \({\bar \Phi _1}\) represents the nominal values of the uncertain parameters, and u1 is defined by

$${u_1} = - {{\rho _1^2r} \over {{\rho _1}\left\Vert r \right\Vert + {\varepsilon ^2}}}.$$
(15)

Since Φ1 and \({\bar \Phi _1}\) are bounded constant vectors, hence we can assume that \(\left\Vert {{{\tilde \Phi}_1}} \right\Vert \leq {\alpha _1}\), where \({\tilde \Phi _1} = {\Phi _1} - {\bar \Phi _1}\) and no restriction exists on the magnitude of α1. In (14), the term \( - {Y_1}(\cdot){\bar \Phi _1}\) represents the nonlinearity of robot (but calculated by nominal magnitudes of parameters) and the term −K v r + u1 is used to relieve the mismatch resulted from calculating the nonlinearities of robot with the nominal magnitude of uncertainties.

Now let us introduce ρ 1 and ε through the following equations:

$${\rho _1} = {\alpha _1}\left\Vert {{Y_1}(\cdot)} \right\Vert $$
(16)
$$\dot \varepsilon = - {K_\varepsilon}\varepsilon.$$
(17)

where K ε is a positive constant. Clearly ε is a continuously decaying positive function once ε(0) > 0.

Therefore, from the above equations, it can be concluded that

$$\left\| {\dot I_d } \right\| \leqslant \chi \left( {\left\| e \right\|,\left\| {\dot e} \right\|,\left\| {\ddot e} \right\|,\left\| {\dddot q_d } \right\|} \right).$$
(18)

where χ is a bounded function for bounded variables. Equation (18) implies that if the system tracking errors be bounded, an upper bound can be considered for the first derivative of the desired current as

$$\left\Vert {{{\dot I}_d}} \right\Vert \leq {\alpha _3}.$$
(19)

If we define the desired current tracking error by

$$\eta = I - {I_d}$$
(20)

and substitute I = I d + η in (13), we obtain

$$M\dot r = {Y_1}(\cdot){\tilde \Phi _1} - C(q,\dot q)r - {K_v}r + {u_1} + \eta.$$
(21)

Hence, the electrical dynamics represented by (3) can be written in terms of the current error:

$${L_m}\dot \eta = - {R_m}\eta - {K_{em}}\dot q - {L_m}{\dot I_d} - {R_m}{I_d} + v.$$
(22)

Similar to the mechanical subsystem, we introduce

$${Y_2}(q,\dot q, \eta, t){\Phi _2} = - {R_m}\eta - {K_{em}}\dot q - {R_m}{I_d}$$
(23)

where Y2(·) ∈ Rn×p is the electrical regressor matrix, Φ 2 ∈ Rp is the vector of uncertain electrical parameters, and p represents the number of these parameters. Therefore (22) can be written as

$${L_m}\dot \eta = {Y_2}(\cdot){\Phi _2} - {L_m}{\dot I_d} + v.$$
(24)

Desired current control

The second step in the controller design is introducing a control law for the input voltage such that the motor current tracks the calculated desired current. Let us introduce the following control law for the motor voltage

$$v = - {Y_2}(\cdot){\bar \Phi _2} - r + {u_2}$$
(25)

where u2 is similarly given by

$${u_2} = - {{\rho _2^2\eta} \over {{\rho _2}\left\Vert \eta \right\Vert + {\mu ^2}}}.$$
(26)

Similar to \({\tilde \Phi _1}\), it can be assumed that \(\left\Vert {{{\tilde \Phi}_2}} \right\Vert \leq {\alpha _2}\) where \({\tilde \Phi _2} = {\Phi _2} - {\bar \Phi _2}\) and no restriction exists on the magnitude of α2.

In the above equation, ρ2 is defined by

$${\rho _2} = {\alpha _2}\left\Vert {{Y_2}(\cdot)} \right\Vert + l{\alpha _3}$$
(27)

where l is a constant greater than the maximum eigenvalue of matrix L and again similar to ε, μ is an augmented state with the following dynamics as

$$\dot \mu = - {K_\mu}\mu.$$
(28)

μ is also a continuously decaying positive function once μ(0) and K μ are positive constants.

Substituting (25) and (26) in (24), it can be deduced that

$${L_m}\dot \eta = - {L_m}{\dot I_d} + {Y_2}(\cdot){\tilde \Phi _2} - {{\rho _2^2\eta} \over {{\rho _2}\left\Vert \eta \right\Vert + {\mu ^2}}} - r.$$
(29)

Stability analysis

Stability and performance of the whole control system in the trajectory tracking is analyzed by the following theorem. The Theorem 1 is developed based on the Lyapunov arguments where a positive definite Lyapunov function is shown to have a negative definite time derivative starting from a bounded initial state vector γ =[eT, ėT]T.

  • Theorem 1. The input control voltage calculated by (25) results in semi-globally asymptotic stability of position and velocity tracking error, i.e.,

    $$\mathop {\lim}\limits_{t \rightarrow \infty} e = 0,\quad \mathop {\lim}\limits_{t \rightarrow \infty} \dot e = 0$$
    (30)

    provided that the desired trajectory tracking and the initial system errors γ being bounded.

  • Proof. Consider a so called positive definite Lyapunov function defined by

    $$V(E) = {1 \over 2}{E^{\rm{T}}}PE$$
    (31)

    where E = [rT,ηT,ε, μ]T is the augmented state vector and

    $$P = {\rm{diag}}\{M,{L_m},K_\varepsilon ^{- 1},K_\mu ^{- 1}\}.$$
    (32)

Differentiating (31) with respect to time, we obtain

$$\dot V = {r^{\rm{T}}}M\dot r + {\eta ^{\rm{T}}}{L_m}\dot \eta + {1 \over 2}{r^{\rm{T}}}\dot Mr - {\varepsilon ^2} - {\mu ^2}.$$
(33)

Substituting (21) and (24), it can be concluded that

$$\matrix{{\dot V = {r^{\rm{T}}}\left[ {Y(\cdot){{\tilde \Phi}_1} - {K_v}r - {{\rho _1^2r} \over {{\rho _1}\left\Vert r \right\Vert + {\varepsilon ^2}}}} \right] +} \hfill \cr {\quad \;{r^{\rm{T}}}\left[ {{1 \over 2}\dot M - C(q,\dot q)} \right]\;\;r + {\eta ^{\rm{T}}}\left[ {- {L_m}{{\dot I}_d} + {Y_2}(\cdot){{\tilde \Phi}_2}} \right. -} \hfill \cr {\quad \;\left. {{{\rho _2^2\eta} \over {{\rho _2}\left\Vert \eta \right\Vert + {\mu ^2}}}} \right] - {\varepsilon ^2} - {\mu ^2}.} \hfill \cr}$$
(34)

Utilizing Property 2 and considering (7) and the facts that for any arbitrary vectors such as a and b, we have aTb ≤ ∥a∥ ∥b∥ and aTa = ∥a∥2, we can simplify (34) to obtain

$$\matrix{{\dot V \leq \left\Vert {{Y_1}(\cdot)} \right\Vert \left\Vert {{{\tilde \Phi}_1}} \right\Vert \left\Vert r \right\Vert - {K_{{v_m}}}{{\left\Vert r \right\Vert}^2} - {{\rho _1^2{{\left\Vert r \right\Vert}^2}} \over {{\rho _1}\left\Vert r \right\Vert + {\varepsilon ^2}}} +} \hfill \cr {\quad \;\;\left\Vert {{Y_2}(\cdot)} \right\Vert \left\Vert {{{\tilde \Phi}_2}} \right\Vert \left\Vert \eta \right\Vert + \left\Vert {{L_m}} \right\Vert \left\Vert {{{\dot I}_d}} \right\Vert \left\Vert \eta \right\Vert -} \hfill \cr {\quad \;\;{{\rho _2^2{{\left\Vert \eta \right\Vert}^2}} \over {{\rho _2}\left\Vert \eta \right\Vert + {\varepsilon ^2}}} - {\varepsilon ^2} - {\mu ^2}.} \hfill \cr}$$
(35)

Consider two bounded sets such as \({\Omega _1} = \{E(t)\vert \;\left\Vert {E(t)} \right\Vert \leq \ell \}, \;{\Omega _2} = \{E(0)\vert \;\left\Vert {E(0)} \right\Vert \leq \sqrt {{\textstyle{{{P_m}} \over {{P_M}}}}\ell} \}\) where ℓ is a selected positive scalar which defines the boundary of the sets. For any trajectory in Ω1, since e and ė are bounded (21) results in bounded ë, too. Utilizing (16), (19) and (27) in (35), for any trajectory in Ω1 it can be stated that

$$\matrix{{\dot V \leq - {K_{{v_m}}}{{\left\Vert r \right\Vert}^2} + {\rho _1}\left\Vert r \right\Vert - {{\rho _1^2{{\left\Vert r \right\Vert}^2}} \over {{\rho _1}\left\Vert r \right\Vert + {\varepsilon ^2}}} +} \hfill \cr {\quad {\rho _2}\left\Vert \eta \right\Vert - {{\rho _2^2{{\left\Vert \eta \right\Vert}^2}} \over {{\rho _2}\left\Vert \eta \right\Vert + {\varepsilon ^2}}} - {\varepsilon ^2} - {\mu ^2} \leq} \hfill \cr {\quad - {K_{{v_m}}}{{\left\Vert r \right\Vert}^2} - {{{\varepsilon ^4}} \over {{\rho _1}\left\Vert r \right\Vert + {\varepsilon ^2}}} - {{{\mu ^4}} \over {{\rho _2}\left\Vert \eta \right\Vert + {\varepsilon ^2}}}} \hfill \cr}$$
(36)

and consequently

$$\dot V \leq - {K_{{v_m}}}{\left\Vert r \right\Vert ^2}.$$
(37)

Since Ω2 is a subset of Ω1, for any trajectory initialized in Ω2 one can integrate (37) to obtain

$$V(t) - V(0) \leq - {K_{{v_m}}}\int_0^t {{{\left\Vert r \right\Vert}^2}{\rm{d}}t.} $$
(38)

Using (7) in the above equation, we can write

$$\matrix{{{1 \over 2}{P_m}{{\left\Vert {E(t)} \right\Vert}^2} \leq V(t) \leq V(0) - {K_{{v_m}}}{{\int_0^t {\left\Vert r \right\Vert}}^2}{\rm{d}}t \leq} \hfill \cr {\quad \quad {1 \over 2}{P_M}{{\left\Vert {E(0)} \right\Vert}^2} - {K_{{v_m}}}{{\int_0^t {\left\Vert r \right\Vert}}^2}{\rm{d}}t} \hfill \cr}$$
(39)

or

$$\left\Vert {E(t)} \right\Vert \leq \sqrt {{{{P_M}} \over {{P_m}}}} \left\Vert {E(0)} \right\Vert \leq \ell.$$
(40)

Therefore, from the definition of Ω2 for any trajectory initialized in Ω2, it can be stated that

$$\left\Vert {E(t)} \right\Vert \leq \ell, \quad \forall t > 0$$
(41)

which concludes that any trajectory starting in Ω2 will remain in Ω1.

Also from (39) we can conclude that

$$\mathop {\lim}\limits_{t \rightarrow \infty} {\left\Vert {E(t)} \right\Vert ^2} \leq {{{P_M}} \over {{P_m}}}{\left\Vert {E(0)} \right\Vert ^2} - {{{K_{{v_m}}}} \over {{P_m}}}{\int_0^\infty {\left\Vert r \right\Vert} ^2}{\rm{d}}t.$$
(42)

Hence it can be stated that

$$\mathop {\lim}\limits_{t \rightarrow \infty} \left\Vert r \right\Vert = 0.$$
(43)

Note that (10) is a stable first-order differential equation driven by the input r. Therefore, by standard linear control arguments and (10), we can state

$$\mathop {\lim}\limits_{t \rightarrow \infty} e = 0\;{\rm{and}}\;\mathop {\lim}\limits_{t \rightarrow \infty} \dot e = 0.$$
(44)

The above results state that the tracking errors e and ė are asymptotically stable. □

Applications to robotic systems interacting with environment

In Section 3, a robust controller is designed for nonconstrained serial manipulators. In many industrial/manufacturing applications such as welding, forming, assembling, and grinding, a robot manipulator is required to come into a planned contact with the environment. In these applications, the environment somehow imposes some constraints on the trajectories that the robot must follow. In this section, the proposed control method will be extended to the case of nonredundant constrained robotic systems.

Constrained robot dynamics

Dynamic motion of constrained robotic systems interacting with rigid environment is described by [27]:

$$\matrix{{{M^\prime}(q)\ddot q + {C^\prime}(q,\dot q)\dot q + {g^\prime}(q) + J_e^{\rm{T}}{f_n} +} \hfill \cr {\quad \quad J_e^{\prime {\rm{T}}}{\tau _d} + {f^\prime}(\dot q) = \tau} \hfill \cr}$$
(45)

where q, M′, C′, g′, τ d ,J′ f , f′, τ have the same definitions as serial robot manipulators. f n ∈ Rn denotes the end-effector normal forces of contact described in the task space and J e ∈ Rn×n represents the Jacobian matrix of the system.

Here we assume that the manipulator operates away from any singularity and that the manipulator motion is holonomically constrained by m algebraic equations. These constraints in the velocity space are expressed by

$$D\dot X = D\;{J_e}(q)\dot q = 0$$
(46)

where Ẋ represents the task space velocity of the end effector and D ∈ Rm×n is a full row rank matrix.

The normal contact force can be represented by

$${f_n} = {D^{\rm{T}}}\lambda $$
(47)

where λ denotes the generalized Lagrangian multiplier. Consider the matrix D e denoted by

$${D_e} = D(q)\,{J_e}(q).$$
(48)

As mentioned in [27], without loss of generality one can partition the columns of the matrix D e as

$${D_e} = [{D_{ml}}\vert {D_m}]$$
(49)

where D m ∈ Rm×m is an m squared nonsingular matrix and D ml ∈ Rm×l, l = n − m.

Due to m holonomic constraints, the joint space of the robot has only l independent variables and one can always partition the joint position vector to q l ∈ Rl and q m ∈ Rm as

$$q = \left[ {\matrix{{{q_l}} \cr {{q_m}} \cr}} \right].$$
(50)

Due to m holonomic constraints, it can be mentioned that q = Ω(ql) where Ω is a nonlinear mapping function which is bounded for bounded state variable q l . It then follows that

$$\dot q = {J_l}(q){\dot q_l}$$
(51)

where

$${J_l}(q) = \left[ {\matrix{{{I_l}} \cr {- D_m^{- 1}{D_{ml}}} \cr}} \right]$$
(52)

and I l ∈ Rl×l is an identity matrix. It is not difficult to see that

$$J_l^{\rm{T}}D_e^{\rm{T}} = 0.$$
(53)

Equation (53) is very useful in the controller design and stability analysis of the system.

By the following change of variables, one can decouple the robot dynamic into two individual blocks: a reduced position block and a reduced force block. It is worth to mention that the constrained force does not appear in the reduced position model. Considering (4), (51) and (53), the reduced position block can be represented by

$$\matrix{{{M_l}(q){{\ddot q}_l} + {C_l}(q,{{\dot q}_l}){{\dot q}_l} + {G_l}(q) +} \cr {J_l^{\rm{T}}(J_f^{\rm{T}}{\tau _d} + f(\dot q)) = {I_l}} \cr}$$
(54)

where

$$\matrix{{{M_l}(q) = K_{Tm}^{- 1}J_l^{\rm{T}}{M^\prime}(q){J_l}} \hfill \cr {{C_l}(q,{{\dot q}_l}) = K_{Tm}^{- 1}J_l^{\rm{T}}\left({{M^\prime}(q){{\dot J}_l} + {C^\prime}(q,{{\dot q}_l})} \right)} \hfill \cr {{G_l}(q) = K_{Tm}^{- 1}J_l^{\rm{T}}{g^\prime}(q)} \hfill \cr {{J_f} = J_f^\prime K_{Tm}^{- {\rm{T}}},\quad f(\dot q) = K_{Tm}^{- 1}{f^\prime}(\dot q)} \hfill \cr {{I_l} = J_l^{\rm{T}}I.} \hfill \cr}$$
(55)

The brushed DC (BDC) motors dynamics can be modeled as

$${L_m}{\dot I_l} = {L_m}\dot J_l^{\rm{T}}I - J_l^{\rm{T}}{R_m}I - J_l^{\rm{T}}{K_{em}}\dot q + {v_l}$$
(56)

where \({v_l} = J_l^{\rm{T}}\;v\), I and v represent the motor current and motor voltage, respectively. And L m ,R m ,K em represent the actuators inductance matrix, the actuators resistance matrix and the motors back emf coefficient matrix, respectively.

It is worth to mention that the matrix M l (q) is positive definite, and that the matrix \({\textstyle{1 \over 2}}{\dot M_l}(q) - {C_l}(q,{\dot q_l})\) is skew symmetric.

Controller design

Let us define the filtered tracking error by

$${r_l} = {\dot e_l} + \Lambda {e_l}$$
(57)

where \({\dot e_l} = {\dot q_l} - {\dot q_{ld}},\;{e_l} = {q_l} - {q_{ld}}\) and q ld , \({\dot q_{ld}}\) are the desired values of reduced position and velocity vectors, respectively.

Also, let us define

$$\matrix{{{Y_{l1}}(q,\dot q,t){\Phi _{l1}} = {M_l}(\Lambda {{\dot e}_l} - {{\ddot q}_{ld}}) - {g_l}(q) -} \hfill \cr {\quad {C_l}(q,\dot q)(- \Lambda {e_l} + {{\dot q}_{ld}}) - J_l^{\rm{T}}(J_f^{\rm{T}}{\tau _d} + f(\dot q))} \hfill \cr {\quad {Y_{l2}}(q,\dot q,I,t){\Phi _{l2}} = {L_m}\dot J_L^{\rm{T}}I - J_L^{\rm{T}}({R_m}I + {K_{em}}\dot q)} \hfill \cr}$$
(58)

where Y l 1(·) is the mechanical regressor matrix, Y l 2(·)is the electrical regressor matrix, Φl1 represents uncertain mechanical parameters and Φl2 represents uncertain electrical parameters.

Consider the current tracking error defined by

$${\eta _l} = {I_l} - {I_{ld}}$$
(59)

where I ld represents the desired current trajectory calculated by

$${I_{ld}} = - {K_v}{r_l} - {Y_{l1}}(\cdot){\bar \Phi _{l1}} - {{\rho _{l1}^2{r_l}} \over {{\rho _{l1}}\left\Vert {{r_l}} \right\Vert + {\varepsilon ^2}}}$$
(60)

where

$${\rho _{l1}} = {\alpha _{l1}}\left\Vert {{Y_{l1}}(\cdot)} \right\Vert $$
(61)
$$\dot \varepsilon = - {K_\varepsilon}\varepsilon.$$
(62)

\({\bar \Phi _{l1}}\) represents the nominal values of the uncertain mechanical parameters and we can assume that \(\left\Vert {{{\tilde \Phi}_{l1}}} \right\Vert \leq {\alpha _{l1}}\), where \({\tilde \Phi _{l1}} = {\Phi _{l1}} - {\bar \Phi _{l1}}\) and no restriction exists on the magnitude of α l 1. Let us introduce the control law for the motor voltage as

$${v_l} = - {Y_{l2}}(\cdot){\bar \Phi _{l2}} - {r_l} - {{\rho _{l2}^2{\eta _l}} \over {{\rho _{l2}}\left\Vert {{\eta _l}} \right\Vert + {\mu ^2}}}$$
(63)

where

$${\rho _{l2}} = {\alpha _{l2}}\left\Vert {{Y_{l2}}(\cdot)} \right\Vert + l{\alpha _{l3}}$$
(64)
$$\dot \mu = - {K_\mu}\mu.$$
(65)

Similar to Φl1, it can be assumed that \(\left\Vert {{{\tilde \Phi}_{l2}}} \right\Vert \leq {\alpha _{l2}}\) where \({\tilde \Phi _{l2}} = {\Phi _{l2}} - {\bar \Phi _{l2}}\) and no restriction exists on the magnitude of α l 2. α l 3 is defined similar to α3, i.e., \(\left\Vert {{{\dot I}_{ld}}} \right\Vert \leq {\alpha _{l3}}\).

Consequently, the position and current error dynamics can be represented by

$$\matrix{{{M_l}{{\dot r}_l} = {Y_{l1}}(\cdot){{\tilde \Phi}_{l1}} - {C_l}(q,{{\dot q}_l}){r_l} - {K_v}r -} \cr {{{\rho _{l1}^2{r_l}} \over {{\rho _{l1}}\left\Vert {{r_l}} \right\Vert + {\varepsilon ^2}}} + {\eta _l}} \cr {{L_m}{{\dot \eta}_l} = - {L_m}{{\dot I}_{ld}} + {Y_{l2}}(\cdot){{\tilde \Phi}_{l2}} - {{\rho _{l2}^2{\eta _l}} \over {{\rho _{l2}}\left\Vert {{\eta _l}} \right\Vert + {\mu ^2}}} - {r_l}.} \cr}$$
(66)

The stability and performance of the whole control system in trajectory tracking is analyzed by Theorem 2.

  • Theorem 2. The input control voltage calculated by (63), results in semi-global asymptotic stability of position and velocity tracking error, i.e.,

    $$\mathop {\lim}\limits_{t \rightarrow \infty} \,{e_l} = 0,\quad \mathop {\lim}\limits_{t \rightarrow \infty} \,{\dot e_l} = 0$$
    (67)

    provided that the desired trajectory tracking and the initial system errors being bounded.

The stability of the system can be proved by the same procedure presented in Section 4, utilizing the following Lyapunov function:

$$V({E_l}) = {1 \over 2}E_l^{\rm{T}}P{E_l}$$
(68)

where \({E_l} = {[r_l^{\rm{T}},\eta _l^{\rm{T}},\varepsilon, \mu ]^{\rm{T}}}\) is the augmented state vector and

$$P = {\rm{diag\{}}{M_l},\,{L_m},\,K_\varepsilon ^{- 1},\,K_\mu ^{- 1}\}.$$
(69)

Experimental and numerical implementation

In order to validate the proposed method, in this section experimental and numerical results are presented for two different systems: A two link serial manipulator and a four-bar linkage system.

Experimental setup

The developed controller is implemented experimentally on a two link planar manipulator shown in Fig. 1 and the experimental results are compared with those of the simulation results for the same system parameters. Each axis is driven by a Maxon servomotor set consisting of a BDC, an encoder and a gear reduction unit. The mass and the length of the links, without considering the mass of the motors, are approximately about 0.54 kg and 43 cm for the first link and 0.24 kg and 47 cm for the second one. The mass of the first and the second motors sets are 0.45 kg and 0.32 kg, respectively.

Fig. 1
figure 1

The two link planar manipulator employed for experimental results

Full size image

The base and elbow joints have the capability of making up to 0.85 and 1.6 revolutions per second and each one has maximum position feedback resolution of up to 14 400 counts per revolution. The base motor is capable of generating up to 16.7 N·m torque and the elbow motor up to 2.2 N·m. The effective torque constant at the joint ends are 6.1 N·m/A for the first axis and 1.95 N·m/A for the second one.

Real-time control is performed with a host computer (Pentium IV 2.0 GHz dual-core) and a servo 400 MHz DSP. Each motor is mounted on two ball bearings after gearbox. The gearboxes have planar clearance of approximately up to 1 deg. This leads to a resultant clearance of 1.5 cm at the end-effecter point. For the velocity feedback, a one step numerical differentiation of the joint position measurements with a sampling period of 4 ms has been used.

Experimental and numerical results for a two link manipulator

Using the above mentioned numerical values of system parameters and employing the proposed algorithm, the controller is developed. The following are used as the control gains:

$$\matrix{{{K_v} = {\rm{diag\{100,}}\,{\rm{100\}}}} \hfill \cr {{K_\varepsilon} = {K_\mu} = 0.001} \hfill \cr {\varepsilon (0) = \mu (0) = 100} \hfill \cr {\Lambda = {\rm{diag\{10,}}\,{\rm{10\}}}{\rm{.}}} \hfill \cr}$$
(70)

The robot is assumed to track a harmonic desired trajectory defined by (71), while the electrical and mechanical parameters are in fact uncertain.

$${q_{1d}} = {q_{2d}} = 0.5\sin {{2\pi} \over 5}t.$$
(71)

The position and velocity tracking errors, both for the experimental results and numerical simulation are given in Figs. 2 and 3.

Fig. 2
figure 2

Time history of position tracking errors

Full size image
Fig. 3
figure 3

Time history of velocity tracking errors

Full size image

Fig. 2 shows that the absolute maximum position tracking error for joint 1 is about 0.06 rad (3.43 deg) and it is about 0.02 rad (1.14 deg) for joint 2 in the experimental case, once the initial errors get settled down. These values are 0.003 rad (0.17 deg) for link 1 and 0.001rad (0.05 deg) for link 2 in the simulation results, once the initial errors get settled down.

The velocity tracking errors are given in Fig. 3. There is an initial spike in the velocity tracking error at t =0. This can be seen again in experimental and simulation results. It is due to the initial condition errors. This figure shows that in the experimental case the velocity tracking errors are bounded within 0.15 rad/s for both links, once the initial errors get settled down. However, in the simulation case they are bounded to 0.006 rad/s and 0.003 rad/s, respectively.

Fig. 4 shows time history of the motors input voltage. Except for noisy behavior of the experimental results, similarity and closeness of the experimental results and simulation results can be clearly observed.

Fig. 4
figure 4

Time history of input voltage

Full size image

Numerical results for a four-bar linkage system

In this section, the validity of the theorem presented in Section 5 is verified by the numerical simulation executed on a four-bar linkage, as an example of constrained robotic systems. The schematic of the system is shown in Fig. 5 which is driven by a motor installed on the first link.

Fig. 5
figure 5

Schematic of a four-bar linkage

Full size image

The dynamics of the system is calculated by (54) and (56), and the inertia and Coriolis and gravity terms are calculated for a three link robotic arm utilizing the Maple software.

A four-bar linkage has two constraint equations defined by

$$\matrix{{{l_1}{c_1} + {l_2}{c_{12}} + {l_3}{c_{123}} = a} \hfill \cr {{l_1}{s_1} + {l_2}{s_{12}} + {l_3}{s_{123}} = 0.} \hfill \cr}$$
(72)

Also D(q) and J e (q) are defined by

$$\begin{array}{*{20}c} {D = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right],} & {J_e = \left[ {\begin{array}{*{20}c} { - l_1 s_1 } & { - l_2 s_{12} } & { - l_3 s_{123} } \\ {l_1 c_1 } & {l_2 c_{12} } & {l_3 c_{123} } \\ \end{array} } \right].} \\ \end{array} $$
(73)

Considering q l = q1 and q m = [q2, q3]T and utilizing the Maple software, the reduced order dynamics of the system in the form of (45) is computed. The electromechanical parameters of the system are selected by

$$\matrix{{{m_1} = 1\,{\rm{kg,}}\,{m_2} = 1\,{\rm{kg,}}\,{m_3} = 1\,{\rm{kg,}}} \hfill \cr {{l_1} = 1\,{\rm{m,}}\,{l_2} = 1\,{\rm{m,}}\,{l_3} = 1\,{\rm{m,}}\,a = 2\,{\rm{m,}}} \hfill \cr {{K_T} = 1,\,{L_m} = 0.1\,{\rm{H,}}\,{K_{em}} = 0.2\,{\rm{V}} \cdot {\rm{s/rad,}}\,{R_m} = 5\Omega.} \hfill \cr}$$
(74)

The uncertain mechanical parameter vector is Φ1 = [m1, m2, m3]T and the uncertain electrical parameter vector is Φ2 = [Lm, K em , R m ]T. The desired trajectory for q1 is described by

$${q_{ld}} = \sin t.$$
(75)

The nominal values of the uncertain parameters are assumed to be \({\bar \Phi _1} = {[6,6,6]^{\rm{T}}},{\bar \Phi _2} = {[2,2,8]^{\rm{T}}}\). The nominal magnitude of parameters are selected far from their actual values to show the effectiveness of the method against great degrees of uncertainties.

Here, for the convenience of simulation, the entire initial conditions are assumed to be zero and the controller gains for the proposed method are chosen to be

$$\matrix{{{K_v} = 100,\,\Lambda = 3} \hfill \cr {{K_\varepsilon} = {K_\mu} = 0.001} \hfill \cr {\varepsilon (0) = \mu (0) = 100.} \hfill \cr}$$
(76)

The simulation results are presented in Figs. 6–8. The angular position tracking error, e l , is represented in Fig. 6. The angular velocity tracking error, ė l , is shown in Fig. 7. The motor voltage is plotted in Fig. 8.

Fig. 6
figure 6

Time history of position tracking error

Full size image
Fig. 7
figure 7

Time history of velocity tracking error

Full size image
Fig. 8
figure 8

Time history of input voltage

Full size image

From this comparative simulation, it can be concluded that the joint position and velocity of the robot system converge towards the desired trajectories.

Conclusions

In this paper, a robust control law has been presented to ensure trajectory tracking for electrically driven robotic systems considering both the robot and actuators uncertainties. In the presented method, no statistical information about the uncertain elements is assumed. The proposed robust control law has two advantages over the previous ones. First, the proposed control law results in asymptotic stability while the majority of the robust methods guarantee the boundedness of the tracking error. The second advantage comes from considering both robot and actuators uncertainties. The method is employed to control two different case studies; a two link serial manipulator and a four-bar linkage system. Both numerical and experimental results show the effectiveness of the method in controlling the system.