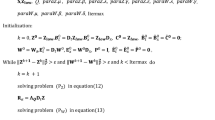Introduction

Seismic wave propagation in strata is actually a filtering process accompanied with amplitude attenuation, phase distortion and frequency reduction (Yang and Zhu 2018). The seismic signals received by geophones are the convolution results of the structure reflectivity and the attenuated wavelet in the time domain. However, owing to the inherent band-limited nature of the source wavelet and the absorption attenuation of the formation pore fluid, the seismic signals become band-limited and lose some essential geologic details. One objective of exploration geophysics is to reveal the subsurface structural features and the physical properties by using broadband seismic signals. Various inversion methods have been successfully used for a long time in broadening seismic bandwidth (e.g., van der Baan and Pham 2008; Gholami 2014; Yuan et al. 2017; Li et al. 2018). The inversion can estimate the broadband reflectivity or impendence from the band-limited seismogram (e.g., Oldenburget al. 1983; Zhang and Castagna 2011) and further bridge the recorded seismic data and the stratigraphic structure. Nevertheless, the traditional unconstrained inversion frequently exposes a serious ill-conditioned problem, that is, multi-solution or non-uniqueness. It is mainly attributed to data uncertainty and inherent flaw of the under-determined inverse problem (e.g., Yang et al. 2018; Yang et al. 2019; Li et al. 2019a). More abundant seismic information, such as sparse assumption of signals, spatial continuity, the intrinsic quality factor (Q) from the reflected seismic data and correlations with other multi-scale geophysical data, is also essential for a unique solution. In the 1960s, Tikhonov regularization method (Tikhonov 1962) was proposed to mitigate the ill-conditioned problem in the unconstrained traditional inversion. The regularization can not only suppress noise and stabilize different inverse problems (e.g., Gholami and Hosseini 2013; Tian et al. 2016; Ma et al. 2019a, b; Li et al. 2019b), but also integrate prior geological information and further excavate the characteristics of seismic signals.

The conventional inversion is mostly an independent single-trace operation which generates a high-resolution data profile or volume through trace-by-trace. Although the trace-by-trace processing is operationally convenient for low computational burden, the inverted results usually suffer from poor spatial continuity and mask some key geologic features in imaging. It is an indisputable fact that the ignored correlation among traces destroys the spatial stability of the inverted reflectivity or impedance (Wang et al. 2013). The single-trace theory holds that the received signals by a geophone are only related to the seismic response at the same location and independent of other traces. Therefore, this technology is intrinsically subjected to spatial low-wavenumber matching and instability. According to the sedimentary rule of strata, the subsurface medium is dominantly determined by the layered structure and the seismic reflected events generally show excellent spatial coherence (Wang et al. 2018). Seismic profile or volume should remain strong spatial continuity and less difference along the structural direction, especially among the adjacent traces. Consequently, these trace-by-trace technologies expose with spatially discontinuous problem while improving the vertical temporal resolution (e.g., Zhang et al. 2013; Yuan et al. 2015).

There has been much recent research (e.g., Kazemi and Sacchi 2014; Pereg et al. 2017; Ji et al. 2019) on the subject of multi-trace inversion for addressing the spatial instability of the trace-by-trace technology (Yuan et al. 2015). Lavielle (1991) proposed a multi-trace inversion method by using the lateral coherence as prior information. By combining with adaptive FX filtering, Wang et al. (2006) developed a structure-preserving sparse inversion method to improve the coherence of multi-trace data. Auken (2005) applied multi-trace lateral constraint to maintain the lateral continuity of resistivity data. Inspired by Auken’s study, Hamid and Pidlisecky (2015, 2016, 2017) used the lateral l2-norm regularization in multi-trace seismic impedance inversion and extended their research to multi-trace structural l2-norm regularization for highlighting richer structural details. Cheng et al. (2018) first designed a series of one inclined-layer reflectivity models with different dips and quantitatively illustrated the structural constraint inversions are superior to the lateral constraint and trace-by-trace inversions.

Although the above-mentioned stationary multi-trace inversion provides spatially continuous reflectivity or impedance, it cannot restore the amplitude attenuation and phase distortion related to earth’s Q-effects. To compensate for Q-attenuation, an alternative to the stationary technology is to employ a nonstationary inversion scheme (van der Baan 2008). As well, the inverse-Q filtering can be applied simultaneously with inversion (nonstationary inversion) (e.g., Margrave et al. 2011; Oliveira and Lupinacci 2013; Chai et al. 2014; Yuan et al. 2017) where the Q-structure is given or estimated as prior information. A kind of semi-blind nonstationary inversion (e.g., Gholami 2015; Aghamiry and Gholami 2017, 2018; Ma et al. 2018) was broadly developed to estimate both Q-models and reflectivity simultaneously in various forms. Gholami (2015) pointed out that the Q-related attenuation diminishes the sparsity of the earth impulse response and hence determined Q-model by optimization (minimization) over the sparsity value of the inverted reflectivity. This makes it possible to estimate the original reflectivity from the attenuated seismic records without prior Q-information.

In summary, the reflectivity inversion aims to extract the reflectivity closest to the original earth impulse response from seismic data as much as possible. The reflectivity should be relatively sparse and spatially continuous when Q- and wavelet-filtering effects are both eliminated. Therefore, we proposed a multi-trace nonstationary inversion, by considering Q-effects and using mixed-norm regularization in this paper. Using the sparse representation function represented as l0.1-norm, a suitable Q-model, as well as the corresponding inverted reflectivity, is simultaneously estimated from attenuated seismic data. The vital superiority of our method can excavate the latent information from seismic data fully and drive the nonstationary inverted result to be sparse and structurally preserved without requiring the prior Q-information.

Theory

Generally, the seismic trace is simulated as the convolution of a seismic wavelet and a reflectivity series (Robinson and Treitel 1980) and equivalently expressed as a matrix–vector product form

$${\mathbf{s}}_{j} = {\mathbf{Wr}}_{j},$$
(1)

where sjand rjare the j-th trace seismic record and reflectivity, respectively,

$${\mathbf{W}} = \left[ {\begin{array}{*{20}c} {w_{1} } & {} & {} & {} \\ {w_{2} } & {w_{1} } & {} & {} \\ \vdots & {w_{2} } & \ddots & {} \\ {w_{L} } & \vdots & \ddots & {w_{1} } \\ {} & {w_{L} } & \ddots & {w_{2} } \\ {} & {} & \ddots & \vdots \\ {} & {} & {} & {w_{L} } \\ \end{array} } \right]$$
(2)

is a Toeplitz matrix for seismic wavelet w = [w1, w2,…,wL]Twhose length is L. We define the length of vectors sj and rj as N, which is commonly larger than L. Thus, the size of the wavelet matrix W is N × N. To further simplify the forward-modeling, the wavelet is provided as a stationary form. Equation (1) illustrates the traditional convolution model in matrix form and can be extended for the multi-trace seismic records as

$${\mathbf{d}} = {\mathbf{Gm}},$$
(3)

in which d = vec(s1, s2,…, sM), m = vec(r1, r2,…, rM), G = kron(I, W), I is an identity matrix, vec means rearranging all vectors sjor rjinto a tall vector in seismic trace order, and kron represents a Kronecker product operator that could reformulate the matrix–matrix multiplication for two any size matrices into a relevant giant matrix. Therefore, the length of vectors d and m is M × N and the size of the matrix G is (M × N) × (M × N). Apparently, G is a huge block diagonal matrix because of the function of identity matrix I.

Supposing that the observed multi-trace seismic data are dobs, the error sum square E between the observed and synthetic seismic data is

$$E = \left\| {{\mathbf{d}}^{{{\text{obs}}}} - {\mathbf{Gm}}} \right\|_{2}^{2},$$
(4)

where ||·||2 denotes the l2-norm of a vector. Direct reflectivity estimation from Eq. (4) will present seriously ill-conditioned. One popular consensus is that the reflectivity is a kind of sparse signal, which maps the underground structure and can be represented by a linear combination of a few eigenvectors. Therefore, the purpose of seismic inversion is to deduce the sparse and structurally related reflectivity or impedance from seismic records. To achieve this goal, a regularization method (Cheng et al. 2018), which combines a temporal lp-norm (0 < p < 1) and a spatial (lateral or structural) l2-norm, is proposed to constrain the data misfit term. The objective function (Eq. (4)) is redefined as

$$O({\mathbf{m}}) = \frac{1}{2}\left\| {{\mathbf{d}}^{obs} - {\mathbf{Gm}}} \right\|_{2}^{2} + \frac{{\lambda_{{1}} }}{2}\left\| {{\mathbf{Cm}}} \right\|_{{2}}^{{2}} { + }\frac{{\lambda_{{2}} }}{p}\left\| {\mathbf{m}} \right\|_{p}^{p},$$
(5)

where λ1 and λ2 are regularization parameters which adjust the proportional weights of data misfit, spatial and sparse constraints, ||·||p denotes the lp-norm (0 < p < 1) of a vector. Matrix C is a spatial (lateral, vertical or structural) smooth filter, which not only improves the spatial matching degree among traces, but also may weaken or directly destroy data misfit, spatial matching and sparsity if neglected or inaccurate. Generally speaking, the temporal lp-norm (0 < p < 1) and structural l2-norm regularizations force the inversion to approach a temporally sparse and structurally smooth solution. By calculating the first-order vertical and lateral matrices of dataset, the formation dipping-angle matrix θ can be extracted as

$${{\varvec{\uptheta}}} = arctan{\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {{{{\mathbf{C}}_{x} {\mathbf{d}}^{obs} .} \mathord{\left/ {\vphantom {{{\mathbf{C}}_{x} {\mathbf{d}}^{obs} .} {{\mathbf{C}}_{z} {\mathbf{d}}^{obs} }}} \right. \kern-\nulldelimiterspace} {{\mathbf{C}}_{z} {\mathbf{d}}^{obs} }}} \right),$$
(6)

where Cx(Cz) represents the first-order lateral (vertical) difference matrix which can act as a lateral or vertical filter in Eq. (5), arctan is the arctangent symbol, and the symbol “./” represents the element-wise division. Equation (6) is essentially a gradient method for dipping-angle estimation from seismic data. In this paper, when considering matrix C as a structural filter, we calculate the structural difference operator matrix Cparl as

$${\mathbf{C}}_{{{\text{parl}}}} = {\mathbf{Q}}_{{\cos}} {\mathbf{C}}_{x} + {\mathbf{Q}}_{{\sin}} {\mathbf{C}}_{z},$$
(7)

where Qcos (Qsin) is a matrix each element of which is a cosine(sine) value of the dipping angle of the corresponding position of matrix θ. However, the inversion based on Eq. (5) mainly focuses on the stationary case which ignores the inherent nonstationary characteristics of seismic signals. To solve the nonstationary problem, the quality factor (Q) associated with attenuation is typically incorporated into seismic wavelet to keep it time-varying. Depending on 1D acoustic theory and frequency-independence constant Q-model, the traditional nonstationary forward model (e.g., Bickel and Natarajan 1985; Margrave et al. 2011; van der Baan 2012) is modified from the traditional form (Eq. (3)) and written as

$${\mathbf{d}} = {\mathbf{G}}\left( Q \right){\mathbf{m}},$$
(8)

where Q represents the equivalent quality factor (Q). Because of the Q-attenuation, G(Q) is no longer stationary, but accompanies with amplitude attenuation, phase distortion and frequency reduction. The larger is the Q-value, the smaller the corresponding seismic attenuation will be. Obviously, when Q approaches infinity, that is, the attenuation tends to zero. Meanwhile, Eq. (8) will degenerate into the traditional stationary convolution model for infinity Q-value. Based on Eq. (5), we combined quality factor (Q) and proposed a nonstationary inversion scheme as following

$$O({\mathbf{m}}) = \frac{1}{2}\left\| {{\mathbf{d}}^{obs} - {\mathbf{G}}(Q){\mathbf{m}}} \right\|_{2}^{2} + \frac{{\lambda_{{1}} }}{2}\left\| {{\mathbf{Cm}}} \right\|_{{2}}^{{2}} { + }\frac{{\lambda_{{2}} }}{p}\left\| {\mathbf{m}} \right\|_{p}^{p}.$$
(9)

In image restoration, it has been shown that the image gradients of the natural image can be better modeled with 0.5 ≤ p ≤ 0.8 (Krishnan and Fergus 2009; Zuo et al. 2013). Referring to the p-selection in image restoration, we control p-value between 0.5 and 0.8 in Eq. (9), such as 0.7, for all synthetic and field examples in this paper. Minimization of Eq. (9) aims to eliminate the wavelet- and Q-filtering effect simultaneously, and to seek an adequate sparse and spatially correlated solution which is more satisfied with the geological characteristics. Unfortunately, directly minimizing Eq. (9) is severely ill-posed and computationally infeasible while the reflectivity and attenuation mechanism, especially, Q-model are both uncertain. If the attenuation mechanism and the source wavelet are known or estimated, we can extract the reflectivity by minimizing Eq. (9) as

$${\mathbf{m}} = \left[ {{\mathbf{G}}(Q)^{T} {\mathbf{G}}(Q) + \lambda_{{1}} {\mathbf{C}}^{T} {\mathbf{C}} + \lambda_{{2}} {\mathbf{U}}} \right]^{ - 1} {\mathbf{G}}^{T} {\mathbf{d}}^{obs},$$
(10)

where T is the transpose of a matrix, U = Diag (|mi|p−2), Diag is the symbol of the diagonal matrix. In general, the repeated weighted iterative algorithm (Chartrand and Yin 2008) can solve Eq. (10) for the optimal m. Assuming that mk−1 is the (k − 1)th iterative result, the repeated weighted matrix Uk−1 for the next (kth) iteration is defined as

$${\mathbf{U}}^{k - 1} = {\text{Diag}}\left( {\left| {m_{i}^{k - 1} } \right|^{p - 2} } \right),$$
(11)

Thus, Eq. (10) is rewritten again as

$${\mathbf{m}}^{k} = \left[ {{\mathbf{G}}(Q)^{T} {\mathbf{G}}(Q) + \lambda_{{1}} {\mathbf{C}}^{T} {\mathbf{C}} + \lambda_{{2}} {\mathbf{U}}^{k - 1} } \right]^{ - 1} {\mathbf{G}}^{T} {\mathbf{d}}^{obs},$$
(12)

where Uk−1(k ≥ 1) is essentially the weight of each iteration. Set the initial iterative reflectivity model m0 and the maximum iterative number kmax. The iteration process starts from k = 1 until the maximum iteration number kmax is reached. Note that when k = 1, the corresponding U0 represents the initial repeated weighted matrix for the iteration and could be constructed by m0. For nonstationary sparse inversion, Gholami (2015) pointed out that once the Q-model is determined to be infinitely approximated to the true Q-structure, the corresponding inverted result will remain relatively sparse. This makes it possible to estimate Q-model and reflectivity simultaneously. Without prior Q-information, a scanning-Q strategy (e.g., Gholami 2015; Aghamiry and Gholami 2017, 2018; Ma et al. 2018) was proposed for Q- and reflectivity-estimation by using nonstationary sparse inversion. In this paper, we set the scanning-Q range as [Qmin ≤ Q1, Q2, …, Qn ≤ Qmax] for Eq. (9), and the corresponding attenuated wavelet matrix and inverted reflectivity are [G(Q1), G(Q2),…,G(Qn)] and [m(Q1), m(Q2),…,m(Qn)]. Based on the sparse assumption of the reflectivity, a sparse l0.1-norm function

$$l_{0.1} \left( {\mathbf{m}} \right) = \left\| {\mathbf{m}} \right\|_{0.1},$$
(13)

is ordinarily used to measure the sparsity of the inverted reflectivity corresponding each scanned Q. By using Eq. (13), we can obtain the sparsest inverted reflectivity (the maximum sparsity or the minimum l0.1-norm value) and the corresponding Q-model. Compared with previous studies, our proposed method combines sparse constraint, structural constraint and Q-attenuation effect. By using scanning-Q inversion strategy, we can estimate Q, as well as the corresponding inverted reflectivity with Q-compensation and structural preservation.

Examples

In this section, the synthetic attenuated and field examples are presented to illustrate the accuracy, structure-preservation, Q-estimation and Q-compensation capability of the proposed multi-trace nonstationary inversion. We also compare the influence of structural regularization, lateral regularization and without structural and lateral regularization (that is, only sparse constraint) for Q-estimation and sparse inversion. Moreover, the initial model m0 = GTdobs and the maximum iteration number of 10 are used for the repeated weighted iterative algorithm.

Synthetic attenuated data example

To compare and analyze the effectiveness of the proposed multi-trace nonstationary sparse inversion with structural constraint, we design a reflectivity model shown in Fig. 1a. The size of this model is 401(traces) × 186(sampling points) with a 2 ms sampling interval. The initial (source) wavelet is Ricker wavelet with a 30 Hz main frequency, 61 sampling points and a 2 ms sampling interval. We set an equivalent-Q as 30 to construct attenuated wavelet matrix and then synthesize attenuated data. The noisy attenuated seismic data (Fig. 1b) are generated by dividing the clean attenuated seismic profile into five sub-profiles with time ranges of 0–92 ms, 94–184 ms, 186–276 ms and 278–370 ms, respectively, and adding 5% random noise (i.e., noise energy to signal energy of each seismic sub-profile is 5%) to each divided sub-profile separately. Figure 1c shows the stationary inverted reflectivity from noisy synthetic attenuated data with the temporal lp-norm (0 < p < 1) and structural l2-norm constraints. Obviously, the energies of the bottom reflection events are extremely weak for ignoring Q-compensation when inverting. To further explore the Q-compensation and structural constraint on nonstationary sparse inversion, we design three nonstationary inversion cases with the temporal lp-norm (0 < p < 1) constraint (i.e., C = 0 in Eq. (9) which degenerates to trace-by-trace inversion), the lateral l2-norm (C = Cx in Eq. (9)) and temporal lp-norm (0 < p < 1) constraints, and the structural l2-norm (C = Cparl in Eq. (9)) and temporal lp-norm(0 < p < 1) constraints, respectively, and mark them as case 1, case 2 and case 3 for distinguishing. Moreover, we set p = 0.7, and the scanning-Q range to be 10 to 100 with an interval of 5. Regularization parameters λ1 and λ2 are used to control the weights between spatial (lateral or structural) and sparse constraint. When choosing regularization parameters for inversion, we should consider computational efficiency. Firstly, we set spatial regularization parameter λ1 = 0 and try to test several sparse constraint parameter λ2, such as 0.5, 0.05, 0.005 and 0.0005. By comparing the sparsity of inverted profiles and l0.1-norm curves of inverted reflectivity corresponding to each scanned equivalent-Q, we determine an appropriate λ2 = 0.005 when the l0.1-norm curve appears a stable concave (minimum) point. Secondly, fix the determined sparse regularization parameter λ2 = 0.005 and try to test several λ1, such as 0.5, 0.05, 0.005 and 0.0005. By comparing the sparsity of inverted profiles and l0.1-norm curves of inverted reflectivity corresponding to each scanned equivalent-Q, the corresponding λ1 both represented as a lateral or structural regularization parameter is determined as 0.05 when the l0.1-norm curve shows a stable concave (minimum) point. The regularization parameters selected in the above way can not only ensure the sparsity and the spatial correlation of inverted reflectivity, but also help to estimate a stable equivalent-Q from the attenuated seismic data. In particular, when only considering the temporal lp-norm (0 < p < 1) regularization, the spatial regularization parameter λ1 is assigned as 0. After successfully setting the relevant parameters, Eq. (9) can be solved by repeated weighted iteration for eliminating the wavelet- and Q-filtering effect step-by-step. We use an l0.1-norm to measure the sparsity of inverted result corresponding to different scanned Q and determine the optimal Q and the corresponding inverted reflectivity by minimization over these sparsity values.

Fig. 1
figure 1

The synthetic attenuated data and the inverted results: a the true reflectivity, b the noisy synthetic attenuated data convoluted by the attenuated wavelet and the true reflectivity and added 5% random noise, c the stationary inverted reflectivity constrained by the structural l2-norm and the temporal lp-norm (0 < p < 1), d case 1: the l0.1-norm curve with an optimal equivalent Q = 25, e case 1: the nonstationary inverted reflectivity corresponding to the optimal Q = 25, f case 1: the inverse-Q filtering result convoluted by the inverted reflectivity (e) and the initial wavelet, g case 2: the l0.1-norm curve with an optimal equivalent Q = 35, h case 2: the nonstationary inverted reflectivity corresponding to the optimal Q = 35, i case 2: the inverse-Q filtering result convoluted by the inverted reflectivity (h) and the initial wavelet, j case 3: the l0.1-norm curve with an optimal equivalent Q = 30, k case 3: the nonstationary inverted reflectivity corresponding to the optimal Q = 30, l case 3: the inverse-Q filtering result convoluted by the inverted reflectivity (k) and the initial wavelet, m the nonstationary inverted reflectivity constrained by the temporal lp-norm (0 < p < 1) with a correct equivalent Q = 30, n the nonstationary inverted reflectivity constrained by the lateral l2-norm and the temporal lp-norm (0 < p < 1) with a correct equivalent Q = 30. Case 1, case 2 and case 3 represent inversion constrained by the temporal lp-norm (0 < p < 1), the lateral l2-norm and temporal lp-norm (0 < p < 1) and the structural l2-norm and temporal lp-norm (0 < p < 1), respectively

Full size image

For the noisy attenuated synthetic data, these three kinds of nonstationary sparse inversion methods are used for simultaneous Q- and reflectivity-estimation. The l0.1-norm curves (Fig. 1d, g, j) for the three cases all present strong concavity, and the corresponding Q-values of concave or minimum points are 25, 35 and 30, respectively. The equivalent-Q estimated by the l0.1-norm curve is comparatively stable and less different from the correct value 30. We pick the Q-values at the concave (minimum) points of l0.1-norm curves and the corresponding inverted reflectivity as the final estimated (inverted) results. Here, one notable problem is that the shapes of bottom reflection events (the positions indicated by the red arrows) on all inverted profiles are not well recognized and recovered because of the strong interferences among these thin layers of the bottom. Compared with the conventional stationary inverted result (Fig. 1c), the nonstationary inversion (Fig. 1e, h. k) can adequately compensate for Q-attenuation. If the lateral and structural l2-norm constraints are both ignored, the nonstationary inversion will only obtain a poor spatial continuity and low signal-to-noise ratio result (as shown in Fig. 1e) from synthetic seismic data. When the lateral l2-norm is used as a spatial regularization, the nonstationary sparse inverted result (as shown in Fig. 1h) has been significantly improved inthe lateral continuity and the signal-to-noise ratio. The red dashed rectangles in Fig. 1h indicate that the lateral constraint is still difficult to remain the continuity in complex structures. However, the continuity of complex or large dipping-angle structures can be effectively recovered (the red dashed rectangles shown in Fig. 1k) when the nonstationary inversion is with the structural l2-norm and the temporal lp-norm (0 < p < 1) constraints (i.e., our proposed method). Constrained by the structural l2-norm and the temporal lp-norm (0 < p < 1), the stationary (shown in Fig. 1c) and nonstationary (shown in Fig. 1k) inverted results are both structurally continuous and temporally sparse. However, due to Q-related compensation, the energy of the inverted reflectivity in Fig. 1k becomes stronger than that in Fig. 1c, especially in the deep. For further Q-compensation exploration, the inverse-Q filtering results are convoluted by the initial (source) wavelet and the nonstationary inverted reflectivity for the three cases and shown in Fig. 1f, i, l. Compared with the original attenuated data, the proposed method dramatically recovers the lost energy for Q-attenuation, especially with enormous potential to compensate for deep reflection energy. The processing of synthetic attenuated data presents that our proposed method can not only estimate accurate equivalent Q-model, but also invert a structurally continuous and temporally sparse reflectivity profile with Q-compensation.

Through l0.1-norm sparse representation function expressed in Eq. (13), our method case 3 estimates a more accurate equivalent-Q value of 30 than case 1 (estimated equivalent-Q = 25) and case 2 (estimated equivalent-Q = 35). To explore the influence of the slight deviation of Q on the inversion, we provide another two inverted profiles (Fig. 1m, n) with the correct equivalent-Q value of 30, which are generated from the attenuated seismic data of Fig. 1b with the lp-norm (0 < p < 1) constraint and the structural l2- and lp-norm (0 < p < 1) constraints, respectively. Figure 1m shows the inverted reflectivity constrained by the lp-norm (0 < p < 1) when equivalent-Q is 30. The inverted profile is sufficiently compensated for the Q-attenuation (especially at the deep), but with poor spatial continuity. Figure 1n is the inverted profile with the structural l2- and lp-norm (0 < p < 1) constraints when equivalent-Q is 30. It is obviously observed that the inverted profile (Fig. 1n) is not only adequately compensated for Q-attenuation (especially the deep reflection), but also more laterally continuous than that in Fig. 1m. However, the red dotted rectangles in Fig. 1n show that lateral constraint do not ensure the restoration of structural continuity. By comparing Fig. 1e, m or Fig. 1h, n, it is interesting to note that Q-model with slight deviation will not destroy the quality of nonstationary inverted results. Therefore, the estimated equivalent-Q values of 25, 30 or 35 are reasonable for the nonstationary inversion here.

Field data example

After the successful application in synthetic attenuated example, the proposed method is expanded to 2D field seismic data for Q- and reflectivity-estimation. The size of the field data is 201 (traces) × 201 (sampling points) with a 2 ms-sampling interval. The first vertical (temporal) 50 points of seismic data (the red rectangle shown in Fig. 2a) are extracted to estimate the initial (source) Ricker wavelet. According to the spectrum analysis, the main frequency of these window data is determined to be approximately 36 Hz (shown in Fig. 2b).We assign the initial Ricker wavelet with the same main frequency of 36 Hz as these window data, 81 sampling points and a 2-mssampling interval. We set p = 0.7, and the scanning-Q range to be 20–100 with an interval of 5 in Eq. (9). Referring to the selection strategy of regularization parameters in the synthetic example, we decide λ1 = 0.005 and λ2 = 0.005. Through the above way, three parameters, p, λ1 andλ2, are determined for inversion. Obviously, the more stable the concave point of l0.1-norm curve is, the stronger the robustness of the combination of p, λ1 and λ2 is. Here, we still compare three nonstationary inversion cases with the temporal lp-norm (0 < p < 1) constraint (C = 0 in Eq. (9)), the lateral l2-norm (C = Cx in Eq. (9)) and temporal lp-norm(0 < p < 1) constraints, and the structural l2-norm (C = Cparl in Eq. (9)) and temporal lp-norm (0 < p < 1) constraints, respectively, and mark them as case 1, case 2 and case 3 for distinguishing.

Fig. 2
figure 2

The field seismic data and the inverted results: a the field seismic data, b the amplitude spectrum of the window seismic data in a, c the stationary inverted reflectivity constrained by the temporal lp-norm (0 < p < 1) and the structural l2-norm, d case 1: the l0.1-norm curve with an optimal equivalent Q = 40, e case 1: the nonstationary inverted reflectivity corresponding to the optimal Q = 40, f case 1: the inverse-Q filtering result convoluted by the inverted reflectivity (e) and the initial wavelet, g case 2: the l0.1-norm curve with an optimal equivalent Q = 45, h case 2: the nonstationary inverted reflectivity corresponding to the optimal Q = 45, i case 2: the inverse-Q filtering result convoluted by the inverted reflectivity (h) and the initial wavelet, j case 3: the l0.1-norm curve with an optimal equivalent Q = 45, k case 3: the nonstationary inverted reflectivity corresponding to the optimal Q = 45, l case 3: the inverse-Q filtering result convoluted by the inverted reflectivity (k) and the initial wavelet. Case 1, case 2 and case 3 represent nonstationary inversion with the temporal lp-norm (0 < p < 1) constraint, the lateral l2-norm and temporal lp-norm (0 < p < 1) constraints, and the structural l2-norm and temporal lp-norm (0 < p < 1) constraints, respectively

Full size image

By optimizing the l0.1-norm of the inverted results corresponding to different scanned Q values (shown in Fig. 2d, g, j), we can estimate the equivalent-Q values to be 40, 45 and 45 for case 1, case 2 and case 3, respectively. The final inverse-Q filtering results (Fig. 2f, i, l) are obtained by convolution of the initial (source) wavelet and the nonstationary inverted reflectivity (Fig. 2e, h, k). Compared with the original profile of Fig. 2a, all three kinds of nonstationary processing greatly enhance the seismic energy after Q-compensation (shown in Fig. 2f, i, l). However, when omitted the lateral and structural l2-norm constraints, the inverted reflectivity and the subsequent inverse-Q filtering profiles are subjected to spatial instability which appear as the noodle-like trails among traces (shown in Fig. 2e, f). Compared with case 1, the lateral l2-norm constraint is powerfully helpful in improving the spatial correlation of inverted result (Fig. 2h), especially the lateral continuity. However, for the relatively complex structures, such as the areas marked by red circles in Fig. 2h, the lateral constraint hardly provides an accurate characterization along these complex or large dipping-angle structures. When the lateral l2-norm constraint is replaced by the structural l2-norm constraint in the nonstationary sparse inversion, the structural details are better recovered and more following geological sedimentary rule than that of case 1 and case 2 (pointed out by the red circles in Fig. 2k). It is mainly rooted in the role of the structural l2-norm constraint on the structure preservation and the good wavenumber matching among different traces. Constrained by the temporal lp-norm (0 < p < 1) and the structural l2-norm, the stationary (Fig. 2c) and nonstationary (Fig. 2k) inverted reflectivity profiles are both temporally sparse and structurally continuous. Related Q-estimation and compensation, the energy of Fig. 2k is stronger than that of Fig. 2c. Moreover, due to the smooth filtering of the lateral and structural l2-norm in the objective function, the inverted reflectivity profiles of Fig. 2h, k remain highly laterally and structurally continuous, but are visually less sparse than that of in Fig. 2e, especially in red dashed circles. Although accompanied with an acceptable reduction in sparsity, the proposed method improves the seismic energy by Q-estimation and compensation and fulfills the purpose of structure preservation.

For the field example, the initial Ricker wavelet is estimated by a window data extracted from the top of attenuated seismic data. To further explore the influence of the window on the final inverted result, seismic data with different window lengths are used to estimate the initial Ricker wavelet for inversion. Here, we consider the temporal lp-norm (0 < p < 1) and structural l2-norm constraints for the nonstationary inversion. Table 1 shows the window length and the corresponding main frequency of the initial Ricker wavelet estimated from these window data. Along with the increase in window length, the main frequency of the estimated Ricker initial wavelet rapidly becomes lower because of the cumulative Q-attenuation amount growth. Using the scanning-Q inversion strategy, the estimated equivalent-Q of the whole seismic profile are 45, 50 and 55 when provided the initial Ricker wavelet with a 36 Hz, 33 Hz and 31 Hz main frequency, respectively. Evidently, the difference between the initial Ricker wavelets results in the estimated-Q variation. Figure 3 shows the inverted reflectivity profiles with different initial Ricker wavelet and corresponding estimated-Q. By comparison, the nonstationary inversion with different initial Ricker wavelet and Q-model bring the Q-compensation and structure-preservation distinctions, especially in the red rectangular areas. Although the window extracted from the top of attenuated seismic data will affect initial Ricker wavelet estimation and further Q-estimation, the comprehensive effect of different initial Ricker wavelets and corresponding estimated-Q always ensures that the nonstationary inverted results are not significantly different.

Table 1 Variation of the extracted initial wavelet with the window length extracted from the top of the attenuated seismic data
Full size table
Fig. 3
figure 3

The nonstationary inverted reflectivity with the initial wavelet and corresponding estimated-Q in Table 1: a the nonstationary inverted reflectivity with the structural l2-norm and temporal lp-norm (0 < p < 1) constraints when the main frequency of the initial Ricker wavelet is 36 and estimated equivalent-Q is 45, b the nonstationary inverted reflectivity with the structural l2-norm and temporal lp-norm (0 < p < 1) constraints when the main frequency of the initial Ricker wavelet is 33 and estimated equivalent-Q is 50, c the nonstationary inverted reflectivity with the structural l2-norm and temporal lp-norm (0 < p < 1) constraints when the main frequency of the initial Ricker wavelet is 31and estimated equivalent-Q is 55

Full size image

Conclusion

By comprehensively considering the inherent attenuation characteristics and multi-trace spatially structural correlation of seismic data, we proposed a multi-trace nonstationary inversion which is constrained by a structural geosteering l2-norm and a temporal lp-norm (0 < p < 1) in this paper. Due to the attenuation mechanism or Q-model, seismic wavelet is not stationary, but a time-varying signal with amplitude attenuation and phase distortion in this technique. A sparse l0.1-norm is provided to quantify the sparsity of the multi-trace reflectivity obtained by scanning-Q strategy, and to find the optimal equivalent-Q and the corresponding nonstationary inverted reflectivity further. Tested by the synthetic attenuated and field examples, the proposed method is capable of simultaneously estimating a stable equivalent-Q model and a structurally continuous and temporally sparse reflectivity with sufficient Q-compensation. Impressively, the complex structures probably, especially for pinch-outs, faults, folds and cleavages, present higher-quality spatial imaging, which is mainly attributed to the structural l2-norm constraint. Thus, the developed technique can be used not only for nonstationary sparse inversion and structural preservation, but also a resolution enhancement tool with the estimated Q-model for compensation.