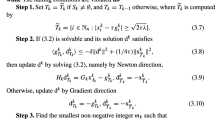Regularized quasi-monotone method for stochastic optimization

Abstract

We adapt the quasi-monotone method, an algorithm characterized by uniquely having convergence quality guarantees for the last iterate, for composite convex minimization in the stochastic setting. For the proposed numerical scheme we derive the optimal convergence rate of $\text{ O }\left( \frac{1}{\sqrt{k+1}}\right)$ in terms of the last iterate, rather than on average as it is standard for subgradient methods. The theoretical guarantee for individual convergence of the regularized quasi-monotone method is confirmed by numerical experiments on $\ell _1$-regularized robust linear regression.

1 Introduction

In the minimization of nonsmooth convex functions, typically, algorithms generate a sequence of iterates using subgradients or estimates thereof. The convergence rates are then derived for some linear combination of the iterates, rather than for the last estimate computed. Obtaining guarantees on the last iterate per se is often a challenging task. A significant contribution in that direction – sometimes also refered to as individual convergence – was given in [5] with the quasi-monotone subgradient method. The corresponding analysis was simplified and extended to solving minimization problems on decentralized networks in [4]. In this paper we extend the work of [5] in two important directions, first we consider a composite minimization problem with a simple additive function (usually a regularizer), and second we consider the stochastic case. We develop the Lyapunov-like analysis from [4] to handle the new elements and present numerical experiments confirming the performance guarantees. We obtain the convergence rate of order $\text{ O }\left( \frac{1}{\sqrt{k+1}}\right)$ in expectation of function evaluations, which is optimal for nonsmooth convex optimization.

Let us briefly comment on the related literature. In [6] the authors introduce an adaptation of mirror descent in order to attain the optimal individual convergence. They successively apply the latter for regularized nonsmooth learning problems in the stochastic setting. As shown in [7], the Nesterov’s acceleration alternatively provides the individual convergence of projected subgradient methods as applied to nonsmooth convex optimization. Especially, the suggested methodology guarantees the regularization structure while keeping an optimal rate of convergence. Our contribution to individual convergence consists in theoretically justifying that also the initially proposed quasi-monotone subgradient method from [5] can be successively adjusted for composite minimization in the stochastic setting. We note that the setting we consider is distinct from the specialized algorithms that also adapt mirror descent for the important case wherein there are separable linear constraints, e.g., the classical [3] or more recent alternating minimization [2] and proximal point based method [1], but extending to this setting could be an interesting topic to pursue for future work.

2 Regularized quasi-monotone method

We consider the composite minimization problem

$$\begin{aligned} \min _{x} F(x)={\bar{f}}(x)+g(x), \end{aligned}$$

(1)

where ${\bar{f}}, g: {\mathbb {R}}^n \rightarrow {\mathbb {R}} \cup \{+\infty \}$ are closed convex functions. Moreover,

$$\begin{aligned} {\bar{f}}(x)={\mathbb {E}}\left[ f(x,\xi )\right] \end{aligned}$$

for some f closed and convex in the first argument and $\xi$ is a sample from some random space $\varXi$. We assume that $\text{ dom }(f(\cdot ,\xi )) \subset \text{ dom }(g)$ for a.e. $\xi$, and $\text{ dom }(g)$ is closed. Usually, ${\bar{f}}$ plays the role of a loss function, whereas g is used for regularization. In our setting, f need not to be differentiable, but unbiased finite variance estimates of its subgradients, i.e. $w(x,\xi )\sim \nabla f(x,\cdot )$ with ${\mathbb {E}}\left[ w(x,\xi )\right] \in \partial {{\bar{f}}}(x)$, should be available. Here, we use $\nabla {{\bar{f}}}(x)$ to denote an element of the convex subdifferential $\partial {{\bar{f}}}(x)=\partial {\mathbb {E}}[f(x,\xi )]$, i.e.

$$\begin{aligned} {\bar{f}}(y) \ge {\bar{f}}(x) + \langle \nabla {{\bar{f}}}(x), y - x\rangle , \quad y \in \text{ dom }(g). \end{aligned}$$

(2)

In addition, g has to be simple. The latter means that we are able to find a closed-form solution for minimizing the sum of g with some simple auxiliary functions. For that, we assume that for the effective domain of g there exists a prox-function $\varPsi :{\mathbb {R}}^n \rightarrow {\mathbb {R}} \cup \{+\infty \}$ w.r.t. an arbitrary but fixed norm $\Vert \cdot \Vert$. The prox-function $\varPsi$ has to fulfil:

• (i) $\varPsi (x) \ge 0$ for all $x \in \text{ dom }(g)$.

• (ii) $\varPsi$ is strongly convex on $\text{ dom }(g)$ with convexity parameter $\beta >0$, i.e. for all $x,y \in \text{ dom }(g)$ and $\alpha \in [0,1]$ it holds:

  $$\begin{aligned} \varPsi \big (\alpha x + (1-\alpha )y\big ) \le \alpha \varPsi (x) + (1-\alpha ) \varPsi (y) - \frac{\beta }{2} \alpha (1-\alpha ) \Vert x-y\Vert ^2. \end{aligned}$$

• (iii) The auxiliary minimization problem

  $$\begin{aligned} \min _{x} \left\{ \langle s,x\rangle + g(x) + \gamma \varPsi (x)\right\} \end{aligned}$$

  is easily solvable for $s \in {\mathbb {R}}^n$ and $\gamma > 0$.

In our analysis, we consider that g is strongly convex with convexity parameter $\sigma \ge 0$ w.r.t. the norm $\Vert \cdot \Vert$. Note that $\sigma =0$ corresponds to the mere convexity of g.

For stating our method, we choose a sequence of positive parameters $(a_k)_{k \ge 0}$, which is used to average the subdifferential information of f. We set:

$$\begin{aligned} A_k = \sum _{\ell =0}^{k} a_\ell . \end{aligned}$$

Equivalently, it holds:

$$\begin{aligned} A_{k+1}=A_k+a_{k+1}. \end{aligned}$$

(3)

Another sequence of positive parameters $(\gamma _k)_{k \ge 0}$ controls the impact of the prox-function $\varPsi$. We assume:

$$\begin{aligned} \gamma _{k+1} \ge \gamma _k, \quad k \ge 0. \end{aligned}$$

(4)

Now, we are ready to formulate the regularized quasi-monotone method for solving the composite minimization problem (1):

Regularized Quasi-Monotone Method (RQM)
0. Initialize $\displaystyle x_{0} = \text{ arg } \min _{x} \left\{ A_{0} g(x) + \gamma _{0}\varPsi (x)\right\}$, $s_{-1}=0$.
1. Sample $\xi _k\sim \varXi$.
2. Compute $w\left( x_k,\xi _k\right)$ and set $\displaystyle s_{k}=s_{k-1} + a_{k} w\left( x_k,\xi _k\right)$.
3. Forecast $\displaystyle x^+_{k} = \text{ arg } \min _{x} \left\{ \left\langle s_{k}, x \right\rangle + A_{k+1} g(x) + \gamma _{k+1}\varPsi (x)\right\}$.
4. Update $\displaystyle x_{k+1} = \frac{A_{k}}{A_{k+1}} x_k + \frac{a_{k+1}}{A_{k+1}} x^+_{k}$.

It is clear that iterates of (RQM) are convex combinations of forecasts:

$$\begin{aligned} x_{k} = \frac{1}{A_k} \left( a_0 x_0 + \sum _{\ell =1}^{k} a_{\ell } x^+_{\ell -1} \right) . \end{aligned}$$

(5)

In order to achieve convergence rates for RQM, the control parameters $\left( a_k\right) _{k\ge 0}$ and $\left( \gamma _k\right) _{k\ge 0}$ should be properly specified. How to do this, will be clear from our convergence analysis in the next section, cf. possible choices in (18), (21) and (22) below.

3 Convergence analysis

Before performing the convergence analysis of (RQM), let us deduce some useful properties of the following auxiliary function:

$$\begin{aligned} \varphi _{k}(s) = \max _{x\in {\mathbb {R}}^n} \left\{ \left\langle s, x \right\rangle - A_{k} g(x) - \gamma _{k}\varPsi (x)\right\} , \quad s \in {\mathbb {R}}^n. \end{aligned}$$

(6)

Since $A_{k} g + \gamma _{k}\varPsi$ is strongly convex with convexity parameter

$$\begin{aligned} \mu _{k} = A_{k} \sigma + \gamma _{k} \beta , \end{aligned}$$

(7)

the convex function $\varphi _{k}$ is differentiable and its gradient $\nabla \varphi _k$ is $\frac{1}{\mu _{k}}$-Lipschitz continuous. The latter property means:

$$\begin{aligned} \varphi _{k}(s') \le \varphi _{k}(s) + \langle \nabla \varphi _{k}(s), s'-s \rangle + \frac{1}{2 \mu _{k}} \Vert s'-s\Vert _*^2, \quad s,s' \in {\mathbb {R}}^n. \end{aligned}$$

(8)

Moreover, it holds:

$$\begin{aligned} \nabla \varphi _{k}(-s_{k-1}) = x_{k-1}^+. \end{aligned}$$

(9)

Let us derive the convergence rate of (RQM). For that, we set:

$$\begin{aligned} B_k = \frac{1}{2} \sum _{\ell =0}^{k} \frac{a_\ell ^2}{\mu _{\ell }} {\mathbb {E}}\left\| w(x_\ell ,\xi _{\ell })\right\| _*^2, \quad k\ge 0, \end{aligned}$$

(10)

where $\Vert \cdot \Vert _*$ denotes the dual norm of $\Vert \cdot \Vert$. We shall denote, as standard, the filtration $\sigma$-algebra corresponding to the sequence of iterates as $\{\mathcal {F}_k\}$.

Theorem 1

Let $x_* \in \text{ dom }(g)$ solve the composite optimization problem (1), and the sequence $\left( x_k\right) _{k\ge 0}$ be generated by (RQM). Then, it holds for $k \ge 0$ that:

$$\begin{aligned} {\mathbb {E}}\left[ F(x_k)\right] - F(x_*) \le \displaystyle \frac{\gamma _{k}}{A_k}\varPsi (x_*) + \frac{B_k}{A_k}. \end{aligned}$$

(11)

Proof

Let us define the stochastic Lyapunov function:

$$\begin{aligned} \begin{array}{rcl} V_k= & {} A_k \left( F(x_k) - F(x_*)\right) \displaystyle + \varphi _{k}(-s_k) + \langle s_k, x_*\rangle + A_k g(x_*) - B_k. \end{array} \end{aligned}$$

We consider the expected difference:

$$\begin{aligned} \begin{array}{rcl} {\mathbb {E}}\left[ V_{k+1}|\mathcal {F}_k\right] - V_{k} &{} = &{} \underbrace{A_{k+1}\left( {\mathbb {E}}\left[ F(x_{k+1})|\mathcal {F}_k\right] - F(x_*)\right) - A_k \left( F(x_k) - F(x_*)\right) }_{\text{=I }} \\ \\ &{} &{} + \underbrace{{\mathbb {E}}\left[ \varphi _{k+1}(-s_{k+1})|\mathcal {F}_k\right] - \varphi _{k}(-s_k)}_{\text{=II }} \\ \\ &{} &{} + \underbrace{{\mathbb {E}}\left[ \langle s_{k+1}, x_*\rangle |\mathcal {F}_k\right] + A_{k+1} g(x_*) - \langle s_k, x_*\rangle - A_k g(x_*)}_{\text{=III }} \\ \\ &{} &{} \displaystyle \underbrace{-{\mathbb {E}}\left[ B_{k+1}|\mathcal {F}_k\right] + B_k}_{\text{=IV }}. \end{array} \end{aligned}$$

Let us estimate the expressions I-IV from above.

Estimation of I We split:

$$\begin{aligned} \begin{array}{rcl} \text{ I } &{} = &{} \underbrace{A_{k+1}\left( {\mathbb {E}}\left[ {\mathbb {E}}\left[ f(x_{k+1},\xi )\right] |\mathcal {F}_k\right] - {\mathbb {E}}\left[ f(x_*,\xi )\right] \right) - A_k \left( {\mathbb {E}}\left[ f(x_k,\xi )\right] - {\mathbb {E}}\left[ f(x_*,\xi )\right] \right) }_{=\text{ I}_f} \\ \\ &{}&{} +\underbrace{A_{k+1}\left( {\mathbb {E}}\left[ g(x_{k+1})|\mathcal {F}_k\right] - g(x_*)\right) - A_k \left( g(x_k) - g(x_*)\right) }_{=\text{ I}_g}. \end{array} \end{aligned}$$

Due to convexity of f, the definitions of $A_{k}$ and $x_{k}$, we obtain:

$$\begin{aligned} \begin{array}{rcl} \text{ I}_f &{} \overset{(3)}{=} &{} a_{k+1} \left( {\mathbb {E}}\left[ {\mathbb {E}}\left[ f(x_{k+1},\xi )\right] |\mathcal {F}_k\right] - {\mathbb {E}}\left[ f(x_*,\xi )\right] \right) \\ \\ &{}&{}+ A_k \left( {\mathbb {E}}\left[ {\mathbb {E}}\left[ f(x_{k+1},\xi )\right] |\mathcal {F}_k\right] - {\mathbb {E}}\left[ f(x_k,\xi )\right] \right) \\ \\ &{} \overset{(2)}{\le } &{} a_{k+1} {\mathbb {E}}\left[ \left\langle \nabla {{\bar{f}}}(x_{k+1}), x_{k+1} - x_*\right\rangle |\mathcal {F}_k\right] + A_k {\mathbb {E}}\left[ \left\langle \nabla {{\bar{f}}}(x_{k+1}), x_{k+1} - x_k\right\rangle |\mathcal {F}_k\right] \\ \\ &{} \overset{\mathbf{4.}}{=} &{} {\mathbb {E}}\left[ \left\langle a_{k+1}\nabla {{\bar{f}}}(x_{k+1}), x^+_{k} - x_*\right\rangle |\mathcal {F}_k\right] . \end{array} \end{aligned}$$

By using convexity of g, it also follows:

$$\begin{aligned} \begin{array}{rcl} \text{ I}_g &{} \overset{\mathbf{4.}}{\le } &{} \displaystyle A_{k+1}\left( \frac{A_k}{A_{k+1}}g(x_{k}) + \frac{a_{k+1}}{A_{k+1}}{\mathbb {E}}\left[ g(x^+_{k})|\mathcal {F}_k\right] - g(x_*)\right) - A_k \left( g(x_k) - g(x_*)\right) \\ \\ &{} \overset{(3)}{=} &{} a_{k+1}\left( {\mathbb {E}}\left[ g(x^+_{k})|\mathcal {F}_k\right] -g(x_*)\right) . \end{array} \end{aligned}$$

Overall, we deduce:

$$\begin{aligned} \text{ I } \le {\mathbb {E}}\left[ \left\langle a_{k+1} \nabla {{\bar{f}}}(x_{k+1}), x^+_{k} - x_*\right\rangle |\mathcal {F}_k\right] + a_{k+1}\left( {\mathbb {E}}\left[ g(x^+_{k})|\mathcal {F}_k\right] -g(x_*)\right) . \end{aligned}$$

Estimation of II First, in view of the definitions of $\varphi _k$, $A_k$, and $x^+_{k}$, we obtain:

$$\begin{aligned} \begin{array}{rcl} {\mathbb {E}}\left[ \varphi _{k}(-s_k)| \mathcal {F}_k\right] &{} \overset{(6)}{\ge } &{} {\mathbb {E}}\left[ \displaystyle \left\langle -s_k, x^+_{k} \right\rangle \right] - A_{k} {\mathbb {E}}\left[ g(x^+_{k}) - \gamma _{k}\varPsi (x^+_{k})|\mathcal {F}_k\right] \\ \\ &{} \overset{(3)}{=} &{} {\mathbb {E}}\left[ \left\langle -s_k, x^+_{k} \right\rangle - A_{k+1} g(x^+_{k}) - \gamma _{k+1}\varPsi (x^+_{k})\right] \\ \\ &{}&{} +{\mathbb {E}}\left[ a_{k+1} g(x^+_{k}) + \left( \gamma _{k+1} - \gamma _{k}\right) \varPsi (x^+_{k})|\mathcal {F}_k\right] \\ \\ &{} \overset{\mathbf{3.}}{=} &{} {\mathbb {E}}\left[ \varphi _{k+1}(-s_k) + a_{k+1} g(x^+_{k}) + \left( \gamma _{k+1} - \gamma _{k}\right) \varPsi (x^+_{k})|\mathcal {F}_k\right] . \end{array} \end{aligned}$$

(12)

Second, due to Lipschitz continuity of $\nabla \varphi _k$ and definitions of $s_k$ and $x_k^+$, we have:

$$\begin{aligned} \begin{array}{rcl} {\mathbb {E}}\left[ \varphi _{k+1}(-s_{k+1})\right] &{} \overset{(8)}{\le } &{} \displaystyle {\mathbb {E}}\left[ \varphi _{k+1}(-s_k) + \langle \nabla \varphi _{k+1}(-s_k), -s_{k+1}+s_{k} \rangle |\mathcal {F}_k\right] \\ \\ &{}&{}\displaystyle + \frac{1}{2 \mu _{k+1}} {\mathbb {E}}\left[ \Vert -s_{k+1}+s_{k}\Vert _*^2|\mathcal {F}_k\right] \\ \\ &{} \overset{\mathbf{2.}, (9)}{=} &{} \displaystyle {\mathbb {E}}\left[ \varphi _{k+1}(-s_k) - \langle x^+_{k}, a_{k+1}w(x_{k+1},\xi _{k+1}) \rangle |\mathcal {F}_k\right] \\ \\ &{}&{} \displaystyle + \frac{a_{k+1}^2}{2 \mu _{k+1}} {\mathbb {E}}\left[ \Vert w(x_{k+1},\xi _{k+1}) \Vert _*^2|\mathcal {F}_k\right] . \end{array} \end{aligned}$$

(13)

By using these two auxiliary inequalities, we are ready to estimate:

$$\begin{aligned} \begin{array}{rcl} \text{ II } &{} = &{} {\mathbb {E}}\left[ \varphi _{k+1}(-s_{k+1}) - \varphi _{k}(-s_k)|\mathcal {F}_k\right] \\ \\ &{} \overset{(12)}{\le } &{} {\mathbb {E}}\left[ \varphi _{k+1}(-s_{k+1}) - \varphi _{k+1}(-s_k) - a_{k+1} g(x^+_{k}) - \left( \gamma _{k+1} - \gamma _{k}\right) \varPsi (x^+_{k})|\mathcal {F}_k\right] \\ \\ &{} \overset{(13)}{\le } &{} \displaystyle - {\mathbb {E}}\left[ \langle a_{k+1} w(x_{k+1},\xi _{k+1}), x^+_{k} \rangle + \frac{a_{k+1}^2}{2 \mu _{k+1}} \Vert w(x_{k+1},\xi _{k+1}) \Vert _*^2|\mathcal {F}_k\right] \\ \\ &{}&{} - {\mathbb {E}}\left[ a_{k+1} g(x^+_{k}) - \left( \gamma _{k+1} - \gamma _{k}\right) \varPsi (x^+_{k})|\mathcal {F}_k\right] . \end{array} \end{aligned}$$

Estimation of III

The definitions of $s_k$ and $A_k$ provide:

$$\begin{aligned} \text{ III } \overset{\mathbf{2.}}{=} {\mathbb {E}}\left[ \langle a_{k+1} w(x_{k+1},\xi _{k+1}), x_*\rangle |\mathcal {F}_k\right] + a_{k+1}g(x_*). \end{aligned}$$

Estimation of IV

Here, we have:

$$\begin{aligned} \text{ IV } \overset{(10)}{=} -\frac{a^2_{k+1}}{2\mu _{k+1}} {\mathbb {E}}\left[ \left\| w(x_{k+1},\xi _{k+1})\right\| _*^2|\mathcal {F}_k\right] . \end{aligned}$$

Altogether, we can see that

$$\begin{aligned} \begin{array}{rcl} {\mathbb {E}}\left[ V_{k+1}|\mathcal {F}_k\right] - V_k &{}\le &{} {\mathbb {E}}\left[ \langle a_{k+1} w(x_{k+1},\xi _{k+1}), x_*-x^+_k\rangle |\mathcal {F}_k\right] \\ \\ &{} &{} -{\mathbb {E}}\left[ \left\langle a_{k+1} \nabla f(x_{k+1}), x^+_{k} - x_*\right\rangle |\mathcal {F}_k\right] \\ \\ &{}&{}- \left( \gamma _{k+1} - \gamma _{k}\right) \varPsi (x^+_{k}). \end{array} \end{aligned}$$

Since $x^+_k$ is defined given $\mathcal {F}_k$, we have:

$$\begin{aligned} {\mathbb {E}}\left[ \langle a_{k+1} w(x_{k+1},\xi _{k+1}), x_*-x^+_k\rangle |\mathcal {F}_k\right] = {\mathbb {E}}\left[ \langle a_{k+1} \nabla {{\bar{f}}}(x_{k+1}), x_*-x^+_k\rangle |\mathcal {F}_k\right] . \end{aligned}$$

By additionally using that the sequence $(\gamma _k)_{k \ge 0}$ is by assumption nondecreasing, and $\varPsi (x) \ge 0$ for all $x \in \text{ dom }(g)$, we obtain:

$$\begin{aligned} {\mathbb {E}}\left[ V_{k+1}|\mathcal {F}_k\right] - V_k \le 0. \end{aligned}$$

Hence, we get by induction and taking total expectations:

$$\begin{aligned} {\mathbb {E}}[V_k] \le {\mathbb {E}}[V_0]. \end{aligned}$$

(14)

It turns out that the expectation of $V_0$ is nonnegative. For that, we first estimate due to the choice of $x_0$:

$$\begin{aligned} \begin{array}{rcl} \varphi _0(-s_0) &{}\overset{(8)}{\le }&{} \displaystyle \varphi _{0}(0) + \langle \nabla \varphi _{0}(0), -s_0 \rangle + \frac{1}{2 \mu _{0}} \Vert s_0\Vert _*^2 \\ \\ &{}\overset{\mathbf{0.}}{=}&{} \displaystyle - a_0 g(x_0) - \gamma _0 \varPsi (x_0) - \left\langle x_0, a_0 w(x_0,\xi _0) \right\rangle \\ \\ &{}&{}+ \displaystyle \frac{a_0^2}{2\mu _{0}} \left\| w(x_0,\xi _0)\right\| _*^2. \end{array} \end{aligned}$$

(15)

This gives:

$$\begin{aligned} \begin{array}{rcl} {\mathbb {E}}[V_0] &{}=&{} \displaystyle A_0 {\mathbb {E}}\left[ F(x_0) - F(x_*)\right] + {\mathbb {E}}\left[ \varphi _{0}(-s_0) + \langle s_0, x_*\rangle \right] \\ \\ &{}&{}+ A_0 g(x_*) - B_0 \\ \\ &{}\overset{(2)}{\le }&{} \displaystyle a_0\left\langle \nabla {{\bar{f}}}(x_0), x_0 \right\rangle + {\mathbb {E}}[\varphi _{0}(-s_0)] + a_0 g(x_0) - B_0 \\ \\ &{}\overset{(15),(10)}{\le }&{} \displaystyle - \gamma _0 \varPsi (x_0) \le 0, \end{array} \end{aligned}$$

(16)

where again the last inequality is due to the assumptions on $\gamma _0$ and $\varPsi$. Additionally, it holds by definition of $\varphi _k$:

$$\begin{aligned} \varphi _{k}(-s_k) \ge \left\langle -s_k, x_* \right\rangle - A_{k} g(x_*) - \gamma _{k}\varPsi (x_*). \end{aligned}$$

(17)

Hence, we obtain:

$$\begin{aligned} \begin{array}{rcl} A_k {\mathbb {E}}\left[ \left( F(x_k) - F(x_*)\right) \right] &{}=&{} \displaystyle {\mathbb {E}}\left[ V_k - \varphi _{k}(-s_k) - \langle s_k, x_*\rangle \right] - A_k g(x_*) + B_k \\ &{}\overset{\begin{array}{c} (14) \\ (16), (17) \end{array}}{\le }&\displaystyle \gamma _{k}\varPsi (x_*) + B_k. \end{array} \end{aligned}$$

The assertion (11) then follows.

Now, let us show that the convergence rate of (RQM) derived in Theorem 1 is optimal for nonsmooth optimization, i.e. it is of order $\text{ O }\left( \frac{1}{\sqrt{k+1}}\right)$. For that, we exemplarily consider the following choice of control parameters:

$$\begin{aligned} a_k = 1, \quad \gamma _k = \sqrt{k+1}, \quad k \ge 0. \end{aligned}$$

(18)

We also assume that the subgradients’ estimates of f have uniformly bounded second moments, i.e. there exists $G >0$ such that

$$\begin{aligned} {\mathbb {E}}\left[ \Vert w(x,\xi ) \Vert _* \right] \le G, \quad x \in \text{ dom }(f). \end{aligned}$$

(19)

Corollary 1

Let $x_* \in \text{ dom }(g)$ solve the composite optimization problem (1), and the sequence $\left( x_k\right) _{k\ge 0}$ be generated by (RQM) with control parameters from (18). Then, it holds for all $k\ge 0$:

$$\begin{aligned} {\mathbb {E}}\left[ F(x_k)\right] - F(x_*) \le \displaystyle \left( \varPsi (x_*) + \frac{G^2}{\beta }\right) \frac{1}{\sqrt{k+1}}. \end{aligned}$$

(20)

Proof

In order to obtain (20), we estimate the terms in (11) which involve control parameters:

$$\begin{aligned}&\frac{\gamma _k}{A_k} = \frac{\sqrt{k+1}}{k+1} = \frac{1}{\sqrt{k+1}}, \\&\quad \begin{array}{rcl} \displaystyle \frac{B_k}{A_k} &{}=&{} \displaystyle \frac{1}{2(k+1)} \sum _{\ell =0}^{k} \frac{1}{\mu _{\ell }} {\mathbb {E}}\left[ \left\| w(x_\ell ,\xi _\ell )\right\| _*^2\right] \overset{(7), (19)}{\le } \frac{G^2}{2 \beta (k+1)} \sum _{\ell =0}^{k} \frac{1}{\sqrt{\ell +1}} \\ \\ &{} \le &{} \displaystyle \frac{G^2}{2 \beta (k+1)} \int _{-\frac{1}{2}}^{k + \frac{1}{2}} \frac{\text{ d } \tau }{\sqrt{\tau +1}} = \frac{G^2}{\beta (k+1)} \left( \sqrt{k+\frac{3}{2}} - \sqrt{\frac{1}{2}} \right) \\ \\ &{}\le &{} \displaystyle \frac{G^2}{\beta \sqrt{k+1}}. \end{array} \end{aligned}$$

$\square$

From the proof of Corollary 1 we see that also other choices of control parameters guarantee the optimal convergence rate of RQM. E.g., we may have chosen:

$$\begin{aligned} a_k = k, \quad \gamma _k = (k+1)^{\frac{3}{2}}, \quad k \ge 0. \end{aligned}$$

(21)

We show that the convergence rate of (RQM) derived in Corollary 1 can be improved to $\text{ O }\left( \frac{\ln k}{k}\right)$ if the regularizer g turns out to be strongly convex. Additionally, an estimate in terms of generated iterates can be obtained. For that, consider the control parameters as follows:

$$\begin{aligned} a_k = 1, \quad \gamma _k = \ln (2 k +3), \quad k \ge 0. \end{aligned}$$

(22)

Corollary 2

Let $x_* \in \text{ dom }(g)$ solve the composite optimization problem (1), and the sequence $\left( x_k\right) _{k\ge 0}$ be generated by (RQM) with control parameters from (22). Additionally, let g be strongly convex with convexity parameter $\sigma >0$. Then, it holds for all $k\ge 0$:

$$\begin{aligned}&{\mathbb {E}}\left[ F(x_k)\right] - F(x_*) \le \displaystyle \left( \varPsi (x_*) + \frac{G^2}{\sigma }\right) \frac{\ln (2 k +3)}{k+1}. \end{aligned}$$

(23)

$$\begin{aligned}&\quad {\mathbb {E}}\left\| x_k - x_* \right\| ^2 \le \displaystyle \frac{2}{\sigma } \left( \varPsi (x_*) + \frac{G^2}{\sigma }\right) \frac{\ln (2 k +3)}{k+1}. \end{aligned}$$

(24)

Proof

In order to obtain (23), we estimate the terms in (11) which involve control parameters:

$$\begin{aligned}&\frac{\gamma _k}{A_k} = \frac{\ln (2 k +3)}{k+1}, \\&\quad \begin{array}{rcl} \displaystyle \frac{B_k}{A_k} &{}=&{} \displaystyle \frac{1}{2(k+1)} \sum _{\ell =0}^{k} \frac{1}{\mu _{\ell }} {\mathbb {E}}\left[ \left\| w(x_\ell ,\xi _\ell )\right\| _*^2\right] \overset{(7), (19)}{\le } \frac{G^2}{2 \sigma (k+1)} \sum _{\ell =0}^{k} \frac{1}{\ell +1} \\ \\ &{} \le &{} \displaystyle \frac{G^2}{2 \sigma (k+1)} \int _{-\frac{1}{2}}^{k + \frac{1}{2}} \frac{\text{ d } \tau }{\tau +1} = \frac{G^2}{\sigma (k+1)} \left( \ln \left( k+\frac{3}{2}\right) - \ln {\frac{1}{2}} \right) \\ \\ &{}=&{} \displaystyle \frac{G^2}{\sigma }\cdot \frac{\ln (2k+3)}{k+1}. \end{array} \end{aligned}$$

For (24), we use the assumption that g is strongly convex, hence, also F is. In particular, we obtain:

$$\begin{aligned} F(x_k) \ge F(x_*) + \left\langle s, x_k -x_* \right\rangle + \frac{\sigma }{2} \left\| x_k - x_*\right\| ^2, \quad s \in \partial F(x^*). \end{aligned}$$

Since $x_*$ solves (1), we have $0 \in \partial F(x_*)$ and it follows:

$$\begin{aligned} \left\| x_k - x_*\right\| ^2\le \frac{2}{\sigma } \left( F(x_k) - F(x_*) \right) . \end{aligned}$$

By taking expectation and recalling (23), we are done. $\square$

Finally, we note that estimating convergence rates for the generated sequence of iterates itself is a hard task in the framework of subgradient methods. We refer e.g. to [8], where the dual averaging methods were adjusted for stochastic composite minimization. There, just the boundedness of iterates could be in general shown. If g is strongly convex, an estimate was nevertheless provided. This is also the case for RQM as we have shown in Corollary 2.

4 Numerical experiments

We performed numerical experiments on two representative synthetic problems with various parameters for the data generation and observed two general patterns in regards to the relative performance of solvers.

For each problem instance we ran one hundred trials of (RQM) in order to investigate the robustness and spread of the performance. Note that the initial $x_0$ set by (RQM) is the zero vector. First, we compare the parameter choice Parameters A as in (18), i.e. $a_k=1$ and, thus, $A_k=k+1$, with $\gamma _k=\sqrt{k+1}$, to the choice of $a_k=k$ and, thus, $A_k = \frac{k(k+1)}{2}$, with the more aggressive constant step-size $\gamma _k= 10$ Parameters B.

We also compare (RQM) to the stochastic regularized subgradient (SRSG) with Nesterov’s extrapolation from [7]. There, by choosing control parameters

$$\begin{aligned} \theta _k = \frac{2}{k+1}, \quad \gamma _k = (k+1)^{3/2}, \end{aligned}$$

the authors iterate:

$$\begin{aligned} \begin{array}{l} y_{k} = {\hat{x}}_{k}+\theta _k\left( \theta ^{-1}_{k-1}-1\right) \left( {\hat{x}}_k- {\hat{x}}_{k-1}\right) , \\ \\ \displaystyle {\hat{x}}_{k+1} = \text{ arg } \min _{x} \left\{ \left\langle w(y_k,\xi _k), x \right\rangle + g(x) + \gamma _{k}\varPsi (x- y_k)\right\} . \end{array} \end{aligned}$$

(25)

Finally, we also compare the procedure to the standard mirror descent algorithm, in this case the update becomes,

$$\begin{aligned} x_{k+1} = \text{ arg } \min _{x} \left\{ \left\langle w(x_k,\xi _k), x \right\rangle + g(x) + \gamma _{k}\varPsi (x- x_k)\right\} . \end{aligned}$$

(26)

In the experiments we use the Euclidean dual map $\varPsi (x)=\frac{1}{2}\Vert x\Vert ^2_2$ and the theoretically optimal rate $\gamma _k=\sqrt{k+1}$.

4.1 Huber loss and $\ell _1$-regularization

Consider linear regression with a robust Huber loss and $\ell _1$-regularization, i.e.

$$\begin{aligned} \min \limits _{\mathbf {a},b} \,\,\sum \limits _{i=1}^N L_{\delta }\left( \mathbf {a}^T x_i+b-y_i\right) +\lambda \Vert (\mathbf {a},b)\Vert _1, \end{aligned}$$

where

$$\begin{aligned} L_{\delta }(z)=\left\{ \begin{array}{ll} \displaystyle \frac{1}{2} z^2 &{} \quad \text {for } |z|\le \delta ,\\ \displaystyle \delta \left( |z|-\frac{1}{2}\delta \right) &{} \quad \text {otherwise}. \end{array}\right. \end{aligned}$$

Here, we expect the number N of data samples to be large. The $\ell _1$-regularization on the parameters encourages sparsity, i.e. most of the parameters to become zero. The Huber loss is a means of mitigating the impact of outliers on the stability of the regression estimate, i.e. by enforcing linear as opposed to quadratic growth of the loss beyond the influence boundary $\delta$. We take the subgradients

$$\begin{aligned} \partial L_{\delta }(z) \ni \left\{ \begin{array}{ll} z &{} \quad \text {for } |z|\le \delta , \\ \displaystyle \delta \cdot \text {sign}(z) &{} \quad \text {otherwise}. \end{array}\right. \end{aligned}$$

Denoting $x=(\mathbf {a},b)$ and choosing as prox-function $\varPsi (x)=\frac{1}{2}\Vert x\Vert ^2_2$, the subproblem in (RQM) admits an explicit solution:

$$\begin{aligned} \begin{array}{rcl} x^+ &{}=&{} \displaystyle \arg \min _x \left\{ \langle s,x\rangle + A \lambda \Vert x\Vert _1+\frac{\gamma }{2} \Vert x\Vert ^2_2\right\} \\ \\ {} &{}=&{} \displaystyle \text {sgn}\left( -\frac{s}{\gamma }\right) \max \left\{ \left| -\frac{s}{\gamma }\right| - \frac{ A\lambda }{\gamma },0\right\} . \end{array} \end{aligned}$$

The explicit solution of the subproblem in (25) is

$$\begin{aligned} \begin{array}{rcl} {\hat{x}} &{}=&{} \displaystyle \arg \min _x \left\{ \langle w,x\rangle + \lambda \Vert x\Vert _1+\frac{\gamma }{2} \Vert x - y\Vert ^2_2\right\} \\ \\ {} &{}=&{} \displaystyle \text {sgn}\left( y-\frac{w}{\gamma }\right) \max \left\{ \left| y-\frac{w}{\gamma }\right| - \frac{\lambda }{\gamma },0\right\} . \end{array} \end{aligned}$$

Now we describe the generation of the synthetic data used to generate the problem for comparison. We let $\mathbf {a}\in {\mathbb {R}}^{10}$, $\delta =2$, and $N=10000$ and conduct the following procedure:

• 1. Choose 4 components of $\mathbf {a}$ to be nonzero. Randomly sample these components and b.

• 2. Choose 10000 input samples $\{x_i\}$ uniformly in $[-5,5]$.

• 3. With probability 0.95 generate $y_i \sim \mathcal {N}\left( \mathbf {a}^T x_i+b,1\right)$, and otherwise $y_i \sim \mathcal {N}\left( \mathbf {a}^T x_i+b,5\right)$.

• 4. Run (RQM).

We set $\lambda =0.1$. The trajectory of the objective value with the associated one standard deviation confidence interval is shown in Fig. 1. Note that for the Nesterov’s extrapolation algorithm we report the objective value on ${\hat{x}}_k$, as this is what the theoretical convergence guarantees in [7] are derived for. We see that SRSG with Nesterov’s extrapolation performs better that our method with the theoretically optimal choice of Parameters A. However, it is worth mentioning that alternative parameter choices (Parameter B) may work better in practice. In any case, all the methods produce convergent sequences w.r.t. the function value.

Fig. 1

Evolution of the objective error with the iterations for Huber Loss and $\ell _1$-Regularization

4.2 $\ell _1$-regression and box constraint

Now, we present a problem and data generation parameters for which the theoretically optimal algorithm RQM exhibit the better comparative performance. The optimization problem is defined to be $\ell _1$-regression with an indicator of membership to a box constraint

$$\begin{aligned} \min \limits _{\mathbf {a},b} \,\,\sum \limits _{i=1}^N \left| \mathbf {a}^T x_i+b-y_i\right| +\mathbf {1}_C(\mathbf {a},b), \end{aligned}$$

where

$$\begin{aligned} C=\{x:x_l\le x \le x_u\}. \end{aligned}$$

In this case, the subproblem uses a stochastic subgradient of the loss term, i.e., for sample i, we have that s or w, respectively for the two algorithms is given by

$$\begin{aligned} \text {sign}\left( \mathbf {a}^T x_i+b-y_i\right) \begin{pmatrix} x_i \\ 1 \end{pmatrix}. \end{aligned}$$

Additionally, we use the same prox-function $\varPsi (x)=\frac{1}{2}\Vert x\Vert ^2_2$. Finally, incorporating the indicator in the subproblem is simply projection onto the box C. We let $\mathbf {a}\in {\mathbb {R}}^{5}$ and $N=1000$ and generate the data as follows:

• 1. Randomly sample $\mathbf {a} \sim \mathcal {N}\left( 0,7\mathbf {I}\right)$ and $b\sim \mathcal {N}(0,8)$.

• 2. Choose 1000 input samples $\{x_i\}$ uniformly in $[-15,15]$.

• 3. Generate $y_i \sim \mathcal {N}\left( \mathbf {a}^T x_i+b,1\right)$.

• 4. Finally $\mathbf {x}_l=x_l\mathbf {1}$ was chosen randomly uniformly in $[-20,0]$ and $\mathbf {x}_u=x_u\mathbf {1}$ in [0, 20].

We can see now in Fig. 2 that in this case the theoretically optimal choice of Parameters A exhibit the best performance.

Fig. 2

Evolution of the objective error with the iterations for $\ell _1$-Regression and Box Constraint