Minsum scheduling with acceptable lead-times and optional job rejection

Abstract

In our current fast-paced era, customers are often willing to pay extra premium for shorter lead times, which motivates further research on the scheduling problem with due-date assignment and customer-specified lead times. As part of this effort, we extend the classic minsum ‘DIF’ scheduling model to allow optional job-rejection, thus adding an important component of real-life applications, namely, the possibility that the scheduler decides to process only a subset of the jobs and outsource the disjoint set. The scheduler is penalised for rejecting certain jobs by setting job-dependent rejection costs, and he is limited by a given upper bound on the total rejection cost. The most general version of the minsum DIF problem includes job-dependent cost parameters and lead-times, and it is strongly NP-hard. Therefore, we study six variants of the problem, where either only the cost parameters or the lead-times are job dependent. All alternatives are extended by optional job-rejection that possibly bounds the constraints or the underlying cost functions. We establish that all studied problems are NP-hard in the ordinary sense and present pseudo-polynomial dynamic programming algorithms and extensive numerical studies for most solutions.

1 Introduction

The objective of scheduling with due-dates is to find the sequence of jobs that optimises performance under specific due-date constraints. In the DIF method for solving this scheduling problem, the due-dates are decision variables (i.e., an integral part of the solution, rather than part of the input), the assignment is unrestricted, and the scheduler is penalised if the job-dependent due-dates exceed given deadlines, known as lead-times. Thus, the scheduler must find the optimal sequence and due-dates that minimise the sum of three component costs: earliness, tardiness, and due-date tardiness. In the original DIF model [15], the scheduler is penalised if the due dates exceed the lead-times, reflecting the potential loss in sales; since delivering early has no cost in this model, the difference between the due date and lead time is represented by a linear function. The DIF method is highly appropriate in the rapidly increasing field of e-commerce, where retail sales are expected to exceed several trillion dollars in the next few years. Indeed, the commitment of the supplier to deliver the goods earlier than the customers’ acceptable lead-time is pivotal in e-commerce, and late delivery may void the contract.

Several studies addressed the minsum DIF model, e.g., Shabtay and Steiner [18], who study job-dependent lead-times; Shabtay and Steiner [19, 20] and Leyvand et al. [11], who extend the model by considering controllable job processing times, and Shabtay [16], who addresses the model with batch delivery costs. Others address the minmax version of the DIF model, e.g., Mor et al. [12], who consider job-dependent cost parameters and lead-times; Gerstl and Mosheiov [5, 6], who extend the model to a time window for acceptable lead-times and solve both the minmax and minsum versions, respectively; and Gerstl et al. [3], who focus on the minmax version with either position-dependent processing times or optional job rejection. In the current study, we follow the approach of Gerstl et al. [3] and extend the minsum DIF problem to include possible job rejection. Shabtay et al. [17] claim that optional job rejection is justified in highly loaded production industries where the scheduler may prefer to reject or outsource some orders, rather than imposing a greater loss. Subsequently, the supplier may incur a considerable rejection cost that must be evaluated already at the scheduling phase. Numerous studies addressed the combination of due-date scheduling with optional job-rejection, including, among others, Zhao et al. [24], who study due-date assignments with job-rejection and position-dependent processing times; Gerstl and Mosheiov [4], who address scheduling with generalised due dates and job rejection; and Mosheiov and Pruwer [14], who focus on minmax common due-date problems with position-dependent processing times.

Shabtay and Steiner [18] prove that the DIF problem, with job-dependent acceptable lead-times and job-dependent cost parameters for earliness, tardiness, and due-date tardiness, is strongly NP-hard. Since this proof implies the lack of a pseudo polynomial-time solution unless P is equal to NP, we study several variations of the problem, where either the cost parameters or the lead-times are job-dependent. All alternatives are extended by an optional job-rejection, possibly bounding the constraints or the underlying cost functions. We establish that all studied problems are NP-hard in the ordinary sense and provide pseudo-polynomial DP algorithms. We present an extensive numerical study that proves that all the DP algorithms are extremely efficient for medium-size problems.

This paper is constructed as follows: Sect. 2 provides the formulation of the problem; Sect. 3 presents preliminary analyses and important known results in scheduling theory; Sect. 4 presents the solution to the problem with job-dependent cost parameters and a common (zero) lead-time, as well as its complementary problem; Sect. 5 focuses on the variant with common cost parameters and common lead-time and its complementary problem; Sect. 6 addresses the case of job-dependent cost parameters and common lead-times; Sect. 7 discusses common cost parameters and job-dependent lead-times; and Sect. 8 presents our numerical study.

2 Notations and formulation

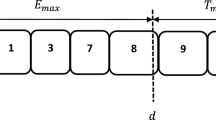
Given is a set ${\mathcal{J}}$ of $n$ jobs that need to be processed on a single machine. The processing time of job $j$ is denoted by $p_{j} ,~j = 1, \ldots ,n$, the total processing time of the jobs in set ${\mathcal{J}}$ is denoted by $P~\left( { = \sum\nolimits_{{j \in {\mathcal{J}}}} {p_{j} } } \right)$, and the longest processing time among all jobs in set ${\mathcal{J}}$ is denoted by $p_{{max}} ~\left( { = \max _{{j \in {\mathcal{J}}}} \left\{ {p_{j} } \right\}} \right)$. The due-date of job $j$ is a decision variable denoted by $d_{j} , \, j = 1, \ldots ,n.$ For a given schedule, let $C_{j}$ denote the completion time of job $j,~j = 1, \ldots ,n$. We consider a job-dependent lead-time, denoted by $l_{j} ,~j = 1, \ldots ,n$; as common in the DIF model, if the due-date of job $j$ is set to be later than its upper bound, the scheduler is penalised. For given schedule and due-dates, let $E_{j} = \max \left\{ {0,d_{j} - C_{j} } \right\}$, $T_{j} = \max \left\{ {0,C_{j} - d_{j} } \right\}$, and $A_{j} = \max \left\{ {0,d_{j} - l_{j} } \right\}$ denote the earliness, tardiness, and due-date tardiness of job $j,~j = 1, \ldots ,n$, respectively. For each job $j,~j = 1, \ldots ,n$, three job-dependent unit costs are considered: the earliness unit cost, $\alpha _{j}$, the tardiness unit cost, $\beta _{j}$, and the due-date tardiness unit cost, $\gamma _{j}$. Following Seidmann et al. [15] and Shabtay and Steiner [18], the objective function studied is of the minsum type. We extend the DIF model by allowing job rejection, i.e., we consider a job-dependent rejection cost, denoted by $r_{j} ,~~j = 1, \ldots ,n$, and we assume a given upper bound on the total rejection cost of all rejected jobs, denoted by $R$.

Let ${\mathcal{J}}_{P}$ and ${\mathcal{J}}_{R}$ denote the set of accepted (processed) jobs and the set of rejected (outsourced) jobs, respectively, such that ${\mathcal{J}} = {\mathcal{J}}_{P} \cup {\mathcal{J}}_{R}$ and ${\mathcal{J}}_{P} \cap {\mathcal{J}}_{R} = \emptyset$. The goal is to find the optimal schedule and due-dates that minimise the total (summed) cost of the earliness, tardiness, and due-date tardiness of set ${\mathcal{J}}_{P}$, i.e., $~Z = \sum\nolimits_{{j \in {\mathcal{J}}_{P} }} {\left( {\alpha _{j} E_{j} + \beta _{j} T_{j} + \gamma _{j} A_{j} } \right)}$, under the constraint that the total rejection cost of set ${\mathcal{J}}_{R}$ is not larger than the rejection cost limit, i.e., $\sum\nolimits_{{j \in {\mathcal{J}}_{R} }} {r_{j} \le R}$. We also consider two complementary problems where the goal is to minimise the total rejection cost, subject to the constraint that the total weighted completion time or the total weighted tardiness cannot exceed a given upper bound, denoted by $Q$.

We first extend the problem addressed by Shabtay and Steiner [18], wherein the cost parameters are considered to be job dependent and the lead-time is common to all jobs and is set to zero, i.e., $l_{j} = 0,~j = 1, \ldots ,n$. Thus, the objective function is $Z = \sum\nolimits_{{j \in {\mathcal{J}}_{P} }} {\left( {\alpha _{j} E_{j} + \beta _{j} T_{j} + \gamma _{j} A_{j} } \right)}$ and, using the three-field notation, the problem is

$$ \boldsymbol{P}1.1:~1| {l_{j} = 0,~~\mathop \sum \limits_{{j \in {\mathcal{J}}_{R} }} r_{j} \le R} |\mathop \sum \limits_{{j \in {\mathcal{J}}_{P} }} \left( {\alpha _{j} E_{j} + \beta _{j} T_{j} + \gamma _{j} A_{j} } \right) $$

(1)

and its complementary problem,

$$ \boldsymbol{P}1.2:1~| {l_{j} = 0,~\mathop \sum \limits_{{j \in {\mathcal{J}}_{P} }} \left( {\alpha _{j} E_{j} + \beta _{j} T_{j} + \gamma _{j} A_{j} } \right) \le Q} |\sum \limits_{{j \in {\mathcal{J}}_{R} }} r_{j} . $$

Next, we adjoin job rejection to the problem studied in Seidman et al. [15], i.e., common cost parameters and a common lead-time. Thus, for $j = 1, \ldots ,n$, $\alpha _{j} = \alpha ,~\beta _{j} = \beta ,~\gamma _{j} = \gamma$ and $l_{j} = l$, and the second problem studied here is

$$ \boldsymbol{P}2.1:~1| {l_{j} = l,~~\mathop \sum \limits_{{j \in {\mathcal{J}}_{R} }} r_{j} \le R} |\mathop \sum \limits_{{j \in {\mathcal{J}}_{P} }} \left( {\alpha E_{j} + \beta T_{j} + \gamma A_{j} } \right) $$

(2)

and its complementary problem,

$$ \boldsymbol{P}2.2:1~| {l_{j} = l,~\mathop \sum \limits_{{j \in {\mathcal{J}}_{P} }} \left( {\alpha _{j} E_{j} + \beta _{j} T_{j} + \gamma _{j} A_{j} } \right) \le Q} |\sum \limits_{{j \in {\mathcal{J}}_{R} }} r_{j} . $$

Third, we consider job-dependent cost parameters and a common lead-time with job-rejection:

$$ \boldsymbol{P}3:~1| {l_{j} = l,~~\mathop \sum \limits_{{j \in {\mathcal{J}}_{R} }} r_{j} \le R} |\mathop \sum \limits_{{j \in {\mathcal{J}}_{P} }} \left( {\alpha _{j} E_{j} + \beta _{j} T_{j} + \gamma _{j} A_{j} } \right) $$

(3)

Finally, we assume common cost parameters and job-dependent lead-times, implying that

$$ \boldsymbol{P}4:~1| {l_{j} ,\mathop \sum \limits_{{j \in {\mathcal{J}}_{R} }} r_{j} \le R} |\mathop \sum \limits_{{j \in {\mathcal{J}}_{P} }} \left( {\alpha E_{j} + \beta T_{j} + \gamma A_{j} } \right). $$

(4)

3 Preliminary analysis

Shabtay and Steiner [18] studied the most general form of the DIF model with acceptable lead-times, i.e., where the unit cost parameters and lead-times are job-dependent:

$$ 1\parallel \sum \left( {\alpha _{j} E_{j} + \beta _{j} T_{j} + \gamma _{j} A_{j} } \right). $$

(5)

The authors referred to the problem as Total Weighted Earliness and Tardiness with Due Date Assignment (TWETD) and proved the following essential properties and theorem:

Property 1

In an optimal schedule, no job is early, i.e., $E_{j} ~ = ~0~,$ for all $~j~ = ~1,~.~.~.~,~n$.

Property 2

In an optimal schedule, if $\gamma _{j} \le \beta _{j}$ then the optimal due date of job $j~$ is $d_{j} = C_{j}$. Otherwise, $d_{j} = \min \left\{ {l_{j} ,~C_{j} } \right\}$.

$$ {\text{Let:}}\quad w_{j} = \min \left\{ {\beta _{j} ,\gamma _{j} } \right\}, $$

(6)

Following the above properties, the TWETD problem can be re-formulated as

$$ 1~\parallel \sum w_{j} \max \left\{ {0,~C_{j} - l_{j} } \right\}. $$

(7)

Thus, to solve the TWETD problem, one must find the sequence that minimises (7), which leads to the following important theorem:

Theorem 0

The TWETD problem is equivalent to a $1~\parallel \sum w_{j} T_{j}$ problem. Therefore, TWETD is strongly NP-hard, even if $\beta _{j} = \gamma _{j} \left( { = w_{j} } \right),~j = 1, \ldots ,n$. Furthermore, the TWETD problem with uniform penalties, i.e., with $\alpha _{j} = ~\beta _{j} = \gamma _{j} = w,~j = 1, \ldots ,n$, is ordinary NP-hard.

The theorem follows from the facts that ${\text{~}}1\parallel \sum w_{j} T_{j}$ is NP-hard in the strong sense and that $1||\sum wT_{j}$ is NP-hard in the ordinary sense. Since TWETD is strongly NP-hard and a pseudo polynomial-time solution does not exist unless P is equal to NP, we focus here on the special cases in which either the unit cost parameters or the acceptable lead-times are job-dependent; these problems can be solved in polynomial time. Below, we establish that these problems, when extended to allow job rejection, are ordinary NP-hard and present DP solutions.

4 Problem $\boldsymbol{P}1.1\;1\left| {\boldsymbol{l}_{\boldsymbol{j}} = 0,\sum_{{\boldsymbol{j} \in {{\mathcal{J}}}_{\boldsymbol{R}} }} {\boldsymbol{r}_{\boldsymbol{j}} \le \boldsymbol{R}} } \right|\sum_{{\boldsymbol{j} \in {{\mathcal{J}}}_{\boldsymbol{P}} }} {\left( {\boldsymbol{\alpha }_{\boldsymbol{j}} \boldsymbol{E}_{\boldsymbol{j}} + \boldsymbol{\beta }_{\boldsymbol{j}} \boldsymbol{T}_{\boldsymbol{j}} + \boldsymbol{\gamma }_{\boldsymbol{j}} \boldsymbol{A}_{\boldsymbol{j}} } \right)}$ and its complementary problem $\boldsymbol{P}1.2\;1\,\left| {\boldsymbol{l}_{\boldsymbol{j}} = 0,\sum_{{\boldsymbol{j} \in {{\mathcal{J}}}_{\boldsymbol{P}} }} {\left( {\boldsymbol{\alpha }_{\boldsymbol{j}} \boldsymbol{E}_{\boldsymbol{j}} + \boldsymbol{\beta }_{\boldsymbol{j}} \boldsymbol{T}_{\boldsymbol{j}} + \boldsymbol{\gamma }_{\boldsymbol{j}} \boldsymbol{A}_{\boldsymbol{j}} } \right)} \le \boldsymbol{Q}} \right|\sum \limits_{{j \in {\mathcal{J}}_{R} }} \boldsymbol{r}_{\boldsymbol{j}}$

Shabtay and Steiner [18] consider the DIF model with job-dependent cost parameters and a common lead-time, such that $l_{j} = 0$ for $j = 1, \ldots ,n$. The authors claim that setting the upper bound of the lead-time to zero is realistic when the customer requests that the order is delivered as soon as possible and may even agree to pay for a faster delivery. Based on Properties 1 and 2 and formulation (7), $1\left| {l_{j} = 0} \right|\sum\nolimits_{{j \in {\mathcal{J}}_{P} }} {\left( {\alpha _{j} E_{j} + \beta _{j} T_{j} + \gamma _{j} A_{j} } \right)} ~$ is equivalent to the elementary problem $1\parallel \sum w_{j} C_{j}$, where $w_{j} = \min \left\{ {\beta _{j} ,\gamma _{j} } \right\}$. Thus, Problem $\boldsymbol{P}1.1$ is reduced to

$$ 1~|\sum r_{j} \le R~|\sum w_{j} C_{j} . $$

(8)

and its complementary problem, $\boldsymbol{P}1.2$, is reduced to $1~\left| {\sum w_{j} C_{j} \le Q} \right|\sum r_{j}$.

Cao et al. [1] proved that this problem is binary NP-hard and presented a pseudo polynomial-time DP algorithm and a fully polynomial-time approximation scheme (FPTAS). Their DP computational complexity is $O\left( {n^{3} p_{{max}} w_{{max}} } \right)$, where $w_{{\max }} = \max _{{1 \le j \le n}} \left\{ {w_{j} } \right\}$. Next, we suggest a DP solution to P1.1 with a faster processing time of $O\left( {n \cdot P \cdot R} \right)$.

Problem $1\parallel \sum w_{j} C_{j}$ is known to be solved by sorting the jobs in a Weighted Shortest Processing Time first (WSPT) order, i.e., in a non-decreasing order of $\frac{{p_{j} }}{{w_{j} }},j = 1,~ \ldots ,n$; hence, we start our DP by sorting the jobs in a WSPT order.

Let f(j, t, r) denote the total weighted completion time for the partial schedule of jobs 1, …, j, with a completion time t and a maximum rejection cost r. At each iteration of the DP, one needs to decide whether to accept or reject job j. In the former case, the total weighted completion time cost is increased; in the latter, the rejection cost of job j does not exceed the current rejection limit. The formal DP (denoted by DP1.1) given by its recursion formula is:

Dynamic programming algorithm DP1:

$$ f\left( {j,t,r} \right) = \left\{ {\begin{array}{*{20}l} {\infty ,} \hfill & {p_{j} > t~and~r_{j} > r} \hfill \\ {f\left( {j - 1,t - p_{j} ,r} \right) + w_{j} t,} \hfill & {p_{j} \le t~and~r_{j} > r} \hfill \\ {f\left( {j - 1,t,r - r_{j} } \right),} \hfill & {p_{j} > t~and~r_{j} \le r} \hfill \\ {\min \left( {~f\left( {j - 1,t - p_{j} ,r} \right) + w_{j} t,f\left( {j - 1,t,r - r_{j} } \right)} \right),} \hfill & {p_{j} \le t~and~r_{j} \le r} \hfill \\ \end{array} } \right. $$

(9)

In this equation, the first line reflects an unfeasible case, the second line reflects the option of processing job $j$, the third line represents the option of rejecting job $j$, and the fourth line reflects the case in which job $j$ may be either processed or rejected, such that the option that achieves the minimal cost is selected.

The boundary conditions are: $f\left( {0,0,r} \right) = 0$ and $f\left( {0,t,r} \right) = \infty$ if $t \ne 0$, $t \le P$, for all $r \le R$. $f\left( {j,t,0} \right) = \sum\nolimits_{{k = 1}}^{j} {w_{k} C_{k} }$, and $t = \sum\nolimits_{{k = 1}}^{j} {p_{k} }$.

The optimal solution is given by $\min \left\{ {f\left( {n,t,r} \right)|0 \le t \le P,~0 \le r \le R~} \right\}$. Note that, in the case of $R \ge \sum\nolimits_{{j = 1}}^{n} {r_{j} }$, the solution is trivial because all jobs may be rejected with a zero cost. Thus, the variable $r$ is assumed to be bounded by $R$.

Theorem 1

Algorithm DP1.1 solves Problem $\boldsymbol{P}1.1$.

Proof

By induction on $j$, $t$ and $r$.

Base case: The case $j = 0$ indicates an empty set. Therefore, in this case, the total completion time, $t$, is also equal to 0 and $f\left( {0,0,r} \right) = 0$, whereas $f\left( {0,t,r} \right) = \infty$ for $0 \ne t \le P$ and $r \le R$. If $j \ne 0$ and the rejection upper bound is 0, all jobs should be processed. That is, the total completion time is $t = \sum\nolimits_{{k = 1}}^{j} {p_{k} }$ and $f\left( {j,t,0} \right) = \sum\nolimits_{{k = 1}}^{j} {w_{k} C_{k} }$ is the cost of the processed jobs when no job is rejected.

We assume the correctness of $f\left( {i,s,u} \right)$ in the case that at least one of $0 \le i < j$ or $0 \le s < t$ or $0 \le u < r$ holds, and we prove the correctness of $f\left( {j,t,r} \right)$. In the case that job $j$ must be processed, that is, its rejection cost cannot be added to the total rejection cost without violating the rejection upper bound, i.e., $r_{j} > r$, the reference cost is $f\left( {j - 1,t - p_{j} ,r} \right)$, which is assumed to be correct by the induction hypothesis. This cost considers the first $j - 1$ jobs with a total completion time $t - p_{j}$, which is applicable only when the processing time of job $j$ can fit in the total completion time, i.e., $p_{j} \le t$. The cost is updated by $w_{j} t$, considering the additional cost for processing job $j$ and leaving the total rejection cost unchanged, as seen on line 2 of Eq. (9). If the processing time of job $j$ cannot fit in the total completion time, i.e., $p_{j} > t$, then the job should be rejected. Accordingly, the cost is equal to that of $f\left( {j - 1,t,r - r_{j} } \right)$, which is known to be correct by the induction hypothesis. This is applied only in the case of $r_{j} \le r$; otherwise, the case is impossible with infinity cost, as reflected by the first line of Eq. (9). In cases where the job may be either processed or rejected, its processing time is not higher than the total completion time. In these cases, the rejection cost can be added without violating the rejection upper bound, i.e., $p_{j} \le t~$ and $r_{j} \le r$, and the minimum cost between case 2 and case 3 is chosen. By the induction hypothesis, as $f\left( {j - 1,t - p_{j} ,r} \right) + w_{j} t$ and $f\left( {j - 1,t,r - r_{j} } \right)$ are optimal, the minimum is optimal for $f\left( {j,t,r} \right)$.$\hfill{\square}$

Theorem 2

The computational complexity of $DP1.1$ is $~O\left( {n \cdot P \cdot R} \right).$

Proof

Using the recursive formula in (9), the DP is calculated for every job $j,~1 \le j \le n$, every possible processing time (which is bounded by $P$), and every rejection cost $r~$ (which is bounded by $~R$), resulting in a processing time of $O\left( {n \cdot P \cdot R} \right)$. The calculation of the optimal solution, $f\left( {n,t_{0} ,r_{0} } \right) = \min \left\{ {f\left( {n,t,r} \right)|0 \le t \le P,~0 \le r \le R~} \right\}$, is done in $O\left( R \right)$. The reconstruction of the solution is done by backtracking, starting at $f\left( {n,t_{0} ,r_{0} } \right)$ and ending at $f\left( {0,0,0} \right)$, for an addition of $O\left( {n + P + R} \right)$ operations. We conclude that the total processing time is still $O\left( {n \cdot P \cdot R} \right)$. $\hfill{\square }$

Example 1

Consider the following six-job problem, in which the rejection cost limit is ${{R}} = 72$ and the common lead-time is ${{l}} = 0$. The processing times are $p_{j} = \left( {18,~26,~35,~40,~30,~31} \right)$, the rejection costs are ${\text{~}}r_{j} = \left( {35,~47,~43,~14,~32,~46} \right)$, and the job-dependent cost parameters are $\alpha _{j} = \left( {13,~12,~19,~23,~21,~1} \right)$, $\beta _{j} = \left( {3,~9,~8,~4,~3,~2} \right)$, and $\gamma _{j} = \left( {4,~4,~4,~23,~10,~20} \right)$. Our solution starts by utilizing $w_{j} = \min \left\{ {\beta _{j} ,\gamma _{j} } \right\}$, resulting in $w_{j} = \left( {3,~4,~4,~4,~3,~2} \right)$. Subsequently, ${\text{~}}\frac{{p_{j} }}{{w_{j} }} = \left( {6.0,~6.5,~8.75,~10.0,~10.0,~15.5} \right)$, implying that the jobs are sequenced in a WSPT order.

Executing $DP1.1$, the set of rejected jobs is ${\mathcal{J}}_{R} = \left\{ {J_{3} ,~J_{4} } \right\}$ with a total rejection cost $\sum\nolimits_{{j \in {\mathcal{J}}_{R} }} {r_{j} = 57 \le 72 = ~R}$.

The set of accepted jobs is the complementary set ${\mathcal{J}}_{P} = \left( {J_{1} ,~J_{2} ,~J_{5} ,~J_{6} } \right)$, the jobs’ due dates are $d_{j} = \left( {0,~44,~0,~0} \right)$, their tardiness values are $T_{j} = \left( {18,~0,74,~105} \right)$, and their due-tardiness values are $A_{j} = \left( {0,~44,~0,~0} \right)$. Consequently, the total processing cost is $Z = 662$.

In the next subsection, we focus on Problem $\boldsymbol{P}1.2$. As mentioned above, this is the complemeary problem of $\boldsymbol{P}1.1$ and the goal is to minimize the total rejection costs, subject to the constraint that the total weighted completion cannot exceed a given upper bound ($Q$). Thus, our problem, denoted as $\boldsymbol{P}1.2$, is $1~\left| {\sum w_{j} C_{j} \le Q} \right|\sum r_{j}$. Shabtay et al. [17] indicated that since the decision version of Problem $\boldsymbol{P}1.1$ is identical to that of $\boldsymbol{P}1.2$, then $\boldsymbol{P}1.2$ is also NP-hard. Hence, we turn our attention toward providing a DP solution for the problem at hand.

Let $g\left( {j,t,r} \right)~$ denote the total rejection cost for the partial schedule of jobs $1, \ldots ,j$, having a completion time $t$ and a total rejection cost $r$. Similar to DP1.1, we first sort the jobs in a WSPT order. At each iteration of the DP, the scheduler then needs to decide whether to reject job $j$, implying that the total rejection cost is increased, or accept job $j$, which increases in the total weighted completion time. In the suggested DP, we must keep track of the scheduling measure to ensure that its value does not exceed the dictated upper bound. To this end, we utilize a variable, $h_{j}$, which represents the total weighted completion time of the accepted jobs of subset $\left\{ {1, \ldots ,j} \right\}$, defined as follows:

$$ h_{j} = \left\{ {\begin{array}{*{20}l} {h_{{j - 1}} + w_{j} t,} \hfill & {{\text{if~job}}\;j\;{\text{is~accepted}}} \hfill \\ {h_{{j - 1}} ,} \hfill & {{\text{else}}} \hfill \\ \end{array} } \right.,\quad {\text{where}}\quad h_{0} = 0. $$

Dynamic programming algorithm DP1.2:

$$ g\left( {j,t,r} \right) = \left\{ {\begin{array}{*{20}l} {\infty ,} \hfill & {p_{j} > t\quad {\text{and}}\quad r_{j} > r} \hfill \\ {g\left( {j - 1,t - p_{j} ,r} \right),} \hfill & {p_{j} \le t\quad {\text{and}}\quad h_{j} \le Q\quad {\text{and}}\quad r_{j} > r} \hfill \\ {g\left( {j - 1,t,r - r_{j} } \right) + r_{j} ,} \hfill & {p_{j} > t\quad {\text{and}}\quad r_{j} \le r} \hfill \\ {\min \left\{ {\begin{array}{*{20}l} {g\left( {j - 1,t - p_{j} ,r} \right)} \hfill \\ {g\left( {j - 1,t,r- r_{j} } \right)} +r_{j},\hfill \\ \end{array} ,} \right.} \hfill & {p_{j} \le t\quad {\text{and}}\quad h_{j} \le Q\quad {\text{and}}\quad r_{j} \le r} \hfill \\ \end{array} } \right. $$

(10)

In this equation, the first line reflects an unfeasible case, the second line reflects the option of processing job $j$, the third line represents the option of rejecting job $j$, the fourth line reflects the case in which job $j$ may be either processed or rejected and the option that achieves the minimal cost is selected. The boundary conditions are $g\left( {0,0,0} \right) = 0$, $g\left( {0,t,r} \right) = \infty$ if $0 < t \le \sum p_{j} = P$, and $0 < r \le \sum r_{j}$. The optimal solution is given by $\min \left\{ {g\left( {n,t,r} \right)|0 \le t \le P,~0 \le r \le \sum r_{j} } \right\}$.

Theorem 3

Algorithm DP1.2 solves Problem P1.2 and its computational complexity is $O\left( {n \cdot P \cdot \sum r_{j} } \right).$

Proof

The proof is similar to those given for Theorems 1 and 2. Therefore, it is omitted here.

5 Problem $\boldsymbol{P}2.1\;1\left| {\boldsymbol{l}_{\boldsymbol{j}} = \boldsymbol{l},\,\,\sum_{{\boldsymbol{j} \in {\mathcal{J}}_{\boldsymbol{R}} }} {\boldsymbol{r}_{\boldsymbol{j}} \le \boldsymbol{R}} } \right|\sum_{{\boldsymbol{j} \in {\mathcal{J}}_{\boldsymbol{P}} }} {\left( {\boldsymbol{\alpha E}_{\boldsymbol{j}} + \boldsymbol{\beta T}_{\boldsymbol{j}} + \boldsymbol{\gamma A}_{\boldsymbol{j}} } \right)}$ and its complementary problem $\boldsymbol{P}2.2\;1\left| {\boldsymbol{l}_{\boldsymbol{j}} = \boldsymbol{l},\,\sum_{{\boldsymbol{j} \in {\mathcal{J}}_{\boldsymbol{P}} }} {\left( {\boldsymbol{\alpha E}_{\boldsymbol{j}} + \boldsymbol{\beta T}_{\boldsymbol{j}} + \boldsymbol{\gamma A}_{\boldsymbol{j}} } \right)} \le \boldsymbol{Q}} \right|\sum_{{\boldsymbol{j} \in {\mathcal{J}}_{\boldsymbol{R}} }} {\boldsymbol{r}_{\boldsymbol{j}} }$

In this section, we extend the classic DIF model introduced by Seidman et al. [15], which postulates common cost parameters and a common lead time, by considering job-rejection. Employing Property 2 and setting $w = \min \left\{ {\beta ,\gamma } \right\}$ and $l_{j} = l$, for $~j = 1, \ldots ,n$ in (7), we obtain

$$ 1~\left| {~l_{j} = l,~\sum r_{j} \le R} \right|w\sum \max \left( {0,~C_{j} - l} \right). $$

(11)

Shabtay and Steiner [18] show that the TWETD problem is equivalent to the well-known problem $1\left| {d_{j} = d} \right|\sum T_{j}$. Replacing $l_{j}$ by $d_{j}$, for $j = 1, \ldots ,n$ and $l$ by $d$, we conclude that Problem $\boldsymbol{P}2.1$ can be reformulated as:

$$ 1~\left| {~d_{j} = d,~\sum r_{j} \le R~} \right|w\sum T_{j} , $$

(12)

and its complementary problem, $\boldsymbol{P}2.2$, is reduced to

$$ 1~\left| {d_{j} = d,~w\sum T_{j} \le Q} \right|\sum r_{j} . $$

Zhang et al. [23] proved that (12) is binary NP-hard by reduction from Knapsack; subsequently, Problem $\boldsymbol{P}2.1$ is also NP-hard. Below, we provide a pseudo-polynomial time DP algorithm for Problem $\boldsymbol{P}2.1$, establishing that it remains ordinary NP-hard. Following Seidman et al. [15], we start the DP by sorting the jobs in a Shortest Processing Time first (SPT) order.

At each iteration of the DP, we compute the minimum due-date tardiness of jobs 1 to $j$ that have a total processing time $t$ and an upper bound $r$ on the rejection cost. The computation is based on the results obtained for jobs 1 to $j - 1$ that have:

• (i) Completion time $t - p_{j}$ and an upper bound rejection cost $r$;

• (ii) Completion time $t$ and an upper bound rejection cost $r - r_{j}$.

At each stage, one needs to decide whether to accept or reject job $~j$:

• (i) Job $j$ must be accepted if its rejection cost exceeds the current rejection limit $r$.

• (ii) Job $j$ may be accepted if its contribution minimises the total due-date tardiness.

• (iii) Job $j$ may be rejected if it minimises the objective function.

The recursive formula is given in the following dynamic programming algorithm DP2.1:

$$ f\left( {j,t,r} \right) = \left\{ {\begin{array}{*{20}l} {\infty ,} \hfill & {p_{j} > t\quad {\text{and}}\quad r_{j} > r} \hfill \\ {f\left( {j - 1,t - p_{j} ,~r} \right) + w\max \left( {0,{\text{~}}t - l} \right),} \hfill & {p_{j} \le t\quad {\text{and}}\quad r_{j} > r} \hfill \\ {f\left( {j - 1,t,r - r_{j} } \right),} \hfill & {p_{j} > t\quad {\text{and}}\quad r_{j} \le r} \hfill \\ {\min \left\{ {\begin{array}{*{20}l} {f\left( {j - 1,t - p_{j} ,~r} \right) + w\max \left( {0,{\text{~}}t - l} \right)} \hfill \\ {f\left( {j - 1,t,r - r_{j} } \right)} \hfill \\ \end{array} ,} \right.} \hfill & {p_{j} \le t\quad {\text{and}}\quad r_{j} \le r} \hfill \\ \end{array} } \right. $$

(13)

The boundary conditions are $f\left( {0,0,r} \right) = 0$ for $~0 \le r \le R$, $f\left( {0,t,r} \right) = \infty$ for $0 \le r \le R,~0 < t \le P \, {\text{and}} \, f\left( {j,t,0} \right) = \sum\nolimits_{{k = 1}}^{j} {w~\max \left( {0,t - l} \right)}$, and $t = \sum\nolimits_{{k = 1}}^{j} {p_{k} }$. The optimal solution is given by $\min \left( {f\left( {n,t,r} \right){\text{|}}0 \le t \le P,~0 \le r \le R} \right)$.

Theorem 4

Algorithm DP2 solves Problem P2.1 .

Proof

The correctness proof is identical to the proof of Theorem 1 by substituting the additional cost incurred by job $j$ $w_{j} t$ by $w\max \left( {0,{\text{~}}t - l} \right)$. $\hfill{\square }$

Theorem 5

The computational complexity of ${\text{DP}}2.1$ is $O\left( {n \cdot P \cdot R} \right)$.

Proof

The proof is similar to the proof of Theorem 2. $\hfill{\square }$

Example 2

Assume a six-job problem with $R = 13$, $\alpha = 16,~~\beta = 5,~\gamma = 15$, and $l = 15$. The processing times (sequenced in an SPT order and renumbered) are $p_{j} = \left( {6,~7,~8,~9,~11,~16} \right)$, and their rejection costs are $r_{j} = \left( {11,~8,~2,~3,~9,~13} \right)$. Since $\beta = 5 \le 15 = \gamma$, all processed jobs are tardy, i.e., $A_{j} = 0,~\forall j \in {\mathcal{J}}_{P}$. Applying $DP2$, the following optimal solution is attained.

The set of rejected jobs is ${\mathcal{J}}_{R} = \left\{ {J_{2} ,~J_{3} ,~J_{4} } \right\}$, with a total rejection cost of $\sum\nolimits_{{j \in {\mathcal{J}}_{R} }} {r_{j} = 13 \le 13 = ~R}$.

The set of accepted jobs is ${\mathcal{J}}_{P} = \left( {J_{1} ,~J_{5} ,~J_{6} } \right)$, the due dates of these jobs is $d_{j} = \left( {6,~15,~15} \right)$, and their tardiness is $T_{j} = \left( {0,~2,~18} \right)$. The total processing cost is, therefore, $Z = 100$.

In what follows, we concentrate on the complementary problem of $\boldsymbol{P}2.1$. Our goal is to minimise the total rejection cost subject to the constraint that the total weighted tardiness cannot exceed a given upper bound ($Q$). Thus, our problem, denoted $\boldsymbol{P}2.2$, is $1~\left| {w\sum T_{j} \le Q} \right|\sum r_{j}$. Let $g\left( {j,t,r} \right)~$ denote the total rejection cost for the partial schedule of jobs $1, \ldots ,j$, with a completion time $t$ and a total rejection cost $r$. At each iteration of the DP, the scheduler must decide whether to reject job $j$, implying that the total rejection cost is increased, or to accept job $j$, and that the total weighted tardiness time is increased. Similar to the explanation of DP1.2, in the current DP, we need to keep track to the total weighted tardiness, which is defined as follows:

$$ h_{j} = \left\{ {\begin{array}{*{20}l} {h_{{j - 1}} + w\max \left\{ {0,~t - l} \right\},} \hfill & {{\text{if~job}}\;j\;{\text{is~accepted}}} \hfill \\ {h_{{j - 1}} ~,} \hfill & {{\text{else}}} \hfill \\ \end{array} ,\quad {\text{where}}\quad h_{0} = 0.} \right. $$

Dynamic programming algorithm DP2.2:

$$ g\left( {j,t,r} \right) = \left\{ {\begin{array}{*{20}l} {\infty ,} \hfill & {p_{j} > t\quad {\text{and}}\quad r_{j} > r} \hfill \\ {g\left( {j - 1,t - p_{j} ,r} \right),} \hfill & {p_{j} \le t\quad {\text{and}}\quad h_{j} \le Q\quad {\text{and}}\quad r_{j} > r} \hfill \\ {g\left( {j - 1,t,r - r_{j} } \right) + r_{j} ,} \hfill & {p_{j} > t\quad {\text{and}}\quad r_{j} \le r} \hfill \\ {\min \left\{ {\begin{array}{*{20}l} {g\left( {j - 1,t - p_{j} ,r} \right)} \hfill \\ {g\left( {j - 1,t,r - r_{j} } \right) + r_{j} } \hfill \\ \end{array} ,} \right.} \hfill & {p_{j} \le t\quad {\text{and}}\quad h_{j} \le Q\quad {\text{and}}\quad r_{j} \le r} \hfill \\ \end{array} } \right. $$

(14)

The boundary conditions are $g\left( {0,0,0} \right) = 0$, $g\left( {0,t,r} \right) = \infty$ if $0 < t \le \sum p_{j} = P$, and $0 < r \le \sum r_{j}$. The optimal solution is given by $\min \left\{ {g\left( {n,t,r} \right)|0 \le t \le P,~0 \le r \le \sum r_{j} } \right\}$.

Theorem 6

Algorithm DP2.2 solves Problem ${\mathbf{P}}2.2$ and its computational complexity is $O\left( {n \cdot P \cdot \sum r_{j} } \right).$

Proof

The proof is similar to those given for Theorems 4 and 5.

6 Problem $\boldsymbol{P}3\;1\left| {\boldsymbol{l}_{\boldsymbol{j}} = \boldsymbol{l},\sum\nolimits_{{\boldsymbol{j} \in {\mathcal{J}}_{\boldsymbol{R}} }} {\boldsymbol{r}_{\boldsymbol{j}} \le \boldsymbol{R}} } \right|\sum\nolimits_{{\boldsymbol{j} \in {\mathcal{J}}_{\boldsymbol{P}} }} {\left( {\boldsymbol{\alpha}_{\boldsymbol{j}} \boldsymbol{E}_{\boldsymbol{j}} + \boldsymbol{\beta}_{\boldsymbol{j}} \boldsymbol{T}_{\boldsymbol{j}} + \boldsymbol{\gamma}_{\boldsymbol{j}} \boldsymbol{A}_{\boldsymbol{j}} } \right)}$

Next, we consider job-dependent cost parameters and a common lead-time with optional job-rejection, formally given in (3) and rewritten as:

$$ 1~\left| {~l_{j} = l~,~\sum r_{j} \le R~} \right|\sum \left( {\alpha _{j} E_{j} + \beta _{j} T_{j} + \gamma _{j} A_{j} } \right). $$

(14)

Using Property 2 and setting $w_{j} = \min \left\{ {\beta _{j} ,\gamma _{j} } \right\}$ and $l_{j} = l$ for $j = 1, \ldots ,n$ in (7), we obtain:

$$ 1\left| {~l_{j} = l,~\sum r_{j} \le R} \right|\sum w_{j} \max \left( {0,~C_{j} - l} \right). $$

(15)

If job-rejection is not allowed, then the problem is equivalent to minimising the total weighted tardiness with a common due date, i.e., $1\left| {d_{j} = d} \right|\sum w_{j} T_{j}$. This problem was proved to be NP-hard by Yuan [22], hence, $\boldsymbol{P}3$ is also NP-hard. Below, we present an $O\left( {n^{2} \cdot l \cdot R} \right)$ DP algorithm solution for $\boldsymbol{P}3$.

Kellerer and Strusevich [8] propose an $O\left( {nP\left( {W^{{UB}} } \right)^{2} } \right)$ time DP algorithm solution, where $W^{{UB}}$ is the upper bound on the total weighted tardiness with a common due date on a single machine. Kianfar and Moslehi [9] suggest an $O\left( {n^{2} d} \right)$ pseudo-polynomial DP algorithm time extending the algorithm of Kacem [7]. This running time also improves the complexity of the algorithm of Kellerer and Strusevich because $n < W^{{UB}}$ and $d < P$ for non-trivial cases. Our solution to P3 also extends the solution of Kacem [7] by considering all cases and the option of job rejection [13]. For completeness of exposition, we report it briefly here. Early jobs are scheduled starting at time 0, while tardy jobs are scheduled so that they are completed at time $P$, going backwards. Let $t$ denote the completion time of the last early job (scheduled before $l$), let $r \in \left\{ {0,1, \ldots ,R} \right\}$ denote the allowed rejection costs, and let $f$ denote the minsum DIF of the corresponding schedule. The DP solution, given in Algorithm $DP3$, generates a set of states, $v_{k}$, for each iteration $k$, $1 \le k \le n$. Each state in $v_{k}$ is represented by an ordered triple $\left( {r,t,f} \right)$, implying a completion time $t$, a rejection cost $r$, and a cost $f$ for the first $k$ jobs. The initial sorting of the jobs is in a Weighted Longest Processing Time first (WLPT) rule order; however, eventually, the tardy jobs are sequenced in accordance with the WSPT rule. In an optimal schedule, the early jobs are processed starting at time zero, and they may be followed by a straddling job that starts before time l and is completed, at least, at time l; the straddling job, in turn, is followed by the tardy jobs. The loop starting on line 6 of Algorithm $DP3$, below, addresses straddling jobs, as each job can potentially be the straddling job; the remaining $n - 1$ jobs can be either early (line 4) or late (line 5), but not straddling. When a job $k$ is rejected, the cost of the tardy jobs scheduled thus far—those scheduled to the right of $k$, i.e., jobs with $p_{j} /w_{j} \ge p_{k} /w_{k}$—must be updated. For a given schedule $\sigma$, let $q_{T} \subseteq {\mathcal{J}}_{P}$ be the set of tardy jobs of $\sigma$. The following Lemma is proved in Mor and Shapira [13].

Lemma 1

The difference in the minsum DIF between accepting and rejecting job $k$ is $\sum\nolimits_{\begin{subarray}{l} j \in q_{T} \\ j < k \end{subarray} } {w_{j} p_{k} }$.

It follows that, for each state, we additionally store the summation of the weights of the tardy jobs that have already been scheduled. Thus, the value of the minsum DIF is updated in constant time, when a certain job $k$ is rejected. In Algorithm $DP3$ the loop $r \in \left\{ {0,1, \ldots ,R} \right\}$, which starts on line 2 of this algorithm, examines, on line 5(iii), all possible rejection costs.

Dynamic programming algorithm $DP3$:

Theorem 7

Algorithm DP3 solves Problem P3 and its computational complexity is $O\left( {n^{2} \cdot l \cdot R} \right)$.

Proof

The correctness of DP3 follows from the reduction of $\boldsymbol{P}3$ to $1\left| {~l_{j} = l,~\sum r_{j} \le R} \right|\sum w_{j} \max \left( {0,~C_{j} - l} \right)$ and from the correctness of Lemma 1. For the running time of DP3, the inner loop is applied $n - 1$ times on each triplet in $\upsilon _{{k - 1}}^{j}$ at each iteration $1 \le k \le n$. Each triplet can be examined to see whether step (1) or step (3) should be applied, such that traversing the states in $\upsilon _{{k - 1}}^{j}$ is, in fact, done only once—in a linear order. As stated by Kacem [7], the complexity of the inner loop of $DP3$ is proportional to $\sum\nolimits_{{k = 1}}^{n} {\left| {v_{k}^{j} } \right|}$, where $\left| {v_{k}^{j} } \right|$ denotes the size of $v_{k}^{j}$. By choosing the state $\left( {r,t,f} \right)$ with the smallest value $f$ at each iteration $k$ and for every $t$, the time is bounded by $O\left( {n \cdot l} \right)$, as $d$ is the maximum value that $t$ can reach. The next outer loop is then applied $R$ times for each possible total rejection cost. Finally, the outer loop is applied $n$ times for each potential straddling job, for a total of $O\left( {n^{2} \cdot l \cdot R} \right)$. Returning the minimum cost on the last line requires a linear scan of all ordered triples in $\upsilon _{n}^{j}$, which does not increase the asymptotic running time. Therefore, the total running time is $O\left( {n^{2} \cdot l \cdot R} \right)$. $\hfill{\square }$

Example 3

Consider the following six-job problem, where the rejection cost limit is $R = 12$ and the common lead time is $l = 28$. The processing times, sequenced in WLPT order and renumbered, are $p_{j} = \left( {27,~12,~32,~27,~32,~5} \right)$, with rejection costs $r_{j} = \left( {8,~11,~7,~9,~1,~6} \right)$. The job-dependent cost parameters are $\alpha _{j} = \left( {20,~16,~17,~5,~14,~8} \right)$, $\beta _{j} = \left( {1,~15,~7,~8,~11,~16} \right)$, and $\gamma _{j} = \left( {4,~1,~7,~18,~17,~12} \right)$.

Calculating the weights using (6), we obtain $w_{j} = \min \left\{ {\beta _{j} ,\gamma _{j} } \right\} = \left( {1,~1,~7,~8,~11,~12} \right)$ and, subsequently, $\frac{{p_{j} }}{{w_{j} }} = \left( {27.000,~12.000,~4.571,~3.375,~2.909,~0.417} \right)$. Applying DP3, the set of rejected jobs is ${\mathcal{J}}_{R} = \left\{ {J_{3} ,~J_{5} } \right\}$, implying that $\sum\nolimits_{{j \in {\mathcal{J}}_{R} }} {r_{j} = 8 \le 12 = R}$. The set of accepted jobs is ${\mathcal{J}}_{P} = \left( {~J_{6} ,~J_{4} ,~J_{2} ,~J_{1} } \right)$. Using Property 2, $d_{j} = \left( {5,~28,~64,~28} \right)$ and, therefore, $T_{j} = \left( {0,~4,~0,~43} \right)$, $A_{j} = \left( {0,~0,~16,~0} \right)$, and the total processing cost is $Z = 91$.

7 Problem $\boldsymbol{P}4\;1\left| {\boldsymbol{l}_{\boldsymbol{j}} ,\sum\nolimits_{{\boldsymbol{j} \in {\mathcal{J}}_{\boldsymbol{R}} }} {\boldsymbol{r}_{\boldsymbol{j}} \le \boldsymbol{R}} } \right|\sum\nolimits_{{\boldsymbol{j} \in {\mathcal{J}}_{\boldsymbol{P}} }} {\left( {\boldsymbol{\alpha E}_{\boldsymbol{j}} + \boldsymbol{\beta T}_{\boldsymbol{j}} + \boldsymbol{\gamma A}_{\boldsymbol{j}} } \right)}$

In this section, we study common cost parameters and job-dependent lead-times. Setting $w = \min \left\{ {\beta ,\gamma } \right\}$ in (6), $\boldsymbol{P}4$ can be reformulated as:

$$ 1\left| {l_{j} ,~\sum r_{j} \le R} \right|w\sum \max \left( {0,~C_{j} - l_{j} } \right). $$

(16)

Denoting by $\boldsymbol{P}^{'} 4$ the problem $\boldsymbol{P}4$ without the option of job-rejection, it follows from (16) that $\boldsymbol{P}^{'} 4$ is equivalent to the fundamental problem, $1\left| ~ \right|\sum T_{j}$. This fundamental problem was studied by Lawler [10] and proved by Du and Leung [2] to be ordinary NP-hard. Assuming that the weights of the jobs are agreeable, i.e., that $p_{i} < p_{j}$ implies that $w_{i} \ge w_{j}$, Lawler showed that an optimal sequence can be found by a DP algorithm with a worst-case running time of $O\left( {n^{4} P} \right)$ or $O\left( {n^{5} p_{{\max }} } \right)$. Steiner and Zhang [21] studied a problem related to $P^{'} 4$, namely, $1\left| {l_{j} } \right|\sum \max \left( {0,~d_{j} - l_{j} } \right) + \sum \beta _{j} U_{j}$, where $\alpha$ is the delivery time quotation cost per extended time unit, $\beta _{j}$ is the job-dependent tardiness cost (which can be treated as a rejection cost), and $U_{j}$ is a binary variable, such that $U_{j} = \left\{ {\begin{array}{*{20}c} {1,~~C_{j} > d_{j} } \\ {0,~~C_{j} \le 0} \\ \end{array} } \right.$, $j = 1, \ldots ,n$. They proved that this problem is equivalent to the problem of minimising the total tardiness with rejection, and they presented an $O\left( {n^{4} P^{3} } \right)$ time DP algorithm and an $O\left( {n^{4} Z^{3} } \right)$ time FPTAS algorithm, where $Z$ is an upper bound on the optimal solution, based on Lawler [10]. Based on the DP provided in Lawler [10], we introduce a DP algorithm with a worst-case running time of either $O\left( {n^{4} \cdot P \cdot R} \right)$ or $O\left( {n^{5} \cdot p_{{\max }} \cdot R} \right)$ for Problem $\boldsymbol{P}4$, proving that it remains NP-hard in the ordinary sense.

First, we claim that, because $w_{j} = w,~~~j = 1, \ldots ,n$ in our problem, Lawler’s agreeability assumption is clearly valid. We start by ordering the jobs in an Earliest Due Date first (EDD) order, $1,2, \ldots ,n$. Following Lawler, we denote by $S\left( {i,j,k} \right)$ the subset of jobs in $i,i + 1, \ldots ,j~$ that have processing times shorter than those of job $k$, formally $S\left( {i,j,k} \right) = \left\{ {j^{'} {\text{|}}i \le j^{'} \le j,p_{{j^{'} }} < p_{k} ~} \right\}$. We define $T\left( {S\left( {i,j,k} \right),t,r} \right)$ as the total weighted tardiness for an optimal schedule of the jobs in $S\left( {i,j,k} \right)$, starting at time $t$ and with a total rejection cost $R$.

Lawler [10] proved that for some $\delta$, $0 \le \delta \le n - k$ there exists an optimal schedule so that:

• 1. Jobs $1,2, \ldots ,k - 1,k + 1,~ \ldots ,k + \delta$ in some sequence start at time $t$, followed by

• 2. Job $k$, with a completion time of $C_{k} \left( \delta \right) = t + \mathop \sum \limits_{{j \le k + \delta {\text{~}}}} p_{j}$, followed by

• 3. Jobs $k + \delta + 1,k + \delta + 2, \ldots ,n$ in some sequence starting at time $C_{k} \left( \delta \right)$.

For simplicity, we present the DP algorithm in two stages: first for computing the total weighted tardiness, and then for allowing rejection. Based on Lawler’s DP algorithm:

$T\left( {S\left( {i,j,k} \right),t,r} \right) = {\text{min}}_{\delta } \left\{ {T\left( {S\left( {i,k^{'} + \delta ,k^{'} } \right),t,r} \right) + w_{{k^{'} }} \cdot \max \left( {0,~C_{{k^{'} }} \left( \delta \right) - d_{{k^{'} }} } \right) + T\left( {S\left( {k^{'} + \delta + 1,j,k^{'} } \right),C_{{k^{'} }} \left( \delta \right),r} \right)} \right\}$, where $k^{'}$ is the job with the maximal processing time within $S\left( {i,j,k} \right)$, and

$$\begin{aligned} & C_{{k^{'} }} \left( \delta \right) = t + \sum_{{j^{'} \le k^{'} + \delta ~}} p_{{j^{'} }} . \\ & T\left( {\left\{ {1,2, \ldots ,n} \right\},t,r} \right) = \min \left( {T\left( {\left\{ {1,2, \ldots ,n} \right\},t,r} \right),\min _{k} \left\{ {T\left( {S\left( {i,j,k} \right),t,r - r_{k} } \right)} \right\}} \right). \end{aligned}$$

(17)

The boundary conditions are $T\left( {\emptyset ,t,r} \right) = 0$, $T\left( {\left\{ j \right\},t,0} \right) = w_{j} \cdot \max \left( {0,~t - p_{j} - l_{j} } \right)$ and if $r > 0,~T\left( {\left\{ j \right\},t,r} \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {r_{j} \le r} \hfill \\ {T\left( {\left\{ j \right\},t,0} \right)} \hfill & {{\text{else}}} \hfill \\ \end{array} } \right.$.

Theorem 8

Algorithm DP4 solves Problem P4 and its computational complexity is$O\left( {n^{4} \cdot P \cdot R} \right)$.

Proof

By induction on $r$. The correctness of the base case of the induction follows directly from the correctness of $T\left( {S\left( {i,j,k} \right),t,r} \right)$ for $r = 0$ using the truth of the algorithm of Lawler. The correctness of $T\left( {\left\{ {1,2, \ldots ,n} \right\},t,r} \right)$ then follows from the induction hypothesis, which assumes correctness for all values lower than $r$ and for all groups of cardinality lower than $n$ in Eq. (17).

The correctness of the running time follows directly from the definition of $T\left( {S\left( {i,j,k} \right),t,r} \right)$. The group $S\left( {i,j,k} \right)$ is defined for each $i,j,k$, where $1 \le i,j,k \le n$, $t$ is defined for each $1 \le t \le P$, and $r$ is defined for each $1 \le r \le R$. Calculating $T\left( {S\left( {i,j,k} \right),t,r} \right)$ requires another factor of $n$ for the minimum calculation running over all $\delta$ s, $1 \le \delta \le n$. $\hfill{\square }$

Example 4

Assume a problem of five jobs with $R = 5$, $\alpha = 7,~~\beta = 6,~~\gamma = 11$, $w = \min \left\{ {\beta ,\gamma } \right\} = 6$, and $l_{j} = \left( {24,~28,~35,~36,~67} \right)$. The processing times, sequenced in their EDD order, are $~p_{j} = \left( {17,~16,~14,~19,~15} \right)$, and their rejection costs are $r_{j} = \left( {3,~3,~4,~3,~2} \right)$. Since $\beta = 6 \le 11 = \gamma$, all processed jobs are tardy. By applying the solution shown above, the set of rejected jobs in the optimal solution is ${\mathcal{J}}_{R} = \left\{ {J_{1} ,~J_{5} } \right\}$, with a total rejection cost of $5 \le ~5 = R$. The set of processed jobs is ${\mathcal{J}}_{P} = \left( {J_{2} ,~J_{3} ,~J_{4} } \right)$, their due-dates are $d_{j} = \left( {16,~30,~36} \right)$, and their tardiness is $T_{j} = \left( {0,~1,~13} \right)$. The total processing cost is, therefore, $Z = 84$.

8 Numerical study

We performed numerical tests to measure the running time of algorithms $DP1.1$, $DP2.1$, and $DP3$. Throughout this experimental study, the job processing times ($p_{j} )$ and rejection costs ($r_{j} )$ were generated uniformly in the interval $\left[ {1,~50} \right]$, and the cost parameters ($\alpha _{j} ,\beta _{j} ,~\gamma _{j}$) were generated uniformly in the interval $\left[ {1,~20} \right]$. We denote by $\bar{p}$ and $\bar{r}$ the maximum possible value of jobs’ processing times and rejection costs, respectively; thus, $\bar{p} = \bar{r} = 50$. The different C++ programs were executed on an Intel (R) Core™ i7-8650U CPU @ 1.90 GHz, 16.0 GB RAM platform. All numerical results are presented in tables constructed in the same format; the columns indicate the number of jobs, $n$, the range of the rejection cost, $R$, and the average and worst-case running times.

$DP1.1$: Instances with $n = 15,~30,~45,$ and 60 jobs were generated, where the cost parameters are job-dependent and the common lead time set to zero. The upper bound on the total rejection cost, $R$, was generated uniformly in three intervals: $\left[ {0.0025,~~0.0050} \right]\bar{r}n,~\left[ {0.0075,~~0.010} \right]\bar{r}n$, and $\left[ {0.015,~~0.020} \right]\bar{r}n$. Note that these intervals roughly reflect rejections of 5%, 10%, and 15% of the jobs, respectively. For each combination of $n$ and $R$, 20 instances were generated and solved. The results in Table 1 demonstrate that $DP1.1$ is efficient for solving medium-size problems. The worst-case running time for problems of 60 jobs and 15% rejected jobs did not exceed 12 ms.

Table 1 Average and worst-case running times of the DP1 algorithm for Problem P1, with either 5%, 10%, or 15% rejected jobs (top, middle, and bottom tables, respectively)

$DP2.1$: Instances with $n = 50,~75,~100,~125$, and 150 jobs were generated. The cost parameters are common to all jobs and the common lead time was generated uniformly in the interval $\left[ {0,~0.25} \right]n\bar{p}$. The upper bound on the total rejection cost was generated uniformly in the intervals $\left[ {0.005,~0.010} \right]n\bar{r},\left[ {0.015,~0.020} \right]n\bar{r}$, and $\left[ {0.025,~0.030} \right]n\bar{r}$, reflecting approximately 10%, 15%, and 20% of rejected jobs. Table 2 presents the average and worst-case running times of Algorithm $DP2.1$ for solving 20 randomly generated instances of $n$ and $R$. Note that the worst-case running time for problems of 150 jobs and 20% rejected jobs did not exceed 3 s, demonstrating that, similar to $DP1$, $DP2.1$ is exceptionally efficient in solving medium-size problems.

Table 2 Average and worst-case running times of the DP2 algorithm for Problem P2, with either 10%, 15%, or 20% rejected jobs (top, middle, and bottom tables, respectively)

$DP3$: Instances were generated with $n = 10,~20,~30$, and 40 jobs. The cost parameters are job dependent. A tightness factor $~\varepsilon = 0.20,~0.30,~0.40$ was used to generate the common lead time for each instance, as a factor of the total processing times, using $l = \varepsilon P$. The total rejection cost $R$ was generated uniformly in the interval $\left[ {0.02,~0.04} \right]n\bar{r}$, replicating approximately 20% of rejected jobs. For each set of $n$ and $l$, 20 cases were constructed and solved. Table 3 presents the average and worst-case running times (in seconds) for $\varepsilon = 0.20,~0.30,~$ and 0.40. The results demonstrate that $DP3$ is efficient and can solve medium-size problems. In particular, the worst-case running times for problems with $n = 40$, $\varepsilon = 0.40$, and 20% of rejected jobs is less than 4.1 s.

Table 3 Average and worst-case running times of the DP3 algorithm for Problem P3, with a tightness factor ($\varvec{\varepsilon}$) of either 0.2, 0.3, or 0.4 (top, middle, and bottom tables, respectively)

9 Conclusions

We studied a single-machine scheduling and due-date assignment problem, known as DIF, with the extension of optional job rejection that possibly bounds the constraints or the underlying cost functions. As DIF with job-dependent cost parameters and lead times is strongly NP-hard, we focused on several restricted versions of the problem, in which either the cost parameters or the lead times are job dependent. We established that all studied problems are NP-hard in the ordinary sense and introduced efficient pseudo-polynomial dynamic programming algorithms that are suitable for solving real-life, medium-sized instances. Solutions to larger instances may perhaps be addressed by FPTAS, metaheuristics, or machine learning. A challenging problem for future research is to provide a heuristic or branch and bound solution for the general problem of job-dependent cost parameters and lead times with an optional job-rejection, and to extend the setting to a more complex machine such as flowshops and parallel machines.