An efficient heuristic for a hub location routing problem

Abstract

This paper examines a new model for hub location known as the hub location routing problem. The problem shares similarities with the well studied uncapacitated single allocation p-hub median problem except that the hubs are now connected to each other by a cyclical path (or tour) known as the global route, each cluster of non-hub nodes and assigned hub is also connected by a single tour known as a local route, and the length of the local routes is constrained to a maximum number of nodes. Thus, aside from the normal tasks of hub selection and allocation of non-hub nodes, up to p + 1 travelling salesman problems need to be solved. A heuristic based on the general variable neighborhood search framework is proposed here to solve this very complicated problem. The improvement phase of the algorithm uses a sequential variable neighborhood descent with multiple neighborhoods required to suit the complex nature of the problem. A best sequencing of the neighborhoods is established through empirical testing. The perturbation phase known as the shaking procedure also uses a well-structured selection of neighborhoods in order to effectively diversify the search to different regions of the solution space. Extensive computational testing shows that the new heuristic significantly outperforms the state-of-the-art. Out of 912 test instances from the literature, we are able to obtain 691 new best known solutions. Not only are the improvements in objective values quite impressive, but also these new solutions are obtained in a small fraction of the time required by the competing algorithms.

1 Introduction

The aim of a transportation/communication network is to facilitate transport/communication between all origin–destination (O–D) pairs. Establishing direct transport/communication between all O–D pairs may be unreasonable for many reasons especially from the economic (or cost) perspective. As an alternative approach, the idea of hub networks has been proposed. The main feature of a hub network that differentiates it from other types is the existence of special nodes (hubs) designated to enable the connection between O–D pairs. Namely, instead of having a direct path between each pair of nodes, nodes communicate via hubs. For example, if we have an origin node O and a destination D, a valid path between them may have the form $O - hub_1 - hub_2 -D$. More precisely, the flow from O to D is first collected at $hub_1$ then transferred to $hub_2$ and finally delivered to node D. So, the main principle of hub networks is that direct connection between non-hub nodes is not possible, and instead, all transport/communication is performed via hub nodes. Hub nodes have a role to collect, consolidate and transfer, and finally distribute the flow in a hub network. Note that on a path $O - hub_1 - hub_2 -D$, hub nodes $hub_1$ and $hub_2$ may be the same. In this case the same hub is used for collection, consolidation and transfer, and distribution purposes,.

During the past years, many variants of the hub location problem, including those with and without capacity constraints, or with different allocation strategies, topologies and objective functions, have been studied. For more details on the classification, solution approaches and applications of hub location problems, we refer the reader to [1, 3,4,5,6, 8,9,10,11, 14,15,17, 21,22,23, 29,30,31, 34,35,36].

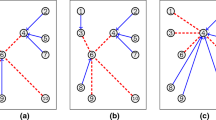
In this paper, we study a relatively new type of hub location problem known as the hub location routing problem. The main feature that differentiates this variant is the existence of local and global routes. A local route starts and ends at a hub that serves one or more non-hub nodes, while the global route is used to interconnect hub nodes, and its main purpose is to transfer the flow between hubs (see Fig. 1).

Fig. 1

A solution of a hub location routing problem

The problem studied in this paper consists of designating p nodes on a given network to serve as hubs, assigning each non-hub node to exactly one hub, connecting non-hub nodes assigned to the same hub by a route and linking hub nodes by a route so that the total routing cost is minimized. A constraint is placed on the maximum length of the local routes by specifying the maximum number of non-hub nodes allowed on a route. There is neither a capacity limitation imposed on the hubs nor a cost for hub installation. However, as in other hub location problems, a discount factor, $0 \le \alpha \le 1$, is applied when calculating the cost of the global route. The problem studied in this paper is referred to as the p-hub location routing problem (pHLRP).

The problem is formally defined on a graph $G=(V, E)$, where V is a given set of nodes and $E =\{(i,j)| i,j \in V \}$ is the set of edges that connect them. A non-negative cost $c_e$ is associated with each edge $e\in E$ representing the routing cost along that edge. A feasible solution of the problem provides p nodes from set V to serve as hubs. Each of these hubs is the root point of a local route starting and ending at it. Each local route is composed of non-hub nodes, and may contain at most C nodes including the hub. If we denote the chosen hubs as $hub_1, hub_2, \dots , hub_p$ and corresponding local routes as $r_1, r_2, \dots , r_p$, where $r_i$ is an ordered list of nodes, then $r_1 \cup r_2 \cup \dots \cup r_p =V$, and $r_i \cap r_j = \emptyset$, $i \ne j$. In other words, each non-hub node is assigned to exactly one hub. If we suppose that $r_i = \{hub_i, n_1^i, \dots , n_k^i,hub_i,\}$ then the cost of the route is calculated as

$$\begin{aligned} cost(r_i) = c_{(hub_i, n_1^i)} +\sum _{m=1}^{k-1} c_(n_m^i,n_{m+1}^i) + c_{(n_k^i, hub_i)}. \end{aligned}$$

If we suppose that the cost of a tour linking the hubs is $cost(hub\_tour)$ then the overall cost of the solution defined by hubs $hub_1, hub_2, \dots , hub_p$ and, corresponding local routes $r_1, r_2, \dots , r_p$, is calculated as: $\sum _{i=1}^p cost(r_i) + \alpha cost(hub\_tour)$. Note that the length of route $r_i$, with the above notation is, $length_i=k+1$. Note also that a route $r_i$ may contain no non-hub nodes at all. In this case the length of the local route is 1, i.e., it contains the trip from hub $hub_i$ to itself.

Applications of the pHLRP may be found, for example, in public and urban transportation systems such as subway and train lines. For example, in subway and train transportation, the inter-hub route consists of platforms that are used to consolidate passengers from many origins and allow their delivery to many destinations. In addition, some of these platforms are served by bus lines which are actually local routes that connect the passengers to the platforms. Another application of this problem arises when designing distributed data networks.

Regarding solution approaches for the problem, there are three heuristic methods available so far [20]: (i) a multi-start variable neighborhood descent, (ii) a Biased Random-Key Genetic Algorithm (BRKGA), and (iii) Local Solver version 6.0. According to the documentation, Local Solver combines different search techniques, constraint propagation, and linear mixed-integer as well as nonlinear programming. The multi-start variable neighborhood descent, in each iteration, applies a variable neighborhood descent (VND) on a random initial solution. Two different variable neighborhood descents (VND) are proposed in [20]. They both explore the same neighborhood structures defined by inserting non-hub nodes from one tour to another; exchanging two non-hub nodes; and changing a hub node. In addition both use the Lin-Kernighan heuristic to improve tours. As search strategies, both VNDs use neither a first nor best improvement search strategy, but execute a random improvement move. However, they differ in the way the exploration of neighborhoods is organized. The first one uses a nested VND scheme, while the other performs consecutive nested Neighborhood Search (CNS). The multi-start VND based on nested VND is denoted by M-VND, while the one using CNS is denoted as M-CNS. Both M-VND and M-CNS exhibit better performance than BRKGA.

In this paper we propose a general variable neighborhood search (GVNS) based approach. GVNS also employs VND as a local search but does not use a completely random re-start to resolve local optimum traps as is the case in M-VND and M-CNS. Instead, it modifies the current solution to varying degrees in order to resolve a local optimum trap. In addition, our GVNS differs from M-VND and M-CNS in the VND procedure. The difference comes from the number of neighborhood structures, the way the neighborhoods are organized in VND, and the search strategy. More precisely, our VND explores seven neighborhood structures in a sequential way using the first improvement strategy. This is a completely different approach from that used in [20]. In addition, our VND does not use the Lin-Kernighan heuristic, but adopts instead other neighborhood structures applicable to the traveling salesman problem (TSP).

The proposed GVNS approach is validated on benchmark instances, and its performance demonstrates both a superior efficiency and effectiveness. Namely, our GVNS succeeds to establish a large number of new best-known solutions. In addition, it turns out to be very efficient in solving large problem instances in a short time. Namely, in almost all large instances it provides significantly better solutions than previous ones in a fraction of the time. Hence, the contributions of the paper may be summarized as:

• A new heuristic for pHLRP is proposed and tested. It is based on exploring seven neighborhoods within a GVNS framework.

• The proposed approach outperforms the previous ones from the literature to a great extent, particularly on large scale instances.

• 691 out of 912 best-known solutions are improved by the proposed GVNS heuristic;

• The algorithm is also very fast compared to the previous methods.

The rest of the paper is organized as follows. The next section details the different components of the new heuristic, and puts them all together within the GVNS framework. This is followed by extensive computational work, which includes a validation of the selected VND structure and parameter specifications, a comparison with the state-of-the-art, and a statistical analysis that confirms the superiority of the new heuristic. Lastly, we provide some conclusions and suggestions for future research.

2 Proposed variable neighborhood search approach

In this section, we provide a detailed description of our solution approach. The section starts by describing the solution representation and the procedure for generating an initial solution. After that, details are provided on the various neighborhood structures used to refine the solution. Finally, the main ingredients of the proposed general variable neighborhood search are described.

2.1 Solution representation

Any solution of the pHLRP may be represented by the three following components: set $H=\{hub_1, hub_2, \dots , hub_p\}$ containing the p selected hub nodes, set $R =\{r_1, r_2, \dots , r_p\}$ containing the local routes assigned to the hubs, and the global route denoted as $hub\_tour$ which connects the hubs from set H. In the established notation each local route $r_i$ originates at hub node $hub_i$. In other words, each route $r_i$ has the form $hub_i - n_1^i - \dots - n_k^i -hub_i$ where $n_1^i- n_2^i \dots -n_k^i$ is the ordered sequence of non-hub nodes visited along the route starting and ending at $hub_i$. Hence, the solution is represented as the triplet $S=(H,hub\_tour, R)$.

2.2 Initial solution

To construct an initial solution we proceed in the following way. From the set V we choose p nodes at random to constitute set H. After that, we assign nodes to hubs and form routes as follows. For each non-hub node the corresponding hub is chosen at random from the set H, and the node is added at the end of the route of the chosen hub. The assignment is made while respecting the imposed constraint on the route length. The $hub_tour$ is constructed as a tour that connects hubs $hub_1, hub_2, \dots , hub_p$ in this order. The outline of the procedure is given by Algorithm 1. Note that a feasible solution is generated in this way.

2.3 Neighborhood structures

The solution generated by procedure Algorithm 1 will likely be far from the optimal one. However, it may be improved by replacing a hub by a node which is not a hub, or moving a non-hub node from one route to another, or changing the order of visiting nodes in the local routes and in the global route. Accordingly, we define the following neighborhoods:

• Insert neighborhood (${N}_{insert}$)- This neighborhood is based on a move that takes a single non-hub node from one local route and inserts it in another local route, while respecting the capacity of the local routes.

• Exchange (${N}_{exhange}$) - This neighborhood is based on a move that exchanges two non-hub nodes from two different local routes. Note that these moves preserve the number of non-hub nodes in each local route.

• Change hub (${N}_{change\_hub}$) - This neighborhood is based on moves that replace a single hub node by a non-hub node from the local route originating at this hub.

• LocalRoute neighborhoods - The purpose of LocalRoute neighborhoods is to optimize the order of visiting non-hub nodes within local routes as well as hub nodes within the global route. Here we adopt some k-opt neighborhoods used for solving the Traveling Salesman Problem (TSP) and its variants (see e.g. [12, 24, 28]). They are: 1-opt, 2-opt and OR-opt-1. The 2-opt neighborhood is based on a move that inverts a part of the route. A simplified variant of the 2-opt move is the 1-opt move, which inverts a part of a tour consisting of 2 consecutive nodes. The OR-opt-1 neighborhood is based on an insertion move that relocates a node from one position to another. Two types of insertion move may be distinguished: forward and backward insertion moves depending on whether a node is moved forward or backward in the tour, respectively. 1-opt, 2-opt, OR-opt-1 forward and OR-opt-1 backward will be denoted as ${N}_{1opt}$, ${N}_{2opt}$, ${N}_{Oropt1for}$ and ${N}_{Oropt1back}$, respectively.

Note that all of these neighborhood allow feasible moves only, i.e., moves that respect the capacity constraints (i.e., do not violate the maximum length of a local route). The change in value of the objective function caused by performing any of these moves may be calculated in constant time O(1).

2.4 Variable Neighborhood descent

The above neighborhood structures do not necessarily yield the same local optima. That is, a local optimum with respect to one neighborhood structure is not necessarily a local optimum with respect to another. In order to efficiently exploit the defined neighborhood structures we embed them in a sequential variable neighborhood descent (VND) framework [7, 13, 24]. In this way, the VND takes a feasible solution at the input and as the output returns a solution which is a local optimum with respect to all employed neighborhood structures. The steps of the VND procedure are provided in Algorithm 2. As observed in previous works on VND (see e.g. [24]), the ordering of the neighborhood structures in the search as well as the search strategy may have a significant impact on the final performance of the VND procedure. Due to the large size of the neighborhood structures we selected a first improvement search strategy, i.e., as soon as an improving solution is detected in some neighborhood structure it replaces the incumbent solution, and the search is re-started from it. Regarding the order of neighborhoods within the VND, we then performed an empirical study to identify a most suitable one (see Sect. 3). This empirical study provided the final selected order shown in line 1 of the algorithm. The statement LocalSearch$(S,{N}_k$) in line 3 denotes the local search with respect to the kth neighborhood in the ordered list N of neighborhoods.

2.5 General variable neighborhood search

In this section we describe our general variable neighborhood search (GVNS) heuristic. Recall that GVNS is a variant of variable neighborhood search [13, 26] that uses a variable neighborhood descent (VND) in the intensification phase (instead of a basic local search with a single neighborhood (see e.g., [2, 25])) and the usual shaking procedure in the diversification phase. Our implementation employs the VND presented in Algorithm 2 for the intensification (or improvement) phase, while at the diversification phase we employ the shaking procedure presented in Algorithm 3. The shaking procedure moves the search to new regions of the solution space by relocating non-hub nodes to different routes and changing the order of visitation of a single local route. The improvement phase and the shaking procedure together with the neighborhood change step are executed alternately until a predefined stopping criterion is met. Here the stopping criterion is given by a limit on CPU time ($T_{max}$) (see line 10 in Algorithm 4). GVNS has an additional parameter $k_{max}$ which denotes the maximum number of iterations (moves) that may be performed within a single shake (Algorithm 3) and which affects the level of diversification obtained by the shaking procedure. The parameter $k_{max}$ is determined empirically in our study (see Sect. 3).

3 Computational results

In this section, we present the results obtained by our GVNS heuristic on benchmark instances from the literature. In addition, we present the results of preliminary testing used to determine the order of neighborhoods within the VND, as well as to determine an appropriate value of the parameter $k_{max}$. Also note that a CPU time limit $T_{max}$ of 60 s is imposed on all runs of the GVNS heuristic.

The experiments are conducted on a machine with an Intel(R) Core(TM) i5-3470 CPU @ 3.20 GHz and 16 GB of RAM.

3.1 Benchmark instances

For testing purposes, the benchmark instances originally proposed in [20] are used. The benchmark set is derived from 76 TSPLIB instances by varying the value of parameter $\alpha$ and considering different scenarios on the tour length C, and the requested number of hubs p. More precisely, the value of the parameter $\alpha$ is taken from the set $\{0.2, 0.4, 0.6, 0.8\}$, while three scenarios are considered for values of C and p:

• Scenario ST $p=\lceil 0.2|V| \rceil$ and $C=\lceil \frac{|V|}{p} \rceil$. In this case the local routes are forced to be non-empty and tight.

• Scenario SL $p=\lceil 0.2|V| \rceil$ and $C=\lfloor 1.8\lceil \frac{|V|}{p} \rceil \rfloor$. Here some local routes may be very large and some may be empty.

• Scenario SQ $p=C=\lceil \sqrt{|V|} \rceil$ . Here local routes may be large or empty, but not as loose as scenario SL .

Hence, in total we have $76\times 4 \times 3 =912$ test instances. The instances with 100 nodes or less are classified as small, while the remaining ones are large.

3.2 Determining the best order of neighborhoods

The aim of this section is to determine the best order of neighborhoods inside our VND procedure. Due to the large number of neighborhood structures considered here, examining all possible orders would be far too time consuming. For this reason, we divide the neighborhood structures into two groups: hub-location neighborhoods and LocalRoute neighborhoods. Hub-location neighborhoods are those that concern the selection of hubs and node-hub assignments, while LocalRoute neighborhoods are those that “optimize” local tours. Having such a division of neighborhoods, we are now interested to determine the best order of neighborhood groups. The order of neighborhoods within the set of hub-location neighborhoods may be determined so that those based on changing node-hub allocations are examined first followed by those that change the hubs. Such a way of exploring neighborhoods is suggested for example in [16]. Hence, respecting the rule that the neighborhoods of smaller cardinality are examined first, we obtain the following order of neighborhoods within the hub-location group: ${N}_{hub}:=\{{N}_{insert},{N}_{exchange}$, ${N}_{change\_hub}\}$. In similar fashion, we order neighborhood structures within the LocalRoute neighborhood group as ${N}_{LocalRoute}:= \{{N}_{1opt}, {N}_{2opt}, {N}_{Oropt1back}$, ${N}_{Oropt1for}\}$. To validate this order we note the following observations: the lowest cardinality neighborhood is examined first; the 2-opt neighborhood should be examined before the OR-opt neighborhoods (e.g., as noted in [24]); ORopt_backward should be examined before ORopt_forward (see e.g., [12, 27, 32] ).

Now that the order of neighborhoods within each group is specified, we examine the best order of groups within the VND paradigm. Hence, we consider the following orders: 1) hub-location neighborhoods, LocalRoute neighborhoods; 2) LocalRoute neighborhoods; hub-location neighborhoods, and 3) hybrid order, where after each neighborhood in the hub-location group we apply the LocalRoute neighborhoods. To differentiate these three VNDs we designate them as:

• VND_1-order of neighborhoods: ${N}_{LocalRoute},{N}_{hub}$;

• VND_2-order of neighborhoods: ${N}_{hub},{N}_{LocalRoute}$;

• VND_3-order of neighborhoods: ${N}_{insert},{N}_{LocalRoute}, {N}_{exchange},{N}_{LocalRoute}, {N}_{change\_hub}, {N}_{LocalRoute}$;

To assess the performance of the above three VNDs, each one is executed 50000 times on a selected subset of instances, each time starting from a different initial solution generated at random as described in Algorithm 1. For testing purposes, we selected a subset of 240 instances with different topologies. This subset is based on the following 20 TSPlib instances: a280, li535, att532, bier127, brg180, ch130, d198, d493, fl417, gil262, gr137, gr202, gr229, gr431, kroA150, kroA200, lin318, pa561, pcb442, pr144. Each of these instances is considered under 3 different scenarios and 4 different values of the parameter $\alpha$. For each VND, the average results taken over 20 instances, all using the same scenario and the same value of parameter $\alpha$, are provided in Table 1. More precisely, we report the averages of the best, the average and the worst solution values (Columns ‘Best’, ‘Avg.’ and ‘Worst’, respectively), as well as the average time-to-target (Columns ‘time’) in seconds. The time-to-target represents the CPU time consumed by a method to reach a final solution value reported at the output.

From the reported results we observe, that average times-to-target of all three VNDs are almost the same. Regarding solution quality, VND_1 exhibits the poorest performance. Comparing VND_2 and VND_3, we observe that in all cases but one (see the line corresponding to the scenario SL and $\alpha =0.8$), VND_2 provides better (best) solutions. In addition, in 9 out of 12 cases, we see that the averages of best, average and worst solution values provided by VND_2 are better than the corresponding ones of VND_3. Consequently, VND_2 may be identified as the best VND. This further implies that the best order of neighborhoods is:

${N}_{insert},{N}_{exchange},{N}_{change\_hub}, {N}_{1opt}, {N}_{2opt}, {N}_{Oropt1back}, {N}_{Oropt1for}$.

Table 1 Examining the order of neighborhoods

3.3 Assessing the value of parameter $k_{max}$

After detecting the best order, we needed to also tune parameter $k_{max}$, which determines the level of diversification that will be used within GVNS to resolve local optimum traps. It is known that for larger values of parameter $k_{max}$, the corresponding VNS heuristic tends to behave as a random multi-start heuristic (i.e., a heuristic that generates a completely random solution at each re-start that does not retain any features of the current best solution). In order to avoid this worst-case scenario, we want to keep the $k_{max}$ value as small as possible while having at the same time high quality results. Since the number of local routes in a solution is expressed by the parameter p, we try to keep the number of local routes affected by the shaking procedure to be as small as possible by attempting the following settings: $k_{max} =\min (5, p)$, $k_{max} = \min (10, p)$ and $k_{max} = \min (20,p)$. In all testing, the time limit parameter $T_{max}$ is set to 60 s as noted above, and for each choice of $k_{max}$ GVNS is executed 20 times, each time starting from a different initial solution generated by Algorithm 1. For testing purposes, we used the same subset of 240 instances as described above. The average results taken over 20 instances, all using the same scenario and the same value of parameter $\alpha$, are provided in Table 2. The column headings are defined in the same way as previously described.

From the reported results, it follows that for scenarios ST and SL the best choice is $k_{max} =\min (10, p)$, regardless of the value of $\alpha$. This choice of the value of parameter $k_{max}$, yields better best and average solution values than the other choices. On the other hand for the SQ scenario the best choice turns out to be $k_{max} =\min (5, p)$. Hence, in all subsequent testing, we will use $k_{max} =\min (10, p)$ for the ST and SL scenarios, and $k_{max} =\min (5, p)$ for the scenario SQ. It should also be emphasized that regardless of the value of $k_{max}$, our GVNS exhibits a good stability with respect to time-to-target.

Table 2 Examining the best value of parameter $k_{max}$

An interesting observation may be deduced after comparing the results reported in Table 1 (multi-start VND) and Table 2 (GVNS). Namely, in all test cases, the solutions obtained by the proposed GVNS are much better than the ones reached by the multi-start VND. Hence, it follows that the proposed shaking procedure resolves local optimum traps more effectively than the random re-start used within the multi-start VND.

3.4 Comparison with the state-of-the-art

In this section we compare our GVNS against the state-of-the-art heuristics presented in [20]: M-VND, M-CNS, and LocalSolver. In all tests the parameters of our GVNS are set as previously described, i.e., $T_{max}=60$ s, $k_{max}=\min (10, p)$ on scenarios ST and SL, and $k_{max}=\min (5, p)$ on scenario SQ. As an improvement routine, VND_2 is used. On each of the 912 instances tested GVNS is executed 20 times, each time starting from a different initial solution generated by Algorithm 1.

The detailed comparison may be found at the following webpage: http://www.mi.sanu.ac.rs/~nenad/p-hubLR/, while here we present the summary results. All instances of the same size type (small or large), tested under the same scenario (ST, SL or SQ) and the same value of the parameter $\alpha \in$ $\{0.2, 0.4, 0.6,$ $0.8\}$ are considered as a test case. Hence, for each test case, we report the average results over all instances in that test case. Table 3 reports the results on small instances, while Table 4 provides results on large instances. The column headings are defined as follows. Columns ‘Scenario’ and ‘$\alpha$’ provide information on the scenario considered and the value of parameter $\alpha$, respectively. The next column ‘Best Known’ provides the average of best-known solution values obtained from the literature for each test case. After that, in the next columns, for each of methods M-VND, M-CNS, and LocalSolver (LS), we report the average percentage deviations of their solution values from the best-known solution values and the average time-to-target. For our GVNS, we report the averages of the best and average solution values on each test case, the average time-to-target and the average percentage deviations of the best found solution values from the current best known values. For each method, the percentage deviation is calculated as:

$$\begin{aligned} \frac{value-best\_known}{best\_known}\times 100, \end{aligned}$$

where value stands for the solution value found by the considered method and $best\_known$ is the best-known solution value reported in the literature [20]. Note that the percentage deviations for M-VND, M-CNS, and LocalSolver are taken directly from [20] as well as all other data related to these methods.

Table 5 provides the following information for each test case: number of instances where the proposed GVNS establishes a new best-known solution (columns ‘Better’); number of instances where it reaches the previous best-known solution (columns ‘Same’); and number of instances where it fails to improve or reach the previous best-known solution (columns ‘Worse’).

Table 3 Comparison on small instances

Table 4 Comparison on large instances

From the results reported on small size instances in Table 3, we observe that our GVNS provides very good solution values in short time. On all 12 test cases, the averages of best and average solution values are less than the averages of best-known values. The previous best-known solution values are improved up to 0.73%. Just on two test cases (SL, 0.20 and SL, 0.80), our GVNS provides higher percentage deviation from the best known solution values than LS. In the remaining 10 cases our GVNS not only provides less percentage deviation than LS but also improves previous best-known solution values. The total number of new best-known solutions established by our GVNS is 135 (see Table 5). On 138 instances, our GVNS matches the previous best-known solutions, while on 63 instances it fails to improve or match the previous best-known solutions.

Comparing the results on large scale instances, it follows that our GVNS exhibits better performance than any other solution approach. On every instance it either improves or matches the previous best-known solution. The average percentage improvement is in the range of 5.32 and 11%. It should be emphasized that our GVNS consumes a lot less CPU time-to-target than any other method. M-VND has very high percentage deviation from the previous best-known solution values, reaching as high as 14.51%. M-CNS and LS exhibit better performance than M-VND, but still worse than GVNS. For example, on test case SL 0.60, where percentage deviations of M-CNS and LS are both 4.51%, our GVNS improves best-known solutions by 6.52%. Moreover, our GVNS improves the previous best-known solutions on 556 out of 576 test instances (see Table 5). It should be emphasized that, as reported in [20], M-CNS and LS exhibit the same performance on all large instances.

Overall, we see that GVNS improves best known solution values on 691 out of 912 instances; matches the previous best-known solution values on 138 instances, while on only 83 instances it neither improves nor reaches the previous best-known solution values. Thus as of now, 829 out of 912 best-known solutions are attributed to the proposed GVNS, i.e., around 90% of the current best-known solutions. In addition, it follows that the proposed GVNS is highly suitable for solving large scale instances in a short time by providing high quality solutions within 60 s. This further implies that our GVNS successfully responds to the main requirement of a heuristic approach, that is, to provide high quality solutions in short time.

Table 5 Number of instances where GVNS provides a better, same or worse solution than best-known from the literature

3.5 Statistical tests

The aim of this section is to determine if the difference in performance between our GVNS and each other method in the comparison is statistically significant or not. In this regard, the Wilcoxon signed-rank test is performed with a significance level of 0.05. The outcome of the tests is provided in Table 6. For each test case, the corresponding row provides p-values obtained after applying the Wilcoxon signed-rank test on the results found by the proposed GVNS and the methods shown in the column headings. A p-value less than 0.05 indicates that there is a significant difference between the two methods, otherwise there is insufficient evidence. From the table we see that on large instances all p-values are orders of magnitude less than 0.05, which implies that there is a significant difference between the proposed GVNS and each of the previously proposed methods. Since, on large instances, the proposed GVNS provides better solution values than any existing method (see Table 4), it may be inferred that the GVNS is the superior method on large size instances, in terms of the solution quality. Similar conclusions may be drawn when comparing GVNS with M-VND and M-CNS on small instances. When comparing the GVNS and LS on small instances, the previous conclusions are applicable on all test cases except for small instances and scenario SL, where no significant differences between GVNS and LS are observed.

Table 6 p-values of the Wilcoxon signed-rank test

4 Conclusions

In this paper an established hub location routing problem is studied, and an efficient solution approach is proposed. The new solution approach follows the general variable neighborhood search framework where in our case seven different neighborhood structures are identified to exploit the nature of the problem. These seven neighborhoods are embedded in a sequential variable neighborhood descent scheme in an efficient and effective ordering determined from a detailed empirical study. In addition, all other parameters and components of our approach are carefully tailored with the aim to obtain high-quality solutions in a short time. Comparing our heuristic with the state-of-the-art approaches reveals that we succeeded to do so to a great extent. Our heuristic established 691 new best-known solutions on a benchmark set of 912 instances while consuming orders of magnitude less CPU time than all competitors. In addition, 829 out of 912 current best-known solutions can be attributed to the proposed GVNS. The statistical tests we conducted strongly confirm the superiority of our approach over the previous ones.

The SL small-sized instances with poor GVNS performance should be the subject of future work in order to detect possible anomalies in the solution space of these instances. As additional future research directions, we suggest the hybridization of the proposed solution method with some exact approaches to hopefully obtain guaranteed optimal solutions, as well as extending the study to other hub location routing problems. Some variants to be studied include for example, capacitated variants of the current problem, with capacities on the edges or at the hubs, allowing the assignment of non-hub nodes to more than one hub, and allowing for different configurations such as a tree structure for inter-hub connections.

In addition, some recent works use an adaptive search strategy, which combines first and best improvement strategies. More specifically, the best improvement is selected for small- and medium-sized instances, and the first improvement for the solution of large problem instances [18, 19]. Therefore, this approach may be also a promising future work direction. Moreover, in [19] new adaptive shaking approaches can be found, which may further enhance the efficiency of GVNS. Hence, this is one more possible research direction. Another possible research direction may be to examine the use of an adaptive neighborhoods’ ordering mechanism of neighborhood structures as was done in [33], for example.