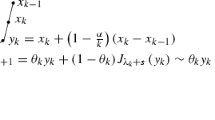Abstract
We consider a class of inertial second order dynamical system with Tikhonov regularization, which can be applied to solving the minimization of a smooth convex function. Based on the appropriate choices of the parameters in the dynamical system, we first show that the function value along the trajectories converges to the optimal value, and prove that the convergence rate can be faster than \(o(1/t^2)\). Moreover, by constructing proper energy function, we prove that the trajectories strongly converges to a minimizer of the objective function of minimum norm. Finally, some numerical experiments have been conducted to illustrate the theoretical results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent years, convex optimization problems draw many researchers’ attention due to its arisen in a lot of application areas, such as machine learning [10, 30], statistics [18], image processing [20, 32] and so on. Hence, various algorithms have been proposed for solving different structured convex optimization problems. One simple and often powerful algorithm is Nesterov accelerated gradient algorithm, whose convergence rate can be \(O(1/t^2)\). Many accelerated algorithms based on Nesterov’s accelerated technique has been proposed since then, we refer the readers to [11, 19, 25, 26, 29, 31] and the reference therein for an overview of these algorithms.
Most literatures consider Nesterov’s accelerated method by using different numerical optimization techniques. However, differential equations are also important and efficient tools to study numerical algorithms. Recently, Su, Boyd, Candés [28] propose a class of second order differential equations to study Nesterov’s accelerated gradient method, which is
where \(\Phi \) is convex and differentiable, and \(\nabla \Phi \) is Lipschitz continuous, \(t_0>0\). They show that this system can be seen as the continuous version of Nesterov’s accelerated gradient method. In addition, they prove that the convergence rate of the function value along the trajectories of (1.1) is \(O(1/t^2)\), if \(\alpha \) is chosen as 3, which is the same as the convergence rate of Nesterov’s accelerated gradient method. Moreover, they show that 3 is the minimum constant that guarantees the convergence rate of \(O(1/t^2)\).
Su, Boyd, Candés work [28] motivates subsequent studies on the second order differential equation (1.1), see, for example, [3, 8, 13,14,15,16, 24, 33]. Particularly, Attouch, Chbani, Peypouquet and Redont [3] establish the weak convergence of the trajectory if \(\alpha > 3\), and they also show that the convergence rate of the objective function along the trajectory is \(o(1/t^2)\). Later, Attouch, Chbani and Riahi [5] consider the convergence properties under the condition that \(\alpha <3\). They prove that the convergence rate is
In order to establish the strong convergence of the trajectory, Attouch, Chbani and Riahi [4] propose the following second order dynamical system:
which add a Tikhonov regular term compared with system (1.1). They show that the function value along the trajectory converges to the optimal value fast, if \(\varepsilon (t)\) decreases to 0 rapidly. In addition, they establish the strong convergence of the trajectory x(t) to the element of minimum norm of \(\arg \min \Phi \), if \(\varepsilon (t)\) tends slowly to zero. There are many other literatures considering the Tikhonov regular techniques, the readers can result the references [1, 2, 9, 17, 23].
In 2019, Attouch, Chbani and Riahi [6, 7] study another differential equation:
where \(\gamma (t)\) and \(\beta (t)\) are scalar functions. They first consider the convergence properties of (1.3). Then a discretized numerical algorithm for solving structured convex composite optimization problem based on the differential equation has been proposed. Inspired by the proof of the convergence of the trajectory of (1.1), they establish the convergence and convergence rate of the algorithm. Concretely, they obtain that the convergence rate of \(\Phi (x(t))\) is
where \(\Gamma \left( t \right) = p\left( t \right) \int _t^{ + \infty } {\frac{1}{{p\left( u \right) }}du} \), \(p\left( t \right) = {e^{\int _{{t_0}}^t {\gamma \left( u \right) du} }}\). In particular, if \(\gamma (t)\) is chosen as \({\frac{\alpha }{t}}\), the convergence rate becomes
According to the above relation, it can be easily seen that the convergence rate of \(\Phi (x(t))\) can be faster than \(O\left( {\frac{1}{{{t^2}}}} \right) \), if we choose proper \(\beta (t)\). For the nonsmooth optimization problems, which means the objective function is not differentiable, differential equations can not be applied directly, we recommend the readers to [12, 21] to see the details.
From the above literatures, we note that some work consider the strong convergence of the trajectory x(t), the other work study the faster convergence rate of objective \(\Phi (x(t))\). A natural question is that whether we can combine these discussions together. In this work, both the strong convergence property of the trajectory x(t) and the fast convergence rate of objective \(\Phi (x(t))\) are studied under different choice of the parameters. To this end, this paper mainly considers the following differential equation:
where \(\Phi \) is convex and differentiable, \(\nabla \Phi \) is Lipschitz continuous, \({u_0},{v_0} \in {\mathcal {H}}\), \(t_0>0\), \(\alpha \) is a positive parameter, \(\beta (t)\) is a time scaling parameter, and \({\varepsilon \left( t \right) x\left( t \right) }\) is a Tikhonov regularization term. Throughout the whole paper, we assume that
Our main contributions are as follows:
-
By constructing proper energy function, we first prove that the existence and uniqueness of the global solution of dynamical system (1.4);
-
We establish the fast convergence rate of \(\Phi (x(t))\) and strong convergence of the trajectory x(t) of system (1.4). In details, under the condition that \(\int _{{t_0}}^{ + \infty } {t\beta \left( t \right) \varepsilon \left( t \right) dt < + \infty }\), we establish the global convergence rate of \(\Phi (x(t))\) which is
$$\begin{aligned} \Phi \left( {x\left( t \right) } \right) - \min \Phi = o\left( {\frac{1}{{{t^2}\beta \left( t \right) }}} \right) . \end{aligned}$$Moreover, if \(\int _{{t_0}}^{ + \infty } {\frac{{\varepsilon \left( t \right) \beta \left( t \right) }}{t}dt = + \infty } \), we show that the global solution x(t) of (1.4) satisfies the following ergodic convergence result:
$$\begin{aligned} \mathop {\lim }\limits _{t \rightarrow \infty } \frac{1}{{\int _{{t_0}}^t {\frac{{\varepsilon \left( \tau \right) \beta \left( \tau \right) }}{\tau }d\tau } }}\int _{{t_0}}^t {\frac{{\varepsilon \left( \tau \right) \beta \left( \tau \right) }}{\tau }\left\| {x\left( \tau \right) - p} \right\| ^2d\tau } = 0, \end{aligned}$$where p is the element of minimal norm of \(\arg \min \Phi \). In addition, we prove that \(\mathop {\lim \inf }\limits _{t \rightarrow \infty } \left\| {x\left( t \right) - p} \right\| = 0.\)
The rest of the paper is organized as follows: Section 2 presents some basic notation and preliminary materials. In Sect. 3, the global existence and uniqueness result is established for (1.4). In Sect. 4, we first establish the fast convergence rate of \(\Phi (x(t))\) based on the condition \(\int _{{t_0}}^{ + \infty } {t\beta \left( t \right) \varepsilon \left( t \right) dt < + \infty }\), and then show that the trajectory x(t) of (1.4) converges to a minimizer of the objective function of minimum norm. In Sect. 5, we perform some numerical experiments to illustrate our theoretical results.
2 Notation and preliminaries
The problems we consider in this paper are all in Hilbert space \(\mathcal {H}\) , and we denote its inner product by \(\langle \cdot ,\cdot \rangle \), the corresponding norm is denoted as \(\left\| \cdot \right\| \).
For the real valued convex and differentiable function \(\Phi :\mathcal {H}\rightarrow \mathbb R\), the gradient of \(\Phi \) is said to be \(L_{\Phi }\)-Lipschitz continuous, if
We say that \(\Phi \) is a \(\sigma \)-strongly convex if and only if \(\Phi \left( \cdot \right) - \frac{\sigma }{2}{\left\| \cdot \right\| ^2}\) is convex, \(\sigma >0\). Moreover, if \(\Phi \) is continuously differentiable, then
A function \(x:[0,\infty )\rightarrow \mathcal {H}\) is called locally absolutely continuous if \(x:[0,\infty )\rightarrow \mathcal {H}\) is absolutely continuous on every compact interval, which means that there exists an integrable function \(y:\left[ {{t_0}, T } \right) \rightarrow {\mathcal {H}}\) such that
For a locally absolutely continuous function, we would like to point out the following property, which will be used in the following sections.
Remark 2.1
Every locally absolutely continuous function \(x:\left[ {{t_0}, + \infty } \right) \rightarrow {\mathcal {H}}\) is differentiable almost everywhere and its derivative coincides with its distributional derivative almost everywhere and one can recover the function from its derivative \(\dot{x} = y\) by the integration formula above.
Before ending this section, we state some lemmas which will be used in our convergence analysis.
Lemma 2.1
Suppose that \(F:\left[ {0, + \infty } \right) \rightarrow \mathbb {R}\) is locally absolutely continuous and bounded below and that there exist \(G \in {L^1}\left( {\left[ {0, + \infty } \right) } \right) \) such that for almost every \(t \in \left[ {0, + \infty } \right) \)
Then there exists \(\mathop {\lim }\limits _{t \rightarrow \infty } F\left( t \right) \in \mathbb {R}\).
Now, we will introduce an energy function we used in the paper, which is
where \({\Phi _t}\left( x \right) = \Phi \left( x \right) + \frac{{\varepsilon \left( t \right) }}{2}{\left\| x \right\| ^2}\).
Next, we will give two important results, which play important roles in the analysis of asymptotic behavior of system (1.4).
Lemma 2.2
Let W be defined by (2.1), we have
Proof
From the definition of \(\Phi _{t}(x(t))\), we immediately have
On the other hand, by taking the derivative of the energy function (2.1) and using the definition of \({\Phi _t}\left( x \right) = \Phi \left( x \right) + \frac{{\varepsilon \left( t \right) }}{2}{\left\| x \right\| ^2}\), we have
Combining (2.2) with the above relation, we obtain further that
By rearranging terms and using the fact that \( \varepsilon (t)\) is continuously differentiable and nonincreasing, we have
where the last inequality is from the fact that \(\dot{\varepsilon }(t) \le 0\) and \(\beta (t)\ge 0\). Moreover, according to system (1.4), we have
Combining (2.3) and (2.4) together, we obtain that
which implies our desired conclusion immediately.
In the following, we introduce another auxiliary function
where \(z\in \arg \min \Phi \), then we will give the following property of \(h_z\).
Lemma 2.3
Suppose \({h_z}\left( t \right) \) is defined as (2.5), then
-
(i)
\({{\ddot{h}}_z}\left( t \right) + \frac{\alpha }{t}{{\dot{h}}_z}\left( t \right) \leqslant {\left\| {\dot{x}\left( t \right) } \right\| ^2} - \beta \left( t \right) \left( {\Phi _t}\left( {x\left( t \right) } \right) - \min \Phi - \frac{{\varepsilon \left( t \right) }}{2}{{\left\| z \right\| }^2} + \frac{{\varepsilon \left( t \right) }}{2} \left\| x\left( t \right) - z \right\| ^2 \right) .\)
-
(ii)
\(\mathop {\sup }\limits _{t \geqslant {t_0}} \frac{{\left| {{{\dot{h}}_z}\left( t \right) } \right| }}{t} < + \infty \) if \(\mathop {\sup }\limits _{t \geqslant {t_0}} \left\| {\dot{x}\left( t \right) } \right\| < + \infty .\)
Proof
(i): From the definition of \(h_{z}(t)\), we immediately obtain that
Hence
According to (1.4), we have
Combining this relation with (2.7), we obtain further that
On the other hand, recall \(\Phi \) is convex function, from this with the definition \(\Phi _{t}\) , we see that \(\Phi _{t}\) is \({\varepsilon \left( t \right) }\)-strongly convex function. Hence, we have
which implies that
Since z is a minimizer of \(\Phi \), by (2.9) and the definition of \({\Phi _t}\left( z \right) = \Phi \left( z \right) + \frac{{\varepsilon \left( t \right) }}{2}{\left\| z \right\| ^2} = \min \Phi + \frac{{\varepsilon \left( t \right) }}{2}{\left\| z \right\| ^2}\), we obtain further that
Using this, the fact \(\beta (t)\ge 0\) from \(H_1\) and (2.8), we have
This completes the proof of (i).
Now we prove (ii). By the definition of \({{\dot{h}}_z}\left( t \right) \) in (2.6) , the assumption that \(\mathop {\sup }\limits _{t \geqslant {t_0}} \left\| {\dot{x}\left( t \right) } \right\| < + \infty \) and Schwartz’s inequality, we obtain that
In addition,
Combining the above inequality, the assumption \(\mathop {\sup }\limits _{t \geqslant {t_0}} \left\| {\dot{x}\left( t \right) } \right\| < + \infty \) with (2.10), we immediately deduce that
where \({\tilde{C}}>0\) is a constant. Thus, \(\mathop {\sup }\nolimits _{t \geqslant {t_0}} \frac{{\left| {{{\dot{h}}_z}\left( t \right) } \right| }}{t} < + \infty .\) This completes the proof.
3 Existence and uniqueness of the solution of (1.4)
In this section, we will prove the existence and uniqueness of a global solution of dynamical system (1.4). We first give the definition of a strong global solution of (1.4).
Definition 3.1
We say that \(x:\left[ {{t_0}, + \infty } \right) \rightarrow {\mathcal {H}}\) is a strong global solution of (1.4), if it satisfies the following properties:
-
(a)
\(x,\dot{x}:\left[ {{t_0}, + \infty } \right) \rightarrow {\mathcal {H}}\) are locally absolutely continuous, in other words, absolutely continuous on each interval \(\left[ {{t_0},T} \right] \) for \({t_0}< T < + \infty \);
-
(b)
\(\ddot{x}\left( t \right) + \frac{\alpha }{t}\dot{x}\left( t \right) + \beta \left( t \right) \left( {\nabla \Phi \left( {x\left( t \right) } \right) + \varepsilon \left( t \right) x\left( t \right) } \right) = 0\) for almost every \(t \geqslant {t_0}\);
-
(c)
\(x\left( {{t_0}} \right) = {u_0}\) and \(\dot{x}\left( {{t_0}} \right) = {v_0}\).
We are now ready to prove the existence and uniqueness of system (1.4). We mainly use Cauchy-Lipschitz-Picard theorem for absolutely continuous trajectories (see, for example [22], proposition 6.2.1], [27], Theorem 54]) to establish the result. The proof is based on the idea that rewriting (1.4) as a particular first order dynamical system in a suitably chosen product space (see also [8, 17]).
Theorem 3.1
For any initial points \({u_0},{v_0} \in {\mathcal {H}}\), there exists a unique \(C^2\)-global solution of the dynamical system (1.4).
Proof
Define \(X\left( t \right) = \left( {x\left( t \right) ,\dot{x}\left( t \right) } \right) \), and \(F:\left[ {{t_0}, + \infty } \right) \times {\mathcal {H}} \times {\mathcal {H}} \rightarrow {\mathcal {H}} \times {\mathcal {H}}\) as
Hence, from (1.4), (3.1) and the definition of X(t), we see that (1.4) can be rewritten as a first order dynamical system, which is
We will first show that \(F\left( {t, \cdot , \cdot } \right) \) is L(t)-Lipschitz continuous for every \(t\geqslant {t_0}\). And the Lipschitz constant is a function of time with the property that \(L\left( \cdot \right) \in L_{loc}^1\left( {\left[ {{t_0}, + \infty } \right) } \right) \). Concretely, for every \(\left( {u,v} \right) ,\left( {\overline{u} ,\overline{v} } \right) \in {\mathcal {H}} \times {\mathcal {H}}\), by (3.1), we have
Using the fact that \({\left( {a + b} \right) ^2} \leqslant 2{a^2} + 2{b^2}\) and the above formula, we have
From this relation and the fact \({\nabla \Phi }\) is \(L_{\Phi }\)-Lipschitz continuous in the assumption, we obtain further that
where the last inequality follows from the fact \(\sqrt{a^2+b^2}\le a+b\) if \(a\ge 0, b\ge 0\), and \(\alpha >0, \beta (t)\ge 0, \varepsilon (t)\ge 0\). Define \(L(t)={1 + \sqrt{2} \frac{\alpha }{t}{\text { + 2}}{L_\Phi }\beta \left( t \right) {\text { + 2}}\beta \left( t \right) \varepsilon \left( t \right) } ,\) then we have
Hence \(F\left( {t, \cdot , \cdot } \right) \) is L(t)-Lipschitz continuous for every \(t\geqslant {t_0}\). Recall that \(\frac{\alpha }{t}\), \(\beta (t)\) and \(\varepsilon (t)\) are continuous for any \(t\ge t_0\). Thus we see that L(t) is integrable on \(\left[ {{t_0},T} \right] \), consequently, \(L\left( \cdot \right) \in L_{loc}^1\left( {\left[ {{t_0}, + \infty } \right) } \right) \).
Next, we will show that \(F\left( { \cdot ,u,v} \right) \in L_{loc}^1\left( {\left[ {{t_0}, + \infty } \right) ,{\mathcal {H}} \times {\mathcal {H}}} \right) \) for all \(u,v \in {\mathcal {H}}\). Take any \(u,v \in {\mathcal {H}}\), by the definition of F, for \({t_0}< T < + \infty \), we have
where the first inequality follows from the fact \(\Vert a+b\Vert ^2\le 2\Vert a\Vert ^2 + 2\Vert b\Vert ^2\), the last inequality follows from that the points \(u,v\in {\mathbb {R}^n}\) are fixed.
Hence, by (3.4) and the fact \(\frac{\alpha }{t}\), \(\beta (t)\) and \(\varepsilon (t)\) are continuous for any \(t\ge t_0\), we immediately obtain that
Combining this relation with (3.3) and the result \(L\left( \cdot \right) \in L_{loc}^1\left( {\left[ {{t_0}, + \infty } \right) } \right) \), and using the Cauchy-Lipschitz-Picard theorem, we see that there exists a unique global solution of system (3.2), which implies the existence of a unique \(C^2\)-global solution of (1.4) by the Lipschitz continuity of \(\nabla \Phi \) and the the continuities of \(\beta (t)\) and \(\varepsilon (t)\). This completes the proof.
4 Convergence analysis of the trajectory of (1.4)
In this section, we will establish the convergence and convergence rate of the trajectory x(t) of (1.4). The proof of convergence will be casted into the following two cases.
Case 1: \(\int _{{t_0}}^{ + \infty } {t\beta \left( t \right) \varepsilon \left( t \right) dt < + \infty }\). In this case, we will show in Theorem 4.1 that for any global solution trajectory of (1.4), the function \(\Phi \left( {x\left( t \right) } \right) \) satisfies the fast convergence property
Case 2: \(\int _{{t_0}}^{ + \infty } {\frac{{\varepsilon \left( t \right) \beta \left( t \right) }}{t}dt = + \infty } \). In this case, we will show in Theorem 4.2 that for any global solution trajectory of (1.4), the following ergodic convergence result holds
where p is the element of minimal norm of \(\arg \min \Phi \). Moreover, the strong global convergence of x(t) will be established, which is
Now we are ready to present the convergence results case by case.
4.1 Case \(\int _{{t_0}}^{ + \infty } {t\beta \left( t \right) \varepsilon \left( t \right) dt < + \infty }\)
For simplicity, we set \(m = \min \Phi \). Take any \(z \in \arg \min \Phi \), we will introduce another auxiliary function for \(\alpha \ne 1\), which is
where \(\Phi _t\) is the same function as defined in (2.1). Let \({g\left( t \right) = \frac{t}{{\alpha - 1}}}\), then by simply computing, we immediately have
From this relation and the definition of \(E\left( t \right) \) in (4.1), we can rewrite \(E\left( t \right) \) as the following formula
Combining (4.3) with the definition of \(W\left( t \right) \) in (2.1) , \(h_z\) in (2.5) and \(\dot{h}_z\) in (2.6), we obtain that
Next, we will prove that the global convergence rate of \(\Phi \left( {x\left( t \right) } \right) \) is \(o\left( {\frac{1}{{{t^2}\beta \left( t \right) }}} \right) \).
Theorem 4.1
Let \(\Phi : \mathcal {H} \rightarrow \mathbb {R}\) be a convex continuously differentiable function such that \(\arg \min \Phi \) is nonempty. Assume that \(\varepsilon (t)\), \(\beta (t)\) satisfies condition \((H_1)\), \(\alpha >1\), \(\int _{{t_0}}^{ + \infty } {t\beta \left( t \right) \varepsilon \left( t \right) dt < + \infty }\) and there exist \(b>0\) such that \(t\dot{\beta }\left( t \right) \leqslant \left( {\alpha - 3-b} \right) \beta \left( t \right) \). Let \(x(\cdot )\) be a classical global solution of (1.4), consider the energy function (4.4), then
-
(i)
\(\dot{E}\left( t \right) \leqslant \frac{1}{{2\left( {\alpha - 1} \right) }}t\beta \left( t \right) \varepsilon \left( t \right) {\left\| z \right\| ^2}\).
-
(ii)
\(\int _{{t_0}}^{ + \infty } {t\beta \left( t \right) \left( {{\Phi _t}\left( {x\left( t \right) } \right) - m} \right) dt < } + \infty \).
-
(iii)
The following fast convergence of \(\Phi (x(t))\) holds:
$$\begin{aligned} \Phi \left( {x\left( t \right) } \right) - m = o\left( {\frac{1}{{\beta \left( t \right) {t^2}}}} \right) . \end{aligned}$$ -
(iv)
Moreover, the trajectory \(x\left( \cdot \right) \) is bounded on \(\left[ {{t_0}, + \infty } \right) \) and
$$\begin{aligned} \int _{{t_0}}^{ + \infty } {t\beta \left( t \right) \varepsilon \left( t \right) {{\left\| {x\left( t \right) } \right\| }^2}dt < } + \infty . \end{aligned}$$
Proof
We first prove (i). From the definition of E(t) in (4.4), we immediately have
where the last inequality follows from the Lemma 2.2.
On the other hand, according to (4.2) and Lemma 2.3, we have
Combining the (4.5) and (4.6), we obtain further that
By rearranging terms, we have
where the second equality follows from the fact \({g\left( t \right) = \frac{t}{{\alpha - 1}}}\) and \(1 + \dot{g}\left( t \right) = \frac{\alpha }{t}g\left( t \right) \) from (4.2).
Recall that \({g\left( t \right) = \frac{t}{{\alpha - 1}}}\) and \(1 + \dot{g}\left( t \right) = \frac{\alpha }{t}g\left( t \right) \) from (4.2), combining this with the assumption \(t\dot{\beta }\left( t \right) \leqslant \left( {\alpha - 3-b} \right) \beta \left( t \right) \) and \(\alpha >1\), we obtain that
Thus, according to this relation, the fact that \(g(t)\ge 0\), \(\beta (t)\ge 0\), \(\varepsilon (t)\ge 0\), \( {{\Phi _t}\left( {x\left( t \right) } \right) - m} \ge 0\) and (4.7), we obtain further that
Moreover, using the fact that \(g\left( t \right) ,\beta \left( t \right) ,\varepsilon \left( t \right) \geqslant 0\) and \({g\left( t \right) = \frac{t}{{\alpha - 1}}}\), we finally have
which proves (i).
We now prove (ii). From the assumption \(\int _{{t_0}}^{ + \infty } {t\beta \left( t \right) \varepsilon \left( t \right) dt < + \infty }\) and (4.9), we deduce that the positive part of \(\dot{E}\left( t \right) \) belongs to \({L^1}\left( {{t_0}, + \infty } \right) \). Using this and the fact that E is bounded from below, we obtain that E(t) has a limit as \(t \rightarrow + \infty \) due to Lemma 2.1. Hence, there exists \(C_1>0\) such that \(|E(t)|\le C_1\).
In addition, according to (4.7), we have
Recall the fact that \({g\left( t \right) = \frac{t}{{\alpha - 1}}}\), \(\beta (t)\ge 0\) and the assumption that \(t\dot{\beta }\left( t \right) \leqslant \left( {\alpha - 3-b} \right) \beta \left( t \right) \), \(\alpha >1\), we obtain further that
Integrating this inequality, and using that \(\int _{{t_0}}^{ + \infty } {t\beta \left( t \right) \varepsilon \left( t \right) dt < + \infty }\) and the fact \(E\left( t \right) \) is bounded from below, we have
which proves (ii).
We now prove (iii). According to Lemma 2.2, we have
After integration by parts on \((t_0 ,t)\), we obtain
From the definition of W(t) in (2.1), we immediately have
From the assumption \(t\dot{\beta }\left( t \right) \leqslant \left( {\alpha - 3-b} \right) \beta \left( t \right) \), we obtain further that
According to (ii), there exists a constant \({\tilde{C}}\) such that \(\frac{\alpha -1-b}{{(\alpha - 1)^2}}\int _{{t_0}}^{+\infty } s\beta \left( s \right) \left( {\Phi _s}\left( {x\left( s \right) } \right) - m \right) ds < {\tilde{C}}\). Then,
From the definition of W(t) in (2.1), we have
which implies that
In addition, according to the Lemma 2.2, we have
which the last inequality is due to \(\alpha >1\). Recall the assumption that \(t\dot{\beta }\left( t \right) \leqslant \left( {\alpha - 3-b} \right) \beta \left( t \right) \), we immediately have
According to (ii), we see that the positive part of \(\frac{d}{{dt}}\left( {\frac{{{t^2}}}{{{{\left( {\alpha - 1} \right) }^2}}}W\left( t \right) } \right) \) belongs to \({L^1}\left( {{t_0}, + \infty } \right) \). As a result,
which implies that
Otherwise, there would exist a constant \(\bar{C} > 0\) such that \(\frac{{{t^2}}}{{{{\left( {\alpha - 1} \right) }^2}}}W\left( t \right) \geqslant \bar{C}\) for t sufficiently large, i.e. \(\frac{t}{{{{\left( {\alpha - 1} \right) }^2}}}W\left( t \right) \geqslant \frac{{\bar{C}}}{t}.\) According to (4.10), we have \(\int _{{t_0}}^{ + \infty } {\frac{{\bar{C}}}{t}dt < } + \infty \), which leads to a contradiction. According to the definition of W(t) in (2.1) again, we have
Recall that \({\Phi _t}\left( x \right) = \Phi \left( x(t)\right) + \frac{{\varepsilon \left( t \right) }}{2}{\left\| x(t) \right\| ^2}\) and \(\mathop {\lim }\limits _{t \rightarrow + \infty } \varepsilon \left( t \right) = 0\). Combining these facts with the above relation, we obtain further that
which proves (iii).
Finally, we prove (iv). According to (4.8),we have
By integrating (4.11) from \(t_0\) to \(\infty \), we obtain that
which follows from the fact \({g\left( t \right) = \frac{t}{{\alpha - 1}}}\), the assumption \(\int _{{t_0}}^{ + \infty } {t\beta \left( t \right) \varepsilon \left( t \right) dt < + \infty }\), and the positive part of \(\dot{E}\left( t \right) \) belongs to \({L^1}\left( {{t_0}, + \infty } \right) \). Using again the definition of \(g(t) = \frac{t}{{\alpha - 1}}\), the assumption \(\alpha >1\), and (4.12), we immediately have
Combining this relation with the assumption that \(\int _{{t_0}}^{ + \infty } {t\beta \left( t \right) \varepsilon \left( t \right) dt < + \infty }\) and the fact \(\left\| {x\left( t \right) } \right\| ^2 \le 2\left\| {x\left( t \right) - z} \right\| ^2 + 2\left\| z \right\| ^2\), \(t>0\), \(\beta (t)\ge 0\), \(\varepsilon (t)\ge 0\), we obtain further that
Next, we begin to establish the boundedness of the trajectory of (1.4). Recall the definition of E(t) in (4.3) and the result E(t) is bounded from the discussion in the proof of (ii), we see there exists \(C_2>0\) such that
Moreover, we have
After dividing (4.15) by \(p\left( t \right) = {\left( {\frac{t}{{{t_0}}}} \right) ^\alpha }\), we obtain that
Combing this relation with the definition of \({h_z}\left( t \right) = \frac{1}{2}{\left\| {x\left( t \right) - z} \right\| ^2}\) in (2.5) and \( {{\dot{h}}_z}\left( t \right) = \left\langle {\dot{x}\left( t \right) ,x\left( t \right) - z} \right\rangle \) from (2.6), we obtain further that
where \(q(t)= \frac{{g\left( t \right) }}{{p\left( t \right) }}\). Using the definition of \({g\left( t \right) = \frac{t}{{\alpha - 1}}}\) and \(p\left( t \right) = {\left( {\frac{t}{{{t_0}}}} \right) ^\alpha }\), we can easily compute q(t) as \(q(t)= \frac{{g\left( t \right) }}{{p\left( t \right) }} = \frac{t}{{\alpha - 1}}\cdot \frac{t_0^\alpha }{t^\alpha } = \frac{{t_0^\alpha {t^{1 - \alpha }}}}{{\alpha - 1}}\). Hence, we have \(\dot{q}(t) = - \frac{1}{{p\left( t \right) }}\) and q(t) is bounded due to the fact \(\alpha >1\) from the assumption. From these discussion, we can rewrite (4.16) as
dividing this equation by \(q{\left( t \right) ^2}\), we have
which is equivalent to
Hence, by integrating the above inequality from \(t_0\) to t, we see that there exists \(C_3>0\) such that
Note that q(t) is bounded due to the fact \(\alpha >1\) from the assumption, combining this with the definition of \(h_z(t) = \frac{1}{2}{\left\| {x\left( t \right) - z} \right\| ^2}\), we immediately obtain that x(t) is bounded. This completes the proof.
Remark 4.1
From Theorem 4.1, we see that if \(\beta (t) = 1\), then we have
which is just the result obtained by Attouch, Chbani, Riahi [4]. Furthermore, the assumption \(t\dot{\beta }\left( t \right) \leqslant \left( {\alpha - 3-b} \right) \beta \left( t \right) \) and the assumption \(\int _{{t_0}}^{ + \infty } {t\beta \left( t \right) \varepsilon \left( t \right) dt < + \infty }\) in Theorem 4.1 reduced to \(\alpha > 3\) and \(\int _{{t_0}}^{ + \infty } {t\varepsilon \left( t \right) dt < + \infty }\) in [4]. Hence our results are more general.
Remark 4.2
From Theorem 4.1, we see that if \(\beta (t) = t\), then we have
Furthermore, the assumption \(t\dot{\beta }\left( t \right) \leqslant \left( {\alpha - 3-b} \right) \beta \left( t \right) \) and the assumption \(\int _{{t_0}}^{ + \infty } t\beta \left( t \right) \varepsilon \left( t \right) dt < + \infty \) in Theorem 4.1 reduced to \(\alpha \geqslant 4+b\) and \(\int _{{t_0}}^{ + \infty } t^2\varepsilon \left( t \right) dt < + \infty \), respectively. This also shows that the convergence rate of the function value is faster than \(O\left( {\frac{1}{{{t^2}}}} \right) \) if \(\alpha >3\).
4.2 Case \(\int _{{t_0}}^{ + \infty } {\frac{{\varepsilon \left( t \right) \beta \left( t \right) }}{t}dt = + \infty } \)
For each \(\varepsilon > 0\), we use \(x_\varepsilon \) to denote the unique solution of the strongly convex minimization problem
From the first order optimality condition, we immediately have
Let us recall the Tikhonov approximation curve, \(\varepsilon \mapsto {x_\varepsilon }\), which satisfies the well-known strong convergence property:
where p is the element of minimal norm of the closed convex nonempty set \(\arg \min \Phi \). Moreover, by the monotonicity property of \(\nabla \Phi \) , and \(\nabla \Phi \left( p \right) = 0\), \(\nabla \Phi \left( {{x_\varepsilon }} \right) = - \varepsilon {x_\varepsilon }\), we have
which, after dividing by \(\varepsilon > 0\), and by Cauchy-Schwarz inequality gives
Theorem 4.2
Let \(\Phi :\mathcal {H} \rightarrow \mathbb {R}\) be a convex continuously differentiable function such that \(\arg \min \Phi \) is nonempty. Suppose that \(\varepsilon (t)\), \(\beta (t)\) satisfies condition \((H_1)\), \(\beta (t)\) is a nonincreasing function such that \(\int _{{t_0}}^{ + \infty } {\frac{{\varepsilon \left( t \right) \beta \left( t \right) }}{t}dt = + \infty } \) and \(\alpha > 1\) hold. Let \(x(\cdot )\) be a classical global solution of (1.4). Then \(\mathop {\lim \inf }\limits _{t \rightarrow \infty } \left\| {x\left( t \right) - p} \right\| = 0,\) where p is the element of minimal norm of \(\arg \min \Phi \). Moreover, the ergodic convergence property holds, which is
Proof
From Lemma 2.2, we have
According to the assumption that \(\beta (t)\) is a nonincreasing function, we have
Hence, W(t) is nonincreasing, and \(\mathop {\lim }\limits _{t \rightarrow + \infty } W\left( t \right) \) exists in \(\mathbb {R}\). Then, by the definition of W(t) in (2.1), we obtain further that \(\mathop {\sup }\limits _{t \geqslant {t_0}} \left\| {\dot{x}\left( t \right) } \right\| < + \infty \) and that
Now, we introduce an auxiliary function \(h_{p}(t)\), which is defined by
where p is the element of minimal norm of \(\arg \min \Phi \). By taking the derivative and second derivative of the \(h_{p}(t)\), we have
Hence, we deduce that
Moreover, recall the definition \({\Phi _t}\left( x \right) = \Phi \left( x \right) + \frac{{\varepsilon \left( t \right) }}{2}{\left\| x \right\| ^2}\) in (2.1), from this and the assumption \(\varepsilon (t)\ge 0\), we see that \(\Phi _t\) is strongly convex with modulus \(\varepsilon (t)\). Then we have
Combining this relation with system (1.4), we obtain further that
From this relation and the definition of h(p) in (4.20), we have
By the definition of \(x_\varepsilon \) and \(\Phi _t\), we immediately get
Combining (4.23) with the above relation, we obtain further that
Since p is the element of minimal norm of \(\arg \min \Phi \), we have \(\Phi \left( p \right) \leqslant \Phi \left( {{x_\varepsilon }\left( t \right) } \right) \). Using this and the definition of \(\Phi _t\), we obtain that
Combining (4.24) with (4.25) together, we obtain further that
Multiply both sides of the above formula by \(\beta (t)\), we have
Combining (4.22) with (4.26) together, we obtain that
On the other hand, by simply computing, we have
Hence, from the above relation and (4.27), we obtain that
Dividing both sides of the above formula by t, we deduce that
Define \(\delta \left( t \right) = \frac{1}{2}\left( {{{\left\| p \right\| }^2} - {{\left\| {{x_\varepsilon }\left( t \right) } \right\| }^2}} \right) \), from the assumption \(\lim \limits _{t\rightarrow \infty } \varepsilon (t) =0\) and (4.17),(4.18) we see that \(\mathop {\lim }\limits _{t \rightarrow \infty } \delta \left( t \right) = 0\). Moreover,
By rearranging terms, we have
By integrating (4.28) on \([t_0,t]\), there exists \(C_4>0\) such that
which follows from (4.19).
Next, we begin to analyze the right terms in the above formula, i.e., \(\int _{{t_0}}^t {\frac{1}{{{s^{\alpha + 1}}}}} \frac{d}{{ds}}\left( {{s^\alpha }{{\dot{h}}_p}\left( s \right) } \right) ds\). According to the integration rule, we have
where \(C_5\) is other constant. Recall the definition of \(h_{p}(t)\) in (4.20), we see that \(h_{p}(t)\) is nonnegative. From this with the fact \(\alpha >1\), we have
Combining the above formula with (4.29), we have
where \(C_6\) is other constant.
From the fact \(\mathop {\sup }\limits _{t \geqslant {t_0}} \left\| {\dot{x}\left( t \right) } \right\| < + \infty \) , similar to Lemma 2.3 (ii) , we have \(\mathop {\sup }\limits _{t \geqslant {t_0}} \frac{{\left| {{{\dot{h}}_p}\left( t \right) } \right| }}{t} < + \infty .\) Using this result and (4.30), we obtain that there exists another constant \(\bar{C}>0\) such that
Since \(\int _{{t_0}}^{ + \infty } {\frac{{\varepsilon \left( t \right) \beta \left( t \right) }}{t}dt = + \infty } \) from the assumption, by (4.31), we obtain further that
Note that \(\mathop {\lim }\limits _{t \rightarrow \infty } \delta \left( t \right) = 0\), hence, \(\mathop {\lim \inf }\limits _{t \rightarrow \infty } {h_p}\left( t \right) = 0,\) which implies that \(\mathop {\lim \inf }\limits _{t \rightarrow \infty } \left\| {x\left( t \right) - p} \right\| = 0.\) This proves the strong convergence of the trajectory x(t).
In the following, we will prove the trajectory x(t) is ergodicly convergent to the solution with minimal norm of the solution of (1.4). Note that
where the last inequality follows from (4.31). Dividing both sides of the above formula by \(\int _{{t_0}}^t {\frac{{\varepsilon \left( \tau \right) \beta \left( \tau \right) }}{\tau }} d\tau \), then we have
where the first inequality follows from the fact \(\varepsilon (t)\ge 0, \beta (t)\ge 0\), and the last equality follows from the assumption that \(\mathop {\lim }\limits _{t \rightarrow \infty } \int _{{t_0}}^t {\frac{{\varepsilon \left( \tau \right) \beta \left( \tau \right) }}{\tau }} d\tau = + \infty \) and the fact that \(\mathop {\lim }\limits _{t \rightarrow \infty } \delta \left( t \right) = 0.\) Then, by the definition of \(h_p\), we have
Since, all the terms in the left side of (4.32) are nonnegative, we obtain further that
This completes the proof.
5 Numerical experiments
In this section, we perform numerical experiments to illustrate our theoretical results of dynamical system (1.4). All the experiments are performed by Matlab 2014b on a 64-bit Thinkpad laptop with an Intel(R) Core(TM) i7-6600U CPU (2.60GHz) and 12GB of RAM.
In our numerical tests, we consider three optimization problems: the first two examples are two dimensional strongly convex problem and convex problem respectively, the third is a convex and twice continuously differentiable one-dimensional problem and the minimizer is not unique, this example comes from reference [17]. We use Runge Kutta 4-5 adaptive method to solve them.
The first two examples are mainly to emphasize the fast convergence rate of the function value (Theorem 4.1), and the third example is to show the strong convergence of the trajectory (Theorem 4.2). A detailed description is given below.
In the next two subsections, we choose \(b \in (0,1)\) and \((\alpha , \beta (t), \varepsilon (t))=\left( 5, t, \frac{1}{t^4}\right) \), \((\alpha , \beta (t), \varepsilon (t))=\left( 7, t^3, \frac{1}{t^6}\right) \), \((\alpha , \beta (t), \varepsilon (t))=\left( 9, t^5, \frac{1}{t^8}\right) \) respectively. All the choices of \(\alpha , \beta (t), \varepsilon (t)\) satisfy the assumptions in Theorem 4.1. Hence, by Theorem 4.1, the function value along the trajectory is convergent fast.
5.1 Strongly convex function
In this subsection, we consider the strongly convex optimization problem:
By simply computing, we obtain that \(\nabla {\Phi _1}\left( {{x_1},{x_2}} \right) = \left( {4{x_1} - 4,10{x_2} + 10} \right) ^T\) and \({x^ * } = \left( {1, - 1} \right) ^T\) is the unique minimizer of \(\Phi _1\), hence the optimal value is \({\Phi _1}^ * = {\Phi _1}\left( {1, - 1} \right) = 0\).
To illustrate the fast convergence rate of \(\Phi (x(t))\), we plot in Fig. 1 the trajectory of \(|{\Phi _1}\left( {x\left( t \right) } \right) - {\Phi _1}^ * |\) versus the time t, the horizontal axis represents t, the initial point is chosen as \(u_0=v_0=(-5,30)^T\). According to Fig. 1a, we see that \(\Phi _1(x(t))\) converges to \(\Phi _1^ *\) fast for all the choices of \(\alpha \), \(\beta (t)\) and \(\varepsilon (t)\). Fig. 1b shows the performance of \(|{\Phi _1}\left( {x\left( t \right) } \right) - {\Phi _1}^ * |\) under the choice of \(\alpha =5\), \(\beta (t)=t\), \(\varepsilon (t)=1/t^4\) and the case \(\alpha =5\), \(\beta (t)=1\), \(\varepsilon (t)=1/t^4\), where the latter choice is from [4]. We see from Fig. 1b that the choice \(\beta (t)=t\) in (1.4) are comparable with \(\beta (t)=1\).
Error analysis with different parameters in dynamical system (1.4) for a strong convex objective function \(\Phi _1\). The red, green, black and blue line correspond to the three choices, \(\alpha =5\), \(\beta (t)=t\), \(\varepsilon (t)=1/t^4\); \(\alpha =7\), \(\beta (t)=t^3\), \(\varepsilon (t)=1/t^6\); \(\alpha =9\), \(\beta (t)=t^5\), \(\varepsilon (t)=1/t^8\); \(\alpha =5\), \(\beta (t)=1\), \(\varepsilon (t)=1/t^4\), respectively
5.2 Convex function
In this subsection, we consider convex optimization problem:
We can easily deduce that \(\nabla {\Phi _2}\left( {{x_1},{x_2}} \right) = \left( {4{x_1}^3 - 4,10{x_2} -10} \right) ^T\) and \({x^ * } = \left( {1, 1} \right) ^T\) is the minimizer of \(\Phi _2\), thus the optimal value is \({\Phi _2}^ * = {\Phi _2}\left( {1, 1} \right) = 0.\)
The computational results are presented in Fig. 2. We plot \(|{\Phi _1}\left( {x\left( t \right) } \right) - {\Phi _2}^ * |\) versus the time t in the following figures, the horizontal axis represents t, and the initial point is chosen as \(u_0=v_0=(-1,5)^T\). From Fig. 2a, we see that \(\Phi _2(x(t))\) converges to \(\Phi _2^ *\) fast for all the choices of \(\alpha \), \(\beta (t)\) and \(\varepsilon (t)\). Figure 2b shows the comparison between the case \(\alpha =5\), \(\beta (t)=t\), \(\varepsilon (t)=1/t^4\) and the case \(\alpha =5\), \(\beta (t)=1\), \(\varepsilon (t)=1/t^4\), where the latter case is from [4]. From the numerical results, we see that the convergence rate of \(\Phi _2(x(t))\) are comparable under both choices of \(\alpha \), \(\beta (t)\), \(\epsilon (t)\).
Error analysis with different parameters in dynamical system (1.4) for a convex objective function \(\Phi _2\). The red, green, black and blue line correspond to the three choices, \(\alpha =5\), \(\beta (t)=t\), \(\varepsilon (t)=1/t^4\); \(\alpha =7\), \(\beta (t)=t^3\), \(\varepsilon (t)=1/t^6\); \(\alpha =9\), \(\beta (t)=t^5\), \(\varepsilon (t)=1/t^8\); \(\alpha =5\), \(\beta (t)=1\), \(\varepsilon (t)=1/t^4\), respectively
5.3 One-dimensional function
In this subsection, we conduct numerical experiments to illustrate the influence of Tikhonov regularization on the strong convergence of the trajectory x(t). We consider \((\alpha , \beta (t), \varepsilon (t))=\left( 3, \frac{1}{{\sqrt{1 + \ln t} }}, \frac{1}{{\sqrt{1 + \ln t} }}\right) \) and \((\alpha , \beta (t), \varepsilon (t))=\left( 3, \frac{1}{{\sqrt{1 + \ln t} }}, 0\right) \) respectively, and the choice of \((\alpha , \beta (t), \varepsilon (t))=\left( 3, \frac{1}{{\sqrt{1 + \ln t} }}, \frac{1}{{\sqrt{1 + \ln t} }}\right) \) satisfies the assumptions in Theorem 4.2.
The optimization problem we consider in this part is as follows:
By easily computing, we can deduce that \(\arg \min \Phi =[-1,1]\) and \(x^*=0\) is its minimum norm solution.
Our computational results are presented in Fig. 3. We plot the trajectory x(t) generated by (1.4) versus the time t in the following figure, the horizontal axis represents t. We see from the figure that x(t) generated by (1.4) with the choice \((\alpha , \beta (t), \varepsilon (t))=\left( 3, \frac{1}{{\sqrt{1 + \ln t} }}, \frac{1}{{\sqrt{1 + \ln t} }}\right) \) converges to the minimum norm solution \(x^*=0\), which conforms with our theory. However, the trajectory x(t) under the case \((\alpha , \beta (t), \varepsilon (t))=\left( 3, \frac{1}{{\sqrt{1 + \ln t} }}, 0\right) \) (without the Tikhonov regularization) converges to the optimal solution, but not the minimum norm solution.
The red line shows the trajectories of the dynamical system with Tikhonov regularization \(\varepsilon (t)=\frac{1}{{\sqrt{1 + \ln t} }}\) are approaching the minimum norm solution \(x^* = 0\); the green line shows the trajectories of the dynamical system without Tikhonov regularization are approaching the optimal solution, but not the minimum norm solution
6 Conclusion, perspective
In this paper, we mainly study the convergence behavior of a second order gradient system with Tikhonov regularization (1.4). We first prove the existence and uniqueness of the \(C^2\)-global solution of (1.4). Next, under the assumption \(\int _{{t_0}}^{ + \infty }t\beta \left( t\right) \varepsilon \left( t\right) dt < +\infty \), we establish the global convergence of \(\Phi \left( {x\left( t \right) } \right) \) to the optimal value of \(\Phi \). Moreover, we show that the convergence rate of \(\Phi (x(t))\) to \(\min \Phi \) is \(o(1/t^2\beta (t))\), which can be faster than \(o(1/t^2)\). In the case \(\int _{{t_0}}^{ + \infty } {\frac{{\varepsilon \left( t \right) \beta \left( t \right) }}{t}dt = + \infty } \), by constructing proper energy function, we show that the trajectory x(t) strongly converges to p, where p is the element of minimal norm of \(\arg \min \Phi \). In addition, we also prove the ergodic convergence of x(t). Finally, we conduct some numerical experiments to illustrate the theoretical results.
At the end of this paper, we would like to list some possible directions of future research related to the dynamical sytem (1.4):
-
(i)
A natural direction is to propose some proper numerical algorithms via time discretization of (1.4). Furthermore, one can investigate their theoretical convergence properties, and confirm them with numerical experiments;
-
(ii)
One can also consider (1.4) endowed with an additional Hessian driven damping, see for example [8, 17];
-
(iii)
Another direction is to consider the non-smooth optimization problems, which mean the objective functions are not differentiable, then we can not apply (1.4) directly. One can use the monotone inclusion to solve it, see for example [8, 12, 21].
References
Attouch, H., Cominetti, R.: A dynamical approach to convex minimization coupling approximation with the steepest descent method. J. Differ. Equ. 128(2), 519–540 (1996)
Attouch, H., Czarnecki, M.O.: Asymptotic control and stabilization of nonlinear oscillators with non-isolated equilibria. J. Differ. Equ. 179(1), 278–310 (2002)
Attouch, H., Chbani, Z., Peypouquet, J., Redont, P.: Fast convergence of inertial dynamics and algorithms with asymptotic vanishing viscosity. Math. Program. 168(1–2), 123–175 (2018)
Attouch, H., Chbani, Z., Riahi, H.: Combining fast inertial dynamics for convex optimization with Tikhonov regularization. J. Math. Anal. Appl. 457(2), 1065–1094 (2018)
Attouch, H., Chbani, Z., Riahi, H.: Rate of convergence of the Nesterovs accelerated gradient method in the subcritical case \(\alpha \le 3\), ESAIM: control. Optim. Calculus Var. 25, 2 (2019)
Attouch, H., Chbani, Z., Riahi, H.: Fast convex optimization via time scaling of damped inertial gradient dynamics, https://hal.archives-ouvertes.fr/hal-02138954
Attouch, H., Chbani, Z., Riahi, H.: Fast proximal methods via time scaling of damped inertial dynamics. SIAM J. Optim. 29(3), 2227–2256 (2019)
Attouch, H., Peypouquet, J., Redont, P.: Fast convex minimization via inertial dynamics with Hessian driven damping. J. Differ. Equ. 261(10), 5734–5783 (2016)
Bolte, J.: Continuous gradient projection method in Hilbert spaces. J. Optim. Theory Appli. 119(2), 235–259 (2003)
Bach, F.: Learning with submodular functions: a convex optimization perspective. Found. Trends Mach. Learn. 6(2–3), 145–373 (2013)
Becker, S., Bobin, J., Cands, E.J.: NESTA: a fast and accurate first-order method for sparse recovery. SIAM J. Imag. Sci. 4(1), 1–39 (2011)
Bot, R.I., Csetnek, E.R.: Second order forward-backward dynamical systems for monotone inclusion problems. SIAM J. Control Optim. 54(3), 1423–1443 (2016)
Bot, R.I., Csetnek, E.R.: Approaching nonsmooth nonconvex optimization problems through first order dynamical systems with hidden acceleration and Hessian driven damping terms. Set-Valued Variation. Anal. 26(2), 227–245 (2018)
Bot, R.I., Csetnek, E.R.: A second-order dynamical system with Hessian-driven damping and penalty term associated to variational inequalities. Optimization 68(7), 1265–1277 (2019)
Bot, R.I., Csetnek, E.R., László, S.C.: Second-order dynamical systems with penalty terms associated to monotone inclusions. Anal. Appl. 16(05), 601–622 (2018)
Bot, R.I., Csetnek, E.R., László, S.C.: A second-order dynamical approach with variable damping to nonconvex smooth minimization. Appl. Anal. 99(3), 361–378 (2020)
Bot, R.I., Csetnek, E.R., László, S.C.: Tikhonov regularization of a second order dynamical system with Hessian driven damping. Math. Program. (2020). https://doi.org/10.1007/s10107-020-01528-8
Bach, F., Jenatton, R., Mairal, J., Obozinski, G.: Structured sparsity through convex optimization. Stat. Sci. 27(4), 450–468 (2012)
Beck, A., Teboulle, M.: A fast iterative shrinkage-threshoiding algorithm for linear inverse problems. SIAM J. Imag. Sci. 2(1), 183–202 (2009)
Condat, L.: A primal-dual splitting method for convex optimization involving Lipschitzian, proximable and linear composite terms. J. Optim. Theory Appl. 158(2), 460–479 (2013)
Csetnek, E.R.: Continuous dynamics related to monotone inclusions and non-smooth optimization problems. Set Valued Variation. Anal. (2020). https://doi.org/10.1007/s11228-020-00548-y
Haraux, A.: Systèmes dynamiques dissipatifs et applications, Rech. Math. Appl. 17, Masson, Paris. (1991)
May, R.: On the strong convergence of the gradient projection algorithm with Tikhonov regularizing term, arXiv preprint arXiv:1910.07873, (2019)
Muehlebach, M., Jordan, M. I.: A dynamical systems perspective on Nesterov acceleration, arXiv preprint arXiv:1905.07436, (2019)
Mitchell, D., Ye, N., Sterck, H.D.: Nesterov acceleration of alternating least squares for canonical tensor decomposition. Numer. Linear Algbera Appl. (2020). https://doi.org/10.1002/nla.2297
Nesterov, Y.: A method of solving a convex programming problem with convergence rate \(O(1/k^2)\). Soviet Math. Doklady 27(2), 372–376 (1983)
Sontag, E.D.: Mathematical Control Theory Deterministic Finite-Dimensional Systems. Texts in Applied Mathematics, vol. 6, 2nd edn. Springer, New York (1998)
Su, W., Boyd, S., Candés, E.J.: A differential equation for modeling Nesterovs accelerated gradient method: theory and insights. J. Mach. Learn. Res. 17, 1–43 (2016)
Sutskever, I., Martens, J., Dahl, G., et al.: On the importance of initialization and momentum in deep learning. In: International Conference on Machine Learning, pp. 1139–1147 (2013)
Sra, S., Nowozin, S., Wright, S.J.: Optimization for Machine Learning. Mit Press, Cambridge (2012)
Tseng, P.: On accelerated proximal gradient methods for convex-concave optimization, http://pages.cs.wisc.edu/~brecht/cs726docs/Tseng.APG.pdf (2008). Accessed 2019
Wright, J., Ganesh, A., Rao, S.: Robust principal component analysis: Exact recovery of corrupted low-rank matrices via convex optimization. Advances in Neural Information Processing Systems 22, 2080–2088 (2009)
Wilson, A. C., Recht, B., Jordan, M. I.: A lyapunov analysis of momentum methods in optimization, arXiv preprint arXiv:1611.02635, (2016)
Acknowledgements
The authors would like to thank the editor and anonymous reviewers for their insight and helpful comments and suggestions which improve the quality of the paper. This work is also supported in part by NSFC 11801131, Natural Science Foundation of Hebei Province (Grant No. A2019202229), Science and Technology Project of Hebei Education Department (Grant No. QN2018101).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Xu, B., Wen, B. On the convergence of a class of inertial dynamical systems with Tikhonov regularization. Optim Lett 15, 2025–2052 (2021). https://doi.org/10.1007/s11590-020-01663-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11590-020-01663-3