On minimization of a quadratic function with one negative eigenvalue

Abstract

It is well known that a quadratic programming minimization problem with one negative eigenvalue is NP-hard. However, in practice one may expect such problems being not so difficult to solve. We suggest to make a single partition of the feasible set in a concave variable only so that a convex approximation of the objective function upon every partition set has an acceptable error. Minimizing convex approximations on partition sets provides an approximate solution of the nonconvex quadratic program that we consider. These minimization problems are to be solved concurrently by parallel computing. An estimation of the number of partition sets is given. The study presents a computational comparison with a standard branch-and-bound procedure.

1 Introduction

Quadratic nonconvex programming has a wide range of applications and is an intensively studied field of global optimization. The number of publications devoted to this topic is quite impressive, see, for example, [1,2,3] and references therein. The main issue of the paper is connected to the result published in [4]. Namely, nonconvex quadratic programming problem with one negative eigenvalue in the objective is NP-hard. Properties of a quadratic function with one negative eigenvalue and the corresponding theoretical results can be found in [5, 6]. We get interested in how difficult on average the problem of global minimization of quadratic objective is with exactly one negative eigenvalue. We assume that the eigenvalues and eigenvectors of the matrix in the minimized function are known. Testing the problem from [4] showed that NP-hardness follows from exponential growth of the size of the feasible set. If the size is bounded then the problem can be solved in a reasonable time. The paper investigates this topic in details.

2 Problem formulation

We consider a quadratic programming problem

$$\begin{aligned} f(x)= & {} x^{\mathsf {T}} Qx + x^{\mathsf {T}} c \rightarrow \min _x \, , \end{aligned}$$

(1)

$$\begin{aligned} x\in X= & {} \{ x\in {\mathbb {R}}^n \mid Ax \leqslant b \} \, , \end{aligned}$$

(2)

where Q is an indefinite $n\times n$ matrix with exactly one negative eigenvalue, A is an $m\times n$ matrix. The feasible set X is assumed to be nonempty and bounded. Here $x^{\mathsf {T}}$ denotes the transpose of vector x.

Let us represent the matrix Q such that

$$\begin{aligned} Q = W \varLambda W^{\mathsf {T}}, \qquad \varLambda =\mathop {\mathrm {diag}}\{\lambda _1, \lambda _2, \ldots , \lambda _n \} \, , \end{aligned}$$

(3)

where $\lambda _1, \lambda _2, \ldots , \lambda _n$ are the eigenvalues of the matrix Q rearranged by increasing order, i.e. $\lambda _1 \leqslant \ldots \leqslant \lambda _n$, $\lambda _1<0$, $\lambda _i \geqslant 0$, $i=2,\ldots ,n$; W is a matrix, which columns are the eigenvectors of Q sorted according to its eigenvalues. $\varLambda$ is a diagonal matrix with $\lambda _1, \lambda _2, \ldots , \lambda _n$ as the diagonal elements. It is well known [7] that $W^{-1} = W^{\mathsf {T}}$. The linear transformation

$$\begin{aligned} y = W^{\mathsf {T}} x \end{aligned}$$

(4)

reduces the problem (1), (2) to the separable form, thus we get the following problem with the separable objective function:

$$\begin{aligned} g(y)= & {} \sum \limits _{i=1}^n \lambda _i y_i^2 + y^{\mathsf {T}} d \rightarrow \min _y \, , \end{aligned}$$

(5)

$$\begin{aligned} y\in Y= & {} \{ y\in {\mathbb {R}}^n \mid Dy \leqslant b \} \, , \end{aligned}$$

(6)

where $d = W^{\mathsf {T}}c$ and $D = AW$. The problems (1), (2), and (5), (6) are equivalent in the sense that $x^*$ is a solution of (1), (2) iff $y^*= W^{\mathsf {T}} x^*$ solves (5), (6). Moreover values of the objectives also coincide. The further discussion refers mainly to the latter optimization statement since it is more convenient for analysis.

3 Minimization procedure

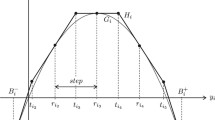
The objective function (5) is concave in $y_1$ and is convex in other variables. Therefore the main idea of the minimization procedure for problem (5), (6) is a partition of the feasible set Y in variable $y_1$ only. Let

$$\begin{aligned} {\widetilde{Y}} = \{ y_1 \in {\mathbb {R}}^1 \mid \alpha \leqslant y_1 \leqslant \beta \} \end{aligned}$$

be a projection of the set Y onto the $y_1$-axis. Divide the set ${\widetilde{Y}}$ into p intervals:

$$\begin{aligned} {\widetilde{Y}} = \bigcup _{i=1}^p \{ y_1\in {\mathbb {R}}^1 \mid \alpha _i \leqslant y_1 \leqslant \beta _i \} \, , \end{aligned}$$

(7)

where $\alpha \leqslant \alpha _i < \beta _i \leqslant \beta$,  $\beta _i = \alpha _{i+1}$ for $i = 1,\ldots ,p-1$, and $\alpha _1 = \alpha$, $\beta _p = \beta$. Then we define a partition $\{Y_1,Y_2, \ldots ,Y_p\}$ of Y as follows:

$$\begin{aligned} Y = \bigcup _{i=1}^p Y_i \, , \qquad Y_i = \{ y\in Y \mid \alpha _i \leqslant y_1 \leqslant \beta _i \} \, , \quad i = 1, 2, \ldots , p \, . \end{aligned}$$

(8)

For every partition set $Y_i$ we underestimate the concave part $\lambda _1 y_1^2$ of the objective by an affine function $l_i$ such that $\lambda _1 y_1^2$ and $l_i$ intersect at points $\alpha _i$ and $\beta _i$:

$$\begin{aligned} \lambda _1 y_1^2 \geqslant l_i(y_1) = \lambda _1(\alpha _i + \beta _i) y_1 - \lambda _1 \alpha _i \beta _i \, , \qquad \alpha _i\leqslant y_1 \leqslant \beta _i \, . \end{aligned}$$

(9)

From (9) we obtain a convex approximation of g:

$$\begin{aligned} g(y) \geqslant \varphi _i(y) = l_i(y_1) + \sum \limits _{i=2}^n \lambda _i y_i^2 + y^{\mathsf {T}} d \, , \quad y\in Y_i \, , \qquad i=1,2,\ldots ,p \, . \end{aligned}$$

This inequality can be presented in the following equivalent form:

$$\begin{aligned} g(y) \geqslant \varphi (y) = \min _{1\leqslant i \leqslant p} l_i(y_1) + \sum \limits _{i=2}^n \lambda _i y_i^2 + y^{\mathsf {T}} d \, , \qquad y\in Y \, . \end{aligned}$$

It is known [8] that

$$\begin{aligned} g(y) - \varphi _i(y) \leqslant -\frac{1}{4} \lambda _1 (\alpha _i - \beta _i)^2 \, , \qquad y\in Y_i \, , \end{aligned}$$

which results in the following estimation of the approximation error upon the entire feasible set:

$$\begin{aligned} g(y) - \varphi (y) \leqslant -\frac{1}{4} \lambda _1 \max _{1\leqslant i \leqslant p} \left\{ (\alpha _i - \beta _i)^2 \right\} \, , \qquad y\in Y \, . \end{aligned}$$

(10)

Theorem 1

For a given $\varepsilon > 0$, let the partition (7) satisfy

$$\begin{aligned} \beta _i - \alpha _i \leqslant 2 \sqrt{\frac{\varepsilon }{|\lambda _1|}} \, , \qquad i=1,2,\ldots ,p \, , \end{aligned}$$

(11)

and $y^*$ be a minimum point of $\varphi$ upon Y. Then the following inequality holds:

$$\begin{aligned} g(y^*) \leqslant g(y) + \varepsilon \, , \qquad y \in Y . \end{aligned}$$

(12)

Proof

The inequalities (11) are equivalent to

$$\begin{aligned} \varepsilon \geqslant -\frac{1}{4} \lambda _1 \max _{1\leqslant i \leqslant p} \left\{ (\alpha _i - \beta _i)^2 \right\} \, . \end{aligned}$$

(13)

As $\varphi (y^*) \leqslant \varphi (y)$ for every $y\in Y$, (12) directly follows from (10) and (13).$\square$

From (10) to (13) we have that for every given tolerance $\varepsilon >0$ we may define a partition of Y with sufficiently small widths of intervals in $y_1$, so that

$$\begin{aligned} g(y) - \varphi (y) \leqslant \varepsilon \, , \qquad y\in Y \, . \end{aligned}$$

(14)

Underestimation of g by $\varphi$ in that manner allows us to perform the partition (8) only once such that the inequality (14) holds. By Theorem 1, every minimizer of $\varphi$ upon Y is an approximate solution of (5), (6). In order to minimize $\varphi$, we solve p convex quadratic programming problems

$$\begin{aligned} \varphi _i(y) \rightarrow \min \, , \quad y\in Y_i \, , \qquad i=1,2,\ldots ,p \, . \end{aligned}$$

(15)

Let $y^{*i}$ be a solution of the ith problem in (15). Then

$$\begin{aligned} \min \varphi (y) = \min _{1\leqslant i \leqslant p} \varphi _i (y^{*i})\, , \end{aligned}$$

and a minimum point of $\varphi$ is the corresponding vector among $y^{*1}, \ldots , y^{*p}$. The optimization problems (15) are suggested to solve concurrently by parallel computing, since they are independent of each other.

As every partition set implies solving a convex quadratic program, the number of partition intervals p has a significant impact on how fast the set of problems (15) would be solved. For a particular problem (5), (6), one can compute the value of p satisfying (11) by

$$\begin{aligned} p = \Bigg \lceil \frac{1}{2} (\beta - \alpha ) \sqrt{ \frac{ |\lambda _1| }{ \varepsilon } } \; \Bigg \rceil \, , \end{aligned}$$

(16)

where $\lceil a \rceil$ is the least integer greater than or equal to a number a. Additionally, an upper estimation of p needed to meet (11) may be established. Since X is bounded, there exists a box constrained set ${\widehat{X}} = \left\{ x\in {\mathbb {R}}^n \mid x^{\min } \leqslant x \leqslant x^{\max } \right\}$ such that $X \subseteq {\widehat{X}}$. It is better to choose ${\widehat{X}}$ so that it has the minimal diameter.

Theorem 2

For a given $\varepsilon >0$, there exists a positive integer p satisfying

$$\begin{aligned} p \leqslant \Bigg \lceil \frac{1}{2} \sqrt{ \frac{n |\lambda _1|}{\varepsilon } } \max _{1\leqslant i \leqslant n} \left\{ x^{\max }_i - x^{\min }_i \right\} \Bigg \rceil \end{aligned}$$

(17)

such that the partition (7) meets (11).

Proof

Inscribe ${\widehat{X}}$ in a ball $B = \left\{ x\in {\mathbb {R}}^n \mid \Vert x - x_0 \Vert \leqslant r \right\}$, where $x_0 = \frac{1}{2}(x^{\min } + x^{\max })$, $r = \Vert x^{\max } - x_0 \Vert$, and $\Vert \cdot \Vert$ is the 2-norm. As $W^{\mathsf {T}} W = I$, where I is the identity matrix, the projection of B onto the $y_1$-axis after the transformation (4) has the length equal to the diameter 2r of B. Since $X\subset B$, there exist an integer p and bounds $(\alpha _i, \beta _i)$, $i=1,\ldots ,p$, such that (11) holds and $p \leqslant \lceil 2r / l \rceil$, where $l = 2\sqrt{ \varepsilon / |\lambda _1| }$. The latter inequality directly implies (17). $\square$

It follows from Theorem 2 that, if $X \subseteq {\widehat{X}}$ and $\lambda _1$, $x^{\min }$, $x^{\max }$ do not depend on n, then the number of intervals p(n) has growth rate $\sqrt{n}$. In the next section we consider an example, where the first component of $x^{\max }$ grows rapidly as n increases.

4 Computational experiment

The proposed method with a single partition was computationally compared with a standard branch-and-bound procedure [9]. Let denote the former method by SP and the latter one by BB. In BB algorithm, partitioning is performed by bisection and, additionally, partition sets that certainly do not admit a solution are excluded from the consideration. More precisely, a partition set should be neglected if its lower bound of the objective exceeds the best known objective value (the record). For a particular partition set $Y_i$ in BB procedure, lower bound is a minimum of $\varphi _i$ on $Y_i$.

We consider three groups of test problems. For every group, the result of the computation for both SP and BB algorithms is presented in a separate table. The names of columns are as follows. n is the number of variables, m is the number of linear constraints in (2) excluding box constraints, SP Int. is the number of intervals p computed by (16), SP Th.Int. is the theoretical estimation of p computed by (17), SP Time is the time of SP algorithm in seconds, BB Int. is the number of convex problems solved in BB algorithm, BB Time is the time of BB algorithm in seconds, Rel.Err. stands for an actual relative error computed after the solution is obtained. In all tables, every row corresponds to a single randomly generated problem. All random values were chosen from specific intervals according to a uniform distribution. To compute the right hand side of (17), we took box constraints of the problems’ definitions as the set ${\widehat{X}}$.

The program was implemented in AIMMS 4.66 modelling environment [10], problems (15) in both methods were solved by IBM ILOG CPLEX 12.9 solver [11]. In the SP method, we solved problems (15) concurrently in parallel using AIMMS GMP library facilities and, additionally, the number of threads used by one CPLEX session was limited to 1. In BB, problems of type (15) were solved sequentially, however the number of threads used by one CPLEX session was not limited so that every convex problem in BB was solved by multiple threads. We used default values for all other CPLEX parameters. Computation was performed on a computer with AMD Ryzen 7 1700X @ 3.4GHz CPU (8 cores, 16 threads), 16 Gb RAM. Preliminary experiments showed that the time of SP is minimal when the method uses 8 threads on this computer. Hence, for the SP algorithm, the number of simultaneous solution of convex problems was limited to 8.

Example 1

In problem (1), (2), set $c = - (Q - \lambda _1 I ) x^*$,   $x^*= (1, -1,\ldots ,1,-1)^{\mathsf {T}}$,  $X = \{ x\in {\mathbb {R}}^n \mid -1 \leqslant x \leqslant 1 \}$. Vector $x^*$ is a solution of (1), (2) [12]. Values of $\lambda _1$, $\lambda _i$, $i=2,\ldots ,n$, and of elements of W were randomly chosen from intervals $[-11,-7]$, [0, 20], $[-10,10]$ respectively. Eigenvectors of Q were computed by applying the Gram–Schmidt process to columns of W. Then we defined Q by (3). For these problems, we set $\varepsilon = 10^{-2}$, because it provided an acceptable relative error in a solution point. The computational results of SP and BB methods are in Table 1. We did not apply the SP algorithm to problems with $n > 500$ due to considerable time of computation, more than 10 minutes per one problem. In all instances both algorithms found the solution $x^*$. As there are box constraints only, $m=0$ for all problems. The number of intervals turns out to be close to its theoretical estimation (17) and grows in accordance with it as n increases. On the other hand, in the BB algorithm, the number of convex problems solved by the method is small and is approximately constant for all dimensions we considered. The “bottleneck” in this case is the time CPLEX spends for solving one quadratic programming problem.

Table 1 Results of experiment for problems with known solution (Example 1)

Table 2 Results of experiment for random problems (Example 2)

Example 2

In this case of (1), (2) all parameters of the objective function were generated randomly in the same way as in Example 1, except for vector c, the elements of which were randomly chosen from $[-30,30]$. Elements of A were generated from $[-15,15]$. Vector b was computed such that every constraint in (2) defined a tangent hyperplane to a ball with the radius 4 and random center, the elements of which were from $[-5,5]$. In order to guarantee the boundedness, we added box constraints $-10\leqslant x \leqslant 10$. We set $\varepsilon = 10^{-2}$. Table 2 contains the result of experiment. It shows that the number of intervals in SP is significantly larger than in Example 1. The reason for it is that variables have a larger bounds so that the length of projection ${\widetilde{Y}}$ increases. Inspite of the promising estimation (17), large number of intervals together with a significant time of solving convex QP leads to considerable time of the SP method. The number of convex problems solved in BB slightly exceeds that in Example 1, but still is nearly constant as n increases. The number m of non-box linear constraints increases the time CPLEX needs to solve a QP problem. One can observe this effect if we compare the columns BB Int. and BB Time for problems with the same n. For example, the problem with $n=1000$, $m=1500$ takes more than 1.5 times of computation time compared with the problem with the same n and $m=800$. For the SP algorithm, the similar result takes place.

Example 3

As stated in [4], a specifically defined QP problem with one negative eigenvalue is equivalent to the maximum clique problem. For the graph with the set of vertices $V=\{1,\ldots ,v\}$ and the set of edges E this QP is

$$\begin{aligned}&-w^2 + z - (x_1 + \cdots + x_v) \rightarrow \min _{(w,z,x,y)}\, , \quad 0 \leqslant x \leqslant 1 \, , \quad y\geqslant 0 \, , \nonumber \\&\quad w = bx_1 + b^2 x_2 + \cdots + b^v x_v \, ,\nonumber \\&\quad z = b^2 x_1 + b^4 x_2 + \cdots + b^{2v} x_v + \sum _{1\leqslant i< j \leqslant v} 2b^{i+j} y_{ij} \, , \nonumber \\&\quad y_{ij} \geqslant x_i + x_j - 1\, , \quad 1\leqslant i <j \leqslant v \, ,\qquad x_i + x_j \leqslant 1 \, , \quad (i,j) \notin E \, , \end{aligned}$$

(18)

where $b=4$. Without loss of generality, we add the constraint $y \leqslant 1$ to provide the boundedness. The key feature that makes this problem difficult to solve is that the length of projection ${\widetilde{Y}}$ onto w-axis (assuming $y_1 = w$) rapidly grows as v increases. Indeed, due to (18) this length may be estimated by $b + b^2 + \cdots + b^v$. Inspite of this, we made some experiments to illustrate how behaviour of the methods differs from the previous two examples. We assume $\varepsilon = 10^{-4}$. The set E was generated randomly in the form of a symmetric adjacency (0, 1)-matrix with zeros on its diagonal. We did not apply the SP algorithm due to a very large number of partition intervals in almost all problems we considered (see the column SP Int. in Table 3). This number exceeds $10\,000$ even for the graph with 4 vertices. The number of convex problems in the BB procedure also increases fast. It is easy to see that problems (15) are linear for this statement, however large numbers in coefficients raise numerical issues with increasing of v.

Table 3 Results of experiment for the maximum clique problem (Example 3)

5 Conclusion

We consider a quadratic programming problem with one negative eigenvalue. In general, it is NP-hard. However, if input parameters such as the negative eigenvalue and the feasible set do not depend on the number of variables, then a solution can be found by solving an acceptable number of convex quadratic programming problems. The experiment shows that, for the standard branch-and-bound procedure, the number of these convex problems is nearly constant for different dimensions.