Scheduling with common due date assignment to minimize generalized weighted earliness–tardiness penalties

Abstract

We investigate a single-machine common due date assignment scheduling problem with the objective of minimizing the generalized weighted earliness/tardiness penalties. The earliness/tardiness penalty includes not only a variable cost which depends upon the job earliness/tardiness but also a fixed cost for each early/tardy job. We provide an $O(n^3)$ time algorithm for the case where all jobs have equal processing times. Under the agreeable ratio condition, we solve the problem by formulating a series of half-product problems, which permits us to devise a fully polynomial-time approximation scheme with $O(n^3/\epsilon )$ time. $\mathcal {NP}$-hardness proof is proved for a very special case and fast FPTASes with $O(n^2/\epsilon )$ running time are identified for two special cases.

1 Introduction

In just-in-time (JIT) manufacturing systems, the decision-maker would like to find a production plan such that all orders are completed neither too early nor too tardy. Usually, JIT scheduling models presume the existence of order due dates and penalize both early orders and tardy orders. The orders that are completed early/tardy will result in penalties. These penalties include not only a variable penalty cost which depends upon the earliness/tardiness of the order [2, 9], but also a fixed charge which is incurred once an order is not on time regardless of how early/tardy it is [21, 23]. As a result, in order to avoid earliness–tardiness penalties, assigning attainable order due dates are very crucial for the manufacturer. On the one hand, prescribing shorter due dates would increase the probability that the order will be delivered late. But then, setting longer due dates would be undesirable to the customer or cause a customer to shut down operations. Therefore, there is an essential tradeoff between offering shorter due dates and longer due dates. Furthermore, due date quotation is also an important issue in a make-to-order JIT environment [4]. The due date assignment methods usually used consist of common due date (CON), equal slack (SLK), total work time (TWK), individual due date (DIF), etc.

The JIT scheduling problems have been an object of extensive research since the early 1990s. In scheduling terms, a manufacturing facility is seen as a machine and an order is seen as a job. Various scheduling criteria and machine environments have been studied in the literature [10]. In this paper, we address a single-machine JIT scheduling problem with generalized earliness–tardiness penalties.

1.1 Notation and problem formulation

To formally describe the problem under study, we start with defining the notations that will be used throughout this paper.

• $\mathcal {J}=\{J_1, J_2, \ldots , J_n\}$: the set of n jobs,

• $p_j$: the processing time of job $J_j$,

• P: the total processing time of all jobs in $\mathcal {J}$, i.e., $P=\sum _{j=1}^n p_j$,

• $C_j$: the completion time of job $J_j$ in a given schedule,

• D: the assignable common due date for all jobs,

• $V_j$: the early indictor variable of job $J_j$, where $V_j=1$ if $C_j <D$ and $V_j=0$ otherwise,

• $U_j$: the tardy indictor variable of job $J_j$, where $U_j=1$ if $C_j >D$ and $U_j=0$ otherwise,

• $E_j$: the earliness of job $J_j$, where $E_j=\max \{0, D-C_j\}$,

• $T_j$: the tardiness of job $J_j$, where $T_j =\max \{0, C_j -D\}$,

• $\mathcal {A}$: the set of early jobs, i.e., $\mathcal {A}=\{J_j: C_j <D\}$,

• $\mathcal {B}$: the set of tardy jobs, i.e., $\mathcal {B}=\{J_j: C_j > D\}$,

• $\alpha$: the unit due date assignment cost,

• $\beta _j$: the unit earliness cost of job $J_j$,

• $\gamma _j$: the unit tardiness cost of job $J_j$,

• $\delta _j$: the early weight of job $J_j$,

• $\theta _j$: the tardy weight of job $J_j$,

• [j]: the subscript of the job scheduled in the jth position in a given sequence $\pi$.

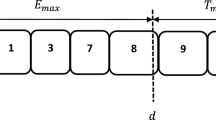
The studied problem can be stated as follows. A set $\mathcal {J}=\{J_1, J_2, \ldots , J_n\}$ of n jobs has to be scheduled without preemption on a single machine. All jobs in $\mathcal {J}$ are simultaneously available at time zero. Each job $J_j$ has an integer processing time $p_j$. A common due date D has to be determined for all jobs.

For a feasible schedule $\pi$ of the n jobs, let $C_j$ be the completion time of job $J_j$. If $C_j < D$, then job $J_j$ is said to be early; if $C_j = D$, then job $J_j$ is said to be on time; if $C_j > D$, then job $J_j$ is said to be tardy. No penalty cost is incurred if a job is on time. However, if job $J_j$ is early, it incurs a variable penalty cost $\beta _j E_j$ and a fixed penalty cost $\delta _j$; and if job $J_j$ is tardy, it incurs a variable penalty cost $\gamma _j T_j$ and a fixed penalty cost $\theta _j$. The goal is to determine a schedule $\pi$ and a common due date D simultaneously that minimizes the generalized weighted earliness–tardiness penalties which can be expressed as follows:

$$\begin{aligned} F(\pi , D)=\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j}), \end{aligned}$$

(1)

where all parameters $\alpha$, $\beta _j$, $\gamma _j$, $\delta _j$ and $\theta _j$ are assumed to be nonnegative integers.

Adopting the traditional 3-field scheme for scheduling problem, the studied problem is denoted by $1|\mathrm {CON} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j})$, where CON indicates that all jobs are assigned a common due date.

As a practical application of the scheduling problem under study, we consider the production and delivery of the rotten perishable goods in the manufacturing industry. Assume that all these goods constitute a single client’s order, so a common delivery date to be prescribed for all the jobs has to be negotiated between the manufacturer and client. When a job is finished after the delivery date, it will incur a tardiness penalty which is composed of two components, tardiness and weighed number of tardy job. The first component is usually concerned with the manufacturer’s contract compensation for the client, which relies on how late the finished jobs are delivered, while the second component is owing to the loss of client’s goodwill or the cost of delivery, both of them are fixed charges. When a job is finished before the delivery date, it will incur an earliness penalty which is also composed of two components, earliness and weighted number of early job. The first component is associated with the inventory cost which depends on how early the jobs are produced, and the second component is due to the rotten perishable goods of short shelf life. The disposal of these rotten goods has to be dealt with a discounted price, or even results in a loss of fixed manufacturing cost. Based on these reasons, the above described situation can be modeled a CON scheduling problem with the objective of minimizing the integrated cost that consists of due date assignment, earliness, tardiness, weighed number of early jobs and weighted number of tardy jobs.

Note that the studied problem is clearly $\mathcal {NP}$-hard since problem $1|\mathrm {CON} |\sum _{j=1}^{n} \beta _{j} (E_{j}+T_{j})$ is already $\mathcal {NP}$-hard [11]. Designing fully polynomial-time approximation schemes for the $\mathcal {NP}$-hard problems that require strongly polynomial time are of special interest [8, 27].

For a minimization problem, a polynomial-time algorithm $\mathcal {H}$ is called a $(1+\rho )$-approximation algorithm if it delivers a solution that is at most of $(1+\rho )$ times the optimal solution. A family of algorithms $\{\mathcal {H}_{\epsilon }: \epsilon >0 \}$ is called a fully polynomial-time approximation scheme (FPTAS) if, for each $\epsilon >0$, algorithm $\mathcal {H}_{\epsilon }$ is a $(1 + \epsilon )$-approximation algorithm that runs in polynomial time in the input size and $1/{\epsilon }$.

1.2 Literature review

Models related to JIT scheduling in the context of CON assignment have been an topic of extensive research since the early 1980s. Panwalkar et al. [26] provided an $O(n \log n)$ time matching algorithm for the problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\alpha D +\beta E_{j}+\gamma T_{j})$. De et al. [5] showed that the problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\alpha \max \{0, D-D_0\} +\theta _{j} U_{j})$ is $\mathcal {NP}$-hard in the ordinary sense, where $D_0$ is a fixed threshold value that represents a standard or an expected waiting period. When the threshold value $D_0$ is zero, they gave an O(n) time algorithm for the problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\alpha D +\theta _{j} U_{j})$. Hall and Posner [11] showed that the symmetric weighted problem $1|\mathrm {CON} |\sum _{j=1}^{n} \beta _{j} (E_{j}+T_{j})$ is $\mathcal {NP}$-hard and presented an O(nP) pseudo-polynomial-time dynamic programming (DP) algorithm, while the complexity issue of the asymmetric weighted problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\beta _{j} E_{j}+\gamma _{j} T_{j})$ is still open whether it is pseudo-polynomial-time solvable or strongly $\mathcal {NP}$-hard. Under the agreeable assumption that $\beta _i/p_i \ge \beta _j/p_j \Longleftrightarrow \gamma _i/p_i \ge \gamma _j/p_j$ for all $i,j=1,2, \ldots , n$, Lee et al. [22] designed an O(nP) time DP algorithm for the problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\beta _{j} E_{j}+\gamma _{j} T_{j} +\theta _{j} U_{j})$. They also developed an $(n^2)$ time algorithm for the unweighted problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\beta E_{j}+\gamma T_{j} +\theta U_{j})$. For the mean squared deviation problem $1|\mathrm {CON} |\sum _{j=1}^{n} (E_{j}^2+ T_{j}^2)$, which is equivalent to the completion time variance problem $1| |\sum _{j=1}^{n} (C_j-\overline{C})^2$, where $\overline{C}=\sum _{j=1}^n C_j/n$ is mean completion time of all the jobs, Kubiak [20] showed that it is $\mathcal {NP}$-hard; De et al. [6] first proposed an $(n^2P)$ pseudo-polynomial DP algorithm, then by using the interval partitioning technique, they designed an FPTAS with $O(n^3/\epsilon )$ time. Kahlbacher and Cheng [13] addressed a CON assignment scheduling problem with a nonlinear objective function $g(D)+\sum _{j=1}^{n} (h(E_j)+\theta _{j} U_{j})$, where $g(\cdot )$ and $h(\cdot )$ are nondecreasing functions with $g(0)=h(0)=0$. They showed that the problems $1|\mathrm {CON} |g(D)+\sum _{j=1}^{n} \theta _{j} U_{j}$ and $1|\mathrm {CON} |\sum _{j=1}^{n} (h(E_j)+\theta _{j} U_{j})$ are both $\mathcal {NP}$-hard. For the problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\alpha D +\beta E_{j}+\theta _{j} U_{j})$, Kahlbacher and Cheng [13] solved the problem in $O(n^4)$ time by modeling a series of assignment problems; Koulamas [17] presented a faster DP algorithm with $O(n^2)$ time. For the $\mathcal {NP}$-hard problem $1|\mathrm {CON} |\sum _{j=1}^{n} \beta _{j} (E_{j}+T_{j})$, Kovalyov and Kubiak [19] developed an FPTAS that requires $O(n^2 \log ^3(\max _{j}\{p_j, w_j, n, 1/\epsilon \})/\epsilon ^2)$ time; Erel and Ghosh [7] proposed an improved FPTAS that requires $O(n^2 \log (\max _{j}\{p_j, w_j, n, 1/\epsilon \})/\epsilon )$ time; Kellerer and Rustogi [14] provided an FPTAS with $O(n^2/\epsilon )$ time. Mosheiov and Yovel [25] proposed an $O(n^4)$ time algorithm for the problem $1|\mathrm {CON}, p_j=p|\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j})$, while Tuong and Soukhal [28] developed an improved algorithm with $O(n^3)$ time. Recently, Koulamas [18] presented an $O(n^3)$ time algorithm for the problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\alpha D +\beta E_{j}+\gamma T_{j} +\delta _{j} V_{j} +\theta _{j} U_{j})$, and $O(n^2)$ time algorithm for the problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\alpha D +\theta _{j} U_{j}+\lambda C_j)$. For more about CON assignment with JIT scheduling, the reader is referred to Gordon et al. [9, 10], Janiak et al. [12], and the references therein.

1.3 Motivation and contribution

The motivation and contributions of this research are made as follows. The first one is to explore the real-life JIT scheduling problem concerning some existing unexplored problems that need to be addressed. In the previous research, almost all JIT scheduling models consider only the cost of earliness and tardiness, or weighted number of early jobs and tardy jobs, respectively, whereas all these components are incorporated in our objective function. The second one is to ascertain the computational complexity boundaries and provide solution algorithms for various special cases. Specifically, a comprehensive comparison in terms of models and the computational complexity boundaries between the known research and our work is summarized in Table 1. Third, by incorporating penalties for the weighted number of early and tardy jobs, we propose an $O(n^3)$ time algorithm for the problem $1|\mathrm {CON}, p_j=p |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j})$ by modeling it as a rectangular assignment problem, which generalizes the problem $1|\mathrm {CON}, p_j=p |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j})$ studied by Mosheiov and Yovel [25] and Tuong and Soukhal [28]. Fourth, when the ratios of the job processing times to the earliness–tardiness penalties are agreeable, we solve the asymmetric weighted problem $1|\mathrm {CON}, \mathrm {Arg} |\sum _{j=1}^{n} (\alpha d +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j})$ by first formulating it in terms of a series of half-product problems. Then by employing the continuous relaxation of the convex quadratic programming method and the rounding technique [15, 16], we obtain a pair of valid lower and upper bounds for the optimal solution. Finally, we obtain an FPTAS that runs in $O(n^3/\epsilon )$ time by employing the approach used in Erel and Ghosh [7]. Note that the running time is strongly polynomial, which allows us solving large-size instances with a chosen accuracy in a reasonable computation time. Also, this result also partially resolves the open asymmetric weighted problem $1|\mathrm {CON}|\sum _{j=1}^{n} (\beta _{j} E_{j}+\gamma _{j} T_{j})$ posed in the literature [11, 16].

Table 1 Summary of the computational complexity boundaries of the problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j})$

The remainder of this paper is organized as follows. In Sect. 2, we give some preliminary results. In Sect. 3, we show that the equal processing time problem $1|\mathrm {CON}, p_j=p |\sum _{j=1}^{n} (\alpha d +\beta _{j} E_{j}+\gamma _{j} T_{j} +\delta _{j} V_{j} +\theta _{j} U_{j})$ can be solved in $O(n^3)$ time by formulating it as a rectangular assignment problem. In Sect. 4, under the agreeable ratio assumption, we first show that the problem $1|\mathrm {CON}, \mathrm {Arg} |\sum _{j=1}^{n} (\alpha d +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j})$ can be solved in $O(n^3/\epsilon )$ time, then we show that the problem $1|\mathrm {CON}, \mathrm {Arg} |\sum _{j=1}^{n} (\alpha d +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta V_{j} +\theta _{j} U_{j})$ can be solved in $O(n^2/\epsilon )$ time, finally we show that the problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\alpha d +\beta _{j} E_{j}+\theta _{j} U_{j})$ is $\mathcal {NP}$-hard even if $\alpha =0$ and admits an FPTAS with $O(n^2/\epsilon )$ running time. In Sect. 5, we give some concluding remarks.

2 Preliminaries

In this section, we establish several useful structural properties for the optimal solutions. The following result implies that there exists an optimal solution without inserted idle times. It can be easily proved and the details are omitted.

Lemma 2.1

For problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j})$, there exists an optimal solution in which the jobs are processed continuously from time zero until the last job is completed.

In view of Lemma 2.1, we can focus our attention on those schedules without idle times. Therefore, we can define a solution by the job processing sequence and the common due date D. The following result implies that the optimal common due date is equal to the completion time of some job.

Lemma 2.2

For problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j})$, there exists an optimal solution in which the common due date D is equal to $C_{[h]}$ for a certain $h \in \{0, 1, \ldots , n\}$, where $J_{[j]}$ is the jth job in a sequence and $C_{[0]}=0$.

Proof

Consider an optimal job sequence $\pi =(J_{[1]}, J_{[2]}, \ldots , J_{[n]})$ in which the required property is violated. Then there exists a certain h, $0 \le h \le n-1$, with $C_{[h]}< D < C_{[h+1]}$ in $\pi$. Write $x=D-C_{[h]}$ and $y=C_{[h+1]}-D$. Clearly, $\min \{x, y\} >0$ and $x+y=p_{[h+1]}$. By simple calculation, the objective function (1) can be formulated as

$$\begin{aligned} F(\pi , D)= n \alpha D + \sum _{j=1}^{h} ( \beta _{[j]} (D-C_{[j]})+\delta _{[j]})+\sum _{j=h+1}^n(\gamma _j (C_{[j]}-D)+\theta _{[j]}). \end{aligned}$$

If $n \alpha +\sum _{j=1}^h \beta _{[j]} \ge \sum _{j=h+1}^n \gamma _{[j]}$, we set $D'=C_{[h]}$. By simple calculation, we have

$$\begin{aligned} F(\pi , D)- F(\pi , D') =\left( n \alpha +\sum _{j=1}^h \beta _{[j]} - \sum _{j=h+1}^n \gamma _{[j]}\right) x +\delta _{[h]} \ge 0. \end{aligned}$$

If $n \alpha +\sum _{j=1}^h \beta _{[j]} < \sum _{j=h+1}^n \gamma _{[j]}$, we set $D'=C_{[h+1]}$. By simple calculation, we have

$$\begin{aligned} F(\pi , D)- F(\pi , D') =-\,\left( n \alpha +\sum _{j=1}^h \beta _{[j]} - \sum _{j=h+1}^n \gamma _{[j]}\right) y +\theta _{[h+1]} \ge 0. \end{aligned}$$

Hence, we can obtain an alternative optimal solution by setting D either to $C_{[h]}$ or to $C_{[h+1]}$. $\square$

In view of Lemma 2.2, we can characterize an optimal solution $S^{*}$ in the form $S^{*}= \mathcal {A} \cup \{J\} \cup \mathcal {B}$ with $D=\sum _{J_j \in \mathcal {A}} p_j +p$, where $\mathcal {A}$ is the set of early jobs, J is some job that is completed on time and p is its processing time, and $\mathcal {B}$ is the set of tardy jobs. Note that $\mathcal {A}$ or $\mathcal {B}$ may be empty.

The following result gives the processing sequence of the jobs in set $\mathcal {A}$ and $\mathcal {B}$, which can be proved by the job interchange argument.

Lemma 2.3

For problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j})$, the early jobs in set $\mathcal {A}$ are sequenced in nondecreasing order of $\beta _j/p_j$, and the tardy jobs in set $\mathcal {B}$ are sequenced in non-increasing order of $\gamma _j/p_j$.

The next two lemmas state that when no job is early or tardy, then the optimal schedule can be found in $O(n \log n)$ time.

Lemma 2.4

For problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j})$, an optimal schedule can be obtained in $O(n \log n)$ time if no job is early (i.e., $\mathcal {A}=\emptyset$).

Proof

In this case, by Lemmas 2.1 and 2.2, if there exists an on time job, i.e., $D=C_{[1]}=p_{[1]}$, then the objective function (1) can be written as

$$\begin{aligned} F(\pi , D)= n \alpha p_{[1]} +\sum _{j=2}^{n} (\gamma _{[j]} T_{[j]}+\theta _{[j]}) =n \alpha p_{[1]} -\theta _{[1]} +\sum _{j=2}^{n} \gamma _{[j]} \sum _{k=2}^j p_{[k]}+ \sum _{j=1}^{n} \theta _{j}, \end{aligned}$$

(2)

otherwise, all jobs are tardy, i.e., $D=0$, then the objective function (1) can be written as

$$\begin{aligned} F(\pi , D)=\sum _{j=1}^{n} (\gamma _{[j]} T_{[j]}+\theta _{[j]}) =\sum _{j=1}^{n} \gamma _{[j]} \sum _{k=1}^j p_{[k]}+ \sum _{j=1}^{n} \theta _{j}. \end{aligned}$$

(3)

By Lemma 2.3, the jobs in set $\mathcal {B}$ should be sequenced in non-increasing order of $\gamma _j/p_j$. W.l.o.g., assume that the jobs in $\mathcal {J}$ are indexed in non-increasing order of $\gamma _j/p_j$, i.e., $\gamma _1/p_1 \ge \gamma _2/p_2 \ge \cdots \ge \gamma _n/p_n$. Clearly, the minimum objective function (3) is $F(0)=\sum _{j=1}^{n} \gamma _{j} \sum _{k=1}^j p_{k}+ \sum _{j=1}^{n} \theta _{j}$. Set

$$\begin{aligned} F(k)=n \alpha p_{k} -\theta _{k} +\sum _{j=1}^{k-1} \gamma _{j} \sum _{i=1}^j p_{i} +\sum _{j=k+1}^{n} \gamma _{j} \left( \sum _{i=1}^j p_{i}-p_k\right) + \sum _{j=1}^{n} \theta _{j}, \end{aligned}$$

which represents the objective function value when job $J_k$ is on time. To compute the minimum value of function (2), we have to enumerate all possible k. By simple calculation, we deduce

$$\begin{aligned} F(k+1)=F(k)+ n \alpha (p_{k+1}-p_k) - (\theta _{k+1}-\theta _k)+(\gamma _k-\gamma _{k+1})\sum _{j=1}^{k-1} p_j +(\gamma _k p_k-\gamma _{k+1} p_{k+1}). \end{aligned}$$

Note that all F(k) can be computed in O(n) time for $k=1, 2, \ldots , n$ (given that the values $\sum _{j=1}^h p_j$ are computed in advance for all $h=1, 2, \ldots , n$). Then the optimal objective function value is given by $\min \{F(k): 0 \le k \le n\}$. Since the indexing operation requires $O(n \log n)$ time, the result holds. $\square$

Lemma 2.5

For problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j})$, an optimal schedule can be obtained in $O(n \log n)$ time if no job is tardy (i.e., $\mathcal {B}=\emptyset$).

Proof

In this case, by Lemmas 2.1 and 2.2, we have $D=C_{[n]}=\sum _{j=1}^n p_j$, then the objective function (1) can be written as

$$\begin{aligned} F(\pi , D)= n \alpha \sum _{j=1}^n p_j +\sum _{j=1}^{n-1} (\beta _{[j]} E_{[j]}+\delta _{[j]}) = \sum _{j=1}^n (n \alpha p_j +\delta _j) -\delta _{[n]} +\sum _{j=1}^{n-1} \beta _{[j]} \sum _{k=j+1}^n p_{[k]}. \end{aligned}$$

(4)

By Lemma 2.3, the jobs in set $\mathcal {A}$ should be sequenced in nondecreasing order of $\beta _j/p_j$. W.l.o.g., assume that the jobs in $\mathcal {J}$ are indexed in nondecreasing order of $\beta _j/p_j$, i.e., $\beta _1/p_1 \le \beta _2/p_2 \le \cdots \le \beta _n/p_n$. Set

$$\begin{aligned} F(k)=\sum _{j=1}^n (n \alpha p_j +\delta _j) -\delta _{k} +\sum _{j=1}^{k-1} \beta _{j} \left( \sum _{i=j+1}^n p_{i}-p_k\right) +\sum _{j=k+1}^{n} \beta _{j} \sum _{i=j+1}^n p_{i}, \end{aligned}$$

which represents the objective function value when job $J_k$ is on time. To compute the minimum value of function (4), we have to enumerate all possible k. By simple calculation, we deduce

$$\begin{aligned} F(k+1)=F(k)+ (\delta _k -\delta _{k+1}) + (p_k-p_{k+1})\sum _{j=1}^{k-1} \beta _j +(\beta _k-\beta _{k+1})\sum _{j=k+2}^n p_j. \end{aligned}$$

Similar to analysis of Lemma 2.4, all F(k) can be computed in O(n) time for $k=1, 2, \ldots , n$. Then the optimal objective function value is given $\min \{F(k): 1 \le k \le n\}$. Since the indexing operation requires $O(n \log n)$ time, the result holds. $\square$

3 $1|\mathrm {CON}, p_j=p |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j})$

In this section, we study the scenario where all jobs have equal processing times, i.e., $p_j=p$ for $1 \le j \le n$. Scheduling problems with equal processing times arise in many real-life fields of application, such as, shampoo packing in batch oriented production systems [28], burn-in operations in integrated circuit manufacturing [24], production planning in the microbiological laboratory [3], etc. We solve the problem $1|\mathrm {CON}, p_j=p |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j})$ in $O(n^3)$ time by formulating it as a rectangular assignment problem.

By Lemmas 2.4 and 2.5, the general problem can be solved in $O(n \log n)$ time if no job is early or tardy, thus we only consider the solutions in which there exist at least one early job and one tardy job. Assume that the number of early and tardy jobs in $\mathcal {A}$ and $\mathcal {B}$ are $n_1$ and $n_2$, respectively, where $1 \le n_1 \le n-2$, $1 \le n_2 \le n-2$, and $n_1+n_2+1=n$.

Let $\pi _{\mathcal {A}}=(J_{(n_1)}, J_{(n_1-1)}, \ldots , J_{(1)})$ denote the processing sequence of early jobs in set $\mathcal {A}$, and let $\pi _{\mathcal {B}}=(J_{\langle 1\rangle }, J_{\langle 2\rangle }, \ldots , J_{\langle n_2 \rangle })$ denote the processing sequence of tardy jobs in set $\mathcal {B}$. Then we use $\pi =(\pi _{\mathcal {A}}, J, \pi _{\mathcal {B}})$ to represent the job sequence on the machine, where J is the on time job.

From the definition of $\pi$, we have $C_{(j)}=(n_1-j+1)p$ for $j=1, 2, \ldots , n_1$; $D=(n_1+1)p$; $C_{\langle j \rangle }= (n_1+j+1)p$ for $j=1, 2, \ldots , n_2$. Then we obtain that $E_{(j)}=D-C_{(j)}=j p$ for $j=1, 2, \ldots , n_1$, and $T_{\langle j \rangle }=C_{\langle j \rangle }-D= jp$ for $j=1, 2, \ldots , n_2$. Hence, the following result holds.

Lemma 3.1

For problem $1|\mathrm {CON}, p_j=p |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j})$, if $\pi =(\pi _{\mathcal {A}}, J, \pi _{\mathcal {B}})$ is the given job sequence, then the objective function (1) can be written as

$$\begin{aligned} F(\pi , D)=n \alpha p+\sum _{j=1}^{n_1} (n \alpha p+ \beta _{(j)} j p+\delta _{(j)}) +\sum _{j=1}^{n_2} (\gamma _{\langle j \rangle } j p+\theta _{\langle j \rangle }). \end{aligned}$$

Next, we formulate this problem as a rectangular assignment problem with an $n \times m$ cost matrix $\mathbf {C}=(c_{j,k})$ with n rows, each corresponding to a job $J_j \in \mathcal {J}$, and $m=2n-3$ columns. Let $x_{j,k}$ be a Boolean variable indicating whether job $J_j$ is assigned to the kth position(i.e., $x_{jk}=1$ if $J_j$ is at position k, and $x_{jk}=0$ otherwise, $j, k=1, 2, \ldots , n$). Note that $x_{j,k}=1$ indicates that job $J_j$ is the $(n-2-k+1)$th last job sequenced in set $\mathcal {A}$ if $1 \le k \le n-2$; $x_{j,k}=1$ indicates job $J_j$ is the on time job if $k=n-1$; and $x_{j,k}=1$ indicates that job $J_j$ is the $(k-n+1)$th job sequenced in set $\mathcal {B}$ if $n \le k \le 2n-3$. Let $c_{j,k}$ denote the cost of assigning job $J_j$ to position k. Then by Lemma 3.1, we have

$$\begin{aligned} c_{j,k}=\left\{ \begin{array}{ll} n \alpha p+(n-2-k+1)p\beta _j+\delta _j, &{} \quad \hbox {for} \quad k=1, 2, \ldots , n-2;\\ n \alpha p, &{}\quad \hbox {for} \quad k=n-1; \\ (k-n+1)p \gamma _j+\theta _j, &{} \quad \hbox {for} \quad k=n, n+1, \ldots , 2n-3. \end{array} \right. \end{aligned}$$

(5)

Therefore, the problem of minimizing the objective function (1) can be formulated as a rectangular assignment problem given below.

$$\begin{aligned} \mathrm {Min}&\sum _{j=1}^{n}\sum _{k=1}^{2n-3}c_{j,k} ~ x_{j,k} \end{aligned}$$

(6)

$$\begin{aligned} \mathrm { s.t.}&\sum _{k=1}^{2n-3}x_{j,k}=1, ~~ j=1, 2, \ldots , n, \end{aligned}$$

(7)

$$\begin{aligned}&\sum _{j=1}^{n} x_{j,k} \le 1, ~~ k=1, 2, \ldots , 2n-3, \end{aligned}$$

(8)

$$\begin{aligned}&x_{j,k} \in \{0, 1\}, ~~ j=1, 2, \ldots , n; ~~ k=1, 2, \ldots , 2n-3. \end{aligned}$$

(9)

In the above rectangular assignment problem, expression (6) minimizes the objective function (1), constraint set (7) ensures that each job is assigned to a position, and constraint set (8) ensures that no position is selected more than once. Since the rectangular assignment problem with an $n \times m$ cost matrix can be solved in $O(n^3+mn)$ time [27], the following result holds.

Theorem 3.2

Problem $1|\mathrm{CON}, p_j=p |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j})$ can be solved in $O(n^3)$ time.

4 $1|\mathrm {CON}, \mathrm {Arg} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j})$

In this section, we study the problem under the assumption that the ratios of the job processing times to the earliness–tardiness penalties are agreeable, i.e.,

$$\begin{aligned} \beta _i/p_i \ge \beta _j/p_j \Longleftrightarrow \gamma _i/p_i \ge \gamma _j/p_j ~\quad \mathrm {for}~ i, j=1,2, \ldots , n. \end{aligned}$$

(10)

Note that if the agreeable assumption does not hold, the complexity status of the basic problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\beta _{j} E_{j}+\gamma _{j} T_{j})$ remains open [11, 14]. A practical motivation for this assumption is the anticipation that if job $J_i$ is comparatively more important than job $J_j$, both its unit earliness and tardiness will be larger than that of job $J_j$ [22]. This problem is denoted by $1|\mathrm {CON}, \mathrm {Arg} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j})$. We formulate the problem as a series of a Boolean programming problem with a quadratic objective, known as half-product in the literature [1], which permits us to devise an FPTAS that runs in $O(n^3/\epsilon )$ time.

Let $\mathbf{x} =(x_1, x_2, \ldots , x_k)$ denote a vector with k Boolean variables. A half-product is a pseudo-Boolean function of the following form:

$$\begin{aligned} H(\mathbf x )=\sum _{1 \le i <j \le k} a_i b_j x_i x_j -\sum _{j=1}^k c_j x_j, \end{aligned}$$

(11)

where for each j, $1 \le j \le k$, the coefficients $a_j$ and $b_j$ are non-negative integers, and $c_j$ is an integer which can be either positive or negative.

Let $\mathbf x ^{*} =(x_1^{*}, x_2^{*}, \ldots , x_k^{*})$ denote a Boolean vector that minimizes the objective function (11). Badics and Boros [1] showed that the problem of minimizing function (11) is $\mathcal {NP}$-hard even if $a_j=b_j$ for $j=1, 2, \ldots , k$. Erel and Ghosh [7] presented an FPTAS with $O(k^2/\epsilon )$ time for minimizing function (11). Since computing the objective value for a given solution $\mathbf x$ requires $O(k^2)$ time, the running time is seen as the best possible. Numerous applications has been found for half-product in machine scheduling problems [16]. Notice that in most scheduling applications, the objective function is usually written as

$$\begin{aligned} F(\mathbf x )=H(\mathbf x )+K, \end{aligned}$$

(12)

where K is a given additive constant.

Lemma 4.1

[7] For the problem of minimizing function (12) (or equivalently, (11)), it admits two pseudo-polynomial DP algorithms that run in $O(k(\sum _{j=1}^k a_j))$ and $O(k(\sum _{j=1}^k b_j))$ time, respectively.

For problem $1|\mathrm {CON}, \mathrm {Arg} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j})$, due to the arbitrary weights $\delta _j$ and $\theta _j$, we cannot determine the on time job in advance. Thus in order to solve the problem, we select each job as a possible on time job. Let p denote the processing time of the job J that is the chosen on time job. W.l.o.g., assume that the remaining $m=n-1$ jobs are indexed in such a way that

$$\begin{aligned} \beta _1/p_1 \ge \beta _2/p_2 \ge \cdots \ge \beta _m/p_m, \end{aligned}$$

(13)

or equivalently, the jobs are indexed in such a way that

$$\begin{aligned} \gamma _1/p_1 \ge \gamma _2/p_2 \ge \cdots \ge \gamma _m/p_m. \end{aligned}$$

(14)

By Lemma 2.3, the jobs in $\mathcal {B}$ are sequenced in the order of their numbering, and the jobs in $\mathcal {A}$ are sequenced in the order opposite to their numbering. Introduce Boolean variables $x_j$, $j=1, 2, \ldots , m$, in such a way that

$$\begin{aligned} x_j=\left\{ \begin{array}{ll} 1, &{}\quad \hbox {if} \quad \hbox {job}\quad J_j \quad \hbox {is early, i.e.,} ~ J_j \in \mathcal {A}; \\ 0, &{}\quad \hbox {if} \quad \hbox {job}\quad J_j \quad \hbox {is tardy, i.e.,} ~ J_j \in \mathcal {B}. \end{array} \right. \end{aligned}$$

(15)

For simplicity, let $R(\mathbf x )=\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j})$ denote the objective function (1). Taking the jobs in order of their numbering given by (13) (or equivalently, (14)), it follows that if job $J_j$ is early, its earliness is given by $E_j=p+\sum _{i=1}^{j-1} p_i x_i$; if job $J_j$ is tardy, its tardiness is given by $T_j=\sum _{i=1}^{j} p_i (1-x_i)$; and the final common due date is given by $D=p+\sum _{j=1}^m p_j x_j$.

Lemma 4.2

For problem $1|\mathrm {CON}, \mathrm {Arg} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j})$, if J is the chosen on time job and p is its processing time, then the objective function $R(\mathbf x )$ can be reformulated as $R(\mathbf x )=H(\mathbf x )+K$, where $H(\mathbf x )$ is the half-product function of the form (11), with $k:=m=n-1$, $a_j:= p_j$, $b_j:= \beta _j+\gamma _j$, $c_j:=\gamma _j (\sum _{i=1}^{j-1} p_i) +p_j (\sum _{i=j}^m \gamma _i) +\theta _j-n \alpha p_j - p \beta _j-\delta _j$, $1 \le j \le m$, and $K:=n \alpha p+\sum _{j=1}^m(p_j \gamma _j+\theta _j)$.

Proof

Recall that $x_j^2=x_j$ and $(1-x_j)^2=1-x_j$. From the previous discussion, it follows that the objective function (1) can be written as

$$\begin{aligned} R(\mathbf x )= & {} \sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j}) \nonumber \\= & {} n \alpha (p+\sum _{j=1}^m p_j x_j)+\sum _{j=1}^m \beta _jx_j(p+\sum _{i=1}^{j-1} p_i x_i) +\sum _{j=1}^m\gamma _j(1-x_j) \sum _{i=1}^{j} p_i (1-x_i)\nonumber \\&+ \sum _{j=1}^m \delta _jx_j+\sum _{j=1}^m \theta _j(1-x_j) \end{aligned}$$

(16)

$$\begin{aligned}= & {} \sum _{j=1}^m \beta _jx_j\sum _{i=1}^{j-1} p_i x_i +\sum _{j=1}^m\gamma _j(1-x_j) \sum _{i=1}^{j-1} p_i (1-x_i) \nonumber \\&+\sum _{j=1}^m (n \alpha p_j+ p \beta _j+\delta _j) x_j+\sum _{j=1}^m(p_j \gamma _j+\theta _j)(1-x_j)+n \alpha p \end{aligned}$$

(17)

$$\begin{aligned}= & {} \sum _{1 \le i < j \le m} p_i (\beta _j+\gamma _j)x_i x_j -\sum _{j=1}^m(\gamma _j (\sum _{i=1}^{j-1} p_i) +p_j (\sum _{i=j}^m \gamma _i) +\theta _j-n \alpha p_j \nonumber \\&- p \beta _j-\delta _j)x_j +n \alpha p+\sum _{j=1}^m(p_j \gamma _j+\theta _j). \end{aligned}$$

(18)

Therefore, the result follows from (18). $\square$

Notice that the problem of minimizing function (11) is equivalent to the problem of minimizing function (12). However, it is known that an FPTAS for minimizing the function (11) does not necessarily behave as an FPTAS for minimizing the function (12). This is due to the fact that the optimal value of function (11) is negative and K can be positive (see [7, 16] for details).

Let $F_{\mathrm {L}}$ and $F_{\mathrm {U}}$ be the lower and upper bounds on the optimal solution value of the function (12), i.e., $F_{\mathrm {L}} \le F(\mathbf x ^{*}) \le F_{\mathrm {U}}$. To minimize the objective function (12), the following approach that is employed in Erel and Ghosh [7] is very useful for designing an FPTAS.

Lemma 4.3

[7] For the problem of minimizing function (12), if the lower bound $F_{\mathrm {L}}$ and the upper bound $F_{\mathrm {U}}$ can be obtained in T(k) time, then there exists an approximation algorithm that outputs a solution $\hat{\mathbf{x }}$ such that $F(\hat{\mathbf{x }}) \le (1+\epsilon ) F_{\mathrm {L}}$ in $O(T(k)+v k^2 /\epsilon )$ time, where $F_{\mathrm {U}}/F_{\mathrm {L}} \le v$.

According to Lemmas 4.2 and 4.3, for the purpose of obtaining an FPTAS for the problem $1|\mathrm {CON}, \mathrm {Arg} |\sum _{j=1}^{n} (\alpha d +\beta _{j} E_{j}+\gamma _{j} T_{j} +\theta _{j} U_{j})$, we only need to determine a valid lower bound $R_{\mathrm {L}}$ and an upper bound $R_{\mathrm {U}}$ on the optimal solution value of $R(\mathbf x ^{*})$ and to ensure that the ratio $R_{\mathrm {U}}/R_{\mathrm {L}}$ is as small as possible.

Assume that the integrality condition of the Boolean variables $x_j$ is relaxed (referred as continuous relaxation), i.e., the condition $x_j \in \{0, 1\}$ is replaced by $0 \le x_j \le 1$, $j=1, 2, \ldots , k$. Let $\mathbf x ^r = (x_1^r, x_2^r, \ldots , x_k^r)$, $0 \le x_j^r \le 1$, be the corresponding solution vector of the continuous relaxation of the problem of minimizing function (18). Obviously, $R(\mathbf x ^r) \le R(\mathbf x ^{*})$, so we can set $R_{\mathrm {L}}=R(\mathbf x ^r)$ as a lower bound on $R(\mathbf x ^{*})$.

If the items are numbered such that $b_1/a_1 \ge b_2/a_2 \ge \cdots \ge b_k/a_k$, Kellerer and Strusevich [15] showed that the half-product function (12) is convex, and the continuous relaxation of the problem of minimizing a convex function (12) can be solved in $O(k^2)$ time. In our case, the required numbering is ensured by (13) and (14), so that the objective function as given in (18) is convex, and the lower bound $R_{\mathrm {L}}=R(\mathbf x ^r)$ can be computed in $O(n^2)$ time.

In order to obtain a valid upper bound $R_{\mathrm {U}}$, a simple rounding of the fractional components of vector $\mathbf x ^r$ is performed, which can be described as follows.

Algorithm $\mathcal {H}_{J,p}$

Step 1.:

Solve the continuous relaxation of the problem of minimizing a convex function $R(\mathbf x )$ of the form (18), and let $\mathbf x ^r = (x_1^r, x_2^r, \ldots , x_m^r)$, $0 \le x_j^r \le 1$, be the corresponding solution vector.

Step 2.:

Determine the sets $\mathcal {A}=\{J_j \in \mathcal {J} {\setminus } \{J\}: x_j^r \le \frac{1}{2}\}$ and $\mathcal {B}=\{J_j \in \mathcal {J} {\setminus } \{J\}: x_j^r > \frac{1}{2}\}$, and define a vector $\mathbf x ' = (x'_1, x'_2, \ldots , x'_m)$ with $x'_j=0$ if $J_j \in \mathcal {A}$, and $x'_j=1$ if $J_j \in \mathcal {B}$.

Step 3.:

Deliver vector $\mathbf x ' = (x'_1, x'_2, \ldots , x'_m)$ as an approximation solution to the problem of minimizing function (18), and therefore, function (17).

Recall that $m=n-1$. Then the running time of Algorithm $\mathcal {H}_{J,p}$ is $O(n^2)$, which is dominated by Step 1. Obviously, we have $R(\mathbf x ^r) \le R(\mathbf x ^{*}) \le R(\mathbf x ')$. Therefore, we can set $R_{\mathrm {U}}=R(\mathbf x ')$ as an upper bound on $R(\mathbf x ^{*})$. Then, we can estimate the ratio $v=R_{\mathrm {U}}/R_{\mathrm {L}}=R(\mathbf x ')/R(\mathbf x ^r)$.

Theorem 4.4

Let $\mathbf x ^r$ be an optimal solution to the continuous relaxation of the problem of minimizing function R(x) of the form (18), and $\mathbf x '$ be the approximation solution found by Algorithm $H_{J,p}$. Then, we have $v=R(\mathbf x ')/R(\mathbf x ^r) \le 4$.

Proof

For a vector $\mathbf x ^r$, let $\mathcal {A}$ and $\mathcal {B}$ be the job sets found in Step 2 of Algorithm $\mathcal {H}_{J,p}$. For an arbitrary vector $\mathbf x =(x_1, x_2, \ldots , x_m)$, $0 \le x_j \le 1$, using the expression (17), define

$$\begin{aligned} R_1(\mathbf x ) = \sum _{{\mathop {J_i, J_j \in \mathcal {A}}\limits ^{1 \le i<j \le m}}} p_i \beta _j x_i x_j +\sum _{{\mathop {J_i, J_j \in \mathcal {A}}\limits ^{1 \le i <j \le m}}} p_i \gamma _j (1-x_i)(1-x_j); \end{aligned}$$

$$\begin{aligned} R_2(\mathbf x ) = \sum _{{\mathop {J_i \in \mathcal {A}, J_j \in \mathcal {B}}\limits ^{1 \le i<j \le m}}} p_i \beta _j x_i x_j +\sum _{{\mathop {J_i \in \mathcal {A}, J_j \in \mathcal {B}}\limits ^{1 \le i <j \le m}}} p_i \gamma _j (1-x_i)(1-x_j); \end{aligned}$$

$$\begin{aligned} R_3(\mathbf x ) = \sum _{{\mathop {J_i \in \mathcal {B}, J_j \in \mathcal {A}}\limits ^{1 \le i<j \le m}}} p_i \beta _j x_i x_j +\sum _{{\mathop {J_i \in \mathcal {B}, J_j \in \mathcal {A}}\limits ^{1 \le i <j \le m}}} p_i \gamma _j (1-x_i)(1-x_j); \end{aligned}$$

$$\begin{aligned} R_4(\mathbf x ) = \sum _{{\mathop {J_i, J_j \in \mathcal {B}}\limits ^{1 \le i<j \le m}}} p_i \beta _j x_i x_j +\sum _{{\mathop {J_i, J_j \in \mathcal {B}}\limits ^{1 \le i <j \le m}}} p_i \gamma _j (1-x_i)(1-x_j); \end{aligned}$$

$$\begin{aligned} R_5(\mathbf x ) = \sum _{J_j \in \mathcal {A}} (n \alpha p_j+ p \beta _j+\delta _j) x_j +\sum _{J_j \in \mathcal {A}}(p_j \gamma _j+\theta _j)(1-x_j); \end{aligned}$$

$$\begin{aligned} R_6(\mathbf x ) = \sum _{J_j \in \mathcal {B}} (n \alpha p_j+ p \beta _j+\delta _j) x_j +\sum _{J_j \in \mathcal {B}}(p_j \gamma _j+\theta _j)(1-x_j). \end{aligned}$$

By the rounding conditions in Step 2 of Algorithm $\mathcal {H}_{J,p}$, we deduce

$$\begin{aligned} R_2(\mathbf x ')=R_3(\mathbf x ')=0, \end{aligned}$$

while

$$\begin{aligned} R_1(\mathbf x ')=\sum _{{\mathop {J_i, J_j \in \mathcal {A}}\limits ^{1 \le i<j \le n}}} p_i \gamma _j; \quad \quad \quad \quad \quad R_1(\mathbf x ^r) \ge \frac{1}{4} \sum _{{\mathop {J_i, J_j \in \mathcal {A}}\limits ^{1 \le i <j \le n}}} p_i \gamma _j; \end{aligned}$$

$$\begin{aligned} R_4(\mathbf x ')=\sum _{{\mathop {J_i, J_j \in \mathcal {B}}\limits ^{1 \le i<j \le n}}} p_i \beta _j; \quad \quad \quad \quad \quad R_4(\mathbf x ^r) \ge \frac{1}{4} \sum _{{\mathop {J_i, J_j \in \mathcal {B}}\limits ^{1 \le i <j \le n}}} p_i \beta _j; \end{aligned}$$

$$\begin{aligned} R_5(\mathbf x ')=\sum _{J_j \in \mathcal {A}} (p_j \gamma _j+\theta _j); \quad \quad \quad \quad R_5(\mathbf x ^r) \ge \frac{1}{2} \sum _{J_j \in \mathcal {A}} (p_j \gamma _j+\theta _j); \end{aligned}$$

$$\begin{aligned} R_6(\mathbf x ')=\sum _{J_j \in \mathcal {B}} (n \alpha p_j+ p \beta _j+\delta _j); \quad R_6(\mathbf x ^r) \ge \frac{1}{2} \sum _{J_j \in \mathcal {B}} (n \alpha p_j+ p \beta _j+\delta _j). \end{aligned}$$

Therefore, we obtain

$$\begin{aligned} R(\mathbf x ')= & {} \sum _{i=1}^6 R_i(\mathbf x ')+n \alpha p\\= & {} R_1(\mathbf x ')+F_4(\mathbf x ')+R_5(\mathbf x ')+R_6(\mathbf x ')+n \alpha p\\\le & {} 4 R_1(\mathbf x ')+4 R_4(\mathbf x ')+2 R_5(\mathbf x ')+2 R_6(\mathbf x ')+n \alpha p\\\le & {} 4 \sum _{i=1}^6 R_i(\mathbf x ^r)+4 n \alpha p=4 R(\mathbf x ^r), \end{aligned}$$

as required. $\square$

For each choice of the on time job J with processing time p, integrating the results obtained in Lemmas 4.1–4.3 and Theorem 4.4, the problem admits an FPTAS and a pseudo-polynomial DP algorithm that run in $O(n^2/\epsilon )$ and O(nP) time, respectively. To find an approximate solution to the problem $1|\mathrm {CON}, \mathrm {Arg} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j})$, we need to run the FPTAS for each chosen on time job. Thus, we obtain the following statement.

Theorem 4.5

Problem $1|\mathrm {CON}, \mathrm {Arg} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j})$ possesses an FPTAS that requires $O(n^3/\epsilon )$ time and a pseudo-polynomial algorithm that requires $O(n^2 P)$ time.

When $\beta _j=\gamma _j$ for all $j=1, 2, \ldots , n$, the agreeable ratio assumption clearly holds, so the following result holds.

Corollary 4.6

Problem $1|\mathrm{CON}|\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\beta _{j} T_{j}+\delta _{j} V_{j} +\theta _{j} U_{j})$ possesses an FPTAS that requires $O(n^3/\epsilon )$ time and a pseudo-polynomial algorithm that requires $O(n^2 P)$ time.

4.1 $1|\mathrm{CON}, \mathrm {Arg} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta V_{j} +\theta _{j} U_{j})$

In this subsection, we study the scenario where the agreeable ratio assumption (10) holds and $\delta _j=\delta$ for all $j=1, 2, \ldots , n$. This case often occurs in the disposal of rotten perishable goods of short shelf life. Each early job may have to be dealt with a common discounted price, or result in a loss of fixed manufacturing cost. This problem is denoted by $1|\mathrm {CON}, \mathrm {Arg} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta V_{j} +\theta _{j} U_{j})$. In this case, we can strengthen the result of Lemma 2.3 as follows.

Lemma 4.7

For problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta V_{j}+\theta _{j} U_{j})$, the non-tardy jobs (including early jobs and on time job) are sequenced in nondecreasing order of $\beta _j/p_j$, and the tardy jobs are sequenced in non-increasing order of $\gamma _j/p_j$.

Under the agreeable ratio assumption (10), by Lemma 4.7, we can assume that the jobs in $\mathcal {J}$ are indexed according to (13) with $m=n$. In contrast with (15), we define the Boolean variables

(19)

Similar to analysis of Lemma 4.2, the following result holds.

Lemma 4.8

For problem $1|\mathrm {CON}, \mathrm {Arg} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta V_{j} +\theta _{j} U_{j})$, the objective function $R(\mathbf x )$ can be reformulated as $R(\mathbf x )=H(\mathbf x )+K$, where $H(\mathbf x )$ is the half-product function of the form (11), with $k:=n$, $a_j:= p_j$, $b_j:= \beta _j+\gamma _j$, $c_j:=\gamma _j (\sum _{i=1}^{j-1} p_i) +p_j (\sum _{i=j}^n \gamma _i) +\theta _j-n \alpha p_j -\delta$, $1 \le j \le n$, and $K:=\sum _{j=1}^n(p_j \gamma _j+\theta _j)-\delta$.

Clearly, the rounding algorithm and Theorem 4.4 still hold. Thus, integrating the results of Lemmas 4.1–4.8 and Theorem 4.4, we immediately obtain the following statement.

Theorem 4.9

Problem $1|\mathrm {CON}, \mathrm {Arg} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\gamma _{j} T_{j}+\delta V_{j}+\theta _{j} U_{j})$ possesses an FPTAS that requires $O(n^2/\epsilon )$ time and a pseudo-polynomial algorithm that requires O(nP) time.

When $\beta _j=\gamma _j$ for all $j=1, 2, \ldots , n$, the agreeable ratio assumption (10) clearly holds, so the following result holds.

Corollary 4.10

Problem $1|\mathrm {CON}|\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\beta _{j} T_{j}+\delta V_{j} +\theta _{j} U_{j})$ possesses an FPTAS that requires $O(n^2/\epsilon )$ time and a pseudo-polynomial algorithm that requires O(nP) time.

4.2 $1|\mathrm{CON} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\theta _{j} U_{j})$

In this subsection, we study the problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j} +\theta _{j} U_{j})$. This case occurs in the situations in which one has to pay an inventory cost that is proportional to the inventory time (i.e., earliness) $E_j$ of job $J_j$, and an additional amount of resource $\theta _{j}$ has to be spent to handle a tardy job $J_j$. Recall that when $\beta _{j}=\beta$ for all $j=1, 2, \ldots , n$, Kahlbacher and Cheng [13] and Koulamas [17] have proposed $O(n^4)$ and $O(n^2)$ time algorithms for the unweighted problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\alpha D +\beta E_{j} +\theta _{j} U_{j})$, respectively. We next show that the weighted problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\theta _{j} U_{j})$ is $\mathcal {NP}$-hard even if $\alpha =0$.

Theorem 4.11

Problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\theta _{j} U_{j})$ is $\mathcal {NP}$-hard even if $\alpha =0$.

Proof

The decision variant of the problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\theta _{j} U_{j})$ is clearly in $\mathcal {NP}$. The proof uses the reduction from the binary $\mathcal {NP}$-complete SUBSET SUM problem [8], which is defined as follows:

SUBSET SUM: Given n positive integers $y_1,y_2, \ldots , y_{n}$ with $\sum _{j=1}^n y_j=Z$ and an integer Y, is there a subset $\mathcal {Y}$ of the index set $\{1, 2, \ldots , n\}$ with $\sum _{y_j \in \mathcal {Y}} y_j = Y$?

For any given instance of the SUBSET SUM problem, we construct an instance of the problem $1|\mathrm {CON} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\theta _{j} U_{j})$ with a set $\mathcal {J}=\{J_1, J_2, \ldots , J_n\}$ of n jobs. The unit due date assignment cost is $\alpha =0$; for each job $J_j \in \mathcal {J}$, its processing time is $p_j=y_j$, its unit earliness cost is $\beta _j=y_j$, and its tardy weight is $\theta _j=Y y_j-\frac{1}{2}y_j^2$. The threshold value is $L=YZ+\frac{1}{2}Y^2-\frac{1}{2}\sum _{j=1}^n y_j^2$.

Let $\mathcal {N}$ and $\mathcal {B}$ denote the set of non-tardy and tardy jobs in a given schedule, respectively. Since $\beta _j=p_j=y_j$ for all $J_j \in \mathcal {J}$, then by Lemma 4.7, we know that the sequence of the non-tardy jobs does not affect the objective value. Based on this fact and substituting the relevant parameters, the objective function can be written as follows:

$$\begin{aligned} \begin{array}{ll} \sum \limits _{j=1}^{n} (\beta _{j} E_{j}+\theta _{j} U_{j}) &{}=\sum \limits _{J_j \in \mathcal {N}} \beta _{j} E_{j}+\sum \limits _{J_j \in \mathcal {B}} \theta _{j} \\ &{}=\sum \limits _{J_j \in \mathcal {N}} \beta _{j} \sum \limits _{{\mathop {1 \le i <j \le n}\limits ^{J_i, J_j \in \mathcal {N}}}}p_i +\sum \limits _{J_j \in \mathcal {B}} \left( Y y_j-\frac{1}{2}y_j^2\right) \\ &{}=\sum \limits _{J_j \in \mathcal {N}} y_{j} \sum \limits _{{\mathop {1 \le i \le j \le n}\limits ^{J_i, J_j \in \mathcal {N}}}}y_i +\sum \limits _{J_j \in \mathcal {B}} \left( Y y_j-\frac{1}{2}y_j^2\right) -\sum \limits _{J_j \in \mathcal {N}} y_{j}^2\\ &{}=\frac{1}{2}\left( \sum \limits _{J_j \in \mathcal {N}} y_{j}\right) ^2 +\sum \limits _{J_j \in \mathcal {B}} \left( Y y_j-\frac{1}{2}y_j^2\right) -\frac{1}{2}\sum \limits _{J_j \in \mathcal {N}} y_{j}^2\\ &{}=\frac{1}{2}\left( \sum \limits _{J_j \in \mathcal {N}} y_{j}\right) ^2 +Y \sum \limits _{J_j \in \mathcal {B}} y_j -\frac{1}{2}\sum \limits _{j=1}^n y_{j}^2. \end{array} \end{aligned}$$

(20)

Define $\rho =\sum _{j \in \mathcal {N}} y_j$, then $\sum _{j \in \mathcal {B}} y_j=Z-\rho$. Because the last term in (20) does not depend on the the choice of $\mathcal N$, we only have to minimize the following function

$$\begin{aligned} \frac{1}{2}\left( \sum \limits _{J_j \in \mathcal {N}} y_{j}\right) ^2 +Y \sum \limits _{J_j \in \mathcal {B}} y_j=\frac{1}{2} \rho ^2+Y(Z-\rho ) =\frac{1}{2}(\rho -Y)^2+YZ+\frac{1}{2}Y^2. \end{aligned}$$

(21)

The function (21) has a unique minimum of $YZ+\frac{1}{2}Y^2$ at $\rho =Y$, i.e, when $\sum _{j \in \mathcal {N}}y_j=Y$. Therefore, the instance of SUBSET SUM has a solution if and only if the objective value to the instance of $1|\mathrm {CON} |\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j}+\theta _{j} U_{j})$ does not exceed $YZ+\frac{1}{2}Y^2-\frac{1}{2}\sum _{j=1}^n y_{j}^2$. $\square$

Since $\gamma _j=0$ for all $j=1, 2, \ldots , n$, the agreeable assumption (10) clearly holds, by Theorem 4.9, the following result holds.

Corollary 4.12

Problem $1|\mathrm {CON}|\sum _{j=1}^{n} (\alpha D +\beta _{j} E_{j} +\theta _{j} U_{j})$ possesses an FPTAS that requires $O(n^2/\epsilon )$ time and a pseudo-polynomial algorithm that requires O(nP) time.

5 Conclusions

In this paper, we address the single-machine common due date assignment problem with the generalized weighted earliness–tardiness penalties. The earliness/tardiness penalty includes not only a variable cost which depends upon the job earliness/tardiness but also a fixed cost for each early/tardy job. A comprehensive comparison in terms of models and computational complexity boundaries between the known research and our work is summarized in Table 1.

Since the running times of the proposed optimal algorithm for the case with equal processing times is strongly polynomial and the approximation schemes designed for those $\mathcal {NP}$-hard problems are also strongly polynomial, they can be used by the industry decision-maker to solve large-size instances exactly or with a chosen accuracy in a reasonable computation time.

As for future research, it is interesting to study the common due date assignment problem with the generalized earliness–tardiness objective function in parallel machines. Another interesting research direction is to investigate the problem of minimizing the generalized weighted earliness–tardiness penalties under other due date assignment methods such as SLK and DIF.