Abstract
We address the problem of testing weak optimality of a given solution of a given interval linear program. The problem was recently wrongly stated to be polynomially solvable. We disprove it. We show that the problem is NP-hard in general. We propose a new algorithm for the problem, based on orthant decomposition and solving linear systems. Running time of the algorithm is exponential in the number of equality constraints. In particular, the proposed algorithm runs in polynomial time for interval linear programs with no equality constraints.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, we address the following problem:
Given an interval linear program, decide whether a given weakly feasible solution is weakly optimal.
This problem was recently wrongly stated to be polynomially solvable in [18]. Our aims are the following:
-
to show a counterexample to the method proposed by [18] and explain what is wrong in their proof,
-
to show that the problem is actually NP-hard in general,
-
to propose an algorithm for the problem,
-
to describe some polynomial cases.
Structure of the paper. In Sect. 1.1, we introduce the notion of interval linear programming and define our problem formally. Section 1.2 provides an overview of related work and some motivation for our paper. The introductory part of the paper is finalized by Sect. 2.1, which provides a counterexample to the method proposed in [18] and also points to the weakness in the proof therein.
The main results of the paper are contained in Sects. 3 and 4. In the former section, we prove that our problem is NP-hard (via reduction from testing solvability of interval linear systems). In the latter section, we prove that weak optimality of a given solution of a given interval linear program can be tested by solving \(2^k\) linear programs (of the same size), where k is the number of equality constraints in the interval linear program.
In particular, this means that if an interval linear program contains only inequality constraints, weak optimality of a given solution can be tested in polynomial time with one linear program. More generally, the test can be performed in polynomial time as long as the number of equality constraints remains “small” (for example constant or logarithmic in the number of variables and inequality constraints).
Our method is based on strong duality characterization, or, more precisely, on the Karush–Kuhn–Tucker (KKT) conditions, similiarly as the former method in [18]. The difference is, however, in the way how we deal with nonlinearity in the formulas. We use a variant of disjunctive programming and orthant decomposition.
To avoid confusion at this point, we premise that reasons of distinguishing equality and inequality constraints (which is not necessary in classical linear programming) will be clarified in Remark 1.5.
1.1 Notation, intervals and interval linear programming
For two real matrices  such that
such that  , an interval matrix is the set of matrices
, an interval matrix is the set of matrices  . The set of all interval matrices of dimension \({m\times n}\) is denoted by \({\mathbb {IR}^{m\times n}}\). Interval vectors and scalars are defined analogously.
. The set of all interval matrices of dimension \({m\times n}\) is denoted by \({\mathbb {IR}^{m\times n}}\). Interval vectors and scalars are defined analogously.
The multiplication of a real and an interval is defined as follows. Assume \({\alpha \in \mathbb {R}}\) and  . If \({\alpha < 0}\), then
. If \({\alpha < 0}\), then  , otherwise
, otherwise  .
.
Throughout the paper, bold symbols are reserved for interval matrices, vectors and scalars, while symbols in italics represent structures of real numbers. The symbol 0 denotes the zero matrix or vector of suitable dimension. Also, e is the vector of suitable dimension containing ones. Generally, we omit declaration of dimensions of matrix or vector variables wherever no confusion should arise. Vectors are understood columnwise.
The ith row of a (possibly interval) matrix A is denoted by \({A_i}\). Similarly, \({a_i}\) denotes \({i}\hbox {th}\) element of a given vector a. The symbol \({{{\mathrm{diag}}}(a)}\) for \({a\in \mathbb {R}^n}\) is the diagonal matrix with entries of a.
Definition 1.1 introduces the notion of interval linear programming and also the interval linear systems.
Definition 1.1
(Interval linear programming)
-
a)
Let the following interval matrices and vectors with dimensions in brackets be given:

accompanied with interval vectors
 .
.Define
 and
and  . The sets \({D^\mathrm {p}}\) will be called data of an interval linear program. Analogously, \({D^\mathrm {s}}\) will be data of an interval linear system.
. The sets \({D^\mathrm {p}}\) will be called data of an interval linear program. Analogously, \({D^\mathrm {s}}\) will be data of an interval linear system. -
b)
Denote a tuple from \({D^\mathrm {s}}\) by

Any tuple from \({D^\mathrm {p}}\), say

is called scenario of interval linear program. Sometimes, also \({s^\mathrm {s}}\) will be called scenario of interval linear system.
To every scenario, a linear program (1.1) (shortly LP), denoted by
 , is associated:
, is associated: 
Analogously, to every \({s^\mathrm {s}\in D^\mathrm {s}}\), a linear system (1.1b)–(1.1d) is assigned; such a system is denoted by \({\textit{LS}(s^\mathrm {s})}\).
-
c)
An interval linear program (shortly ILP) with data \({D^\mathrm {p}}\), denoted by \({\textit{ILP}(D^\mathrm {p})}\), is the family of linear programs \({\{\textit{LP}(s^\mathrm {p}):\,s^\mathrm {p}\in D^\mathrm {p}\}}\).
-
d)
An interval linear system with data \({D^\mathrm {s}}\), denoted by \({\textit{ILS}(D^\mathrm {s})}\) is the family of linear systems
 .
.
To simplify, an interval linear program is the family of linear programs with coefficients varying along given intervals. Similarly an interval linear system is the family of linear systems.
We will use interval linear programs and systems quite often. For convenience and readability, we will write them in short form: the interval linear program with data \({D^\mathrm {p}}\) reads

the interval linear system will be written in an analogous way.
Remark 1.2
(on notation) Some symbols in the paper have upper indices. These should simplify orientation in the (not very small) amount of different symbols. The indices are “\({\mathrm {p}}\)” for “of a program”, “\({\mathrm {s}}\)” for “of a system”, “\({\mathrm {f}}\)” for “free” (variables) and “\({\mathrm {n}}\)” for “nonnegative” (variables).
Feasibility and optimality in classical linear programming Properties of feasibility and optimality are well known when dealing with linear systems or programs. This holds also for feasible or optimal solution of a linear system or program.
For all the above properties, one can define a decision problem in form “does the particular property hold for a given (solution of) linear program/system?”. Note that all such decision problems can be solved using algorithms for linear programming.
Feasibility and optimality in interval linear programming For interval linear systems and programs, the above properties and associated decision problems are not so straightforward to formulate. There are at least two quite natural ways to build analogous problems. For our paper, the analogies that could be called weak problems are interesting. In Definitions 1.3 and 1.4, we build analogies to all the above properties. Actually, we are especially interested in Definitions 1.3a and 1.4b. For other concepts of feasibility and optimality in interval linear programming, see Remark 1.6.
Definition 1.3
(Weak feasibility) Assume that data \({D^\mathrm {s}}\) of a system \({\textit{ILS}(D^\mathrm {s})}\) are given.
-
a)
The system \({\textit{ILS}(D^\mathrm {s})}\) is weakly feasible, if there exists \({s^\mathrm {s}\in D^\mathrm {s}}\) such that \({\textit{LS}(s^\mathrm {s})}\) is feasible.
-
b)
A given
 is a weakly feasible solution of \({\textit{ILS}(D^\mathrm {s})}\), if there exists \({s^\mathrm {s}\in D^\mathrm {s}}\) such that x is a feasible solution of \({\textit{LS}(s^\mathrm {s})}\).
is a weakly feasible solution of \({\textit{ILS}(D^\mathrm {s})}\), if there exists \({s^\mathrm {s}\in D^\mathrm {s}}\) such that x is a feasible solution of \({\textit{LS}(s^\mathrm {s})}\).
Definition 1.4
(Weak optimality) Assume that data \({D^\mathrm {p}}\) of a program \({\textit{ILP}(D^\mathrm {p})}\) are given.
-
a)
The program \({\textit{ILP}(D^\mathrm {p})}\) is weakly optimal, if there exists \({s^\mathrm {p}\in D^\mathrm {p}}\) such that \({\textit{LP}(s^\mathrm {p})}\) has an optimum.
-
b)
A given
 is a weakly optimal solution of \({\textit{ILP}(D^\mathrm {p})}\), if there exists
is a weakly optimal solution of \({\textit{ILP}(D^\mathrm {p})}\), if there exists  such that x is an optimal solution of \({\textit{LP}(s^\mathrm {p})}\).
such that x is an optimal solution of \({\textit{LP}(s^\mathrm {p})}\).
Remark 1.5
Unlike for linear programming, the distinguishing of inequality and equality constraints does matter here. The mutual transformation of the types of constraints is not possible in general. For example, an equality constraint  cannot be rewritten to the system
cannot be rewritten to the system  . The former means
. The former means  for all
for all  , while the latter reads
, while the latter reads  for all
for all  . The problem is that we lose the dependency \({A^1 = A^2}\) during the transformation—one calls this the dependency problem.
. The problem is that we lose the dependency \({A^1 = A^2}\) during the transformation—one calls this the dependency problem.
Although the set of all weakly feasible solutions of the system  is the same as the set of all weakly feasible solutions
is the same as the set of all weakly feasible solutions  (see [17]), the transformation can create new weakly optimal solutions (see [7]).
(see [17]), the transformation can create new weakly optimal solutions (see [7]).
For additional details on dependency problem, examples and possible transformations, see [13] and also previously mentioned [7, 17].
The distinguishing of nonnegative and free variables has a bit different primary background. In fact, it turns out that many questions in interval analysis are much simpler with nonnegative variables than with free variables. Hence, the types of variables are often treated separately. For our results, this distinction is not really necessary. We do so just to demonstrate the generality of our results.
The formulation of the problem we are facing follows, in two variants.
Our problems
-
(P1)
Given data \({D^\mathrm {p}}\) of an interval linear program and a solution
 , test whether x is weakly optimal, i.e. decide whether x is optimal for some scenario \({s^\mathrm {p}\in D^\mathrm {p}}\).
, test whether x is weakly optimal, i.e. decide whether x is optimal for some scenario \({s^\mathrm {p}\in D^\mathrm {p}}\). -
(P2)
Decide (P1). If the answer is yes, find a scenario witnessing it.
The problem (P2) is a constructive version of (P1). Note also that a scenario is a sufficient witness of weak optimality.
Remark 1.6
Note that the weak problems ask in general the following question: Given a property of classical linear program/system, is the property satisfied for at least one scenario of a given interval linear program/system?”. If the quantifier “at least one scenario” is interchanged for “every scenario”, one obtains strong problems. For example, a feasible x is a strongly optimal solution of a given \({\textit{ILP}(D^\mathrm {p})}\), if x is an optimal solution of \({\textit{LP}(s^\mathrm {p})}\) for every \({s^\mathrm {p}\in D^\mathrm {p}}\). The survey on results regarding both the weak and strong problems in interval linear programming can be found in [8] and the corresponding problems related to interval linear systems of equations and inequalities in [26].
Remark 1.7
Another difference between classical linear programming and interval linear programming is in the relation between feasibility and optimality. In linear programming, a problem of testing optimality (of a linear program) can be transformed to a problem of testing feasibility (of a linear system) using strong duality characterization. However, we cannnot perform such a transformation from a problem of testing weak optimality of an interval linear program to a problem of testing weak feasibility of an interval linear system due to the dependency problem. We discuss this in Sect. 2, see Lemma 2.1 and Remark 2.2. This is the reason we cannot directly use the results on interval linear systems from the book [26].
1.2 Related work
Since the early works [4, 15, 21], interval linear programming became an intensively developing discipline. A survey on results can be found in [8]. A lot of effort was devoted to the problem of calculating the range of optimal values and the related computational complexity issues [5, 6, 22, 25]. Considerably less attention was paid to the more challenging problem of characterizing and tightly approximating the optimal solutions. This problem becomes easier in the case when there is a basis that is optimal for each scenario [4, 14, 15, 24]. Despite the fact that checking such basis stability is a co-NP-hard problem [10], there are practically usable conditions, and once a basis stability is observed, many interval linear programming problems turn to be tractable. On the other hand, if basis stability is not confirmed, much less is known and can be said.
The problem in question of testing weak optimality of a given solution of an interval linear program naturally emerged when dealing with various questions and problems regarding interval linear programming. Since that time, a partial characterization of the weakly optimal solution set was given in [2] and an inner approximation was considered in [1]. More general concepts of solutions, extending weak and strong solutions, were recently addressed in [16, 19, 20]. Particular quantified solutions were also studied in [11, 12]. Duality in interval linear programming, which helps in charaterizing of weak optimality, among others, was studied in [23].
2 Auxiliary result: strong duality in LP
In the next sections, we will strongly rely on the obvious characterization of the set of optimal solutions of an interval linear program using strong duality theorem for linear programming. To be precise, note that the characterization uses complementarity constraints from KKT conditions instead of the classical zero-duality-gap constraint. However, for linear objective functions, this makes no difference.
Lemma 2.1
(Characterization of weak optimality using strong duality) Consider an interval linear program  . The solution
. The solution  is a weakly optimal solution of \({\textit{ILP}(D^\mathrm {p})}\), if and only if
is a weakly optimal solution of \({\textit{ILP}(D^\mathrm {p})}\), if and only if  is a feasible solution of the system
is a feasible solution of the system


for some  and
and  .
.
For a fixed scenario \({s^\mathrm {p}}\), the constraints (2.1a) correspond to the feasibility of primal program, the constraints (2.1b) to the feasibility of dual program, and the constraints (2.1c) and (2.1d) to the complementary slackness.
Proof
(of Lemma2.1) If  is a weakly optimal solution, there exists a scenario \({s^\mathrm {p}\in D^\mathrm {p}}\) such that x is an optimal solution of \({\textit{LP}(s^\mathrm {p})}\). Using the well known strong duality theorem we know that there exists a tuple
is a weakly optimal solution, there exists a scenario \({s^\mathrm {p}\in D^\mathrm {p}}\) such that x is an optimal solution of \({\textit{LP}(s^\mathrm {p})}\). Using the well known strong duality theorem we know that there exists a tuple  such that
such that  solves (2.1).
solves (2.1).
Similarly, if  is a feasible solution of (2.1), we obtain that
is a feasible solution of (2.1), we obtain that  is a weakly optimal solution of \({\textit{ILP}(D^\mathrm {p})}\) for scenario \({s^\mathrm {p}}\) from application of the strong duality theorem. \(\square \)
is a weakly optimal solution of \({\textit{ILP}(D^\mathrm {p})}\) for scenario \({s^\mathrm {p}}\) from application of the strong duality theorem. \(\square \)
Remark 2.2
Note that the system (2.1)
-
is nonlinear and remains nonlinear even for fixed
 ,
, -
can be rewritten to a linear system for fixed \({s^\mathrm {p}}\),
-
is not a standard interval linear system due to the dependency problem: note the multiple occurrences of individual coefficients that could be considered interval coefficients (see Remark 1.5). It is rather a linear parametric system, where parameters attain values from given intervals. This is actually what makes the weak optimality harder to grasp than weak feasibility for interval linear program (cf. this with classical linear program, where optimality and feasibility are essentially the same problems).
2.1 The weakness in the method in [18] and an counterexample
The characterization provided by Lemma 2.1 is actually fundamental for both the method presented in the paper [18] and our method. Here, we describe how the earlier method was intended to work and what is wrong in its derivation.
Assume a weakly feasible solution x is to be tested for weak optimality of a given interval linear program \({\textit{ILP}(D^\mathrm {p})}\). Concrete values of  and b are selected such that x is weakly feasible—using the formulas suggested in [9]. Now, these values and also
and b are selected such that x is weakly feasible—using the formulas suggested in [9]. Now, these values and also  are fixed, meaning that (2.1) is a linear system, so the intention is to simply test such this linear system for feasibility.
are fixed, meaning that (2.1) is a linear system, so the intention is to simply test such this linear system for feasibility.
The problem is that the method selects coefficients of constraints without taking dual program into account. In particular, the objective vectors do not influence the selected scenario at all. Then, the weakness of the proof of the main theorem (Theorem 3.1 in the original paper) is in the “only if” part, namely in the first sentence on page 84. The paper states that there exists a solution satisfying the systems (20) and (21) therein (read “there exists an optimal solution of the dual program”), however, this is not ensured, since the scenario was chosen to satisfy the primal feasibility only.
Example 2.3
Consider the \({\textit{ILP}((0,([0,2],[0,2]),0,0,2,0,0,(0,1){}^{\mathrm {T}}))}\) with two nonnegative variables and one equality constraint

Assume we want to test the weak optimality of \({x = \left( {\begin{array}{c}1\\ 1\end{array}}\right) }\). The method of [18] selects the scenario with  and says that x is weakly optimal if and only if the system with variables \({y^1 \in \mathbb {R}, c^1 \in \mathbb {R}^2}\) (we use the notation of the original paper)
and says that x is weakly optimal if and only if the system with variables \({y^1 \in \mathbb {R}, c^1 \in \mathbb {R}^2}\) (we use the notation of the original paper)
is feasible. Note that the same system can be obtained from (2.1d) and (2.1e).
This yields the result that x is not weakly optimal. This is wrong, since x is optimal for a scenario with  .
.
Note that it actually doesn’t matter what  was selected by the method. The main concern is that it was selected without taking objective vector into account. Assume that the method selects some
was selected by the method. The main concern is that it was selected without taking objective vector into account. Assume that the method selects some  such that
such that  is feasible and that the example is modified such that
is feasible and that the example is modified such that  . Now, the method says that
. Now, the method says that  is not a weakly optimal solution, while it is: for the scenario with
is not a weakly optimal solution, while it is: for the scenario with  .
.
3 NP-hardness proof
In this section, we prove that the problem (P1) is NP-hard. We show this by a reduction from weak feasibility testing of an interval system of inequalities with free variables. We lean on the well-known result stated in Lemma 3.1.
Lemma 3.1
(NP-hardness of weak feasibility, Rohn [26, p. 58]) Consider the family of interval linear systems with free variables and inequality constraints only, in form

i.e. the family of interval systems with data  .
.
The problem “given data \({D^\mathrm {s}}\), decide whether \({\textit{ILS}(D^\mathrm {s})}\) is weakly feasible” is NP-hard.
Our result follows:
Theorem 3.2
The problem (P1) is NP-hard.
Proof
Consider the family of interval linear programs with nonnegative variables and equality constraints only, i.e. the family of interval linear programs with data in form  .
.
Using Lemma 2.1 we know that a given x is a weakly optimal solution of \({\textit{ILP}(D^\mathrm {p})}\) if and only if the system (2.1) has a solution for the fixed x. Hence, the system reads (zero rows and summands are omitted)

Now, assume that we want to test weak optimality of the solution  . The system (3.2) becomes
. The system (3.2) becomes

We have that  is a weakly optimal solution of \({\textit{ILP}(D^\mathrm {p})}\) if and only if the inequality system (3.3a) is feasible for at least one
is a weakly optimal solution of \({\textit{ILP}(D^\mathrm {p})}\) if and only if the inequality system (3.3a) is feasible for at least one  , which actually is exactly the problem of testing weak feasibility of the interval linear system with data
, which actually is exactly the problem of testing weak feasibility of the interval linear system with data  . For such an interval linear system, testing weak feasibility is NP-hard due to Lemma 3.1.
. For such an interval linear system, testing weak feasibility is NP-hard due to Lemma 3.1.
Now, since an algorithm for the problem (P1) can be used to solve an NP-hard problem (namely the problem of testing weak feasibility of interval inequality system from Lemma 3.1), we can conclude that the problem (P1) is at least as hard. \(\square \)
4 Algorithm for (P2)
In this section, we describe an algorithm for solving the problem (P2). First, we demonstrate the idea on a simpler case with no equality constraint. Then we show that it can be rewritten to treat interval linear programs in their full generality.
Recall the notation introduced in Definition 1.1: the symbol k denotes the number of equality constraints, the number of inequality constraints is denoted by \({\ell }\). Our method will be able to test weak optimality of a given point by solving \({2^k}\) feasibility problems of classical linear systems.
4.1 The simple case: inequality constraints
Weak optimality of a given  can be tested via solving the nonlinear system (2.1) by Lemma 2.1. Our key idea is the following: if \({k=0}\), the nonlinear system (2.1) can be rewritten as a linear system. A nice geometric trick takes place here: a special form of disjunctive programming (see e.g. [3]) can be utilized. Disjunctive programming is a tool for modelling (hulls of) disjunctions of some suitably represented sets (e.g. convex polyhedra).
can be tested via solving the nonlinear system (2.1) by Lemma 2.1. Our key idea is the following: if \({k=0}\), the nonlinear system (2.1) can be rewritten as a linear system. A nice geometric trick takes place here: a special form of disjunctive programming (see e.g. [3]) can be utilized. Disjunctive programming is a tool for modelling (hulls of) disjunctions of some suitably represented sets (e.g. convex polyhedra).
It is based on the observation that polyhedra can be scaled by scaling right hand sides only. Consider \({P^1 = \{x: A^1 x \le b^1 \}}\) and \({P^2 = \{x: A^2 x \le b^2\}}\). The natural way to express the conic hull of \({P^1 \cup P^2}\) is
which is apparently nonlinear. However, the coefficients \({y^1}\) and \({y^2}\) can be moved into the description of \({P^1}\) and \({P^2}\), removing nonlinearity:
Note that we actually use substitution \({z^i = y^i x^i}\). This is possible since since \({y^i \ge 0}\). Note also that if one of the coefficients, say \({y^i}\), is zero, it means that \({z^i}\) is also zero.
The above linearization applied on the system (2.1) allows for deriving Theorem 4.1. Similarly as in the above simple example, we scale the limits of the intervals in  and
and  by the corresponding dual variables and substitute new variables
by the corresponding dual variables and substitute new variables  . In particular, note that the nonlinear constraints (2.1c) are rewritten as constraints (4.1b). If
. In particular, note that the nonlinear constraints (2.1c) are rewritten as constraints (4.1b). If  for some i, then \(i\hbox {th}\) row of (4.1b) is of the form \({0=0}\). If
for some i, then \(i\hbox {th}\) row of (4.1b) is of the form \({0=0}\). If  , then the constraint
, then the constraint  takes place, exactly as the complementarity constraint (2.1c) does.
takes place, exactly as the complementarity constraint (2.1c) does.
Theorem 4.1
Let an interval linear program \({\textit{ILP}(D^\mathrm {p})}\) with data

be given.
A given  is a weakly optimal solution of \({\textit{ILP}(D^\mathrm {p})}\) if and only if it is a weakly feasible solution of
is a weakly optimal solution of \({\textit{ILP}(D^\mathrm {p})}\) if and only if it is a weakly feasible solution of  and there exists a solution
and there exists a solution  of the system
of the system

If so, a scenario witnessing weak optimality of x is

where \(i\hbox {th}\) row of  is determined as follows:
is determined as follows:
-
if
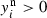 , then
, then  ,
, -
else
 is determined as a solution of linear system
is determined as a solution of linear system  (4.3)
(4.3)
and \(i\hbox {th}\) row of  is determined as
is determined as

Proof
“\({\Rightarrow }\)”: We know that x is a weakly optimal solution, hence there is a scenario  and a vector
and a vector  solving the system (2.1) for the fixed x. Then also
solving the system (2.1) for the fixed x. Then also  solves the system (4.1), since
solves the system (4.1), since
-
the rows in relations (4.1a) are only scaled or nullified rows of some constraints in the system (2.1)
-
constrains (4.1c)–(4.1f) are actually contained in system (2.1), and
-
an \(i\hbox {th}\) row of (4.1b) either has the form \({0 = 0}\) (if
 ), or (otherwise) is satisfied via \(i\hbox {th}\) row of (2.1a), which is satisfied as equality due to \(i\hbox {th}\) complementarity constraint in (2.1c).
), or (otherwise) is satisfied via \(i\hbox {th}\) row of (2.1a), which is satisfied as equality due to \(i\hbox {th}\) complementarity constraint in (2.1c).
“\({\Leftarrow }\)” and “If so”: Assume  solves (4.1) for a given weakly feasible x. Since x is weakly feasible, a solution
solves (4.1) for a given weakly feasible x. Since x is weakly feasible, a solution  of the system (4.3) exists for every \({i=1,\dots ,\ell }\). Hence, we can construct the scenario \({s^w}\) in (4.2).
of the system (4.3) exists for every \({i=1,\dots ,\ell }\). Hence, we can construct the scenario \({s^w}\) in (4.2).
Now, note that  and \({s^w}\) solve (2.1) (and hence x is weakly optimal):
and \({s^w}\) solve (2.1) (and hence x is weakly optimal):
-
an \(i\hbox {th}\) row of (2.1a) follows either from rescaling the corresponding row of (4.1b) (for
 ), or from (4.3) (for
), or from (4.3) (for  ),
), -
the dual feasibility constraint (2.1b) is obtained simply by substitution to (4.1c),
-
the complementarity constraints are obviously satisfied: if \({y_i >0}\), then \(i\hbox {th}\) row of primal feasibility is satisfied as equality, if \(x_i>0\), \(i\hbox {th}\) row of dual feasibility is satisfied as equality,
-
the “scenario feasibility” constraints (2.1e) are satisfied, since the scenario \({s^w}\) is clearly correctly built.\(\square \)
Corollary 4.2
The problem (P2) is polynomially solvable via checking feasibility of a linear system if the underlying interval linear program has no equality constraints (i.e. \({k=0}\)).
The weak optimality test itself can be done by solving the system (4.1). If a scenario witnessing optimality is also necessary, it can be obtained using (4.2) by solving additional systems of form (4.3).
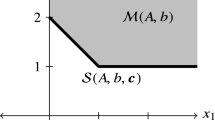
Illustration of Example 4.3. The space of rows of the matrix  is depicted. For example, the line
is depicted. For example, the line  contains pairs of coefficients
contains pairs of coefficients  such that second to fourth constraint is satisfied as equality for the given x
such that second to fourth constraint is satisfied as equality for the given x
Example 4.3
We demonstrate the idea on a small example. The geometry behind Theorem 4.1 is depicted on Fig. 1. The figure shows the space of coefficients of constraints.
The setting is the following: assume that we are given interval linear program

with

i.e. there are two free variables and the objective function is crisp. We are to test weak optimality for  .
.
Note that the third constraint can’t be satisfied as equality for the given x. This enforces \({y_3 = 0}\). Hence the third rows of (4.1a) and (4.1b) are null.
Our given x is weakly optimal if c is in the conic hull of all the feasible  and
and  (see the bold triangle and the bold line segment in the figure). The conic hull itself is depicted with dashed pattern. Note that it corresponds to left hand sides of the constraints (2.1b) and (4.1c).
(see the bold triangle and the bold line segment in the figure). The conic hull itself is depicted with dashed pattern. Note that it corresponds to left hand sides of the constraints (2.1b) and (4.1c).
The gray cones are cones of all the feasible  and
and  . Since their conic hull contains c, we have that x is weakly optimal.
. Since their conic hull contains c, we have that x is weakly optimal.
Just for illustration, there is also an additional fourth constraint

in the figure. There is no  such that x is feasible. With this fourth constraint x is not weakly optimal.
such that x is feasible. With this fourth constraint x is not weakly optimal.
4.2 The general case: equations are allowed
Now consider the problem (P2) in its full generality. The key in the special case was in the nonnegativity of  . Assuming equality constraints, we need to consider also free dual variables
. Assuming equality constraints, we need to consider also free dual variables  . However, the linearization based on disjunctive programming requires variables with a fixed sign (nonnegative or nonpositive ones). The underlying problem is that a nonconvex set cannot be described by just one linear system, as shows Example 4.4:
. However, the linearization based on disjunctive programming requires variables with a fixed sign (nonnegative or nonpositive ones). The underlying problem is that a nonconvex set cannot be described by just one linear system, as shows Example 4.4:
Illustration of Example 4.4. The space of rows of the matrix  is depicted. For example, the line
is depicted. For example, the line  contains pairs of coefficients
contains pairs of coefficients  such that second constraint is satisfied
such that second constraint is satisfied
Example 4.4
Consider now the ILP from Example 4.3 with equalities instead of inequalities (and also only with the first two constraints):

where

Again, we are to test weak optimality for  .
.
The space of  and
and  is depicted on Fig. 2. The meaning of elements of the figure is analogous to Fig. 1.
is depicted on Fig. 2. The meaning of elements of the figure is analogous to Fig. 1.
The sets of all primarily feasible normals  and
and  can now be scaled by both positive and negative factors. The resulting sets are nonconvex double-cones.
can now be scaled by both positive and negative factors. The resulting sets are nonconvex double-cones.
Note that for a classical linear program, these double-cones are degenerated to a single line, which is actually a convex set.
To emphasize: from the perspective of the method presented in Sect. 4.1, the problem is that we cannot linearize the dual feasibility constraint, because we need to sum up points from possibly nonconvex sets. Alternatively, the problem can be viewed in the constraints (4.1a). Consider a constraint  for some
for some  and
and  . If \({y \ge 0}\) (or \({y \le 0}\)), it can rewritten as
. If \({y \ge 0}\) (or \({y \le 0}\)), it can rewritten as  (or
(or  ), however, if y can be arbitrary, the two cases must be distinguished.
), however, if y can be arbitrary, the two cases must be distinguished.
However, the standard orthant decomposition of  -space can be apparently used here. We do so in Theorem 4.6.
-space can be apparently used here. We do so in Theorem 4.6.
Definition 4.5
For given data  of an ILP and a given sign vector \({\sigma \in \{-1,1\}^{k}}\), the testing system for\({D^\mathrm {p}}\)in orthant\({\sigma }\) is the system (4.6) in the form
of an ILP and a given sign vector \({\sigma \in \{-1,1\}^{k}}\), the testing system for\({D^\mathrm {p}}\)in orthant\({\sigma }\) is the system (4.6) in the form

Theorem 4.6
Assume ILP with data  . A solution
. A solution  is weakly optimal if and only if x is a weakly feasible solution of \({\textit{ILP}(D^\mathrm {p})}\) and there is \({\sigma \in \{-1,1\}^{k}}\) such that the testing system for \({D^\mathrm {p}}\) in orthant \({\sigma }\) is feasible for the fixed x. If so, a scenario witnessing optimality of x is
is weakly optimal if and only if x is a weakly feasible solution of \({\textit{ILP}(D^\mathrm {p})}\) and there is \({\sigma \in \{-1,1\}^{k}}\) such that the testing system for \({D^\mathrm {p}}\) in orthant \({\sigma }\) is feasible for the fixed x. If so, a scenario witnessing optimality of x is

where \(i\hbox {th}\) row of  is determined as follows:
is determined as follows:
-
if
 , then
, then  ,
, -
else
 is determined as a solution of the linear system
is determined as a solution of the linear system

\(i\hbox {th}\) row of  is determined as follows:
is determined as follows:
-
if
 , then
, then  ,
, -
else
 is determined as a solution of (4.3),
is determined as a solution of (4.3),
and \(i\hbox {th}\) row of  is determined as
is determined as

Proof
Very analogous to the proof of Theorem 4.1. \(\square \)
Corollary 4.7
The problem (P2) for an ILP with data \({D^\mathrm {p}}\) can be solved by solving \({2^k}\) linear systems, one for every \({\sigma \in \{-1,1\}^k}\). Recall that k is the number of equality constraints in the ILP. The size of the linear systems to be solved is linear in the number of variables and constraints of the ILP.
5 Conclusions
We proved that the problem of testing weak optimality of a given solution of a given interval linear program is NP-hard. We proposed an algorithm, based on orthant decomposition, which can decide the problem via solving of \({2^k}\) linear systems, where k is the number of equality constraints in the given interval linear program. In particular, this means that the proposed method works in polynomial time for interval linear programs with inequality constraints only.
References
Allahdadi, M., Mishmast Nehi, H.: The optimal solution set of the interval linear programming problems. Optim. Lett. 7(8), 1893–1911 (2013)
Ashayerinasab, H.A., Nehi, H.M., Allahdadi, M.: Solving the interval linear programming problem: a new algorithm for a general case. Expert Syst. Appl. 93(Suppl. C), 39–49 (2018)
Balas, E.: Disjunctive programming: properties of the convex hull of feasible points. Discrete Appl. Math. 89(1–3), 3–44 (1998). https://doi.org/10.1016/S0166-218X(98)00136-X
Beeck, H.: Linear programming with inexact data. technical report TUM-ISU-7830, Technical University of Munich, Munich (1978)
Chinneck, J.W., Ramadan, K.: Linear programming with interval coefficients. J. Oper. Res. Soc. 51(2), 209–220 (2000)
Gabrel, V., Murat, C.: Robustness and duality in linear programming. J. Oper. Res. Soc. 61(8), 1288–1296 (2010)
Garajová, E., Hladík, M., Rada, M.: Interval Linear Programming Under Transformations: Optimal Solutions and Optimal Value Range (2018). arXiv:1802.09872
Hladík, M.: Interval linear programming: a survey. In: Mann, Z.Á. (ed.) Linear Programming-New Frontiers in Theory and Applications, Mathematics Research Developments, pp. 85–120. Nova Science Publishers, Hauppauge (2012)
Hladík, M.: Weak and strong solvability of interval linear systems of equations and inequalities. Linear Algebra Appl. 438(11), 4156–4165 (2013). https://doi.org/10.1016/j.laa.2013.02.012
Hladík, M.: How to determine basis stability in interval linear programming. Optim. Lett. 8(1), 375–389 (2014)
Hladík, M.: Robust optimal solutions in interval linear programming with forall-exists quantifiers. Eur. J. Oper. Res. 254(3), 705–714 (2016)
Hladík, M.: On strong optimality of interval linear programming. Optim. Lett. 11(7), 1459–1468 (2017)
Hladík, M.: Transformations of interval linear systems of equations and inequalities. Linear Multilinear Algebra 65(2), 211–223 (2017)
Koníčková, J.: Sufficient condition of basis stability of an interval linear programming problem. Z. Angew. Math. Mech. 81(Suppl. 3), 677–678 (2001)
Krawczyk, R.: Fehlerabschätzung bei linearer Optimierung. In: Nickel, K. (ed.) Interval Mathemantics: Proceedings of the International Symposium, Karlsruhe, West Germany, May 20–24, 1975, LNCS, vol. 29, pp. 215–222. Springer (1975)
Li, H.: Necessary and sufficient conditions for unified optimality of interval linear program in the general form. Linear Algebra Appl. 484, 154–174 (2015)
Li, W.: A note on dependency between interval linear systems. Optim. Lett. 9(4), 795–797 (2015). https://doi.org/10.1007/s11590-014-0791-1
Li, W., Liu, P., Li, H.: Checking weak optimality of the solution to interval linear program in the general form. Optim. Lett. 10(1), 77–88 (2016). https://doi.org/10.1007/s11590-015-0856-9
Li, W., Liu, X., Li, H.: Generalized solutions to interval linear programmes and related necessary and sufficient optimality conditions. Optim. Methods Softw. 30(3), 516–530 (2015)
Luo, J., Li, W., Wang, Q.: Checking strong optimality of interval linear programming with inequality constraints and nonnegative constraints. J. Comput. Appl. Math. 260, 180–190 (2014)
Machost, B.: Numerische Behandlung des Simplexverfahrens mit intervallanalytischen Methoden. Technical Report 30, Berichte der Gesellschaft für Mathematik und Datenverarbeitung, 54 pages, Bonn (1970)
Mráz, F.: Calculating the exact bounds of optimal values in LP with interval coefficients. Ann. Oper. Res. 81, 51–62 (1998)
Novotná, J., Hladík, M., Masařík, T.: Duality gap in interval linear programming. In: Zadnik Stirn, L. et al. (ed.) Proceedings of the 14th International Symposium on Operational Research SOR’17, pp. 501–506. Slovenian Society Informatika, Ljubljana, Slovenia (2017)
Rohn, J.: Stability of the optimal basis of a linear program under uncertainty. Oper. Res. Lett. 13(1), 9–12 (1993)
Rohn, J.: Complexity of some linear problems with interval data. Reliab. Comput. 3(3), 315–323 (1997)
Rohn, J.: Interval linear programming. In: Fiedler, M., et al. (eds.) Linear Optimization Problems with Inexact Data, Chap. 3, pp. 79–100. Springer, New York (2006)
Acknowledgements
The work of M. Rada was supported by the Czech Science Foundation Grant P403/17-13086S. The work of M. Hladík and E. Garajová was supported by the Czech Science Foundation Grant P403/18-04735S. The work of E. Garajová was also supported by Grant No. 156317 of Grant Agency of Charles University.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Rada, M., Hladík, M. & Garajová, E. Testing weak optimality of a given solution in interval linear programming revisited: NP-hardness proof, algorithm and some polynomially-solvable cases. Optim Lett 13, 875–890 (2019). https://doi.org/10.1007/s11590-018-1289-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11590-018-1289-z




 .
. and
and  . The sets
. The sets 

 , is associated:
, is associated: 
 .
. is a weakly feasible solution of
is a weakly feasible solution of  is a weakly optimal solution of
is a weakly optimal solution of  such that x is an optimal solution of
such that x is an optimal solution of  , test whether x is weakly optimal, i.e. decide whether x is optimal for some scenario
, test whether x is weakly optimal, i.e. decide whether x is optimal for some scenario  ,
,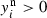 , then
, then  ,
, is determined as a solution of linear system
is determined as a solution of linear system 
 ), or (otherwise) is satisfied via
), or (otherwise) is satisfied via  ), or from (
), or from ( ),
),

 , then
, then  ,
, is determined as a solution of the linear system
is determined as a solution of the linear system , then
, then  ,
, is determined as a solution of (
is determined as a solution of (