1 Introduction

The facility layout problem involves positioning facilities in a certain area in order to optimize an objective function. Usually the objective is to minimize the total cost of transporting materials among facilities (departments, machines, etc). Facility layout problems often occur in practice, for example, in the design of automated manufacturing systems. An automated manufacturing system consists of a set of machines and an automated material handling device that transports materials among machines. A designer should plan a physical configuration of the machines that minimizes the material handling cost. An automated guided vehicle (AGV) is commonly utilized as the material handling device. For greater efficiency, the AGV is set to move along a straight line. In that context, the designer can implement a single row layout, i.e. a layout in which all machines are arranged on the same side of a straight line corridor; Alternatively, a double row layout may be implemented, i.e. a layout in which machines may lie on both sides of a corridor (see [13]). These types of layouts give rise, respectively, to the single row facility layout problem (SRFLP) (e.g. [1, 2, 8, 17]); and the double-row layout problem (DRLP) (e.g. [6, 11]).

The DRLP is how to arrange a given number of machines on either side of the corridor so that the total cost to transport materials among these machines is minimized. Chung and Tanchoco [11] described a practical application of the DRLP in an LCD manufacturing line.

The DRLP is an NP-Hard combinatorial optimization problem (e.g. [6]), and therefore, as the number of machines to be arranged increases, the computational cost to solve the problem increases considerably. In recent years, several authors in the literature have applied integer programming to different facility layout problems to exactly solve medium sized problems (e.g. [3, 7, 9, 10, 12, 14,15,16]). Specifically for the DRLP, a mixed-integer programming (MIP) model was presented by Chung and Tanchoco [11]. Amaral [6] proposed a different MIP model for the DRLP, which proved to be more efficient than the model of Chung and Tanchoco [11]. In this paper, we propose modifications to the MIP model of Amaral [6], obtaining a tighter model. The new model leads to significant reduction in computer time and in the number of branch-and-bound nodes needed to solve problems.

2 The model of Amaral [6]

The mixed-integer programming (MIP) model of Amaral [6] considers the following definitions.

2.1 Parameters

n

Number of machines

\(N=\{1,\ldots ,n\}\)

Set of machines

\(R=\){upper row, lower row}

Set of rows that define a corridor

\(c_{ij}\)

Amount of flow between machines i e j (\(1\le i<j\le n\))

\(\ell _{i}\)

Length of machine i

\(L=\sum _{i=1}^{n}\ell _{i}\)

 

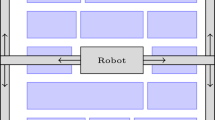
It is assumed that the corridor lies along the x axis in the range \([0,\,L]\), the width of the corridor is neglectable and the distance between two machines is taken between their centers (see Fig. 1).

Fig. 1
figure 1

A double row layout. The distance \(d_{ij}\) between two machines i and j is the horizontal distance between their centers

Full size image

2.2 Variables

\(x_{i}\)

Abscissa of the center of machine i (\(1\le i\le n\))

\(d_{ij}\)

Distance between machines i e j (\(1\le i<j\le n\))

\(\alpha _{ij}\)

Binary variable that equals 1 if machine i is on the left of machine j, both on the same row; and 0 otherwise (\(1\le i,\,j\le n\), \(i\ne j\))

Amaral [6] proposes the following MIP formulation for the double row layout problem:

$$\begin{aligned} \text {M0: }~~&\min \sum _{(i,j);i<j}c_{ij}d_{ij}&\end{aligned}$$
(1)
$$\begin{aligned}&d_{ij}\ge x_{i}-x_{j},&i<j\end{aligned}$$
(2)
$$\begin{aligned}&d_{ij}\ge x_{j}-x_{i},&i<j\end{aligned}$$
(3)
$$\begin{aligned}&d_{ij}-\alpha _{ij}(\ell _{i}+\ell _{j})/2-\alpha _{ji}(\ell _{i}+\ell _{j})/2\ge 0,&i<j\end{aligned}$$
(4)
$$\begin{aligned}&x_{i}+(\ell _{i}+\ell _{j})/2\le x_{j}+L(1-\alpha _{ij}),&i\ne j\end{aligned}$$
(5)
$$\begin{aligned}&x_{p}\le x_{q},&(p,\,q)=\arg \min _{i<j}c_{ij}\end{aligned}$$
(6)
$$\begin{aligned}&-\alpha _{ij}-\alpha _{ji}+\alpha _{ik}+\alpha _{ki}+\alpha _{jk}+\alpha _{kj}\le 1,&i<j,\,k\ne i,\,k\ne j\end{aligned}$$
(7)
$$\begin{aligned}&-\alpha _{ij}+\alpha _{ji}+\alpha _{ik}-\alpha _{ki}-\alpha _{jk}+\alpha _{kj}\le 1,&i<j,\,k<j,\,k\ne i\end{aligned}$$
(8)
$$\begin{aligned}&\alpha _{ij}+\alpha _{ji}+\alpha _{ik}+\alpha _{ki}+\alpha _{jk}+\alpha _{kj}\ge 1,&i<j<k\end{aligned}$$
(9)
$$\begin{aligned}&\alpha _{ij}\in \{0,1\},&i\ne j\end{aligned}$$
(10)
$$\begin{aligned}&x_{i}\in [\ell _{i}/2,\,L-\ell _{i}/2],&1\le i\le n \end{aligned}$$
(11)

The objective function (1) minimizes the total flow among machines; Constraints (2) and (3) provide the distance between each pair of machines; (4) ensures that if machines i and j are allocated at the same row, then the distance between their centers is at least \((\ell _{i}+\ell _{j})/2\); (5) prohibits overlap between machines; (6) avoids symmetry; (7)–(10) characterize the incidence vectors ( \(\alpha _{ij}\)) of a DRLP solution.

3 The new model

Based on the model of Amaral [6], we propose to modify Constraint (4) in order to consider the machines allocated between machines i e j. For \(i<j\), \(k\ne i\), \(k\ne j\), we define the binary variable \(e_{kij}\) such that \(e_{kij}=1\) if machine k is between machines i and j, all at the same row; and 0 otherwise. These types of variables have been used before in [4]. Note that if there is a set \(S_{ij}\subset N\) of machines allocated between machines i and j, all of them at the same row, then we can narrow the right hand side of constraint (4) to \(\sum _{k\in S_{ij}}\ell _{k}\) . Further, \(d_{ij}>(\ell _{i}+\ell _{j})/2\), when \(S_{i,j}\ne \oslash \) so that restriction (5) can also be reformulated by replacing \((\ell _{i}+\ell _{j})/2\), the lower bound for \(|x_{i}-x_{j}|\), by the tighter bound \(d_{ij}\). Thus, we obtain the following model:

$$\begin{aligned} \text {M: }~~\min \sum _{(i,j);i<j}c_{ij}d_{ij}\nonumber \\ (2),(3),(6)\hbox {--}(11)\nonumber \\ \sum _{k;k\ne i,j}\ell _{k}e_{kij}\le & {} d_{ij}-\alpha _{ij}(\ell _{i}+\ell _{j})/2-\alpha _{ji}(\ell _{i}+\ell _{j})/2,\quad i<j\end{aligned}$$
(12)
$$\begin{aligned} x_{i}+d_{ij}\le & {} x_{j}+2(L-\ell _{i}/2-\ell _{j}/2)(1-\alpha _{ij}),\quad i<j\end{aligned}$$
(13)
$$\begin{aligned} x_{i}+d_{ji}\le & {} x_{j}+2(L-\ell _{i}/2-\ell _{j}/2)(1-\alpha _{ij}),\quad i>j\end{aligned}$$
(14)
$$\begin{aligned} e_{kij}\ge & {} \alpha _{ik}+\alpha _{kj}-1,\quad i<j,\,k\ne i,\,k\ne j\end{aligned}$$
(15)
$$\begin{aligned} e_{kij}\ge & {} \alpha _{jk}+\alpha _{ki}-1,\quad i<j,\,k\ne i,\,k\ne j\end{aligned}$$
(16)
$$\begin{aligned} e_{kij}\in & {} \{0,1\},\quad i<j,\,k\ne i,\,k\ne j \end{aligned}$$
(17)

Note that Constraint (12) is the reformulation of Constraint (4). It is easy to see that \(d_{ij}-2(L-\ell _{i}/2-\ell _{j}/2)\le x_{j}-x_{i}\) is always valid, implying validity of constraints (13) and (14), which represent the reformulation of constraint (5). The constraints (15)–(17) together with the objective impose that the variables \(e_{kij}\) assume only values according to their definition. In Model M0 there are \(\frac{n}{2}(2n^{2}-n-1)+1\) constraints, \(\frac{n}{2}(n-1)+n\) continuous variables and \(n(n-1)\) binary variables. In the proposed Model (M), there are \(n(n^{2}-3n+2)\) additional restrictions, and \(\frac{n}{2}(n^{2}-3n+2)\) additional binary variables. However, the reformulation (12), (13) and (14) of the constraints (4) and (5) contribute to the gain of performance in relation to Model M0.

3.1 Valid inequalities

As inter-machine distance is a semi-metric, the following inequalities are valid:

$$\begin{aligned} d_{ij}\le d_{ik}+d_{jk},\quad d_{ik}\le d_{ij}+d_{jk},\quad d_{jk}\le d_{ij}+d_{ik} \end{aligned}$$
(18)

The variable \(e_{kij}\) is zero if machines k, i, and j are not all on the same side of the corridor. The following inequalities are, therefore, valid:

$$\begin{aligned} e_{kij}\le \alpha _{ik}+\alpha _{ki},\quad e_{kij}\le \alpha _{ij}+\alpha _{ji},\quad e_{kij}\le \alpha _{jk}+\alpha _{kj} \end{aligned}$$
(19)

4 Computational experiments

All tests were performed using CPLEX 12.7.1.0 on an Intel Core i7-3770 CPU 3.40 GHz with 8 GB of RAM with the Windows 8 operating system. The problem instances tested include instances (S9, S9H, S10, S11) introduced by Simmons [17], instances (12a, 12b, 13a, 13b) of Amaral [5] and the instance P15 of Amaral [1]. Besides, there are two new instances (14a, 14b), which are available from the authors. For all of the instances tested here, we assume that clearances have already been included in the lengths of the machines.

In order to analyze the effects of inequalities (18) and (19), we tested Model M and its following variants:

  • MC: Model M with the inequalities (18) used as cuts, inserted on demand;

  • MT: Model M with the inequalities (18) inserted as constraints;

  • MTC: Model MT with the inequalities (19) used as cuts.

These are compared against models:

  • M0: the model, which was given in [6];

  • M0T: Model M0 with the inequalities (18) inserted as constraints.

Computational results are presented in Tables 1 and 2. For each problem instance, the first two columns of Table 1 specify the problem instance. The next six columns show a comparison of each model (M0T, M0, M, MC, MT, MTC) in terms of time required to solve the problems. Table 2 displays for each model (M0T, M0, M, MC, MT, MTC), the number of enumeration tree nodes consumed to solve each instance to optimality. All tests ended with optimality gap equal to zero.

Table 1 Comparison of times (s) required to solve problems using Models M0T, M0, M, MT, MC, MTC
Full size table
Table 2 Comparison of number of nodes required to solve problems using Models M0T, M0, M, MT, MC, MTC
Full size table

From Table 1 it can be seen that for every instance the solution process with Model M is often much faster than with Model M0. Moreover, each of the models MT, MC or MTC provides some performance improvement over Model M and hence, over Model M0. Among the six models shown in the table, the smallest processing time for each instance was obtained either with MTC, MT or MC.

The solution times for Models MC and MT indicate that for the larger instances it may be better to insert the triangular inequalities (18) as constraints in Model M. Note that MT was specially fast for the largest instance (P15). However, the inclusion of Inequalities (18) in M0 does not help with speed up the solution process, as M0T is the slowest model for every instance, but S10.

Regarding the use of cuts (19) in MT or MTC, it has been observed that MT was particularly fast for solving Instance P15. However, for the instances with \(n<15\), there is a similar time performance between MTC and MT.

From Table 2 it is seen that for all instances the number of nodes consumed with the models M, MC, MT or MTC is smaller than with M0, which indicates that the proposed models are tighter than M0. Particularly, with MT or MTC, the number of nodes has been drastically reduced in relation to M0, for all instances. Therefore, with the presented models we can obtain optimal solutions for larger instances (with 14 and 15 departments) more efficiently than before.

5 Conclusions

In this article, we considered the double row layout problem (DRLP), which has large applicability, particularly in the design of manufacturing systems. We proposed modifications to the mixed-integer programming formulation of the DRLP given by Amaral [6] (denoted here as M0), thus obtaining a model M, which is more efficient than M0. Moreover, we described three variants of the model M, which were called: MC, MT and MTC. These variants are tighter than M, and hence tighter than M0. Computational tests with the proposed model M and its variants have shown that they perform considerably better than M0 leading to both smaller solution times and smaller number of nodes.

We believe that improvements on the proposed formulation are possible. In future works, valid inequalities other than those used here can be applied to the proposed model leading to a further performance gain.