1 Introduction

The facility location problem is a classic problem of operations research and computer science. It has wide applications [12, 16, 19, 21]. The most important variant of the facility location problem is the uncapacitated facility location problem (UFLP). In the UFLP, we are given a facility set and a client set. Opening a facility will incur an opening cost, and assigning a client to a facility will incur a serving cost. We want to open some facilities to serve all the clients such that the total opening cost as well as serving cost is minimized.

Since the UFLP is an NP-hard problem, various approximation algorithms for the UFLP have been proposed over the years [2,3,4, 6, 8,9,10, 13, 15, 18, 20]. Among all the existing algorithms, Shmoys et al. [18] give the first constant 3.16-approximation algorithm, which is based on LP rounding method. Li [13] proposes the currently best 1.488-approximation algorithm, which is based on randomized rounding and dual fitting. The inapproximability lower bound for the UFLP is known as 1.463 [8].

A limitation for the UFLP is that some distant clients (i.e., outliers) may have a powerful influence on the problem. In order to overcome the limitation, Charikar et al. [5] give two important variants for the UFLP, namely the robust facility location problem (RFLP) and the facility location problem with penalties (FLPWP). In both variants, a small subset of clients can be rejected to serve. In the RFLP, a nonnegative integer \(q < n\) is also given, where n is the number of all the clients. We aim to open some facilities to serve at least \(n-q\) clients such that the sum of opening cost and serving cost is minimized. For the RFLP, Charikar et al. [5] give a 3-approximation algorithm by using the technique of primal–dual. In the FLPWP, each client also has a penalty cost. A client can either be served by a facility or be penalized. We aim to open some facilities to serve some of the clients and pay penalty cost for the rest of clients, such that the sum of opening cost, serving cost and penalty cost is minimized. For the FLPWP, Charikar et al. [5] present the first 3-approximation algorithm, and Li et al. [14] give the currently best approximation ratio of 1.5148.

Another variant of the UFLP is the facility leasing problem (FLE). In the FLE, we are given a facility locations set, a client locations set, time periods from 1 to T. At each time period, a subset of clients will arrive. There are K lease types for all facilities. We can lease a facility at any time. Leasing a facility i of a type k at any time period s will incur a leasing cost \(f_i^{k}\) such that facility i is opened at time period s with a lease length \(l_k\). Each client can only be assigned to a facility whose open interval contains the arrival time of the client. Assigning a client j to a facility i will incur a serving cost \(c_{ij}\). We want to lease a set of facilities to serve all the clients such that the total leasing cost as well as serving cost is minimized. Anthony and Gupta [1] first introduced the FLE and give an O(K)-approximation algorithm for this problem, where K is the number of the lease types. Inspired by the primal–dual algorithm for the UFLP, which is proposed by Jain and Vazirani [10], Nagarajan and Williamson [17] give a currently best 3-approximation algorithm for the FLE. The only result for the FLE with outlier is given by de Lima et al. [7]. They propose the facility leasing problem with penalties (FLEWP), and give a primal–dual 3-approximation algorithm.

In this work, we propose the robust facility leasing problem (RFLE), which is a new variant for the FLE with outlier. Denote n as the number of all the clients. Comparing with the FLE, we are further given a nonnegative integer \(q (< n) \) as the outlier number in the RFLE. We aim to open a set of facilities to serve at least \(n-q\) clients such that the total cost including leasing and serving cost is minimized. Inspired by the works of Nagarajan and Williamson [17] on the FLE and Charikar et al. [5] on the FLPWP, we obtain a preliminary primal–dual 6-approximation algorithm for the RFLE. Furthermore, we modify the phase of constructing an integer primal feasible solution with a careful recognition on the leasing facilities. This refined algorithm leads to an improved approximation ratio 3.

The remainder structure of our paper is as follows. In Sect. 2, we describe the RFLE and give the integer program, the linear program relaxation and the dual program. Section 3 presents a basic primal–dual 6-approximation algorithm along with the analysis. Section 4 offers an improved 3-approximation algorithm which is based on the first algorithm. In Sect. 5, some discussions are given.

2 Preliminaries

In the RFLE, we are given a facility location set F, a client location set D of cardinality n, time periods \(\{1, 2, \ldots , T\}\) and a nonnegative integer \(q < n\). At each time period \(t \in \{1, 2, \ldots , T\}\), a subset of clients \(D_t \subseteq D\) will arrive. These subsets is a partition of D. For simplicity, we denote a client by a binary (j, t), where \(j \in D\) is the location of the client and \(t \in \{1, 2, \ldots , T\}\) is the arrival time of the client. Let \({\mathcal {D}}\) denote the set of client binaries (j, t). There are K lease types for all facilities. Let \({\mathcal {L}}\) be the set of lease types, where \(|{\mathcal {L}}| = K\). For any lease type \(k \in {\mathcal {L}}\), a lease length \(l_k\) is also given. Without loss of generality, we assume that \(l_k\) is an integer for any \(k \in {\mathcal {L}}\). We can start leasing a facility at any time period. Leasing a facility \(i \in F\) for a type \(k \in {\mathcal {L}}\) at a time period \(s \in \{1, 2, \ldots , T\}\) incurs a leasing cost \(f_i^k\) such that facility i is opened during time interval \([s, s+l_k)\). For any time period s and lease type k, denote \(I^k_s\) as time interval \([s, s+l_k)\). For simplicity, we denote a facility by a triple (i, k, s), where \(i \in F\) is the location of the facility, \(k \in {\mathcal {L}}\) is the lease type for the facility, and \(s \in \{1, 2, \ldots , T\}\) is the start time of leasing the facility. Let \({\mathcal {F}}\) denote the set of facility triples (i, k, s). For any client \((j, t) \in {\mathcal {D}}\), it can only be assigned to some facility \((i, k, s) \in {\mathcal {F}}\) whose open interval contains t. That means, a client (j, t) can be assigned to a facility (i, k, s) if \(t \in I^k_s\). Assigning a client (j, t) to a facility (i, k, s) incurs a serving cost \(c_{ij}\). We assume that the serving costs are non-negative, symmetric, and satisfy the triangle inequality. Our goal is to lease a set of facilities \({\mathcal {S}} \subseteq {\mathcal {F}}\) to serve at least \(n-q\) clients such that the total cost including the leasing and serving cost is minimized. Note that if we set \(q=0\) for the RFLE, it simplifies to the FLE.

We introduce the following three types of binary variables (\(\{y_{iks}\}\), \(\{x_{iks, jt}\}\), \(\{z_{jt}\}\)) to describe the integer program of the RFLE.

  • For any facility \((i, k, s) \in {\mathcal {F}}\), variable \(y_{iks}\) indicates whether facility \(i \in F\) is leased for type \(k \in {\mathcal {L}}\) at time period \(s \in \{1, 2, \ldots , T\}\).

  • For any facility \((i, k, s) \in {\mathcal {F}}\), client \((j, t) \in D\), the variable \(x_{iks, jt}\) indicates whether client (j, t) is served by facility (i, k, s).

  • For any client \((j, t) \in {\mathcal {D}}\), the variable \(z_{jt}\) indicates whether client (j, t) is rejected to serve.

The RFLE can be formulated as the following integer program:

$$\begin{aligned} \mathrm{\min }&\sum \limits _{(i, k, s) \in {\mathcal {F}}} f_i^k y_{iks} + \sum \limits _{(i, k, s) \in {\mathcal {F}} : t \in I^k_s} \sum \limits _{(j, t) \in {\mathcal {D}}} c_{ij} x_{iks, jt} \nonumber \\ \mathrm{s.\ t.}&\sum \limits _{(i, k, s) \in {\mathcal {F}} : t \in I^k_s} x_{iks, jt} + z_{jt } \ge 1, \qquad \forall (j, t) \in {\mathcal {D}}, \nonumber \\&x_{iks, jt} \le y_{iks}, \qquad \qquad \qquad \qquad ~~~\forall (i, k, s) \in {\mathcal {F}}, (j, t) \in {\mathcal {D}}, \nonumber \\&\sum \limits _{(j, t) \in {\mathcal {D}}} z_{jt} \le q, \nonumber \\&x_{iks, jt}, y_{iks}, z_{jt} \in \{0, 1\}, \qquad \qquad ~~ \forall (i, k, s) \in {\mathcal {F}}, (j, t) \in {\mathcal {D}}. \end{aligned}$$
(1)

The objective function is composed of leasing cost and serving cost. The first constraints guarantee that a client \((j, t) \in {\mathcal {D}}\) is either served by a facility \((i, k, s) \in {\mathcal {F}}\) whose open interval contains t or rejected to serve. The second constraints guarantee that if a client \((j, t) \in {\mathcal {D}}\) is assigned to a facility \((i, k, s) \in {\mathcal {F}}\), then facility (i, k, s) must be leased. The third constraint guarantees that at most q clients can be rejected to serve (i.e., at least \(n-q\) clients must be served).

By relaxing all the variables, we obtain the following linear program relaxation.

$$\begin{aligned} \mathrm{\min }&\sum \limits _{(i, k, s) \in {\mathcal {F}}} f_i^k y_{iks} + \sum \limits _{(i, k, s) \in {\mathcal {F}} : t \in I^k_s} \sum \limits _{(j, t) \in {\mathcal {D}}} c_{ij} x_{iks, jt} \nonumber \\ \mathrm{s.\ t.}&\sum \limits _{(i, k, s) \in {\mathcal {F}} : t \in I^k_s} x_{iks, jt} + z_{jt } \ge 1, \qquad \forall (j, t) \in {\mathcal {D}}, \nonumber \\&x_{iks, jt} \le y_{iks}, \qquad \qquad \qquad \qquad ~~~\forall (i, k, s) \in {\mathcal {F}}, (j, t) \in {\mathcal {D}}, \nonumber \\&\sum \limits _{(j, t) \in {\mathcal {D}}} z_{jt} \le q, \nonumber \\&x_{iks, jt}, y_{iks}, z_{jt} \ge 0, \qquad \qquad \qquad ~~ \forall (i, k, s) \in {\mathcal {F}}, (j, t) \in {\mathcal {D}}. \end{aligned}$$
(2)

We remark that the above linear program relaxation has an unbounded integrality gap (cf. [5]).

Using the duality theory, we obtain the dual program of the RFLE.

$$\begin{aligned} \mathrm{\max }&\sum \limits _{(j, t) \in {\mathcal {D}}} \alpha _{jt} - q \gamma \nonumber \\ \mathrm{s. \ t.}&\sum \limits _{(j, t) \in {\mathcal {D}}} \beta _{iks, jt} \le f_i^k, ~~~~~ \forall (i, k, s) \in {\mathcal {F}}, \nonumber \\&\alpha _{jt} - \beta _{iks, jt} \le c_{ij}, \qquad \forall (i, k, s) \in {\mathcal {F}}, (j, t) \in {\mathcal {D}}, t \in I^k_s, \nonumber \\&\alpha _{jt} \le \gamma , \qquad \qquad \qquad ~~\forall (j, t) \in {\mathcal {D}}, \nonumber \\&\alpha _{jt}, \beta _{iks, jt}, \gamma \ge 0, \qquad ~~ \forall (i, k, s) \in {\mathcal {F}}, (j, t) \in {\mathcal {D}}. \end{aligned}$$
(3)

In program (3), the dual variable \(\alpha _{jt}\) can be viewed as the budget of client (j, t), and the dual variable \(\beta _{iks, jt}\) can be viewed as the contribution of client (j, t) to facility (i, k, s).

3 A preliminary primal–dual 6-approximation algorithm

In Sect. 3.1, we present a preliminary primal–dual approximation algorithm. We show that the algorithm is implementable in Sect. 3.2. We present the approximation ratio analysis in Sect. 3.3.

3.1 Our main algorithm

Let \({{\mathcal {I}}}{{\mathcal {N}}}\) denote an original instance of the RFLE. Recall that the linear program relaxation (2) has an unbounded integrality gap. Therefore, we cannot use it to design an LP-based algorithm of the RFLE. In order to obtain a linear program relaxation with a bounded integrality gap, we construct a modified instance \(\mathcal {IN^\prime }\) of the original instance \({{\mathcal {I}}}{{\mathcal {N}}}\) as follows. We guess a facility \((i^{\prime }, k^{\prime }, s^{\prime }) \in {\mathcal {F}}\) with the most expensive leasing cost \(f_{i^{\prime }}^{k^{\prime }}\) in the optimal solution of \({{\mathcal {I}}}{{\mathcal {N}}}\). We obtain \(\mathcal {IN^{\prime }}\) by setting the leasing cost of \((i^{\prime }, k^{\prime }, s^{\prime })\) to 0 and setting the leasing cost of any facility whose leasing cost is greater than \(f_{i^{\prime }}^{k^{\prime }}\) to \(\infty \). Note that for any facility \((i^{\prime }, k^{\prime }, s^{\prime \prime })\) with \(s^{\prime \prime } \ne s^{\prime }\), its leasing cost is still \(f_{i^{\prime }}^{k^{\prime }}\).

Now we are ready to give our preliminary algorithm which consists of two phases. In Phase 1, we construct a dual feasible solution of the instance \(\mathcal {IN^\prime }\). In Phase 2, we obtain an integer primal feasible solution of the original instance \({{\mathcal {I}}}{{\mathcal {N}}}\).

Algorithm 1

  1. Phase 1.

    Constructing a dual feasible solution of \({{\mathcal {I}}}{{\mathcal {N}}}^\prime \).

    1. Step 1.0.

      (Initialization.) Set \({\mathcal {T}} := \emptyset \), \(\mathcal {{\widetilde{D}}} := \emptyset \), \({\mathcal {O}} := {\mathcal {D}}\). For any \((j, t) \in {\mathcal {D}}\), set \(\alpha _{jt}:=0\). For any \((i, k, s) \in {\mathcal {F}}\), \((j, t) \in {\mathcal {D}}\) such that \(t \in I^k_s\), set \(\beta _{iks, jt} := \mathrm{max} \{\alpha _{jt} - c_{ij}, 0\}\). For any \((i, k, s) \in {\mathcal {F}}\), \((j, t) \in {\mathcal {D}}\) such that \(t \notin I^k_s\), set \(\beta _{iks, jt} :=0\). Set \(\gamma := 0\).

    2. Step 1.1.

      Increase the dual variables \(\alpha _{jt}\) associated with the clients \((j, t) \in {\mathcal {O}}\) and the dual variable \(\gamma \) uniformly until one of the following events happens.

      1. Event 1.

        There exist a facility \((i, k, s) \in {\mathcal {T}}\) and a client \((j, t) \in {\mathcal {O}}\), such that \(\alpha _{jt} = c_{ij}\) and \(t \in I^k_s\).

      2. Event 2.

        There exist a facility \((i, k, s) \in \mathcal {F {\setminus } T}\) such that the facility constraint becomes tight, namely, \(\sum _{(j, t) \in {\mathcal {D}}} \beta _{iks, jt} = f_i^k\).

      If Event 1 happens, stop increasing \(\alpha _{jt}\) of the client (j, t). Update \(\mathcal {{\widetilde{D}}}:=\mathcal {{\widetilde{D}}} \cup \{(j, t)\}\) and \({\mathcal {O}} := {\mathcal {O}} {\setminus } \{(j, t)\}\). We call facility (i, k, s) the connecting witness of (j, t). If Event 2 happens, we say that facility (i, k, s) is paid for and it is temporarily opened. Stop increasing \(\alpha _{jt}\) for any \((j, t) \in {\mathcal {O}}\) such that \(\beta _{iks, jt} > 0\). Define \(N_{(i, k, s)} = \{(j, t) \in {\mathcal {O}} : \beta _{iks, jt} > 0\}\). We call facility (i, k, s) the connecting witness of any client \((j, t) \in N_{(i, k, s)}\). Update \({\mathcal {T}}={\mathcal {T}} \cup \{(i, k, s)\}\), \(\mathcal {{\widetilde{D}}}:=\mathcal {{\widetilde{D}}} \cup N_{(i, k, s)}\) and \({\mathcal {O}} := {\mathcal {O}} {\setminus } N_{(i, k, s)}\). If multiple events happen simultaneously, we break ties arbitrarily.

    3. Step 1.2.

      If \(|{\mathcal {O}}|>q\), go to Step 1.1. Otherwise, stop increasing \(\gamma \) and stop Phase 1.

  2. Phase 2

    Constructing an integer primal feasible solution of \({{\mathcal {I}}}{{\mathcal {N}}}\).

    1. Step 2.1.

      Let facility \((i_f, k_f, s_f)\) denote the last temporarily opened facility. If \(|{\mathcal {O}}|=q\), go to Step 2.2. Otherwise, facility \((i_f, k_f, s_f)\) must be paid at the terminal time of Phase 1. Arbitrary select \(q - |{\mathcal {O}}|\) clients in \(N_{(i_f, k_f, s_f)}\). Let \({\mathcal {O}}_f\) be these clients. Update \(\mathcal {{\widetilde{D}}}:=\mathcal {{\widetilde{D}}} {\setminus } {\mathcal {O}}_f\) and \({\mathcal {O}} := {\mathcal {O}} \cup {\mathcal {O}}_f\).

    2. Step 2.2.

      We construct a graph G as follows. Every facility in \({\mathcal {T}}\) is a vertex in G. For any facility \((i, k, s) \in {\mathcal {F}}\) and any client \((j, t) \in {\mathcal {D}}\), if \(\beta _{iks, jt} > 0\), we say that client (j, t) contributes to facility (i, k, s). There is an edge between two vertices in G if there exists a client that contributes to both the corresponding facilities in \({\mathcal {T}}\).

    3. Step 2.3.

      Order the facilities in \({\mathcal {T}}\) according to non-increasing lease lengths. Then, find a maximal independent set of the vertices in G by greedily selecting the vertices in this order. Let \({\mathcal {I}} \subseteq {\mathcal {T}}\) denote the corresponding facility set of the maximal independent set.

    4. Step 2.4.

      For any facility \((i, k, s) \in {\mathcal {F}}\), we say that facilities (i, k, s), (i, k, \( \mathrm{max} \{s - l_k, 0\})\) and \((i, k, s+l_k)\) correspond to facility (i, k, s) and use \({\mathcal {F}}_{(i, k, s)}\) to denote them, i.e., \({\mathcal {F}}_{(i, k, s)}: = \{(i, k, s), (i, k, \mathrm{max}\{s-l_k, 0\}), (i\), \(k, s+l_k) \}\). For any facility \((i, k, s) \in {\mathcal {I}}\), we lease the facilities in \({\mathcal {F}}_{(i, k, s)}\). Let \(\mathcal {I^{\prime }}\) denote all the facilities that are leased in this step.

    5. Step 2.5.

      For any client \((j, t) \in \mathcal {{\widetilde{D}}}\), connect it to its closest facility \((i, k, s) \in \mathcal {I^\prime }\) such that \(t \in I^k_s\).

At the end of Phase 1, the produced dual solution is feasible for instance \(\mathcal {IN^\prime }\), since our dual ascending process does not violate any constraint of the dual program (3). At the end of Phase 2, \(\mathcal {I^{\prime }}\) is the open facility set, \(\mathcal {{\widetilde{D}}}\) is the served client set, and \({\mathcal {O}}\) is the rejected client set of cardinality q.

3.2 The analysis of the feasibility

An essential issue for Algorithm 1 is that we are not sure whether Step 2.5 can be successfully performed. In this subsection, we will give an answer for this.

According to the construction process of the facility set \(\mathcal {I^\prime }\), we have the following lemma.

Lemma 1

For any client \((j, t) \in \mathcal {{\widetilde{D}}}\), there must exist some facility \(({\bar{i}}, {\bar{k}}, {\bar{s}}) \in \mathcal {I^\prime }\) such that \(t \in I^{{\bar{k}}}_{{\bar{s}}}\).

Proof

For any client \((j, t) \in \mathcal {{\widetilde{D}}}\), its connecting witness (i, k, s) has the following two properties:

  1. (1)

    Facility (i, k, s) is temporarily opened in Phase 1 (i.e., \((i, k, s) \in {\mathcal {T}}\)).

  2. (2)

    Facility (i, k, s) is opened at the arrival time of client (j, t) (i.e., \(t \in I^k_s\)).

Note that the facility set \({\mathcal {T}}\) can be partitioned into sets \(\mathcal {T \cap I}\) and \(\mathcal {T {\setminus } I}\). We split our analysis of this lemma into two cases, a simple one when the connecting witness \((i, k, s) \in \mathcal {T\cap I}\) and a slightly more complicated one when \((i, k, s) \in \mathcal {T {\setminus } I}\).

  • Case 1 The connecting witness \((i, k, s) \in \mathcal {T\cap I}.\) If facility \((i, k, s) \in \mathcal {T \cap I}\), according to the construction process of the facility set \(\mathcal {I^{\prime }}\), we have that \((i, k, s) \in \mathcal {I^\prime }\). The proof is completed under this case, since (i, k, s) is a facility in \(\mathcal {I^\prime }\) such that \(t \in I^k_s\).

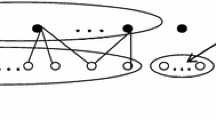
  • Case 2 The connecting witness \((i, k, s) \in \mathcal {T {\setminus } I}.\) In this case, there must exist a client \(({\tilde{j}}, {\tilde{t}}) \in {\widetilde{D}}\) that contributes to both facility (i, k, s) and some facility \(({\tilde{i}}, {\tilde{k}}, {\tilde{s}}) \in {\mathcal {I}}\) such that \(l_{{\tilde{k}}} \ge l_k\). Recall that

    $$\begin{aligned} {\mathcal {F}}_{({\tilde{i}}, {\tilde{k}}, {\tilde{s}})} = \{ ({\tilde{i}}, {\tilde{k}}, {\tilde{s}}), ({\tilde{i}}, {\tilde{k}}, \mathrm{max}\{{\tilde{s}} - l_{{\tilde{k}}}, 0\}), ({\tilde{i}}, {\tilde{k}}, {\tilde{s}}+l_{{\tilde{k}}}) \}. \end{aligned}$$

    We have the following claim. Claim If the connecting witness (i, k, s) of client (j, t) belongs to \(\mathcal {T {\setminus } I}\), then there must exist a facility in \({\mathcal {F}}_{({\tilde{i}}, {\tilde{k}}, {\tilde{s}})} (\subseteq {\mathcal {I}}^\prime )\), whose open interval contains t. For the sake of intuition, we illustrate the claim in Fig. 1. If the claim is true, it is obvious that our proof is completed under this case. Proof of Claim. Since client \(({\tilde{j}}, {\tilde{t}})\) contributes to both (i, k, s) and \(({\tilde{i}}, {\tilde{k}}, {\tilde{s}})\), we obtain that \({\tilde{t}} \in I^k_s\) and \({\tilde{t}} \in I^{{\tilde{k}}}_{{\tilde{s}}}\). Thus, \(I^k_s \cap I^{{\tilde{k}}}_{{\tilde{s}}} \ne \emptyset \). Combing with \(t \in I^k_s\) and \(l_{{\tilde{k}}} \ge l_k\), we have

    $$\begin{aligned} t \in I^k_s =[s, s+l_k) \subseteq [ \mathrm{max}\{{\tilde{s}} - l_{{\tilde{k}}}, 0\}, {\tilde{s}}+2l_{{\tilde{k}}})=I^{{\tilde{k}}}_{{\tilde{s}}}\cup I^{{\tilde{k}}}_{ \mathrm{max}\{{\tilde{s}} - l_{{\tilde{k}}}, 0\}} \cup I^{{\tilde{k}}}_{{\tilde{s}}+l_{{\tilde{k}}}}. \end{aligned}$$

    This completes the proof of this claim.

\(\square \)

Fig. 1
figure 1

Illustration of the claim

Full size image

Lemma 1 guarantees that Step 2.5 of Phase 2 in Algorithm 1 can be proceeded successfully. Thus, we can obtain an integer primal feasible solution of instance \({{\mathcal {I}}}{{\mathcal {N}}}\) from Algorithm 1.

3.3 The analysis of the approximation ratio

In this subsection, we analyze the approximation ratio of Algorithm 1. Let OPT denote the optimal solution cost of the original instance \({{\mathcal {I}}}{{\mathcal {N}}}\). We separate OPT into the most expensive leasing cost \(f_{i^\prime }^{k^\prime }\) and the rest cost of it. Let \(OPT^{\prime }\) denote the rest cost. We have \(OPT = f_{i^\prime }^{k^{\prime }} + OPT^{\prime } \).

For any client \((j, t) \in \mathcal {{\widetilde{D}}}\), if there exists some facility \((i, k, s) \in {\mathcal {I}}\) such that \(\beta _{iks, jt} > 0\), we call it a directly connected client and say that (j, t) is directly connected to facility (i, k, s). Note that a client in \(\mathcal {{\widetilde{D}}}\) can be directly connected to at most one facility in \({\mathcal {I}}\). Denote \(\mathcal {{\widetilde{D}}}_1\) as the set of directly connected clients. For any client \((j, t) \in \mathcal {{\widetilde{D}}}\), if there is no facility \((i, k, s) \in {\mathcal {I}}\) such that \(\beta _{iks, jt} > 0\), we call it an indirectly connected client. Denote \(\mathcal {{\widetilde{D}}}_2\) as the set of indirectly connected clients. If a client \((j, t) \in \mathcal {{\widetilde{D}}}_1\) and it is directly connected to facility \((i, k, s) \in {\mathcal {I}}\), let \(\alpha _{jt}^f = \alpha _{jt} - c_{ij}\) and \(\alpha _{jt}^s = c_{ij}\). If a client \((j, t) \in \mathcal {{\widetilde{D}}}_2\), let \(\alpha _{jt}^f = 0\) and \(\alpha _{jt}^s = \alpha _{jt}\). Note that we have \(\alpha _{jt} = \alpha _{jt}^f + \alpha _{jt}^s\) for any client \((j, t) \in \mathcal {{\widetilde{D}}}\).

Let C denote the serving cost of the clients in \(\mathcal {{\widetilde{D}}}\). The following lemma provides an upper bound of C.

Lemma 2

$$\begin{aligned} C \le 3 \sum \limits _{(j, t) \in \mathcal {{\widetilde{D}}}} \alpha _{jt}^s. \end{aligned}$$

Proof

Algorithm 1 shows that the serving cost C is associated with the client set \(\mathcal {{\widetilde{D}}}\). Note that \(\mathcal {{\widetilde{D}}}\) can be partitioned into sets \(\mathcal {{\widetilde{D}}}_1\) and \(\mathcal {{\widetilde{D}}}_2\). We can connect any client \((j, t) \in \mathcal {{\widetilde{D}}}\) to some facility in \(\mathcal {I^\prime }\) according to the following two cases.

  • Case 1 Client \((j, t) \in \mathcal {{\widetilde{D}}}_1\). In this case, there exists a facility \((i, k, s) \in {\mathcal {I}}\) for client (j, t) such that \(\beta _{iks, jt} > 0\). Note that facility (i, k, s) must belong to \({\mathcal {I}}^\prime \). We can connect client (j, t) to (i, k, s). The serving cost of (j, t) is \(c_{ij} = \alpha _{jt}^s\).

  • Case 2 Client \((j, t) \in \mathcal {{\widetilde{D}}}_2\). In this case, we will show that client (j, t) can be assigned to either its connecting witness or some facility that is related to its connecting witness. Assume that facility (i, k, s) is the connecting witness of client (j, t). Thus, we have \(c_{ij} = \alpha _{jt}\). If \((i, k, s) \in \mathcal {T \cap I} = {\mathcal {I}}\), it must belong to \({\mathcal {I}}^\prime \). We can connect client (j, t) to (i, k, s) and it will incur a serving cost of \(c_{ij} = \alpha _{jt} = \alpha _{jt}^s\). If \((i, k, s) \in \mathcal {T {\setminus } I}\), there must exist a client \(({\tilde{j}}, {\tilde{t}}) \in {\widetilde{D}}\) that contributes to both facility (i, k, s) and some facility \(({\tilde{i}}, {\tilde{k}}, {\tilde{s}}) \in {\mathcal {I}}\) such that \(l_{{\tilde{k}}} \ge l_k\). As we claimed in the proof of Lemma 1, client (j, t) can be connected to one of the three facilities that are leased corresponding to \(({\tilde{i}}, {\tilde{k}}, {\tilde{s}})\) (i.e., facilities \(({\tilde{i}}, {\tilde{k}}, {\tilde{s}})\), \(({\tilde{i}}, {\tilde{k}}, \mathrm{max}\{{\tilde{s}} - l_{{\tilde{k}}}, 0\})\) and \(({\tilde{i}}, {\tilde{k}}, {\tilde{s}}+l_{{\tilde{k}}}\))). The serving cost of (j, t) is \(c_{{\tilde{i}}j}\). Since client \(({\tilde{j}}, {\tilde{t}})\) contributes to both facility (i, k, s) and facility \(({\tilde{i}}, {\tilde{k}}, {\tilde{s}})\), we have \(c_{i{\tilde{j}}} \le \alpha _{{\tilde{j}}{\tilde{t}}}\) and \(c_{{\tilde{i}}{\tilde{j}}} \le \alpha _{{\tilde{j}}{\tilde{t}}}\). Let \(\gamma _{(i, k, s)}\) and \(\gamma _{({\tilde{i}}, {\tilde{k}}, {\tilde{s}})}\) be the value of \(\gamma \) when we temporarily open facility (i, k, s) and \(({\tilde{i}}, {\tilde{k}}, {\tilde{s}})\), respectively. We have that

    $$\begin{aligned} \alpha _{{\tilde{j}} {\tilde{t}}} \le \mathrm{min} \{\gamma _{(i, k, s)}, \gamma _{({\tilde{i}}, {\tilde{k}}, {\tilde{s}})}\} \le \gamma _{(i, k, s)} \le \alpha _{jt}. \end{aligned}$$

    Since the serving costs satisfy the triangle inequality (Fig. 2), we have

    $$\begin{aligned} c_{{\tilde{i}}j} \le c_{ij} + c_{i{\tilde{j}}} + c_{{\tilde{i}}{\tilde{j}}} \le \alpha _{jt} + 2 \alpha _{{\tilde{j}}{\tilde{t}}} \le 3 \alpha _{jt} = 3 \alpha _{jt}^s. \end{aligned}$$
Fig. 2
figure 2

Illustration of the serving cost of client \((j, t) \in \mathcal {{\widetilde{D}}}_2\)

Full size image

Combining the results of Cases 1 and 2, we complete the proof of this lemma. \(\square \)

Let \(\mathcal {{\widetilde{I}}}\) denote the facility set of \({\mathcal {I}} {\setminus } \{(i^\prime , k^\prime , s^\prime ), (i_f, k_f, s_f)\}\), where \((i^\prime , k^\prime , s^\prime )\) is the guessed facility with most expensive leasing cost and \((i_f, k_f, s_f)\) is the last temporarily opened facility. Let \(\bar{{\mathcal {I}}}\) be all the finally leased facilities which correspond to \(\mathcal {{\widetilde{I}}}\), i.e.,

$$\begin{aligned} \bar{{\mathcal {I}}} : = \bigcup \limits _{(i, k, s) \in \mathcal {{\widetilde{I}}}} {\mathcal {F}}_{(i, k, s)}. \end{aligned}$$

Denote F as the leasing cost of \(\bar{{\mathcal {I}}}\). The following lemma provides an upper bound of F.

Lemma 3

$$\begin{aligned} F \le 3 \sum \limits _{(j, t) \in \mathcal {{\widetilde{D}}}} \alpha _{jt}^f. \end{aligned}$$

Proof

It is clear that only the clients belong to \(\mathcal {{\widetilde{D}}}_1\) can contribute to the facilities in \(\widetilde{{\mathcal {I}}}\). For any facility \((i, k, s) \in \mathcal {{\widetilde{I}}}\), let \(N_{(i, k, s)}^{\mathrm{con}}\) be all the clients that contribute to (i, k, s) (i.e., \(N_{(i, k, s)}^{\mathrm{con}} := \{(j, t) \in \mathcal {{\widetilde{D}}}_1 : \beta _{iks, jt} > 0 \}\)). We have

$$\begin{aligned} \sum \limits _{(j, t) \in N_{(i, k, s)}^{\mathrm{con}}}\alpha _{jt}^f = \sum \limits _{(j, t) \in N_{(i, k, s)}^{\mathrm{con}}}(\alpha _{jt} - c_{ij}) = \sum \limits _{(j, t) \in N_{(i, k, s)}^{\mathrm{con}}} \beta _{iks, jt} =f_i^k. \end{aligned}$$

Note that any client \((j, t) \in \mathcal {{\widetilde{D}}}_1\) contributes to at most one facility in \(\mathcal {{\widetilde{I}}}\). It means that we have \( N_{(i_1, k_1, s_1)}^{\mathrm{con}} \cap N_{(i_2, k_2, s_2)}^{\mathrm{con}} = \emptyset \) for any \((i_1, k_1, s_1), (i_2, k_2, s_2) \in \mathcal {{\widetilde{I}}}\). Then we have

$$\begin{aligned} \sum \limits _{(i, k, s) \in \mathcal {{\widetilde{I}}}} f_i^k =\sum \limits _{(i, k, s) \in \mathcal {{\widetilde{I}}}} ~ \sum \limits _{(j, t) \in N_{(i, k, s)}^{\mathrm{con}}}\alpha _{jt}^f \le \sum \limits _{(j, t) \in \mathcal {{\widetilde{D}}}_1} \alpha _{jt}^f \le \sum \limits _{(j, t) \in \mathcal {{\widetilde{D}}}} \alpha _{jt}^f. \end{aligned}$$

Thus

$$\begin{aligned} F = \sum \limits _{(i, k, s) \in \bar{{\mathcal {I}}}} f_i^k = 3 \sum \limits _{(i, k, s) \in \mathcal {{\widetilde{I}}}} f_i^k \le 3 \sum \limits _{(j, t) \in \mathcal {{\widetilde{D}}}} \alpha _{jt}^f. \end{aligned}$$

\(\square \)

Now we are ready to give the main result of Algorithm 1.

Theorem 4

Algorithm 1 is a 6-approximation algorithm for the RFLE.

Proof

Combining Lemmas 2 and 3 together, we get

$$\begin{aligned} C + F \le 3 \sum \limits _{(j, t) \in \mathcal {{\widetilde{D}}}} \left( \alpha _{jt}^s + \alpha _{jt}^f \right) = 3 \sum \limits _{(j, t) \in \mathcal {{\widetilde{D}}}} \alpha _{jt}. \end{aligned}$$

Note that we have \(\alpha _{jt} = \gamma \) for any client \((j, t) \in \mathcal {{\widetilde{O}}}\), that \(|\mathcal {{\widetilde{O}}}|= q\), and that the optimal solution of instance \({{\mathcal {I}}}{{\mathcal {N}}}\) is feasible for the modified instance \({{\mathcal {I}}}{{\mathcal {N}}}^\prime \) with a cost of \(OPT^\prime =OPT-f_{i^\prime }^{k^\prime }\). We have

$$\begin{aligned} C + F\le & {} 3 \sum \limits _{(j, t) \in \mathcal {{\widetilde{D}}}} \alpha _{jt}\\= & {} 3\left( \sum \limits _{(j, t) \in {\mathcal {D}}} \alpha _{jt} - \sum \limits _{(j, t) \in \mathcal {{\widetilde{O}}}} \alpha _{jt} \right) \\= & {} 3 \left( \sum \limits _{(j, t) \in {\mathcal {D}}} \alpha _{jt} - q \gamma \right) \\\le & {} 3 OPT^{\prime }. \end{aligned}$$

Since the solution of Algorithm 1 may lease the kinds of facilities that are corresponding to facility \((i^\prime , k^\prime , s^\prime )\) or \((i_f, k_f, s_f)\) or both (i.e., maybe we have \((i^\prime , k^\prime , s^\prime ) \in {\mathcal {I}}\) or \((i_f, k_f, s_f) \in {\mathcal {I}}\) or both), the total cost of our solution is at most

$$\begin{aligned} C+F+3f_{i^\prime }^{k^\prime } + 3 f_{i_f}^{k_f} \le 3 OPT^{\prime } + 6 f_{i^\prime }^{k^\prime } \le 6 OPT. \end{aligned}$$

This completes the proof of this theorem. \(\square \)

4 A refined primal–dual 3-approximation algorithm

In this section, we propose a primal–dual 3-approximation algorithm for the RFLE by modifying Phase 2 of Algorithm 1 with a careful recognition on the leasing facilities.

Recall the definitions of \((i^\prime , k^\prime , s^\prime )\) and \((i_f, k_f, s_f)\) in Algorithm 1. Let \({\mathcal {F}}^\prime \) denote all the facilities that are corresponding to facility \((i^\prime , k^\prime , s^\prime )\) or facility \((i_f, k_f, s_f)\), i.e.,

$$\begin{aligned} {\mathcal {F}}^\prime : = {\mathcal {F}}_{(i^\prime , k^\prime , s^\prime )} \cup {\mathcal {F}}_{(i_f, k_f, s_f)}. \end{aligned}$$

One shortcoming of Algorithm 1 is that we may lease all the facilities in \({\mathcal {F}}^\prime \). Since there are six facilities in \({\mathcal {F}}^\prime \), the leasing cost of \({\mathcal {F}}^\prime \) is upper bounded by \(6 f_{i^\prime }^{k^\prime }\). In order to obtain a tighter upper bound, we carefully re-construct the maximal independent set which allows us to open only two facilities in \({\mathcal {F}}^\prime \). This refined construction results in the modification of Steps 2.2–2.4 of Algorithm 1. Using the same pre-process in Sect. 3, we construct the associated modified instance \({{\mathcal {I}}}{{\mathcal {N}}}^\prime \) for any given instance \({{\mathcal {I}}}{{\mathcal {N}}}\). We present our refined primal–dual algorithm as follows.

Algorithm 2

  1. Phase 1.

    Constructing a dual feasible solution of \({{\mathcal {I}}}{{\mathcal {N}}}^\prime \) (cf. Phase 1 in Algorithm 1).

  2. Phase 2.

    Constructing a integer primal feasible solution of \({{\mathcal {I}}}{{\mathcal {N}}}\).

    1. Step 2.1.

      Same as Step 2.1. in Algorithm 1.

    2. Step 2.2.

      We construct a graph G as follows. Let \({\mathcal {T}}^\prime \) denote the facility set of \({\mathcal {T}} {\setminus } \{(i^\prime , k^\prime , s^\prime ), (i_f, k_f, s_f)\}\). Every facility in \({\mathcal {T}}^\prime \) is a vertex in G. For any facility \((i, k, s) \in {\mathcal {F}}\) and any client \((j, t) \in {\mathcal {D}}\), if \(\beta _{iks, jt} > 0\), we say that client (j, t) contributes to facility (i, k, s). There is an edge between two vertices in G if there exists a client that contributes to both the corresponding facilities in \({\mathcal {T}}^\prime \).

    3. Step 2.3.

      Order the facilities in \({\mathcal {T}}^\prime \) according to non-increasing lease lengths. Then, find a maximal independent set of the vertices in G by greedily selecting the vertices in this order. Let \({\mathcal {I}} \subseteq {\mathcal {T}}^{\prime }\) denote the corresponding facilities of the maximal independent set.

    4. Step 2.4.

      For any facility \((i, k, s) \in {\mathcal {F}}\), we say that facilities (i, k, s), (i, k, \( \mathrm{max} \{s - l_k, 0\})\) and \((i, k, s+l_k)\) correspond to facility (i, k, s) and use \({\mathcal {F}}_{(i, k, s)}\) to denote them, i.e., \({\mathcal {F}}_{(i, k, s)}: = \{(i, k, s), (i, k, \mathrm{max}\{s-l_k, 0\}), (i\), \(k, s+l_k) \}\). For any facility \((i, k, s) \in {\mathcal {I}}\), we lease the facilities in \({\mathcal {F}}_{(i, k, s)}\). We also lease facility \((i^\prime , k^\prime , s^\prime )\) and facility \((i_f, k_f, s_f)\). Let \(\mathcal {I^{\prime }}\) denote all the facilities that are leased in this step.

    5. Step 2.5.

      Same as Step 2.5. in Algorithm 1.

Now we give the performance analysis of Algorithm 2 as follows.

Theorem 5

Algorithm 2 is a 3-approximation algorithm for the RFLE.

Proof

Note that Algorithm 2 is the same as Algorithm 1 before Step 2.2. Obviously, we have Lemmas 1–3 for Algorithm 2. Therefore, we obtain

$$\begin{aligned} C + F \le 3 OPT^{\prime }. \end{aligned}$$

Since facility \((i^\prime , k^\prime , s^\prime )\) and facility \((i_f, k_f, s_f)\) are leased in the produced solution of Algorithm 2, the total cost of the solution is at most

$$\begin{aligned} C+F+f_{i^\prime }^{k^\prime } + f_{i_f}^{k_f} \le 3 OPT^{\prime } + 2 f_{i^\prime }^{k^\prime } \le 3 OPT. \end{aligned}$$

This completes the proof of this theorem. \(\square \)

5 Discussions

In this paper, we study a new variant of the FLE, namely, the RFLE. By using the primal–dual technique, we propose two approximation algorithms for the RFLE. The first one has an approximation ratio of 6. We further improve the ratio to 3 by making some modifications of the first algorithm.

In the FLE, the number of time periods T and each subset of clients \(D_t \subseteq D\) that arrives at time period \(t \in \{1, 2, \ldots , T\}\) are given as input. In the online version of the FLE (OFLE), this information is unknown. The results for the OFLE are given in [11, 17]. In the future, we are interested in investigating the OFLE with outlier which includes two variants, the robust OFLE and the OFLE with penalties.