1 Introduction

The aim of this paper is to analyze the global exponential stability of the equilibrium points of a dynamical system described by variational inequalities. Such a system has numerous applications, in particular in the fields of mathematical programming, network economics, transportation research, and game theory [13, 18]. Furthermore, this system can also be seen as a mathematical model allowing to study important concepts as systems of nonlinear equations, necessary optimality conditions for optimization problems, complementarity problems, obstacle problems, network equilibrium problems (see, e. g., [2, 12]).

Many numerical methods have been proposed for solving variational inequality problems. The most well-known methods are the projection methods, the gap-function methods and the bundle methods [2, 13, 20]. In particular, the projection-type methods have been widely used. They are simple and efficient when the projection can be easily computed. This is the case for solving engineering applications such as signal processing, system identification and robot motion control [14, 27]. Often projection-type methods are combined with continuous dynamical systems based on circuit implementation [4, 21].

In recent years, dynamical systems have been widely investigated for solving linear and nonlinear variational inequalities with a particular attention to optimization problems [1, 5, 7, 8, 15, 16, 19, 22, 23, 26]. The global convergence and the global asymptotic stability of the trajectories generated by the dynamical systems can be obtained by imposing a monotonicity assumption on the corresponding operator [22, 23]. The global exponential stability of the trajectories, which is important for proving the convergence of a dynamical system, can also be deduced but under a strong monotonicity condition on the operator [1, 19, 24, 25]. Finally, let us mention that the global exponential stability implies the global asymptotic stability but not the converse.

Recently, Hu and Wang [6, 7] studied the convergence of the projected dynamical system proposed in [1, 19, 22, 25] for solving pseudomonotone variational inequalities with the consequence that they can extend the class of concerned convex optimization problems to the class of pseudoconvex optimization problems. They also prove the global convergence and the global asymptotic stability of the dynamical system under the assumption that the corresponding operator is pseudomonotone and Lipschitz continuous. However, to obtain the global exponential stability, Hu and Wang have to impose some restrictive conditions between the modulus of strong pseudomonotonicity and the modulus of Lipschitz continuity of the corresponding operator. These conditions are never satisfied for the class of strongly monotone and Lipschitz continuous variational inequalities (see Remark 2 below). Therefore, the global exponential stability obtained by Hu and Wang can be hardly used for extending the results proposed in [1, 19, 22, 25].

This paper provides two new contributions. The first one is the existence and uniqueness of the equilibrium point of the proposed dynamical system when the corresponding operator is strongly pseudomonotone and continuous. In that case, the existence assumption supposed to be satisfied in [6, 7] is no more necessary. In the second contribution, we establish the global exponential stability of the dynamical system without imposing any condition between the modulus of strong pseudomonotonicity and the modulus of Lipschitz continuity of the corresponding operator. Therefore, the results obtained in this paper improve and extend the results proposed in [1, 6, 7, 19, 22, 25] .

The remainder of the paper is organized as follows: in Sect. 2, we recall some preliminaries useful for establishing our main results. In Sect. 3, we first state the existence and uniqueness of the equilibrium point of the proposed dynamical system and then prove the global exponential convergence of the trajectory generated by this dynamical system. Some illustrative examples and numerical simulations are described in Sect. 4. Section 5 gives the conclusion of the paper.

2 Preliminaries

Let \(\varOmega \) be a nonempty closed convex subset of the Euclidean space \(\mathbb {R}^n\) and let \(F: \varOmega \rightarrow \mathbb {R}^n\) be a continuous operator. The problem of finding \(x^*\in \varOmega \) such that

$$\begin{aligned} (F(x^*))^{T} (x-x^*) \ge 0 \quad \forall x\in \varOmega , \end{aligned}$$

is called a variational inequality problem. We denote this problem by VI(\(F, \varOmega \)) and its solution set by Sol(\(F, \varOmega \)).

Very often one considers problem VI(\(F,\varOmega \)) with some additional properties imposed on the operator F such as Lipschitz continuity, monotonicity, strong monotonicity, pseudomonotonicity, and strong pseudomonotonicity. Let us recall here some well-known definitions (see, e.g., [9]).

Definition 1

The operator F is said to be

  1. (a)

    strongly monotone with modulus \(\gamma \) on \(\varOmega \) if there exists \(\gamma >0\) such that

    $$\begin{aligned} (F(x)-F(y))^{T} (x-y) \ge \gamma \,\Vert x-y\Vert ^2 \quad \forall x,y\in \varOmega ; \end{aligned}$$
  2. (b)

    monotone on \(\varOmega \) if

    $$\begin{aligned} (F(x)-F(y))^{T} (x-y) \ge 0 \quad \forall x,y\in \varOmega ; \end{aligned}$$
  3. (c)

    strongly pseudomonotone with modulus \(\gamma \) on \(\varOmega \) if there exists \(\gamma >0\) such that

    $$\begin{aligned} (F(x))^{T} (y-x) \ge 0 \; \Longrightarrow \; (F(y))^{T} (y-x) \ge \gamma \,\Vert x-y\Vert ^2 \end{aligned}$$

    for all \(x,y\in \varOmega \);

  4. (d)

    pseudomonotone on \(\varOmega \) if

    $$\begin{aligned} (F(x))^{T} (y-x) \ge 0 \; \Longrightarrow \; (F(y))^{T} (y-x) \ge 0 \end{aligned}$$

    for all \(x,y\in \varOmega \).

Remark 1

The implications (a) \(\Longrightarrow \) (b), (a) \(\Longrightarrow \) (c), (c) \(\Longrightarrow \) (d) and (b) \(\Longrightarrow \) (d) are evident.

Definition 2

The operator F is said to be Lipschitz continuous with modulus L on \(\varOmega \) if there exists a constant \(L>0\) such that

$$\begin{aligned} \Vert F(x)-F(y)\Vert \le L\, \Vert x-y\Vert \quad \forall x,y\in \varOmega . \end{aligned}$$

Remark 2

When the operator F is strongly monotone with modulus \(\gamma \) and Lipschitz continuous with modulus L, it follows from the Cauchy–Schwarz inequality that

$$\begin{aligned} \gamma \Vert x-y\Vert ^2\le & {} (F(x)-F(y))^T (x-y)\\\le & {} \Vert F(x)-F(y)\Vert \, \Vert x-y\Vert \\\le & {} L \Vert x-y\Vert ^2, \end{aligned}$$

which implies \(\gamma \le L\).

Next we recall the definition of the projection operator. Let \(\varOmega \) be a nonempty closed convex subset of \(\mathbb {R}^n\). Then, for each \(x\in \mathbb {R}^n\), there exists a unique point in \(\varOmega \), (see, e.g.,[12]), denoted by \(P_{\varOmega }(x)\), such that

$$\begin{aligned} \Vert x-P_{\varOmega }(x)\Vert \le \Vert x-y\Vert \quad \forall y\in \varOmega , \end{aligned}$$

where \(\Vert \cdot \Vert \) denotes the \(l_2\)-norm of \(\mathbb {R}^n\). Some well-known properties of the metric projection \(P_{\varOmega }:\mathbb {R}^n \rightarrow \varOmega \) are given in the following lemma.

Lemma 1

Assume that the set \(\varOmega \) is a nonempty closed convex subset of \(\mathbb {R}^n\). Then

  1. (a)

    \(P_{\varOmega }(\cdot )\) is a nonexpansive operator, i.e., for all \(x,y\in \mathbb {R}^n\), it holds

    $$\begin{aligned} \Vert P_{\varOmega }(x)-P_{\varOmega }(y)\Vert \le \Vert x-y\Vert ; \end{aligned}$$
  2. (b)

    For any \(x\in \mathbb {R}^n\) and \(y\in \varOmega \), it holds

    $$\begin{aligned} (x-P_{\varOmega }(x))^{T} (y-P_{\varOmega }(x)) \le 0. \end{aligned}$$

Proof

See [12]. \(\square \)

Remark 3

The operator \(P_{\varOmega }(\cdot )\) is Lipschitz continuous with Lipschitz modulus \(L=1\).

For solving problem VI(\(F, \varOmega \)), we consider the following projected dynamical system

$$\begin{aligned} \frac{dx}{dt}=\lambda \, \{-x +P_{\varOmega }(x-\alpha F(x))\}, \end{aligned}$$
(1)

where \(\lambda >0\) and \(\alpha >0\) are two scaling factors.

The dynamical system (1) was developed in [1, 19, 22] for solving monotone variational inequalities. In particular, it was proved that \(x^*\) is a solution of problem VI\((F,\varOmega )\) if and only if it is an equilibrium point of the dynamical system, i.e., if \(P_\varOmega (x^*-\alpha F(x^*))=x^*\).

The asymptotic stability of this dynamical system holds under conditions as the operator F is monotone and Lipschitz continuous with modulus L and \(\alpha <1/L\) [22]. When the monotonicity of F is replaced by the strong monotonicity, the dynamical system has global exponential stability provided that \(\alpha < 2\gamma / L^2 \) [1, 19]. The stable properties of this dynamical system have been recently extended by Hu and Wang [6] to the class of pseudomonotone variational inequalities with some additional assumptions on F. When the operator F is strongly pseudomonotone with modulus \(\gamma >0\) and Lipschitz continuous with modulus \(L>0\), it has been proved that this dynamical system is globally exponentially stable provided that it has an equilibrium point and that \(\gamma > 2L\). However, it follows from Remark 2 that the last inequality is never satisfied for the class of strongly monotone and Lipschitz continuous variational inequalities.

Remark 4

The explicit discretization of dynamical system (1) with respect to the time variable t, with step size \(h_n>0\) and initial point \(x_0 \in \mathbb {R}^n\), yields the following iterative scheme:

$$\begin{aligned} \frac{x_{n+1}-x_n}{h_n}=\lambda \, \{-x_n +P_{\varOmega }(x_n-\alpha F(x_n))\}. \end{aligned}$$

For \(h_n=1\), this becomes

$$\begin{aligned} x_{n+1}=(1-\lambda )\,x_n+\lambda P_{\varOmega }(x_n-\alpha F(x_n)), \end{aligned}$$

which is the relaxed projection method for solving variational inequalities with relaxation parameter \(\lambda \). It is known, at least in the situation \(\lambda =1\), that the iterative sequence generated by this algorithm converges linearly to a solution when F is strongly (pseudo)-monotone and Lipschitz continuous [2, 10].

3 Global exponential stability

It is known that \(x^*\) is a solution of problem VI(\(F, \varOmega \)) if and only if it is an equilibrium point of the dynamical system (1), see for example, [3, 22]. Moreover, it follows from Theorem 2.1 in [11] that if the operator F is continuous and strongly pseudomonotone, then problem VI(\(F, \varOmega \)) has a unique solution. The existence of solutions for strongly pseudomonotone continuous variational inequalities has also been recently established in the more general setting of equilibrium problems [17]. Therefore, as a consequence, we have:

Theorem 1

Suppose that the operator F is continuous and strongly pseudomonotone with modulus \(\gamma >0\) on a nonempty closed convex set \(\varOmega \). Then the variational inequality VI(\(F, \varOmega \)) has a unique solution which is the unique equilibrium point of the dynamical system (1).

We are now in a position to establish the global exponential stability of the dynamical system (1) without the restrictive assumption \(\gamma > 2L\) imposed in [6]. In that purpose, we first recall the stability concepts of an equilibrium point of the general dynamical system

$$\begin{aligned} \frac{dx}{dt} = f(x), \quad x \in \mathbb {R}^n \end{aligned}$$
(2)

where f is a continuous function from \(\mathbb {R}^n\) to \(\mathbb {R}^n\).

Definition 3

[19]

  1. (a)

    A point \(x^*\) is an equilibrium point for (2) if \(f(x^*)=0\);

  2. (b)

    An equilibrium point \(x^*\) of (2) is stable if, for any \(\epsilon >0\), there exists \(\delta >0\) such that, for every \(x_0 \in B(x^*, \delta ) \), the solution x(t) of the dynamical system with \(x(0)=x_0\) exists and is contained in \(B(x^*, \epsilon )\) for all \(t>0\), where \(B(x^*, r )\) denotes the open ball with center \(x^*\) and radius r;

  3. (c)

    A stable equilibrium point \(x^*\) of (2) is asymptotically stable if there exists \(\delta >0\) such that, for every solution x(t) with \(x(0) \in B(x^*, \delta )\), one has

    $$\begin{aligned} \lim _{t \rightarrow +\infty } x(t)=x^*; \end{aligned}$$
  4. (d)

    An equilibrium point \(x^*\) of (2) is exponentially stable if there exist \(\delta >0\) and constants \(\mu >0\) and \(\eta >0\) such that, for every solution x(t) with \(x(0) \in B(x^*, \delta )\), one has

    $$\begin{aligned} \Vert x(t) -x^* \Vert \le \mu \, \Vert x(0)-x^*\Vert \, e^{- \eta t} \quad \forall t \ge 0. \end{aligned}$$
    (3)

    Furthermore, \(x^*\) is globally exponentially stable if (3) holds true for all solutions x(t) of (2).

Theorem 2

Assume that the operator F is strongly pseudomonotone with modulus \(\gamma >0\) and Lipschitz continuous with modulus \(L>0\). Then the unique equilibrium solution of dynamical system (1) is globally exponentially stable when \(\alpha < 2\gamma /L^2\).

Proof

Under the assumptions made, it follows from Theorem 1 that problem VI(\(F, \varOmega \)) has a unique solution denoted \(x^*\). Setting \(y=P_{\varOmega }(x-\alpha F(x)) \) and replacing x by \(x-\alpha F(x)\) in Lemma 1(b) we have

$$\begin{aligned} (x-\alpha F(x)-y)^T (z-y)\le 0 \quad \forall z\in \varOmega . \end{aligned}$$

Substituting \(z=x^*\in \varOmega \) into the last inequality yields

$$\begin{aligned} (x-\alpha F(x)-y)^T (x^*- y) \le 0, \end{aligned}$$

or equivalently

$$\begin{aligned} (x-y)^T (x^*- y) \le \alpha (F(x))^T( x^*-y). \end{aligned}$$
(4)

On the other hand, since \(y=P_{\varOmega }(x-\alpha F(x)) \in \varOmega \) and \(x^*\) is the unique solution of problem VI(\(F, \varOmega \)), it holds that

$$\begin{aligned} (F(x^*))^T (y-x^*)\ge 0. \end{aligned}$$

Hence, by the strong pseudomonotonicity property of F we have

$$\begin{aligned} (F(y))^T(y-x^*)\ge \gamma \,\Vert y-x^*\Vert ^2. \end{aligned}$$

Using the Cauchy–Schwarz inequality, the strong pseudomonotonicity and the Lipschitz continuity of F, we obtain

$$\begin{aligned} 2\alpha (F(x) )^T(x^*-y)= & {} -2\alpha (F(y) )^T(y-x^*)+2\alpha (F(x) -F(y))^T(x^*-y) \nonumber \\\le & {} -2\alpha \gamma \Vert y-x^*\Vert ^2+2\alpha \Vert F(x)-F(y)\Vert \Vert y-x^*\Vert \nonumber \\\le & {} -2\alpha \gamma \Vert y-x^*\Vert ^2+2\alpha L\Vert x-y\Vert \Vert y-x^*\Vert \nonumber \\\le & {} -2\alpha \gamma \Vert y-x^*\Vert ^2+ \Vert x-y\Vert ^2+(\alpha L)^2\Vert y-x^*\Vert ^2. \end{aligned}$$
(5)

Combining (4) with (5) one has

$$\begin{aligned} 2(x-y)^T (x^*- y)\le & {} 2\alpha (F(x) )^T(x^*-y) \nonumber \\\le & {} -2\alpha \gamma \Vert y-x^*\Vert ^2+ \Vert x-y\Vert ^2+(\alpha L)^2\Vert y-x^*\Vert ^2. \end{aligned}$$
(6)

We note that \(2a^Tb=\Vert a\Vert ^2+\Vert b\Vert ^2-\Vert a-b\Vert ^2\) for all \(a,b\in \mathbb {R}^n\).

Substituting \(a=x-y\) and \(b=x^*-y\) into this inequality we obtain

$$\begin{aligned} 2(x-y)^T (x^*- y)= & {} \Vert x-y\Vert ^2+\Vert x^*-y\Vert ^2-\Vert (x-y)-(x^*-y)\Vert ^2 \nonumber \\= & {} \Vert y-x^*\Vert ^2+\Vert y-x\Vert ^2-\Vert x-x^*\Vert ^2. \end{aligned}$$
(7)

Then it follows from (6) and (7) that

$$\begin{aligned}&\Vert y-x^*\Vert ^2+\Vert y-x\Vert ^2-\Vert x-x^*\Vert ^2\\&\quad \le -2\alpha \gamma \Vert y-x^*\Vert ^2+ \Vert x-y\Vert ^2+(\alpha L)^2\Vert y-x^*\Vert ^2 \end{aligned}$$

or equivalently

$$\begin{aligned} (1+\alpha (2\gamma -\alpha L^2)) \Vert y-x^*\Vert ^2 \le \Vert x-x^*\Vert ^2. \end{aligned}$$
(8)

Since \(\alpha <2\gamma / L^2\) it holds \(1+\alpha (2\gamma -\alpha L^2)>1\). Thus, from (8), one has

$$\begin{aligned} \Vert y-x^*\Vert \le \frac{1}{\sqrt{1+\alpha (2\gamma -\alpha L^2)}}\, \Vert x-x^*\Vert . \end{aligned}$$
(9)

Consider the Lyapunov function

$$\begin{aligned} V(x(t))=\frac{1}{2}\,\Vert x(t)-x^*\Vert ^2 \quad \forall x(t) \in \varOmega . \end{aligned}$$

From (1), time derivative of V can be expressed as

$$\begin{aligned} \frac{dV}{dt}= & {} (x-x^*)^T\, \frac{dx}{dt} \\= & {} \lambda \left\{ (x-x^*)^T(y-x)\right\} \\= & {} \lambda \left\{ (x-x^*)^T(y-x^*)-\Vert x-x^*\Vert ^2\right\} . \end{aligned}$$

Therefore, it follows from the Cauchy–Schwarz inequality and (9) that

$$\begin{aligned} \frac{dV}{dt}\le & {} \lambda \, \left\{ \Vert x-x^*\Vert \Vert y-x^*\Vert -\Vert x-x^*\Vert ^2\right\} \\\le & {} \lambda \left[ \frac{1}{\sqrt{1+\alpha (2\gamma -\alpha L^2)}}-1 \right] \Vert x-x^*\Vert ^2 \\= & {} -\beta \Vert x-x^*\Vert ^2, \end{aligned}$$

where

$$\begin{aligned} \beta =\lambda \left[ 1-\frac{1}{\sqrt{1+\alpha (2\gamma -\alpha L^2)}}\right] >0. \end{aligned}$$
(10)

Therefore, for all \(t>0\), we have

$$\begin{aligned} \Vert x(t)-x^*\Vert \le \Vert x(0)-x^*\Vert \, e^{-\beta t}. \end{aligned}$$

This means that the equilibrium solution \(x^*\) of the dynamical system (1) is globally exponentially stable. \(\square \)

Remark 5

According to Theorem 2, the unique equilibrium point \(x^*\) is globally exponentially stable if parameter \(\alpha \) is small enough. Therefore, it is interesting to study the value of \(\alpha \) which maximizes the convergence rate of the trajectories. Considering \(\beta \) in (10) as a function of \(\alpha \in \left( 0,2\gamma /L^2 \right) \), we can see that the maximum convergence rate of the trajectory x(t) is

$$\begin{aligned} \beta ^*=\lambda \left[ 1-\frac{L}{\sqrt{L^2+\gamma ^2}}\right] , \end{aligned}$$

which is attained at \(\alpha =\alpha ^*=\gamma /L^2\).

As a consequence of Theorem 2, we have the following corollary:

Corollary 1

[19] Assume that the operator F is strongly monotone with modulus \(\gamma >0\) and Lipschitz continuous with modulus \(L>0\). Then the unique equilibrium solution of dynamical system (1) is globally exponentially stable when \(\alpha < 2\gamma /L^2\).

Remark 6

It should be mentioned that the result obtained in Theorem 2 extends the global exponential stability proposed in [19] for the class of strongly monotone variational inequalities to a broader class of variational inequalities, namely the class of strongly pseudomonotone variational inequalities.

4 Examples and numerical results

In this section, we give some examples to illustrate the effectiveness of the theoretical results presented above.

Example 1

Let \(\varOmega =[0,1]\) and \(F: \varOmega \rightarrow \mathbb {R}^n\) defined for all \(x \in \varOmega \) by \(F(x)=\frac{1}{1+x}\). First we prove that F is strongly pseudomonotone with modulus \(\gamma =\frac{1}{2}\) and Lipschitz continuous with modulus \(L=1\) on \(\varOmega \).

Indeed, suppose that, for \(x,y \in \varOmega \), we have \((F(x))^{T} (y-x) \ge 0\), then \( \frac{y-x}{1+x} \ge 0\), or equivalently \(y\ge x\). Since \(x,y \in \varOmega =[0,1]\), it holds

$$\begin{aligned} (y-x)(1+y)\le 2, \end{aligned}$$

which implies

$$\begin{aligned} \frac{1}{1+y}\ge \frac{1}{2}(y-x). \end{aligned}$$

Multiplying the last inequality by \(y-x\ge 0\), one has

$$\begin{aligned} \frac{1}{1+y}\,(y-x)\ge \frac{1}{2}\,\Vert y-x\Vert ^2. \end{aligned}$$

This means that

$$\begin{aligned} (F(y))^{T} (y-x) \ge \frac{1}{2}\,\Vert y-x\Vert ^2, \end{aligned}$$

i.e., F is strongly pseudomonotone with modulus \(\gamma =\frac{1}{2}\) on \(\varOmega \).

On the other hand

$$\begin{aligned} \Vert F(x)-F(y)\Vert= & {} \left\| \, \frac{1}{1+x}-\frac{1}{1+y} \,\right\| \\= & {} \left\| \,\frac{y-x}{(1+x)(1+y)} \,\right\| \\\le & {} \Vert x-y\Vert , \end{aligned}$$

which means that F is Lipschitz continuous with modulus \(L=1\) on \(\varOmega \).

It follows from Theorem 1 that the dynamical system (1) has a unique equilibrium point. It is easy to see that \(x^*=0\) is this point.

Note that F is neither monotone nor strongly monotone because

$$\begin{aligned} (F(x)-F(y))^{T} (x-y)= & {} \left( \frac{1}{1+x}-\frac{1}{1+y} \right) (x-y)\\= & {} \frac{-(x-y)^2}{(1+x)(1+y)} \le 0. \end{aligned}$$

According to Theorem 2, the trajectory of the dynamical system (1) always globally exponentially converges to the unique solution \(x^*=0\) when \(\alpha <1\).

The next example comes from [11].

Example 2

Let

$$\begin{aligned} \varOmega =\{x\in \mathbb {R}^{n}\, |\, \Vert x\Vert \le 5\} \quad \text{ and }\quad F(x)=(8-\Vert x\Vert )\,x \text{ for } \text{ all } x \in \varOmega . \end{aligned}$$

The operator F is both Lipschitz continuous and strongly pseudomonotone on \(\varOmega \). Indeed, for any \(x, y \in \varOmega \), we have

$$\begin{aligned} \Vert F(x)-F(y)\Vert= & {} \Vert (8-\Vert x\Vert )\,x-(8-\Vert y\Vert )\,y\Vert \\= & {} \Vert 8(x-y)-\Vert x\Vert (x-y)-(\Vert x\Vert -\Vert y\Vert )\,y\Vert \\\le & {} 8\Vert x-y\Vert +\Vert x\Vert \Vert x-y\Vert +|\Vert x\Vert -\Vert y\Vert |\,\Vert y\Vert \\\le & {} 8\Vert x-y\Vert +5\,\Vert x-y\Vert +5\,\Vert x-y\Vert \\= & {} 18\,\Vert x-y\Vert . \end{aligned}$$

Hence F is Lipschitz continuous on \(\varOmega \) with modulus \(L=18\). Suppose that \(x, y \in \varOmega \) are such that \((F(x))^T(y-x)\ge 0\), or equivalently

$$\begin{aligned} (8-\Vert x\Vert )\,x^T(y-x)\ge 0. \end{aligned}$$

This implies that \(x^T(y-x) \ge 0\) because \(\Vert x\Vert \le 5<8\). Observe that

$$\begin{aligned} (F(y))^T(y-x)= & {} (8 -\Vert y\Vert ) (y^T(y-x))\\\ge & {} (8 -\Vert y\Vert ) (y^T(y-x)-x^T(y-x) )\\= & {} (8 -\Vert y\Vert ) \Vert x-y\Vert ^2. \end{aligned}$$

Since \(\Vert y\Vert \le 5\), it holds that \(8 -\Vert y\Vert \ge 3\). This implies

$$\begin{aligned} (F(y))^T(y-x)\ge (8 -\Vert y\Vert ) \Vert x-y\Vert ^2 \ge 3 \Vert x-y\Vert ^2. \end{aligned}$$

Therefore F is strongly pseudomonotone on \(\varOmega \) with modulus \(\gamma =3\).

Moreover, F is neither strongly monotone nor monotone on \(\varOmega \). To see this, it suffices to choose

$$\begin{aligned} x=(4, 0, \ldots , 0),\ y=(5,0, \ldots ,0) \in \varOmega \end{aligned}$$

and note that

$$\begin{aligned} (F(x)-F(y))^T(x-y)= -1<0. \end{aligned}$$

It is easy to check that \(x^*=0\) is the unique solution of VI\((F,\varOmega )\). According to Theorem 2, the trajectory of dynamical system (1) always globally exponentially converges to the unique solution \(x^*=0\) when \(\alpha <\frac{2\gamma }{L^2}\).

The following example is due to Hu and Wang [6].

Example 3

Consider a two dimensional variational inequality \(VI(F,\varOmega )\) with a spherical constraint defined, for all \(x=(x_1,x_2)\), by

$$\begin{aligned} F(x)=\left( 0.5x_1x_2-2x_2-10^7, -4x_1+0.1x_2^2-10^7 \right) ^T, \end{aligned}$$

and

$$\begin{aligned} \varOmega =\{x\in \mathbb {R}^2\, |\, (x_1-2)^2+(x_2-2)^2 \le 1\}. \end{aligned}$$

This problem \(VI(F,\varOmega )\) has a unique solution \(x^*=(2.7071, 2.7071)^T\). Furthermore, F is not monotone and using a Monte Carlo approach, Hu and Wang [6] verified that F is strongly pseudomonotone with modulus \(\gamma =11\) and Lipschitz continuous with modulus \(L=5\). The numerical results have been displayed in [6] with some different starting points. According to Theorem 2, the trajectory of dynamical system (1) always globally exponentially converges to the unique solution \(x^*=(2.7071, 2.7071)^T\) when \(\alpha < 2\gamma /L^2\).

Remark 7

In Example 3, since \(\gamma >2L\), the theoretical results in [6] can be applied. However, in the first two examples, condition \(\gamma >2L\) is violated, therefore the global exponential stability of these examples cannot be guaranteed by the results established in [6].

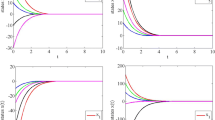
Next, we give the numerical results for the above examples. The codes are written in MATLAB and the experiments were performed in MATLAB version R2014b on a desktop Intel Core i7 with 8GB RAM. All the simulations confirm that the trajectory of dynamical systems (1) always globally exponentially converges to the unique solution \(x^*\) of the problem. For instance, in Figs. 1, 2 and 3, some results for Example 2 are displayed in various dimensional spaces with different initial points and parameters. For Example 3, we obtain the unique solution \(x^*=(2.7071, 2.7071)^T\) in one step even with different initial points and parameters.

Fig. 1
figure 1

The trajectory of dynamical system (1) in Example 2, when \(n=3, \lambda =1, \alpha =0.018\). On the left, \(x_0=(-\,2,1,3)^T\), on the right \(x_0=(4,-\,2,1)^T\)

Full size image
Fig. 2
figure 2

The trajectory of dynamical system (1) in Example 2, when \(n=5, \lambda =1, \alpha =0.015\). On the left, \(x_0=(1,-\,1,2,3,-\,2)^T\), on the right \(x_0=(-\,3,1,-\,2,3,-\,1)^T\)

Full size image
Fig. 3
figure 3

The trajectory of dynamical system (1) in Example 2, when \(n=10, \lambda =1, \alpha =\gamma /L^2\) and \(x_0=(-\,5,-\,4,-\,3,-\,2,-\,1,1,2,3,4,5)^T\)

Full size image

5 Conclusion

In this paper, we have further analyzed the global stability of a dynamical system for solving strongly pseudomonotone Lipschitz continuous variational inequalities considered in [1, 6, 19, 22]. The existence and uniqueness of the equilibrium points of these dynamical systems are stated. The global exponential stability of the trajectory is established without imposing restrictive conditions on the original data of the problem. Some examples are analyzed and numerical tests are given to illustrate the effectiveness of the theoretical results. It should be noticed that the results presented in this paper are still valid in infinite dimensional Hilbert space. Studying the global stability of this dynamical system without monotonicity assumption is an interesting subject for future research.