1 Introduction and motivation

The vehicle routing problem (VRP) is a well-studied problem [6, 10]. In its simplest form, it seeks to route a fleet of homogeneous vehicles to deliver identical packages from a depot to a number of customer locations while minimizing the total travel cost. Following recent advancements in drone technology, Amazon [2, 8], DHL [4], Federal Express [3], and other large companies with an interest in package delivery, have begun investigating the viability of incorporating drone delivery into their commercial package delivery services. Drone delivery (from trucks) would enable trucks to visit customers located centrally on the route and drones to visit farther-away customers. In other words, trucks would get “close enough” to more distant customers and then dispatch drones. Drone delivery could reduce the number of required trucks and drivers on the road. Perhaps more significantly, drones might speed up delivery.

In 2013, Jeff Bezos, CEO of Amazon, expressed his desire to use drones to offer delivery to Amazon’s elite customers within 30 min of ordering [9]. This is a primary motivation for our work. Given Amazon’s focus on speed of delivery, we think the most appropriate objective function here is to minimize the time until the last delivery. However, since all vehicles have to return to the depot, we seek to minimize the completion time. This is a good approximation to the time until last delivery when the last customer is close to the depot.

To date, there has been very little research on drone delivery of packages from trucks. Three recent papers are Murray and Chu [7], Agatz et al. [1], and Gambella et al. [5]. All of these focus on developing computational techniques (either exact or heuristic) for solving a variant of this problem. As far as we know, our paper is the first to study the problem from a worst-case point of view. Given the emerging status of drone and truck delivery technology, we think our results are especially valuable. They indicate, in a quantitative way, that the maximal potential savings relative to a traditional truck-based model to companies like Amazon and others are very substantial. Actualizing even a fraction of the maximal potential savings would likely justify the cost of adopting this technology.

2 Problem description

Suppose there are n customers to be served by a homogeneous fleet of m trucks, each carrying k drones. Every customer demands one parcel, which can be delivered by either a truck or a drone. There is no service time for a delivery. A truck has a capacity of C parcels. We make the following assumptions about the drone behaviors:

  1. A1.

    A drone can carry at most one parcel when airborne.

  2. A2.

    A drone has a battery life of U time units, which initially is arbitrarily large (the effect of a limited battery life on the worst-case ratio will be studied in a sequel paper).

  3. A3.

    The trucks and drones follow the same distance metric. More specifically, we assume that the truck and drone must travel from a to b along the street network. Restricting drones to travel along the street network is a natural initial assumption. Furthermore, in following the street network, drones will avoid obstacles and private airspace. (In a sequel paper, we will relax this assumption.)

  4. A4.

    Upon returning to the truck, the time required to prepare the drone for another launch with a new package and a fresh battery is negligible.

  5. A5.

    The speed of the drone is \(\alpha \) times the speed of the truck.

We make the following assumptions about the coordination between the truck and drones:

  1. A6.

    A drone launched from a truck must be picked up by the same truck.

  2. A7.

    The truck can dispatch and pick up a drone only at a node, i.e., the depot or a customer location. The truck can continue serving customers after a drone is dispatched and pick up the drone at, possibly, a different node.

  3. A8.

    The vehicle (truck or drone) that arrives at the pick-up node first has to wait for the other one.

The objective is to minimize the completion time, i.e., from the time the trucks are dispatched from the depot with the drones to the time when the last truck or the last drone returns to the depot.

We will refer to this new vehicle routing problem as the Vehicle Routing Problem with Drones, denoted by VRPD\(_{m,\alpha ,k}\), where m is the number of trucks in the fleet and \(\alpha \) is the ratio of the drone speed to the truck speed. Common notation used in the remainder of this paper is listed below:

  • Z(P): The optimal objective function value of problem P (e.g., VRPD\(_{m,\alpha ,k}\))

  • \(Z^f(P)\): The objective function value of a feasible solution f to the problem P (the feasible solution will be specified whenever the notation is used)

  • \(L_r\): The length of route r

  • \(T^{\text {veh}}_r\): The travel time by vehicle veh (veh = trc for truck, and veh = drn for drone) on route r

  • \(W^{\text {veh}}_r\): The waiting time by vehicle veh on route r

  • \(D^{\text {veh}}_r=T^{\text {veh}}_r+W^{\text {veh}}_r\): The duration of route r by vehicle veh.

The plan for the rest of the paper is as follows: In Sect. 3, we present the main results of our analysis. In Sect.  4, we present our conclusions and directions for future work. In a sequel paper, we will relax some of the model assumptions, explicitly consider limited battery life, different distance metrics for drones and trucks, and a general cost function. We will also explore the connection between the VRPD and some related problems.

3 Main results

Before a company like Amazon commits to a delivery strategy predicated on the utilization of drones, it might want to know the answer to a key question: At maximum, how much time could be saved, in the best case, using trucks and drones vs. using trucks only? If we look at this question from another angle, it becomes: How much longer will deliveries take with trucks only? This is commonly referred to as worst-case analysis.

In this section, our goal is to provide theoretical bounds on the benefit from using drones. In each of the theorems presented, we compare two related problems \(P_t\) and \(P_{td}\). The two problems have the same set of customers, but different fleets. In \(P_t\), the fleet consists of trucks only. In \(P_{td}\), the fleet consists of trucks and drones. The fleet in \(P_{td}\) can serve the customers faster (due to parallelization). That is, we expect \(Z(P_{td}) \le Z(P_t)\). We want to determine the lowest upper bound on the ratio \(\frac{Z(P_t)}{Z(P_{td})}\). For example, in the theorem below, we compare the VRPD\(_{1,1,k}\) with the TSP (traveling salesman problem), i.e., the problem of finding a min-cost closed tour that visits every node at least once.

Theorem 1

\(\frac{Z(\text {TSP})}{Z(\text {VRPD}_{1,1,k})}\le k+1\) and the bound is tight.

Remark 1

Theorem 1 is a special case of later theorems; nonetheless, we present a proof here because it serves as an easy-to-follow template for the other proofs. We remind the reader that k is the number of drones per truck throughout this paper.

Proof of Theorem 1

We start with the optimal VRPD\(_{1,1,k}\) solution, and construct a closed (not necessarily simple) walk of all the nodes. We then convert the closed walk to a feasible TSP solution with bounded duration.

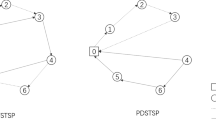
A VRPD\(_{1,1,k}\) solution can be decomposed into \(k+1\) routes: one truck route and k drone routes. Figures 1 and 2 illustrate the decomposition of a solution with \(k=2\). The square labeled 0 represents the depot and the eight circles labeled 1–8 represent the customers. The black line represents the path followed by the truck and the red and blue lines are paths followed by the two drones, respectively. The dashed red (or blue) lines are paths of the drone while in the air and the solid red (or blue) lines are paths of the drone while it is on the truck. Therefore, the red drone is launched from the truck at customer 1 to serve customer 2, and picked up at customer 5 where it is immediately launched again to serve customer 7. The red drone is finally picked up at customer 4 and returns to the depot with the truck. The blue drone is dispatched from the depot to serve customer 8 and picked up at customer 4. This VRPD solution can be decomposed into three routes as shown in Fig. 2c. The truck route is shown in Fig. 2a. Its duration is the sum of the travel time of cycle \(0\rightarrow 1\rightarrow 6\rightarrow 5\rightarrow 3\rightarrow 4 \rightarrow 0\) and the waiting time at customer 5. The red drone route is shown in Fig. 2b. Its duration is the sum of the travel time of cycle \(0\rightarrow 1\rightarrow 2\rightarrow 5\rightarrow 7\rightarrow 4 \rightarrow 0\) and the waiting time at customer 4. The blue drone route is shown in Fig. 2. Its duration is the sum of the travel time of cycle \(0 \rightarrow 8 \rightarrow 4 \rightarrow 0\) and the waiting time at customer 4. All three routes have the same duration, which is equal to the objective function value.

Fig. 1
figure 1

A VRPD\(_{1,1,k}\) solution with \(k=2\)

Full size image
Fig. 2
figure 2

Decomposition of a VRPD\(_{1,1,k}\) solution

Full size image

Given an optimal VRPD\(_{1,1,k}\) solution, we decompose it into \(k+1\) routes, and construct a giant route, denoted by R, that traverses the \(k+1\) routes, one after another. In the example shown in Fig. 1, the sequence that the nodes are traversed in R is \(0\rightarrow 1\rightarrow 6\rightarrow 5\rightarrow 3\rightarrow 4 \rightarrow 0\rightarrow 1\rightarrow 2\rightarrow 5\rightarrow 7\rightarrow 4 \rightarrow 0 \rightarrow 8 \rightarrow 4 \rightarrow 0\). Every node is visited at least once in R and some are visited multiple times. In particular, the depot is always visited \(k+2\) times, if we include both the start and the end of the route. We have the travel time of R,

$$\begin{aligned} T_R^{\text {trc}} \le D_R^{\text {trc}} = (k+1)Z(\text {VRPD}_{1,1,k}). \end{aligned}$$
(1)

A feasible TSP solution can be obtained from R by deleting repeated customers and keeping depots only at the beginning and the end. For the example shown in Fig. 1, the feasible TSP solution is \(0\rightarrow 1\rightarrow 6\rightarrow 5\rightarrow 3\rightarrow 4 \rightarrow 2\rightarrow 7 \rightarrow 8 \rightarrow 0\) as shown in Fig. 3. Since the optimal TSP solution visits every node at least once, we must have \(Z^f(\text {TSP}) \le T_R^{\text {trc}}\). Therefore,

$$\begin{aligned} Z(\text {TSP}) \le Z^f(\text {TSP}) \le (k+1)Z(\text {VRPD}_{1,1,k}) \end{aligned}$$
(2)

or

$$\begin{aligned} \frac{Z(\text {TSP})}{Z(\text {VRPD}_{1,1,k})} \le (k+1). \end{aligned}$$
(3)
Fig. 3
figure 3

A feasible TSP solution from the optimal VRPD solution

Full size image

To show that the bound is tight, we consider an example with \(k+1\) customers, \(c_0\), \(c_1\), \(\ldots \), \(c_k\). All customers are located at a distance 1 from the depot. The distance between every pair of customers is 2. (See Fig. 4a for the case with \(k=2\). The distances are given in parentheses next to the edges.) Both the truck and the drones travel at a speed of 1. The capacity of the truck \(C=k+1\). An optimal TSP solution visits the customers \(c_0\) to \(c_k\) in sequence, and \(Z(\text {TSP})=2(k+1)\) (see Fig. 4c). A feasible VRPD\(_{1,1,k}\) solution serves customer \(c_0\) with the truck and serves each of the remaining customers using a drone, which is launched at the depot and picked up at the depot. All vehicles return to the depot at the same time with \(Z^f(\text {VRPD}_{1,1,k})=2\) (see Fig. 4b). In this example,

$$\begin{aligned} \frac{Z(\text {TSP})}{Z(\text {VRPD}_{1,1,k})} \ge \frac{Z(\text {TSP})}{Z^f(\text {VRPD}_{1,1,k})} = \frac{2(k+1)}{2}=k+1. \end{aligned}$$
(4)

\(\square \)

Fig. 4
figure 4

A worst-case VRPD\(_{1,1,k}\) example with \(k=2\)

Full size image

Theorem 2 uses the same construction procedure as in Theorem 1 and generalizes Theorem 1.

Theorem 2

If \(\alpha \ge 1\), \(\frac{Z(\text {TSP})}{Z(\text {VRPD}_{1,\alpha ,k})}\le \alpha k+1\) and the bound is tight.

Proof of Theorem 2

Without loss of generality, we assume the truck speed is 1 and the drone speed is \(\alpha \) (since we are interested in only the ratio of the objective function values). As in our proof of Theorem 1, we decompose an optimal VRPD\(_{1,\alpha ,k}\) solution into \(k+1\) routes, denoted by \(r_0\), \(r_1\), \(\ldots \), \(r_k\), and traverse them one after another to form a giant route R. If R is traveled by the truck, the travel time

$$\begin{aligned} T^{\text {trc}}_R = \sum _{j=0}^k T^{\text {trc}}_{r_j} = T^{\text {trc}}_{r_0}+\sum _{j=1}^k \frac{L_{r_j}}{1} \le T^{\text {trc}}_{r_0}+\sum _{j=1}^k \alpha T ^{\text {drn}}_{r_j}. \end{aligned}$$
(5)

In Eq. (5), we have the length of a drone route \(L_{r_j} \le \alpha T_{r_j}^{\text {drn}}\), but not \(L_{r_j} = \alpha T_{r_j}^{\text {drn}}\), because some part of \(L_{r_j}\) might be traveled at the truck speed, which is not greater than the drone speed. After we remove the revisited customers and depots in the middle of R, we obtain \(Z^f(\text {TSP})\). This yields

$$\begin{aligned} Z(\text {TSP}) \le Z^f(\text {TSP}) \le T^{\text {trc}}_R \le T^{\text {trc}}_{r_0}+\sum _{j=1}^k \alpha T^{\text {drn}}_{r_j}. \end{aligned}$$
(6)

Therefore,

$$\begin{aligned} Z(\text {VRPD}_{1,\alpha ,k})&= \max \lbrace D^{\text {trc}}_{r_0}, D^{\text {drn}}_{r_1}, \dots , D^{\text {drn}}_{r_k}\rbrace \end{aligned}$$
(7)
$$\begin{aligned}&\ge \max \lbrace T^{\text {trc}}_{r_0}, T^{\text {drn}}_{r_1}, \dots , T^{\text {drn}}_{r_k}\rbrace \end{aligned}$$
(8)
$$\begin{aligned}&\ge \frac{1}{\alpha k+1}\left( T^{\text {trc}}_{r_0}+\sum _{j=1}^k \alpha T^{\text {drn}}_{r_j}\right) \end{aligned}$$
(9)
$$\begin{aligned}&\ge \frac{Z(\text {TSP})}{\alpha k+1}. \end{aligned}$$
(10)

Inequality (8) is valid because travel time on a route is never greater than the duration of the route. Inequality (9) is valid because the maximum is never less than any weighted average. Inequality (10) is due to inequality (6). Rearranging the terms, we have,

$$\begin{aligned} \frac{Z(\text {TSP})}{Z(\text {VRPD}_{1,\alpha ,k})}\le \alpha k+1. \end{aligned}$$
(11)

To show the tightness of the bound, we consider an example with \(k+1\) customers, \(c_0\), \(c_1\), \(\ldots \), \(c_k\). \(c_0\) is at a distance of 1 from the depot and \(c_j\), \(j>0\), is at a distance of \(\alpha \) from the depot. The distance between \(c_0\) and \(c_j\), \(j>0\), is \(1+\alpha \) and the distance between \(c_i\) and \(c_j\), \(i \ne j\) and \(i,j>0\), is \(2\alpha \). (An example with \(k=2\) is shown in Fig. 5.) The truck speed is 1 and the drone speed is \(\alpha \). The capacity of the truck \(C=k+1\). An optimal TSP solution serves \(c_0\) to \(c_k\) in sequence and \(Z(\text {TSP})=2\alpha k+2\). A feasible VRPD\(_{1,\alpha ,k}\) solution serves customer \(c_0\) with the truck and each of the other customers using a drone, which is launched at the depot and picked up at the depot. All vehicles return to the depot at the same time with \(Z^f(\text {VRPD}_{1,\alpha ,k})=2\). In this example,

$$\begin{aligned} \frac{Z(\text {TSP})}{Z(\text {VRPD}_{1,\alpha ,k})} \ge \frac{Z(\text {TSP})}{Z^f(\text {VRPD}_{1,\alpha ,k})} = \frac{2\alpha k+2}{2}=\alpha k+1. \end{aligned}$$
(12)

\(\square \)

Fig. 5
figure 5

A worst-case VRPD\(_{1,\alpha ,k}\) example with \(k=2\)

Full size image

Suppose the drone can travel \(50~\%\) faster than the truck and that the truck carries \(k=2\) drones. Then, Theorem 2 tells us that completion time can be up to 4 times as long without using drones as it is with drones. Based on this, it is easy to understand the widespread interest in drones for package delivery.

The next theorem does not involve drones in particular, but its proof uses the same approach as in the proofs of Theorems 1 and 2. We decompose an optimal VRPD solution into several routes and traverse them one after another to form a giant route R, from which we construct a feasible TSP solution with bounded objective value.

Theorem 3

Let n customers be served by a fleet of m trucks of different speeds, \(v_1\), \(v_2\), \(\ldots \), \(v_m\), such that the combined speed, \(V=\sum _{i=1}^m v_i\). Denote the optimal (min-max) objective function value by \(Z(\text {VRP*})\). If these customers are served by one truck with speed v and of sufficient capacity, the optimal objective function value is denoted by \(Z(\text {TSP}_v)\). We have

$$\begin{aligned} \frac{Z(\text {TSP}_v)}{Z(\text {VRP*})} \le \frac{V}{v} \end{aligned}$$

and the bound is tight.

Proof of Theorem 3

See “Proof of Theorem 3” in Appendix. \(\square \)

In view of Theorem 3, we have an alternate proof of the inequality in Theorem 2. There are two differences between VRPD\(_{1,\alpha ,k}\) and VRP*. First, in VRP*, there is no waiting time, but in VRPD\(_{1,\alpha ,k}\), duration is the sum of travel and waiting times. Second, in VRP*, every route i is traversed at a constant speed, \(v_i\), but in VRPD\(_{1,\alpha ,k}\), a drone route is traversed at the truck speed when the drone is on the truck and traversed at the drone speed when the drone is in the air. We introduce average speeds in looking at the optimal solution to the VRPD\(_{1,\alpha ,k}\) so that it can be converted into a feasible VRP* solution. The average speed on a route is the ratio of the route length to the route duration. The average speed of the truck route \(r_0\) is \(v_0 \le 1\) because of possible waiting time by the truck. (We normalize the vehicle speed so that the truck speed is always 1). The average speed on a drone route \(r_j\) is \(v_j \le \alpha \), \(j>0\), because of lower truck speed and possible waiting by the drone. Therefore, the optimal VRPD\(_{1,\alpha ,k}\) solution can be viewed as a feasible VRP* solution with a combined speed as defined in Theorem 3, \(V \le \alpha k+1\). Therefore,

$$\begin{aligned} \frac{Z(\text {TSP}_{v=1})}{Z(\text {VRPD}_{1,\alpha ,k})} = \frac{Z(\text {TSP}_{v=1})}{Z^f(\text {VRP*})} \le \frac{Z(\text {TSP}_{v=1})}{Z(\text {VRP*})} \le \alpha k+1. \end{aligned}$$
(13)

The worst-case example is the same as in the original proof (see Fig. 5).

We generally expect that the drone travels faster than the truck, i.e., \(\alpha > 1\), but we also consider the case in which drones travel slower, due to possible regulatory restrictions. Both the original and the alternate proof of Theorem 2 encounter difficulty if we relax the assumption \(\alpha \ge 1\) in Theorem 2. In the original proof, the inequality in (5) fails. In the alternate proof, the average speed of drone route \(r_j\), \(v_j, j>0\), may be greater than \(\alpha \), and, therefore, the combined speed, V, as defined in Theorem 3, may be greater than \(\alpha k+1\). Nevertheless, the worst-case bound still holds even if we drop the assumption \(\alpha \ge 1\), because of the following theorem.

Theorem 4

\(\frac{Z(\text {TSP})}{Z(\text {VRPD}_{1,\alpha ,k})}\le \alpha k+1\) and the bound is tight.

Proof of Theorem 4

We start with the truck route, denoted by \(r_0\), in the optimal VRPD\(_{1,\alpha ,k}\) and add customers served by the drones to form a feasible TSP solution.

We denote the duration of the truck route by \(D^{\text {trc}}_{r_0}\). (Note that \(D^{\text {trc}}_{r_0}=Z(\text {VRPD}_{1,\alpha ,k})\).) We add all the customers served by the first drone to \(r_0\). The goal is to show the increase in duration is not greater than \(\alpha D^{\text {trc}}_{r_0}\). Suppose customer k is served by the first drone that is dispatched at node i and picked up at node j. Denote, by \(D^{\text {trc}}_{ij}\), the time taken from the drone dispatchment at i to the truck’s arrival at j. Denote, by \(W^{\text {trc}}_j\), the possible waiting time of the truck at j. Denote the lengths from i to k and from k to j by \(L_{ik}\) and \(L_{kj}\), respectively. Let the possible waiting time of the drone at j be \(W^{\text {drn}}_j\). We must have

$$\begin{aligned} D^{\text {trc}}_{ij}+W^{\text {trc}}_j=\frac{L_{ik}+L_{kj}}{\alpha }+W^{\text {drn}}_j. \end{aligned}$$
(14)

Both sides of Eq. (14) measure the time elapsed from the launch of the drone to the pick-up of the drone. The left-hand side measures it from the perspective of the truck and the right-hand side measures it from the perspective of the drone. Rearranging Eq. (14), we have

$$\begin{aligned} L_{ik}+L_{kj}&=\alpha (D^{\text {trc}}_{ij}+W^{\text {trc}}_j-W^{\text {drn}}_j)\end{aligned}$$
(15)
$$\begin{aligned}&\le \alpha (D^{\text {trc}}_{ij}+W^{\text {trc}}_j). \end{aligned}$$
(16)

If \(L_{ik} \le L_{kj}\), we loop customer k at i to form part of the route \(i-k-i-\cdots -j\). We have the duration of this part of the route

$$\begin{aligned} 2L_{ik}+D^{\text {trc}}_{ij}+W^{\text {trc}}_j&\le (L_{ik}+L_{kj})+D^{\text {trc}}_{ij}+W^{\text {trc}}_j\end{aligned}$$
(17)
$$\begin{aligned}&\le \alpha (D^{\text {trc}}_{ij}+W^{\text {trc}}_j)+D^{\text {trc}}_{ij}+W^{\text {trc}}_j\end{aligned}$$
(18)
$$\begin{aligned}&= (1+\alpha )(D^{\text {trc}}_{ij}+W^{\text {trc}}_j). \end{aligned}$$
(19)

Inequality (17) is due to the assumption that \(L_{ik}\le L_{kj}\). Inequality (18) is due to inequality (16). From (19), the additional duration is bounded by \(\alpha (D^{\text {trc}}_{ij}+W^{\text {trc}}_j)\). If \(L_{ik} > L_{kj}\), we loop customer k at j to form the partial route \(i-\cdots -j-k-j\), and the argument is the same.

In Fig. 6a, we show a typical part of an optimal VRPD\(_{1,\alpha ,k}\) solution. The truck route is in black and the drone route is in red. At customer 1, the drone is launched to visit customer 8. At customer 4, the truck waits to pick up the drone, which is then launched at customer 5 to serve customer 6. The drone reaches and waits at customer 7, where it is picked up. In Fig. 6b, we show part of the intermediate route when customers 8 and 6, previously served by the drone, are added to the truck route. Since customer 1 is nearer than customer 4 to customer 8, we form a loop \(1\rightarrow 8\rightarrow 1\) around customer 1. Similarly, we loop customer 6 around customer 7, instead of customer 5. (After all drone customers, including those served by other drones, are inserted, we skip the revisited customers 1 and 7 to get part of the feasible TSP solution shown in Fig. 6c.)

Fig. 6
figure 6

Adding drone customers to truck route

Full size image

For a particular drone, there is no overlap of the truck path on which this drone is not with the truck. For example, in Fig. 6a, the path \(1 \rightarrow 2\rightarrow 3 \rightarrow 4\) and \(5\rightarrow 9\rightarrow 10\rightarrow 7\) do not overlap. Therefore, we can add all the customers served by a drone in the same manner such that the additional duration is bounded by \(\alpha D^{\text {trc}}_{r_0}\).

We then add the customers served by the second drone, and the third, and so on until the \(k{\text {th}}\) drone. Each time the increase in duration is bounded by \(\alpha D^{\text {trc}}_{r_0}\). After all customers served by the drones are added to the truck route, the duration is no greater than \((\alpha k+1)D^{\text {trc}}_{r_0}\). A feasible TSP solution is generated by removing all the truck-related waiting time and revisits to customers. The objective function value is also bounded by \((\alpha k+1)D^{\text {trc}}_{r_0}\) and we have shown that the inequality holds (recall that \(D^{trc}_{r_0} = Z(VRPD_{1,\alpha , k}))\).

To show the bound is tight, consider a VRPD\(_{1,\alpha ,k}\) with \(k+1\) customers. Customer \(c_0\) is located at a distance of 1 from the depot. Customers \(c_1\), \(c_2\), \(\ldots \), \(c_k\) are located at a distance of \(\alpha \) from the depot. The distances between \(c_0\) and \(c_j\), \(j>0\) are \(1+\alpha \). The distances between any two customers \(c_i\) and \(c_j\), \(i>0,j>0\), are \(2\alpha \). The speed of the truck is 1. An optimal TSP solution is to visit the customers in the sequence \(c_0\), \(c_1\), \(\dots \), \(c_k\), so \(Z(\text {TSP})=2(\alpha k+1)\). A feasible VRPD\(_{1,\alpha ,k}\) solution is to dispatch the k drones at the depot to serve customers \(c_1\) to \(c_k\), while the truck serves customer \(c_0\). All vehicles will return to the depot at the same time, after 2 time units. Therefore, \(Z^f(\text {VRPD}_{1,\alpha ,k})=2\). So \(\frac{Z(\text {TSP})}{Z(\text {VRPD}_{1,\alpha ,k})} \ge \frac{Z(\text {TSP})}{Z^f(\text {VRPD}_{1,\alpha ,k})}=\alpha k+1\). \(\square \)

We constructed different TSP solutions from the same optimal VRPD\(_{1,\alpha ,k}\) solution. We compare the construction using the example shown in Fig. 1. The giant route in the proofs of Theorems 1 and 2 and the intermediate route in the proof of Theorem 4 are shown in Fig. 7. The feasible TSP solutions are shown in Fig. 8.

Fig. 7
figure 7

Comparison of the intermediate routes in TSP route construction

Full size image
Fig. 8
figure 8

Comparison of the TSP solutions constructed in the proofs

Full size image

In the next theorem, we consider VRPD\(_{m,\alpha ,k}\) with m trucks, each carrying k drones.

Theorem 5

\(\frac{Z(\text {TSP})}{Z(\text {VRPD}_{m,\alpha ,k})}\le m(\alpha k+1)\) and the bound is tight.

Proof of Theorem 5

Given an optimal VRPD\(_{m,\alpha ,k}\) solution, we can decompose the problem into m subproblems. Let \(S_i\) be the set of customers served by either the \(i{\text {th}}\) truck or a drone on the \(i{\text {th}}\) truck. The \(i{\text {th}}\) subproblem is a VRPD\(_{1,\alpha ,k}\) on the set of customers \(S_i\). The optimal VRPD\(_{m,\alpha ,k}\) solution gives feasible solutions to all m subproblems. If we denote the TSP on \(S_i\) by TSP\(^{(i)}\), by Theorem 4, we have

$$\begin{aligned} Z(\text {TSP}^{(i)}) \le (\alpha k+1)Z(\text {VRPD}_{1,\alpha ,k}^{(i)}) \le (\alpha k+1)Z^f(\text {VRPD}_{1,\alpha ,k}^{(i)}). \end{aligned}$$
(20)

We join the TSP solutions to subproblems to form a giant route that serves all the customers and then we skip the visits to the depot in the middle of the route. The result is a feasible TSP solution over all the customers. Therefore,

$$\begin{aligned} Z(TSP)&\le \sum _{i=1}^m Z^f(TSP^{(i)})\end{aligned}$$
(21)
$$\begin{aligned}&\le \sum _{i=1}^m (\alpha k+1)Z^f(\text {VRPD}_{1,\alpha ,k}^{(i)})\end{aligned}$$
(22)
$$\begin{aligned}&\le (\alpha k+1) \sum _{i=1}^m Z(\text {VRPD}_{m,\alpha ,k})\end{aligned}$$
(23)
$$\begin{aligned}&= m(\alpha k+1)Z(\text {VRPD}_{m,\alpha ,k}). \end{aligned}$$
(24)

Inequality (21) holds because its right-hand side is the duration of a route that visits every customer exactly once and visits the depot \(m+1\) times. Inequality (22) holds because of inequality (20). Inequality (23) holds because \(Z(\text {VRPD}_{m,\alpha ,k})=\max _i\lbrace Z^f(\text {VRPD}^{(i)}_{1,\alpha ,k})\rbrace \).

Rearranging the terms, we prove the inequality in Theorem 5. To prove that the bound is tight, we consider a VRPD\(_{m,\alpha ,k}\) with \(m(k+1)\) customers, \(c_j^{(i)}\), where \(i \in I=\lbrace 1,2,\dots , m\rbrace \) and \(j \in J=\lbrace 0,1,\cdots ,k\rbrace \). The truck capacity is \(C=m(k+1)\) parcels. The speeds of the trucks and the drones are 1 and \(\alpha \), respectively. The distance metric is described below:

  • Distance between the depot and customer \(c_0^{(i)}\) is 1, \(\forall i\in I\)

  • Distance between the depot and customer \(c_j^{(i)}\) is \(\alpha \), \(\forall i \in I, \forall j \in J\backslash \lbrace 0\rbrace \)

  • Distance between customers \(c_0^{(i_1)}\) and \(c_0^{(i_2)}\) is 2, \(\forall i_1,i_2 \in I, i_1 \ne i_2\)

  • Distance between customers \(c_0^{(i_1)}\) and \(c_j^{(i_2)}\) is \(1+\alpha \), \(\forall i_1,i_2 \in I\) and \(\forall j \in J\backslash \lbrace 0\rbrace \)

  • Distance between customers \(c_{j_1}^{(i_1)}\) and \(c_{j_2}^{(i_2)}\) is \(2\alpha \), \(\forall i_1,i_2 \in I,\forall j_1,j_2 \in J\backslash \lbrace 0\rbrace , (i_1,j_1) \ne (i_2, j_2)\).

An example with \(m = 2\) and \(k = 2\) is illustrated in Fig. 9. The example is intentionally constructed as a symmetric example with perfect synchronicity between trucks and drones by placing “drone nodes” at distance \(\alpha \) and “truck nodes” at distance 1 from the depot. This allows for zero wait time, constant utilization of all vehicles, and knowledge that we are utilizing the most direct routes possible.

Fig. 9
figure 9

A worst-case VRPD\(_{m,\alpha ,k}\) example with \(k=2\)

Full size image

An optimal TSP solution has duration \(Z(\text {TSP})=2m(\alpha k+1)\). In fact, serving the customers in any sequence will result in duration of \(2m(\alpha k+1)\). A feasible VRPD\(_{m, \alpha ,k}\) solution dispatches all drones at the depot. The \(j{\text {th}}\) drone on the \(i{\text {th}}\) truck serves customer \(c_j^{(i)}\). The \(i{\text {th}}\) truck serves customer \(c_0^{(i)}\) on a dedicated route. All vehicles return to the depot at the same time and \(Z^f(\text {VRPD}_{m,\alpha ,k})=2\). Therefore, in this example, we have

$$\begin{aligned} \frac{Z(\text {TSP})}{Z(\text {VRPD}_{m,\alpha ,k})} \ge \frac{Z(\text {TSP})}{Z^f(\text {VRPD}_{m,\alpha ,k})}=\frac{2m(\alpha k+1)}{2}=m(\alpha k+1), \end{aligned}$$
(25)

which proves the bound in Theorem 5 is achieved and, therefore, tight. \(\square \)

In the next theorem, we compare the VRPD\(_{m,\alpha ,k}\) to the min-max VRP, denoted by VRP*, with a fleet of m trucks and no drones.

Theorem 6

\(\frac{Z(\text {VRP*})}{Z(\text {VRPD}_{m,\alpha ,k})}\le \alpha k+1\) and the bound is tight.

Proof of Theorem 6

The proof relies on the same decomposition used in the proof of Theorem 5. Denote the set of customers served by the \(i{\text {th}}\) truck or a drone on the \(i{\text {th}}\) truck by \(S_i\). The route in the optimal VRPD\(_{m,\alpha ,k}\) solution that serves customers in \(S_i\) is feasible to the subproblem VRPD\(^{(i)}_{1,\alpha , k}\). We denote the TSP on \(S_i\) by TSP\(^{(i)}\) and reproduce inequality (20) below.

$$\begin{aligned} Z(\text {TSP}^{(i)}) \le (\alpha k+1)Z^f(\text {VRPD}_{1,\alpha ,k}^{(i)}). \end{aligned}$$
(26)

The optimal objective function value of the min-max VRP is never greater than the maximum of the \(Z(\text {TSP}^{(i)})\)’s; otherwise we have a better VRP* solution consisting of the routes from the optimal TSP\(^{(i)}\) solutions.

$$\begin{aligned} Z(\text {VRP*})&\le \max \lbrace Z(\text {TSP}^{(1)}), Z(\text {TSP}^{(2)}), \ldots , Z(\text {TSP}^{(m)})\rbrace \end{aligned}$$
(27)
$$\begin{aligned}&\le (\alpha k+1) \max _i \lbrace Z^f(\text {VRPD}_{1,\alpha ,k}^{(i)})\rbrace \end{aligned}$$
(28)
$$\begin{aligned}&= (\alpha k+1) Z(\text {VRPD}_{m,\alpha ,k}). \end{aligned}$$
(29)

Rearranging the terms, we have the inequality in Theorem 6.

To show that the bound is tight, we consider the same example of \(m(k+1)\) customers as in the proof of Theorem 5. In the optimal VRP* solution, we serve the customers \(c_j^{(i)}\), \(\forall j \in J\), by the \(i{\text {th}}\) truck. All routes have the same duration and \(Z(\text {VRP*})=2(\alpha k+1)\) is the optimal objective function value because if \(Z(\text {VRP*})<2(\alpha k+1)\), we will have a TSP solution over all the \(m(k+1)\) customers and the depot with \(Z(\text {TSP})<2m(\alpha k+1)\). A feasible VRPD\(_{m,\alpha ,k}\) solution described in the proof of Theorem 5 has \(Z^f(\text {VRPD}_{m,\alpha ,k})=2\). Therefore, in this example,

$$\begin{aligned} \frac{Z(\text {VRP*})}{Z(\text {VRPD}_{m,\alpha ,k})} \ge \frac{Z(\text {VRP*})}{Z^f(\text {VRPD}_{m,\alpha ,k})}=\frac{2(\alpha k+1)}{2}=\alpha k+1. \end{aligned}$$
(30)

\(\square \)

The next theorem compares VRPD\(_{m,\alpha ,k}\) and VRPD\(_{m,\beta ,k}\), i.e., VRPD with different drone speeds. The idea is to address the following question: If a more advanced (and faster) set of drones becomes available, how much time can we save in delivering all packages?

Theorem 7

Let \(\alpha < \beta \). We have \(\frac{Z(\text {VRPD}_{m,\alpha ,k})}{Z(\text {VRPD}_{m,\beta ,k})} \le \frac{\beta }{\alpha }\) and the bound is tight.

To prove Theorem 7, we first define a regular feasible solution as one in which a truck leaves a pick-up node as soon as it picks up all the drones it must pick up at that node. We then introduce a lemma that is true for all regular feasible solutions of VRPD. Suppose an ant crawls onto the truck just before it is dispatched from the depot. The ant can crawl from a drone to the truck or from the truck to a drone, only when the drone is on the truck. It stays on one of the vehicles (the truck or a drone) until the fleet returns to the depot.

The duration of the route followed by the ant, i.e., the sum of the travel times on one or more vehicles plus the waiting times, is equal to the objective function value of the feasible solution because the ant starts its journey when the fleet leaves the depot and finishes its journey when all vehicles return to the depot.

Lemma 1

For every regular feasible solution to the VRPD, there is a strategy for the ant to always stay on a vehicle that is in motion.

Proof of Lemma 1

See “Proof of Lemma 1” in Appendix. \(\square \)

We illustrate the ant’s strategy using the example in Fig. 1. The truck returns to the depot with the two drones, so the ant stays on the truck on the last leg LG\(_{A_N,0}^{(N)}\). Tracing the truck route backwards, the first drone pick-up is at customer 4 (\(A_N=B_{N-1}=4\)), where the truck arrives after the two drones. The ant stays on the truck on the leg LG\(_{A_{N-1},4}^{(N-1)}\). Tracing the truck route backwards, the next pick-up is at 5 (\(A_{N-1}=B_{N-2}=5\)), where the red drone arrives last. The ant, therefore, stays on the red drone on the leg LG\(_{A_{N-2},5}^{(N-2)}\). This leg starts at 1 (\(A_{N-2}=B_{N-3}=1\)), where the red drone is dispatched. The ant stays on the truck on the leg LG\(_{A_{N-3},1}^{(N-3)}\). When we trace the truck route backwards from \(B_{N-3}=1\), we encounter the depot again, so \(A_{N-3}=0\) and \(N-3=1\). The ant route is \(0\text {(on the truck)} \rightarrow 1 \text {(crawls onto the red drone)} \rightarrow 2 \text {(on the red drone)} \rightarrow 5 \text {(crawls back onto the truck)} \rightarrow 3\text {(on the truck)} \rightarrow 4 \text {(on the truck)} \rightarrow 0(\text {on the } \text {truck)}\). There is no waiting time on this route. In addition, the ant route can be segmented according to the vehicle that the ant stays on. In the above example, the segments are \(0 \rightarrow 1\) on the truck, \(1 \rightarrow 2 \rightarrow 5\) on the drone, and \(5 \rightarrow 3 \rightarrow 4 \rightarrow 0\) on the truck.

With Lemma 1 proved, we now prove Theorem 7.

Proof of Theorem 7

We start with a fleet with only one truck with k drones and show first

$$\begin{aligned} \frac{Z(\text {VRPD}_{1,\alpha ,k})}{Z(\text {VRPD}_{1,\beta ,k})} \le \frac{\beta }{\alpha }. \end{aligned}$$
(31)

Suppose we have a regular optimal VRPD\(_{1, \beta ,k}\) solution. (A regular optimal solution always exists because we can dispatch the truck immediately after it picks up all the drones it is supposed to pick up at the node.) We construct a feasible VRPD\(_{1, \alpha ,k}\) solution by following the same routing plan, but serving the customers with the \(\alpha \) drones. It is possible that with the \(\beta \) drones, the truck is the last vehicle to arrive at a pick-up node, but now with the slower \(\alpha \) drones, a drone is the last vehicle to arrive at a pick-up node. Nevertheless, the solution is still regular. In this VRPD\(_{1,\alpha ,k}\) solution, there is a strategy for the ant to always stay on a moving vehicle by Lemma 1. The ant never waits, so its travel time is the duration of the ant route (\(R_\alpha \)), which is also the objective value of the solution to the VRPD\(_{1, \alpha ,k}\). The ant route can be partitioned into segments based on the vehicle the ant is on. On the other hand, if the ant chooses the same path (\(R_\beta \)) in the optimal VRPD\(_{1,\beta ,k}\) solution, there may be waiting times. The duration of \(R_\beta \) is equal to the optimal objective function value of the VRPD\(_{1,\beta ,k}\). \(R_\beta \) has the same length as \(R_\alpha \) but different duration because of shorter travel times and possible waiting times. \(R_\beta \) can be partitioned in exactly the same way as \(R_\alpha \). For every element of the partition, if the path is traveled with the truck speed, the travel time on that path in both the VRPD\(_{1, \alpha ,k}\) and VRPD\(_{1,\beta ,k}\) solutions are equal; if the path is traveled by the drone, the travel time of that path in the VRPD\(_{1,\alpha ,k}\) solution is no more than \(\frac{\beta }{\alpha }\) times the travel time of the path in the VRPD\(_{1, \beta ,k}\) solution. Therefore, the total travel time by the ant in the VRPD\(_{1,\alpha ,k}\) solution is no more than \(\frac{\beta }{\alpha }\) times the travel time in the VRPD\(_{1, \beta ,k}\) solution. Because of possible waiting times on route \(R_\beta \) and because there is no waiting time on route \(R_\alpha \), the duration of \(R_\alpha \) is no more than \(\frac{\beta }{\alpha }\) times the duration of \(R_\beta \). Hence, inequality (31) holds.

To generalize inequality (31) to problems with multiple trucks, we partition the VRPD\(_{m,\beta ,k}\) into m subproblems of VRPD\(_{1,\beta ,k}\) according to the optimal VRPD\(_{m,\beta ,k}\) solution. Let \(S_i\) be the set of customers served by either the \(i{\text {th}}\) truck or a drone on the \(i{\text {th}}\) truck. The problem of serving all customers in \(S_i\) using one truck and k \(\beta \) drones is the \(i\text {th}\) subproblem, denoted by VRPD\(_{1,\beta ,k}^{(i)}\). We assume the \(i{\text {th}}\) route in the optimal VRPD\(_{m,\beta ,k}\) solution also solves the subproblem VRPD\(^{(i)}_{1,\beta , k}\) optimally. (If not, we can always replace the \(i{\text {th}}\) route of the VRPD\(_{m,\beta ,k}\) solution with the optimal solution to the VRPD\(^{(i)}_{1,\beta , k}\) without increasing the objective function value of the VRPD\(_{m,\beta ,k}\) solution.) We solve the \(i{\text {th}}\) subproblem using the \(\alpha \) drones to obtain an optimal solution whose objective function value is denoted by \(Z(\text {VRPD}_{1,\alpha ,k}^{(i)})\). By inequality (31), we have

$$\begin{aligned} Z(\text {VRPD}_{1,\alpha ,k}^{(i)})&\le \frac{\beta }{\alpha } Z(\text {VRPD}_{1,\beta ,k}^{(i)})\end{aligned}$$
(32)
$$\begin{aligned} \max _{i}Z(\text {VRPD}_{1,\alpha ,k}^{(i)})&\le \frac{\beta }{\alpha } \max _{i}Z(\text {VRPD}_{1,\beta ,k}^{(i)})=\frac{\beta }{\alpha }Z (\text {VRPD}_{m,\beta ,k}). \end{aligned}$$
(33)

We put the optimal solutions to the m subproblems VRPD\(_{1,\alpha ,k}^{(i)}\) together to form a feasible solution to the VRPD\(_{m,\alpha ,k}\). This yields the desired inequality:

$$\begin{aligned} Z(\text {VRPD}_{m,\alpha ,k}) \le Z^f(\text {VRPD}_{m,\alpha ,k}) = \max _{i}Z(\text {VRPD}_{1,\alpha ,k}^{(i)}) \le \frac{\beta }{\alpha }Z (\text {VRPD}_{m,\beta ,k}).\nonumber \\ \end{aligned}$$
(34)

To show the bound is tight, we consider two cases. If \(1 \le \alpha < \beta \), let customer \(c_0\) be the only customer, which is at a distance of 1 from the depot. Since, the drones travel faster than the truck in both VRPD\(_{1,\alpha ,k}\) and VRPD\(_{1,\beta ,k}\), it is optimal to have a drone to serve \(c_0\). \(Z(\text {VRPD}_{1,\alpha ,k})=\frac{1}{\alpha }\) and \(Z(\text {VRPD}_{1,\beta ,k})=\frac{1}{\beta }\). Therefore, \(\frac{Z(\text {VRPD}_{1,\alpha ,k})}{Z(\text {VRPD}_{1,\beta ,k})} = \frac{\beta }{\alpha }\) in this example.

If \(\alpha < 1\), we consider an example with the number of drones per truck \(k \ge \frac{1}{\alpha }\). Let the number of customers be \(k+1\). Customer \(c_0\) is at a distance of 1 from the depot and customers \(c_1\) to \(c_k\) are at a distance of \(\beta \) from the depot. The distance between \(c_0\) and \(c_j\) with \(j>0\) is \(1+\beta \) and the distance between \(c_i\) and \(c_j\) with \(i,j>0\) is \(2\beta \). A feasible solution, denoted by \(S_\alpha \), to VRPD\(_{1,\alpha ,k}\) is to serve \(c_0\) by the truck and \(c_1\) to \(c_k\) by the drones. The objective function value of \(S_\alpha \) is \(\frac{2\beta }{\alpha }\). \(\frac{2\beta }{\alpha }\) is also a lower bound of all feasible solutions to VRPD\(_{1,\alpha ,k}\). If a customer \(c_j\) with \(j>0\) is served by a drone, it is on a route with duration at least \(\frac{2\beta }{\alpha }\). If all customers \(c_j\) with \(j>0\) are served by the truck, the duration of the truck route is at least \(2k\beta \ge \frac{2\beta }{\alpha }\). Therefore, \(S_\alpha \) is also the optimal solution and \(Z(\text {VRPD}_{1,\alpha ,k})=\frac{2\beta }{\alpha }\). A feasible solution to the VRPD\(_{1,\beta ,k}\) is to have the truck serving \(c_0\) and the drones serving \(c_j\) with \(j>0\) and the objective function value is \(Z^f(\text {VRPD}_{1,\beta ,k})=2\). Therefore, in this example,

$$\begin{aligned} \frac{Z(\text {VRPD}_{1,\alpha ,k})}{Z(\text {VRPD}_{1,\beta ,k})} \ge \frac{Z(\text {VRPD}_{1,\alpha ,k})}{Z^f(\text {VRPD}_{1,\beta ,k})}=\frac{\beta }{\alpha } \end{aligned}$$

\(\square \)

If we can replace our current set of drones with an advanced set of drones which travel twice as fast, we can reduce the delivery completion time by up to \(50~\%\).

4 Conclusions and future work

The idea of delivering packages by drones (launched from trucks) as well as directly from trucks, as is the common practice, is intriguing and is being seriously considered by numerous prominent companies in the U.S. and in Europe. There are, however, numerous technological and regulatory obstacles to overcome. In order for the commercialization of this idea to make sense, the potential savings in delivery completion time must be considerable.

After describing the VRPD and defining notation, we prove several worst-case theorems. Each result reveals the amount of time that could be saved, in the best case, as a result of using trucks and drones rather than trucks alone in delivering packages to customers. For example, suppose a drone travels \(50~\%\) faster than a truck, there are m trucks, and at most two drones per truck. Theorem 6 tells us that, in the best case, we can reduce delivery completion time by \(75~\%\).

In future work, we will present a number of interesting extensions and explore connections to related problems (e.g., the close enough VRP). There is also a need for smart exact and heuristic approaches to solve the VRPD and simulation studies that aim to determine the expected benefits of using drones and trucks to deliver packages rather than trucks alone.

Overall, we think the VRPD represents a very exciting new direction in logistics. We expect to see substantial progress on this problem in both the academic literature and in practice over the next decade. Furthermore, we expect the academic and practitioner communities to feed off of one another. What we have shown represent bounds on maximal savings. Further research could give us better indications of actual savings in real-life settings.