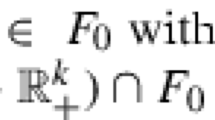An inexact restoration approach to optimization problems with multiobjective constraints under weighted-sum scalarization

Abstract

We apply a flexible inexact-restoration (IR) algorithm to optimization problems with multiobjective constraints under the weighted-sum scalarization approach. In IR methods each iteration has two phases. In the first phase one aims to improve the feasibility and, in the second phase, one minimizes a suitable objective function. We show that with the IR framework there is a natural way to explore the structure of the problem in both IR phases. Numerical experiments are conducted on Portfolio optimization, the Moré–Garbow–Hillstrom collection, and random fourth-degree polynomials, where we show the advantages of exploiting the structure of the problem.

1 Introduction

We consider the constrained optimization problem in the form:

$$\begin{aligned} \text{ min } f(x) \quad \text{ s.t. } \quad h(x) = 0, \quad x \in \Omega , \end{aligned}$$

(1)

where $\Omega \subset \mathbb {R}^n$ is a polytope, $f: \mathbb {R}^n \rightarrow \mathbb {R}$, $h: \mathbb {R}^n \rightarrow \mathbb {R}^m$ and both f and h have Lipschitz continuous gradients.

One goal of this paper is to demonstrate the practical efficiency of the Flexible Inexact Restoration algorithm introduced in [5]. In addition, we propose a way to minimize an objective function over the Pareto set of a multiobjective problem, which fits well with the case when the user already has a current decision. For this type of formulation we show that the Inexact Restoration approach has several advantages. Numerical tests concerning problems with this structure will be shown to elucidate both the applicability of IR methods in this situation as well as the gain in performance resulting from the innovations proposed in [5].

Let us define the Flexible Inexact Restoration algorithm. See [5] for details.

For all $x \in \Omega$ and $\lambda \in \mathbb {R}^m$, we define the Lagrangian $L(x, \lambda )$ by:

$$\begin{aligned} L(x, \lambda ) := f(x) + \sum _{i=1}^m \lambda _i h_i(x). \end{aligned}$$

Given a penalty parameter $\theta \in [0, 1]$, we consider, for all $x \in \Omega , \lambda \in \mathbb {R}^m$, the sharp Lagrangian merit function:

$$\begin{aligned} \Phi (x, \lambda , \theta ) := \theta L(x, \lambda ) + (1 - \theta ) \Vert h(x)\Vert , \end{aligned}$$

(2)

where $\Vert \cdot \Vert$ is the Euclidean norm.

Algorithm Flexible Inexact Restoration with sharp Lagrangian.

Step 0. Initialization

Set parameters $r\in [0,1[$ and $s\in [0,r]$. As initial approximation we choose, arbitrarily, $x^0 \in \Omega$ and $\lambda ^{0} \in \mathbb {R}^m$. We initialize $\theta _{-1} \in \; ]0, 1[$ and $k \leftarrow 0$.

Step 1. Restoration step

Compute $y^{k+1} \in \Omega$ such that:

$$\begin{aligned} \Vert h(y^{k+1})\Vert \le r \Vert h(x^k)\Vert . \end{aligned}$$

(3)

If this is not possible, the algorithm stops declaring a failure in the Restoration step.

Step 2. Estimation of Lagrange Multipliers

Compute $\lambda ^{k+1} \in \mathbb {R}^m$ as an approximation for the Lagrange multipliers associated with the constraints $h(x) = 0$.

Step 3. Descent direction

Compute the direction $d^k$ as the solution of the following problem:

$$\begin{aligned} \text{ min } \frac{1}{2} d^T H_k d + \nabla L(y^{k+1}, \lambda ^{k+1})^T d \end{aligned}$$

(4)

$$\begin{aligned} \text{ s.t. } \nabla h(y^{k+1})^T d = 0, \;\; y^{k+1} + d \in \Omega , \end{aligned}$$

(5)

where $H_k$ is an approximation to the Hessian of the Lagrangian.

Step 4. Globalization

Step 4.1 Penalty parameter computation

Compute $\theta _k$ as the supremum of the values of $\theta \in [0, \theta _{k-1}]$ such that

$$\begin{aligned} \Phi (y^{k+1}, \lambda ^{k+1}, \theta ) \le \Phi (x^k, \lambda ^{k}, \theta ) + \frac{1-s}{2}(\Vert h(y^{k+1})\Vert - \Vert h(x^k)\Vert ). \end{aligned}$$

(6)

Step 4.2. Line search

If $\Vert d^k\Vert =0$ we define $t_k := 1$.

Otherwise, compute $t_k \in ]0, 1]$, the largest number of the form $2^{-\ell }, \ell =0,1,\ldots$, such that

$$\begin{aligned} L(y^{k+1} + t_k d^k, \lambda ^{k+1}) < L(y^{k+1}, \lambda ^{k+1}) \end{aligned}$$

(7)

and

$$\begin{aligned} \Phi (y^{k+1} + t_k d^k, \lambda ^{k+1}, \theta _k) \le \Phi (x^k, \lambda ^{k}, \theta _k) + \frac{1-r}{2} (\Vert h(y^{k+1})\Vert - \Vert h(x^k)\Vert ). \end{aligned}$$

(8)

Step 4.3. Iteration update

Set

$$\begin{aligned} x^{k+1} = y^{k+1} + t_k d^k, \end{aligned}$$

(9)

update $k \leftarrow k+1$ and go to Step 1.

In [5] it was proved that, under reasonable assumptions, the algorithm is well defined and every limit point of a sequence $(x^k,\lambda ^k)$ generated by the Algorithm is a feasible Karush–Kuhn–Tucker pair of (1).

2 Application to optimization with multiobjective constraints under the weighted-sum scalarization

Inexact Restoration methods are useful in problems in which there is a natural way to deal with feasibility and optimality in different phases. This is the case of Bilevel Optimization problems [8], in which Restoration consists of minimizing a function of the state variables for fixed values of the controls [1, 20]. In this section we deal with Bilevel problems coming from the weighted-sum scalarization approach to Multiobjective Optimization. Given q functions $f_1, \ldots , f_q$, a set of constraints $h_i(x) = 0, i = 1, \ldots , p$ and a polytope $\Omega \subset \mathbb {R}^n$, we are interested in the multiobjective problem

$$\begin{aligned} \text{ Minimize } (f_1(x),\ldots ,f_q(x)) \quad \text{ subject } \text{ to } \quad h(x)=0,\quad x \in \Omega . \end{aligned}$$

(10)

There are some classical concepts of solution for multiobjective problems (e.g. see [17]). One of them states that a feasible point $x^*$ of a multiobjective problem is called a Pareto efficient solution, if there is no other feasible point x such that $f_i(x)\le f_i(x^*)$ for all $i=1,\ldots ,q$ and $f(x)\ne f(x^*)$. In this paper we deal with a weak notion of solution called weak Pareto efficiency, which states that there is no other feasible point x such that $f_i(x)<f_i(x^*)$ for all $i=1,\ldots ,q$. Given non-negative weights $w_i\ge 0, i=1,\ldots ,q$ with $\sum _{i=1}^qw_i=1$, we define Z(w) as the set of solutions of the weighted-sum scalarization

$$\begin{aligned} \text{ Minimize } \text{(with } \text{ respect } \text{ to } \text{ x) } \sum _{i=1}^q w_i f_i(x) \quad \text{ subject } \text{ to } \quad h(x)=0,\quad x \in \Omega . \end{aligned}$$

(11)

It can be shown that every solution in Z(w) is a weak Pareto efficient solution and that these notions coincide under convexity. See [17].

Given $x_c \in \mathbb {R}^n$, we are interested in the following problem:

$$\begin{aligned} \text{ Minimize } \Vert x - x_c\Vert ^2\quad \text{ subject } \text{ to } \quad x \in Z, \end{aligned}$$

(12)

where $Z = \bigcup \{Z(w) \;|\; w_i\ge 0, i=1,\ldots ,q \text{ and } \sum \nolimits _{i=1}^q w_i = 1\}$. Therefore, problem (12) is an instance of the problem of Optimization over a subset of the weak Pareto efficient set (see [4, 7, 26] and references therein). The objective function of (12) reflects the necessity of taking a decision x with minimal variation with respect to a possible previous decision $x_c$. For instance, if the goals of a portfolio program are to maximize profit and minimize variance it is natural to establish that the best multiobjective solution is the one that differs less from the present portfolio.

Note that if we choose positive weights $w_i>0, i=1,\ldots ,q$ with $\sum _{i=1}^qw_i=1$, solutions in Z(w) are true Pareto efficient solutions. In fact, it can be shown that, in this case, solutions in Z(w) are proper Pareto solutions, in the sense that the marginal gain in one criterion can not be made arbitrarily large relative to each of the marginal losses in other criteria. See [14, 16, 17]. Therefore, if we consider (12) with Z replaced by $\bigcup \{Z(w) \;|\; w_i\ge \varepsilon , i=1,\ldots ,q \text{ and } \sum _{i=1}^q w_i = 1\}$, where $\varepsilon >0$ is a small tolerance, we can recover proper Pareto solutions. We note that proper Pareto solutions and solutions of Z(w) with positive weights coincide under convexity [17]. Also, under suitable convexity and compacity assumptions, the set of proper Pareto solutions is dense in the set of Pareto solutions. See [3, 23].

We choose to search for weak Pareto solutions under the weighted-sum scalarization approach for simplicity, but many other scalarizations have been introduced for nonconvex problems [6, 9, 10, 22] and one could also consider them.

In order to develop an affordable algorithm for solving (12) we rely on Nonlinear Optimization approaches. Problem (12) may be expressed as a standard Nonlinear Programming problem replacing the constraint $x \in Z$ with the KKT conditions of the problem (11). However, the KKT conditions of (11) do not reflect accurately the constraint $x \in Z$. This constraint imposes that x must be a minimizer of problem (11), not merely a stationary point.

For simplicity, let us describe here the situation in which (11) is an unconstrained optimization problem. In this case, the Nonlinear Programming reformulation yields:

$$\begin{aligned} \text{ Minimize } \Vert x - x_c\Vert ^2 \quad \text{ subject } \text{ to } \; \sum _{i = 1}^q w_i \nabla f_i(x) = 0, \quad \sum _{i=1}^q w_i = 1, \quad \text{ and }\quad w \ge 0. \end{aligned}$$

(13)

Problem (13) is a standard constrained optimization problem with $n +q$ variables (x and w), $n + 1$ equality constraints, and bound constraints $w_i \ge 0, i = 1, \ldots , q$. The fulfillment of the constraints of (13) by a pair (x, w) is not sufficient to guarantee that $x \in Z(w)$, except in the case that all the functions are convex. Furthermore, non KKT points of (11) may be attractors for nonlinear programming softwares when solving (13). Consider, for example, that $n=q=1$ and $f_1(x) = \frac{3}{4}x^4-\frac{7}{3}x^3+\frac{5}{2}x^2.$ In this case $x^*=0$ is the only KKT point of (11), although $x=1$ is a local minimizer of the infeasibility measure $|f_1'(x)|$. For this reason we have that $x=1$ will be likely found by a standard nonlinear optimization method when solving (13) with an initial point close to $x=1$.

When dealing with the constrained case, the situation is even harder. One could have that a solution of problem (11) may not be a KKT point. Consider, for example, that $n=q=1$, $f_1(x) = x$, and $h(x)=x^2$. In this case $x^*=0$ is the solution of (11) but the feasible set of the reformulated problem is empty.

On the other hand, the Inexact Restoration approach seems to be adequate for these situations since, essentially, allows one to consider the problem (12) under a formulation that evokes more properly the essence of the problem:

$$\begin{aligned}&\text{ Minimize } \frac{1}{2}\Vert x-x_c\Vert ^2 \quad \text{ subject } \text{ to } \quad w_i \ge 0,\quad \sum _{i=1}^q w_i=1,\quad \text { and }\\&\quad x \text { is a minimizer of (11)}. \end{aligned}$$

Moreover, assuming that, given a set of weights $w_1, \ldots , w_q$, it is possible to minimize, approximately, $\sum _{i=1}^q w_i f_i(x)$, the Inexact Restoration necessarily finds a point that fulfills the L-AGP optimality condition [2], not requiring constraint qualifications at all. The objective of this paper is to show how these theoretical properties are reflected in practical computations.

In order to fully exploit the potentiality of IR we need to define the specific restoration procedure that we want to employ. The natural procedure is, given the (generally infeasible) current point $(x^k, w^k)$, to keep fixed $w^k$ and to obtain the restored point $y^{k+1}$ by inexact minimization of the weighted function $\sum _{i=1}^q w^k_i f_i(x)$.

Although the Restoration Phase of the IR algorithm involves only the variables x, the Optimality Phase involves both vectors of variables x and w. Moreover, even in the Optimality Phase, we are able to maintain the fulfillment of the constraints $\sum _{i=1}^q w_i = 1$ and $w \ge 0$ throughout the process by means of the following definition of the polytope $\Omega$ in (1):

$$\begin{aligned} \Omega = \left\{ (x, w) \in \mathbb {R}^{n+q} \;|\; \sum _{i=1}^q w_i = 1\quad \text{ and } \quad w \ge 0\right\} . \end{aligned}$$

As a consequence, in the Optimization Phase we will solve Quadratic Programming problems with the constraints defined by $\Omega$ and the tangent space (involving both variables x and w) to the manifold defined by $\sum _{i=1}^q w_i \nabla f_i(x) = \sum _{i=1}^q w^k_i \nabla f_i(x^k)$. Moreover, the presence of $\Omega$ as a constraint of all the Optimization Phases guarantees the strength of the condition L-AGP in this case.

In the numerical experiments we used three families of problems.

• 1. Portfolios: This family of problems is related to the well-known Mean-Variance problem in portfolio optimization. The investor aims to maximize return and to minimize the risk of the investment. In our simulation we used seven shares from the London exchange market: AZN.L, BARC.L, KGF.L, LLOY.L, MKS.L, TSCO.L and VOD.L, plus a risk-free asset. We consider scenarios using the historical data on daily returns from July 16 (2012) to October 10 (2012) available in [25]. The expected profit was defined as $f_1(x)=-v^Tx$ and, using the variance as a measure of the risk, we have that $f_2(x)= x^T M x$, where v is the expected return and M is the covariance matrix for the generated scenarios. Combining the data of these assets we can generate as many assets as desired. Therefore, we could address this problem using up to 1000 variables. The constraints of the multiobjective problem are $\sum _{i=1}^n x_i=1$ and $x_i \ge 0$ for all $i = 1, \ldots , n$. We defined the current decision $x_c$ as a random point that satisfies the constraints. Note that, in this case, (11) is a linearly constrained optimization problem. This means that the variables of the problem, as well as in the Optimization Phase of IR, are the primal variables x, the optimal weights w, and the Lagrange multipliers of (11).

• 2. MGH-generated problems: The MGH Collection of Moré et al. [21] was used to generate 120 different multiobjective problems. We used the functions 3, 4, 5, 9, 12, 14, 16, 18, 20, 21, 22, 23, 24, 25, 26, and 35 of this collection and, for each pair $(i, j) (i \ne j)$ of this set we defined the problem in which $f_1$ is the function i and $f_2$ is the function j. The number of variables n was defined to be the maximum of $n_i$ and $n_j$, where $n_i$ was the number of variables of the function i in the MGH collection and $n_j$ was the number of variables of the function j. In all the problems the domain was the box with bounds $-10$ and 10 and we defined $x_c = 0$.

• 3. Quartic polynomials: The third class of problems with multiobjective constraints consisted of considering two objectives where each one is a random fourth-degree polynomial in several variables. For simplicity, we considered only separable polynomials. The objective functions $f_1(x)$ and $f_2(x)$ were defined as

  $$\begin{aligned} f_i(x)= \sum _{j=1}^{n} a_{ij}x_j^4+b_{ij}x_j^3+ c_{ij}x_j^2+ d_{ij}x_j, \end{aligned}$$

  where $a_{ij}$ was random in [0, 10] and $b_{ij}, c_{ij}$, and $d_{ij}$ were randomly chosen in $[-10,10]$. The current decision $x_c$ was also random, with each coordinate between $-10$ and 10. We considered three instances of this problem, with $n \in \{1, 10, 20\}$ and 100 different problems in each case.

3 Implementation and numerical results

Our numerical tests were designed to check the effectiveness of the IR algorithms. More precisely, our tests are designed to corroborate (or not) that the IR framework provides a better alternative than the straightforward Nonlinear Programming approach for minimizing a function over the stationary points of the weighted-sum scalarization problem (11).

The code that implements IR was written in Fortran, employing double precision and the following computer environment: Intel(R) Core(TM) i5-2400 CPU @ 3.10 GHz with 4 GB of RAM memory. For solving the quadratic subproblems in the Optimization Phase we employed Fletcher’s subroutine qlcpd.f [12] and for Restoration steps we minimized the weighted-sum scalarization problem (11) using Fletcher’s filterSD.f. The problems (12) were solved using different Inexact Restoration instances and were also tackled using a consolidated Constrained Optimization code using the Nonlinear-Programming reformulation. For this purpose, we also employed Fletcher’s filterSD.f [12], which uses Sequential Linearly Constrained Programming with globalization provided by a Trust Region Filter scheme. Linearly Constrained subproblems are solved by glcpd.f, which is a limited memory spectral gradient method based on Ritz values. The subroutines qlcpd.f and filterSD.f were always used with their default parameters [12].

At each iteration of the IR algorithm, before the execution of Step 1, we test the stopping criteria

$$\begin{aligned} \Vert h(x^k)\Vert \le \varepsilon _{feas} \end{aligned}$$

(14)

and

$$\begin{aligned} \Vert P_{\Omega } (x^k - [\nabla f(x^k) + \nabla h(x^k) \lambda ^{k}]) - x^k\Vert \le \varepsilon _{opt}, \end{aligned}$$

(15)

where $P_{\Omega }$ is the Euclidean projection operator onto $\Omega$. In the experiments we used $\varepsilon _{feas} = \varepsilon _{opt} = 10^{-8}$. In the Initialization Step we chose $x^0=x_c$, $\lambda ^0=0$, and $\theta _{-1}=0.99$.

We tested four instances of the IR algorithm:

• FF: This version corresponds, essentially, to the the Fischer–Friedlander approach to Inexact Restoration [11]. The approximations to the Lagrange multipliers are all null, which means that the merit function is a nonsmooth penalty $\phi (x,\theta )= \theta f(x)+ (1-\theta ) \Vert h(x)\Vert$. The direction obtained in the optimization phase is the projection of the gradient on the tangent space, which correspond to set $H_k$ equal to the identity in (4) for all the iterations. We also enforce a 50% improvement in the feasibility phase and we set $r=s = 0.5$ for all k.

• Flex-FF: This is a flexible version of FF. In this version we still do not make use of the Lagrange multipliers and we choose the direction at the optimization phase as in the FF method. However we increase the chance of the optimization step to be accepted by choosing $r=0.99$ and taking $s=0$.

• Q-FF: In this version we use $\phi (x,\theta )= \theta f(x)+ (1-\theta ) \Vert h(x)\Vert$ as the merit function. On the other hand we use the Lagrange multipliers estimators to set $d^k$ as the solution of the quadratic problem (4)–(5) with $H_k=\nabla ^2 L(y^{k+1},{\lambda }^{k+1})$, where ${\lambda }^{k+1}$ is the vector of Lagrange multipliers of the subproblem solved at the previous Optimization Phase subproblem. We set $r=0.5$ and $s=0$.

• New IR: This is the complete version the flexible Algorithm. Here we use $r=0.5$, $s=0$, and we use the approximations of Lagrange multipliers both in the merit function as in the definition of the quadratic Hessian. In other words, we obtain the direction $d^k$ as the solution of the quadratic problem (4)–(5) with $H_k=\nabla ^2 L(y^{k+1},\lambda ^{k+1})$, and we use the sharp Lagrangian $\Phi (x, \lambda , \theta ) = \theta L(x, \lambda ) + (1 - \theta ) \Vert h(x)\Vert$ as the merit function.

The Nonlinear Programming reformulation of problem (12) consists of replacing the constraint that says that x minimizes $\sum _{i=1}^q w_if_i(x)$ with the KKT conditions of this problem. This approach will be denominated “KKT” form now on.

The results of the comparison of the IR approach against “KKT” are reported below. Note that this is not a comparison between IR and the Nonlinear Programming code described in [12] since, in fact, we used this Nonlinear Programming code, or a subroutine of it, both in our Restoration and in our Optimization Phase. It is a comparison between the approach that tries to solve (12) using the KKT conditions as constraints, without further information, and the IR algorithms that employ the minimization structure of those constraints.

• 1. Portfolios: All these problems were successfully solved both by the IR algorithms as by the Nonlinear Programming reformulation using $n \in \{8,100,1000\}$. The execution time for the two first cases was smaller than 1 s and for $n = 1000$ it was smaller than 1.5 s. This was expected due to convexity. Nevertheless, the running time for the IR approach is compatible with the KKT approach.

• 2. MGH-generated problems: In Fig. 1 we show the data profile for the MGH-generated problems. We note that by reformulating the lower level problem with its KKT conditions, only 45 % of the problems are solved, however, when the problem is solved, the computer time is much smaller than the one used by the IR algorithms. The original FF approach solves 85.8 % of the problems, while Flex-FF solves 79.17 %. Therefore, the strategy of accepting more steps aiming to avoid the Maratos effect, resulted in a weaker performance. On the other hand, the use of second order information and Lagrange multipliers in Q-Flex really improves the performance, increasing to 90.8 % the number of solved problems. The full IR version of the inexact restoration method including Lagrange multipliers at the merit functions performed best in this test by solving 92.5 % of the problems.

• 3. Quartic polynomials: We solved 100 problems for each value of $n \in \{1, 10, 20\}$. In all the 300 problems the IR algorithm found a Pareto point. However, using the KKT approach, we obtained Pareto points only in 87 problems with $n=1$, 16 problems with $n=10$ and none of the problems for $n=20$. This shows that the KKT reformulation approach can fail dramatically, while the IR approach finds a reasonable solution.

Fig. 1

Data profile for the 120 test problems based on the Moré-Garbow–Hillstrom test collection

4 Conclusions

Modern Inexact Restoration methods share the following characteristics:

• Very mild assumptions on the method are used for Restoration.

• Approximate minimization, on the tangent set, of a function that resembles the objective function restricted to the feasible region (the function itself, the Lagrangian, or their linear or quadratic approximations).

Different methods differ in two main aspects:

• Mechanism used to accept or reject trial points;

• Functions employed to compare a current iterate with a trial point.

With respect to the first item above we distinguish between methods that use trust regions, filters or line searches. The second item distinguishes between methods that use Lagrange multipliers in the comparison current-trial and those which rely only on functional and constraint values.

With these parameters we are able to construct the following table, where we classify the methods by Martínez and Pilotta [19], Martínez [18], Gonzaga, Karas and Vanti [15], Fischer and Friedlander [11] and the flexible method presented in [5].

Methods	Mechanism	Comparison current-trial
Martínez–Pilotta	Trust regions	Objective function and infeasibility
Martínez	Trust regions	Lagrangian and infeasibility
Gonzaga-Karas-Vanti	Filters	Objective function and infeasibility
Fischer–Friedlander	Line searches	Objective function and infeasibility
Flexible method	Line searches	Lagrangian and infeasibility

The methods of Fischer and Friedlander and the flexible one presented in [5] are, in principle, preferable over the ones of Martínez and Pilotta and Martínez because they allow one to truly prove boundedness of the penalty parameter. Boundedness arguments are also present in the other methods but only in proofs by contradiction. (In [18, 19] boundedness is proved under the false assumption of non-convergence. Therefore, the penalty parameters could be unbounded for these methods in the case of convergence). A boundedness proof for the methods given in [18] and [19] remains to be an open problem. Of course this question makes no sense in the case of filter-based methods.

Methods based on Lagrangians should be less prone to Maratos-like effects than methods based only on the true objective functions. Lagrangians on the tangent space are better representations of the objective function on the feasible region than the true objective function, a fact that leads one to conjecture that Newtonian methods based on Lagrangians share the non-Maratos properties of unconstrained Newton methods, for which the unitary step is always acceptable. However, the proof that the methods in which the merit function is the sharp Lagrangian are Maratos-free is still an open problem.

The Inexact Restoration framework fits well to problems that have some structure that can be explored in the Restoration and/or in the Optimization phase. We introduced a new approach to minimize a function over the Pareto set of a multiobjective problem, under the weighted-sum scalarization approach. Those problems have the appropriate structure to be solved with Inexact Restoration algorithms. We tested our algorithms using a set of problems that includes Portfolio Decisions, 120 problems derived from the MGH collection, and 300 fourth degree polynomial problems. The numerical results show that most theoretical improvements contribute to a better practical performance of the algorithm.

Future research will include the application of alternative IR approaches to wider families of multiobjective problems [24] and the application of the IR techniques introduced in this paper to minimization on the Pareto frontier using more sophisticated scalarizations [6, 9, 10, 22]. Moreover, restoration procedures not based on scalarizations [13] should also be analyzed from the point of view of Inexact Restoration.