1 Introduction

In a recent paper [1], we considered a binary mixture of gases in which the single constituents are non-dissipative gases (Eulerian gases) and we have studied the shock-structure profile. In particular, we have classified all possible regions of concentration and Mach number for which we can have sub-shocks formation. This paper aims to obtain results in a more realistic case where single constituents have dissipation. More specifically, we consider polyatomic gases in which the bulk viscosity is dominant, and we can neglect the shear viscosity and heat conductivity. For this kind of mixture, we use the simple model in the framework of Rational Extended Thermodynamics (RET) proposed by Arima, Ruggeri, Sugiyama, and Taniguchi [2] (see also [3]).

The main aim of this paper is to give a study to evaluate dissipation’s effects by comparing the profile of shock waves and sub-shocks with the ones obtained in a mixture of Eulerian fluids for some possible kinds of mixtures and some Mach numbers.

2 Model of a binary mixture of RET\(_6\) gases

In [4,5,6], a hyperbolic model for a single fluid with 6 fields (RET\(_6\)) was proposed in the framework of RET, considering only the dynamical pressure as a dissipative mechanism and the shear viscosity and the heat conductivity are neglected. This simplified theory preserves the main physical properties of the more complex theory of 14 variables [7], in particular when the bulk viscosity plays a more important role than the shear viscosity and the heat conductivity. This situation is observed in many gases. In fact, the usefulness of the RET\(_6\) theory is shown through the analysis of the ultrasonic sounds in a hydrogen gas [8] and the shock structure in a carbon dioxide gas [9, 10] (see the book [11] for more details).

Starting from this model, in the paper [2], a model for a mixture in which each component is this kind of gas was proposed. In the case of a binary mixture and one-space dimension reads:Footnote 1

$$\begin{aligned}&\frac{\partial \rho _1 }{\partial t} + \frac{\partial \rho _1 v_1 }{\partial x} = 0, \nonumber \\&\frac{\partial \rho _1 v_1 }{\partial t}+ \frac{\partial }{\partial x} \left\{ \rho _1 v^2_1 + p_1 + \Pi _1 \right\} = {\hat{m}}_1,\nonumber \\&\frac{\partial }{\partial t} \left( \rho _1 v^2_1 + 2 \rho _1 \varepsilon _1 \right) + \frac{\partial }{\partial x}\left\{ \left[ \rho _1 v^2_1 + 2\rho _1 \varepsilon _1 + 2 p_1 + 2\Pi _1 \right] v_1 \right\} = 2({\hat{e}}_1 + {\hat{m}}_1 v), \nonumber \\&\frac{\partial }{\partial t}\left\{ \rho _1 v_1^2 + 3(p_1 +\Pi _1 )\right\} + \frac{\partial }{\partial x}\left\{ \left[ \rho _1 v_1^2 + 5 (p_1 +\Pi _1 )\right] v_1 \right\} = - \frac{3 \Pi _1}{\tau _1} + 2 ({\hat{\omega }}_1 + {\hat{m}}_1 v), \nonumber \\&\frac{\partial \rho _2 }{\partial t} + \frac{\partial \rho _2 v_2 }{\partial x} = 0, \nonumber \\&\frac{\partial \rho _2 v_2 }{\partial t}+ \frac{\partial }{\partial x} \left\{ \rho _2 v^2_2 + p_2 + \Pi _2 \right\} = -{\hat{m}}_1, \nonumber \\&\frac{\partial }{\partial t} \left( \rho _2 v^2_2 + 2 \rho _2 \varepsilon _2 \right) + \frac{\partial }{\partial x}\left\{ \left[ \rho _2 v^2_2 + 2\rho _2 \varepsilon _2 + 2 p_2 + 2\Pi _2 \right] v_2 \right\} = -2({\hat{e}}_1 + {\hat{m}}_1 v), \nonumber \\&\frac{\partial }{\partial t}\left\{ \rho _2 v_2^2 + 3(p_2 +\Pi _2 )\right\} + \frac{\partial }{\partial x}\left\{ \left[ \rho _2 v_2^2 + 5 (p_2 +\Pi _2 )\right] v_2 \right\} = - \frac{3 \Pi _2}{\tau _2} -2 ({\hat{\omega }}_1 + {\hat{m}}_1 v), \end{aligned}$$
(1)

where the quantities with suffix \(\alpha \) \((= 1, 2)\) represent the corresponding quantities for the constituent \(\alpha \): \(\rho _\alpha \), \(v_\alpha \), \(p_\alpha \), \(\varepsilon _\alpha \), and \(\Pi _\alpha \) are, respectively, the mass density, the velocity, the pressure, the specific internal energy, and the dynamical non-equilibrium pressure. On the right-hand side, \(\tau _\alpha \) is the relaxation time for the dynamic pressure and the production terms, \({\hat{m}}_\alpha \), \({\hat{e}}_\alpha \), and \({\hat{\omega }}_\alpha \) represent the production terms evaluated for zero velocity due to the interchange of the momentum, the energy, and the momentum flux, respectively with the condition: \({\hat{m}}_2=-{\hat{m}}_1\), \({\hat{e}}_2=-{\hat{e}}_1\), \({\hat{\omega }}_2=-{\hat{\omega }}_1\) in such way for the the whole mixture is conserved mass, momentum and energy.

We consider a mixture of rarefied polyatomic gases described by the following thermal and caloric equations of state:

$$\begin{aligned} p_{\alpha } = \rho _{\alpha } \frac{k_B}{m_{\alpha }}T_{\alpha }, \quad \varepsilon _{\alpha } = \frac{D_{\alpha }}{2}\frac{k_B}{m_{\alpha }} T_{\alpha }, \end{aligned}$$
(2)

where \(T_{\alpha }\), \(k_B\), \(m_\alpha \), and \(D_\alpha \) are, respectively, the temperature, the Boltzmann constant, the mass of a molecule, and the degrees of freedom of a molecule. In the present analysis, we consider polytropic gases in which the specific heat is independent of the temperature, and therefore the degrees of freedom of a molecule \(D_\alpha \) is a constant. We recall that the ratio of the specific heats \(\gamma _\alpha \) is related to \(D_\alpha \) by the relation:

$$\begin{aligned} \gamma _\alpha = \frac{D_\alpha +2 }{D_\alpha }. \end{aligned}$$

The production terms are determined by the entropy principle in [2] and are given:

$$\begin{aligned} \begin{aligned} {\hat{m}}_1 = \psi _{11} {\hat{\Lambda }}_1, \quad {\hat{e}}_1 = 2(\theta _{11} {\hat{\eta }}_1 + \kappa _{11} {\hat{\zeta }}_1), \quad {\hat{\omega }}_1 = 2(\kappa _{11} {\hat{\eta }}_1 + \phi _{11} {\hat{\zeta }}_1 ) \end{aligned} \end{aligned}$$

with

$$\begin{aligned} \begin{aligned}&{\hat{\Lambda }}_1 = - \frac{u_1}{T_1}\left( 1- \frac{\Pi _1}{p_1}\right) + \frac{u_2}{T_2}\left( 1- \frac{\Pi _2}{p_2}\right) , \\&{\hat{\eta }}_1 = \frac{1}{2 T_1} \left( 1- \frac{\Pi _1}{p_1}\right) - \frac{1}{2 T_2} \left( 1- \frac{\Pi _2}{p_2}\right) , \\&{\hat{\zeta }}_1 = - \frac{1}{2 T_1 }\frac{D_1}{(D_1-3)}\frac{\Pi _1}{p_1} + \frac{1}{2 T_2}\frac{D_2}{(D_2-3)}\frac{\Pi _2}{p_2}, \\ \end{aligned} \end{aligned}$$

where \(\psi _{11} >0\) and the matrix

$$\begin{aligned} \begin{pmatrix} \theta _{11} &{} \kappa _{11}\\ \kappa _{11} &{} \phi _{11} \end{pmatrix} \quad \text {is positive definite. } \end{aligned}$$

Here, \(u_\alpha = v_\alpha - v\) is the diffusion velocity, where v is the mixture velocity \(v = \frac{1}{\rho }\sum _{\alpha =1}^{2}\rho _\alpha v_\alpha \) and \(\rho \) is the total mass density \(\rho =\sum _{\alpha =1}^{2}\rho _\alpha \).

By taking sum of (1), we have the following equivalent system

$$\begin{aligned}&\frac{\partial \rho }{\partial t} + \frac{\partial \rho v}{\partial x} = 0, \nonumber \\&\frac{\partial \rho v}{\partial t}+ \frac{\partial }{\partial x} \left( \rho v^2 + p + \Pi - \sigma \right) = 0,\nonumber \\&\frac{\partial }{\partial t} \left( \frac{1}{2}\rho v^2 + \rho \varepsilon \right) +\frac{\partial }{\partial x}\left\{ \left( \frac{1}{2}\rho v^2 + \rho \varepsilon + p + \Pi -\sigma \right) v + q \right\} = 0,\nonumber \\&\frac{\partial }{\partial t}\left\{ \rho v^2 + 3(p+\Pi )\right\} + \frac{\partial }{\partial x}\left\{ \left[ \rho v^2 + 5 (p+\Pi ) - 2 \sigma \right] v + 2 Q \right\} = \nonumber \\&\quad \quad - 3\left( \frac{\Pi _{1}}{\tau _1}+\frac{\Pi _{2}}{\tau _2}\right) ,\nonumber \\&\frac{\partial \rho _1 }{\partial t} + \frac{\partial \rho _1 v_1 }{\partial x} = 0, \nonumber \\&\frac{\partial \rho _1 v_1 }{\partial t}+ \frac{\partial }{\partial x} \left\{ \rho _1 v^2_1 + p_1 + \Pi _1 \right\} = {\hat{m}}_1, \nonumber \\&\frac{\partial }{\partial t} \left( \rho _1 v^2_1 + 2 \rho _1 \varepsilon _1 \right) + \frac{\partial }{\partial x}\left\{ \left[ \rho v^2_1 + 2\rho _1 \varepsilon _1 + 2 p_1 + 2\Pi _1 \right] v_1 \right\} = 2({\hat{e}}_1 + {\hat{m}}_1 v), \nonumber \\&\frac{\partial }{\partial t}\left\{ \rho _1 (v_1 )^2 + 3(p_1 +\Pi _1 )\right\} + \frac{\partial }{\partial x}\left\{ \left[ \rho _1 v_1^2 + 5 (p_1 +\Pi _1 )\right] v_1 \right\} \nonumber \\&= - \frac{3 \Pi _1}{\tau _1} +2 ({\hat{\omega }}_1 + {\hat{m}}_1 v), \end{aligned}$$
(3)

where the total pressure p, the global specific internal energy \(\varepsilon \), the global dynamic pressure \(\Pi \), the deviatoric part of the global shear stress \(\sigma \), the global heat flux q, and a new quantity Q are given by [2]:

$$\begin{aligned} \begin{aligned}&p=\sum _{\alpha =1}^{2}p_\alpha , \\&\rho \varepsilon = \rho \varepsilon _{\text {int}} +\frac{1}{2} \sum _{\alpha =1}^{2}\rho _\alpha u_\alpha ^2, \quad \varepsilon _{\text {int}} =\frac{1}{\rho } \sum _{\alpha =1}^{2}\rho _\alpha \varepsilon _\alpha , \\&\sigma = { - \frac{2}{3} \sum _{\alpha =1}^{2}\rho _\alpha u_\alpha ^2} = - \frac{2}{3} \frac{\rho _{1} \rho }{\rho _{2}} u_1^2,\\&\Pi =\sum _{\alpha =1}^{2}\left( \Pi _\alpha + \frac{1}{3}\rho _\alpha u_\alpha ^2\right) = \Pi _1+\Pi _2 -\frac{\sigma }{2},\\&q = \sum _{\alpha =1}^{2}\left( \frac{1}{2}\rho _\alpha u_\alpha ^2 + \rho _\alpha \varepsilon _\alpha + p_\alpha + \Pi _\alpha \right) u_\alpha ,\\&Q = \sum _{\alpha =1}^{2}\left\{ \frac{1}{2}\rho _\alpha u_\alpha ^2 + \frac{5}{2}\left( p_\alpha + \Pi _\alpha \right) \right\} u_\alpha . \end{aligned} \end{aligned}$$
(4)

It is noticeable that there appear in the system (3) global shear stress and global heat flux due to the presence of the diffusion velocity even if we neglect these dissipative quantities in the field equations for each constituent.

The system (3) with (2) and (4) is a hyperbolic system of 8 scalar equations in 1-dim for the 8 components of the fields \({\textbf{U}}\), namely, the total mass density, the mixture velocity, the global internal energy or an average temperature, the global dynamic pressure, and the corresponding variables for the species 1.

In equilibrium in which \(T_1=T_2=T\) the global pressure and the internal intrinsic energy can be written in the form

$$\begin{aligned} p^{(E)} = \frac{k_{B}}{m} \rho T, \quad \rho {\varepsilon ^{(E)}_{\text {int}} } = \frac{D}{2} \frac{k_{B}}{m} \rho T \end{aligned}$$
(5)

provided that we introduce [12]

$$\begin{aligned} \begin{aligned} \frac{1}{m} = \frac{c}{ m_{1}} + \frac{(1-c)}{ m_{2}},\quad D(c) = c \frac{m(c)}{m_{1}} D_{1} + (1 - c) \frac{m(c)}{m_{2}} D_{2}, \end{aligned} \end{aligned}$$
(6)

with m and D being the average mass, and a sort of average degrees of freedom D of molecules, respectively, and c (\(0< c < 1\)) being the concentration related to the mass densities:

$$\begin{aligned} \rho _{1} = \rho c, \quad \rho _{2} = \rho (1 - c). \end{aligned}$$

The associate equilibrium subsystem of (3), according to the definition given in [13], is given by the conservation laws (3)\(_{1,2,3,5}\) where we put the equilibrium values \( v_1 = v_2= v \), \( T_1 = T_2 = T \), and \(\Pi _1 = \Pi _2 = 0\) in which the production terms in (3)\(_{4,6,7,8}\) vanishing:

$$\begin{aligned} \begin{aligned}&\frac{\partial \rho }{\partial t} + \frac{\partial \rho v}{\partial x} = 0,\\&\frac{\partial \rho _1 }{\partial t} + \frac{\partial \rho _1 v }{\partial x} = 0, \\&\frac{\partial \rho v}{\partial t}+ \frac{\partial }{\partial x} \left( \rho v^2 + p^{(E)} \right) = 0,\\&\frac{\partial }{\partial t} \left( \frac{1}{2}\rho v^2 + \rho {\varepsilon ^{(E)}_{\text {int}} }\right) +\frac{\partial }{\partial x}\left\{ \left( \frac{1}{2}\rho v^2 + \rho {\varepsilon ^{(E)}_{\text {int}} } + p^{(E)} \right) v \right\} = 0,\\ \end{aligned} \end{aligned}$$
(7)

with \(p^{(E)}\) and \({\varepsilon ^{(E)}_{\text {int}} }\) given in (5). The equilibrium subsystem is of course the same as the Eulerian mixture.

3 Characteristic velocities in equlibrium

The characteristic velocities for a single fluid with RET\(_6\) were evaluated in [6] and as the left-hand side of the system (1) are two blocks of single fluids, we have the following characteristic velocities in an equilibrium state in which \(v_1=v_2=v\) and \(T_1=T_2=T\):

$$\begin{aligned} \begin{aligned}&v - \sqrt{\frac{5}{3} \frac{k_{\textrm{B}}}{m_{1}} T}, \quad v - \sqrt{\frac{5}{3} \frac{k_{\textrm{B}}}{m_{2}} T}, \quad v \, (\text {with multiplicity} \,\, 4),\\&v + \sqrt{\frac{5}{3} \frac{k_{\textrm{B}}}{m_{2}} T}, \quad v + \sqrt{\frac{5}{3} \frac{k_{\textrm{B}}}{m_{1}} T} \end{aligned} \end{aligned}$$

while the characteristic velocities of the equilibrium subsystem (7) are

$$\begin{aligned} v - \sqrt{\gamma \frac{k_{\textrm{B}}}{m} T}, \quad v \,\, \text {(twice)}, \quad v + \sqrt{\gamma \frac{k_{\textrm{B}}}{m} T}, \end{aligned}$$

where

$$\begin{aligned} \gamma = \frac{D+2}{D}. \end{aligned}$$

From now we consider the positive eigenvalues with respect to the rest frame of the fluid and introduce the characteristic velocities in an equilibrium state for constituents 1 and 2

$$\begin{aligned} \lambda _1 = v + \sqrt{\frac{5}{3} \frac{k_{\textrm{B}}}{m_{1}} T}, \quad \lambda _2 = v + \sqrt{\frac{5}{3} \frac{k_{\textrm{B}}}{m_{2}} T} \end{aligned}$$
(8)

and the characteristic velocities of the equilibrium subsystem

$$\begin{aligned} {\bar{\lambda }} = v + \sqrt{\gamma \frac{k_{\textrm{B}}}{m} T}. \end{aligned}$$
(9)

We notice that the expressions of the characteristic velocities of the full system are independent of the ratio of specific heat of the constituents \(\gamma _\alpha \) while the ones of the equilibrium subsystem depend on \(\gamma \). This is a peculiar property of the system of RET\(_6\) according to a general theorem given in [14].

We consider the first species the one for which \(m_1 \le m_2\) and we call \(\mu \) the ratio of the masses of the constituents defined by

$$\begin{aligned} \mu = \frac{m_{1}}{m_{2}}, \quad 0 < \mu \le 1, \end{aligned}$$

and with this choice \(\lambda _2 \le \lambda _1\) holds.

The subcharacteristic conditions for convexity argument according to a theorem in [13] hold and we have:

$$\begin{aligned} {\bar{\lambda }} \le \lambda _{1}. \end{aligned}$$

Now we need to evaluate for the following if \({\bar{\lambda }}\) is greater or less than \(\lambda _2\). It is easy, taking into account (8) and (9), to prove the following result:

Statement 1

- For any \(\, 1< \gamma _1 < {5}/{3}\),   and \(\, 1< \gamma _2 < {5}/{3}\),

$$\begin{aligned} \begin{aligned}&\text {case A): } \quad \text {If} \quad \mu \le \mu ^* ={3 \gamma _1}/{5} \in ]0,1[, \, \text {there exists a} \,\, c^* \in \, ]0,1[ \,\, \text {such that: } \\&\qquad \qquad \qquad \text {for}\,\,\, 0< c \le c^*, \quad {\bar{\lambda }} \le \lambda _2< \lambda _1 \\&\qquad \qquad \qquad \text {for}\,\,\, c^*< c< 1, \quad \lambda _2< {\bar{\lambda }}< \lambda _1 \\&\qquad \qquad \qquad \text {where} \,\, c^* \text {is solution of} \,\, {\bar{\lambda }} = \lambda _2, \,\, \text {i.e.} \,\, \gamma /m = 5/(3m_2); \\&\text {case B): } \quad \text {If} \quad \mu > \mu ^*, \quad \text {then} \quad \,\, \lambda _2< {\bar{\lambda }} < \lambda _1 \quad \text {for any} \,\, c \in \, ]0,1[ \, . \end{aligned} \end{aligned}$$
(10)

4 Shock-structure solution

The shock structure is a traveling wave solution, depending on a single variable \(\varphi = x - s t\) with s being the velocity of the shock wave,

$$\begin{aligned} {\textbf{U}}\equiv {\textbf{U}}(\varphi ), \qquad \varphi = x - s t \end{aligned}$$

with constant equilibrium boundary conditions at infinity:

$$\begin{aligned} \lim _{\varphi \rightarrow + \infty } {\textbf{U}} ={\textbf{U}}_0, \qquad \lim _{\varphi \rightarrow - \infty } {\textbf{U}} = {\textbf{U}}_\textrm{I}. \end{aligned}$$

We call the state \({\textbf{U}}_0\) as the unperturbed state and the state \({\textbf{U}}_\textrm{I}\) as the perturbed state, respectively. Hereafter, the quantities with the subscript 0 represent the quantities evaluated in the unperturbed state, and the quantities with subscript I represent the ones evaluated in the perturbed state.

We can choose without loss of generality the unperturbed velocity \(v_0=0\). The equilibrium states are:

$$\begin{aligned} {\textbf{U}}_{0} = \left( \begin{array}{c} \rho _{0} \\ v_0=0 \\ T_{0} \\ \Pi _0 = 0\\ \left( \rho _1\right) _{0} = c_0 \rho _0 \\ \left( v_1\right) _{0} =v_0=0 \\ \left( T_1\right) _{0}=T_0 \\ \left( \Pi _1\right) _{0}=0\\ \end{array} \right) , \quad {\textbf{U}}_\textrm{I} = \left( \begin{array}{c} \rho _\textrm{I} \\ v_\textrm{I} \\ T_\textrm{I} \\ \Pi _\textrm{I}=0\\ \left( \rho _1\right) _\textrm{I}= c_\textrm{I} \rho _\textrm{I} \\ \left( v_1\right) _\textrm{I}=v_\textrm{I} \\ \left( T_1\right) _\textrm{I}=T_\textrm{I}\\ \left( \Pi _1\right) _\textrm{I}=0\\ \end{array} \right) . \end{aligned}$$
(11)

As is well known the perturbed equilibrium state is connected with the unperturbed one through the Rankine-Hugoniot equation of the equilibrium sub-system (7), and therefore we have:

$$\begin{aligned} \begin{aligned}&\rho _\textrm{I} = \frac{(1+D_0) M_{0}^{2}}{D_0 + M_{0}^{2}}\rho _0, \quad v_\textrm{I} = \frac{D_0(M_{0}^{2} - 1)}{(D_0 + 1) M_{0}} a_0, \\&T_\textrm{I} = \frac{(D_0 + M_0^2)\{(2+D_0)M_0^2 -1 \}}{(D_0 + 1)^2 M_0^2} T_0, \\&c_\textrm{I} = c_{0}. \end{aligned} \end{aligned}$$
(12)

Here the unperturbed Mach number \(M_0\) is defined as usual by

$$\begin{aligned} M_{0} =\frac{s-v_0}{a_{0}}, \end{aligned}$$
(13)

with \(a_0\) being the sound velocity in the unperturbed state:

$$\begin{aligned} a_{0} = \sqrt{ \gamma _0 \frac{k_{B}}{m_{0}} T_{0} }, \qquad \gamma _0= \frac{D_0+2}{D_0}, \end{aligned}$$

and \(D_0\) being the degrees of freedom of a molecule in the unperturbed state \(D_0 = D(c_0)\) (see (6)\(_2\)), while \(m_{0} = m(c_{0})\) being the equilibrium average mass of the mixture (see (6)\(_1\)).

Note that relations between mixture state variables \(\rho _\textrm{I}\), \(v_\textrm{I}\), \(T_\textrm{I}\) and \(\rho _{0}\), \(u_{0}\), \(T_{0}\), correspond to the solution of the usual Rankine-Hugoniot relations between the state variables at the shock wave for a single fluid for the system of Euler equations. It is also noticeable that the concentration is the same in both equilibrium states, \(c_\textrm{I} = c_{0}\), and in the sequel it will be termed equilibrium concentration, without special regard to upstream or downstream state. Finally, downstream equilibrium can be regarded as a one-parameter family of states parametrized by the Mach number (i.e., shock velocity: see (17)), \({\textbf{U}}_\textrm{I} \equiv {\textbf{U}}_\textrm{I} ({\textbf{U}}_{0}, M_{0})\). In this way, the Mach number is naturally introduced in the model through the boundary conditions.

5 Sub-shocks formation

We consider the shock family bifurcating from the trivial zero shock solution obtained as \(s={\bar{\lambda }}_{0}\). The Lax condition [15] gives the admissibility conditions as \({\bar{\lambda }}_0< s < {\bar{\lambda }}_\textrm{I}\), which can be equivalently expressed as \(M_{0} > 1\).

According to the theorem in [16], the non-existence of the smooth shock structure is proved when the shock velocity is greater than the maximum characteristic velocity in the unperturbed state. Therefore in the present case, see (10) we have the following

Statement 2

  • A continuous \(C^1\) shock-structure solution cannot exist for a binary mixture of gases in which each constituent has a bulk viscosity when the shock velocity satisfies

    $$\begin{aligned} s > \lambda _{10}, \end{aligned}$$
    (14)

i.e. a shock structure with velocity s greater than \(\lambda _{10}\) has a sub-shock inside.

To know if other sub-shock can exist, we recall the observation that a sub-shock can arise when s meets an eigenvalue \(\lambda \) [17]. Now, as we do not know the analytical expression of the eigenvalues along the shock-structure solution, we focus on the eigenvalues in the two equilibrium states. In the unperturbed state \(\textbf{U}_0\), all the eigenvalues \(\lambda _0\) are constant values, while in the perturbed equilibrium one \(\textbf{U}_\textrm{I}\), all \(\lambda _\textrm{I}\) are functions of s. Taking into account that for \(s={\bar{\lambda }}_0\) we have the null shock and therefore \(\lambda _\textrm{I}({\bar{\lambda }}_0) = \lambda _0\). When s increases, for the genuine non-linearity, all \(\lambda _{\textrm{I}}(s)\) are increasing functions of s. As a consequence, the only candidates in the state \({\textbf{U}}_{\mathrm I}\) to meet s are the eigenvalues that are in the unperturbed state \({\textbf{U}}_0\) less than \({\bar{\lambda }}_0\), while s can meet in the state \({\textbf{U}}_0\) all the eigenvalues greater of \({\bar{\lambda }}_0\).

Therefore taking into account the inequalities between the eigenvalues given in (10) we can have:

Statement 3

  • For any \(1< \gamma _1 < {5}/{3}\), and \(1< \gamma _2 < {5}/{3}\), there may exist a sub-shock before the maximum characteristic velocity in the unperturbed state, according with:

$$\begin{aligned} \begin{aligned}&\text {case A): } \quad \text {If} \quad \mu \le {3 \gamma _1}/{5}, \text {and } \\&\qquad \qquad \qquad \text {when}\,\,\, 0< c_0 \le c^* , \,\, \text {for } \, \, s> \lambda _{20}, \\&\qquad \qquad \qquad \text {when}\,\,\, c^*< c_0 < 1, \,\, \text {for } \, \, s> s^*, \,\, \text {solution of } \,\, \lambda _{\textrm{2I}}(s^*)=s^*, \\&\text {case B):} \quad \text {If} \quad \mu>{3\gamma _1}/{5}, \,\, \text {for } \, \, s > \lambda _{20} \quad \text {for any} \,\, c_0 \in \, ]0,1[ \, . \end{aligned} \end{aligned}$$
(15)

Remark 1

  • These conditions are necessary but not sufficient for the existence of the sub-shock. In fact, there are cases in which the singularity is not verified due to an indeterminate form 0/0. For more precise details, see the reference [1].

Using dimensionless variables the condition (14) of Statement 2, taking into account (8), (11), (13) and (6), becomes:

$$\begin{aligned} M_{0} > M_{10} = \frac{\lambda _{10} }{a_0} = \sqrt{\frac{5 m_0 D_0}{3 m_1 (D_0+2)}} = \sqrt{\frac{5 D_0}{3 (D_0+2)\left\{ c_{0} + (1 - c_{0}) \mu \right\} }} \end{aligned}$$

in which we are sure that there is a subshock in the shock profile of species 1.

While the conditions (15) of Statement 3 becomes in the case A) for \(0 < c_0 \le c^*\), \(M_0> M_{20}^*\) with \(M_{20}^*\) being the solution of

$$\begin{aligned} M_\textrm{2I} (M_{20}^*, c_0, \mu )= M_{20}^*, \end{aligned}$$
(16)

where we have indicates \(M_\textrm{2I} = \lambda _\textrm{2I}/a_0\). By inserting the Rankine-Hugoniot conditions (12), we obtain

$$\begin{aligned} M_\textrm{2I} = \frac{D_0(M_{0}^{2} - 1)}{(D_0 + 1) M_{0}} + \sqrt{ \frac{5D_0(D_0 + M_0^2)\{(2+D_0)M_0^2 -1 \}}{3(D_0+2)(D_0 + 1)^2 M_0^2}\frac{m_0}{m_{2}}} \end{aligned}$$

and we obtain the solution of (16):

$$\begin{aligned} M_{20}^* = \sqrt{\frac{D_0 \{5 m_0 + 3 (D_0 + 2) m_2\}}{(D_0 + 2)(5 D_0 m_0 - 3 m_2)}}. \end{aligned}$$

For \(c^*< c_0 < 1\) we may have a subshock if

$$\begin{aligned} M_0 > M_{20} = \frac{\lambda _{20} }{a_0} = \sqrt{\frac{5 m_0 D_0}{3 m_2 (D_0+2)}} = \sqrt{\frac{5 D_0 \mu }{3 (D_0+2)\left\{ c_{0} + (1 - c_{0}) \mu \right\} }}. \end{aligned}$$

In the case B) of Statement 3 have a subshock for \(M_0 > M_{10}\) and may have a subshock for \(M_0 > M_{20}\). In both cases A) and B), the existence of the sub-shock is concerned the shock profile of species 2.

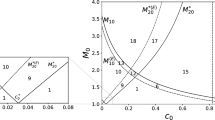
The topology of regions depends on \(M_{20}^*\) that for some values of \(\mu < \mu ^*\) can have an asymptote or can intersect \(M_{10}\). The complete analysis will be an object of a future paper. In the present analysis, we consider only the case A) with \(\mu =0.4\) and we omit also the case B). Our aim is mainly to compare in this case the behavior of the shock structure with the one in which the constituents are Eulerian gases. Using the results in the paper [1], we also depict the corresponding curves predicted by the Eulerian theory as \(M_{10}^\mathrm{(Euler)}\) and \(M_{20}^{*\mathrm (Euler)}\), and we can have the following regions described in Fig. 1.

Fig. 1
figure 1

Different regions in the plane \((c_0, M_0\)) of possible sub-shocks. \(D_1=5\), \(D_2=7\), and \(\mu = 0.4\). The dotted curves are the ones of a mixture of Eulerian gases. The circles represent the parameters adopted for numerical calculations shown in Sec. 6

Full size image

According to (15), for case A), it is sure that no sub-shock arises when \(M_0 < M_{20}\) for \(0 < c_0 \le c^*\) and \(M_0 < M_{20}^*\) for \(c^*< c_0 < 1\), and that a sub-shock for constituent 1 emerges when \(M_0 > M_{10}\). However, it is not sure whether a sub-shock for constituent 2 appears or not when \(M_0 > M_{20}\) or \(M_0 > M_{20}^*\). The possibility of the sub-shock formation is summarized in Table 1. In this table, "Maybe" indicates that the condition is only necessary but not sufficient for the sub-shock existence (see Remark 1).

Table 1 Summary of the possibility of the sub-shock formation for the classified regions in the plane \((c_0, M_0\)) shown in Fig. 1. The symbols \(S_1\) and \(S_2\) represent the sub-shock for constituent 1 and the sub-shock for constituent 2, respectively. The corresponding conclusions for a binary mixture of Eulerian gas are also shown in the last columns
Full size table

6 Numerical analysis

In this section, we perform numerical calculations for obtaining the shock-structure solutions to compare the solutions obtained by the RET\(_6\) mixture theory with the ones by the Eulerian mixture of gas and to verify in the uncertain cases if sub-shocks arise. For this purpose, we solve the Riemann problem for the PDE system (1) instead of solving the ODE system. This strategy is based on the conjecture proposed by Ruggeri and coworkers about the large-time behavior of the Riemann problem with or without structure [18, 19] for a system of balance laws [20,21,22] – following an idea of Liu [23]. According to the conjecture, the solution of the Riemann problem of the whole system converges to the corresponding shock structure for a large time if the Riemann initial data correspond to a shock family \({\mathcal {S}}\) of the equilibrium subsystem. This strategy allows us to use the Riemann solvers [24] for numerical calculations of the shock structure with or without sub-shocks, and it has been validated in several shock phenomena [1, 3, 20, 22, 25,26,27].

In the present analysis, by adopting the Uniformly accurate Central Scheme of order 2 (UCS2) [28], we perform numerical calculations on the shock structure obtained after a long time for the Riemann problem consisting of two equilibrium states \({\textbf{U}}_0\) and \({\textbf{U}}_{\textrm{I}}\) satisfying (11) at \(x = 0\). For convenience, we introduce the following dimensionless variables scaled by the quantities evaluated in the unperturbed state and an arbitrary characteristic time for numerical computations \(t_c\):

$$\begin{aligned}&{\hat{\rho }} = \frac{\rho }{\rho _{0}}, \quad {\hat{v}} = \frac{v}{a_{0}}, \quad \hat{{\mathcal {T}}} = \frac{{\mathcal {T}}}{T_{0}}, \quad {\hat{\Pi }} = \frac{\Pi }{\rho _0\frac{k_B}{m_0}T_{0}}, \nonumber \\&{\hat{\varphi }} = \frac{\varphi }{t_c \, a_0}, \quad {\hat{x}} = \frac{x}{t_c \, a_0}, \quad {\hat{t}} = \frac{t}{t_c}, \quad {\hat{\tau }} = \frac{\tau }{t_c}, \nonumber \\&{\hat{\psi }} = \frac{t_c}{\rho _0 T_0}\psi _{11}, \quad {\hat{\theta }} = \frac{t_c}{\rho _0 \frac{k_B}{m_0} T_0^2}\theta _{11}, \quad {\hat{\kappa }} = \frac{t_c}{\rho _0 \frac{k_B}{m_0} T_0^2}\kappa _{11}, \quad {\hat{\phi }} = \frac{t_c}{\rho _0 \frac{k_B}{m_0} T_0^2}\phi _{11}, \end{aligned}$$
(17)

where \({\mathcal {T}}\) is an average (non-equilibrium) temperature proposed in [29] in an implicit way:

$$\begin{aligned} \rho \varepsilon _{\text {int}} = \rho _1 \varepsilon _1 (\rho _1, {\mathcal {T}}) + \rho _2 \varepsilon _2 (\rho _2, {\mathcal {T}}) = \rho _1 \varepsilon _1 (\rho _1, T_1) + \rho _2 \varepsilon _2 (\rho _2, T_2). \end{aligned}$$

In the present analysis, we adopt the following parameters; \(D_1 = 5\), \(D_2 = 7\), \(\mu = 0.4\), \({\hat{\psi }} = {\hat{\theta }} = {\hat{\kappa }} = 0.2\), \({\hat{\phi }} = 0.3\), \({\hat{\tau }}_1 = 1\), and \({\hat{\tau }}_2 = 2\). We compare the profiles of global quantities predicted by a mixture of RET\(_6\) and Eulerian gases for \(M_0 = 1.15, 1.3, 1.47\) in Figs. 2 – 4, respectively. The parameters correspond to the ones by circles i - iii shown in Fig. 1 and lie in the regions 3, 5, and 8 where the sub-shock formation for constituent 2 is unclear as summarized in Table 1.

Figure 2 shows that the thickness of the shock structure predicted by the RET\(_6\) theory is larger than the one predicted by the Eulerian theory. Moreover, although only the shock-structure solution of the RET\(_6\) theory becomes in principle singular for \(M_0 = 1.15\), we notice that both the RET\(_6\) and Eulerian theories predict continuous shock structure as shown in Fig. 2. These results show the effect of the dissipation makes the shock structure broader and smoother. Similarly, Fig. 3 shows the profiles for \(M_0 = 1.3\) where the parameter lies in the region 5 in which the sub-shock for constituent 2 may exist for both the RET\(_6\) and the Eulerian theories. It is confirmed that the Eulerian theory predicts the sub-shock formation while the RET\(_6\) theory does not.

Fig. 2
figure 2

Profiles of the dimensionless global mass density, mixture velocity, and average temperature at \({\hat{t}} = 100\) (Solid curves). \(D_1 = 5\), \(D_2 = 7\), \(\mu = 0.4\), \(c_0 = 0.25\), and \(M_0 = 1.15\). These parameters lie in the region 3 and are indicated by circle No. i in Fig. 1. The temporal and spatial numerical meshes are \(\Delta {\hat{t}} = 0.005\) and \(\Delta {\hat{x}} = 0.04\). The theoretical predictions by the theory of a mixture of Eulerian gases are also shown (dashed curves)

Full size image
Fig. 3
figure 3

Profiles of the dimensionless global mass density, mixture velocity, and average temperature at \({\hat{t}} = 100\) (Solid curves). \(D_1 = 5\), \(D_2 = 7\), \(\mu = 0.4\), \(c_0 = 0.25\), and \(M_0 = 1.3\). These parameters lie in the region 5 and are indicated by circle No. ii in Fig. 1. The temporal and spatial numerical meshes are \(\Delta {\hat{t}} = 0.0025\) and \(\Delta {\hat{x}} = 0.02\). The theoretical predictions by the theory of a mixture of Eulerian gases are also shown (dashed curves)

Full size image
Fig. 4
figure 4

Profiles of the dimensionless global mass density, mixture velocity, and average temperature at \({\hat{t}} = 100\) (Solid curves). \(D_1 = 5\), \(D_2 = 7\), \(\mu = 0.4\), \(c_0 = 0.25\), and \(M_0 = 1.47\). These parameters lie in the region 8 and are indicated by circle No. iii in Fig. 1. The temporal and spatial numerical meshes are \(\Delta {\hat{t}} = 0.0025\) and \(\Delta {\hat{x}} = 0.02\). The theoretical predictions by the theory of a mixture of Eulerian gases are also shown (dashed curves)

Full size image

Lastly, we show the profiles for \(M_0 = 1.47\) in Fig. 4, which corresponds to the region 8. Only the Eulerian theory predicts the multiple sub-shocks, and the RET\(_6\) theory predicts only-one sub-shock. It is emphasized that the amplitude of the sub-shock predicted by the RET\(_6\) theory is smaller than the one predicted by the Eulerian theory due to the effect of the dissipation, namely, the dynamic pressure.