Gait classification for early detection and severity rating of Parkinson’s disease based on hybrid signal processing and machine learning methods

Abstract

Parkinson’s disease (PD) is one of the cognitive degenerative disorders of the central nervous system that affects the motor system. Gait dysfunction represents the pathology of motor symptom while gait analysis provides clinicians with subclinical information reflecting subtle differences between PD patients and healthy controls (HCs). Currently neurologists usually assess several clinical manifestations of the PD patients and rate the severity level according to some established criteria. This is highly dependent on clinician’s expertise which is subjective and ineffective. In the present study we address these issues by proposing a hybrid signal processing and machine learning based gait classification system for gait anomaly detection and severity rating of PD patients. Time series of vertical ground reaction force (VGRF) data are utilized to represent discriminant gait information. First, phase space of the VGRF is reconstructed, in which the properties associated with the nonlinear gait system dynamics are preserved. Then Shannon energy is used to extract the characteristic envelope of the phase space signal. Third, Shannon energy envelope is decomposed into high and low resonance components using dual Q-factor signal decomposition derived from tunable Q-factor wavelet transform. Note that the high Q-factor component consists largely of sustained oscillatory behavior, while the low Q-factor component consists largely of transients and oscillations that are not sustained. Fourth, variational mode decomposition is employed to decompose high and low resonance components into different intrinsic modes and provide representative features. Finally features are fed to five different types of machine learning based classifiers for the anomaly detection and severity rating of PD patients based on Hohen and Yahr (HY) scale. The effectiveness of this strategy is verified using a Physionet gait database consisting of 93 idiopathic PD patients and 73 age-matched asymptomatic HCs. When evaluated with 10-fold cross-validation method for early PD detection and severity rating, the highest classification accuracy is reported to be $98.20\%$ and $96.69\%$, respectively, by using the support vector machine classifier. Compared with other state-of-the-art methods, the results demonstrate superior performance and support the validity of the proposed method.

Introduction

Parkinson’s disease (PD) is a chronic neurodegenerative brain disorder that mainly affects the motor system of the elderly people to perform regular activities (Balaji et al. 2020). It usually leads to typical symptoms including tremor, bradykinesia, rigidity, gait disturbance and postural instability, among which gait disturbance is one of the early manifestations of PD and evolves over time (Hausdorff et al. 1998; Rehman et al. 2019a). Current diagnosis of PD is commonly based on subjective clinical examination in conjunction with expensive and time-consuming brain imaging techniques (Hoehn and Ravikumar 1998; Rehman et al. 2019b). Recent work has revealed that objective quantification of gait impairments can not only inform early diagnosis, but also rate the severity, which is non-invasive and inexpensive (Mirelman et al. 2019; Del Din et al. 2019). Particularly, features of gait pattern can serve as significant biomarkers which are critical for not only identifying the presence of PD but also quantifying the progression of the disease.

Gait analysis provides clinicians with various parameters including spatiotemporal, kinematic and kinetic types (Morris et al. 1999). They are recognized as variables of influence by gait impairment in PD patients due to their association with clinical attributes. Spatiotemporal parameters concern the foot step pattern which include step length, step velocity, step width, swing time and stance time (Morris et al. 1999). Kinematic parameters refer to variables about the pattern of motion with no consideration of the source of motion, such as the angular displacement of the hips, knees and ankle joints over time (Morris et al. 1999). Kinetic parameters, such as ground reaction force during walking, measure the force that causes the motion. Kinetics refers to the underlying forces, powers and energies of the lower limbs and trunk that enable the person to walk (Winter 1991). Among these parameters, gait kinematics and kinetics provide a more comprehensive description of locomotion as well as highlighting disturbances in the moments and powers contributing to the gait pattern. In addition, kinetic measures permit a deeper analysis at the level of neuromotor processes. Currently, vertical ground reaction force (VGRF) has been widely used in gait analysis, which is a reflection of the net forces exerted by the human body on ground while walking (Manap and Tahir 2013; Alkhatib et al. 2020). It characterizes disorder patterns, diagnosis, rehabilitation clinic, and monitoring of treatment progress, which is widely used as discriminate feature in early detection and severity grading of PD patients. Farashi (2020) proposed some new feature sets from VGRF data for the gait cycle including area under VGRF curve, peak delay of VGRF data and higher-order moments of VGRF data in both time and frequency domains to improve performance of a PD diagnostic approach. Minamisawa et al. (2012) demonstrated the influence of neurological changes and aging on the VGRF components and the difference in fluctuation pattern behavior in healthy controls and PD patients. Detrended fluctuation analysis was used to study characteristics of fluctuation of VGRF. Manap and Tahir (2013) utilized the peak values of VGRF during initial contact, mid-stance and toe off phases to detect gait irregularities in PD patients.

Conventional diagnosis of PD is largely depending on the subjective measures obtained from visual observations and questionnaire of the clinicians. For example, Hoehn & Yahr (HY) scale has been widely used in assessing the severity level of PD, which consists of 5 stages originally and is further extended with additional stage 1.5 and 2.5 (Hoehn and Yahr 1967). The Unified Parkinsons Disease Rating Scale (UPDRS) is more complex and 42 questions are arranged to assess the motor symptoms, daily activities and behavioral characteristics (Martinez-Martin et al. 1994). It is time-consuming and subjective when clinicians employ these scales to rate the severity level of PD patients as several diagnostic criteria use descriptive symptoms. Since these measurements cannot provide a quantified diagnostic basis (Zhao et al. 2018), an objective, quick and computer-aided diagnosis system has been urgently required in the clinical applications.

Machine learning (ML) methods can provide such an objective and efficient diagnosis and severity rating system for PD patients. Widely reported ML models in literature for classification of PD include support vector machine (SVM) (Wu et al. 2019), Naive Bayes (NB) (Cavallo et al. 2019), random forest (RF) (Kuhner et al. 2017), k-nearest neighbour (KNN) (Oung et al. 2018), decision tree (DT) (Sakar et al. 2019), artificial neural networks (ANNs) (Berus et al. 2019), logistic regression (LR) (Cao et al. 2020) and ensemble learning based Adaboost (ELA) (Yang et al. 2021). In addition, ML methods identify the best combination of clinically relevant gait features to address questions around gait characteristics, PD classification and progression detection. The choice of gait features is important for the models so that their findings are easy to interpret. However, based on the literature, extraction and utilization of gait features vary widely, often with no consistency on datasets and data type across studies or rationale for classification of PD (Rehman et al. 2019a). For example, Sakar et al. (2019) applied the tunable Q-factor wavelet transform (TQWT) to the voice signals of PD patients for feature extraction, which has higher frequency resolution than the classical discrete wavelet transform. The feature subsets were fed to multiple classifiers and the predictions of the classifiers were combined with ensemble learning approaches. Caramia et al. (2018) extracted range of motions and spatio-temporal parameters from gait raw data collected by Inertial Measurement Units. These parameters were fed to six different ML classifiers for PD classification and severity rating. Peng et al. (2017) extracted multilevel regions of interest (ROIs) features from T1-weighted brain magnetic resonance images. Filter- and wrapper-based feature selection method and multi-kernel SVM were used for PD classification. Yuvaraj et al. (2018) extracted higher-order spectra bispectrum features from electroencephalography (EEG) signals and fed them to the traditional ML classifiers like KNN, SVM and DT for PD classification. Prabhu et al. (2020) extracted nonlinear features from gait signals by using recurrence quantification analysis and statistical analysis. These features better represented the dynamics of human gait and were fed to SVM and probabilistic neural network for PD identification. Farashi (2020) extracted time, frequency and time-frequency domains features from VGRF data by using wavelet packet decomposition and power spectral density. These feature were fed to the DT classifier for PD detection. Oung et al. (2018) detected and classified PD using signals from wearable motion and audio sensors based on both empirical wavelet transform (EWT) and empirical wavelet packet transform (EWPT). EWT and EWPT decomposed both speech and motion data signals up to different levels and provided the instantaneous amplitudes and frequencies from the coefficients of the decomposed signals by applying the Hilbert transform. These features were fed to KNN for PD detection and severity rating. Balaji (2021) proposed a long short term memory (LSTM) network for severity rating of PD from gait data without any hand crafted features and learned the long-term temporal dependencies in the gait cycle for robust diagnosis of PD. Findings from the above-mentioned studies reveal that different types of features cooperated with different ML methods may provide various ideas and performance for PD classification. Therefore, there is a need to identify suitable ML models and the optimal combination of gait characteristics for detection and severity rating of PD.

Despite the fact that these previous approaches have demonstrated respectable classification accuracy, the potential of dynamical nonlinear features together with ML methods has not been thoroughly investigated. In the present study, we propose a combined and computational method from the area of nonlinear method and ML for PD diagnosis and severity rating. From the gait patterns acquired from 16 foot worn sensors, time series of VGRF data are utilized to represent discriminant gait information. First, phase space of the VGRF is reconstructed, in which the properties associated with the nonlinear gait system dynamics are preserved. Then Shannon energy is used to extract the characteristic envelope of the phase space signal. Third, Shannon energy envelope (SEE) is decomposed into high and low resonance components using dual Q-factor signal decomposition (DQSD) derived from tunable Q-factor wavelet transform (TQWT). Note that the high Q-factor component consists largely of sustained oscillatory behavior, while the low Q-factor component consists largely of transients and oscillations that are not sustained. Fourth, variational mode decomposition (VMD) is employed to decompose high and low resonance components into different intrinsic modes and provide representative features. Finally, features are fed to five supervised ML algorithms namely SVM, DT, RF, KNN and ELA classifiers for the anomaly detection and severity rating of PD patients based on HY scale. This is not only the binary classification but also the multi-class classification problem. Moreover, in order to avoid data overfitting problem and enhance the classification accuracy, 10-fold cross validation technique is utilized.

The remainder of the paper is organized as follows. Section Method depicts the procedure of the proposed method. It also includes the data description, feature extraction and selection, and classification models. Section 3 presents some experimental results. Sections Experimental results and Conclusion give some discussions and conclusions, respectively.

Method

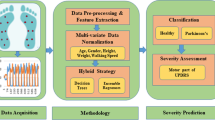
In this section, we simply introduce the procedure of the proposed method for PD identification and severity rating. Figure 1 illustrates the block diagram of the proposed method for the binary and multi-class classification problems. The method includes the feature extraction and classification stages and follows the following steps. In the first step, features are extracted by using hybrid signal processing methods, including PSR, DQSD, VMD and statistical analysis. In the second step, feature vectors are fed into five different types of classification models to discriminate between PD patients and healthy controls (HCs) and classify the stages (healthy, mild, medium and high) of PD patients based on HY scale. Finally, different performance parameters are used to evaluate the classification results.

Fig. 1

Block diagram of the proposed method for PD classification and severity rating using nonlinear features and different classification models

Dataset description

In the present study, we use the publicly available gait database provided by Physionet (Goldberger et al. 2000) (https://physionet.org/content/gaitpdb/1.0.0/), which includes 73 HCs (mean age: 66.3 years; 55$\%$ men) and 93 idiopathic PD patients (mean age: 66.3 years; 63$\%$ men). Demographic and clinical characteristics of the participants are depicted in Table 1. The database contains 55 PD patients with HY scale 2 (mild), 28 PD patients with HY scale 2.5 (medium) and 10 PD patients with HY scale 3 (high). This indicates that most of the PD patients were at the early stage of the disease or with moderate severity, which can serve as a benchmark to assess the proposed early detection and severity rating of PD. The database includes the VGRF records of subjects as they walked at their usual, self-selected pace for approximately 2 minutes on level ground. Underneath each foot were 8 sensors (Ultraflex Computer Dyno Graphy, Infotronic Inc.) that measure force (in Newtons) as a function of time. The output of each of these 16 sensors has been digitized and recorded at 100 samples per second, and the records also include two signals that reflect the sum of the 8 sensor outputs for each foot. Here in Fig. 2, we demonstrate the samples of the total force Y(t) and Z(t) under the left foot and the right foot, respectively, from HCs and PD patients with three types of HY scale.

Table 1 Demographic and clinical characteristics of the participants

Fig. 2

Samples of sum of the 8 sensor outputs for each foot from HCs and PD patients with different HY scales

In order to obtain more efficient features, this study considers parameters from VGRF data Y(t) and Z(t) by using SEE, DQSD and VMD. This helps extraction of discriminative features from human gait system for PD classification and severity rating.

Phase space reconstruction (PSR)

It is sometimes necessary to search for patterns in a time series and in a higher dimensional transformation of the time series (Sun et al. 2015). Phase space reconstruction is a method used to reconstruct the so-called phase space. The concept of phase space is a useful tool for characterizing any low-dimensional or high-dimensional dynamic system. A dynamic system can be described using a phase space diagram, which essentially provides a coordinate system where the coordinates are all the variables comprising mathematical formulation of the system. A point in the phase space represents the state of the system at any given time (Sivakumar 2002; Lee et al. 2014). The VGRF data Y(t) and Z(t) can be written as the time series vector $\upsilon =\{\upsilon _1,\upsilon _2,\upsilon _3,...,\upsilon _K\}$, where K is the total number of data points. The phase space can be reconstructed according to (Lee et al. 2014):

$$\begin{aligned} Y_j=(\upsilon _j,\upsilon _{j+\tau },\upsilon _{j+2\tau },...,\upsilon _{j+(d-1)\tau }) \end{aligned}$$

(1)

where $j=1,2,...,K-(d-1)\tau$, d is the embedding dimension of the phase space and $\tau$ is a delayed time.

The behaviour of the signal over time can be visualized using PSR (especially when $d=$ 2 or 3). In this work, we have confined our discussion to the value of embedding dimension $d=3$, because of their visualization simplicity. In addition, different studies have found this value to best represent the attractor for human biological system (Venkataraman and Turaga 2016; Som et al. 2016). For $\tau$, we either use the first-zero crossing of the autocorrelation function for each time series or the average $\tau$ value obtained from all the time series in the training dataset using the method proposed in (Michael 2005). In this study, we consider the values of time lag $\tau =1$ to test the classification performance. PSR for $d=3$ has been referred to as 3D PSR.

Reconstructed phase spaces have been proven to be topologically equivalent to the original system and therefore are capable of recovering the nonlinear dynamics of the generating system (Takens 1980; Xu et al. 2013). This implies that the full dynamics of the gait system are accessible in this space, and for this reason, features extracted from it can potentially contain more and/or different information than the common features extraction method (Chen et al. 2014).

3D PSR is the plot of three delayed vectors $\upsilon _j,\upsilon _{j+1}$ and $\upsilon _{j+2}$ to visualize the dynamics of human gait system. Euclidian distance (ED) of a point $(\upsilon _j,\upsilon _{j+1},\upsilon _{j+2})$, which is the distance of the point from origin in 3D PSR and can be defined as (Lee et al. 2014)

$$\begin{aligned} ED_j=\sqrt{\upsilon _j^2+\upsilon _{j+1}^2+\upsilon _{j+2}^2} \end{aligned}$$

(2)

ED measures can be used in features extraction and have been studied and applied in many fields, such as clustering algorithms and induced aggregation operators (Merigó and Casanovas 2011).

Figures 3 and 4 demonstrate samples of the PSR of total force Y(t) and Z(t) under the left and right feet from HCs and PD patients with different HY scales.

Fig. 3

Samples of PSR of the total force Y(t) under the left foot from HCs and PD patients with different HY scales

Fig. 4

Samples of PSR of the total force Z(t) under the right foot from HCs and PD patients with different HY scales

Shannon energy envelope (SEE)

The normalized average Shannon energy named as Shannon energy envelope is a well-known technique for the envelope extraction of signals. The extraction of SEE follows the following steps.

Suppose the original signal recorded as s(t). The normalization is applied by setting the variance of the signal to a value of 1. The resulting signals is expressed as

$$\begin{aligned} s_{norm}(t)=\frac{s(t)}{\mid \max \limits _{i=1}^{N}s(i)\mid }, \end{aligned}$$

(3)

where $s_{norm}(t)$ is a normalized amplitude, N denotes the signal length. The Shannon energy of signal $s_{norm}(t)$ is calculated as

$$\begin{aligned} E=-s_{norm}^2(t){\textrm{log}}(s_{norm}^2(t)). \end{aligned}$$

(4)

Then the average Shannon energy is calculated as

$$\begin{aligned} E_a=-\frac{1}{N}\sum \limits _{i=1}^{N}s_{norm}^2(i){\textrm{log}}(s_{norm}^2(i)). \end{aligned}$$

(5)

Energy that better approaches detection ranges in the presence of noise or domains with more width results in fewer errors. Capacity to emphasize medium is the advantage of using Shannon energy rather than classic energy (Beyramienanlou and Lotfivand 2017; Zidelmal et al. 2014). The selected signal is normalized in the following equation (6) for decreasing the signal base and placing the signal below the baseline,

$$\begin{aligned} E_n=\frac{E_a-\nu }{\varsigma }, \end{aligned}$$

(6)

where $E_n$ is the average Shannon Energy standardized or normalized (known as Shannon energy envelope, SEE), $\nu$ is the average value of energy $E_a$, $\varsigma$ is the standard deviation of energy $E_a$. Here, after computing Shannon energy, small spikes around the main peak of the energy are generated. These spikes make main peaks detection difficult. To eliminate this spike, Shannon energy is converted into SEE (Beyramienanlou and Lotfivand 2017).

Figures 5 and 6 demonstrate samples of SEE of the PSR of total force Y(t) and Z(t) under the left and right feet from HCs and PD patients with different HY scales.

Fig. 5

Samples of SEE of PSR of the total force Y(t) under the left foot from HCs and PD patients with different HY scales

Fig. 6

Samples of SEE of PSR of the total force Z(t) under the left foot from HCs and PD patients with different HY scales

Tunable Q-factor wavelet transform (TQWT) and dual Q-factor signal decomposition (DQSD)

Wavelet transform is an effective time-frequency tool for the analysis of non-stationary signals. The tunable Q-factor wavelet transform (TQWT) is a flexible fully-discrete wavelet transform suitable for analysis of oscillatory signals (Selesnick 2011a). TQWT depends on changeable parameters: Q-factor (Q), redundancy (R), and decomposition level (J). Generally, Q measures the oscillatory behavior and waveform shape of wavelet waveform. R helps localize the wavelet in time-domain without affecting its shape. The decomposition level J controls the expansion extent and bandpass location of wavelet waveform. There will be a total of $J+1$ subbands. For the TQWT parameters, the wavelet transform should have a low Q-factor when the signal illustrates small or no oscillatory behavior. On the other hand, the wavelet transform should have a relatively high Q-factor for the analysis and processing of oscillatory signals. It is worth noting that unwanted excessive ringing of wavelets needs to be prevented while performing TQWT by appropriately choosing the value of R greater than or equal to 3 (Selesnick 2011a). Generally, a value of $R=4$ is recommended. The TQWT decomposes gait signals into subbands with a number of decomposition levels by using the input parameters (Q, R, and J). TQWT consists of two iterative band-pass filter banks, i.e., the high resonance component filter $H_{filter}(\omega )$ and the low resonant component filter $L_{filter}(\omega )$. The resonance characteristics of oscillatory signal can be represented by quality factor Q, i.e. the ratio of its center frequency to its bandwidth, $Q=f_c/B_w$, where $f_c$ denotes the center frequency and $B_w$ represents the bandwidth of signal.

Let the low-pass and high-pass scaling factors of the two-channel filter bank be denoted by $\lambda$ and $\sigma$, respectively. In order to prevent excessive redundancy and achieve perfect reconstruction, the scaling factors should be: $0<\lambda <1$, $0<\sigma \le 1$, $\lambda +\sigma >1$. Mathematically, the low-pass filter $L_{filter}(\omega )$ and high-pass filter $H_{filter}(\omega )$ are expressed as follows (Selesnick 2011a), respectively :

$$\begin{aligned} L_{filter}(\omega )=\left\{ \begin{array}{lll} 1, &{} &{} {if~\mid \omega \mid \le (1-\sigma )\pi }\\ \vartheta \left( \frac{\omega +(\sigma -1)\pi }{\lambda +\sigma -1}\right) , &{} &{} {if~(1-\sigma )\pi<\mid \omega \mid <\lambda \pi }\\ 0, &{} &{} {if~\lambda \pi \le \mid \omega \mid \le \pi }\\ \end{array} \right. \end{aligned}$$

(7)

and

$$\begin{aligned} H_{filter}(\omega )=\left\{ \begin{array}{lll} 0, &{} &{} {if~\mid \omega \mid \le (1-\sigma )\pi }\\ \vartheta \left( \frac{\lambda \pi -\omega }{\lambda +\sigma -1}\right) , &{} &{} {if~(1-\sigma )\pi<\mid \omega \mid <\lambda \pi }\\ 1, &{} &{} {if~\lambda \pi \le \mid \omega \mid \le \pi }\\ \end{array} \right. \end{aligned}$$

(8)

where $\vartheta (\omega )$ is the frequency response of Daubechies filter and is defined with the following expression:

$$\begin{aligned} \vartheta (\omega )=0.5\times (1+cos(\omega ))\times \sqrt{2-cos(\omega )},~\mid \omega \mid \le \pi . \end{aligned}$$

(9)

The Q-factor, R and maximum number of decomposition level $J_{max}$ can be expressed in terms of parameters $\lambda$ and $\sigma$ as follows:

$$\begin{aligned} Q=\frac{f_c}{B_w}=\frac{2-\sigma }{\sigma };~R=\frac{\sigma }{1-\lambda };~J_{max}=\frac{\textrm{log}(\sigma L/8)}{\textrm{log}(1/\lambda )}, \end{aligned}$$

(10)

where L is the length of the analysed heart sound signal. Detailed expressions of Q, R, $J_{max}$, $f_c$ and $B_w$ have been provided in (Selesnick 2011a).

Consider sparse representation of a signal using two Q-factors simultaneously. This problem can be used for decomposing a signal into high and low resonance components (Selesnick 2011b), which is also named as dual Q-factor signal decomposition (DQSD).

Consider the problem of expressing SEE of the PSR of a given total force signal Y(t) under left foot as the sum of an oscillatory signal $y_1(t)$ and a non-oscillatory signal $y_2(t)$, that is

$$\begin{aligned} SEE^{PSR^{Y(t)}}=y_1(t)+y_2(t). \end{aligned}$$

(11)

The signal $SEE^{PSR^{Y(t)}}$ is a measured signal, and $y_1(t)$ and $y_2(t)$ are to be determined in such a way that $y_1(t)$ consists mostly of sustained oscillations and $y_2(t)$ consists mostly of non-oscillatory transients. As described in(Selesnick 2011b), such a decomposition is necessarily nonlinear in $SEE^{PSR^{Y(t)}}$, and it cannot be accomplished using frequency-based filtering. One approach is to model $y_1(t)$ and $y_2(t)$ as having sparse representations using high Q-factor and low Q-factor wavelet transforms respectively (Selesnick 2011b). In this case, a sparse representation of the signal $SEE^{PSR^{Y(t)}}$ using both high Q-factor and low Q-factor TQWT jointly, making the identification of $y_1(t)$ and $y_2(t)$ feasible. This approach is based on morphological component analysis (MCA) (Starck 2005), a general method for signal decomposition relying on sparse representations.

Denote $\hbox {TQWT}_1$ and $\hbox {TQWT}_2$ as the TQWT with two different Q-factors (high and low Q-factors). Then the sought decomposition can be achieved by solving the constrained optimization problem:

$$\begin{aligned} \mathop {argmin}\limits _{w_1,w_2}\lambda _1 ||w_1||_1+\lambda _2 ||w_2||_1 \end{aligned}$$

(12)

such that

$$\begin{aligned} SEE^{PSR^{Y(t)}}= \textrm{TQWT}_1^{-1}(w_1)+ \textrm{TQWT}_2^{-1}(w_2). \end{aligned}$$

(13)

For greater flexibility, we will use subband-dependent regularization:

$$\begin{aligned} \mathop {argmin}\limits _{w_1,w_2}\sum \limits _{j=1}^{J_1+1}\lambda _{1,j} ||w_{1,j}||_1+\sum \limits _{j=1}^{J_2+1}\lambda _{2,j} ||w_{2,j}||_1 \end{aligned}$$

(14)

where $w_{i,j}$ denotes subband j of $\hbox {TQWT}_i$ for $i=1,2$, $J_i$ represents the decomposition level of $\hbox {TQWT}_i$ for $i=1,2$.

When $w_1$ and $w_2$ are obtained, we set

$$\begin{aligned} y_1(t)= \textrm{TQWT}_1^{-1}(w_1), y_2=\textrm{TQWT}_2^{-1}(w_2). \end{aligned}$$

(15)

Given the signal $SEE^{PSR^{Y(t)}}$, the function returns signals $y_1(t)$ and $y_2(t)$. In addition, it returns sparse wavelet coefficients $w_1$ and $w_2$ corresponding to $y_1(t)$ and $y_2(t)$, respectively.

Likewise, SEE of the PSR of the total force Z(t) under the right foot can also be expressed as

$$\begin{aligned} SEE^{PSR^{Z(t)}}= z_1(t)+z_2(t). \end{aligned}$$

(16)

$$\begin{aligned} SEE^{PSR^{Z(t)}}= \textrm{TQWT}_1^{-1}(w_1)+ \textrm{TQWT}_2^{-1}(w_2), \end{aligned}$$

(17)

where $w_{i,j}$ denotes subband j of $\hbox {TQWT}_i$ for $i=1,2$, $J_i$ represents the decomposition level of $\hbox {TQWT}_i$ for $i=1,2$.

When $w_1$ and $w_2$ are obtained, we set

$$\begin{aligned} z_1(t)= \textrm{TQWT}_1^{-1}(w_1), z_2=\textrm{TQWT}_2^{-1}(w_2). \end{aligned}$$

(18)

Given the signal $SEE^{PSR^{Z(t)}}$, the function returns signals $z_1(t)$ and $z_2(t)$. In addition, it returns sparse wavelet coefficients $w_1$ and $w_2$ corresponding to $z_1(t)$ and $z_2(t)$, respectively.

It can be seen in Figs. 7 and 8 that this procedure separates the given VGRF signal into two signals that have quite different behavior. One signal (the high Q-factor component) is sparsely represented by a high Q-factor wavelet transform ($Q = 4$). The second signal (the low Q-factor component) is sparsely represented by a low Q-factor wavelet transform ($Q = 1$). Note that the high Q-factor component consists largely of sustained oscillatory behavior, while the low Q-factor component consists largely of transients and oscillations that are not sustained.

Fig. 7

Samples of high and low Q-factor components $y_1(t)$ and $y_2(t)$ of SEE of PSR of the total force Y(t) under the left foot from HCs and PD patients with different HY scales

Fig. 8

Samples of high and low Q-factor components $z_1(t)$ and $z_2(t)$ of SEE of PSR of the total force Z(t) under the right foot from HCs and PD patients with different HY scales

Variational mode decomposition (VMD)

VMD is aiming to decompose a composite input signal x(t) (for example, $y_1(t)$,$y_2(t)$,

$z_1(t)$,$z_2(t)$) into n number of intrinsic modes $\mu _n(t)$, which have specific sparsity properties while reproducing the input signal. The decomposition process can be written as a constrained variational problem with the following function:

$$\begin{aligned}{} & {} \min \limits _{{\mu _n},{\omega _n}}\left\{ \sum \limits _{n = 1}^K\left\| \frac{\partial }{\partial t}\left[ \left( \delta (t)+\frac{j}{\pi t}\right) *\mu _n(t)\right] e^{-j\omega _{k}t}\right\| _2^2\right\} ,\nonumber \\{} & {} \quad ~\mathrm{subject~to}~\sum \limits _{n = 1}^K\mu _n(t)=x(t), \end{aligned}$$

(19)

where K is the number of decomposition modes, $\frac{\partial }{\partial t}[\cdot ]$ denotes the partial derivative of a function, $\delta$ is the Dirac function, ‘$*$’ represents convolution computation, $\mu _n=\{\mu _1,\mu _2,...,\mu _n\}$ is the set of all modes, $\omega _n=\{\omega _1,\omega _2,...,\omega _n\}$ is the set of center frequency, t is the time script, j is the complex square root of $-1$.

Considering a quadratic penalty term and Lagrange multiplier $\eta$, the above-mentioned constrained variational problem can be transferred into an unconstrained optimization problem, which is represented as follows:

$$\begin{aligned} \begin{aligned} L(\{\mu _n\},\{\omega _n\},\eta )&=\alpha \sum \limits _{n = 1}^K\left\| \frac{\partial }{\partial t}\left[ \left( \delta (t)+\frac{j}{\pi t}\right) *\mu _n(t)\right] e^{-j\omega _{k}t}\right\| _2^2\\&\quad +\left\| x(t)-\sum \limits _{n = 1}^K\mu _n(t)\right\| _2^2\\&\quad +\left\langle \eta (t),x(t)-\sum \limits _{n = 1}^K\mu _n(t)\right\rangle , \end{aligned} \end{aligned}$$

(20)

where L denotes the augmented Lagrangian, $\alpha$ is balancing parameter of the data-fidelity constraint,‘$\langle \cdot \rangle$’ represents the inner product.

Alternate direction method of multipliers (ADMM) has been used to generate various decompose modes and centre frequency at the time of shifting operation of each mode (Dragomiretskiy and Zosso 2014). The solution of Eq. (20) can be derived by using ADMM, in which the process of the solution of $\mu _n$ and $\omega _n$ mainly consists of the following steps:

• Step 1: Intrinsic mode update. The Wiener filtering is embedded for updating the mode directly in Fourier domain with a filter tuned to the current center frequency. The solution for updated mode is obtained as follows:

  $$\begin{aligned} {\hat{\mu }}_n^{\kappa +1}=\frac{{\hat{x}}(\omega )-\sum \limits _{i\ne n}{\hat{\mu }}_i(\omega )+\frac{{\hat{\eta }}(\omega )}{2}}{1+2\alpha (\omega -\omega _n)^2}, \end{aligned}$$

  (21)

  where $\kappa$ is the number of iterations, ${\hat{x}}(\omega )$, ${\hat{\mu }}_i(\omega )$ and ${\hat{\eta }}(\omega )$ represent the Fourier transforms of ${\hat{x}}(t)$, ${\hat{\mu }}_i(t)$ and ${\hat{\eta }}(t)$, respectively.

• Step 2: Center frequency update. The center frequency is updated as the center of gravity of the corresponding mode’s power spectrum, which is represented as follows:

  $$\begin{aligned} {\hat{\omega }}_n^{\kappa +1}=\frac{\int _0^{\infty }\omega \vert {\hat{\mu }}_n(\omega )\vert ^2d\omega }{\int _0^{\infty }\vert {\hat{\mu }}_n(\omega )\vert ^2d\omega } \end{aligned}$$

  (22)

The complete algorithm of VMD can be found in (Dragomiretskiy and Zosso 2014). Figures 9, 10, 11 and 12 demonstrate samples of the VMD of VGRF data $y_1(t)$,$y_2(t)$,$z_1(t)$ and $z_2(t)$ from PD patients and HCs.

Fig. 9

Samples of VMD of $y_1(t)$ from HCs and PD patients with different HY scales

Fig. 10

Samples of VMD of $y_2(t)$ from HCs and PD patients with different HY scales

Fig. 11

Samples of VMD of $z_1(t)$ from HCs and PD patients with different HY scales

Fig. 12

Samples of VMD of $z_2(t)$ from HCs and PD patients with different HY scales

The VMD method can effectively capture narrow-band and wide-band modes unlike the fixed bandwidth of subabands as in the case of the wavelet transform based decomposition approach (Babu et al. 2018). It is more robust to noisy data. Since each mode is updated by Wiener filtering in Fourier domain during the optimization process, the updated mode is less affected by noisy disturbances. Therefore, VMD can be more efficient for capturing the signal’s short and long variations (Mishra et al. 2018; Sujadevi et al. 2019). Hence, we apply the VMD method to make up for the disadvantage of TQWT and serve as complementary tool to more effectively extract features from VGRF signals.

Feature extraction and selection

In order to obtain more efficient features, this paper proposes the following extraction scheme.

• (1) PSR of the VGRF data Y(t) and Z(t) under left and right feet from HCs and PD patients.

• (2) Extraction of SEE of the PSR of the VGRF data Y(t) and Z(t).

• (3) DQSD of the SEE of the PSR of the VGRF data Y(t) and Z(t).

• (4) VMD of the high and low Q-factor components of the SEE of the PSR of the VGRF data Y(t) and Z(t). The first six intrinsic modes are selected as feature vectors $[y_1^{\mu _n},y_2^{\mu _n},z_1^{\mu _n},z_2^{\mu _n}]^T,~(n=1,2,...,6)$. These twenty-four features are fed to the following classification models for the early detection and severity rating of PD patients.

Classification models

To carry out a comparative study, five popular ML methods, i.e., the support vector machine (SVM), K-nearest neighbor (KNN), naive Bayes (NB) classifier, decision tree (DT) and ensemble learning based Adaboost (ELA) classifier are evaluated because they are usually utilized to solve the classification problem in nonlinear feature space. For detailed introductions of these models, please refer to references (Vapnik 1998; Zhang et al. 2017; Berger 2013; Tanha et al. 2017; Wang et al. 2014; Freund and Schapire 1996).

Support vector machine (SVM)

SVM is a prevalent ML and pattern classification technique which transforms data points into a high-dimensional feature space and identifies an optimum hyperplane separating the classes present in the data (Vapnik 1998).

K-nearest neighbor (KNN)

KNN is an effective nonparametric classifier which performs the classification by searching for the test data’s k nearest training samples in the feature space (Zhang et al. 2017). It utilizes Euclidean or Manhattan distance as a distance metric for the similarity measurement.

Naive Bayes (NB) classifier

NB classifier is a probabilistic method relying on the assumption that every pair of features involved are independent of each other whose weights are of equal importance (Berger 2013). The main advantages of NB are the conditional independence assumption, which lead to a quick classification and the probabilistic hypotheses (results obtained as probabilities of belonging of each class).

Decision tree (DT)

In DT, features are used as input to construct a tree structure in which several rules are extracted to recognize the class of the test data (Tanha et al. 2017).

Ensemble learning based Adaboost (ELA) classifier

Ensemble learning techniques combine the outputs of several base classification techniques to form an integrated output and enhance classification accuracy. Compared to other ML methods that try to learn one hypothesis from the training data, ensemble learning relies on constructing a set of hypotheses and combines them for use (Wang et al. 2014). For the popular Boosting ensemble method, we adopt the addative boosting (Adaboost) algorithm (Freund and Schapire 1996) in this study.

Each classification model requires one or several parameters that control the prediction outcome of the classifier. Choosing the best values for these parameters is difficult and involves finding a trade-off between the model’s complexity and its generalization ability. In the present study, we adopt the popular radial basis function (RBF) kernel for SVM classifier. The parameter C is the penalty coefficient. The higher C is, the more the classifier cannot tolerate errors, which will lead to overfitting, and the lower C is, the less likely there will be underfitting. The parameter gamma affects the number of support vectors in the model. The relationship between the size of gamma and the number of support vectors is: when gamma is larger, the support vector is lower; when gamma is smaller, the support vector is higher. The penalty coefficient is set C = 2.25, and the gamma in the RBF function is set gamma = 0.028. For KNN classifier, different values for k are tested; the system operates best when the number of neighbors is ten (k = 10). The distance matrix calculation approach is Euclidean, and the distance weight is kept equal. In NB classifier, the Gaussian kernel function with unbounded support vector is configured, and the multivariate multinomial predictor is set for categorical predictions. In DT classifier, Gini’s diversity index is chosen as a split criterion with the maximum number of splits being 100 and the surrogate decision splits per node being 10. In ELA classifier, the number of learners is assigned as 50 and the maximum number of splits is set as 200 with the learning rate of 0.1.

Experimental results

Several experiments are conducted to test the ability of the proposed features on different classifiers. For the evaluation, seven performance parameters are used including the Sensitivity (SEN), the Specificity (SPF), the Accuracy (ACC), the Positive Predictive Value (PPV, which is also referred to as precision), the Negative Predictive Value (NPV), the Matthews Correlation Coefficient (MCC) and F1 score. These measurements are defined as follows (Azar and El-Said 2014):

$$\begin{aligned}{} & {} \textrm{SEN}=\frac{\text{TP}}{\text{TP + FN}}\times 100(\%) \end{aligned}$$

(23)

$$\begin{aligned}{} & {} \textrm{SPF}=\frac{\text{TN}}{\text{TN + FP}}\times 100(\%) \end{aligned}$$

(24)

$$\begin{aligned}{} & {} \textrm{ACC}=\frac{\text{TP + TN}}{\text{TP + TN + FN + FP}}\times 100(\%) \end{aligned}$$

(25)

$$\begin{aligned}{} & {} \textrm{PPV} =\frac{\text{TP}}{\text{TP + FP}}\times 100(\%) \end{aligned}$$

(26)

$$\begin{aligned}{} & {} \textrm{NPV}=\frac{\text{TN}}{\text{TN + FN}}\times 100(\%) \end{aligned}$$

(27)

$$\begin{aligned}{} & {} \textrm{MCC}=\frac{\text{TP}\times \text{TN-FN}\times \text{FP}}{\sqrt{(\text{TP + FN})(\text{TP + FP})(\text{TN + FN})(\text{TN + FP})}} \end{aligned}$$

(28)

$$\begin{aligned}{} & {} \mathrm{F1~score}=\frac{2\times \text{TP}}{2\times \text{TP + FN + FP}} \end{aligned}$$

(29)

where TP is the number of true positives, FN is the number of false negatives, TN is the number of true negatives and FP is the number of false positives. The sensitivity and specificity correspond to the probabilities that PD patients and healthy controls, respectively, are correctly classified. To be accurate, a classifier must have a high classification accuracy, a high sensitivity, as well as a high specificity (Chu 1999). For a larger value of MCC, the classifier performance will be better (Azar and El-Said 2014; Yuan et al. 2007). F1 score, which conveying the accuracy of the model, is the weighted harmonic mean of precision and sensitivity.

Binary and multi-class classification problems are dealt with by using five classification models: SVM, KNN, NB, DT and ELA. 10-fold cross-validation technique is used and performance outcome such as SEN, SPF, ACC, PPV, NPV, MCC and F1 score is calculated to obtain reliable and stable evaluation on the performance of the proposed method. For the 10-fold cross-validation, the data set is divided into ten subsets. Each time, one of the ten subsets is used as the test set and the other night subsets are put together to form a training set. As such, every fold has been used nine times as train data and one time as test data. The final result is the average of the 10 implementations. All experiments described in Table 2 focus on early PD detection and severity rating. Case 1 deals with the binary classification while Case 2 accomplishes four-class classification, respectively.

For a visual display of the classification results between PD patients and HCs, the confusion matrices obtained by the proposed five classifiers are shown in Tables 3, 4, 5, 6 and 7. Summary of the classification performance outcome of Case 1 for the five classifier models is illustrated in Table 8 with 10-fold cross-validation style. Among the five classifier models, the SVM classifier achieves the best classification performance.

Table 2 Different experimental cases in the present study

Table 3 The confusion matrix for Case 1: binary classification with SVM classifier

Table 4 The confusion matrix for Case 1: binary classification with KNN classifier

Table 5 The confusion matrix for Case 1: binary classification with NB classifier

Table 6 The confusion matrix for Case 1: binary classification with DT classifier

Table 7 The confusion matrix for Case 1: binary classification with ELA classifier

Table 8 Performance of the proposed classification approaches evaluated by 10-fold cross-validation method with Case 1: HCs-PD

The classification performance outcome of Case 2 for the five classifier models is illustrated in Tables 9, 10, 11, 12 and 13. Summary of the overall average classification performance of Case 2 for the five classifier models is illustrated in Table 14. Among the five classifier models, the SVM classifier achieves the best classification performance.

Table 9 Performance of the proposed classification approach evaluated by 10-fold cross-validation method for Case 2: four-class classification with SVM classifier

Table 10 Performance of the proposed classification approach evaluated by 10-fold cross-validation method for Case 2: four-class classification with KNN classifier

Table 11 Performance of the proposed classification approach evaluated by 10-fold cross-validation method for Case 2: four-class classification with NB classifier

Table 12 Performance of the proposed classification approach evaluated by 10-fold cross-validation method for Case 2: four-class classification with DT classifier

Table 13 Performance of the proposed classification approach evaluated by 10-fold cross-validation method for Case 2: four-class classification with ELA classifier

Table 14 Summary of the overall average classification performance evaluated by 10-fold cross-validation for Case 2 with five different classifiers

To further elucidate the performance of the five machine learning classifiers, Fig. 13 demonstrates the ROC curves in binary and multi-class classification, respectively.

Fig. 13

The receiver operating characteristics (ROC) curves for five classifiers of binary and multi-class classification task: a Binary classification; b Multi-class classification. The SVM classifier is superior to others classifiers with an AUC under both conditions. AUC: area under the curve

Discussion

Literature reveals that various methods have been proposed in recent years for the classification of gait signals in binary (for example, HVs vs PD patients) and multi-class (for exmaple, HCs vs PD with HY 2 vs PD with HY 2.5 vs PD with HY 3) classification problems. We present and discuss about the experimental results for different cases regarding early PD detection and severity rating. Comparisons with state-of-the-art methods are illustrated in Tables 15 and 16 by using 10-fold cross-validation on the same Physionet database.

For the binary classification, Aydin and Aslan (2021) used Hilbert-Huang Transform (HHT) to extract features from VGRF data coming from sixteen sensors on the bottom of both feet. Then 16 features were fed to the classifier constructed by vibes algorithm and classification and regression trees. The reported accuracy was 96.68$\%$. Alkhatib et al. (2020) extracted features from VGRF by using center of pressure (COP) path and load distribution and fed them to the linear discriminant analysis (LDA) classifier. Overall classification accuracy was recorded to be 95$\%$. Alam et al. (2017) used the swing time, stride time variability, and center of pressure features extracted from VGRF data and fed to the SVM classifier. The reported accuracy was 95.7$\%$. Balaji et al. (2020) proposed statistical analysis for feature selection from 16 VGRF data. Nine discriminant features were selected and fed to four machine learning classifiers for classification and the reported highest accuracy for four-class classification was 99.4$\%$ with a DT classifier. El Maachi et al. (2020) proposed 1D convolutional neural network (1D-Convnet) to build a Deep Neural Network (DNN) classifier. This model was using 18 1D-signals coming from VGRF without any handcrafted features. The reported accuracy for binary and four-class classification was 98.7$\%$ and 85.3$\%$, respectively. Veeraragavan et al. (2020) used VGRF data to compute the initial contact of right foot (ICR), initial contact of left foot (ICL), terminal contact of the right (TCR) and terminal contact of left foot (TCL) as gait features. Then they were fed to the ANN model for classification and the reported accuracy for binary and four-class classification was 87.9$\%$ and 76.08$\%$, respectively.

Overall, our classification approach achieves greatest accuracy, especially in binary classification. For multi-class classification, although our classification accuracy is not higher than that reported in (Balaji et al. 2020), we present a new classification tool together with building a novel feature vector rather than using directly the VGRF signals. In addition, we used 24 features which are less than 26 features reported in (Balaji et al. 2020). The results indicate that the proposed system can be effective for the classification of gait patterns between HCs and PD patients. The proposed method serves not only as a measure of kinematic variability and discrimination between two groups of HCs and PD patients, but also as a potential and useful artificial intelligent tool in planning ongoing prediction of PD progress, as an alternative or supportive technical means to other diagnostic approaches such as MRI, CT, etc.

Table 15 Comparing the performance (10-fold cross-validation style) in binary classification between HCs and PD patients using different methods

Table 16 Comparing the performance (10-fold cross-validation style) in four-class classification between HCs and PD patients with HY scale 2, 2.5 and 3

Conclusion

This study investigated the performance of novel gait features extracted from VGRF data on five classification models for discriminating gait patterns between HCs and PD patients. The results of this study indicate that the pattern classification of VGRF data can offer an objective and non-invasive method to assess the gait disparity between HCs and PD patients with different HY scales. Hybrid signal processing methods can extract discriminant features to figure out the gait disparity between different groups of gait patterns.These results demonstrate the potential of the proposed technique for early PD detection and severity rating through pathological gait patterns represented by VGRF on different classification models. Different from most of the previous machine learning based approaches which deal with binary classification problem that detects only the presence of PD, the proposed approach carries out a multi-class classification and quantify the stages of PD.

In terms of the limitations in the present study, there are two concerns: (1) the method was evaluated on a relatively small size of database. Future work will include a clinical validation of the proposed technique with a larger number of PD patients with different HY scales and age-matched healthy controls. (2) there are only VGRF gait signals extracted from the participants. Various gait signals like joint angles, angular velocity and acceleration, kinetic parameters (force, moment, etc) may also be considered in future work to comprehensively reflect the characteristic of pathological and normal gait patterns between HCs and PD patients. This may offer better prediction of PD stages based on HY scale.