Introduction

The brain is the most complex network, composed of a large number of neurons connected by excitatory and inhibitory synapses. It can receive and process various information, including simple perceptual and complex emotional and thinking activities (Toga and Thompson 2003; Wang Xiao-Jing et al. 2020; Han et al. 2021). To regulate various adaptive responses, the nervous system can continuously vary the neural circuits . The presynaptic neurons produce spikes to the synapses of the postsynaptic neurons through the low electrical resistance of gap junctions, which is called electrical synapses. The presynaptic neurons through the release of neurotransmitters conduce impulses to the postsynaptic neuron synapses, which known as chemical synapses. Because of the special structure of the chemical synapses, the information transmission is unidirectional, while the signal transmission in the electrical synapse is bidirectional. Dynamic changes in synaptic strength occur when the number of synapses between neurons in the cortical network or the number of neurotransmitters released by presynaptic neurons changes, called synaptic plasticity.

Synaptic plasticity, the principal mechanism of information transmission between neurons and information storage in the brain, is the basis for cognitive abilities, such as memory  and learning (Brunel and Wang 2003; Gautam et al. 2015; Clawson et al. 2017). It was first proposed by the psychologist Hebb (Hebb et al. 1949), and has a profound influence on the development of neuroscience. In particular, the experimental evidence for Hebb’s hypothesis was presented in 1997 (Frotscher et al. 1997), and the coupling between neurons was shown to be slightly increased when they both fired. Meanwhile, Bi showed that the changes in synaptic strength between neurons before and after a synapse, can be strengthened or weakened, and the effect of prominent plasticity appeared only within 50 ms of the presynaptic release time interval. This kind of synaptic plasticity which depends on spike time sequence and interval is called the spike-timing-dependent plasticity (STDP) (Sen et al. 2000; Bi and Poo 1998, 2001; Markram et al. 2012). In the past two decades, it has been extensively studied (Haas et al. 2006; Sjöström and Gerstner 2010; Markram et al. 2012; Kim and Lim 2018, 2019; Santos et al. 2019; D’Amour and Froemke 2015; Khoshkhou and Montakhab 2019).

In the cerebral cortex, neural activity changes irregularly and dynamically, as a result of the dynamic balance between the excitatory and inhibitory neurons. The excitatory neurons mainly transmit information in the brain, while the inhibitory interneurons in the brain can release inhibitory neurotransmitters to reduce the excitability of neurons, and jointly maintain the balance of neural networks through their interaction and restriction. This delicate balance is also a key factor affecting the normal function of the nervous system (Chialvo 2010; Plenz 2014; Kesheng et al. 2021; Antonio et al. 2021; Han et al. 2021). Previous observations showed Parkinson’s disease and focal seizures are related to the dynamic changes of excitatory and inhibitory connection strength in the basal ganglia (Galati et al. 2008; Oswal et al. 2021; Nambu 2005; Wang et al. 2017). Many studies were conducted based on the excitatory–inhibitory balanced network (Vogels et al. 2011; Buzsáki and Wang 2012). In 2018, Wang et al. found that the neural rhythm is mainly determined by the ratio of excitatory current to inhibitory current and the balance between excitatory and inhibitory neurons (Wang 2020). These experimental observations showed that the inhibitory synaptic plasticity is crucial for understanding the mechanisms involved in neurodegenerative diseases.

The excitatory-inhibitory balanced network exists in many different regions of the brain (such as the CA3 region of the hippocampus, basal ganglia, and the primary visual cortex) (Hunt David et al. 2018; Shi et al. 2021; Han et al. 2021; Xing et al. 2012). Most of the former studies were abstracted it as a kind of universal network model. Based on the excitatory-inhibitory  balanced network, the influence on network synchronization from different aspects were studied (Rich et al. 2018; Zhang and Liu 2019; Kim and Lim 2020; Zhang and Liu 2019; Batista et al. 2010; Sun and Yang 2010; Yao et al. 2019; Liliia and Shchur Lev 2018). Sang Yoon Kim and Woochang Lim conducted a series of research on synchronization of networks based on synaptic plasticity (Kim and Lim 2021, 2019, 2018, 2020; Khoshkhou and Montakhab 2018, 2020). In particular, a recent research result comprehensively considered the effect of  the synaptic plasticity learning mechanism on the rhythm transition of cluster neural networks by establishing neural networks with complex topology including excitatory and inhibitory clusters (Kim and Lim 2020).

Numerous research on network topology are based on the small-world network, scale-free network and random network, and the difference of the network structure has little influence on synchronization characteristics (Watts and Strogatz 1998; Kim and Lim 2015; Yoon and Woochang 2018; Liliia and Shchur Lev 2018; Kim and Lim 2018; Clawson et al. 2017; Batista et al. 2010; Khoshkhou and Montakhab 2020; Sun et al. 2019). The above factors inspire this paper. A complex network consisting of excitatory (E) pyramidal neurons and inhibitory (I) interneurons was studied, and the effects of the interaction between spike-timing-dependent plasticity and chemical synapses on network synchronization and oscillation behaviors were investigated. Our results will complement and improve the mechanism of neurodegenerative diseases from the theoretical level to providing guidance for their treatments.

The oscillation behaviors also play different functional roles in the synaptic plasticity, and different oscillation frequency bands may correspond to different behavioral states, cognitive capabilities, or human brain locations and information processing. Especially, the \(\gamma\) band rhythm is related to different functions for information integration in a large-scale network model for the primary visual cortex (V1) (Brunet Nicolas et al. 2014; Alina et al. 2021; Stauch et al. 2021; Han et al. 2021). Researching about the effects of spike-timing-dependent plasticity on the synchronization mechanism and oscillation behaviors provide a new insight into the role of synaptic plasticity for the information processing and transmission in human brain.

Accordingly, the outline of this paper is organized as follows: the following “Mathematical model and methods” section introduces the Izhikevich neuron model and methods used in this study. The “Numerical results” section explores the effects of many key parameters on synchronization and oscillation behaviors of the excitatory and inhibitory neuronal networks with different types of synaptic plasticity. The numerical results and relevant analysis are presented. Finally, “Conclusion and discussions” section gives a brief discussion and conclusion of this study.

Mathematical model and methods

With the advantages of the Izhikevich neuron model, that is, the computational is inexpensive, and rich complex spiking and bursting properties of a biological neuron can be exhibited by appropriate parameters selection (Izhikevich Eugene 2003, 2004; Izhikevich 2007), we chose it in this work. The network model consists of Izhikevich neurons, therefore, the different dynamical properties of biological neural networks can be analyzed more efficiently and deeply. As mentioned above, our study mainly uses excitatory and inhibitory neurons, and more details are described below.

Single-cell model and its dynamics

Excitatory cells and Inhibitory cells

We model excitatory neurons by the excitatory regular spiking pyramidal neurons that can fire in trains of single action potentials. For the inhibitory cortical neurons, we use the fast spiking \((\mathrm FS)\) Izhikevich interneurons. The single neuron dynamics is described by a two-dimensional system of ordinary differential equations and can be given as follows.

$$\begin{aligned} \frac{dv_{i}}{dt}=0.04v_{i}^{2}+5v_{i}+140-u_{i}+I^{DC}_{i}+I^{syn}_{i}, \end{aligned}$$
(1)
$$\begin{aligned} \frac{du_{i}}{dt}=a(bv_{i}-u_{i}), \end{aligned}$$
(2)
$$\begin{aligned} \mathrm {if}\quad v_{i}\ge V_{peak}(+30 \mathrm{mV}),\quad \mathrm{then} \quad \left\{ \begin{array}{ll} v_{i}\leftarrow c, \\ u_{i}\leftarrow u_{i}+d. \end{array} \right. \end{aligned}$$
(3)
Fig. 1
figure 1

Typical types of the Izhikevich model correspond to different values of the parameters (a, b, c, d) and the input current \(I^{DC}=10\). Time series of the membrane potential of two typical neurons (The left column) and the corresponding \(f-I\) curves illustrating properties of the Izhikevich model used in this study (The right column). a, b A excitatory regular spiking (RS) pyramidal neuron, and c, d A inhibitory fast spiking (FS) interneuron. In this simulation, the time step is 0.01 ms and the time length is 200 ms

Full size image

In the above equations, \(v_{i}\) denotes the membrane potential and \(u_{i}\) is the recovery current of each neuron i (\(i=1,\cdots ,N\)). \(I^{DC}_{i}\) represents the external current injected into \(i\text {th}\) neuron in the network determining the intrinsic firing rate of uncoupled neurons. To observe the synchronization characteristics of the mixed excitatory and inhibitory neural networks in the paper, the values of \(I^{DC}_{i}\) are chosen randomly from a uniform distribution in the range of [9, 10]. The periodic firing frequency of excitatory neurons is \(22 \text {Hz}\) as shown in Fig. 1(a, b), while for the inhibitory neurons, it is \(136 \text {Hz}\) which is shown in Fig. 1(c, d). The term \(I^{syn}_{i}\) is the sum of all incoming synaptic currents to neuron i, described in more detail below. According to the formula (3), when the membrane potential \(v_{i}\) reaches the maximum voltage, \(V_{peak}=+30\mathrm{mV}\), it is reset to c, and the recovery variable \(u_{i}\) is added by d. The parameters a, b, c and d are dimensionless, and the values of RS neurons or FS neurons are set to be different. In our simulations, we set \(a_{ex}=0.02\), \(b_{ex}=0.2\), \(c_{ex}=-65\text {mV}\), \(d_{ex}=8\) for the excitatory RS pyramidal neurons and \(a_{in}=0.1\), \(b_{in}=0.2\), \(c_{in}=-65\text {mV}\), \(d_{in}=2\) for the inhibitory FS interneurons, as described in the \(1\text {st}\) and \(2\text {nd}\) item of Table 1. The two typical properties of the neurons are illustrated in Fig. 1, and the frequency-current curves (\(f-I\) curve, the periodic firing frequency f as a function of input current density I) of the two typical neurons are plotted. The comparison of the characteristics of the two types of neurons shows a great difference in firing frequency between them, and the firing frequency of FS neurons is much higher than that of RS neurons under the same input current.

Table 1 Parameter values used in our computations
Full size table

Network architecture

As mentioned above, the Izhikevich model was considered as the local node in the system, and the Watts-Strogatz (WS) small-world network as the underlying structure (Watts and Strogatz 1998). The algorithm for constructing the WS small-world is shown as follows. It was started as a regular ring with N nodes for the rewiring probability \(p=0\), where each node is coupled to its k (an even number) nearest neighbors. Then each edge in the network was rewired randomly with probability p, without multiple edges and self-loops. When the probability p is rewired as 1, it evolves into a completely random network.

We have run simulations of \(100 \leqslant N \leqslant 1000\) for many times and found that our results are independent of the size of the neural network. Therefore, the results of \(N = 250\) is used to improve computational efficiency, which is consistent with the model used in the work of Christoph Börgers’ book (Börgers 2017). The symbolic depiction of the excitatory (E) and inhibitory (I) network was shown in Fig. 2. The lines of black arrows represent that the connections of presynaptic neurons is E, and the lines of black circles denote that the connections of presynaptic neurons is I.

This study emphasizes the influence of STDP on network dynamics. To compare the effects of eSTDP and iSTDP on network synchronous transition, we consider the following different network structures of N: a small-world network of purely excitatory neurons (\(\alpha =0\)), in other words, the number of excitatory neurons is \(N_{e}=N\); a small-world network of purely inhibitory neurons (\(\alpha =1\)), that is, the number of inhibitory neurons is \(N_{i}=N\) and a small-world network of mixed excitatory and inhibitory neurons (\(\alpha =0.2\)). Based on the anatomy of a mammalian cortex, the ratio of excitatory to inhibitory neurons is set as 4 : 1, which means \(N_{e}=200\) and \(N_{i}=50\). All the simulations were coded using MATLAB vR2020b.

Fig. 2
figure 2

Symbolic depiction of the excitatory (E) and the inhibitory (I) network. (Color online) Lines with black solid arrows represent the E to E and E to I connections. The connections of I to E and I to I are represented by the lines with black solid circles

Full size image

Synaptic currents and plasticity

Neural information is transmitted mainly through the synaptic connections between neurons. In cultures of dissociated rat hippocampal neurons, Bi and Poo found that both LTP and LTD depended on the activation of NMDA receptors (Bi and Poo 1998). Further research showed that both GABA and AMPA receptors affect the frequency of the neural network oscillations (Brunel and Wang 2003). In general, the major factors that affect the membrane potential of the postsynaptic neurons are neurotransmitters released by chemical synapses, which diffuse through the synaptic cleft to the postsynaptic membrane and bind to specialized receptors. Thus, the ion channels are opened, and then the membrane potential of the neuron is changed. Therefore, in our network, neurons are connected by chemical synapses, and the effect of the pre-synaptic neurons on the post-synaptic neurons can be expressed as \(I^{syn}_{i}\) (Brunel and Wang 2003; Roth and Van Rossum 2009).

$$\begin{aligned} I^{syn}_{i}=\frac{1}{D^{in}_{i}}\sum _{j=1,j\ne i}^N g_{ji}w_{ji}s_{j}(t)(V^{syn}-v_{i}) \end{aligned}$$
(4)
$$\begin{aligned} s_{j}(t)=\frac{\exp\left( -\frac{t-t{j}}{\tau _{d}}\right) -\exp\left( -\frac{t-t_{j}}{\tau _{r}}\right) }{\tau _{d}-\tau _{r}} \end{aligned}$$
(5)

Here, the connectivity matrix \({(w_{ji})}_{N\times N}\) can be defined according to the structure of the complex network. If the neuron j is the presynaptic to the neuron i (\(i\ne j\)), then \(w_{ji}=w_{ij}=1\); otherwise, \(w_{ji}=0\) and \(w_{ii}=0\) for all i. Small world neural network is our main network structure. In addition, \((w_{ji})_{N\times N}\) is an asymmetric and irreducible matrix. And \(D^{in}_{i}\) denotes the in-degree of the ith neuron, which is given by \(D^{in}_{i}=\sum _{j=1,j\ne i}^N w_{ji}\). The function 5 represents the synpatic gating varible of neuron j at time t, where \(\tau _{d}\) and \(\tau _{r}\) are the synaptic rise time and decay time, respectively. \(t_{j}\) is the last spiking time of the pre-synaptic neuron j. \(V^{syn}\) represents the reversal potential of the synapse with \(V^{syn}_{ex} = 0\) for excitatory connections and \(V^{syn}_{in} = -75\) for inhibitory connections, which are listed in the \(3\text {rd}\) item of Table 1. The term \((g_{ji})_{N\times N}\) describes the coupling strength of the synapse from neuron j to neuron i, when firing of the jth neuron instantaneously changes the value \(v_i\) by \(g_{ji}\), which is a variable in our simulations, and \(g_{ji}=g_{ji}+\varDelta g_{ji}\).

Neuroscientific studies have found that the synapses of neurons are plastic, and their connections strength changes over time. The changes in the strength of numerous synapses generate the brain’s memory function. Therefore, we consider the spike-timing-dependent plasticity based on the Hebbian rule. the synapses coupling strength g is adjusted based on the relative timing between the spikes of pre-synaptic and post-synaptic neurons.

According to the nearest-spike mechanism, a pair of spikes was selected between the presynaptic neuron firing instant and the postsynaptic neuron firing instant. The synaptic weights between presynaptic and postsynaptic neurons were modified by the time difference \(\varDelta t= t_{post}-t_{pre}\) between the pre-neuron and post-neuron firing time. \(\varDelta t\) is a key variable that regulates the weight of connections between presynaptic and postsynaptic neurons, and the specific model expression is as follows (Haas et al. 2006, Field et al. 2020, Kim and Lim 2019, Khoshkhou and Montakhab 2019).

$$\begin{aligned} \varDelta g^{e}_{ij}= \left\{ \begin{array}{ll} A_{+}\exp ( -{\varDelta } {t_{ij}}/\tau _{+}), &{} {{\varDelta } {t_{ij}} \ge 0} \\ -{A_{{-}\exp} ( {\varDelta } {t_{ij}} {\tau _{-}})} &{} {{\varDelta } {t_{ij}} < 0}. \end{array} \right. \end{aligned}$$
(6)
$$\begin{aligned} \varDelta g^{i}_{ij}= \left\{ \begin{array}{ll} -A_{+}\exp ( -{\varDelta } {t_{ij}}/{\tau _{+}}) &{} {{\varDelta } {t_{ij}} \ge 0} \\ -A_{-}\frac{{\varDelta } {t_{ij}}}{{\tau _{-}}}\exp ( -{\varDelta } {t_{ij}} {\tau _{-}}) &{} {{\varDelta } {t_{ij}} < 0} \end{array} \right. \end{aligned}$$
(7)

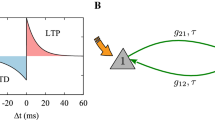
Here \(\varDelta t=t_{i}-t_{j} = t_{post}-t_{pre}\), \(t_{pre}\) and \(t_{post}\) are the last spiking time of the presynaptic and the postsynaptic neurons, respectively. Only the difference in the spiking time of the most recent spike is recorded here. \(A_{+}\) and \(A_{-}\) represent the maximum synaptic increment and inhibition parameters. The temporal parameters of synaptic enhancement and inhibition are represented by symbols \(\tau _{+}\) and \(\tau _{-}\). The specific marking calculation method is shown in Fig.3. Figure 4 shows the time window of eSTDP and iSTDP for \(g^{e}_{ij}\) and \(g^{i}_{ij}\). All the parameters used for Izhikevich neurons, synaptic current and STDP rules are given in Table 1.

Fig. 3
figure 3

Schematic diagram of the nearest spike mechanism. Blue and black lines refer to the firing time of pre-synaptic and post-synaptic neurons in simulated time, respectively

Full size image
Fig. 4
figure 4

Plasticity as a function of the postsynaptic and presynaptic temporal window. \(\varDelta g_{ij}=F(\varDelta t)\). a excitatory (eSTDP) and b inhibitory (iSTDP)

Full size image

Synchrony measure

To explore the effect of synaptic plasticity on the neural network, the Kuramoto order parameter is used to quantify the degree of synchronization activity in the neural population (Kuramoto 1975, 1984). We begin with an instantaneous phase to each neuron expressed by (Pikovsky and Osipov 1997):

$$\begin{aligned} \phi _{j}(t)=2\pi \frac{t-t^m_{j}}{t^{m+1}_{j}-t^m_{j}}. \end{aligned}$$
(8)

where \(t^m_{j}\) represents the instant when a spike \(m (m=0,1,2,\cdots )\) of a neuron j occurs \((t^m_{j}<t<t^{m+1}_{j})\). Then the population average order parameter is given by:

$$\begin{aligned} R(t)= \frac{1}{N} \sum _{j=1}^{N}e^{i\phi _{j}(t)}, \end{aligned}$$
(9)

and the global instantaneous order parameter R defined as:

$$\begin{aligned} R=\left\langle \cdots \right\rangle _{t}=\frac{1}{t_{fin}-t_{ini}}\int _{t_{ini}}^{t_{fin}} R(t)dt \end{aligned}$$
(10)

where R is computed by average temporal length of \(t_{fin}-t_{ini}=5s\). R is bounded between 0 and 1. In particular, \(R=1\) indicates complete synchronization, while \(R=0\) means asynchronization.

In our simulations, all the equations were numerically integrated using the Fourth-Order Runge-Kutta Method with a time-step size equaling to \(10^{-2}\) ms. The simulations of the neuronal network have been improved and after 10 s from random initial conditions, the network reaches a statistically stable state. In this paper, the spatio-temporal patterns of the neuronal network are plotted. The excitatory cells are given the lowest neuron index toward the bottom of the y-axis while the inhibitory cells are given the highest neuron index towards the top of the y-axis.

Numerical results

This section presents the numerical results and relevant analyses. We mainly focus on how the effect of synaptic plasticity on the synchronization transitions of different populations. Therefore, three different networks: a network of purely excitatory neurons with eSTDP \((\alpha =0)\), a network of purely inhibitory neurons with iSTDP \((\alpha =1)\) and a network of excitatory and inhibitory neurons with eSTDP and iSTDP \((\alpha =0.2)\).

A network of purely excitatory neurons with eSTDP

The first focus is the effect of excitatory spike-timing-dependent plasticity (eSTDP) on the synchronization of the purely excitatory neuron network.

Fig. 5
figure 5

a, b, c The variation trend of coupling strength of two excitatory neurons under the action of eSTDP. d, e, f The variation trend of average coupling strength of the whole neural network under eSTDP. In this simulation, the time step is 0.01 ms and the time length is 3000 ms. a, d \(g_{ee}=0.15\),\(k=10\); b, e \(g_{ee}=0.15,k=50\); c, f \(g_{ee}=0.45,k=50\)

Full size image

In the first case, based on the excitatory complex network, the spiking behaviors of two coupled neurons were observed by changing the coupling strength \(g_{ee}\) between excitatory synapses and the number of the nearest neurons k. First of all, a pair of mutually coupled neurons are randomly selected and denoted as \(g_{12}\) and \(g_{21}\), and they are opposite to each other. The initial value of the coupling strength is \(g_{ee}=0.15\), and the number of the nearest neighbor coupled neurons in the small-world network is \(k=10\). As shown in Fig. 5a, when the coupling strength of \(g_{12}\) increases, the coupling strength of \(g_{21}\) decreases, but the interaction between them is not completely symmetric. Figure 5d shows that the coupling strength of the whole network gradually increases from the initial value of 0.15 to 0.3. In Fig. 5b, e, when the number of the nearest neighbor neurons in the small-world network is increased, and k value is 50, \(g_{12}=0.15\) quickly decreases to 0, while \(g_{21}\) increases from 0.15 to 0.6, and continues to increase after \(g_{12}=0\). Therefore, the coupling strength of the overall network tends to increase gradually, which is consistent with Fig. 5e. When the initial value of the coupling strength is \(g_{ee}=0.45\), the value of \(g_{12}\) rapidly increases from 0.45 to 0.6, while that of \(g_{21}\) is decreased from 0.45 to 0, and the average coupling strength of the overall network decreases rapidly. Only 1000 ms was used when the average coupling strength decreased from 0.45 to 0.3, while 3000 ms was adopted for that from 0.15 to 0.3 for the first two cases, as shown in Fig. 5f. Therefore, both the coupling strength between synapses and the number of the nearest neighbor coupling neurons in the small-world network affect the average coupling strength of the network.

Fig. 6
figure 6

The raster plots of the network and the change curve of the synchronization degree of the network. In this simulation, the time step is 0.01 ms and the time length is 3000 ms. a, d \(g_{ee}=0.15,k=10\); b, e \(g_{ee}=0.15,k=50\); c, f \(g_{ee}=0.45,k=50\)

Full size image

Next, to study the synchronization dynamics of the overall neural network, the raster plots of the network and the change curve of the synchronization degree of the network are made, which are shown in Fig. 6. When the values of the coupling strength \(g_{ee}\) and the number of the nearest neighbor neurons k are small, the network shows irregular discharge behavior, as shown in Fig. 6a. As k increases to 50 (Fig. 6b) and \(g_{ee}\) to 0.45 (Fig. 6c), the whole network becomes stable, with regular firing synchronization. In addition, the value of the synchronization parameter R increases rapidly with these two variables. Figure 6e shows that R fluctuates and rises in the initial stage, and finally stabilizes in complete synchronization. It can be found in Fig. 6f that R is stabilizes around 0.9, and the whole network is always in a stable and completely synchronous state.

Fig. 7
figure 7

a Synchrony measure R (color bar) as a function of the coupling strength \(g_{ee}\) and the number of the nearest neighbor neurons k without eSTDP. b Synchrony measure R (color bar) as a function of  the coupling strength \(g_{ee}\) and the number of the nearest neighbor neurons k combined with eSTDP. c The difference of influence on synchronization parameters \(\varDelta R_{ee}\)(color bar) as a function of the  coupling strength \(g_{ee}\) and the number of the nearest neighbor neurons k

Full size image

Both coupling strength \(g_{ee}\) and the number of the nearest neighbor neurons k can promote network synchronization without eSTDP, as shown in Fig. 7a (Wang et al. 2020). To this end, the synchronous changes in the state combined with eSTDP are shown in Fig. 7b. \(\varDelta R_{ee}= R_{eSTDP}-R_{ee}\) is defined as the difference of influence on synchronization parameters after eSTDP is combined, and the specific change diagram is given in Fig. 7c. The observation shows that with the increase of \(g_{ee}\) and k, the degree of synchronization R gradually strengthens. When \(g_{ee}\) is less than 0.3, the network is in a state of chaos with small changes in R. When \(g_{ee}\) is between 0.3 and 0.4, k obviously influences synchronization. When \(g\geq0.4\), the network is completely synchronous. When \(g_{ee}\) is greater than 0.2 and is combined with eSTDP, complete synchronization can be achieved, and the value of k is insensitive to the effects of synchronization. Finally, it can be concluded from Fig. 7c that the addition of synaptic plasticity in the excitatory neural network can greatly promote network synchronization. According to the equation (6), \(\varDelta g^{e}_{ij}\) adjusts based on the different firing time between neurons to promote network synchronization, and the restraining effect of eSTDP makes the network gradually stable.

A network of purely inhibitory neurons with iSTDP

The effect of inhibitory spike-timing-dependent plasticity was considered in the same way when the study of the synchronous dynamic mechanism of the inhibitory neural network is studied.

Fig. 8
figure 8

a, b, The variation trend of the coupling strength of two inhibitory neurons under the action of iSTDP. c, d The variation trend of the average coupling strength of the whole neural network under iSTDP. In this simulation, the time step is 0.01 ms and the time length is 3000 ms. a, c \(g_{ii}=0.15,k=50\); b, d \(g_{ee}=0.45,k=50\)

Full size image

Firstly, we randomly selected a pair of mutually coupled inhibitory neurons and their interaction was observed by changing the coupling strength \(g_{ii}\) between them, as shown in Fig. 8a. When the initial coupling strength is \(g_{ii}=0.15\) and the number of the nearest neighbor neurons is \(k=50,\) \(g_{12}\) and \(g_{21}\) show symmetrical periodic changes, with low variation frequency and continuous changes between 0.3 and 0.6 (Fig. 8a). When the coupling strength \(g_{ii}\) is increased to 0.45, the fluctuation frequency of \(g_{12}\) and \(g_{21}\) is significantly increased (as Fig. 8b). When the initial value of \(g_{ii}\) is 0.15 and 0.45, the average coupling strength can increase to 0.54, and finally stabilize, which is completely different from that in the excitatory neural network.

Fig. 9
figure 9

The raster plots of the network and the change curve of the synchronization degree of the network. In this simulation, the time step is 0.01 ms and the time length is 3000 ms. a, c \(g_{ee}=0.15,k=50\); b, d \(g_{ee}=0.45,k=50\)

Full size image

Figure 9 shows the raster plots and the change curve of the synchronization degree R of the network. The raster plots of the neural network are in the chaotic state of high firing frequency, and the synchronization order parameter R fluctuates irregularly below 0.4, indicating that the irregular firing synchronization characteristics of the network.

Fig. 10
figure 10

a Synchrony measure R (color bar) as a function of the coupling strength \(g_{ii}\) and the number of the nearest neighbor neurons k without iSTDP. b Synchrony measure R (color bar) as a function of  the coupling strength \(g_{ii}\) and the number of the nearest neighbor neurons k combined with iSTDP. c The difference of influence on synchronization parameters \(\varDelta R_{ii}\) (color bar) as a function of the  coupling strength \(g_{ii}\) and the number of the nearest neighbor neurons k

Full size image

In the excitatory neural network mentioned above, we found that the coupling strength, the number of the nearest neighbor neurons and the synaptic plasticity all promoted synchronization. However, in the inhibitory network, no obvious changes were found. Thus, we combine these three factors to consider the overall synchronous dynamic mechanism, as shown in Fig. 10.

The color of Fig. 10a and b changes slightly, the synchronization order parameter is always lower than 0.4, so the network is considered in a chaotic state. Just to clarify our results, similarly, \(\varDelta R_{ii}= R_{iSTDP}-R_{ii}\) is defined as the difference of influence on synchronization parameters after iSTDP is combined, and the specific change diagram is given in Fig. 10c. Its variation is less than 0.3, which means that the synchronization effect of the inhibitory neural networks is insensitive to the iSTDP.

A network of excitatory and inhibitory neurons with mixed eSTDP and iSTDP

The first two sections discuss the effects of the synaptic plasticity on a purely dynamic characteristic network. It can be found that the influence of the synaptic plasticity on the  excitatory and inhibitory networks is quite different. The role of the synaptic plasticity in the excitatory–inhibitory balanced neural network should be clarified.

First, a pair of neurons coupled by excitatory synapses and a pair of neurons coupled by inhibitory synapses were randomly selected to observe the interaction between them. Figure 11a, b shows a pair of excitatorily coupled neurons, and the initial coupling strength is 0.15 and 0.45, respectively. The number of the nearest neighbor neurons k is 50. It was found that the coupling strength of two neurons fluctuated periodically under the action of mixed STDP compared with that in the purely excitatory neural network (Fig. 5). However, the frequency of generating cycles was much smaller than that of the network composed of purely inhibitory neurons (Fig. 8). The coupling strength curve of a pair of inhibitory synaptic coupling neurons was shown in Fig. 11c, d. It was found that the change frequency of the coupling strength of two neurons also fluctuates with the increase of the coupling strength value g. In addition, the frequency of the coupling strength fluctuation was faster than that of the neural network with purely inhibitory coupling (Fig. 8a, b). Mixed STDP is the result of two learning rules, eSTDP and iSTDP, which exert balanced traction on the synaptic coupling of excitatory neurons, leading to periodic fluctuations in the coupling strength.

The variation curves of the four average synaptic coupling strengths of the neural network, including the coupling strengths of excitatory and excitatory neuron connections \(g_{EE}\), the coupling strengths of excitatory and inhibitory neuron connections \(g_{EI}\), the coupling strengths of inhibitory and excitatory neuron connections \(g_{IE}\), and the coupling strengths of inhibitory and inhibitory neuron connections \(g_{II}\), are shown in Fig. 11e, f. Observations indicate that when the initial coupling strength is 0.15, with the addition of synaptic plasticity , the coupling strength of the stable network tends to 0.3. However, when it is 0.45, the coupling strength gradually decreases to 0.3, which means the trend of \(g_{EE}\) is consistent with Fig.5d, e, f. For \(g_{EI}\), \(g_{IE}\) and \(g_{II}\), the coupling intensity of \(g_{EI}\), \(g_{IE}\) and \(g_{II}\) accords with the case of purely inhibitory neural network in Fig. 8. In other words, under the mutual restriction of mixed synaptic plasticity, the average coupling strength of excitatory and excitatory neurons (\(g_{EE}\)) keeps the overall trend of excitatory spike-timing-dependent plasticity and makes the average coupling strength fluctuate periodically. When at least one of the two coupling neurons is inhibitory, the effect of inhibitory spike-timing-dependent plasticity (iSTDP) is manifested. That means, if RS and FS neurons are coupled with each other, the iSTDP between them will promote the firing frequency.

Fig. 11
figure 11

a, b The variation trend of the coupling strength of two excitatory neurons under the action of mixed spike-timing-dependent plasticity. c, d The variation trend of the coupling strength of two inhibitory neurons under the action of mixed spike-timing-dependent plasticity. e, f The variation trend of the average coupling strength of the whole neural network under mixed spike-timing-dependent plasticity. In this simulation, the time step is 0.01 ms and the time length is 3000 ms. a, c, e \(g_{ii}=0.15,k=50\); b, d, f \(g_{ee}=0.45,k=50\)

Full size image

Then, the effect of mixed spike-timing-dependent plasticity on the synchronization dynamics of the whole network is observed through the variation curve of the synchronization degree of the whole network. When the initial coupling strength of neurons was \(g=0.15\), the synchronization order parameters R showed a fluctuating rise and exceeded 0.5 for a time, but the network still did not produce regular synchronous characteristics, as shown in Fig. 12a. In addition, when the coupling strength of initial neurons was increased to \(g = 0.45\), the synchronization degree R remained below 0.5 with the changes of time, which is shown in Fig. 12b. It does not like a purely excitatory network that makes the whole network to achieve complete synchronization and also in the purely inhibitory network on the basis of promoting effect on the degree of synchronization. Therefore, the stimulative effect of  eSTDP and the inhibitory effect of iSTDP jointly  maintain the balance of the E-I network.

Fig. 12
figure 12

The change curve of the synchronization degree of the network. In this simulation, the time step is 0.01 ms and the time length is 3000 ms. a, c \(g_{ee}=0.15,k=50\); b, d \(g_{ee}=0.45,k=50\)

Full size image

The effects of the synaptic coupling strength and mixed spike-timing-dependent plasticity on network synchronization are discussed. In the study of purely excitatory neural network and purely inhibitory neural network, the effect of the number of the nearest neighbor coupling neurons k on the synchronization of the whole neural network is also considered. Then, the synchronization and balance of the excitatory–inhibitory balanced network under the joint action of these two factors is studied.

The change of synchronization order parameter R with the coupling strength g and the number of nearest coupling neurons k of the small-world network is shown by the color diagram in Fig. 13. The synaptic plasticity is not included in the subgraph of Fig. 13a, and the color of R is always blue. That means in the excitation-inhibitory balanced network, no matter how the parameters g and k change, the network is always in a chaotic state, where R is lower than 0.5. Then, eSTDP and iSTDP were added into the excitatory–inhibitory balanced network. Although the color in Fig. 12b became light, R was still lower than 0.5. This is consistent with the result in Fig. 12. The synchronization difference of \({\varDelta R}\) with and without synaptic plasticity fluctuated less than 0.2.

Fig. 13
figure 13

a Synchrony measure R (color bar) as a function of the coupling strength \(g_{ii}\) and the number of the nearest neighbor neurons k without iSTDP. b Synchrony measure R (color bar) as a function of the  coupling strength \(g_{ii}\) and the number of the nearest neighbor neurons k combined with iSTDP. c The difference of influence on synchronization parameters \(\varDelta R_{ii}\)(color bar) as a function of the  coupling strength \(g_{ii}\) and the number of the nearest neighbor neurons k

Full size image

Conclusion and discussions

In this section, we mainly consider the synchronous transition mechanism of the excitatory and inhibitory neural networks with spike-timing-dependent plasticity (STDP). By changing the initial coupling strength of the network, the number of the nearest neighbor coupling neurons of the small-world network, and combined with the STDP of the excitatory and inhibitory impulses, we conducted in-depth exploration based on different network structures.

The research in this section is mainly analyzed and discussed in three different situations.

First, a purely excitatory network composed of RS neurons was constructed, and excitatory spike- timing-dependent plasticity (eSTDP) was added to the network. By changing the initial coupling strength of the network, it is found that the final coupling strength of the network tends to be 0.3, and the synchronization degree is obviously improved. Changing the number of the nearest coupling neurons of the small-world network, that is, the number of connecting edges of the network increases. For a single neuron, the increase in the number of synapses connected to it will lead to an increase in the value of coupling terms, so the synchronization degree of the network will be enhanced. In addition, the STDP of the excitatory pulse adjusted and stabilized the coupling strength at the intermediate strength of 0.3. Finally, the network evolves to complete synchronization and remaines stable.

Then, a purely inhibitory small-world network composed of inhibitory neurons in fast spiking (FS) firing mode is used to add inhibitory spike-timing-dependent plasticity (iSTDP) into the network. There are no similar results between purely excitatory and purely inhibitory neural networks. The initial coupling strength of the network has no effect on the coupling strength of the steady state of the neural networks, and it eventually tends to a large value of 0.55, and the upper bound of the coupling strength is 0.6. However, the interesting finding is that the coupling strength fluctuates periodically, and the frequency of fluctuation increases with the increase of the initial coupling strength. The effect of the number of nearest neighbor coupling neurons on the degree of network synchronization is also negligible. Of course, the most important concern is that the  spike-timing-dependent plasticity of inhibitory impulses did not produce desirable results either.

The two extremes are analyzed above, but the main purpose is to study the role of synaptic plasticity in the excitatory–inhibitory balanced network. Therefore, in the last part, RS neurons and FS neurons jointly constitute the excitatory–inhibitory balanced network at the ratio of 4 : 1. In this network, eSTDP and iSTDP are also added. Under their joint action, the synchronization behaviors of the network are different.

For the coupling strength in the network, when the coupling strength is lower, the enhancement effect keeps the coupling strength curve to fluctuate in low range. When the coupling strength is higher, the coupling strength will be reduced within the scope of the lower curve fluctuations. In addition, in the excitatory–inhibitory balanced network, the mean coupling intensity tends to inhibit the STDP of the inhibitory impulse as long as the inhibitory neurons are involved. Although the proportion of inhibitory neurons is only \(25\%\), the inhibitory effect of iSTDP was dominant.

In recent years, several papers on the emergence of the oscillation and synchronization in the compuational models showed some of the oscillation like gamma band rhythm had stochastic property (Hunt David et al. 2018; Brunet Nicolas et al. 2014; Xing et al. 2012; Chariker et al. 2018, 2016; Saraf and Young 2021). In our simulating results, we did not find the existence of stochastic property which may be due to the lack of complexity of network model structure. We will consider the stochastic property in the follow-up work with specific brain regions.

In terms of network synchronization, in the excitatory–inhibitory balanced network, there is no completely synchronous behavior as in the purely excitatory network, nor is it like the completely chaotic state in the pure inhibitory network. The synchronization degree is balanced around 0.5. That means as eSTDP promots network synchronization, mixed synaptic plasticity inhibites it by iSTDP to maintain network balance. The weight of eSTDP and iSTDP in this paper is the same, and iSTDP has played a strong leading role. More complex situations in this aspect will be studied in the future.

There also have been many researches about not only neuronal synchronization, but also the effects of the synaptic delay on a neuronal network with STDP (Xie et al. 2016; Mojtaba et al. 2017; Lameu et al. 2018). They showed that the neuronal plasticity and synaptic delay are closely linked to the intensity of excitatory couplings. Increasing the time delay, the synchronous behavior of the neural network is suppressed. However, these studies have mainly focused on the effect of time delays on excitatory synapses, and inhibitory synaptic plasticity remains to be further discussed. That’s what we’re going to do next. Excessive synchronization will lead to neurodegenerative diseases, such as seizures and Parkinson’s disease (Schwab et al. 2013; Cian et al. 2018). This study found the joint restriction of eSTDP and iSTDP, which can be used to guide the treatment and further research of the neurodegenerative diseases.