New delay-interval-dependent stability criteria for switched Hopfield neural networks of neutral type with successive time-varying delay components

Abstract

This paper deals with the problem of delay-interval-dependent stability criteria for switched Hopfield neural networks of neutral type with successive time-varying delay components. A novel Lyapunov–Krasovskii (L–K) functionals with triple integral terms which involves more information on the state vectors of the neural networks and upper bound of the successive time-varying delays is constructed. By using the famous Jensen’s inequality, Wirtinger double integral inequality, introducing of some zero equations and using the reciprocal convex combination technique and Finsler’s lemma, a novel delay-interval dependent stability criterion is derived in terms of linear matrix inequalities, which can be efficiently solved via standard numerical software. Moreover, it is also assumed that the lower bound of the successive leakage and discrete time-varying delays is not restricted to be zero. In addition, the obtained condition shows potential advantages over the existing ones since no useful term is ignored throughout the estimate of upper bound of the derivative of L–K functional. Using several examples, it is shown that the proposed stabilization theorem is asymptotically stable. Finally, illustrative examples are presented to demonstrate the effectiveness and usefulness of the proposed approach with a four-tank benchmark real-world problem.

Introduction

Over the past decades, switched neural networks (SNNs) have become a popular research topic that attracts researcher’s attention, various delayed neural networks such as Hopfield NNs, Cohen–Grossberg NNs, cellular NNs and bidirectional associative memory NNs have been extensively investigated. Switched systems are an important class of hybrid dynamical systems which are composed of a family of continuous-time or discrete-time subsystems and a rule that orchestrates the switching among them. Switched systems provide a natural and convenient unified framework for mathematical modeling of many physical phenomena and practical applications, such as autonomous transmission systems, computer disc drivers, room temperature control, power electronics, chaos generators, to name but a few. In recent years, considerable efforts have been focused on the analysis and design of switched systems. In this regard, lots of valuable results in the stability analysis and stabilization for linear or nonlinear hybrid and switched systems were established (see Liberzon and Morse 1999; Song et al. 2008; Zong et al. 2008; Hetel et al. 2008 and references therein).

Within the last few decades, many researcher’s have well-focused on the dynamic analysis of Hopfield NNs, which was first introduced by Hopfield (1982, 1984), has drawn considerable attention due to their many applications in different areas such as pattern recognition, associative memory and combinatorial optimization. Since, the stability is one of the most important behaviors for the NNs, a great deal of results concerning the asymptotic or exponential stability have been proposed (see e.g., Xu 1995; Cao and Ho 2005; Cao et al. 2007, 2008, 2016; Manivannan et al. 2016; Aouiti et al. 2016; Yang et al. 2006; Zhou et al. 2009 and the references therein). It is well known that time delays are often encountered in NNs which may degrade the system performance and cause oscillation, leading to instability. Therefore, it is of great importance to study the asymptotic or exponential stability of NNs with time delay. Meanwhile, neutral time-delay systems are frequently encountered in many practical situations such as in chemical reactors, water pipes, population ecology, heat exchangers, robots in contact with rigid environments (Zhang and Yu 2010; Niculescu 2001), and so on. A neutral time-delay system contains delays both in its state, and in its derivatives of state. Therefore, many dynamical NNs are described with neutral functional differential equations that include neutral delay differential equations as their special case. These NNs are called neutral type NNs or NNs of neural-type.

Since, we know that successive time-varying delay model has a more strapping application background in remote control and control system. For example, we consider a state-feedback networked control, where the physical plant, controller, sensor, and actuator are placed at different places and signals are transmitted from one device to another. Along with the delays, there are two network-induced ones, one from sensor to controller and the other from controller to actuator. Then, the closed loop system will appear with two additive time delays in the state. Thus, in the network transmission settings, the two delays are usually time varying with dissimilar properties. Therefore, it is of substantial importance to study the stability of systems with two additive time-varying delay components. Motivated by the previous discussion, in this paper we are concerned with the problem of stability analysis for SHNNs of neutral type with successive time-varying delay components. In this connection, recently a new form of NNs with two additive time-varying delays has been considered in Zhao et al. (2008), Gao et al. (2008) and Shao and Han (2011). In Lam et al. (2007) and Rakkiyappan et al. (2015a, b), it was mentioned that in network controlled system (NCS), if the signal transmitted from one point to another passes through few segments of networks, then successive delays are induced with different properties owing to variable transmission conditions. That is, if the physical plant and the state-feedback controller are given by $\dot{z}(t)={\mathcal{A}}z(t) + {\mathcal{B}}u(t)$ and $u_c(t)=Kx_c(t)$, then it is appropriate to consider time-delays in the dynamical model as $\dot{z}(t)={\mathcal{A}}z(t) + {\mathcal{B}} Kz(t-h_1(t)-h_2(t))$, where $h_1(t)$ is the time-delay induced from sensor to controller and $h_2(t)$ is the delay induced from controller to the actuator. Therefore, the stability analysis of such system was earlier carried out by adding up all the successive delays into a single delay, that is $h_1(t) + h_2(t)=h(t)$ to develop a sufficient stability condition. Therefore, the problem of stability analysis of NNs with successive time-varying delays in the state has received more and more attention and become more popular in recent years (see Rakkiyappan et al. 2015a, b; Senthilraj et al. 2016; Samidurai and Manivannan 2015; Dharani et al. 2015 and the references therein).

Recently, the stability of systems with leakage delays becomes one of the hot topics and it has been studied by many researcher’s in the literature. The research about the leakage delay (or forgetting delay), which has been found in the negative feedback of system, can be traced back to 1992. In Kosko (1992), it was observed that the leakage delay had great impact on the dynamical behavior of the system. Since then, many researcher’s have paid much attention to the systems with leakage delay and some interesting results have been derived. For example, Gopalsamy (1992), considered a population model with leakage delay and found that the leakage delay can destabilize a system. In Gopalsamy (2007), the bidirectional associative memory (BAM) neural networks with constant leakage delays were investigated based on L–K functions and properties of M-matrices. Inspired by Gopalsamy (2007), recently it is essential important to study the stability of delayed NNs with leakage effects have been existing in Samidurai and Manivannan (2015), Sakthivel et al. (2015), Li et al. (2011, 2015), Lakshmanan et al. (2013), Li and Yang (2015), and Balasubramaniam et al. (2012).

So far, recently Rakkiyappan et al. (2015a, b), established the exponential synchronization of complex dynamical networks with control packet loss and additive time-varying delays. Currently, Senthilraj et al. (2016), proposed the problem of stability analysis of uncertain neutral type BAM neural networks with two additive time-varying delay components. Very recently, robust passivity analysis for delayed stochastic impulsive NNs with leakage and additive time-varying delays have been established by Samidurai and Manivannan (2015). Very recently, Rakkiyappan et al. (2015a, b), analyzed synchronization for singular complex dynamical networks with Markovian jumping parameters and two additive time-varying delay components. More recently, new stability criteria for switched Hopfield NNs of neutral type with additive time-varying discrete delay components and finitely distributed delay were studied by Dharani et al. (2015). Lakshmanan et al. (2013), stability problem concerned with the BAM neural networks with leakage time delay and probabilistic time-varying delays was studied. Li and Yang (2015) analyzed the leakage delay has significant impacts on the dynamical behavior of genetic regulatory networks (GRNs) and can bring tendency to destabilize systems. Recently, in Li et al. (2015) considered stability problem for a class of impulsive NNs model, which includes simultaneously parameter uncertainties, stochastic disturbances and two additive time-varying delays in the leakage term. Balasubramaniam et al. (2012), deals with the problem of delay-dependent global asymptotic stability of uncertain switched Hopfield NNs with discrete interval and distributed time-varying delays and time delay in the leakage term.

Very recently, Sakthivel et al. (2015), considered the issue of state estimation for a class of BAM neural networks with leakage term. Fuzzy cellular NNs with time-varying delays in the leakage terms have been extensively studied by Yang (2014), without assuming the boundedness on the activation functions. In Zhang et al. (2010), studied a class of new NNs referred to as switched neutral-type NNs with time-varying delays, which combines switched systems with a class of neutral-type NNs. By using an average dwell time method and new L–K functional to assure the global exponential stability and decay estimation for a class of switched Hopfield NNs of neutral type in Zong et al. (2010). In Li and Cao (2013), proposed the switched exponential state estimation and robust stability for interval neural networks with the average dwell time. Very recently, Li et al. (2014) concerned with a class of nonlinear uncertain switched networks with discrete time-varying delays, based on the strictly complete property of the matrices system and the delay-decomposing approach. In Ahn (2010) first time, proposed the $H_\infty$ weight learning law to study not only guarantee the asymptotical stability of switched Hopfield NNs, but also reduce the effect of external disturbance to an $H_\infty$ norm constraint.

With the motivation mentioned above, a new delay-interval-dependent stability criterion for SHNNs of neutral type with successive time-varying delay components is proposed in this paper. By fully using the available information about time-delays and activation functions, a novel L–K functional is constructed. Our main goal is to establish the delay-interval-dependent stability criteria, such that the concerned NNs are asymptotically stable. Make use of new technique to estimate the lower and upper bound information of the time-varying delay and L–K functional with double and triple integral terms, we apply WDII, introducing of some zero equations and using the RCC technique and Finsler’s lemma, new stability criteria for a class of SHNNs of neutral type is obtained in terms of LMIs, which ensures the asymptotic stability. Finally, four numerical examples are given to demonstrate the effectiveness and applicability of our theoretical results.

The main contribution of this paper lies in the following aspects:

• A novel L–K functional is introduced which includes more information about successive time-varying delays and slope of the neuron activation function. Such type of L–K functional has not yet been considered in the previous literature on the stability of SHNNs of neutral type with successive time-varying delay components are introduced.

• Different from others in Dharani et al. (2015), Balasubramaniam et al. (2012), Zong et al. (2010), Li and Cao (2013), Li et al. (2014), Cao et al. (2013) and Ahn (2010); several numerical examples are presented to illustrate the validity of the main results with a real-world simulation. This implies that the results of the present paper are essentially new.

• Inspired by the works in Kwon et al. (2014a, (2014b), some zero equations which would include more quadratic and integral terms are introduced. These terms are merged with the time derivative of L–K functional and combined with RCC approach, which in turn can enhance the feasibility region of stability criterion.

• Moreover, WDII Lemma is taken into account to bound the time-derivative of triple integral L–K functionals, this gives more tighter bounding technology to deal with such L–K functionals, this technique has been never used in previous literature for the stability of SHNNs of neutral type.

Notations Throughout this paper, the superscripts T and $-1$ mean the transpose and the inverse of a matrix respectively. ${\mathbb{R}}^n$ denotes the n-dimensional Euclidean space, ${\mathbb{R}}^{n\times m}$ is the set of all $n \times m$ real matrices. For symmetric matrices P and $Q, P > Q$ (respectively, $P = Q$) means that the matrix $P - Q$ is positive definite (respectively, non-negative). $I_n, 0_n$ and $0_m,n$ stands for $n \times n$ identity matrix, $n \times n$ and $n \times m$ zero matrices, respectively and symmetric term in a symmetric matrix is denoted by $*, X^\bot$ denotes a basis for the null-space of X. If the Matrices are not explicitly stated, it is assumed to compatible dimensions.

Problem formulation and preliminaries

Consider the following delayed Hopfield neural network model Dharani et al. (2015) of neutral type with successive time-varying delay components and distributed delay as:

$$\begin{aligned} \dot{y}(t)& = -D y(t-\delta _1(t)-\delta _2(t)) + A f(y(t))\\&\quad + B f(y(t-h_1(t)-h_2(t))) \\&\quad+ C \int _{t-\tau (t)}^t f(y(s)) ds + E \dot{y} (t-\sigma (t)) + J, \\ y(t)& = \varphi (t), \quad t \in [-\overline{r},0], \end{aligned}$$

(1)

where $y(t) = [y_1(t), y_2(t), \dots, y_n(t)]^T \in {\mathbb{R}}^n$ is the state vector of the network at time t, n corresponds to the number of neurons, $f(y(t)) = [f_1(y_1(t)), f_2(y_2(t)), \dots, f_n(y_n(t))]^T \in {\mathbb{R}}^n$ is the neuron activation function. The matrix $D =$diag$(d_1, d_2, \ldots, d_n)$ is a diagonal matrix with positive entries $d_i > 0.\, A, B, C, E$ are the connection weight matrix and coefficient matrix, the discretely delayed connection weight matrix, the distributively delayed connection weight matrix and coefficient matrix of the time derivative of the delayed states, respectively. $J=[J_1,J_2,\dots,J_n]^T$ is the constant external input vector. $\varphi _i(t) (i\in N)$ is a continuous vector-valued initial function on $[-\bar{r},0],\overline{r}=$max$\{\delta _{1U}, \delta _{2U}, h_{1U}, h_{2U}, \tau, \sigma \}$. $\delta _1(t), \delta _2(t)$ and $h_1(t), h_2(t)$ are leakage and discrete interval time-varying continuous functions that represent the two delay components in the state respectively, $\tau (t)$ and $\sigma (t)$ are denotes the distributive and neutral time delays, and which satisfies the following:

$$\begin{aligned}&0 \le \delta _{1L} \le \delta _1(t) \le \delta _{1U}, \quad \delta _{1UL}=\delta _{1U} - \delta _{1L}, \quad \dot{\delta _1}(t) \le \eta _1, \\&0 \le \delta _{2L} \le \delta _2(t) \le \delta _{2U}, \quad \delta _{2UL}=\delta _{2U} - \delta _{2L}, \quad \dot{\delta _2}(t) \le \eta _2, \\&0 \le \delta _{L} \le \delta (t) \le \delta _{U}, \quad \delta _{UL}=\delta _{U} - \delta _{L}, \quad \dot{\delta }(t) \le \eta,\\&0 \le h_{1L} \le h_1(t) \le h_{1U}, \quad h_{1UL}=h_{1U} - h_{1L}, \quad \dot{h_1}(t) \le \mu _1, \\&0 \le h_{2L} \le h_2(t) \le h_{2U}, \quad h_{2UL}=h_{2U} - h_{2L}, \quad \dot{h_2}(t) \le \mu _2, \\&0 \le h_{L} \le h(t) \le h_{U}, \quad \ h_{UL}=h_{U} - h_{L}, \quad \dot{h}(t) \le \mu, \\&0 \le \tau (t) \le \tau, \quad \dot{\tau }(t)\le \tau _D, \quad 0\le \sigma (t) \le \sigma, \quad \dot{\sigma }(t)\le \sigma _D, \end{aligned}$$

(2)

where $\delta _{1U}\ge \delta _{1L}, \delta _{2U}\ge \delta _{2L}, \delta _{U}\ge \delta _{L}, h_{1U}\ge h_{1L}, h_{2U}\ge h_{2L}, h_{U}\ge h_{L}, \tau, \sigma, \eta _1, \eta _2, \mu _1, \mu _2, \tau _D$ and $\sigma _D$ are known real constants. Note that $\delta _{1L}, \delta _{2L}, \delta _L, h_{1L}, h_{2L}, h_L$ may not be equal to 0. we denote

$$\begin{aligned} \delta (t)& = \delta _1(t) + \delta _2(t), \quad h(t) = h_1(t) + h_2(t), \\ \delta _1& = \delta _{1L} + \delta _{1U}, \quad h_1 = h_{1L} + h_{2U}, \\ \delta _2& = \delta _{2L} + \delta _{2U}, \quad h_2 = h_{2L} + h_{2U}, \\ \eta& = \eta _1 + \eta _2, \quad \mu = \mu _1 + \mu _2. \end{aligned}$$

(3)

Remark 2.1

The first term in the right side of (1) variously known as forgetting or leakage term. It is known from the literature on population dynamics [see Gopalsamy (1992)] that time delays in the stabilizing negative feedback terms will have a tendency to destabilize a system. $f_j(\cdot ),\, j=1,2, \dots,n$ are signal transmission functions. Furthermore, system (1) contains some data about the derivative of the past state to further analysis and model the dynamics for such complex neural responses. Hence system (1) has been referred to as neutral-type system, in which the system has both the state delay and the state derivative with delay, the so-called neutral delay.

Throughout this paper, it is assumed that each neuron activation function $f_j(\cdot )$ in (1) satisfies:

Assumption (H)

(Liu et al. 2006) For any $j\in \{1,2,\dots,n\},\, f_j(0)=0$ and their exist constants $k^{-}_{j}$ and $k^{+}_{j}$ such that

$$k^{-}_{j}\le\, {\frac{f_j(\alpha _1)-f_j(\alpha _2)}{\alpha _1-\alpha _2}}\le k^{+}_{j},$$

(4)

for all $\alpha _1\ne \alpha _2$, where $\alpha _1,\alpha _2\in {\mathbb{R}}.$ Then by Brouwer’s fixed-point theorem Cao (2000) and Assumption H, it can be proved that there exist at least one equilibrium point for system (1). Let $z^* = [z^*_1, z^*_2, \ldots, z^*_n]^T$ be one equilibrium point of system (1). For convenience we shift $z^*$ to the origin by making the following transformation: $z(\cdot ) = y(\cdot ) - y^*$ and then system (1) can be rewritten as

$$\begin{aligned} \dot{z}(t)& = - D z(t-\delta (t)) + A g(z(t)) + B g(z(t-h(t))) \\&\quad + C \int _{t-\tau (t)}^t g(z(s)) ds + E \dot{z} (t-\sigma (t)), \\ z(t)& = \phi (t), \quad t \in [-\overline{r},0], \end{aligned}$$

(5)

where $z(t) = [z_1(t), z_2(t),\dots, z_n(t)]^T$ is the state vector of the transformed system, the initial condition $\phi (t) = \varphi (t) - z^*, g(z(t)) = [g_1(z_1(t)), g_2(z_2(t)),\dots, g_n(z_n(t))]^T, g_j(z_j(t)) = f_j (z_j(t) + z^*_j) - f_j(z^*_j), \,\,j=1,2,\dots, n.$ According to Assumption H, function $g_j(\cdot )$ satisfies the following condition:

$$k^{-}_{j}\le {\frac{g_j(\alpha )}{\alpha }}\le k^{+}_{j}, \quad g_j(0)=0, \quad \forall \alpha \in R, \quad \alpha \ne 0, \quad i=1,2,\ldots,n.$$

(6)

The switched Hopfield neural network of neutral type with discrete and distributed delays are described as

$$\begin{aligned} \dot{z}(t)& = - D_{\varrho (t)} z(t-\delta (t)) + A_{\varrho (t)} g(z(t)) + B_{\varrho (t)} g(z(t-h(t))) \\&\quad + C_{\varrho (t)} \int _{t-\tau (t)}^t g(z(s)) ds + E_{\varrho (t)} \dot{z} (t-\sigma (t)), \\ z(t)& = \phi (t), \quad t \in [-\overline{r},0], \end{aligned}$$

(7)

where $\varrho (t)$ is a switching signal which takes its values in the finite set ${\mathcal{K}} = \{1,2, \dots,m\}.$ Define the indicator function $\gamma (t) = [\gamma _1(t), \gamma _2(t), \ldots, \gamma _n(t)]^T$, where

$$\gamma _k(t) = {\left\{ \begin{array}{ll} 1, & {\text{when the switched system is described by the }}k{th} {\text{ mode}}, D_k, A_k, B_k, C_k, E_k, \\ 0, & {\text{otherwise,}} \end{array}\right.}$$

(8)

and $k \in K.$ Thus, the model (8) can also be described by

$$\begin{aligned} \dot{z}(t)&= \sum _{k=1}^m \gamma _k(t) \left[ - D_k z(t-\delta (t)) + A_k g(z(t)) + B_k g(z(t-h(t))) \right. \\& \quad \left. + \;C_k \int _{t-\tau (t)}^t g(z(s)) ds + E_k \dot{z} (t-\sigma (t))\right]. \end{aligned}$$

(9)

As (9) must be satisfied under any switching rules, it follows that $\sum _{k=1}^m \gamma _k(t) = 1.$ Next, we present some preliminary lemmas, which are needed in the proof of our main results.

Lemma 2.1

(Gu 2000) For any positive definite matrix $M \in {\mathbb{R}}^{n\times n}$, scalars $h_2>h_1>0$, vector function $w:[h_1,h_2]\rightarrow {\mathbb{R}}^n$ such that the integrations concerned are well defined, the following inequality holds:

$$-(h_2-h_1) \int _{t-h_2}^{t-h_1} w^T(s) M w(s) ds\le - \left( \int _{t-h_2}^{t-h_1} w(s)ds \right) ^T M \left( \int _{t-h_2}^{t-h_1} w(s)ds \right)$$

Lemma 2.2

(Park et al. 2011) Let $f_1,f_2,\dots,f_N: R^m \longmapsto R$ have positive values in an open subset D of $R^m$. Then, the reciprocally convex combination of $f_i$ over D satisfies

$$\min _{\{\alpha _i|\alpha _i>0, \sum _{i} \alpha _i=1\}} \sum _{i} {\frac{1}{\alpha _i}} f_i(t) = \sum _{i}f_i(t) + \max _{g_{i,j}(t)}\sum _{i\ne j}g_{i,j}(t)$$

subject to

$$\left\{ g_{i,j}:R^m\longmapsto R,g_{j,i}(t)\triangleq g_{i,j}(t), \begin{bmatrix} f_i(t)&g_{i,j}(t) \\ g_{j,i}(t)&f_j(t) \end{bmatrix} \ge 0 \right\}$$

Lemma 2.3

(Park et al. 2015) For a given matrix $M>0$, given scalars a and b satisfying $a<b$, the following inequality holds for all continuously differentiable function in $[a,b] \rightarrow {\mathbb{R}}^n:$

$${\frac{(b-a)^2}{2}}\int _{a}^b\int _{s}^b\dot{x}^T(u)M\dot{x}(u)du ds \ge {{\left( \int _{a}^b \int _{s}^b \dot{x}(u) du ds \right) ^T}M} {\left( \int _{a}^b \int _{s}^b \dot{x}^T(u) du ds \right)} + 2 \Theta _d^T M \Theta _d.$$

where

$$\Theta _d=-\int _{a}^b\int _{s}^b\dot{x}(u)du ds + {\frac{3}{b-a}}\int _{a}^b\int _{s}^b\int _{v}^b\dot{x}(v) dv du ds.$$

Remark 2.2

So far, very recently the WDII is proposed by Park et al. (2015). Employing WDII is sure to get less conservative criteria than applying the Jensen’s inequality. Therefore, this integral inequality takes advantage of the following information from three aspects: the first is to use the information on the state such as x(t),  the second is to benefit information on the integral of the state over the period of the delay such as $\int _{t-\bar{\tau }}^tx(s) ds$ or $\int _{t-\tau (t)}^tx(s) ds$ and the third is to employ the information on the double integral of the state over the period of the delay such as $\int _{-\bar{\tau }}^0\int _{t+u}^tx(s) ds$ or $\int _{-\tau (t)}^0\int _{t+u}^tx(s) ds.$ Therefore, which gives the more information about the plant states such as $x(t),\int _{t-\bar{\tau }}^tx(s) ds$ or $\int _{t-\tau (t)}^tx(s) ds$ and $\int _{-\bar{\tau }}^0\int _{t+u}^tx(s) ds$ or $\int _{-\tau (t)}^0\int _{t+u}^tx(s) ds.$ Hence, Lemma 2.3 may provide tighter bound than the Jensen’s inequality.

Lemma 2.4

(Boyd et al. 1994) Let $\xi \in {\mathbb{R}}^n,\Phi =\Phi ^T \in {\mathbb{R}}^{n \times n}$ such that rank $(B)<n$. The following statements are equivalent

• (i) $\xi ^T \Phi \xi < 0, \quad \forall B \xi = 0, \quad \xi \ne 0,$

• (ii) ${B^\bot }^T \Phi B^{\bot } < 0,$ where $B^{\bot }$ is a right orthogonal complement of B.

Lemma 2.5

(Boyd et al. 1994) For a given matrices $A_{11}, A_{12}, A_{21}, A_{22}$ with appropriate dimensions, $\begin{bmatrix} A_{11}&A_{12} \\ A_{21}&A_{22} \\ \end{bmatrix} < 0$, holds if and only if $A_{22}<0, A_{11}-A_{12}A_{22}^{-1}A_{12}^T < 0$.

Main results

In this section, we will propose a stability criteria for system (9). For the sake of simplicity of matrix and vector representation, $e_i \in {\mathbb{R}}^{56 n \times n}\ (i=1,2, \dots, 56)$ are defined as block entry matrices (for example $\left. e_4^T = \left[ 0_n, \quad 0_n, \quad 0_n, \quad I_n, \quad \underbrace{0_n, \dots \dots \dots, 0_n}_{52 \ times} \right] \right)$. The other notations are defined as

$$\begin{aligned} \zeta (t)& = \left[ z^T(t) \ z^T(t-h_{1L}) \ z^T(t-h_1(t)) \ z^T(t-h_{1U}) \ z^T(t-h_{2L}) \ z^T(t-h_2(t)) \ z^T(t-h_{2U}) \ z^T(t-h_L) \right. \\& \quad z^T(t-h(t)) \ z^T(t-h_U) \ \int _{t-h_{1L}}^t z^T(s) ds \ \int _{t-h_{2L}}^tz^T(s) ds \ \int _{t-h_L}^t z^T(s)ds \ \int _{t-h_1(t)}^{t-h_{1L}}z^T(s)ds \\& \quad \int _{t-h_{1U}}^{t-h_1(t)}z^T(s) ds \ \int _{t-h_2(t)}^{t-h_{2L}}z^T(s)ds \ \int _{t-h_{2U}}^{t-h_2(t)}z^T(s) ds \ \int _{t-h(t)}^{t-h_L}z^T(s)ds \ \int _{t-h_U}^{t-h(t)}z^T(s) ds \\& \quad \int _{-h_{1L}}^0 \int _{t+u}^tz^T(s)dsdu \ \int _{-h_{2L}}^0 \int _{t+u}^tz^T(s)dsdu \ \int _{-h_{L}}^0 \int _{t+u}^tz^T(s)dsdu \ \int _{-h_1(t)}^{-h_{1L}} \int _{t+u}^tz^T(s)dsdu \\& \quad \int _{-h_{1U}}^{-h_1(t)} \int _{t+u}^tz^T(s)dsdu \ \int _{-h_2(t)}^{-h_{2L}}\int _{t+u}^tz^T(s)dsdu \ \int _{-h_{2U}}^{-h_2(t)} \int _{t+u}^tz^T(s)dsdu \ \int _{-h(t)}^{-h_L}\int _{t+u}^t z^T(s)dsdu \\& \quad \int _{-h_U}^{-h(t)}\int _{t+u}^t z^T(s)dsdu \ g^T(z(t)) \ g^T(z(t-h_{1U})) \ g^T(z(t-h_1(t))) \ g^T(z(t-h_{2U})) \ g^T(z(t-h_2(t))) \\& \quad g^T(z(t-h_U)) \ g^T(z(t-h(t))) \ \dot{z}^T(t) \ \dot{z}^T(t-h_{1U}) \ \dot{z}^T(t-h_{2U}) \ \dot{z}^T(t-h_U) \ \int _{t-\tau (t)}^tg^T(z(s))ds \\& \quad z^T(t-\delta _1) \ z^T(t-\delta _1(t)) \ z^T(t-\delta _2) \ z^T(t-\delta _2(t)) \ z^T(t-\delta ) \ z^T(t-\delta (t)) \ \int _{t-\delta _1(t)}^tz^T(s) ds \\& \quad \int _{t-\delta _2(t)}^tz^T(s)ds \ \int _{t-\delta (t)}^tz^T(s)ds \ \int _{t-\delta _1(t)}^{t-\delta _{1L}}z^T(s)ds \ \int _{t-\delta _{1U}}^{t-\delta _1(t)}z^T(s)ds \ \int _{t-\delta _2(t)}^{t-\delta _{2L}}z^T(s)ds \ \int _{t-\delta _{2U}}^{t-\delta _2(t)}z^T(s)ds \\& \quad \left. \int _{t-\delta (t)}^{t-\delta _L}z^T(s)ds \ \int _{t-\delta _U}^{t-\delta (t)}z^T(s) ds \ \dot{z}^T(t-\sigma (t))\right] ^T. \end{aligned}$$

$$\begin{aligned} \Gamma& = \left[ \underbrace{0_n \dots \dots 0_n}_{28 \ times} A_k \quad \underbrace{0_n \dots \dots 0_n}_{5 \ times} B_k \quad \underbrace{0_n \dots \dots 0_n}_{4 \ times} \quad C_k \quad \underbrace{0_n \dots \dots 0_n}_{5 \ times} \quad -D_k \quad \underbrace{0_n \dots \dots 0_n}_{9 \ times} \quad E_k \right], \\ \Pi _1& = \left[ e_1-e_{49} D_k \right], \quad \Pi _2 = \left[ e_{36} - e_1 D_k + (1-\eta ) e_{46} D_k \right], \\ \Pi _3& = 2 \left( e_{29} - k_m e_1 \right) \Lambda _1 e_{36}^T + 2 \left( k_p e_1 - e_{29} \right) \Delta _1 e_{36}^T + 2 \left( e_{30} - k_m e_4 \right) e_{37}^T + 2 \left( k_p e_4 - e_{30} \right) \Delta _2 e_{37}^T \\& \quad+ \,2 \left( e_{32} - k_m e_7 \right) \Lambda _3 e_{38}^T + 2 \left( k_p e_7 - e_{32} \right) \Delta _3 e_{38}^T + 2 \left( e_{34} - k_m e_{10} \right) \Lambda _4 e_{39}^T + 2 \left( k_p e_{10} - e_{34} \right) \Delta _4 e_{39}^T, \\ \Pi _4& = e_{36} (T_1 + T_2 + T_3) e_{36}^T - e_{37}T_1 e_{37}^T - e_{38} T_2 e_{38}^T - e_{39} T_3 e_{39}^T, \\ \Pi _5& = e_1 (P_2 + P_3 + P_4) e_1^T + e_{42}(-(1-\eta _1)P_2 + (1-\eta _1)P_5) e_{42}^T + e_{44}(-(1-\eta _2)P_3 + (1-\eta _2)P_6)e_{44}^T \\& \quad+\, e_{46}(-(1-\eta )P_4-(1-\eta )P_5 -(1-\eta )P_6) e_{46}^T + \left[ e_1 \quad e_{29} \right] \begin{bmatrix} P_7&P_8 \\ *&P_9 \end{bmatrix} \left[ e_1 \quad e_{29} \right] ^T \\& \quad- \, (1-\mu _1) \left[ e_3 \quad e_{31} \right] \begin{bmatrix} P_7&P_8 \\ *&P_9 \end{bmatrix} \left[ e_3 \quad e_{31} \right] ^T + \left[ e_1 \quad e_{29} \right] \begin{bmatrix} P_{10}&P_{11} \\ *&P_{12} \end{bmatrix} \left[ e_1 \quad e_{29} \right] ^T \\& \quad-\, (1-\mu _2) \left[ e_6 \quad e_{33} \right] \begin{bmatrix} P_{10}&P_{11} \\ *&P_{12} \end{bmatrix} \left[ e_6 \quad e_{33} \right] ^T + (1-\mu _1) \left[ e_3 \quad e_{31} \right] \begin{bmatrix} P_{13}&P_{14} \\ *&P_{15} \end{bmatrix} \left[ e_3 \quad e_{31} \right] ^T \\& \quad-\, (1-\mu ) \left[ e_9 \quad e_{35} \right] \begin{bmatrix} P_{13}&P_{14} \\ *&P_{15} \end{bmatrix} \left[ e_9 \quad e_{35} \right] ^T + (1-\mu _2) \left[ e_6 \quad e_{33} \right] \begin{bmatrix} P_{16}&P_{17} \\ *&P_{18} \end{bmatrix} \left[ e_6 \quad e_{33} \right] ^T \\& \quad- \, (1-\mu ) \left[ e_9 \quad e_{35} \right] \begin{bmatrix} P_{16}&P_{17} \\ *&P_{18} \end{bmatrix} \left[ e_9 \quad e_{35} \right] ^T,\\ \Pi _6&= e_1 (Q_1 + Q_2 + Q_3 + Q_6 + Q_9) e_1^T + e_{41}(-Q_1 + Q_4) e_{41}^T + e_{43} (-Q_2 + Q_3) e_{43}^T + e_{45}(-Q_3 - Q_4 - Q_5) e_{45}^T \\& \quad+\, e_1 (Q_7 + Q_{10}) e_{29}^T + e_{29}(Q_8 + Q_{11}) e_{29}^T + \left[ e_1 \quad e_{29}\right] \begin{bmatrix} Q_6&Q_7 \\ *&Q_8 \end{bmatrix} \left[ e_1 \quad e_{29}\right] ^T - \left[ e_4 \quad e_{30}\right] \begin{bmatrix} Q_6&Q_7 \\ *&Q_8 \end{bmatrix} \left[ e_4 \quad e_{30}\right] ^T \\& \quad+ \, \left[ e_1 \quad e_{29}\right] \begin{bmatrix} Q_9&Q_{10} \\ *&Q_{11} \end{bmatrix} \left[ e_1 \quad e_{29}\right] ^T - \left[ e_7 \quad e_{32}\right] \begin{bmatrix} Q_9&Q_{10} \\ *&Q_{11} \end{bmatrix} \left[ e_7 \quad e_{32}\right] ^T + \left[ e_4 \quad e_{30}\right] \begin{bmatrix} Q_{12}&Q_{13} \\ *&Q_{14} \end{bmatrix} \left[ e_4 \quad e_{30}\right] ^T \\& \quad-\, \left[ e_{10} \quad e_{34}\right] \begin{bmatrix} Q_{12}&Q_{13} \\ *&Q_{14} \end{bmatrix} \left[ e_{10} \quad e_{34}\right] ^T + \left[ e_7 \quad e_{32}\right] \begin{bmatrix} Q_{15}&Q_{16} \\ *&Q_{17} \end{bmatrix} \left[ e_7 \quad e_{32}\right] ^T - \left[ e_{10} \quad e_{34}\right] \begin{bmatrix} Q_{15}&Q_{16} \\ *&Q_{17} \end{bmatrix} \left[ e_{10} \quad e_{34}\right] ^T,\\ \Pi _7& = e_1 \left( \delta _{1L}^2 U + \delta _{2L}^2 V + \delta _{1L}^2 W + \delta _{1UL}^2X + \delta _{2UL}^2Y + \delta _{UL}^2Z \right) e_1^T - e_{47}Ue_{47} - e_{48}Ve_{48}^T - e_{49}We_{49}^T - e_{50}X e_{50}^T \\& \quad-\, 2e_{50}Xe_{51}^T - e_{51}Xe_{51}^T - e_{52}Ye_{52}^T - 2e_{52}Y e_{52}^T - e_{53}Ye_{53}^T - e_{54}Ze_{54}^T - 2e_{54}Ze_{55}^T - e_{55}Ze_{55}^T, \\ \Pi _8& = e_2h_{1UL}Q_1e_2^T + e_3 \left( -h_{1UL}Q_1 + h_{1UL}Q_2 \right) e_3^T - e_4 h_{1UL}Q_2e_4^T + e_5h_{2UL}Q_3e_5^T + e_6 \left( -h_{2UL}Q_3 + h_{2UL}Q_4 \right) e_6^T \\& \quad-\, e_7h_{2UL}Q_4e_7^T + e_8h_{UL}Q_5e_8^T + e_9 \left( -h_{UL}Q_5 + h_{UL}Q_6 \right) e_9^T - e_{10}h_{UL}Q_6e_{10}^T, \end{aligned}$$

$$\begin{aligned} \Pi _9& = \left[ e_1 \quad e_{36} \right] \left( h_{1L}^2\bar{U} + h_{2L}^2\bar{V} + h_{L}^2 \bar{W} + h_{1UL}^2\bar{X} + h_{2UL}^2 \bar{Y} + h_{UL}^2 \bar{Z} \right) \left[ e_1 \quad e_{36} \right] ^T - \left[ e_{11} \quad e_{1}-e_{2}\right] \bar{U}\left[ e_{11} \quad e_{1}-e_{2}\right] ^T \\& \quad- \, \left[ e_{12} \quad e_{1}-e_{5}\right] \bar{V}\left[ e_{12} \quad e_{1}-e_{5}\right] ^T - \left[ e_{13} \quad e_{1}-e_{8}\right] \bar{W}\left[ e_{13} \quad e_{1}-e_{8}\right] ^T \\& \quad-\, \left[ e_{14} \quad e_2-e_3 \quad e_{15} \quad e_3-e_4 \right] \begin{bmatrix} \bar{X}&{\mathcal{L}} \\ *&\bar{X} \end{bmatrix} \left[ e_{14} \quad e_2-e_3 \quad e_{15} \quad e_3-e_4 \right] ^T \\& \quad-\, \left[ e_{16} \quad e_5-e_6 \quad e_{17} \quad e_6-e_7 \right] \begin{bmatrix} \bar{Y}&{\mathcal{M}} \\ *&\bar{Y} \end{bmatrix} \left[ e_{16} \quad e_5-e_6 \quad e_{17} \quad e_6-e_7 \right] ^T \\& \quad-\, \left[ e_{18} \quad e_8-e_9 \quad e_{19} \quad e_9-e_{10} \right] \begin{bmatrix} \bar{Z}&{\mathcal{N}} \\ *&\bar{Z} \end{bmatrix} \left[ e_{18} \quad e_8-e_9 \quad e_{19} \quad e_9-e_{10} \right] ^T, \\ \Pi _{10}& = e_{36} \left( {\frac{h_{1L}^4}{4}}R_1 + {\frac{h_{2L}^4}{4}}R_2 + {\frac{h_{L}^4}{4}}R_3 + {\frac{(h_{1U}^2-h_{1L}^2)^2}{4}} R_4 + {\frac{(h_{2U}^2-h_{2L}^2)^2}{4}} R_5 + {\frac{(h_{U}^2-h_{L}^2)^2}{4}} R_6 \right) e_{36}^T \\& \quad-\, e_1 \left( {\frac{3}{2}}R_1 + {\frac{3}{2}}R_2 + {\frac{3}{2}}R_3 + 3R_4 + 3R_5 + 3R_6 \right) e_1^T + e_13R_1e_{20}^T - e_{11}3R_1e_{11}^T + e_{11}{\frac{6}{h_{1L}}}R_1e_{20}^T - e_{20}{\frac{18}{h_{1L}^2}}R_1e_{20}^T \\& \quad+\, e_13R_2e_{21}^T - e_{12}3R_2e_{12}^T + e_{12}{\frac{6}{h_{2L}}}R_2e_{21}^T - e_{21}{\frac{18}{h_{2L}^2}}R_2e_{21}^T + e_13R_3e_{22}^T - e_{13}3R_3e_{13}^T + e_{13}{\frac{6}{h_{L}}}R_3e_{22}^T \\& \quad-\, e_{22}{\frac{18}{h_{L}^2}}R_3e_{22}^T + e_13R_4e_{23}^T - e_{14}3R_4e_{14}^T + e_{14}{\frac{6}{h_{1U}-h_{1L}}}R_4e_{23}^T - e_{23}{\frac{18}{(h_{1U}-h_{1L})^2}}R_4e_{23}^T \\& \quad+ \, e_13R_4e_{24}^T - e_{15}3R_4e_{15}^T + e_{15}{\frac{6}{h_{1U}-h_{1L}}}R_4e_{24}^T - e_{24}{\frac{18}{(h_{1U}-h_{1L})^2}}R_4e_{24}^T + e_13R_5e_{25}^T - e_{16}3R_5e_{16}^T \\& \quad+\, e_{16}{\frac{6}{h_{2U}-h_{2L}}}R_5e_{25}^T - e_{25}{\frac{18}{(h_{2U}-h_{2L})^2}}R_5e_{25}^T + e_13R_5e_{26}^T - e_{17}3R_5e_{17}^T + e_{17}{\frac{6}{h_{2U}-h_{2L}}}R_5e_{26}^T \\& \quad-\, e_{26}{\frac{18}{(h_{2U}-h_{2L})^2}}R_5e_{26}^T + e_13R_6e_{27}^T - e_{18}3R_6e_{18}^T + e_{18}{\frac{6}{h_{U}-h_{L}}}R_6e_{27}^T - e_{27}{\frac{18}{(h_{U}-h_{L})^2}}R_6e_{27}^T \\& \quad+ \, e_13R_6e_{28}^T - e_{19}3R_6e_{19}^T + e_{19}{\frac{6}{h_{U}-h_{L}}}R_6e_{28}^T - e_{28}{\frac{18}{(h_{U}-h_{L})^2}}R_6e_{28}^T, \\ \Pi _{11}& = e_{29}\tau ^2S_1e_{29}^T - e_{40}S_1e_{40}^T + e_{36}S_2 e_{36}^T - e_{56}(1-\sigma _D)S_2e_{56}^T, \\ \Pi _{12}& = e_{36}(-H -H^T)e_{36}^T - 2e_{36}HA_ke_{46}^T + 2e_{36}HB_k e_{29}^T + 2e_{36}HC_ke_{35}^T + 2e_{36}HD_ke_{40}^T + 2e_{36}HE_ke_{56}^T, \\ \Pi _{13}& = -e_1G_1\Sigma _1e_1^T + 2e_1G_1\Sigma _2e_{29}^T - e_{29}G_1e_{29}^T -e_3G_2\Sigma _1e_3^T + 2e_3G_2\Sigma _2e_{31}^T - e_{31}G_2e_{31}^T -e_4G_3\Sigma _1e_4^T \\& \quad+ \, 2e_4G_3\Sigma _2e_{30}^T - e_{30}G_3e_{30}^T -e_6G_4\Sigma _1e_6^T + 2e_6G_4\Sigma _2e_{33}^T - e_{33}G_4e_{33}^T -e_7G_5\Sigma _1e_7^T + 2e_7G_5\Sigma _2e_{32}^T \\& \quad- \, e_{32}G_5e_{32}^T -e_9G_6\Sigma _1e_9^T + 2e_9G_6\Sigma _2e_{35}^T - e_{35}G_6e_{35}^T -e_{10}G_7\Sigma _1e_{10}^T + 2e_{10}G_7\Sigma _2e_{34}^T - e_{34}G_7e_{34}^T, \\ \Xi& = \Pi _1 P \Pi _2^T + \Pi _2 P \Pi _1^T + \sum _{i=3}^{13} \Pi _i, \\ K_p& = diag\left\{ k_1^+,k_2^+, \dots \dots, k_n^+ \right\}, \quad K_m = diag\left\{ k_1^-,k_2^-, \dots \dots, k_n^- \right\}, \\ \Sigma _1& = diag\left\{ k^-_1 k^+_1,k^-_2k^+_2,\dots \dots,k^-_nk^+_n\right\}, \quad \Sigma _2=diag\left\{ {\frac{k^-_1+k^+_1}{2}},{\frac{k^-_2+k^+_2}{2}},\dots \dots,{\frac{k^-_n+k^+_n}{2}} \right\},\\ {\mathcal{F}}_1& = \begin{bmatrix} 0_n&F_1 \\ F_1&0_n \end{bmatrix}, \ \ {\mathcal{F}}_2 =\begin{bmatrix} 0_n&F_2 \\ F_2&0_n \end{bmatrix}, \ \ {\mathcal{F}}_3 =\begin{bmatrix} 0_n&F_3 \\ F_3&0_n \end{bmatrix}, \ \ {\mathcal{F}}_4 =\begin{bmatrix} 0_n&F_4 \\ F_4&0_n \end{bmatrix}, \ \ {\mathcal{F}}_5 =\begin{bmatrix} 0_n&F_5 \\ F_5&0_n \end{bmatrix}, \ \ {\mathcal{F}}_6 =\begin{bmatrix} 0_n&F_6 \\ F_6&0_n \end{bmatrix}. \end{aligned}$$

Theorem 3.1

For given positive scalars - $\delta _{1L}$, $\delta _{1U}$, $\delta _{2L}$, $\delta _{2U}$, $h_{1L}$, $h_{1U}$, $h_{2L}$, $h_{2U}$, $\delta_1$, $\delta_2$, $h_1$, $h_2$, $\tau$, $\sigma$, $\eta_1$, $\eta_2$, $\mu_1$, $\mu_2$, $\tau_D$, $\sigma_D$ and diagonal matrices $K_p,K_m$, then the neural network described by (9) is globally asymptotically stable, for any time-varying delay $\delta (t),h(t),\tau (t)$ and $\sigma (t)$ satisfying (2), if there exist positive definite matrices $P_i (i=1,2, \dots,18)\in {\mathbb{R}}^{n \times n},T_i (i=1,2,3)\in {\mathbb{R}}^{n \times n},Q_i (i=1,2,\dots,17)\in {\mathbb{R}}^{n \times n}U,V,W,X,Y,Z\in {\mathbb{R}}^{n \times n},\bar{U}{\in {\mathbb{R}}^{2n \times 2n}},\bar{V}{\in {\mathbb{R}}^{2n \times 2n}},\bar{W}{\in {\mathbb{R}}^{2n \times 2n}},\bar{X}{\in {\mathbb{R}}^{2n \times 2n}},\bar{Y}{\in {\mathbb{R}}^{2n \times 2n}},\bar{Z}{\in {\mathbb{R}}^{2n \times 2n}}$,$R_i (i=1,2,\dots,6)\in {\mathbb{R}}^{n \times n},S_i (i=1,2)\in {\mathbb{R}}^{n \times n}$, positive diagonal matrices $\Delta _l=\hbox {diag}\left\{ \lambda _{l1}, \lambda _{l2}, \dots, \lambda _{ln}\right\},\Lambda _l=$diag$\left\{ \mu _{l1}, \mu _{l2}, \dots, \mu _{ln}\right\},H\in {\mathbb{R}}^{n \times n},G_i (i=1,2,\dots,7)\in {\mathbb{R}}^{n \times n}$, any symmetric matrices $F_i\in {\mathbb{R}}^{n \times n}(i=1,2, \dots,6)$, any matrices ${\mathcal{L}}, {\mathcal{M}}, {\mathcal{N}}\in {\mathbb{R}}^{2n \times 2n}$ such that the following LMIs hold:

$$(\Gamma ^\perp )^T \ \Xi \ \Gamma ^\perp < 0,$$

(10)

$$\begin{bmatrix} \bar{X} + {\mathcal{F}}_1&{\mathcal{L}} \\ \\ *&\bar{X} + {\mathcal{F}}_2 \end{bmatrix} \ge 0,$$

(11)

$$\begin{bmatrix} \bar{Y} + {\mathcal{F}}_3&{\mathcal{M}} \\ \\ *&\bar{Y} + {\mathcal{F}}_4 \end{bmatrix} \ge 0,$$

(12)

$$\begin{bmatrix} \bar{Z} + {\mathcal{F}}_5&{\mathcal{N}} \\ \\ *&\bar{Z} + {\mathcal{F}}_6 \end{bmatrix} \ge 0,$$

(13)

Proof

Let us consider the following Lyapunov–Krasoskii functional candidate:

$$V(z(t), t) = \sum \limits _{i=1}^{9}V_i(z(t), t),$$

(14)

where

$$\begin{aligned} V_1(z(t),t)& = \left( z(t)-D_k \int _{t-\delta (t)}^tz(s) ds \right) ^T P_1\left( z(t)-D_k \int _{t-\delta (t)}^tz(s) ds \right), \\ V_2(z(t),t)& = 2 \sum _{i=1}^n \left[ \lambda _{1i} \int _{0}^{z_i(t)} \left( g_i(s) - k_i^-s \right) ds + \delta _{1i} \int _{0}^{z_i(t)} \left( k_i^+s - g_i(s) \right) ds \right] \\&+\, 2 \sum _{i=1}^n \left[ \lambda _{2i} \int _{0}^{z_i(t-h_{1U})} \left( g_i(s) - k_i^-s \right) ds + \delta _{2i} \int _{0}^{z_i(t-h_{1U})} \left( k_i^+s - g_i(s) \right) ds \right] \\& \quad+ \,2 \sum _{i=1}^n \left[ \lambda _{3i} \int _{0}^{z_i(t-h_{2U})} \left( g_i(s) - k_i^-s \right) ds + \delta _{3i} \int _{0}^{z_i(t-h_{2U})} \left( k_i^+s - g_i(s) \right) ds \right] \\& \quad+\, 2 \sum _{i=1}^n \left[ \lambda _{4i} \int _{0}^{z_i(t-h_{U})} \left( g_i(s) - k_i^-s \right) ds + \delta _{4i} \int _{0}^{z_i(t-h_{U})} \left( k_i^+s - g_i(s) \right) ds \right], \\ V_3(z(t),t)& = \int _{t-h_{1U}}^t\dot{z}^T(s)T_1 \dot{z}(s) ds + \int _{t-h_{2U}}^t \dot{z}^T(s) T_2 \dot{z}(s) ds + \int _{t-h_{U}}^t \dot{z}^T(s) T_3 \dot{z}(s) ds,\\ V_4(z(t),t)& = \int _{t-\delta _1(t)}^t z^T(s) P_2 z(s) ds + \int _{t-\delta _2(t)}^t z^T(s) P_3 z(s) ds + \int _{t-\delta (t)}^t z^T(s)P_4z(s) ds + \int _{t-\delta (t)}^{t-\delta _1(t)} z^T(s)P_5 z(s) ds \\& \quad+\, \int _{t-\delta (t)}^{t-\delta _2(t)} z^T(s)P_6 z(s) ds + \int _{t-h_1(t)}^t \begin{bmatrix} z(s) \\ g(z(s)) \end{bmatrix}^T \begin{bmatrix} P_7&P_8 \\ *&P_9 \end{bmatrix}\begin{bmatrix} z(s) \\ g(z(s)) \end{bmatrix} ds \\& \quad+\, \int _{t-h_2(t)}^t \begin{bmatrix} z(s) \\ g(z(s)) \end{bmatrix}^T \begin{bmatrix} P_{10}&P_{11} \\ *&P_{12} \end{bmatrix}\begin{bmatrix} z(s) \\ g(z(s)) \end{bmatrix} ds +\int _{t-h(t)}^{t-h_1(t)} \begin{bmatrix} z(s) \\ g(z(s)) \end{bmatrix}^T \begin{bmatrix} P_{13}&P_{14} \\ *&P_{15} \end{bmatrix}\begin{bmatrix} z(s) \\ g(z(s)) \end{bmatrix} ds \\& \quad+\,\int _{t-h(t)}^{t-h_2(t)} \begin{bmatrix} z(s) \\ g(z(s)) \end{bmatrix}^T \begin{bmatrix} P_{16}&P_{17} \\ *&P_{18} \end{bmatrix}\begin{bmatrix} z(s) \\ g(z(s)) \end{bmatrix} ds, \\ V_5(z(t),t)& = \int _{t-\delta _1}^t z^T(s) Q_1 z(s) ds + \int _{t-\delta _2}^t z^T(s) Q_2 z(s) ds + \int _{t-\delta }^t z^T(s)Q_3z(s) ds + \int _{t-\delta }^{t-\delta _1} z^T(s)Q_4 z(s) ds \\& \quad+ \,\int _{t-\delta }^{t-\delta _2} z^T(s)Q_5 z(s) ds + \int _{t-h_{1U}}^t \begin{bmatrix} z(s) \\ f(z(s)) \end{bmatrix}^T \begin{bmatrix} Q_6&Q_7 \\ *&Q_8 \end{bmatrix}\begin{bmatrix} z(s) \\ g(z(s)) \end{bmatrix} ds \\& \quad+\,\int _{t-h_{2U}}^t \begin{bmatrix} z(s) \\ g(z(s)) \end{bmatrix}^T \begin{bmatrix} Q_{9}&Q_{10} \\ *&Q_{11} \end{bmatrix}\begin{bmatrix} z(s) \\ g(z(s)) \end{bmatrix} ds +\int _{t-h_U}^{t-h_{1U}} \begin{bmatrix} z(s) \\ g(z(s)) \end{bmatrix}^T \begin{bmatrix} Q_{12}&Q_{13} \\ *&Q_{14} \end{bmatrix}\begin{bmatrix} z(s) \\ g(z(s)) \end{bmatrix} ds \\& \quad+\,\int _{t-h_U}^{t-h_{2U}} \begin{bmatrix} z(s) \\ g(z(s)) \end{bmatrix}^T \begin{bmatrix} Q_{15}&Q_{16} \\ *&Q_{17} \end{bmatrix}\begin{bmatrix} z(s) \\ g(z(s)) \end{bmatrix} ds, \\ V_6(z(t),t)& = \delta _{1L} \int _{-\delta _{1L}}^0 \int _{t+\theta }^tz^T(s) U z(s) ds d\theta + \delta _{2L} \int _{-\delta _{2L}}^0 \int _{t+\theta }^tz^T(s) V z(s) ds d\theta + \delta _L \int _{-\delta _L}^0 \int _{t+\theta }^tz^T(s) W z(s) ds d\theta \\& \quad+\, \delta _{1UL} \int _{-\delta _{1U}}^{-\delta _{1L}} \int _{t+\theta }^tz^T(s) X z(s) ds d\theta + \delta _{2UL} \int _{-\delta _{2U}}^{-\delta _{2L}} \int _{t+\theta }^tz^T(s) Y z(s) ds d\theta \\& \quad+\, \delta _{UL} \int _{-\delta _U}^{-\delta _L} \int _{t+\theta }^tz^T(s) Z z(s) ds d\theta, \\ V_7(z(t),t)& = h_{1L} \int _{-h_{1L}}^0 \int _{t+\theta }^t\xi ^T(s) \bar{U} \xi (s) ds d\theta + h_{2L} \int _{-h_{2L}}^0 \int _{t+\theta }^t\xi ^T(s) \bar{V} \xi (s) ds d\theta + h_L \int _{-h_L}^0 \int _{t+\theta }^t\xi ^T(s) \bar{W} \xi (s) ds d\theta \\& \quad+\, h_{1UL} \int _{-h_{1U}}^{-h_{1L}} \int _{t+\theta }^t\xi ^T(s) \bar{X} \xi (s) ds d\theta + h_{2UL} \int _{-h_{2U}}^{-h_{2L}} \int _{t+\theta }^t\xi ^T(s) \bar{Y} \xi (s) ds d\theta \\& \quad+\, h_{UL} \int _{-h_U}^{-h_L} \int _{t+\theta }^t\xi ^T(s) \bar{Z} \xi (s) ds d\theta, \\ V_8(z(t),t)& = {\frac{h_{1L}^2}{2}} \int _{-h_{1L}}^0 \int _{\theta }^0 \int _{t+u}^t \dot{z}^T(s) R_1 \dot{z}(s) ds du d\theta + {\frac{h_{2L}^2}{2}} \int _{-h_{2L}}^0 \int _{\theta }^0 \int _{t+u}^t \dot{z}^T(s) R_2 \dot{z}(s) ds du d\theta \\& \quad+\, {\frac{h_L^2}{2}}\int _{-h_L}^0 \int _{\theta }^0 \int _{t+u}^t \dot{z}^T(s) R_3 \dot{z}(s) ds du d\theta + {\frac{h_{1U}^2-h_{1L}^2}{2}} \int _{-h_{1U}}^{-h_{1L}} \int _{\theta }^0 \int _{t+u}^t \dot{z}^T(s) R_4 \dot{z}(s) ds du d\theta \\& \quad+\, {\frac{h_{2U}^2-h_{2L}^2}{2}} \int _{-h_{2U}}^{-h_{2L}} \int _{\theta }^0 \int _{t+u}^t \dot{z}^T(s) R_5 \dot{z}(s) ds du d\theta + {\frac{h_{U}^2-h_{L}^2}{2}} \int _{-h_{U}}^{-h_{L}} \int _{\theta }^0 \int _{t+u}^t \dot{z}^T(s) R_6 \dot{z}(s) ds du d\theta, \\ V_9(z(t),t)& = \tau \int _{-\tau }^0 \int _{t+\theta }^t g^T(z(s)) S_1 g(z(s)) ds d\theta + \int _{t-\sigma (t)}^t \dot{z}^T(s) S_2 \dot{z}(s) ds. \end{aligned}$$

$$\xi ^T(t) =\hbox {col} \left\{ z(t), \dot{z}(t) \right\}.$$

Taking the time derivative of V(z(t), t) along the trajectories of system (9) yields

$$\dot{V}(z(t),t) = \sum \limits _{i=1}^{9}\dot{V_i}(z(t),t),$$

(15)

where

$$\begin{aligned} \dot{V_1}(z(t),t) & \le 2 \left( z(t) - D_k \int _{t-\delta (t)}^t z(s) ds \right) ^TP_1 \left( \dot{z}(t) - D_k z(t) + (1-\eta )D_k z(t-\delta (t)) \right) \\ & \le 2\zeta ^T(t) \Pi _1^T P_1 \Pi _2 \zeta (t), \end{aligned}$$

(16)

$$\begin{aligned} \dot{V_2}(z(t),t)& = 2 \left[ g(z(t)) - k_m z(t) \right] ^T\Lambda _1 \dot{z}(t) + 2 \left[ k_p z(t) - g(z(t)) \right] ^T \Delta _1 \dot{z}(t) \\& \quad+\, 2 \left[ g(z(t-h_{1U})) - k_m z(t-h_{1U}) \right] ^T \Lambda _2 \dot{z}(t-h_{1U}) \\& \quad+\, 2 \left[ k_p z(t-h_{1U}) - g(z(t-h_{1U})) \right] ^T \Delta _2 \dot{z}(t-h_{1U}) \\& \quad+\, 2 \left[ g(z(t-h_{2U})) - k_m z(t-h_{2U}) \right] ^T \Lambda _3 \dot{z}(t-h_{2U}) \\& \quad+\, 2 \left[ k_p z(t-h_{2U}) - g(z(t-h_{2U})) \right] ^T \Delta _3 \dot{z}(t-h_{1U}) \\& \quad+\, 2 \left[ g(z(t-h_{U})) - k_m z(t-h_{U}) \right] ^T \Lambda _4 \dot{z}(t-h_{U}) \\& \quad+\, 2 \left[ k_p z(t-h_{U}) - g(z(t-h_{U})) \right] ^T \Delta _4 \dot{z}(t-h_{U}) \\& = \zeta ^T(t) \Pi _3 \zeta (t), \end{aligned}$$

(17)

$$\begin{aligned} \dot{V_3}(z(t),t)& = \dot{z}^T(t) \left[ T_1 + T_2 + T_3 \right] \dot{z}(t) - \dot{z}^T(t-h_{1U}) T_1 \dot{z}^T(t-h_{1U}) - \dot{z}^T(t-h_{2U}) T_2 \dot{z}^T(t-h_{2U}) \\& \quad-\, \dot{z}^T(t-h_{U}) T_3 \dot{z}^T(t-h_{U}) \\& = \zeta ^T(t) \Pi _4 \zeta (t), \end{aligned}$$

(18)

$$\begin{aligned} \dot{V_4}(z(t),t)& \le z^T(t) \left[ P_2 + P_3 + P_4 \right] z(t) + z^T(t-\delta _1(t))\left[ -(1-\eta _1)P_2 + (1-\eta _1)P_5 \right] z(t-\delta _1(t)) \\& \quad+\, z^T(t-\delta _2(t))\left[ -(1-\eta _2)P_3 + (1-\eta _2)P_6 \right] z(t-\delta _2(t)) \\& \quad+\, z^T(t-\delta (t))\left[ -(1-\eta )P_4 - (1-\eta )P_5 - (1-\eta )P_6 \right] z(t-\delta (t)) \\& \quad+\, \begin{bmatrix} z(t) \\ g(z(t)) \end{bmatrix}^T \begin{bmatrix} P_7&P_8 \\ *&P_9 \end{bmatrix} \begin{bmatrix} z(t) \\ g(z(t)) \end{bmatrix} \\& \quad-\, (1-\mu _1) \begin{bmatrix} z(t-h_1(t)) \\ g(z(t-h_1(t))) \end{bmatrix}^T \begin{bmatrix} P_7&P_8 \\ *&P_9 \end{bmatrix} \begin{bmatrix} z(t-h_1(t)) \\ g(z(t-h_1(t))) \end{bmatrix} \\& \quad+\, \begin{bmatrix} z(t) \\ g(z(t)) \end{bmatrix}^T \begin{bmatrix} P_{10}&P_{11} \\ *&P_{12} \end{bmatrix} \begin{bmatrix} z(t) \\ g(z(t)) \end{bmatrix} \\& \quad-\, (1-\mu _2) \begin{bmatrix} z(t-h_2(t)) \\ g(z(t-h_2(t))) \end{bmatrix}^T \begin{bmatrix} P_{10}&P_{11} \\ *&P_{12} \end{bmatrix} \begin{bmatrix} z(t-h_2(t)) \\ g(z(t-h_2(t))) \end{bmatrix} \\& \quad+\, (1-\mu _1) \begin{bmatrix} z(t-h_1(t)) \\ g(z(t-h_1(t))) \end{bmatrix}^T \begin{bmatrix} P_{13}&P_{14} \\ *&P_{15} \end{bmatrix} \begin{bmatrix} z(t-h_1(t)) \\ g(z(t-h_1(t))) \end{bmatrix} \\& \quad-\, (1-\mu ) \begin{bmatrix} z(t-h(t)) \\ g(z(t-h(t))) \end{bmatrix}^T \begin{bmatrix} P_{13}&P_{14} \\ *&P_{15} \end{bmatrix} \begin{bmatrix} z(t-h(t)) \\ g(z(t-h(t))) \end{bmatrix} \\& \quad+\, (1-\mu _2) \begin{bmatrix} z(t-h_2(t)) \\ g(z(t-h_2(t))) \end{bmatrix}^T \begin{bmatrix} P_{16}&P_{17} \\ *&P_{18} \end{bmatrix} \begin{bmatrix} z(t-h_2(t)) \\ g(z(t-h_2(t))) \end{bmatrix} \\& \quad-\, (1-\mu ) \begin{bmatrix} z(t-h(t)) \\ g(z(t-h(t))) \end{bmatrix}^T \begin{bmatrix} P_{16}&P_{17} \\ *&P_{18} \end{bmatrix} \begin{bmatrix} z(t-h(t)) \\ g(z(t-h(t))) \end{bmatrix} \\& \le \zeta ^T(t) \Pi _5 \zeta (t), \end{aligned}$$

(19)

$$\begin{aligned} \dot{V_5}(z(t),t)& = z^T(t)\left[ Q_1 + Q_2 + Q_3 + Q_6 + Q_9 \right] z(t) + z^T(t-\delta _1)\left[ -Q_1 + Q_4 \right] z(t-\delta _1) \\&+\, z^T(t-\delta _2) \left[ -Q_2 + Q_5 \right] z(t-\delta _2) + z^T(t-\delta ) \left[ -Q_3 -Q_4 -Q_5 \right] z(t-\delta ) \\&+\, z^T(t) \left[ Q_7 + Q_{10} \right] g(z(t)) + g^T(z(t)) \left[ Q_8 + Q_{11} \right] g(z(t)) \\&+\, \begin{bmatrix} z(t) \\ g(z(t)) \end{bmatrix}^T \begin{bmatrix} Q_6&Q_7 \\ *&Q_8 \end{bmatrix} \begin{bmatrix} z(t) \\ g(z(t)) \end{bmatrix} - \begin{bmatrix} z(t-h_{1U}) \\ g(z(t-h_{1U})) \end{bmatrix}^T \begin{bmatrix} Q_6&Q_7 \\ *&Q_8 \end{bmatrix} \begin{bmatrix} z(t-h_{1U}) \\ g(z(t-h_{1U})) \end{bmatrix} \\&+\, \begin{bmatrix} z(t) \\ g(z(t)) \end{bmatrix}^T \begin{bmatrix} Q_9&Q_{10} \\ *&Q_{11} \end{bmatrix} \begin{bmatrix} z(t) \\ g(z(t)) \end{bmatrix} - \begin{bmatrix} z(t-h_{2U}) \\ g(z(t-h_{2U})) \end{bmatrix}^T \begin{bmatrix} Q_9&Q_{10} \\ *&Q_{11} \end{bmatrix} \begin{bmatrix} z(t-h_{2U}) \\ g(z(t-h_{2U})) \end{bmatrix} \\&+\, \begin{bmatrix} z(t-h_{1U}) \\ g(z(t-h_{1U})) \end{bmatrix}^T \begin{bmatrix} Q_{12}&Q_{13} \\ *&Q_{14} \end{bmatrix} \begin{bmatrix} z(t-h_{1U}) \\ g(z(t-h_{1U})) \end{bmatrix} \\&-\, \begin{bmatrix} z(t-h_{U}) \\ g(z(t-h_{U})) \end{bmatrix}^T \begin{bmatrix} Q_{12}&Q_{13} \\ *&Q_{14} \end{bmatrix} \begin{bmatrix} z(t-h_{U}) \\ g(z(t-h_{U})) \end{bmatrix} \\&+\, \begin{bmatrix} z(t-h_{2U}) \\ g(z(t-h_{2U})) \end{bmatrix}^T \begin{bmatrix} Q_{15}&Q_{16} \\ *&Q_{17} \end{bmatrix} \begin{bmatrix} z(t-h_{2U}) \\ g(z(t-h_{2U})) \end{bmatrix} \\&-\, \begin{bmatrix} z(t-h_{U}) \\ g(z(t-h_{U})) \end{bmatrix}^T \begin{bmatrix} Q_{15}&Q_{16} \\ *&Q_{17} \end{bmatrix} \begin{bmatrix} z(t-h_{U}) \\ g(z(t-h_{U})) \end{bmatrix} \\& = \zeta ^T(t) \Pi _6 \zeta (t), \end{aligned}$$

(20)

$$\begin{aligned} \dot{V_6}(z(t),t)& = z^T(t) \left[ \delta _{1L}^2U + \delta _{2L}^2V + \delta _L^2W + \delta _{1UL}^2X + \delta _{2UL}^2Y + \delta _{UL}^2Z \right] z(t) \\&-\, \delta _{1L} \int _{t-\delta _{1L}}^tz^T(s) U z(s) ds - \delta _{2L} \int _{t-\delta _{2L}}^tz^T(s) V z(s) ds \\&-\, \delta _{L} \int _{t-\delta _{L}}^tz^T(s) W z(s) ds - \delta _{1UL} \int _{t-\delta _{1U}}^{t-\delta _{1L}} z^T(s) X z(s) ds \\&-\, \delta _{2UL} \int _{t-\delta _{2U}}^{t-\delta _{2L}} z^T(s) Y z(s) ds - \delta _{UL} \int _{t-\delta _{U}}^{t-\delta _{L}} z^T(s) Z z(s) ds. \end{aligned}$$

Applying Lemma 2.1, we have

$$\begin{aligned} \dot{V_6}(z(t),t)& \le z^T(t) \left[ \delta _{1L}^2U + \delta _{2L}^2V + \delta _L^2W + \delta _{1UL}^2X + \delta _{2UL}^2Y + \delta _{UL}^2Z \right] z(t) \\&- \, \int _{t-\delta _1(t)}^tz^T(s) ds U \int _{t-\delta _1(t)}^t z(s) ds - \int _{t-\delta _2(t)}^tz^T(s) ds V \int _{t-\delta _2(t)}^t z(s) ds \\&- \, \int _{t-\delta (t)}^tz^T(s) ds W \int _{t-\delta (t)}^t z(s) ds - \int _{t-\delta _1(t)}^{t-\delta _{1L}} z^T(s) ds X \int _{t-\delta _1(t)}^{t-\delta _{1L}} z(s) ds \\&- \, 2 \int _{t-\delta _1(t)}^{t-\delta _{1L}} z^T(s) ds X \int _{t-\delta _{1U}}^{t-\delta _1(t)} z^T(s) ds - \int _{t-\delta _{1U}}^{t-\delta _1(t)} z^T(s) ds X \int _{t-\delta _{1U}}^{t-\delta _1(t)} z(s) ds \\&- \, \int _{t-\delta _2(t)}^{t-\delta _{2L}} z^T(s) ds Y \int _{t-\delta _2(t)}^{t-\delta _{2L}} z(s) ds - 2 \int _{t-\delta _2(t)}^{t-\delta _{2L}} z^T(s) ds Y \int _{t-\delta _{2U}}^{t-\delta _2(t)} z^T(s) ds \\&- \, \int _{t-\delta _{2U}}^{t-\delta _2(t)} z^T(s) ds Y \int _{t-\delta _{2U}}^{t-\delta _2(t)} z(s) ds - \int _{t-\delta (t)}^{t-\delta _{L}} z^T(s) ds Z \int _{t-\delta (t)}^{t-\delta _{L}} z(s) ds \\&- \, 2 \int _{t-\delta (t)}^{t-\delta _{L}} z^T(s) ds Z \int _{t-\delta _{U}}^{t-\delta (t)} z^T(s) ds - \int _{t-\delta _{U}}^{t-\delta (t)} z^T(s) ds Z \int _{t-\delta _{U}}^{t-\delta (t)} z(s) ds \\ \dot{V_6}(z(t),t)& \le \zeta ^T(t) \Pi _7 \zeta (t). \end{aligned}$$

(21)

Inspired by the ideas in the works of Kwon et al. (2014a, b), following six zero equalities with any symmetric matrices $F_i, \ i=1,2,\dots,6$ are introduced:

$$0= h_{1UL} \left[ z^T(t-h_{1L})F_1z(t-h_{1L}) - z^T(t-h_1(t))F_1z(t-h_1(t)) - 2 \int _{t-h_1(t)}^{t-h_{1L}} z^T(s) F_1 \dot{z}(s) ds \right],$$

(22)

$$0= h_{1UL} \left[ z^T(t-h_1(t))F_2z(t-h_1(t)) - z^T(t-h_{1U})F_2z(t-h_{1U}) - 2 \int _{t-h_{1U}}^{t-h_1(t)} z^T(s) F_2 \dot{z}(s) ds \right],$$

(23)

$$0= h_{2UL} \left[ z^T(t-h_{2L})F_3z(t-h_{2L}) - z^T(t-h_2(t))F_3z(t-h_2(t)) - 2 \int _{t-h_2(t)}^{t-h_{2L}} z^T(s) F_3 \dot{z}(s) ds \right],$$

(24)

$$0= h_{2UL} \left[ z^T(t-h_2(t))F_4z(t-h_2(t)) - z^T(t-h_{2U})F_4z(t-h_{2U}) - 2 \int _{t-h_{2U}}^{t-h_2(t)} z^T(s) F_4 \dot{z}(s) ds \right],$$

(25)

$$0= h_{UL} \left[ z^T(t-h_{L})F_5z(t-h_{L}) - z^T(t-h(t))F_5z(t-h(t)) - 2 \int _{t-h(t)}^{t-h_{L}} z^T(s) F_5 \dot{z}(s) ds \right],$$

(26)

$$0= h_{UL} \left[ z^T(t-h(t))F_6z(t-h(t)) - z^T(t-h_{U})F_6z(t-h_{U}) - 2 \int _{t-h_{U}}^{t-h(t)} z^T(s) F_6 \dot{z}(s) ds \right].$$

(27)

By summing the above six zero equalities given in the Eqs. (22)–(27), it can be obtained

$$\begin{aligned} 0& = \zeta ^T(t) \Pi _8 \zeta (t) - 2 h_{1UL} \int _{t-h_1(t)}^{t-h_{1L}}z^T(s)F_1\dot{z}(s) - 2 h_{1UL} \int _{t-h_{1U}}^{t-h_1(t)}z^T(s)F_2\dot{z}(s) ds \\&- \, 2 h_{2UL} \int _{t-h_2(t)}^{t-h_{2L}}z^T(s)F_3\dot{z}(s) - 2 h_{2UL} \int _{t-h_{2U}}^{t-h_2(t)}z^T(s)F_4\dot{z}(s) ds \\&- \, 2 h_{UL} \int _{t-h(t)}^{t-h_{L}}z^T(s)F_5\dot{z}(s) - 2 h_{UL} \int _{t-h_{U}}^{t-h(t)}z^T(s)F_6\dot{z}(s) ds, \\ \dot{V_7}(z(t),t)& = \xi ^T(t) \left[ h_{1L}^2\bar{U} + h_{2L}^2\bar{V} + h_L^2\bar{W} + h_{1UL}^2\bar{X} + h_{2UL}^2\bar{Y} + h_{UL}^2\bar{Z} \right] \xi (t) \\&- \, h_{1L} \int _{t-h_{1L}}^t\xi ^T(s) \bar{U} \xi (s) ds - h_{2L} \int _{t-h_{2L}}^t\xi ^T(s) \bar{V} \xi (s) ds \\&- \, h_{L} \int _{t-h_{L}}^t\xi ^T(s) \bar{W} \xi (s) ds - h_{1UL} \int _{t-h_{1U}}^{t-h_{1L}} \xi ^T(s) \bar{X} \xi (s) ds \\&- \, h_{2UL} \int _{t-h_{2U}}^{t-h_{2L}} \xi ^T(s) \bar{Y} \xi (s) ds - h_{UL} \int _{t-h_{U}}^{t-h_{L}} \xi ^T(s) \bar{Z} \xi (s) ds. \end{aligned}$$

(28)

Using Lemma 2.1, the following inequalities hold

$$\begin{aligned} \dot{V_7}(z(t),t)& \le \xi ^T(t) \left[ h_{1L}^2\bar{U} + h_{2L}^2\bar{V} + h_L^2\bar{W} + h_{1UL}^2\bar{X} + h_{2UL}^2\bar{Y} +\;h_{UL}^2\bar{Z} \right] \xi (t) \\&- \, \begin{bmatrix} \int _{t-h_{1L}}^t z(s) ds \\ \\ z(t) - z(t-h_{1L}) \end{bmatrix}^T \begin{bmatrix} \bar{U}_{11}&\bar{U}_{12} \\ \\ *&\bar{U}_{22} \end{bmatrix} \begin{bmatrix} \int _{t-h_{1L}}^t x(s) ds \\ \\ z(t) - z(t-h_{1L}) \end{bmatrix} \\&- \, \begin{bmatrix} \int _{t-h_{2L}}^t z(s) ds \\ \\ z(t) - z(t-h_{2L}) \end{bmatrix}^T \begin{bmatrix} \bar{V}_{11}&\bar{V}_{12} \\ \\ *&\bar{V}_{22} \end{bmatrix} \begin{bmatrix} \int _{t-h_{2L}}^t z(s) ds \\ \\ z(t) - z(t-h_{2L}) \end{bmatrix} \\&- \, \begin{bmatrix} \int _{t-h_{L}}^t z(s) ds \\ \\ z(t) - z(t-h_{L}) \end{bmatrix}^T \begin{bmatrix} \bar{W}_{11}&\bar{W}_{12} \\ \\ *&\bar{W}_{22} \end{bmatrix} \begin{bmatrix} \int _{t-h_{L}}^t z(s) ds \\ \\ z(t) - z(t-h_{L}) \end{bmatrix} \\&- \, h_{1UL} \int _{t-h_{1U}}^{t-h_{1L}} \xi ^T(s) \bar{X} \xi (s) ds - h_{2UL} \int _{t-h_{2U}}^{t-h_{2L}} \xi ^T(s) \bar{Y} \xi (s) ds \\&- \, h_{UL} \int _{t-h_{U}}^{t-h_{L}} \xi ^T(s) \bar{Z} \xi (s) ds. \end{aligned}$$

(29)

By considering integral terms in (29) with the equation (28), if the inequalities in (11), (12) and (13) are holds, then by utilizing Lemmas 2.1 and 2.2, it follows that

$$\begin{aligned}&-h_{1UL} \int _{t-h_{1U}}^{t-h_{1L}}\xi ^T(s) \bar{X}\xi (s) ds - 2 h_{1UL} \int _{t-h_1(t)}^{t-h_{1L}}z^T(s) F_1 \dot{z}(s) ds - 2 h_{1UL} \int _{t-h_{1U}}^{t-h_1(t)} z^T(s) F_2 \dot{z}(s)ds \\&\quad = - h_{1UL} \int _{t-h_1(t)}^{t-h_{1L}} \xi ^T(s) \left\{ \bar{X} + {\mathcal{F}}_1 \right\} \xi (s) ds - h_{1UL} \int _{t-h_{1U}}^{t-h_1(t)} \xi ^T(s) \left\{ \bar{X} + {\mathcal{F}}_2 \right\} \xi (s) ds \\&\quad \le - {\frac{h_{1UL}}{h_1(t)-h_{1L}}} \int _{t-h_1(t)}^{t-h_{1L}} \xi ^T(s) \left\{ \bar{X} + {\mathcal{F}}_1 \right\} \xi (s) ds - {\frac{h_{1UL}}{h_{1U}-h_1(t)}} \int _{t-h_{1U}}^{t-h_1(t)} \xi ^T(s) \left\{ \bar{X} + {\mathcal{F}}_2 \right\} \xi (s) ds \\ &\quad \le - \begin{bmatrix} \int _{t-h_1(t)}^{t-h_{1L}} \xi (s) ds \\ \\ \int _{t-h_{1U}}^{t-h_1(t)} \xi (s) ds \end{bmatrix}^T \begin{bmatrix} \bar{X} + {\mathcal{F}}_1&{\mathcal{L}} \\ \\ *&\bar{X} + {\mathcal{F}}_2 \end{bmatrix} \begin{bmatrix} \int _{t-h_1(t)}^{t-h_{1L}} \xi (s) ds \\ \\ \int _{t-h_{1U}}^{t-h_1(t)} \xi (s) ds \end{bmatrix}, \end{aligned}$$

(30)

and similarly, we have

$$\begin{aligned}&-h_{2UL} \int _{t-h_{2U}}^{t-h_{2L}}\xi ^T(s) \bar{Y}\xi (s) ds - 2 h_{2UL} \int _{t-h_2(t)}^{t-h_{2L}}z^T(s) F_3 \dot{z}(s) ds - 2 h_{2UL} \int _{t-h_{2U}}^{t-h_2(t)} z^T(s) F_4 \dot{z}(s)ds \\&\quad = - h_{2UL} \int _{t-h_2(t)}^{t-h_{2L}} \xi ^T(s) \left\{ \bar{Y} + {\mathcal{F}}_3 \right\} \xi (s) ds - h_{2UL} \int _{t-h_{2U}}^{t-h_2(t)} \xi ^T(s) \left\{ \bar{Y} + {\mathcal{F}}_4 \right\} \xi (s) ds \\&\quad \le - {\frac{h_{2UL}}{h_2(t)-h_{2L}}} \int _{t-h_2(t)}^{t-h_{2L}} \xi ^T(s) \left\{ \bar{Y} + {\mathcal{F}}_3 \right\} \xi (s) ds - {\frac{h_{2UL}}{h_{2U}-h_2(t)}} \int _{t-h_{2U}}^{t-h_2(t)} \xi ^T(s) \left\{ \bar{Y} + {\mathcal{F}}_4 \right\} \xi (s) ds \\ &\quad \le - \begin{bmatrix} \int _{t-h_2(t)}^{t-h_{2L}} \xi (s) ds \\ \\ \int _{t-h_{2U}}^{t-h_2(t)} \xi (s) ds \end{bmatrix}^T \begin{bmatrix} \bar{Y} + {\mathcal{F}}_3&{\mathcal{M}} \\ \\ *&\bar{Y} + {\mathcal{F}}_4 \end{bmatrix} \begin{bmatrix} \int _{t-h_2(t)}^{t-h_{2L}} \xi (s) ds \\ \\ \int _{t-h_{2U}}^{t-h_2(t)} \xi (s) ds \end{bmatrix}, \end{aligned}$$

(31)

$$\begin{aligned}&-h_{UL} \int _{t-h_{U}}^{t-h_{L}}\xi ^T(s) \bar{Z}\xi (s) ds - 2 h_{UL} \int _{t-h(t)}^{t-h_{L}}z^T(s) F_5 \dot{z}(s) ds - 2 h_{UL} \int _{t-h_{U}}^{t-h(t)} z^T(s) F_6 \dot{z}(s)ds \\&\quad = - h_{UL} \int _{t-h(t)}^{t-h_{L}} \xi ^T(s) \left\{ \bar{Z} + {\mathcal{F}}_5 \right\} \xi (s) ds - h_{UL} \int _{t-h_{U}}^{t-h(t)} \xi ^T(s) \left\{ \bar{Z} + {\mathcal{F}}_6 \right\} \xi (s) ds \\&\quad \le - {\frac{h_{UL}}{h(t)-h_{L}}} \int _{t-h(t)}^{t-h_{L}} \xi ^T(s) \left\{ \bar{Z} + {\mathcal{F}}_5 \right\} \xi (s) ds - {\frac{h_{UL}}{h_{U}-h(t)}} \int _{t-h_{U}}^{t-h(t)} \xi ^T(s) \left\{ \bar{Z} + {\mathcal{F}}_6 \right\} \xi (s) ds \\&\quad \le - \begin{bmatrix} \int _{t-h(t)}^{t-h_{L}} \xi (s) ds \\ \\ \int _{t-h_{U}}^{t-h(t)} \xi (s) ds \end{bmatrix}^T \begin{bmatrix} \bar{Z} + {\mathcal{F}}_5&{\mathcal{N}} \\ \\ *&\bar{Z} + {\mathcal{F}}_6 \end{bmatrix} \begin{bmatrix} \int _{t-h(t)}^{t-h_{L}} \xi (s) ds \\ \\ \int _{t-h_{U}}^{t-h(t)} \xi (s) ds \end{bmatrix}. \end{aligned}$$

(32)

From (30)–(32), it is concluded that

$$\begin{aligned}&\dot{V}_7(z(t),t) - 2 h_{1UL} \int _{t-h_1(t)}^{t-h_{1L}}z^T(s)F_1\dot{z}(s) - 2 h_{1UL} \int _{t-h_{1U}}^{t-h_1(t)}z^T(s)F_2\dot{z}(s) ds \\&\qquad - \, 2 h_{2UL} \int _{t-h_2(t)}^{t-h_{2L}}z^T(s)F_3\dot{z}(s) - 2 h_{2UL} \int _{t-h_{2U}}^{t-h_2(t)}z^T(s)F_4\dot{z}(s) ds \\&\qquad - \, 2 h_{UL} \int _{t-h(t)}^{t-h_{L}}z^T(s)F_5\dot{z}(s) - 2 h_{UL} \int _{t-h_{U}}^{t-h(t)}z^T(s)F_6\dot{z}(s) ds \\&\quad \le \xi ^T(t) \left[ h_{1L}^2\bar{U} + h_{2L}^2\bar{V} + h_L^2\bar{W} + h_{1UL}^2\bar{X} + h_{2UL}^2\bar{Y} + h_{UL}^2\bar{Z} \right] \xi (t) \\&\qquad - \, \begin{bmatrix} \int _{t-h_{1L}}^t z(s) ds \\ \\ z(t) - z(t-h_{1L}) \end{bmatrix}^T \begin{bmatrix} \bar{U}_{11}&\bar{U}_{12} \\ \\ *&\bar{U}_{22} \end{bmatrix} \begin{bmatrix} \int _{t-h_{1L}}^t x(s) ds \\ \\ z(t) - z(t-h_{1L}) \end{bmatrix} \\&\qquad - \, \begin{bmatrix} \int _{t-h_{2L}}^t z(s) ds \\ \\ z(t) - z(t-h_{2L}) \end{bmatrix}^T \begin{bmatrix} \bar{V}_{11}&\bar{V}_{12} \\ \\ *&\bar{V}_{22} \end{bmatrix} \begin{bmatrix} \int _{t-h_{2L}}^t z(s) ds \\ \\ z(t) - z(t-h_{2L}) \end{bmatrix} \\&\qquad - \, \begin{bmatrix} \int _{t-h_{L}}^t z(s) ds \\ \\ z(t) - z(t-h_{L}) \end{bmatrix}^T \begin{bmatrix} \bar{W}_{11}&\bar{W}_{12} \\ \\ *&\bar{W}_{22} \end{bmatrix} \begin{bmatrix} \int _{t-h_{L}}^t z(s) ds \\ \\ z(t) - z(t-h_{L}) \end{bmatrix} \\&\qquad - \, \begin{bmatrix} \int _{t-h_1(t)}^{t-h_{1L}} z(s) ds \\ z(t-h_{1L}) - z(t-h_1(t)) \\ \\ \int _{t-h_{1U}}^{t-h_1(t)} z(s) ds \\ z(t-h_1(t)) - z(t-h_{1U}) \end{bmatrix}^T \begin{bmatrix} \bar{X} + {\mathcal{F}}_1&{\mathcal{L}} \\ \\ *&\bar{X} + {\mathcal{F}}_2 \end{bmatrix} \begin{bmatrix} \int _{t-h_1(t)}^{t-h_{1L}} z(s) ds \\ z(t-h_{1L}) - z(t-h_1(t)) \\ \\ \int _{t-h_{1U}}^{t-h_1(t)} z(s) ds \\ z(t-h_1(t)) - z(t-h_{1U}) \end{bmatrix} \\&\qquad - \, \begin{bmatrix} \int _{t-h_2(t)}^{t-h_{2L}} z(s) ds \\ z(t-h_{2L}) - z(t-h_2(t)) \\ \\ \int _{t-h_{2U}}^{t-h_2(t)} z(s) ds \\ z(t-h_2(t)) - z(t-h_{2U}) \end{bmatrix}^T \begin{bmatrix} \bar{Y} + {\mathcal{F}}_3&{\mathcal{M}} \\ \\ *&\bar{Y} + {\mathcal{F}}_4 \end{bmatrix} \begin{bmatrix} \int _{t-h_2(t)}^{t-h_{2L}} z(s) ds \\ z(t-h_{2L}) - z(t-h_2(t)) \\ \\ \int _{t-h_{2U}}^{t-h_2(t)} z(s) ds \\ z(t-h_2(t)) - z(t-h_{2U}) \end{bmatrix} \\ &\qquad - \, \begin{bmatrix} \int _{t-h(t)}^{t-h_{L}} z(s) ds \\ z(t-h_{L}) - z(t-h(t)) \\ \\ \int _{t-h_{U}}^{t-h(t)} z(s) ds \\ z(t-h(t)) - z(t-h_{U}) \end{bmatrix}^T \begin{bmatrix} \bar{Z} + {\mathcal{F}}_5&{\mathcal{N}} \\ \\ *&\bar{Z} + {\mathcal{F}}_6 \end{bmatrix} \begin{bmatrix} \int _{t-h(t)}^{t-h_{L}} z(s) ds \\ z(t-h_{L}) - z(t-h(t)) \\ \\ \int _{t-h_{U}}^{t-h(t)} z(s) ds \\ z(t-h(t)) - z(t-h_{U}) \end{bmatrix} \\ &\quad \le \zeta ^T(t) \Pi _9 \zeta (t), \end{aligned}$$

(33)

$$\begin{aligned} \dot{V_8}(z(t),t)& = \dot{z}^T(t)\left( {\frac{h_{1L}^4}{4}} R_1 + {\frac{h_{2L}^4}{4}} R_2 + {\frac{h_{L}^4}{4}} R_3 + {\frac{(h_{1U}^2 - h_{1L}^2)^2}{4}} R_4 + {\frac{(h_{2U}^2 - h_{2L}^2)^2}{4}} R_5 \right. \\&\left. +\;{\frac{(h_{U}^2 - h_{L}^2)^2}{4}} R_6 \right) \dot{z}(t) - {\frac{h_{1L}^2}{2}}\int _{-h_{1L}}^0 \int _{t+u}^t \dot{z}^T(s) R_1 \dot{z}(s) ds du \\&- \, {\frac{h_{2L}^2}{2}}\int _{-h_{2L}}^0 \int _{t+u}^t \dot{z}^T(s) R_2 \dot{z}(s) ds du - {\frac{h_{L}^2}{2}}\int _{-h_{L}}^0 \int _{t+u}^t \dot{z}^T(s) R_3 \dot{z}(s) ds du \\&- \, {\frac{h_{1U}^2-h_{1L}^2}{2}} \int _{-h_1(t)}^{-h_{1L}} \int _{t+u}^t \dot{z}^T(s) R_4 \dot{z}(s) ds du - {\frac{h_{1U}^2-h_{1L}^2}{2}} \int _{-h_{1U}}^{-h_1(t)} \int _{t+u}^t \dot{z}^T(s) R_4 \dot{z}(s) ds du \\&- \, {\frac{h_{2U}^2-h_{2L}^2}{2}} \int _{-h_2(t)}^{-h_{2L}} \int _{t+u}^t \dot{z}^T(s) R_5 \dot{z}(s) ds du - {\frac{h_{2U}^2-h_{2L}^2}{2}} \int _{-h_{2U}}^{-h_2(t)} \int _{t+u}^t \dot{z}^T(s) R_5 \dot{z}(s) ds du \\&- \, {\frac{h_{U}^2-h_{L}^2}{2}} \int _{-h(t)}^{-h_{L}} \int _{t+u}^t \dot{z}^T(s) R_6 \dot{z}(s) ds du - {\frac{h_{U}^2-h_{L}^2}{2}} \int _{-h_{U}}^{-h(t)} \int _{t+u}^t \dot{z}^T(s) R_6 \dot{z}(s) ds du. \end{aligned}$$

(34)

Applying Lemma 2.3, the integral terms in (34) can be rewritten as

$$\begin{aligned} - {\frac{h_{1L}^2}{2}}\int _{-h_{1L}}^0 \int _{t+u}^t \dot{z}^T(s) R_1 \dot{z}(s) ds du& \le - \left( h_{1L}z(t) - \int _{t-h_{1L}}^t z(s) ds \right) ^TR_1 \left( h_{1L}z(t) - \int _{t-h_{1L}}^t z(s) ds \right) \\&- \, 2 \left( -{\frac{h_{1L}}{2}}z(t) - \int _{t-h_{1L}}^tz(s) ds + {\frac{3}{h_{1L}}} \int _{-h_{1L}}^0 \int _{t+u}^t z(s) ds du \right) ^T R_1 \\&\times \left( -{\frac{h_{1L}}{2}}z(t) - \int _{t-h_{1L}}^tz(s) ds + {\frac{3}{h_{1L}}} \int _{-h_{1L}}^0 \int _{t+u}^t z(s) ds du \right) \\ & \le \zeta ^T(t) \Theta _1 \zeta (t), \end{aligned}$$

(35)

Similarly, we have

$$- {\frac{h_{2L}^2}{2}}\int _{-h_{2L}}^0 \int _{t+u}^t \dot{z}^T(s) R_2 \dot{z}(s) ds du \le \zeta ^T(t)\Theta _2 \zeta (t),$$

(36)

$$- {\frac{h_{L}^2}{2}}\int _{-h_{L}}^0 \int _{t+u}^t \dot{z}^T(s) R_3 \dot{z}(s) ds du \le \zeta ^T(t) \Theta _3 \zeta (t),$$

(37)

$$- {\frac{h_{1U}^2-h_{1L}^2}{2}} \int _{-h_1(t)}^{-h_{1L}} \int _{t+u}^t \dot{z}^T(s) R_4 \dot{z}(s) ds du \le \zeta ^T(t) \Theta _4 \zeta (t),$$

(38)

$$- {\frac{h_{1U}^2-h_{1L}^2}{2}} \int _{-h_{1U}}^{-h_1(t)} \int _{t+u}^t \dot{z}^T(s) R_4 \dot{z}(s) ds du \le \zeta ^T(t) \Theta _5 \zeta (t),$$

(39)

$$- {\frac{h_{2U}^2-h_{2L}^2}{2}} \int _{-h_2(t)}^{-h_{2L}} \int _{t+u}^t \dot{z}^T(s) R_5 \dot{z}(s) ds du \le \zeta ^T(t) \Theta _6 \zeta (t),$$

(40)

$$- {\frac{h_{2U}^2-h_{2L}^2}{2}} \int _{-h_{2U}}^{-h_2(t)} \int _{t+u}^t \dot{z}^T(s) R_5 \dot{z}(s) ds du \le \zeta ^T(t) \Theta _7 \zeta (t),$$

(41)

$$- {\frac{h_{U}^2-h_{L}^2}{2}} \int _{-h(t)}^{-h_{L}} \int _{t+u}^t \dot{z}^T(s) R_6 \dot{z}(s) ds du \le \zeta ^T(t) \Theta _8 \zeta (t),$$

(42)

$$- {\frac{h_{U}^2-h_{L}^2}{2}} \int _{-h_{U}}^{-h(t)} \int _{t+u}^t \dot{z}^T(s) R_6 \dot{z}(s) ds du \le \zeta ^T(t) \Theta _9 \zeta (t).$$

(43)

where

$$\begin{aligned} \Theta _1& = -\left[ h_{1L}e_1 - e_{11} \right] R_1 \left[ h_{1L}e_1 - e_{11} \right] ^T - 2 \left[ -{\frac{h_{1L}}{2}}e_1 - e_{11} + {\frac{3}{h_{1L}}}e_{20} \right] R_1 \left[ -{\frac{h_{1L}}{2}}e_1 - e_{11} + {\frac{3}{h_{1L}}}e_{20} \right] ^T \\ \Theta _2& = -\left[ h_{2L}e_1 - e_{12} \right] R_2 \left[ h_{2L}e_1 - e_{12} \right] ^T - 2 \left[ -{\frac{h_{2L}}{2}}e_1 - e_{12} + {\frac{3}{h_{2L}}}e_{21} \right] R_2 \left[ -{\frac{h_{2L}}{2}}e_1 - e_{12} + {\frac{3}{h_{2L}}}e_{21} \right] ^T, \\ \Theta _3& = -\left[ h_{L}e_1 - e_{13} \right] R_3 \left[ h_{L}e_1 - e_{13} \right] ^T - 2 \left[ -{\frac{h_{L}}{2}}e_1 - e_{13} + {\frac{3}{h_{L}}}e_{22} \right] R_3 \left[ -{\frac{h_{L}}{2}}e_1 - e_{13} + {\frac{3}{h_{L}}}e_{22} \right] ^T, \\ \Theta _4& = -\left[ h_{1UL}e_1 - e_{14} \right] R_4 \left[ h_{1UL}e_1 - e_{14} \right] ^T - 2 \left[ -{\frac{h_{1UL}}{2}}e_1 - e_{14} + {\frac{3}{h_{1UL}}}e_{23} \right] R_4 \left[ -{\frac{h_{1UL}}{2}}e_1 - e_{14} + {\frac{3}{h_{1UL}}}e_{23} \right] ^T, \\ \Theta _5& = -\left[ h_{1UL}e_1 - e_{15} \right] R_4 \left[ h_{1UL}e_1 - e_{15} \right] ^T - 2 \left[ -{\frac{h_{1UL}}{2}}e_1 - e_{15} + {\frac{3}{h_{1UL}}}e_{24} \right] R_4 \left[ -{\frac{h_{1UL}}{2}}e_1 - e_{15} + {\frac{3}{h_{1UL}}}e_{24} \right] ^T,\\ \Theta _6& = -\left[ h_{2UL}e_1 - e_{16} \right] R_5 \left[ h_{2UL}e_1 - e_{16} \right] ^T - 2 \left[ -{\frac{h_{2UL}}{2}}e_1 - e_{16} + {\frac{3}{h_{2UL}}}e_{25} \right] R_5 \left[ -{\frac{h_{2UL}}{2}}e_1 - e_{16} + {\frac{3}{h_{2UL}}}e_{25} \right] ^T, \\ \Theta _7& = -\left[ h_{2UL}e_1 - e_{17} \right] R_5 \left[ h_{2UL}e_1 - e_{17} \right] ^T - 2 \left[ -{\frac{h_{2UL}}{2}}e_1 - e_{17} + {\frac{3}{h_{2UL}}}e_{26} \right] R_5 \left[ -{\frac{h_{2UL}}{2}}e_1 - e_{17} + {\frac{3}{h_{2UL}}}e_{26} \right] ^T, \\ \Theta _8& = -\left[ h_{UL}e_1 - e_{18} \right] R_6 \left[ h_{UL}e_1 - e_{18} \right] ^T - 2 \left[ -{\frac{h_{UL}}{2}}e_1 - e_{18} + {\frac{3}{h_{UL}}}e_{27} \right] R_6 \left[ -{\frac{h_{UL}}{2}}e_1 - e_{18} + {\frac{3}{h_{UL}}}e_{27} \right] ^T, \\ \Theta _9& = -\left[ h_{UL}e_1 - e_{19} \right] R_6 \left[ h_{UL}e_1 - e_{19} \right] ^T - 2 \left[ -{\frac{h_{UL}}{2}}e_1 - e_{19} + {\frac{3}{h_{UL}}}e_{28} \right] R_6 \left[ -{\frac{h_{UL}}{2}}e_1 - e_{19} + {\frac{3}{h_{UL}}}e_{28} \right] ^T. \\ \end{aligned}$$

From (34)–(43), it gives that

$$\begin{aligned} V_8(z(t),t)& \le \zeta ^T(t) \Pi _{10} \zeta (t), \\ V_9(z(t),t)& \le \tau ^2 g^T(z(t)) S_1 g(z(t)) - \tau \int _{t-\tau (t)}^tg^T(z(s)) S_1 g(z(s)) ds + \dot{z}^T(t)T_2\dot{z}(t) \\&+ \, \dot{z}^T(t-\sigma (t))(-(1-\sigma _D)T_2)\dot{z}(t-\sigma (t)). \end{aligned}$$

Utilizing Lemma 2.1, we have

$$\begin{aligned} V_9(z(t),t)& \le g^T(z(t)) \left[ \tau ^2 S_1 \right] g(z(t)) + \left( \int _{t-\tau (t)}^tg(z(s)) ds \right) ^T (-S_1) \left( \int _{t-\tau (t)}^t g(z(s)) ds \right) + \dot{z}^T(t)S_2\dot{z}(t) \\&+ \, \dot{z}^T(t-\sigma (t))(-(1-\sigma _D)S_2)\dot{z}(t-\sigma (t)), \\ & \le \zeta ^T(t) \Pi _{11} \zeta (t). \end{aligned}$$

(44)

On the other hand, for any matrix H with appropriate dimension, it is true that

$$\begin{aligned} 0& = 2 \dot{z}^T(t) H \sum _{k=1}^m \gamma _k(t) \left[ \dot{z}(t) - D_k z(t-\delta (t)) + A_k g(z(t)) + B_k g(z(t-h(t)))\right. \\&\left. + C_k \int _{t-\tau (t)}^t g(z(s)) ds + E_k \dot{z} (t-\sigma (t))\right], \\ & = \zeta ^T(t) \Pi _{12} \zeta (t). \end{aligned}$$

(45)

From (6), the following inequality holds for any positive diagonal matrices $G_i, \ i=1,2, \dots,7$

$$\begin{aligned} 0& = \left\{ \left[ z^T(t) \left( -G_1 \Sigma _1 \right) z(t) + 2 z^T(t) \left( G_1 \Sigma _2 \right) g(z(t)) + g^T(z(t)) \left( -G_1 \right) g(z(t)) \right] \right. \\& \quad+ \, \left[ z^T(t-h_1(t)) \left( -G_2 \Sigma _1 \right) z(t-h_1(t)) + 2 z^T(t-h_1(t)) \left( G_2 \Sigma _2 \right) g(z(t-h_1(t))) \right. \\&\left. \quad + g^T(z(t-h_1(t))) \left( -G_2 \right) g(z(t-h_1(t))) \right] \\& \quad+ \, \left[ z^T(t-h_{1U}) \left( -G_3 \Sigma _1 \right) z(t-h_{1U}) + 2 z^T(t-h_{1U}) \left( G_3 \Sigma _2 \right) g(z(t-h_{1U}))\right. \\&\left. \quad + g^T(z(t-h_{1U})) \left( -G_3 \right) g(z(t-h_{1U})) \right] \\& \quad+ \, \left[ z^T(t-h_2(t)) \left( -G_4 \Sigma _1 \right) z(t-h_2(t)) + 2 z^T(t-h_2(t)) \left( G_4 \Sigma _2 \right) g(z(t-h_2(t)))\right. \\&\left. \quad + g^T(z(t-h_2(t))) \left( -G_4 \right) g(z(t-h_2(t))) \right] \\& \quad+ \, \left[ z^T(t-h_{2U}) \left( -G_5 \Sigma _1 \right) z(t-h_{2U})\right. \\&\left. \quad + 2 z^T(t-h_{2U}) \left( G_5 \Sigma _2 \right) g(z(t-h_{2U})) + g^T(z(t-h_{2U})) \left( -G_5 \right) g(z(t-h_{2U})) \right] \\& \quad+ \, \left[ z^T(t-h(t)) \left( -G_6 \Sigma _1 \right) z(t-h(t)) + 2 z^T(t-h(t)) \left( G_6 \Sigma _2 \right) g(z(t-h(t)))\right. \\&\left. \quad + g^T(z(t-h(t))) \left( -G_6 \right) g(z(t-h(t))) \right] \\& \quad+ \, \left[ z^T(t-h_{U}) \left( -G_7 \Sigma _1 \right) z(t-h_{U})\right. \\&\left. \left. \quad + 2 z^T(t-h_{U}) \left( G_7 \Sigma _2 \right) g(z(t-h_{U})) + g^T(z(t-h_{U})) \left( -G_7 \right) g(z(t-h_{U})) \right] \right\} \\& = \zeta ^T(t) \Pi _{13} \zeta (t). \end{aligned}$$

(46)

From Eqs. (16)–(46), by using S-procedure in Boyd et al. (1994), if Eqs. (11)–(13) hold, then an upper bound of $\dot{V}(z(t),t)$ can be written as

$$\dot{V}(z(t),t)\,\le \,\zeta ^T(t) \Xi \zeta (t).$$

(47)

Based on Lemma 2.4, $\zeta ^T(t) \ \Xi \ \zeta (t) < 0$ with $\Gamma \ \zeta (t) = 0$ is equivalent to $(\Gamma ^\perp )^T \ \Xi \ \Gamma ^\perp <0.$ Therefore, if the inequality (10) holds, the equilibrium point of system (9) is asymptotically stable. This completes the proof

Remark 3.1

For the case of SHNNs without neutral term, we let $E_k = 0$ in (9) and the following corollary can be obtained with a proof similar to Theorem 3.1. In this case, network (9) can be rewritten as

$$\dot{z}(t)= \sum _{k=1}^m \gamma _k(t) \left[ - D_k z(t-\delta (t)) + A_k g(z(t)) + B_k g(z(t-h(t))) + C_k \int _{t-\tau (t)}^t g(z(s)) ds \right].$$

(48)

Corollary 3.1

For given positive scalars $\delta _{1L},\delta _{1U},\delta _{2L},\delta _{2U},h_{1L},h_{1U},h_{2L},h_{2U},\delta _1,\delta _2,h_1,h_2,\tau,\eta _1,\eta _2,\mu _1,\mu _2,\tau _D$, and diagonal matrices $K_p,K_m$, then the neural network described by (48) is asymptotically stable, for any time-varying delay $\delta (t),h(t)$ and $\tau (t)$ satisfying (2), if there exist positive definite matrices $P_i (i=1,2, \dots,18)\in {\mathbb{R}}^{n \times n},T_i (i=1,2,3)\in {\mathbb{R}}^{n \times n},Q_i (i=1,2,\dots,17)\in {\mathbb{R}}^{n \times n}U,V,W,X,Y,Z\in {\mathbb{R}}^{n \times n},\bar{U}{\in {\mathbb{R}}^{2n \times 2n}},\bar{V}{\in {\mathbb{R}}^{2n \times 2n}},\bar{W}{\in {\mathbb{R}}^{2n \times 2n}},\bar{X}{\in {\mathbb{R}}^{2n \times 2n}},\bar{Y}{\in {\mathbb{R}}^{2n \times 2n}},\bar{Z}{\in {\mathbb{R}}^{2n \times 2n}},R_i (i=1,2,\dots,6)\in {\mathbb{R}}^{n \times n},S_1 \in {\mathbb{R}}^{n \times n}$, positive diagonal matrices $\Delta _l=\hbox {diag}\left\{ \lambda _{l1}, \lambda _{l2}, \dots, \lambda _{ln}\right\},\Lambda _l=\hbox {diag}\left\{ \mu _{l1}, \mu _{l2}, \dots, \mu _{ln}\right\},H\in {\mathbb{R}}^{n \times n},G_i (i=1,2,\dots,7)\in {\mathbb{R}}^{n \times n}$, any symmetric matrices $F_i\in {\mathbb{R}}^{n \times n}(i=1,2, \dots,6)$, any matrices ${\mathcal{L}}, {\mathcal{M}}, {\mathcal{N}}\in {\mathbb{R}}^{2n \times 2n}$ such that the following LMIs hold:

$$\left( \overline{\Gamma }^\perp \right) ^T \ \Xi \ \overline{\Gamma }^\perp < 0,$$

(49)

$$\begin{bmatrix} \bar{X} + {\mathcal{F}}_1&{\mathcal{L}} \\ \\ *&\bar{X} + {\mathcal{F}}_2 \end{bmatrix} \ge 0, \quad \begin{bmatrix} \bar{Y} + {\mathcal{F}}_3&{\mathcal{M}} \\ \\ *&\bar{Y} + {\mathcal{F}}_4 \end{bmatrix} \ge 0, \quad \begin{bmatrix} \bar{Z} + {\mathcal{F}}_5&{\mathcal{N}} \\ \\ *&\bar{Z} + {\mathcal{F}}_6 \end{bmatrix} \ge 0,$$

(50)

where $\Xi$ is same as defined in Theorem 3.1 with $E_k = 0.$

Proof

For the proof, consider the same Lyapunov–Krasovskii functional (10) with $S_2 = 0$ in $V_9(z(t),t).$ Then by following the same procedure in Theorem 3.1, we obtain $\Xi$ with $S_2 = 0.$ Then by defining $\overline{\Gamma } = \left[ \underbrace{0_n \dots \dots 0_n}_{28 \ times} A_k \underbrace{0_n \dots \dots 0_n}_{5 \ times} B_k \underbrace{0_n \dots \dots 0_n}_{4 \ times} C_k \underbrace{0_n \dots \dots 0_n}_{5 \ times} -D_k \underbrace{0_n \dots \dots 0_n}_{9 \ times} \right]$ and its right orthogonal complement by $\overline{\Gamma }^T$ we conclude the proof similar to Theorem 3.1. $\square$

Remark 3.2

For the case of SHNNs without leakage and neutral term, we let $E_k = 0$ in (9) and the following corollary can be obtained with a proof similar to Theorem 3.1. In this case, network (9) can be rewritten as

$$\dot{z}(t)= \sum _{k=1}^m \gamma _k(t) \left[ - D_k z(t) + A_k g(z(t)) + B_k g(z(t-h(t))) + C_k \int _{t-\tau (t)}^t g(z(s)) ds \right].$$

(51)

Corollary 3.2

For given positive scalars $h_{1L},h_{1U},h_{2L},h_{2U},h_1,h_2,\tau,\mu _1,\mu _2,\tau _D$, and diagonal matrices $K_p,K_m$, then the neural network described by (51) is asymptotically stable, for any time-varying delay h(t) and $\tau (t)$ satisfying (2), if there exist positive definite matrices $P_i (i=1,7, \dots,18)\in {\mathbb{R}}^{n \times n},T_i (i=1,2,3)\in {\mathbb{R}}^{n \times n},Q_i (i=6,7,\dots,17)\in {\mathbb{R}}^{n \times n},\bar{U}{\in {\mathbb{R}}^{2n \times 2n}},\bar{V}{\in {\mathbb{R}}^{2n \times 2n}},\bar{W}{\in {\mathbb{R}}^{2n \times 2n}},\bar{X}{\in {\mathbb{R}}^{2n \times 2n}},\bar{Y}{\in {\mathbb{R}}^{2n \times 2n}},\bar{Z}{\in {\mathbb{R}}^{2n \times 2n}}$,$R_i (i=1,2,\dots,6)\in {\mathbb{R}}^{n \times n},S_1 \in {\mathbb{R}}^{n \times n}$, positive diagonal matrices $\Delta _l=\hbox {diag}\left\{ \lambda _{l1}, \lambda _{l2}, \dots, \lambda _{ln}\right\},\Lambda _l=\hbox {diag}\left\{ \mu _{l1}, \mu _{l2}, \dots, \mu _{ln}\right\},H\in {\mathbb{R}}^{n \times n},G_i (i=1,2,\dots,7)\in {\mathbb{R}}^{n \times n}$, any symmetric matrices $F_i\in {\mathbb{R}}^{n \times n}(i=1,2, \dots,6)$, any matrices ${\mathcal{L}}, {\mathcal{M}}, {\mathcal{N}}\in {\mathbb{R}}^{2n \times 2n}$ such that the following LMIs hold:

$$\left( \widehat{\overline{\Gamma }}^\perp \right) ^T \ \Xi \ \widehat{\overline{\Gamma }}^\perp < 0,$$

(52)

$$\begin{bmatrix} \bar{X} + {\mathcal{F}}_1&{\mathcal{L}} \\ \\ *&\bar{X} + {\mathcal{F}}_2 \end{bmatrix} \ge 0, \quad \begin{bmatrix} \bar{Y} + {\mathcal{F}}_3&{\mathcal{M}} \\ \\ *&\bar{Y} + {\mathcal{F}}_4 \end{bmatrix} \ge 0, \quad \begin{bmatrix} \bar{Z} + {\mathcal{F}}_5&{\mathcal{N}} \\ \\ *&\bar{Z} + {\mathcal{F}}_6 \end{bmatrix} \ge 0,$$

(53)

where $\Xi$ is same as defined in Theorem 3.1 with $E_k = 0.$

Proof

For the proof, consider the same Lyapunov–Krasovskii functional (10) with $P_i=0,\, i=2,3,\dots,6, \, Q_i, i=1,2,\dots,5,\,U=V=W=X=Y=Z=0,\,S_2 = 0$ in $V_4(z(t),t),V_5(z(t),t),V_6(z(t),t)$ and $V_9(z(t),t).$ Then by following the same procedure in Theorem 3.1, we obtain $\Xi$ with $P_i=0,\, i=2,3,\dots,6,\,Q_i, i=1,2,\dots,5,\,U=V=W=X=Y=Z=0,\,S_2 = 0.$ Then by defining $\widehat{\overline{\Gamma }} = \left[ -D_K \underbrace{0_n \dots \dots 0_n}_{27 \ times} A_k \underbrace{0_n \dots \dots 0_n}_{5 \ times} B_k \underbrace{0_n \dots \dots 0_n}_{4 \ times} C_k \right]$ and its right orthogonal complement by $\overline{\Gamma }^T$ we conclude the proof similar to Theorem 3.1. $\square$

Remark 3.3

We may also consider the case of SHNNs without leakage, distributed and neutral term, we let $\delta (t)=C_k=E_k = 0$ in (9) and the following corollary can be obtained with a proof similar to Theorem 3.1. In this case, network (9) can be rewritten as

$$\dot{z}(t)= \sum _{k=1}^m \gamma _k(t) \left[ - D_k z(t) + A_k g(z(t)) + B_k g(z(t-h(t))) \right].$$

(54)

Corollary 3.3

For given positive scalars $h_{1L},h_{1U},h_{2L},h_{2U},h_1,h_2,\mu _1,\mu _2$, and diagonal matrices $K_p,K_m$, then the neural network described by (54) is asymptotically stable, for any time-varying delay h(t) satisfying (2), if there exist positive definite matrices $P_i (i=1,7, \dots,18)\in {\mathbb{R}}^{n \times n},T_i (i=1,2,3)\in {\mathbb{R}}^{n \times n},Q_i (i=6,7,\dots,17)\in {\mathbb{R}}^{n \times n},\bar{U}{\in {\mathbb{R}}^{2n \times 2n}},\bar{V}{\in {\mathbb{R}}^{2n \times 2n}},\bar{W}{\in {\mathbb{R}}^{2n \times 2n}},\bar{X}{\in {\mathbb{R}}^{2n \times 2n}},\bar{Y}{\in {\mathbb{R}}^{2n \times 2n}},\bar{Z}{\in {\mathbb{R}}^{2n \times 2n}},R_i (i=1,2,\dots,6)\in {\mathbb{R}}^{n \times n}$, positive diagonal matrices $\Delta _l=\hbox {diag}\left\{ \lambda _{l1}, \lambda _{l2}, \dots, \lambda _{ln}\right\},\Lambda _l=\hbox {diag} \left\{ \mu _{l1}, \mu _{l2}, \dots, \mu _{ln}\right\},H\in {\mathbb{R}}^{n \times n},G_i (i=1,2,\dots,7)\in {\mathbb{R}}^{n \times n}$, any symmetric matrices $F_i\in {\mathbb{R}}^{n \times n}(i=1,2, \dots,6)$, any matrices ${\mathcal{L}}, {\mathcal{M}}, {\mathcal{N}}\in {\mathbb{R}}^{2n \times 2n}$ such that the following LMIs hold:

$$\left( \Psi ^\perp \right) ^T \ \Xi \ \Psi ^\perp < 0,$$

(55)

$$\begin{bmatrix} \bar{X} + {\mathcal{F}}_1&{\mathcal{L}} \\ \\ *&\bar{X} + {\mathcal{F}}_2 \end{bmatrix} \ge 0, \quad \begin{bmatrix} \bar{Y} + {\mathcal{F}}_3&{\mathcal{M}} \\ \\ *&\bar{Y} + {\mathcal{F}}_4 \end{bmatrix} \ge 0, \quad \begin{bmatrix} \bar{Z} + {\mathcal{F}}_5&{\mathcal{N}} \\ \\ *&\bar{Z} + {\mathcal{F}}_6 \end{bmatrix} \ge 0,$$

(56)

where $\Xi$ is same as defined in Theorem 3.1 with $\delta (t)=C_k=E_k = 0.$

Proof

For the proof, consider the same Lyapunov–Krasovskii functional (10) with $P_i=0,\, i=2,3,\dots,6,\,Q_i, i=1,2,\dots,5,\,U=V=W=X=Y=Z=0,\,S_1=S_2 = 0$ in $V_4(z(t),t),V_5(z(t),t),V_6(z(t),t)$ and $V_9(z(t),t).$ Then by following the same procedure in Theorem 3.1, we obtain $\Xi$ with $P_i=0,\, i=2,3,\dots,6,\,Q_i, i=1,2,\dots,5,\,U=V=W=X=Y=Z=0,\,S_1=S_2 = 0.$ Then by defining $\Psi = \left[ -D_K \underbrace{0_n \dots \dots 0_n}_{27 \ times} A_k \underbrace{0_n \dots \dots 0_n}_{5 \ times} B_k \underbrace{0_n \dots \dots 0_n}_{4 \ times} \right]$ and its right orthogonal complement by $\Psi ^T$ we conclude the proof similar to Theorem 3.1. $\square$

Remark 3.4

In order to use more information about neuron activation functions, in this paper terms on the slope of neuron activation functions are introduced in the L–K functional to study the stability of addressed NNs. In Shao and Han (2011) have used the term.

$$2\sum _{i=1}^n \int _{0}^{z_i} \delta _i g_i(s)ds, \quad where \quad \delta _i\ge 0, \quad i=1,2, \dots,n$$

in their L–K functional for the neuron activation function $g(z(\cdot ))$. By utilizing the condition (4) about the slope of the neuron activation functions into the L–K functional, the term

$$2\sum _{i=1}^n \left[ \lambda _{1i} \int _{0}^{z_i(t)} (g_i(s)-k_i^- s)ds + \delta _{1i} \int _{0}^{z_i(t)} (k_i^+ s - g_i(s))ds \right],$$

has been introduced in Li et al. (2011). Recently, only few authors have employed delay bounds into the slope of neuron activation functions in the L–K functional, see Kwon et al. (2014a, b). Inspired by these works, in this paper, we consider a new $V_2(z(t),t)$, which indicates that more information about neuron activations has been used and it has not been considered in any of the previous works that deal with the stability of SHNNs with successive time-varying delay components.

Remark 3.5

In order to reduce the conservatism of stability conditions, inspired by the ideas in Kwon et al. (2014b), six zero integral equalities in (22)–(27) are introduced and terms involving these inequalities are merged with Eq. (29) during the calculation of $V_7(z(t),t)$. After then, reciprocal convex combination technique is utilized in the proof of Theorem 3.1, which can lead to a further improvement of the stability criterion. It is noted that introducing augmented L–K functional and zero integral inequalities and utilizing reciprocal convex combination technique can lead to less conservative results.

Remark 3.6

The number of decision variables used in Theorem 3.1 is larger than the previous studies in Rakkiyappan et al. (2015a, b), Senthilraj et al. (2016), and Dharani et al. (2015). Because, the reason is the proposed model consists of an additive interval time-delay components in the state both of discrete delay and leakage delay with newly augmented form of L–K functionals. As we know that, in order to reduce the computational burden the Finsler’s lemma was conducted in the proof of Theorem 3.1, which in turn to reduces the computational burden. As a result, proposed stability criteria gives better results while maintaining lower computational burden.

Remark 3.7

It is important to note that very limited works have been done on stability of switched Hopfield NNs of neutral-type with time-varying delays. More particularly, stability analysis of switched Hopfield NNs of neutral-type with successive interval time-varying delay components in the state both of discrete and leakage delay has not been completely studied in previous literature (see e.g., Rakkiyappan et al. 2015a, b; Senthilraj et al. 2016; Dharani et al. 2015). In order to fill such a gap, in this paper we aimed to obtain new stability criteria for switched Hopfield NNs of neutral-type with successive interval time-varying delay components in the state both of discrete and leakage delay is proposed. Therefore, the results of the present paper are essentially new. Hence, unfortunately we could not provide any comparison results over existing methods in order to show the improvements.

Remark 3.8

It is noted that, very recently Zeng et al. (2015) proposed the free-matrix-based integral inequality and this integral inequality used for handling the double integral L–K functionals, that offers a new tighter information on the upper bounds of time-varying delay and its interval for the time-delay systems. Therefore, we utilizing this integral inequality to deal with such L–K functionals, which turn to reduce the conservatism further. Thus, there is no limit for such improvements on delay bounds of time-delay systems it’s basically depends on choosing good L–K functionals and computing it’s derivative with an newly improved integral inequalities or some other techniques called delay-partitioning approaches and so on. Thus, in the future, the inequality proposed in Zeng et al. (2015) can be used in order to achieve improved results for delayed NNs.

Remark 3.9

It is well-known that most of the existing results concerning the stability problem of delayed switched Hopfield NNs of neutral type. However, switched Hopfield NNs of neutral type with successive interval time-varying delay components in the state of discrete delay and leakage delay has not been considered in the previous works. In contrast to the system models in Rakkiyappan et al. (2015a, b), Senthilraj et al. (2016), Dharani et al. (2015); one can find that their results cannot be applicable to system (1). This indicates that the proposed system model and obtained results are essentially new. There is no doubt that studying stability analysis for the systems described in (9), with leakage and discrete interval time-varying delays is sure not only to enhance the dynamic research theory of system model proposed in (9), but also further enrich the foundation of realistic application for the delayed SHNNs, as shown in the following numerical section.

Numerical examples

In this section, we provide four numerical examples to demonstrate the effectiveness of our delay-dependent stability criteria.

Example 4.1

Consider system (9) with $n = k = 2$ and

$$\begin{aligned} D_1 &= \begin{bmatrix} 5.1&0 \\ 0&4.7 \\ \end{bmatrix}, \quad D_2 = \begin{bmatrix} 4.6&0 \\ 0&4.3 \\ \end{bmatrix}, \quad A_1 = \begin{bmatrix} 1.1&-0.7 \\ 0.9&1.2 \\ \end{bmatrix}, \quad A_2 = \begin{bmatrix} -0.8&-1.1 \\ 0.9&0.8 \\ \end{bmatrix}, \quad B_1 = \begin{bmatrix} 1.2&0.6 \\ 0.8&1 \\ \end{bmatrix}, \\ \quad B_2 &= \begin{bmatrix} -0.6&-0.7 \\ 0.7&0.6 \\ \end{bmatrix}, \ C_1 = \begin{bmatrix} -0.8&-0.9 \\ 0.9&0.8 \\ \end{bmatrix}, \ C_2 = \begin{bmatrix} 0.6&0.6 \\ 0.65&0.6 \\ \end{bmatrix}, \ E_1 = \begin{bmatrix} -0.8&-1.0 \\ 0.9&0.8 \\ \end{bmatrix}, \ E_2 = \begin{bmatrix} -0.9&-1.2 \\ 0.9&0.9 \\ \end{bmatrix}. \end{aligned}$$

The activation functions are assumed to be

$$g_{i}(z_{i})=0.5\left( |z_i+1| - |z_i-1|\right), \ i=1,2.$$

It is easy to check that the activation functions are satisfied (6) with $K_m=\hbox {diag}\left\{ 0,0\right\},K_p=\hbox {diag}\left\{ 1,1\right\}$. Also let $\delta _{1L}=0.10,\delta _{1U}=0.20,\delta _1=0.30,\delta _{2L}=0.15,\delta _{2U}=0.25,\delta _2=0.40,h_{1L}=0.50,h_{1U}=1.0,h_1=1.50,h_{2L}=0.80,h_{2U}=1.0,h_2=1.80,\tau =0.30,\sigma =0.40,\eta _1=0.4,\eta _2=0.5,\mu _1=0.4,\mu _2=0.5,\tau _D=0.5,\sigma _D=0.5.$ By our Theorem 3.1 and Matlab LMI toolbox, it is found that the equilibrium point of system (9) is asymptotically stable. It can also be verified that the LMIs (10)–(13) are feasible for larger upper delay bounds $\delta _1, \delta _2, h_1, h_2, \tau$ and $\sigma$. lt shows that all the conditions stated in Theorem 3.1 have been satisfied and hence system (9) with the above given parameters are asymptotically stable.

Example 4.2

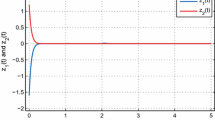
Consider the switched Hopfield neural network without neutral term as in (48) with the parameters $D_k, A_k, B_k, C_k (k = 1, 2)$ as defined in Example 4.1. By choosing $\delta _1(t)=0.1+0.1\cos (0.5t),\delta _2(t)=0.2+0.2\cos (0.5t),h_1(t)=0.6+0.6\sin (0.5t),h_2(t)=0.7+0.7\sin (0.5t),\tau (t)=0.25+0.25\cos (3t)$, we let $\delta _{1L}=0.05,\delta _{1U}=0.15,\delta _1=0.20,\delta _{2L}=0.10,\delta _{2U}=0.30,\delta _2=0.40,h_{1L}=0.40,h_{1U}=0.80,h_1=1.20,h_{2L}=0.50,h_{2U}=1.0,h_2=1.50,\tau =0.50$ and $\eta _1=0.2,\eta _2=0.3,\mu _1=0.4,\mu _2=0.5,\tau _D=0.5.$ Also letting $g_{i}(z_{i})=0.5\left( |z_i+1| - |z_i-1|\right), \ i=1,2.$ it can be easily verified that the activation functions holds with $K_m=\hbox {diag}\left\{ 0,0\right\},K_p=\hbox {diag}\left\{ 1,1\right\}$. By using Matlab LMI toolbox, it is found that LMI (49) and (50) is feasible. Thus, it can be conclude that the switched NNs (48) is asymptotically stable and the state trajectories of the dynamical system is converges to the zero equilibrium point with an initial state $[-0.2,0.2]^T$, it can be shown in Fig. 1. Suppose, if we take leakage time-varying delay $\delta _1(t)=0.15+0.15\cos (0.5t) (\delta _1\ge 0.30),\delta _2(t)=0.25+0.25\cos (0.5t) (\delta _2\ge 0.50)$, it is found that the neural network (48) is actually unstable and the state trajectories of the dynamical system is not converges to the zero equilibrium point, it can be shown in Fig. 2. According to this example, it can be conclude that the leakage delay has a significant effect in the dynamical behaviour of the switched NNs.

Fig. 1

State trajectory of the system (48) in Example 4.2

Fig. 2

State trajectory of the system (48) in Example 4.2

Remark 4.1

As is well-known that the leakage time delays are unavoidable and their occurrence causes instability or oscillation, it can be verified through different simulation results for different time delays especially for the leakage delay that the oscillation of the dynamics increases when time delays are chosen to be larger, which would obviously affect the stability. Thus, time delays in the leakage term have a great impact on the stability of the considered switched system.

Example 4.3

Consider the switched Hopfield neural network without leakage and neutral term as in (51) with the parameters $A_k, B_k, C_k, D_k (k = 1, 2)$ as defined in Example 4.1. By choosing $h_1(t) = 0.8 + 0.8 \sin (0.5t),h_2(t) = 1.2 + 1.2 \sin (0.5t), \tau (t) = 0.5 + 0.5 \cos (3t),$ we let $h_{1L}=0.50,h_{1U}=1.10,h_1 = 1.60,h_{2L}=0.70,h_{2U}=1.70,h_2 = 2.40,\tau = 1.0$ and $\mu _1 = 0.3,\mu _2 = 0.35,\tau _D=0.5$. Also letting $g_1(z) = g_2(z) = 0.5 (|z + 1|- |z- 1|)$, it can be easily verified that the neuron activation function holds with $K_m=\hbox {diag}\left\{ 0,0\right\},K_p=\hbox {diag}\left\{ 1,1\right\}$. By using Matlab LMI toolbox, it is found that LMIs in Corollary 3.2 is feasible. Thus, we can conclude that the model (51) is asymptotically stable. The simulation results for the above mentioned delay values also ensure the asymptotic stability of the model (51). Hence, the convergence of the SHNNs (51) is shown in Fig. 3, with an initial state $[-0.4,0.8]^T$.

Fig. 3

State trajectory of the system (51) in Example 4.3

Example 4.4

So far, originally NNs embody the characteristics of real biological neurons that are connected or functionally related in a nervous system. On the other hand, NNs can represent not only biological neurons but also other practical systems namely the quadruple-tank process system can be shown in Fig. 5. The setup consists of four interacting tanks, two water pumps and two valves. The two process inputs are the voltages $\upsilon _1$ and $\upsilon _2$ supplied to the two pumps. Tank 1 and Tank 2 are placed below Tank 3 and Tank 4 to receive water flow by the action of gravity. Hence as shown in Fig. 4, the quadruple-tank process can be expressed clearly using the neural network model, see for instance, Samidurai and Manivannan (2016), Lee et al. (2013), Huang et al. (2012), Haoussi et al. (2011) and Johansson (2000); proposed the state-space equation of the quadruple-tank process and designed the state feedback controller as follows:

$$\dot{\bar{x}}(t) = \bar{A_0}\bar{x}(t) + \bar{A_1}\bar{x}(t-\tau _1) + \bar{B_0}\bar{u}(t-\tau _2) + \bar{B_1}\bar{u}(t-\tau _3),$$

(57)

where

$$\begin{aligned} \bar{A_0}& = \begin{bmatrix} -0.0021&0&0&0 \\ 0&-0.0021&0&0 \\ 0&0&-0.0424&0 \\ 0&0&0&-0.0424 \end{bmatrix}, \quad \bar{A_1} = \begin{bmatrix} 0&0&0.0424&0 \\ 0&0&0&0.0424 \\ 0&0&0&0 \\ 0&0&0&0 \end{bmatrix}, \\ \quad \bar{B_0}& = \begin{bmatrix} 0.1113 \gamma _1&0&0&0 \\ 0&0.1042 \gamma _2&0&0 \end{bmatrix}^T, \quad \bar{B_1} = \begin{bmatrix} 0&0&0&0.1113(1 - \gamma _1) \\ 0&0&0.1042(1 - \gamma _2)&0 \end{bmatrix}^T, \\ \quad \gamma _1& = 0.333, \quad \gamma _2 = 0.307, \quad \bar{u}=\bar{K}x(t), \\ \quad \bar{K}& = \begin{bmatrix} -0.1609&-0.1765&-0.0795&-0.2073 \\ -0.1977&-0.1579&-0.2288&-0.0772 \end{bmatrix}. \end{aligned}$$

Generally speaking, the differential equations representing the mass balances in the delayed [transport delay $h(t)=h_1(t) + h_2(t)$] equations. To derive a more interesting control problem, transport delays can easily be added by delaying the inlet of water to the tanks, so it is the possible approach used to examine in this paper. Moreover, in this present study transport delays between valves and tanks being additive interval time-varying, it is also taken into account but not exists in previous literature in the following aspects. For simplicity, it was assumed that $\tau _1=0,\ \tau _2=0$ and $\tau _3=h(t)=h_1(t) + h_2(t)$ (since $h_{1L}\le h_1(t)\le h_{1U}$ and $h_{2L}\le h_2(t)\le h_{2U}$). Here, the control input $\bar{u}(t)$, means that the amount of water supplied by the pumps. Therefore, it is true that $\bar{u}(t)$ has a threshold value due to the limited area of the hose and the capacity of the pumps. Therefore, it is natural to consider $\bar{u}(t)$, as a nonlinear function as follows:

$$\begin{aligned} \bar{u}(t)& = \bar{K} \bar{g}(\bar{z}(t)), \\ \bar{u}(t-\tau (t))& = \bar{K} \bar{g}(\bar{z}(t-\tau (t))), \\ \bar{g}(\bar{z}(t))& = \left[ \bar{g_1}(\bar{z_1}(t)),\dots,\bar{g_4}(\bar{z_4}(t))\right] ^T,\\ \bar{g_i}(\bar{z_i}(t))& = 0.1 (\mid \bar{z_i}(t) + 1 \mid - \mid \bar{z_i}(t) - 1 \mid ), \quad i=1,\dots,4. \end{aligned}$$

The quadruple-tank process (57) can be rewritten to the form of system (54) with $k=1$, as follows:

$$\begin{aligned} \dot{z}(t)& = - D_1z(t) + A_1g(z(t)) + B_1g(z(t-h(t))), \\ y(t)& = \varphi (t), \end{aligned}$$

(58)

where $D_1 = -\bar{A_0} - \bar{A_1}, \quad A_1 = \bar{B_0}\bar{K}, \quad B_1 = \bar{B_1}\bar{K}, \quad g(\cdot ) = \bar{g}(\cdot )$. In addition, $K_m=\hbox {diag}\left\{ 0,0,0,0\right\},K_p=\hbox {diag}\left\{ 0.1,0.1,0.1,0.1\right\}$ with $h_{1L}=0.60,h_{1U}=1.20,h_1=1.80,h_{2L}=0.80,h_{1U}=1.50,h_2=2.30,\mu _1=\mu _2=0.5$. Using MATLAB LMI control Toolbox and by solving LMIs in Corollary 3.3, we found that the quadruple-tank process system (58) is asymptotically stable. By choosing $h_1(t) = 0.9 + 0.9 \sin (0.5t),h_2(t) = 1.15 + 1.15 \sin (0.5t),\mu _1=\mu _2=0.5$ and $g_i(z_i)=0.1\left( \mid z_i+1 \mid - \mid z_i-1 \mid \right), \quad i=1,2,\dots, 4$, it can be easily verified that Assumption (H) is holds. Figure 5 shows the state trajectories of the system is converges to zero equilibrium point with an initial state $[-0.3,0.2,0.5,-0.4]$, hence it is found that the dynamical behavior of the quadruple-tank process system (58) is asymptotically stable.

Fig. 4

Schematic representation of the quadruple-tank process. Source: From Johansson (2000)

Fig. 5

State trajectory of the system (58) in Example 4.4

Conclusions

In this paper, the problem of new delay-interval-dependent stability criteria for SHNNs of neutral type with time delays have been investigated. In order to achieving stability results, some suitable L–K functional under the weaker assumption of neuron activation function divided by states are utilized to enhance the feasible region of proposed stability criteria. By using the famous Jensen’s inequality, WDII Lemma, introducing of some zero equations and combined with RCC technique, a novel delay-interval-dependent stability criterion is derived in terms of linear matrix inequalities (LMIs). Then the feasibility and effectiveness of the developed methods have been shown by interesting numerical simulation examples. The proposed approach is finally demonstrate the numerical simulation of the benchmark problem that takes into account additive time-varying delays, showing the feasibility of the proposed approach on a realistic problem. Therefore, our results have an important significance in theory and design, as well as in applications of neutral type SHNNs with delays in leakage terms.