Introduction

Pfeifer et al. (2007) have suggested that locomotion control is not only located in the brain, but that there is a tight coupling between the brain, the body, and the environment, an idea that is usually termed embodiment (Nakajima et al. 2013). The typical example is octopus which has a relatively small central brain which controls the large peripheral nervous system of the arms. It is well known that the nervous system of the octopus is highly distributed throughout the entire body. A typical example showing the effectiveness of this distribution of the nervous system is the reaching behavior (Sumbre et al. 2001; Yekutieli et al. 2005a, b; Gutfreund 1998). Do humans have similar morphological structure to reduce the burden of the brain and control locomotion effectively? The central pattern generator (CPG) for locomotion has been shown to exist in the spinal cord of many animals. The CPG is a neural circuit that can produce rhythmic patterns of neural activity without receiving rhythmic inputs. Many researchers have established the CPG network, i.e., the arrangement of CPGs to the biped robot. These adjacent CPGs are coupled to one another with different values of joint angles (Yu et al. 2014; Kim et al. 2009). This structure is similar to one of the octopus. However, studies show that the locomotion of animals is hierarchically controlled by the central nervous system, from the cerebral cortex level, the brainstem level, to the spinal cord level. In this paper, we study the relationship between the cerebral cortex and the CPG and suggest that some CPGs are embedded in limbs and composed of the parameters space which corresponds to the one of the cerebral cortex.

Central to produce rhythmic patterns is the functional unit called the CPG (Yu et al. 2014; Kim et al. 2009; Lu et al. 2014). Although the CPG can in principle produce basic locomotor rhythm in the absence of inputs from higher brain centers and peripheral sensory feedback (Rybak et al. 2006; Dominici et al. 2011), these inputs shape the timing and magnitude of motoneuron activities, and their processing is conversely influenced by the CPG(Windhorst 2007). In previous works, a model (Lu and Tian 2014) has been established and it showed the relationship between the small-world neural network and the CPG. Other researchers have also studied the interaction between the cerebral cortex and the locomotion (Harris-Warrick 2011; Taga 1998; Sreenvasa et al. 2012; Tani and Ito 2003). Harris-Warrick (2011) argued that neuromodulators determine the active neuronal composition of the CPG, and that modeling the function of neural networks without including the actions of neuromodulators is not possible. Taga (1998) also showed that the neural rhythm generator in the neural system is combined with a system called the discrete movement generator, which receives both the output of the rhythm generator and the visual information regarding the obstacle and generates discrete signals to modify the basic gait pattern. Investigating the coupling relationship between the cerebral cortex and the CPG is therefore important and can help to understand the locomotion control. The main problem is to build a model between the cerebral cortex and the CPG.

An analysis of brain activity reveals the presence of synchronous oscillations. These oscillations are not an epiphenomenon, but they play a crucial role in many important processes of the cortex. The oscillator can produce a wide range of dynamics, including quasi-periodic limit cycles, chaotic waveforms, and intermittent chaotic oscillation (Kozma and Puljic 2013). Jansen and Rit (1995) built the neural mass model (NMM), which simulates electrical brain activity and its intricate cortical structures. Grimbert and Faugeras (2006) investigated the dynamical behavior of the NMM. In their analysis, the rhythmic activities of alpha rhythm and epileptic wave were related to the structure of a set of periodic orbits and their bifurcation. Zheng et al. (2012) developed a model of the local field potential based on the NMM and found that, as neural responses adapt, so too do the excitatory and inhibitory components adapt proportionately. By contrast, previous studies have already revealed that time delays can gradually affect the spatiotemporal dynamics in networks of coupled neurons (Roxin et al. 2005). Cona et al. (2011) and Ursino et al. (2010) showed that brain rhythms may be transmitted to other regions via long range excitatory connections and serve a pivotal role in learning and motion. Dhamala et al. (2004) showed that time-delayed coupling facilitates the existence of the stable synchronized states of two chaotic neurons. Balasubramaniam and Jarina Banu (2014) described the problem of synchronization for discrete-time complex dynamical networks with time-varying delays in the dynamical nodes and the coupling term. The NMM with time delay can therefore be used to describe the dynamical behavior of the cerebral cortex.

This paper is organized as follows. In “Motivation of the research and the new model” section, the motivation of this research is introduced and a new model that shows the coupling relationship between the NMM and the CPG with time delay is presented. Bifurcation analysis is conducted to describe the dynamic characteristics of the new model. Detailed analysis of the parameters’ effects on the NMM and the CPG is shown in “Analyses of the parameters’ effects” section. The conclusions and directions for future study are made in “Discussion and conclusions” section.

Motivation of the research and the new model

Motivation of the research

The locomotor patterns are the product of neural processes. The CPGs—spinal neuronal networks that control the basic rhythms and patterns of motoneuron activation during locomotion—have a crucial function (Lacquaniti et al. 2012). The CPGs in the spinal cord produce motor patterns with appropriate timing. Each generator is affected by sensory feedback from the moving limb and is activated from the locomotor command regions (Grillner 2011). The supraspinal control of locomotion has been investigated in animals (Drew et al. 2008). However, few mathematical models have been established to explain the interaction between the brain and the CPG.

The research discussed a model of the coupling relationship between the NMM and the CPG with time delay. Bifurcation analysis and phase diagram were used to describe changes in the behavior of the system. The new model developed in this work is beneficial in studying the dynamic character of neural processes and help us to understand the relationship between the brain and the locomotion. In the NMM, the excitatory input is represented by parameter p, and k means a latency times than the excitatory impulse response from local neurons. In the CPG, parameter d represents the strength of self inhibition, w is the strength of inhibition among CPGs and e represents the excitatory tonic input. In the new model, changes in parameters k and p can lead to different dynamic behaviors of the system. The influences of the changes in parameters parameters d, e, and w on the NMM and the CPG were also analyzed.

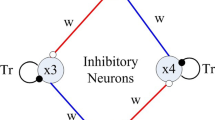
The coupling relationship between the NMM and the CPG with time delay is complex, as shown in Fig. 1.

Fig. 1
figure 1

Coupling relationship between NMM and CPG

Full size image

Many modes for NMM exist, and they are determined by parameter p. Parameter k affects the state of the NMM and CPG. With a change in parameter k, the state of the NMM changes from a chaotic to stable state. When the value of parameters k and p are suitable, the phase diagram of the CPG is the limit cycle, and the state of the NMM is stable. At the same time, various values of w, d, and e can affect the state of the NMM and the CPG.

The CPG model with time delay

The operator of the neural populations in Jansen’s model transforms the average pulse density of action potentials into an average postsynaptic membrane potential. The impulse response function of time delay h d (t) (Huang et al. 2011) is given by

$$h_{d} (t) = \left\{ {\begin{array}{*{20}l} {Aa_{d} te^{{ - a_{d} t}} (t \ge 0)} \hfill \\ {0(t < 0)} \hfill \\ \end{array} } \right.$$
(1)

where A determines the maximal amplitude of the postsynaptic potentials. The parameter a d lumps together the characteristic delays of the synaptic transmission. If the input is x(t), then the output is y(t) = h d  × x(t).

This operator can be described as a second-order ordinary differential equation.

$$\textit{\"{y}}(t) = Aa_{d} x(t) - 2a_{d} \dot{y}(t) - a_{d}^{2} y(t)$$
(2)

It can also be written as follows:

$$\left\{ {\begin{array}{*{20}l} {\dot{y}(t) = z(t)} \hfill \\ {\dot{z}(t) = Aa_{d} x(t) - 2a_{d} z(t) - a_{d}^{2} y(t)} \hfill \\ \end{array} } \right.$$
(3)

Choosing the CPG output (Matsuoka 2011) as the input of Eq. (3), the state equation of the new CPG model is given by.

$$\left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = x_{2} } \hfill \\ {\dot{x}_{2} = Aa_{d} g(x_{3} ) - 2a_{d} x_{2} - a_{d}^{2} x_{1} } \hfill \\ {T_{r} \dot{x}_{3} + x_{3} = - dx_{4} + e} \hfill \\ {T_{a} \dot{x}_{4} + x_{4} = g(x_{3} )} \hfill \\ \end{array} } \right.$$
(4)

In Eq. (4), variables x 1 and x 2 correspond to y and z in Eq. (3), respectively. Function g(·) is a piecewise linear function defined by g(x) = max(0, x), which represents a threshold property of the neurons. g(x 3) is the output of the CPG. The variable x 3 represents the membrane potential, and the self-inhibitory input x 4 represents an adaptation or fatigue property that ubiquitously exists in real neurons. Neuron x 3 receives an excitatory tonic input e (>0), which induces the spontaneous firing of each neuron and an inhibitory input dx 4 from the other neuron x 4. The parameters T r and T a are the time constants that determine the reaction time of the variables x 3 and x 4, respectively. The linear stability analysis is in previous studies (Lu et al. 2014).

Model between CPG and NMM with time delay

In the CPG model (Matsuoka 2011), the input x is a membrane potential of the neuron body, and the output y is the firing rate of the neuron. In the NMM model (Jansen and Rit 1995; Grimbert and Faugeras 2006), the response function h transforms the average pulse density of action potentials into an average postsynaptic membrane potential, and the non-linear sigmoid function Sigm transforms the average membrane potential into an average pulse density. Synchrony in the networks of spatially distributed neurons involves the signal transmission of time delays because of finite propagation speeds and axonal lengths (Matsuoka 1985; David and Friston 2003). The new model is based on these phenomena and constures the coupling relationship between the CPG and the NMM with time delay, as shown in Fig. 2.

Fig. 2
figure 2

Model between NMM and CPG with time delay

Full size image

In Fig. 2, the left and right parts show the CPG and NMM models, respectively. In the CPG model, the variables x 7 and x 8 represent the membrane potential, and y e and y f the firing rate of the neuron. The two variables x 9 and x 10 represent the adaptations or fatigue properties that ubiquitously exist in real neurons. The parameters w and d represent the strength of mutual and self-inhibition, respectively. The output of the CPG model is y e –y f . In the NMM, a single neural population is modeled by a population of pyramidal cells that receive inhibitory and excitatory feedback from local neurons and excitatory input from far and near cortex areas with the connectivity constants C 1, C 2, C 3 and C 4. The excitatory input is represented by an average pulse density p (Huang et al. 2011). Considering the time delay (Adhikari et al. 2011), the CPG output is transformed into an average postsynaptic membrane potential by the function h d (t) and modulated by constant k 1. The average postsynaptic membrane potential is then added into the NMM. By contrast, the output of the NMM is tranformed by h d (t) and k 2 and is fed back into the CPG.

According to the state equation of the CPG (Matsuoka 1985, 2011) and NMM (Jansen and Rit 1995), the state equation of the new model can be described by Eq. (5) when the NMM output x 2–x 3 is attached to the input of the CPG and the CPG output max(0, x 7)–max(0, x 8) is attached to the input of the NMM with time delay. In Eq. (5), a d  = a/k means a latency k times than the excitatory impulse response from the local neurons. Jansen and Rit (1995) set these parameters to simulate the connection between the prefrontal and occipital visual cortex. The two connectivity constants, k 1 and k 2, attenuate the output of one area, before it is fed back into the other. The values of these two parameters are set as 1.

$$\left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = x_{4} } \hfill \\ {\dot{x}_{2} = x_{5} } \hfill \\ {\dot{x}_{3} = x_{6} } \hfill \\ {\dot{x}_{4} = AaSigm(x_{2} - x_{3} ) - 2ax_{4} - a^{2} x_{1} } \hfill \\ {\dot{x}_{5} = AaC_{2} Sigm(C_{1} x_{1} ) - 2ax_{5} - a^{2} x_{2} + Aa(p + k_{1} x_{12} )} \hfill \\ {\dot{x}_{6} = BbC_{4} Sigm(C_{3} x_{1} ) - 2bx_{6} - b^{2} x_{3} } \hfill \\ {T_{r} \dot{x}_{7} + x_{7} = - dx_{9} - w\hbox{max} (0,x_{8} ) + e + k_{2} x_{11} } \hfill \\ {T_{r} \dot{x}_{8} + x_{8} = - dx_{10} - w\hbox{max} (0,x_{7} ) + e + k_{2} x_{11} } \hfill \\ {T_{a} \dot{x}_{9} + x_{9} = \hbox{max} (0,x_{7} )} \hfill \\ {T_{a} \dot{x}_{10} + x_{10} = \hbox{max} (0,x_{8} )} \hfill \\ {\dot{x}_{11} = x_{13} } \hfill \\ {\dot{x}_{13} = Aa_{d} Sigm(x_{2} - x_{3} ) - 2a_{d} x_{13} - a_{d}^{2} x_{11} } \hfill \\ {\dot{x}_{12} = x_{14} } \hfill \\ {\dot{x}_{14} = Aa_{d} [\hbox{max} (0,x_{7} ) - \hbox{max} (0,x_{8} )] - 2a_{d} x_{14} - a_{d}^{2} x_{12} } \hfill \\ \end{array} } \right.$$
(5)

where \(Sigm(v) = \frac{{2e_{0} }}{{1 + e^{{r(v_{0} - v)}} }}\). Here, e 0 determines the maximum firing rate of the neural population, v 0 the postsynaptic potential for which a 50 % firing rate is achieved, and r the steepness of the sigmoidal transformation. x 1, x 2 and x 3 are the outputs of the three postsynaptic potential blocks, respectively. A and B determine the maximal amplitude of the excitatory and inhibitory postsynaptic potentials, respectively. a and b are the lumped representation of the sum of the reciprocal of the time constant of passive membrane and all other spatially distributed delays in the dendritic network. x 11 is the NMM output and x 12 is the CPG output with time delay.

Dynamic performance analysis

To analyze the dynamic performance of the new model, let us consider the following four cases for system (5):

$$\left\{ {\begin{array}{*{20}l} {(a)\hbox{max} (0,x_{7} ) = x_{7},\hbox{max} (0,x_{8} ) = x_{8} .\quad x_{7} > 0,x_{8} > 0} \hfill \\ {(b)\hbox{max} (0,x_{7} ) = 0,\hbox{max} (0,x_{8} ) = 0.\qquad x_{7} \le 0,x_{8} \le 0} \hfill \\ {(c)\hbox{max} (0,x_{7} ) = x_{7} ,\hbox{max} (0,x_{8} ) = 0.\quad x_{7} > 0,x_{8} \le 0} \hfill \\ {(d)\hbox{max} (0,x_{7} ) = 0,\hbox{max} (0,x_{8} ) = x_{8} .\quad x_{7} \le 0,x_{8} > 0} \hfill \\ \end{array} } \right.$$
(6)

Grimbert and Faugeras (2006) treated the input p as a constant and analyzed the dynamic behavior of Jansen’s model as a function of p. Let X = (x 1, x 2, x 3, x 4, x 5, x 6, x 7, x 8, x 9, x 10, x 11, x 12, x 13, x 14)T, then system (5) can be written as

$$\dot{X} = f(X,p)$$
(7)

From f(X, p) = 0, the following fixed points are obtained:

$$\left\{ {\begin{array}{*{20}l} {y_{1} = \frac{A}{a}\left[ {C_{2} Sigm(C_{1} Sigm(C_{1} \frac{A}{a}Sigm(y))) + p} \right] - \frac{B}{b}C_{4} Sigm\left[ {C_{3} \frac{A}{a}Sigm(y)} \right].\quad x_{7} > 0,x_{8} > 0} \hfill \\ {y_{2} = \frac{A}{a}\left[ {C_{2} Sigm(C_{1} Sigm(C_{1} \frac{A}{a}Sigm(y))) + p} \right] - \frac{B}{b}C_{4} Sigm\left[ {C_{3} \frac{A}{a}Sigm(y)} \right].\quad x_{7} \le 0,x_{8} \le 0} \hfill \\ {y_{3} = \frac{A}{a}\left[ {C_{2} Sigm(C_{1} Sigm(C_{1} \frac{A}{a}Sigm(y))) + p + \frac{{k_{1} A}}{{(1 + d)a_{d} }}\left( {\frac{{k_{2} A}}{{a_{d} }}Sigm(y) + e} \right)} \right]} \hfill \\ {\quad \quad - \frac{B}{b}C_{4} Sigm\left[ {C_{3} \frac{A}{a}Sigm(y)} \right].\quad x_{7} > 0,x_{8} \le 0} \hfill \\ {y_{4} = \frac{A}{a}\left[ {C_{2} Sigm(C_{1} Sigm(C_{1} \frac{A}{a}Sigm(y))) + p - \frac{{k_{1} A}}{{(1 + d)a_{d} }}\left( {\frac{{k_{2} A}}{{a_{d} }}Sigm(y) + e} \right)} \right]} \hfill \\ {\quad \quad - \frac{B}{b}C_{4} Sigm\left[ {C_{3} \frac{A}{a}Sigm(y)} \right].\quad x_{7} \le 0,x_{8} > 0} \hfill \\ \end{array} } \right.$$
(8)

where x 2 − x 3 = y, which can be viewed as a function of the parameter p. y 1,y 2,y 3 and y 4 can be thought of as representing the electroencephalography (EEG) activity of the unit in four cases and p is the parameter of interest.

To study the behavior of the system near the fixed points, the system is linearized and calculated its Jacobian matrix at the fixed point. The eigenvalues of J are computed to analyze the stability of the family of equilibrium points. The stability of the equilibrium point is determined by the Jacobian matrix of system (5). The Jacobian matrix all of whose eigenvalues have negative real parts indicates that the equilibrium point is stable for x 7 ≤ 0, x 8 ≤ 0, x 7 > 0, x 8 > 0 and x 7 ≤ 0, x 8 > 0. One positive eigenvalue exists for x 7 > 0, x 8 ≤ 0, therefore, the equilibrium point in this case is unstable.

A bifurcation is a drastic and sudden change in the behavior of a dynamic system, which occurs when one or several of its parameters are varied. Describing the behavior of the new model is related to studying its bifurcations. The initial values are set as [0.04 14.11 11.01 −0.46 −216.07 −189.02 −10.54 0.45 0.25 0.67 0.01 0.05 0.15 0.24] (Huang et al. 2011). The fourth order Runge–Kutta method is used to solve system (5). The bifurcation is obtained in Fig. 3, where the parameter p is varied in the interval [−50, 400] at a step of 0.5.

Fig. 3
figure 3

Bifurcation diagram of the model

Full size image

Figure 3 clearly shows that the main branch changes to two branches when p = 113. The two branches then merge into one branch when p = 137. The system gradually becomes stable when p > 371. In following Fig. 5, the three values of parameter p are the dividing points between two modes of the NMM.

Analyses of the parameters’ effects

Two aspects of the coupling relationship between the NMM and the CPG are examined here. One aspect is the effects of the NMM and the CPG when the parameter p of the NMM and the parameter k of time delay are changed. The other is the effects of the NMM and the CPG when the three parameters d, e and w are varied.

Effects of CPG and NMM when parameters p and k are changed

The standard values of these parameters are determined as A = 3.25 mV, a = 100 s−1, B = 22 mV, b = 50 s−1, r = 0.56 mV−1, e 0 = 2.5 s−1, v 0 = 6 mV, C 1 = 1.25C 2 = 4C 3 = 4C 4 = C=135 (Huang et al. 2011). NMM has four equilibrium points, as the parameter p is varied, as shown in Fig. 4.

Fig. 4
figure 4

Four equilibrium points of NMM

Full size image

In Fig. 4a, the equilibrium point labeled with the red star is defined as the first mode of the NMM. The equilibrium point labeled with the blue star is defined as the fourth mode, and its position is higher than the first mode. In Fig. 4b, the spike-like epileptic activity labeled with the red cycle is defined as the second mode. The alpha-like activity labeled with the blue cycle is defined as the third mode. Other parameters are set as T r  = 0.1, T a  = 1, d = 1.6, e = 10, w = 1.1, k 1 = k 2 = 1, and k = 1000 (Lu and Tian 2014; Matsuoka 2011).

The mode of the NMM changes when the parameter p is varied (Huang et al. 2011). The corresponding relationship between the NMM and the CPG when the parameter p is varied is shown in Fig. 5. The first mode of the NMM exists for p ∈ [0, 113]. At the same time, the CPG output is periodic oscillation, and the phase diagram of the CPG is the limit cycle, as shown in Fig. 5a for p = 60. The first mode switches to the second mode for p ∈ (113,137], as shown in Fig. 5b for p = 115. As the parameter p increases, the second mode turns to the third mode, as shown in Fig. 5c for p = 156. The third mode changes to the fourth mode when p > 372, as shown in Fig. 5d for p = 431. Therefore, the four intervals [0, 113], (113, 137], (137, 371], and (371, 569] correspond to the four modes, respectively.

Fig. 5
figure 5

Phase diagrams and output of the model. a p = 60. b p = 115. c p = 156. d p = 431

Full size image

In this new model, the effects of variations in parameter k on the CPG and NMM are discussed. The maximal Lyapunov exponent (MLE) is used to show the chaotic state of the NMM. The MLE describes the time asymptotic rate of the separation of infinitesimally close trajectories. A positive MLE is usually taken as an indication that the system is chaotic. An MLE of zero indicates that a limit cycle or a quasi-periodic attractor exists in the system and that all the MLEs of a stable fixed point negative. The parameter p is set as p = 60. At the beginning, the fourth mode exists in the NMM, and the CPG output is constant, as shown in Fig. 6a for k = 32. When k > 35, the coexistence of the third and the fourth mode can be observed, and the MLE is 0.012, as shown in Fig. 6b for k = 40. As parameter k is increased, the second, third, and fourth modes coexist, and the MLE is 0.011, as shown in Fig. 6c for k = 45. When k > 49, the coexistence of the four modes can be observed and the MLE is 0.013, as shown in Fig. 6d for k = 120. As parameter k is increased, the coexistence of the first, second and third modes can be observed, and the MLE is 0.005, as shown in Fig. 6e for k = 165. When k = 194, the first and second modes coexist, and the MLE is 0.002, as shown in Fig. 6f. As parameter k is increased, the NMM gradually changes to the first mode, as shown in Fig. 6g for k = 220. The phase diagram of the CPG finally changes to the limit cycle, as shown in Fig. 6h for k = 260.

Fig. 6
figure 6

Phase diagrams and output of the model with p = 60. a k = 32. b k = 40. c k = 45. d k = 120. e k = 165. f k = 194. g k = 220. h k = 260

Full size image

In this section, the second case is discussed when p = 115. At the beginning, the fourth mode exists in the NMM, and the CPG output is constant, as shown in Fig. 7a for k = 37. As parameter k is increased, the third and fourth modes coexist, and the MLE is 0.01, as shown in Fig. 7b for k = 50. When k > 65, the coexistence of the second, third and fourth modes can be observed, and the MLE is 0.023, as shown in Fig. 7c for k = 160. When k > 225, the second and third modes coexist, and the MLE is 0.038, as shown in Fig. 7d for k = 270. As parameter k is increased, the NMM gradually changes to the second mode, as shown in Fig. 7e for k = 400. The phase diagram of the CPG finally changes to the limit cycle, as shown in Fig. 7f for k = 557.

Fig. 7
figure 7

Phase diagrams and output of the model with p = 115. a k = 37. b k = 50. c k = 160. d k = 270. e k = 400. f k = 557

Full size image

In the third case, p = 156. At the beginning, the fourth mode exists in the NMM, and the CPG output is constant, as shown in Fig. 8a for k = 44. As parameter k is increased, the coexistence of the third and fourth modes can be observed, and the MLE is 0.006, as shown in Fig. 8b for k = 90. When k > 290, the NMM changes to the third mode, as shown in Fig. 8c for k = 350. The phase diagram of the CPG changes to the limit cycle, as shown in Fig. 8d for k = 820.

Fig. 8
figure 8

Phase diagrams and output of the model. a k = 44, p = 156. b k = 90, p = 156. c k = 350, p = 156. d k = 820, p = 156

Full size image

In the fourth case, the NMM maintains the fourth mode as parameter k is increased. The phase diagram of the CPG changes to the limit cycle for k = 890.

In these four cases, the CPG output is constant, and the NMM is in the fourth mode at the beginning, which can also be treated as its first state. As parameter k is increased, the coexistence of many modes can be observed, and the NMM state is chaotic because the MLE is positive. This state is treated as the second state. When the phase diagram of the CPG is the limit cycle, the NMM state is in a stable mode, which can be taken as the third state. Therefore, the changes in the parameter k of time delay lead to the conversion of the NMM state and the CPG when the parameter p is fixed. Moreover, the switch of the NMM state is affected by the spatial position. The trends are from high position to low position. When the parameter k is large, the NMM maintains one stable mode, and the phase diagram of the CPG is the limit cycle. The state conversion then does not exist. Moreover, the value of parameter k becomes larger as soon as the value of parameter p becomes larger in one interval corresponding to one stable mode of the NMM. Taking the second NMM mode as an example, the phase diagram of the CPG changes to the limit cycle when p = 114 and k = 600. However, when p = 137, the value of parameter k must be 9500 when the CPG output is a periodic oscillation.

Effects of NMM and CPG when parameters d, e and w are varied

To analyze the effects of parameters d, e and w on the NMM and the CPG, p is set at p = 115, which corresponds to the second mode of the NMM. The parameter k of time delay is set as k = 600. When d ∈ [0, 0.37], the output of the CPG converges to zero, and the coexistence of the second and third modes can be observed, as shown in Fig. 9a for d = 0. As parameter d is increased, the phase diagram of the CPG changes to the limit cycle, the amplitude of the CPG decreases, and the mode of the NMM switches to the second one, as shown in Fig. 9b for d = 1.6. The phase diagram of the CPG finally converges to the zero plane, as shown in Fig. 9c for d = 200.

Fig. 9
figure 9

Phase diagrams and output of the model with the parameter d. a d = 0, p = 115. b d = 1.6, p = 115. c d = 200, p = 115

Full size image

The effects of the parameter w are discussed in what follows. When w ∈ [0, 1], the NMM is in the second mode, and the phase diagram of the CPG is in a stable focus, as shown in Fig. 10a for w = 1. As parameter w is increased, the phase diagram of the CPG changes to the limit cycle, as shown in Fig. 8b for w = 1.1. When w > 1.9, the CPG output converges to zero, and the coexistence of the second and third modes of the NMM can be observed, as shown in Fig. 10b for w = 15.6.

Fig. 10
figure 10

Phase diagrams and output of the model with the parameter w. a w = 1, p = 115. b w = 15.6, p = 115

Full size image

The effects of the parameter e are discussed in what follows. The effects of parameter e on the NMM and the CPG are weak for the whole interval when k = 600. To observe the obvious effects, the parameter is set at k = 490. When e ∈ [0, 0.2], the NMM is in the second mode, and the phase diagram of the CPG is in a stable focus, as shown in Fig. 11a for e = 0. As parameter e is increased, the phase diagram of the CPG changes to the limit cycle and the amplitude of the CPG output increases, as shown in Fig. 11b for e = 800.

Fig. 11
figure 11

Phase diagrams and output of the model with the parameter e. a e = 0, p = 115. b e = 800, p = 115

Full size image

From above analysis, the mode of the NMM and phase diagram of the CPG vary as the three parameters d, e and w are changed. Parameter d represents the strength of self-inhibition. As parameter d is increased, the NMM changes from a chaotic to a stable state, and the phase diagram of the CPG switches to the limit cycle. When parameter d increases, the phase diagram of the CPG converges to the zero plane because of the strong inhibitory effect. Parameter w represents the strength of inhibition among CPGs. When the value of parameter w is at an appropriate interval, the CPG output is a periodic oscillation, and the state of the NMM is in a stable mode. However, when the value increases, the state of the NMM changes to be a chaotic state. Parameter e represents the excitatory tonic input and influences the amplitude of the CPG output.

Discussion and conclusions

Comparing with previous studies (Lu and Tian 2014; Lu et al. 2014), the new model between the NMM and the CPG can show the complex dynamic characters which help us to understand the relationship between the brain and the locomotion. The dynamic character of the new model shows that the state of the NMM and the CPG can be regulated by these parameters, and they have a corresponding relationship. Then the brain can control the locomotor patterns through these parameters, when the NMM is treated as the cerebral cortex and the CPG as the locomotor patterns. Stable patterns are formed by many interactions among the central nervous system, body segments, and the environment, and are consistent with the dynamic behaviors in Figs. 6, 7, 8, 9, 10 and 11. Various values of the parameters lead to changes in the state of the CPG, which reaches the limit cycle given appropriate values of the parameters. At the same time, the mode of the NMM is in a stable mode, corresponding to the state of the CPG. Some CPGs are suggested to be embedded in limbs and composed of parameters space which corresponds to the one of the cerebral cortex. This embodiment of humans can reduce the burden of the brain and simplify the control of the locomotion. This investigation is therefore beneficial in the fields of motor neurology and motor control.

By contrast, the time delay can impair the stability of the CPG and NMM. Reeves et al. (2011) used a simple task of stick balancing to perform the control concepts. They showed that the delay could impair human locomotion. Wang and Xu (2010) used the single inverted pendulum model to demonstrate that a person with a slow reaction can easily lose the stability of his or her quiet standing. In the present study, with an increase in the delay, the phase diagram of the CPG does not maintain the limit cycle, and such effect becomes increasingly strong. This result implies that a person with slow reaction easily loses the stability of his or her locomotion.

Nassour et al. (2014) used the CPG model as the underlying low-level controller of a humanoid robot to generate various walking patterns. However, there are no effective application to realize the natural locomotion control which shows the tight relationship between the brain, the body, and the environment. Then the studies which integrate the high-level regulator (brain) and low-level controller (CPG) are deserved to investigate further.