Auxiliary particle filtering with lookahead support for univariate state space models

Abstract

An essential type of Bayesian recursive filters known as the sequential Monte Carlo (alias, the particle filter) is used to estimate hidden Markov target states from noisy sensor data. Utilising sensor data and a collection of weighted particles, the filter makes an approximation of the posterior probability density of the target state. These particles are made to recursively propagate in time and are then updated using the incoming sensor information. The auxiliary particle filter improves over the traditional particle filter by guiding particles into regions of importance of the probability density using a lookahead scheme. This facilitates in the use of fewer particles and improved accuracy. However, when the sensor observations are extremely informative and the state transition noise is strong, the filter suffers badly. This is because the high state transition noise causes the particles that are determined to be important by the lookahead step could guide themselves to unimportant regions of the posterior in the final sampling process. Recent improvements of the auxiliary particle filter explored better weighting strategies but the said problem has not been explored closely. This paper seeks to solve the problem by adopting an auxiliary lookahead technique with two predictive support points to estimate the particles that will be located in regions of high importance after final sampling. The proposed method is successfully tested using a nonlinear model using simulations.

1 Introduction

Bayesian state estimation provides a recursive state space modelling framework to estimate the hidden Markov state of target(s) $x_{t}$ using all available noisy sensor observations $y_{1:t}$ where $y_{1:t} = \{y_{1}, y_{2}, \ldots , y_{t} \}$ and t is the time index [1]. The state space model comprises of a state transition model that describes the evolution of the target state over time and a sensor observation model that describes the observation. Both models include random measures (noise) that account for the uncertainty in state evolution and observation processes. With all available sensor data at each time instant, the Bayesian state estimation framework computes the posterior probability density function (PDF) of the target state $p(x_{t} | y_{1:t} )$ at every time step [2]. Prediction and updating are the two phases involved in this. The state transition model is used in the prediction step to construct a prediction density $p(x_{t} | y_{1:t-1})$ that creates a target hypothetical prediction. The posterior PDF can then be updated using the prediction density and the observation density (computed from the sensor model) using Bayes’ rule. Bayesian estimation is useful for several applications including target tracking [3], econometric modelling [4], biomedical engineering [5], robotics [6] and more [7].

The Kalman filter is known to be the optimal Bayesian state estimator as it provides an exact solution for computing the posterior PDF [8]. It accomplishes this by computing the first two moments of the PDF analytically. However the filter is limited to linear systems with Gaussian noise. The sequential Monte Carlo (henceforth termed the particle filter (PF)) [9], on the other hand, can be applied to the more general class of nonlinear and non-Gaussian state space models. A group of weighted particles used in the PF serve to represent the posterior PDF of the target state [10]. The PF’s particles can be thought of as weighted point explorers that cluster around regions that are probabilistically highly significant, or regions that contribute to the posterior. Following the Bayesian state estimation framework, the PF also comprises two steps, prediction and update, which together can be termed sequential importance sampling (SIS). The prediction step propagates the particles to the next time step using the state transition model and the update step weights the particle of its importance (or contribution) to the posterior PDF. Degeneracy, which occurs when all but one particle have minimal weight after a few iterations and is a direct result of not sampling from high importance regions, is a problem that SIS by itself experiences. This is overcome by resampling the particles based on their weights [11, 12].

Another strategy to overcome degeneracy is to sample particles from the regions of importance, that is, to guide them into locations in the state space that contribute to the posterior PDF. This can be achieved by leveraging the incoming observation in the sampling process, that is, by sampling from $p(x_{t}|x_{t-1}, y_{t})$ instead of $p(x_{t}| x_{t-1})$. Several methods have been proposed to leverage the incoming observation in SIS. The most popular in this class is the auxiliary particle filter (APF) [13]. The filter samples a lookahead set of particles and computes their weights, then resamples the resultant and uses those resampling indices to propagate the old particles to the next time step using $p(x_{t}| x_{t-1})$. This lookahead sampling scheme impersonates sampling from $p(x_{t}| x_{t-1}, y_t)$ as sampling directly by incorporating the incoming observation is not straightforward. The APF improves over the standard PF and requires fewer particles. Improved weighting strategies for the APF have been proposed in [14, 15]. The recently proposed improved APF (IAPF) [16, 17] has demonstrated enhanced accuracy over the APF, particularly in circumstances where the variance of the noise is small.¹ It built a general framework to compute the weights from the lookahead particles. Other look ahead strategies include adapted placement and others [18,19,20, 23]. The key idea in all these methods is the same: look ahead in time and determine the set of particles which when propagated using SIS will lie in regions of importance, retract, and then propagate those particles. These methods achieve high tracking accuracy by virtue of sampling from high importance regions.

The problem The lookahead strategy of the APF methods determine those particles that will probably be important if sampled from $p(x_{t}|x_{t-1})$. However a large state transition noise and and a low observation noise can lead to perturbing the particles with large target heading disturbance and weighting them using a narrow observation density. This leads to many particles having low probability mass which consequently leads to degeneracy. This also results in over-estimating the mass in the density function tails and inaccurately representing the posterior PDF.

Contribution of this paper In this paper, we propose an improvement of the APF method to overcome the aforementioned problem. The key idea here is to take support from two predictive locations for each particle that lie at the tails of the prediction density. This paper assumes a univariate state space model, hence the density has two support points, one on the left and the other on the right of the mean value, whereas for multivariate models there will be multiple support points. These support points indicate the importance a particle will hold if it is propagated to the next time step. A realisation of the particle prediction to the next time step will almost certainly lie within the posterior density if both support points lie within the bounds of the posterior density. Therefore leveraging the two support points within the sampling process will aid in improved selection of those particles that will contribute to the posterior. This paper presents a scheme to achieve this. The efficacy of the proposal is tested using simulations.

The remainder of this article is organised as follows: Sect. 2 describes the PF and the APF methods. The proposed method in described in Sect. 3 followed by simulation results in Sect. 4. We finally conclude in Sect. 5.

2 Bayesian state estimation

In this section we describe Bayesian state estimation and the PF methodology. Consider the state space model

$$\begin{aligned} x_{t}&= f (x_{t-1}, a_{t}) \end{aligned}$$

(1)

$$\begin{aligned} y_{t}&= h (x_{t}, e_{t}) \end{aligned}$$

(2)

where from (1), the target state $x_{t} \in \mathbb {R}^{d_{x}}$ at time instant $t \in \mathbb {N}$ is a hidden random variable evolves over time for time steps $t=1,...,T$ following an initial distribution $p(x_{0})$ and the Markov state transition density $p(x_{t} | x_{t-1})$ and $d_{x}$ denotes the state dimensionality. From (2), the observation density $p(y_{t} | x_{t})$ is followed by the noisy sensor observation $y_{t} \in \mathbb {R}^{d_{y}}$ and $d_{y}$ stands for the observation dimensionality. State transition and sensor observation (non)linear functions are f(.) and h(.) respectively, while state transition and observation noise are $a_{t}$ and $e_{t}$ respectively.

Using all of the available observations, Bayesian state estimation seeks to iteratively estimate the PDF of the concealed target state. If the posterior PDF $p(\textbf{x}_{t-1} | \textbf{y}_{1:t-1})$ at time $t-1$ is available, then the filter constructs the posterior PDF at time t according to

$$\begin{aligned} p(x_{t}| y_{1:t})&\propto \int p(y_{t}|x_{t}) p(x_t | x_{t-1}) p(x_{t-1}| y_{1:t-1}) \; dx_{t-1} \end{aligned}$$

(3)

$$\begin{aligned}&\propto p(y_{t}|x_{t}) p(x_t | y_{1:t-1}) \end{aligned}$$

(4)

where $p(x_t | y_{1:t-1})$ is the prediction density and $p(y_{t}|x_{t})$ is the observation density. Once the posterior PDF is available, the hidden target state can be estimated using the expected a posteriori (EAP) [2] as

$$\begin{aligned} \hat{ x}_{t}^{\text {EAP}}&= \mathbb {E}(p(x_{t}| y_{1:t})) = \int x_{t} p(x_{t}| y_{1:t}) dx_{t} \end{aligned}$$

(5)

2.1 The standard PF

The PF uses a set of N particles and their associated weights in accordance with $p(x_{t-1} | y_{1:t-1}) \approx \{ x_{t-1}^{i}, w_{t-1}^{i} \}_{i=1}^{N}$ where i is the particle index, to approximate the posterior density at time $t-1$. To move to time t, the PF follows the principle of importance sampling: aims to sample from the target (unknown) density $p(x_{t} | y_{1:t})$ and since it is unknown we sample from a proposal density $q(x_{t} | y_{1:t})$ which has the same support as the target. If the proposal can be factorised as

$$\begin{aligned} q(x_{t}| y_{1:T}) = q(x_{t} | x_{t-1}, y_{t}) q(x_{t-1}| y_{1:t-1}) \end{aligned}$$

(6)

then the particles may be accepted with probability

$$\begin{aligned} w_{t}&= \frac{p(x_{t}|y_{1:t})}{q(x_{t}|y_{1:t})} \end{aligned}$$

(7)

$$\begin{aligned}&= \frac{p(y_{t}|x_{t}) p(x_{t}|x_{t-1})}{q(x_{t}|x_{t-1}, y_{t})} \frac{p(x_{t-1}|y_{1:t-1})}{q(x_{t-1}|y_{1:t-1})} \end{aligned}$$

(8)

$$\begin{aligned}&= \frac{p(y_{t}|x_{t}) p(x_{t}|x_{t-1})}{q(x_{t}|x_{t-1}, y_{t})} w_{t-1} \end{aligned}$$

(9)

Sampling from the proposal $q(x_{t-1}|y_{1:t-1})$ is nontrivial especially for nonlinear transition models. Therefore it is often the practice to chose the state transition density as the proposal density

$$\begin{aligned} q(x_{t-1}|y_{1:t-1})&= p(x_{t}|x_{t-1}) \end{aligned}$$

(10)

Then the PF may be outlined as follows.

Step 1 Sample particles $\bar{x}_{t}^{i} \sim p(x_{t}| x_{t-1}^{i}), i=1,\ldots ,N$.

Step 2 Compute the weights as

$$\begin{aligned} \bar{w}_{t}^{i}&= w_{t-1}^{i} p(y_{t} | x_{t}^{i}), i=1,\ldots ,N \end{aligned}$$

(11)

were the weights are derived by substituting the state transition density in (9). The weights are then normalised so they sum to one. The posterior at time t then is approximated as $p(x_{t} | y_{1:t}) \approx \{ \bar{x}_{t}^{i}, \bar{w}_{t}^{i} \}_{i=1}^{N}$

Step 3 After a few iterations, the weight mismatch grows and degeneracy becomes more evident. To avoid this, the particles are resampled to form a new set $p(x_{t} | y_{1:t}) \approx \{ x_{t}^{i}, w_{t}^{i} \}_{i=1}^{N}$ by sampling an index

$$\begin{aligned} j^{i}: P(j^{i} = m) = \bar{w}_{t}^{m}, m=1,\ldots ,N \end{aligned}$$

(12)

set $x_{t}^{i} = \bar{x}_{t}^{j^{i}}$ and $w_{t} = 1/N$. Particles with tiny weights are removed in this resampling process and replaced with replicas of particles with larger weights [11, 12, 21, 22]. It can be observed that this filter assumes the transition prior as the Markov transition density as shown in (10). As this does not leverage the incoming information $y_t$, there is not guarantee that the particles generated thereof will lie in regions of the state space contributed by $y_t$. That is, particles might not be generated from regions contribute to the posterior $p(x_{t}|y_{1:t})$. The only solution to overcome this problem is to use more particles to ensure there are enough particles to span the regions of high posterior probability density. Consequentially, a lot of computational effort will have to be spent in the sequential resampling process of (12). The entire PF process can be outlined as shown in Algorithm 1.

Algorithm 1

The PF

2.2 The APF

The key solution to overcoming the said problem is to sample particles from regions that contribute to the posterior. This can be achieved by foreseeing which particles will gain probability mass if propagated forward, and then propagating only those to the next time step. This idea, traditionally called the “lookahead strategy,” can be understood from [19]. The APF is the well known method to accomplish the lookahead strategy. The APF, unlike the PF, looks ahead in time to leverage the incoming observation $y_t$ in its sampling process.

The APF aims to impersonate sampling from a proposal that includes the incoming observation. To accomplish this, the filter first determines a set of indices $j^{i}, i=1,\ldots ,N$ such that the particles at time $t-1$ corresponding to these indices will lie in regions that contribute to the posterior pdf. Let the proposal density be factorised as

$$\begin{aligned} q(x_{t}|y_{1:t})&= \underbrace{q(x_{t} | j^{i})}_{\text {Sampling}} \underbrace{q(j^{i} | x_{t-1}, y_{t}) q(x_{t-1}|y_{1:t-1})}_{\text {Lookahead}} \end{aligned}$$

(13)

where we express

$$\begin{aligned} q(j^{i} | x_{t-1}, y_t) \propto q(y_{t}|j^{i}) q(j^{i} | x_{t-1}) \end{aligned}$$

(14)

Sampling the indices $j^{i}$ from $q(j^{i} | x_{t-1}, y_{t})$ is equivalent to drawing from the weighted particle approximation

$$\begin{aligned} j^{i}&\sim \bar{w}_{t}^{i} \delta (x_{t} - \bar{x}_{t}^{i}), i=1,\ldots ,N \end{aligned}$$

(15)

where $\delta (.)$ denotes the Dirac-delta function and where

$$\begin{aligned} \bar{x}_{t}^{i}&= \mathbb {E}(p(x_{t}|x_{t-1}^{i})) \end{aligned}$$

(16)

$$\begin{aligned} \bar{w}_{t}^{i}&= w_{t-1} p(y_{t}|\bar{x}_{t}^{i}) \end{aligned}$$

(17)

and $j^{i}$ is a sample index such that $P(j^{i} = i) = \bar{w}_{t}^{i}$. Note that the weights should be normalised so they sum to one. New particles are then sampled according to $x_{t}^{i} \sim p(x_{t} | x_{t-1}^{j^{i}})$. The weights corresponding to these particles are their observation densities weighed down by the density of the lookahead sample, and given by

$$\begin{aligned} w_{t}^{i} = \frac{p(y_{t}| x_{t}^{i})}{p(y_{t}|\bar{x}_{t}^{j^{i}})} \end{aligned}$$

(18)

The weights again are normalised. The new weighted sample set is then propagated to the next time step. The APF is outlined in Algorithm 2. The key advantage of the APF is that we now need fewer particles since the particles are assuredly drawn from regions that contribute to the posterior probability.

Algorithm 2

The APF

2.3 Improved versions of the APF

Charalampidis and Papavassilopoulos [14] proposed the IAPF. Here a weighting factor $s_t^{j^i}$ was derived to weigh the final weights of the particles in (18) as

$$\begin{aligned} w_{t}^{i} = s_t^{j^i} \frac{p(y_{t}| x_{t}^{i})}{p(y_{t}|\bar{x}_{t}^{j^{i}})} \end{aligned}$$

(19)

This weighting ensures that the weights are set in proportion to the number of their replicates from the resampling step and hence stabilises the weight function. This consequently reduces the Monte Carlo error associated with the final estimate. The recently proposed IAPF [16, 17] developed a general framework for the APF formalism. The first stage weights are computed, instead of (17), as

$$\begin{aligned} \bar{w}_{t}^{i}&= \frac{p(y_{t}|\bar{x}_{t}^{i}) \sum _{j=1}^{N} w_{t-1}^{j} p(\bar{x}_{t}^{i}| x_{t-1}^{j})}{\sum _{j=1}^{N} w_{t-1}^{j} p(\bar{x}_{t}^{i}| x_{t-1}^{j})} \end{aligned}$$

(20)

and the second stage weights are computed, instead of (18), as

$$\begin{aligned} w_{t}^{i} = \frac{p(y_{t}| x_{t}^{i}) \sum _{j=1}^{N}w_{t-1}^{j} p(x_{t}^{i}| x_{t-1}^{j})}{\sum _{j=1}^{N} \bar{w}_{t}^{j} p(x_{t}^{i}|x_{t-1}^j)} \end{aligned}$$

(21)

The weights must be normalised in both cases. Since the full multiple importance sampling formalism is implemented herein, the weights are more stable and hence the Monte Carlo error associated with the final estimate will also be small. Branchini and Elvira, in [23], improvised the APF mechanism including generic multiple importance sampling proposals and optimising the weights using the least squares method. This work, despite being novel, does not fall under the problem being discussed in this paper, and hence not included in the experiments.

The APF and the IAPFs suffer when the observations are highly informative, or when the variance of the error is small. This problem is explained and a method to overcome the same is proposed in the subsequent section.

3 Proposed method

In this section we discuss the problem of the APFs in sampling incorrectly for highly informative observations and propose a method to overcome it. Consider when the observation nose is very small the observation density $p(y_{t}|x_{t})$ stays highly peaked and high state transition noise will cause the predictions to stray away from regions that contribute to the posterior. Hence any leveraging of the incoming observation in the sampling process will be lost.

3.1 Example 1

To understand this further, as an example, consider a univariate state space model governed by a random walk state transition model $x_{t} = x_{t-1} + a_{t}$ where the additive zero mean white noise variable is defined as $a_{t} \sim \mathcal {N}(0, \tau ^2=1)$. Also consider the observation model to be additive Gaussian as $y_{t} = x_{t} + e_{t}$ where the additive zero mean white noise variable is defined as $e_{t} \sim \mathcal {N}(0, \sigma ^2)$. Also suppose that the observation is at the origin $y=0$. Assume there are $N=8$ particles. Table 1 illustrates the problem of the APF/IAPFs for the above model.

Case 1 The first set of rows from $x_{t-1} \longrightarrow w_{t}$ correspond to the case when the observation error variance is $\sigma ^2=0.5$ and is comparable to the state transition noise variance $\tau ^2$. Here, the 1st row corresponds to the means of the particles obtained from the transition kernel $p(x_{t}|x_{t-1})$ and since we use the random walk model, the propagated means $\bar{x}_{t}^{i}, i=1,\ldots ,N$ are equal to the particles at time $t-1$. These means are the lookahead samples. The normalised weights $\bar{w}_{t}^{i}, i=1,\ldots ,N$ then computed and the sampling indices $j^i, i=1\cdots ,N$ are obtained as shown in rows 2, 3 & 4. We then retract to time $t-1$ and select those particles corresponding to the output of the resampler, i.e., $x_{t-1}^{j^i}, i=1,\ldots ,N$ as shown in row 5. These particles are then propagated forward to time t using the Markov transition prior and their weights are recomputed in rows 6 & 7. It is expected that the variance of the weights at the 7th stage will be low, i.e., the propagated particles are more representative of the posterior PDF.

Table 1 Numerical example illustrating the problem of un-leveraging the incoming data into the sampling process

Case 2 The second set of rows, again from $x_{t-1} \longrightarrow w_{t}$, correspond to the case when the observation error variance is $\sigma ^2=0.05$ and is very small compared to the state transition noise variance $\tau ^2$. It can be observed here although the best particles, the 3rd and the 4th, i.e., $x_{t-1}^{(3,4)}= \{0.130022, 0.038661\}$ are propagated forward as shown in row 5, the large difference in the Markov transitional noise variance $\tau ^2$ and the observation noise variance $\sigma ^2$ cause the subsequent weights (shown in row 6) are small and require another step of resampling to avoid the effect of degeneracy. Therefore any leverage of the incoming observation induced by the process of looking ahead using the means of the transition kernel is nullified.

3.2 Example 2

Figure 1 illustrates the same problem for the same model conditions using more particles $N=100$. The yellow circles correspond to the particles at time $t-1$. The blue stems correspond to the weighted particle approximation for $\sigma ^2=0.5$ and the red to $\sigma ^2=0.05$. It can be seen that when $\sigma ^2 \lll \tau ^2$, the variance between the weights is large and this requires another resampling step.

A general opinion of the said problem can be seen in Fig. 2. The figure shows the percentage probability of the number of particles obtaining weights less than 1/N, i.e.,

$$\begin{aligned} L = |i: w_{t}^{i}<1/N| \end{aligned}$$

(22)

for varying observation noise variances keeping $\tau ^2=1$. It can be seen that the average number of low weight particles increases for reducing error variance, thus leading to degeneracy and the need for resampling. In other word, the effect of leveraging the incoming information within the particles by way of looking ahead is annulled in this low error variance conditions.

3.3 Our proposal

Here we propose a method to overcome the said problem. The problem in the APF/IAPFs can be seen in the following perspective: If a realisation of the state transition density $x_{t}^{i} \notin (y_{t} - 3\sigma , y_{t} + 3\sigma )$ then its corresponding weight will be very small $w_{t}^{i} \lll$ since $\sigma ^2 \lll$. And if the state transition noise is high $\tau ^2 \ggg$ then it is almost certain that the probability of prediction will not lie in the 99.95% region of the observation density, i.e.,

$$\begin{aligned} P(x_{t}^{i} \sim p(x_{t}|\bar{x}_{t-1}^{i}) \notin (y_{t} - 3\sigma , y_{t} + 3\sigma )) \ne 0 \end{aligned}$$

(23)

This causes the weights to be extremely small thus causing $\sum _{i=1}^{N} w_{t}^{i} = 0$ and division by zero errors. This situation may happen at the lookahead or the sampling stages.

Here, we propose a improvement to the APF to handle low observation noise scenarios effectively. For the state space model given in Sect. 1, assume the noise in the state transition model in (1) and the observation density in (2) are Gaussian as $a_{t} \sim \mathcal {N}(0,\tau ^2)$ and $e_{t} \sim \mathcal {N}(0, \sigma ^2)$. Also assume $\tau ^2 \ggg$ meaning there is a large diffusion over the state heading and $\sigma ^2 \lll$ meaning the observations are highly informative which in turn cause the observation density to be very peaked.

Fig. 1

Illustration of the problem in APF/IAPFs

Fig. 2

Percentage of the number of particles with weights less than 1/N versus the observation noise variance. The result is averaged over 1000 Monte Carlo runs

The traditional APF looks ahead in time using either the mean or the mode or one realisation of the state transition density $p(x_{t}|x_{t-1})$. Since the observation density is peaked, we need to have enough particles in the regions of importance of the posterior density, else we suffer from degeneracy. Determining the importance of a lookahead particle based on on realisation of its prediction, in all probability, will be a weak determination for the said scenario. Therefore, we propose to include two support predictive points. Chose two support points as

$$\begin{aligned} \bar{x}_{t}^{i,l} = \mathbb {E}(p(x_{t}| x_{t-1}^{i})) - \gamma \tau \end{aligned}$$

(24)

$$\begin{aligned} \bar{x}_{t}^{i,r} = \mathbb {E}(p(x_{t}| x_{t-1}^{i})) + \gamma \tau \end{aligned}$$

(25)

where we set $\gamma =1$ empirically. The l and r in the superscript notate the support values corresponding to the left and right of the mean value respectively. Both the support points ensure that $\bar{x}_{t}^{i,.}: p(x_{t}|x_{t-1}^{i}) \le \gamma$. Determination that the ith sample will be important is made based on a single realisation of the sample. If the sample is determined to be important based on one realisation is a weak determination. That is to say, instead of considering one lookahead particle, we span the transition density of each particle limited by $\gamma$. This will aid in an accurate determination of the importance of the lookahead value.

Sampling the indices $j^{i}$ from $q(j^{i} | x_{t-1}, y_{t})$ is now equivalent to drawing from the weighted particle approximation

$$\begin{aligned} j^{i}&\sim \bar{w}_{t}^{i} (\delta (x_{t} - \bar{x}_{t}^{i,l}) + \delta (x_{t} - \bar{x}_{t}^{i,r})) \end{aligned}$$

(26)

for $i=1,\ldots ,N$ where

$$\begin{aligned} \bar{w}_{t}^{i}&= w_{t-1} \frac{p(y_{t}|\bar{x}_{t}^{i,l}) + p(y_{t}|\bar{x}_{t}^{i,r})}{2} \end{aligned}$$

(27)

As can be seen, we reduce the lookahead sample weights by a factor equal to the average weight of samples that are $\gamma$ standard deviations from the mean value. This prevents particles that might not contribute to the posterior from being deemed relevant and used in the final sampling procedure.

Once the lookahead particles and their weights are obtained, the index $j^{i}$ is a sample index such that $P(j^{i} = i) = \bar{w}_{t}^{i}$. The particles are then sampled according to $x_{t}^{i} \sim p(x_{t} | x_{t-1}^{j^{i}})$ and weighted as (18).

The proposed method can be outlined as follows.

Step 1 Lookahead in time using the support points $\{ \bar{x}_{t}^{i,l}, \bar{x}_{t}^{i,r}\}$ for $i=1,\ldots ,N$.

Step 2 Compute the normalised lookahead weights $\{\bar{w}_{t}^{i}\}_{i=1}^{N}$ according to (27).

Step 3 Sample $j^{i} \sim \sum _{i=1}^{N} \bar{w}_{t}^{i} ( \delta (x_{t} - \bar{x}_{t}^{i,l}) + \delta (x_{t} - \bar{x}_{t}^{i,r}) )$ which relates to the resampling step. In this paper we use the well-known systematic resampling.

Step 4 Retract and sample new particles from the resampled indices as $x_{t}^{i} \sim p(x_{t}|x_{t-1}^{j^{i}})$ and compute the normalised weights according to (18).

The key benefit of this proposal is that taking the support of two predictions instead of one that are $\gamma$ standard deviations from the expected value helps in disallowing particles to be treated as important when only the expectation is considered.

4 Simulation

Here, we demonstrate the effectiveness of the suggested system. We evaluate our system in comparison with the APF [13], the improved APF by Charalampidis and Papavassilopoulos [14] (we name as IAPF-2013) and the improved IAPF by Victor Elvira et al. [17] (we name as IAPF-2019). All the tests are averaged over 1000 Monte Carlo iterations. For the proposed method, we set $\gamma = 1$.

4.1 Linear example

We first use a univariate state space model defined by the following state transition and observation densities as

Fig. 3

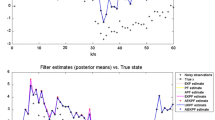
From left to right correspond to time steps $t=25, \; 50, \; 75, \; 100$. The first row corresponds to $N=100, \sigma ^2=0.01$, the second to $N=10000, \sigma ^2=0.01$, the third to $N=100, \sigma ^2=1$ and the fourth to $N=10{,}000, \sigma ^2=1$. The the black represents the Kalman filter, the blue represents the standard PF, the cyan represents the APF, and the red represents the proposed filter

$$\begin{aligned} p(x_{t}|x_{t-1})&= \mathcal {N}(x_{t-1}, \tau ^{2}) \end{aligned}$$

(28)

$$\begin{aligned} p(y_{t}|x_{t})&= \mathcal {N}(x_{t}, \sigma ^{2}) \end{aligned}$$

(29)

for $t=1,\ldots ,T=100$. The state transition noise variance is configured to be $\tau ^2=10$. The initial target state is $x_{t=0}=0$. The filters are initiatlised with $x_{t=0}^{i} \sim \mathcal {N}(0,1)$ for $i=1,\ldots , N$. Employing a linear Gaussian model allows to compare against the optimal Kalman filter. Figure 3 shows the filter estimated posterior densities against the optimal Kalman filter density at time steps $t=25, \; 50, \; 75, \; 100$ for low and high values of noise variance $\sigma ^2$ and for low and high values of the number of particles N. It can be observed that, when the $\sigma ^2 = 0.01$, the APF and the proposed APF suffer from not having sufficient particles to explore the peaked region of importance as can be seen from their very flat densities in the top two rows. On the other hand, the methods compare well with the Kalman filter and the standard PF at moderately higher values of $\sigma ^2$. This demonstrates that the proposed approach is nearly equivalent to the APF with regard to approximating the posterior accurately.

Table 2 shows the root mean square error (RMSE) for low and high values of observation noise $\sigma ^2$ and numbers of particles N. It can be observed that the proposed method shows nearly 8.5% improvement (i.e., reduction in RMSE) over the APF at $\sigma ^2=0.01$. This is by virtue of leveraging the lookahead process on two prediction support values instead of the mean value as does the APF that improves the quality of particles propagated to the next time step. It has been proposed in the APF by Pitt and Shepherd [13] to resample the particles a second time for improved representation of the posterior. However most literature does not employ a second resampling stage as resampling is computationally expensive. In this paper, we do not employ a second resampling to any of the APF methods.

4.2 Nonlinear example

We now use the nonlinear growth model used extensively in the PF literature, given by

$$\begin{aligned} p(x_{t} | x_{t-1})&= \mathcal {N}\bigg ( \frac{x_{t-1}}{2} + \frac{25 x_{t-1}}{1 + x_{t-1}^{2}} + 8 \text {cos}(1.2 t), \tau ^{2} \bigg ) \end{aligned}$$

(30)

$$\begin{aligned} p(y_{t} | x_{t})&= \mathcal {N}\bigg ( \frac{x_{t}^{2}}{20}, \sigma ^2 \bigg ) \end{aligned}$$

(31)

for $t=1,\ldots ,T=100$. We set the state transition noise variance $\tau ^2=10$. The initial target is $x_{t=0}=0$. The filters are initialised with $x_{t=0}^{i} \sim \mathcal {N}(0,1), i=1,\ldots , N$. Firstly, in Fig. 4, we show the estimated effective sample size

$$\begin{aligned} \hat{N}_{\text {eff}} = \frac{1}{N \sum _{i=1}^{N} {w_{i}^{i}}^{2}} \end{aligned}$$

(32)

Table 2 The table shows the RMSE values of the Kalman filter (KF), the standard PF (SPF), the APF and the proposed method for low and high values of $\sigma ^2$ and N for the linear Gaussian example

for the filters for varying numbers of particles at a low noise variance of $\sigma ^2=0.1$. The $\hat{N}_{\text {eff}}$ is a measure of the degeneracy of the filters and a value of zero indicates complete degeneracy and a value of one indicates no degeneracy. We compute this estimate after the final sampling stage for the APFs and proposed method. Since the observation error is small, the observation density is highly peaked, and this causes high degeneracy within the APFs. It can be observed in the figure that all the filters suffer from degeneracy in that they could not achieve more than $\hat{N}_{\text {eff}} = 0.5$ even at $N=1000$. However, it is clear that the suggested method achieves a higher effective sample size value by using two support points to assess a particle’s significance for propagation to the following time step.

Fig. 4

The estimated effective sample size versus the number of particles N at low noise variance of $\sigma ^2=0.1$

Secondly, as mentioned in Sect. 3, the APFs fail completely due division by zero errors caused by particles not being sampled close to the importance regions of the highly peaked observation density. Figure 5 shows the failure probability of the filters calculated empirically at low noise condition, and it can be observed that the proposed filter gains tremendously in terms of avoiding division by zero errors. It has been found to fail only 0.5% of the time while the APF is found to fail 5% of the time and the others fail more than 10% of the time. The filters do not fail as $\sigma ^2$ increases because the increase causes the observation density to flatten.

Fig. 5

The filter failure probability. The first stem corresponds to the APF, the second to the IAPF-2013, the third to the IAPF-2019 and the fourth to the proposed filter at $N=100$ and $\sigma ^2=0.1$

We have until now shown that the two support points influence the avoidance of degeneracy and division by zero errors. This should straightforwardly correlate to the tracking accuracy. Therefore, we show the RMSE of the filters for varying observation error variances at $N=100$ and $N=1000$. This is shows in Fig. 6. It can be observed that the RMSE of the proposed method is magnitude times lower than the conventional APF methods. It can be observed that the reduction in RMSE in the proposed method is consistent across all values of observation error with 26.4%, 29.4% and 12.3% reduction over the APF, the IAPF-2013 and the IAPF-2019 methods respectively. The reason for this is that the particles used for final propagation are a rich collection of those that would contribute to the posterior pdf. This collection is realised by virtue of the proposed support point based lookahead sampling.

Fig. 6

The RMSE versus the noise variance $\sigma ^2$. The top panel corresponds to $N=100$ and the bottom to $N=1000$. The legend of the top panel applies to the bottom also

Finally, we show the computational time (in seconds) of the various filters for the nonlinear model. This is shown in Fig. 7. The standard PF exhibits the lowest computational requirement. This is followed by the APF as it involves an additional look ahead sampling stage. The third is the proposed method. Fourthly, the computationally most expensive are the IAPF variants as they involve more computations in determining the weights. The IAPF-2019 is far more expensive at it involves computing over the generalised form of weights of the multiple importance sampling functions. Summarily, it can be observed that the proposed filter, apart from being stable in low noise conditions than the APF and the IAPFs, is also computationally more efficient than the IAPFs.

Fig. 7

The computational time versus the number of particles

5 Conclusion

In the PF, a proposal density that draws particles leveraging on the previous particles and the incoming observation is known to guide particles into regions of importance of the posterior pdf and thus avoid degeneracy and the need to use many particles. However leveraging the incoming observation in the proposal is not straightforward. The APF and its variants mimic this leveraging process cleverly by first looking ahead in time and determining those particles that would have importance when propagated forward. However when the state transition noise is high and the observation noise is very low, the lookahead strategy of these filters fail due to degeneracy or low weights. This paper proposed to use two support predictive points instead of one, that are located one standard deviation symmetrically from the mean, and use the density in between the two support points to determine the importance of lookahead particles. This will improve the determination process and guides particles that will have higher importance to the next time step. The efficacy of the proposed method is shown using simulations. In the future, the proposed approach will be extended to multivariate state space models.