1 Introduction

In this paper, we consider the following second order nonlinear vector differential equation:

$$\begin{aligned} \ddot{X} + F(X,\dot{X})\dot{X} + H(X) = P(t, X, \dot{X}), \end{aligned}$$
(1.1)

or its equivalent system:

$$\begin{aligned} \dot{X} = Y, ~ \dot{Y} = - F(X,Y)Y - H(X) + P(t, X, Y), \end{aligned}$$
(1.2)

where \( X, Y : \mathbb {R}^+ \rightarrow \mathbb {R}^n, ~\mathbb {R}^+ = [ 0, \infty )\); \( H: \mathbb {R}^n \rightarrow \mathbb {R}^n \); \( P: \mathbb {R}^+ \times \mathbb {R}^n \times \mathbb {R}^n \rightarrow \mathbb {R}^n \); F is an \( n \times n \) continuous symmetric positive definite matrix function dependent on the arguments displayed explicitly and the dots indicate differentiation with respect to variable t. It is assumed that both H and P are continuous with respect to their variables. Furthermore, the existence and uniqueness of the solutions of Eq. (1.1) are assumed. The Jacobian matrix \(J_H(X)\) of H(X) is given by

$$\begin{aligned} J_H(X)= \Big (\frac{\partial h_i}{\partial x_j}\Big ), \end{aligned}$$

where \((i, j = 1, 2, ..., n);\) \( (x_1, x_2, ..., x_n)\) and \((h_1, h_2, ...,h_n)\) represent the components of X and H respectively. We also assumed throughout this paper that the Jacobian matrix \(J_H(X)\) exists and is continuous. The symbol \( \langle X, Y \rangle = \sum _{i = 1}^{n}x_iy_i\) is used to denote the usual scalar product of any two vectors \(X, Y \in \mathbb {R}^n.\)

The study of qualitative behaviour of solutions of second order scalar linear and nonlinear differential equations have been studied by many authors in the literature due to their applications in many fields of science and technology such as biology, physics, chemistry, control theory, economy, communication network, financial mathematics, medicine and mechanics among many other fields. To study the qualitative behaviour of solutions of differential equations, the second method of Lyapunov has proven to be an effective method among other methods available. This method, involves the construction of a suitable functional known as Lyapunov function. Unfortunately, to construct a good lyapunov function especially for nonlinear differential equations remains a difficult task. For further studies on the subject of qualitative behaviour of solutions of differential equations, interested reader(s) may look at papers of Abou-El-Ela and Sadek [1, 2], Adeyanju [5], Adeyanju and Adams [6], Ademola [4], Ademola et al. [3], Ahmad and Rama [7], Alaba and Ogundare [8], Awrejcewicz [9], Baliki [10], Cartwright [13], Chicone [14], Ezeilo [15,16,17], Grigoryan [18], Hale [19], Jordan [20], Loud [21], Ogundare et al. [22], Omeike et al. [23,24,25], Reissig et al. [27], Sadek [28], Smith [29], Tejumola [30,31,32], Tunc [35, 36], Tunc and Mohammed [33, 38, 39], Tunc and Tunc [40], Yoshizawa [41] and Zainab [42].

Ezeilo [16] used the well-known direct method of Lyapunov to examine the convergence of solutions of a certain second order differential equation similar to (1.1) with \(F(X,\dot{X})\equiv C \), C being a real constant \( n \times n \) matrix and \(H(X) = G(X)\). His result was an extension of the convergence result obtained by Loud [21] for the second order scalar differential equation:

$$\begin{aligned} \ddot{x} + c\dot{x} + g(x) = p(t), \end{aligned}$$

where c is a positive constant.

Also worthy of mentioning is the work of Tejumola [31], who considered a certain second order matrix differential equation of the form:

$$\begin{aligned} \ddot{X} + A \dot{X} + H(X) = P(t, X, \dot{X}), \end{aligned}$$

A being a constant \( n \times n\) symmetric matrix, X, H(X), P are \( n \times n\) continuous matrices. He discussed three different properties of this differential equation which are: stability of the trivial solution when \(H(0) = 0\) and \(P \equiv 0\), the ultimate boundedness of all solutions and the existence of periodic solutions. Adeyanju [5] proved some results on the limiting regime in the sense of Demidovic for a certain class of second order vector differential equations similar to Eq. (1.1) with \(F(X,\dot{X})\) being replaced by an \(n \times n\) symmetric, positive definite constant matrix A.

Earlier, Omeike et al. [23] established some conditions for the boundedness of solutions of Eq. (1.1) by using an incomplete Lyapunov function supplemented with a signum function.

The above results of Omeike et al. [23] and other papers mentioned above serve as a motivation for this work. Our goal is to rather use a complete Lyapunov function to study the asymptotic stability of the trivial solution(which was not considered by Omeike et al. [23]) and boundedness of all solutions of the Eq. (1.1) or system (1.2) with simpler conditions.

2 Preliminary results

The following lemmas are very important for the proof of the three theorems contained in this paper.

Lemma 2.1

Let A be a real symmetric \(n \times n\) matrix and

$$\begin{aligned} 0 <\delta _a \le \lambda _i(A) \le \Delta _a, ~ (i = 1, 2,..., n), \end{aligned}$$

where \(\delta _a\) and \( \Delta _a \) are respectively the least and greatest eigenvalues of the matrix A. Then, for any \(X \in \mathbb {R}^n\) we have,

$$\begin{aligned} \Delta _a \Vert X\Vert ^2 \ge \langle AX,X\rangle \ge \delta _a \Vert X\Vert ^2. \end{aligned}$$

Proof

See [2, 11, 33]. \(\square \)

Lemma 2.2

Let H(X)be a continuously differentiable vector function with \(H(0) = 0\). Then,

  1. (i)
    $$\begin{aligned} \langle H(X), X \rangle = \int _0 ^1 X^T J_H(\sigma X)Xd\sigma , \end{aligned}$$
  2. (ii)
    $$\begin{aligned} \frac{d}{dt} \int _0 ^1 \langle H(\sigma X), X \rangle d \sigma = \langle H(X), Y \rangle . \end{aligned}$$

Proof

See [2, 15, 34]. \(\square \)

Lemma 2.3

[19] Suppose \(f(0) = 0\). Let V be a continuous functional defined on \(C_H = C\) with \(V(0) = 0\) and let u(s) be a function, non-negative and continuous for \(0 \le s < \infty \), \(u(s) \rightarrow \infty \) as \(s \rightarrow \infty \) with \(u(0) = 0\). If for all \(\varphi \in C,\) \(u(|\phi (0)|) \le V(\varphi ), ~ V(\varphi ) \ge 0, \dot{V}(\varphi ) \le 0\),then the zero solution of \(\dot{x} = f(x_t)\) is stable.

If we define \( Z = \{ \varphi \in C_H: \dot{V}(\varphi ) = 0\}\), then the zero solution of \(\dot{x} = f(x_t)\)is asymptotically stable, provided that the largest invariant set in Z is \(Q=\{0\}. \)

Definition 2.4

[12, 37] A continuous function \(W: \mathbb {R}^n \rightarrow \mathbb {R}^+\) with \(W(0) = 0\), \(W(s) > 0\) if \(s > 0\), andW strictly increasing is a wedge.

Definition 2.5

[12, 37] Let D be an open set in \(\mathbb {R}^n\) with \(0 \in D.\) A function \( V: [0, \infty ) \times D \rightarrow [0, \infty )\) is called positive definite if \(V(t, 0) = 0\) and if there is a wedge \(W_1\) with \(V(t, x) \ge W_1(|x|),\) and is called a decrescent function if there is a wedge \(W_2\) with \(V(t,x) \le W_2(|x|).\)

Theorem 2.6

[12, 37] If there is a Lyapunov function V for the Eq. (1.1) and wedges satisfying:

  1. (i)

    \(W_1(|\phi (0)|) \le V(t, \phi ) \le W_2(\parallel \phi \parallel )\),  \( ( where ~ W_1(r) ~ and ~ W_2(r) ~ are ~ wedges) \),

  2. (ii)

    \(V^{\prime }(t, \phi ) \le 0,\)

then the zero solution of (1.1) is uniformly stable.

Theorem 2.7

[37, 42] Suppose that there exists a continuous Lyapunov function \(V(t, \phi )\)defined for all\(t \in \mathbb {R}^+\) and \(\phi \in S^*\),which satisfies the following conditions:

  1. (i)

    \(a(|\phi (0)|) \le V(t, \phi ) \le b_1(|\phi (0)|) + b_2(\parallel \phi \parallel )\), where \( a(r), ~ b_1(r), ~b_2(r) \in CI\) (CI denotes the set of continuous increasing functions) and are positive for \(r > H \) and \(a(r) - b_2(r) \rightarrow \infty \) as \(r \rightarrow \infty ,\)

  2. (ii)

    \(V^{\prime }(t, \phi ) \le 0,\)

then the solutions of (1.1) is uniformly bounded.

3 Basic assumptions

In this section, we give the basic assumptions for the main results.

Assumptions

Suppose the following assumptions hold:

  1. (T1)

    \(J_H(X)\) and F(X, Y) are symmetric, positive definite and their eigenvalues \(\lambda _i (J_H(X))\) and \(\lambda _i (F(X,Y))\) respectively satisfy

    $$\begin{aligned} \delta _h \le \lambda _i(J_H(X)) \le \Delta _h, ~ \text{ for } \text{ all }~ X \in \mathbb {R}^n, \end{aligned}$$
    (3.1)
    $$\begin{aligned} \alpha - \epsilon \le \lambda _i(F(X, Y)) \le \alpha , ~ \text{ for } \text{ all }~ X, Y \in \mathbb {R}^n, \end{aligned}$$
    (3.2)

    where \(\delta _h\), \(\alpha \), \(\epsilon \) and \( \Delta _h\) are positive constants and \(H(0) = 0, ~ H(X) \ne 0\) (whenever \(X \ne 0\)), such that

    $$\begin{aligned} \delta \ge \frac{\alpha + \epsilon }{\alpha - \epsilon } >1. \end{aligned}$$
  2. (T2)

    There exist a positive finite constant \(K_2\) and a continuous function \(\theta (t)\) such that vector P(t, X, Y) satisfies:

    $$\begin{aligned} \parallel P(t,X,Y) \parallel \le \theta (t) \{ 1 + (\Vert X\Vert + \Vert Y\Vert )\}, \end{aligned}$$
    (3.3)

    where \( \int ^t_0\theta (s)ds \le K_2 < \infty \) for all \(t \ge 0.\)

4 Main results

Here are the main results of the paper. Let

$$\begin{aligned} P(t,X,Y) \equiv 0, \end{aligned}$$

then we have the following theorem.

Theorem 4.1

Suppose the conditions stated under the basic assumption (T1) above are satisfied, then the zero solution of the Eq. (1.1) or system (1.2) is uniformly stable and asymptotically stable.

Proof: We begin by defining a continuously differentiable function \(V(t) = V(X(t),Y(t))\) by

$$\begin{aligned} {} 2V(t) = \parallel \alpha X + Y \parallel ^2 + 2( \delta + 1) \int _{0}^{1}\langle H(\sigma _1 X), X\rangle d \sigma _1 + \delta \parallel Y \parallel ^2, \end{aligned}$$
(4.1)

\(\alpha \) and \(\delta \) are as defined above. Without doubt, \(V(0,0) = 0\). By Lemma 2.1 and Lemma 2.2 we have

$$\begin{aligned} 2V(t)\ge & {} \delta _h ( \delta + 1) \parallel X \parallel ^2 + \delta \parallel Y \parallel ^2 \\\ge & {} \delta _1 ( \parallel X \parallel ^2 + \parallel Y \parallel ^2), \end{aligned}$$

where \(\delta _1 = \min \{\delta , \delta _h ( \delta + 1)\}\).

Similarly, using Lemma 2.1 and Lemma 2.2, the following is evident

$$\begin{aligned} 2V(t)\le & {} \big ((\Delta _h ( \delta + 1) + 2\alpha ^2\big ) \parallel X \parallel ^2 + (\delta + 2) \parallel Y \parallel ^2 \\\le & {} \delta _2 ( \parallel X \parallel ^2 + \parallel Y \parallel ^2), \end{aligned}$$

where \(\delta _2 = \max \{\big ((\Delta _h ( \delta + 1) + 2\alpha ^2\big ), (\delta + 2)\}.\) It follows that

$$\begin{aligned} {} \delta _1 ( \parallel X \parallel ^2 + \parallel Y \parallel ^2) \le 2V(t) \le \delta _2 ( \parallel X \parallel ^2 + \parallel Y \parallel ^2). \end{aligned}$$
(4.2)

The time derivative of the function V(t) along the solution path of the equation being studied is given by

$$\begin{aligned} \frac{d}{dt}V(t) = \dot{V}(t)= & {} - \alpha \langle X, H(X) \rangle - (\delta + 1) \langle Y, F(X,Y)Y \rangle \nonumber \\&+ \alpha \langle Y, Y \rangle + \alpha \Big (\alpha I - F(X,Y)\Big ) \langle X, Y\rangle , \end{aligned}$$

where I is an \(n \times n\) identity matrix. The above derivative can be written as

$$\begin{aligned} {} \dot{V}(t) = - U_1 - U_2, \end{aligned}$$
(4.3)

where

$$\begin{aligned} U_1 = \frac{\alpha }{2} \langle X, H \rangle - \alpha \langle Y, Y \rangle + \frac{(\delta + 1)}{2} \langle Y, F(X,Y)Y \rangle , \end{aligned}$$

and

$$\begin{aligned} U_2 = \frac{\alpha }{2} \langle X, H \rangle + \frac{(\delta + 1)}{2} \langle Y, F(X,Y)Y \rangle + \alpha \langle X, (F (X,Y) - \alpha I)Y \rangle . \end{aligned}$$

But

$$\begin{aligned} \langle X, (F (X,Y) - \alpha I)Y \rangle= & {} \frac{1}{2} \parallel K_1 (F - \alpha I) Y + K^{-1}_1 X\parallel ^2 - \frac{1}{2 K_1^2} \parallel X \parallel ^2\\- & {} \frac{K^2_1}{2} (F - \alpha I)^2 \parallel Y \parallel ^2\\\ge & {} - \frac{1}{2K_1^2}\parallel X \parallel ^2 - \frac{\epsilon ^2 K_1^2}{2} \parallel Y \parallel ^2. \end{aligned}$$

Also from Lemma 2.2, we have

$$\begin{aligned} \langle X, H \rangle \ge \delta _h \parallel X \parallel ^2. \end{aligned}$$

Hence,

$$\begin{aligned} U_1\ge & {} \frac{1}{2} \alpha \delta _h \parallel X \parallel ^2 + \frac{1}{2}\Big ( (\delta + 1)( \alpha - \epsilon ) - 2 \alpha \Big ) \parallel Y \parallel ^2\\\ge & {} \delta _3 \{\parallel X \parallel ^2 + \parallel Y \parallel ^2\}, \end{aligned}$$

where \(\delta _3 = \frac{1}{2}\min \{\alpha \delta _h; (\delta + 1)( \alpha - \epsilon ) - 2 \alpha \}.\)

Similarly,

$$\begin{aligned} U_2 \ge \frac{\alpha }{2}(\delta _h - K_1^{-2}) \parallel X \parallel ^2 + \frac{1}{2}\Big ( (\delta + 1)(\alpha - \epsilon ) - \alpha \epsilon ^2 K_1^2\Big )\parallel Y \parallel ^2, \end{aligned}$$

let \(K_1^2 = \frac{1}{2} \min \Big ( \frac{1}{\delta _h}, \frac{(\alpha - \epsilon )(\delta + 1)}{\alpha \epsilon ^2} \Big ), \) then

$$\begin{aligned} U_2 \ge 0. \end{aligned}$$

Thus,

$$\begin{aligned} \dot{V}(t) \le -\delta _3 \{ \parallel X \parallel ^2 + \parallel Y \parallel ^2\} \le 0. \end{aligned}$$

The above inequality shows that the derivative with respect to t of the Lyapunov function V(t) along the solution path of Eq. (1.1) is negative semidefinite. Thus, we conclude by Theorem 3 that the zero solution of Eq. (1.1) is stable and also uniformly stable.

Next is to show that the zero solution is asymptotically stable. Define

$$\begin{aligned} W = W(X,Y) \equiv \{(X,Y): \dot{V}(X,Y) = 0\}. \end{aligned}$$

Applying the so-called LaSalle’s invariance principle, it follows that \((X,Y) \in W\) implies that \(X = 0 = Y\). This shows that the largest invariant set contained in the set W is \((0,0) \in W\). We can therefore conclude by Lemma 3 that the zero solution of the Eq. (1.1) is asymptotically stable and thereby conclude the proof of Theorem 4.1.

Our next theorem is on boundedness of solutions of equation (1.1). Let

$$\begin{aligned} P(t,X,Y) \ne 0. \end{aligned}$$

Theorem 4.2

If the assumptions (T1) and (T2) hold, then there exists a positive constant D such that all the solutions of equation (1.1) satisfy the inequalities

$$\begin{aligned} \parallel X \parallel \le D, ~ \parallel Y \parallel \le D \end{aligned}$$

as \(t \rightarrow + \infty \).

Proof: Now that \(P(t,X,Y) \ne 0\), the time derivative of the Lyapunov function V(t) used in the proof of Theorem 5 is given by

$$\begin{aligned} \frac{d}{dt}V(t) = \dot{V}(t)\le & {} -\delta _3 \{ \parallel X \parallel ^2 + \parallel Y \parallel ^2\} + \langle \alpha X + (\delta + 1) Y, P(t,X,Y)\rangle , \\\le & {} \Big ( \alpha \Vert X\Vert + (\delta + 1)\Vert Y\Vert \Big ) \times \Big (\theta (t) + \theta (t)( \Vert X\Vert + \Vert Y\Vert ) \Big ),\\\le & {} \delta _4 \Big ( \Vert X\Vert + \Vert Y\Vert \Big ) \times \Big (\theta (t) + \theta (t)( \Vert X\Vert + \Vert Y\Vert \Big ),\\\le & {} \delta _4 \theta (t) \Big ( \Vert X\Vert + \Vert Y\Vert \Big ) + \delta _4 \theta (t) \Big ( \Vert X\Vert ^2 + \Vert Y\Vert ^2 + 2\Vert X\Vert \Vert Y\Vert \Big ), \end{aligned}$$

where \(\delta _4 = \max \{\alpha ; (\delta + 1)\}.\)

Applying the inequalities,

$$\begin{aligned} \Vert X\Vert \le 1 + \Vert X\Vert ^2, ~ \Vert Y\Vert \le 1 + \Vert Y\Vert ^2, ~ 2\Vert X\Vert \Vert Y\Vert \le \Vert X\Vert ^2 + \Vert Y\Vert ^2, \end{aligned}$$

and (4.2) to \(\dot{V}(t)\) above, we obtain

$$\begin{aligned} {} \dot{V}(t)\le & {} 2\delta _4\theta (t) + 6\delta _1^{-1} \delta _4 \theta (t)V(t),\nonumber \\ \dot{V}(t)\le & {} \delta _5\theta (t) + \delta _6 \theta (t)V(t), \end{aligned}$$
(4.4)

where \( \delta _5 = 2\delta _4\) and \( \delta _6 = 6\delta _1^{-1} \delta _4.\)

Integrating both sides of (4.4) from 0 to \(t(t \ge 0),\) yields

$$\begin{aligned} V(t) - V(0)\le & {} \delta _5 \int _0^t\theta (s)ds + \delta _6 \int _0^t V(s) \theta (s) ds, \\ V(t)\le & {} V(0) + \delta _5 K + \delta _6 \int _0^t V(s) \theta (s) ds. \end{aligned}$$

Setting \(\delta _7 = V(0) + \delta _5 K\), then we get

$$\begin{aligned} V(t) \le \delta _7 + \delta _6 \int _0^t V(s) \theta (s) ds. \end{aligned}$$

Applying Gronwall-Bellman inequality [26] to the above inequality produces

$$\begin{aligned} {} V(t) \le \delta _7 \exp \Big ( \delta _6 \int _0^t \theta (s)ds\Big ) = D_1. \end{aligned}$$
(4.5)

From inequalities (4.5) and left hand side of (4.2) we can deduce that,

$$\begin{aligned} {} \Vert X(t)\Vert ^2 + \Vert Y(t)\Vert ^2 \le 2 \delta ^{-1}D_1 = D^2. \end{aligned}$$
(4.6)

It then follows from (4.6) that,

$$\begin{aligned} {} \Vert X(t)\Vert \le D, ~\text{ and } ~ \Vert Y(t)\Vert \le D. \end{aligned}$$
(4.7)

This completes the proof of Theorem 4.2 and the boundedness of solutions of Eq. (1.1) or system (1.2) is established.

Corollary 4.3

Under the assumptions of Theorem 4.2, all the solutions of equation (1.1) are uniformly bounded.

Theorem 4.4

Under the assumptions of Theorem 4.2 but with modification that

$$ \parallel P(t,X,Y) \parallel \le \theta (t),$$

\(\theta (t) \in L^1[0, \infty )\) for all \(t \in \mathbb {R}^+;\) \( L^1(0, \infty )\) is the space of Lebesgue integrable functions. Then there exists a positive constant \(D_*\) such that all the solutions of equation (1.1) ultimately satisfy the inequalities

$$ \parallel X \parallel \le D_* ~\text{ and }~ \parallel Y \parallel \le D_*$$

as \(t \rightarrow + \infty \).

Proof

From the proof of Theorem 4.2, we have

$$\begin{aligned} \frac{d}{dt}V(t)\le & {} -\delta _3 \{ \parallel X \parallel ^2 + \parallel Y \parallel ^2\} + \langle \alpha X + (\delta + 1) Y, P(t,X,Y)\rangle \\\le & {} \theta (t) \big ( \alpha \Vert X\Vert + (1 + \delta )\Vert Y\Vert \big ) \\\le & {} \delta _4 \theta (t) \big ( \Vert X\Vert + \Vert Y\Vert \big ). \end{aligned}$$

But,

$$\begin{aligned} \Vert X\Vert + \Vert Y\Vert \le 2^{\frac{1}{2}}\sqrt{\parallel X \parallel ^2 + \parallel Y \parallel ^2 }. \end{aligned}$$

On applying this inequality and the left hand side of (4.2), we have

$$\begin{aligned} \frac{d}{dt}V(t)\le & {} 2^{\frac{3}{2}} \delta _4 \delta _1^{ -\frac{1}{2}}\theta (t)V(t)^{ \frac{1}{2}}\\ \frac{d}{dt}V(t)\le & {} 2^{\frac{3}{2}} \delta _4 \delta _1^{ -\frac{1}{2}}\theta (t)V(t). \end{aligned}$$

Integrating both sides of the above inequality from 0 to \(t(t > 0),\) and letting \( \delta _8 = 2^{\frac{3}{2}} \delta _4 \delta _1^{ -\frac{1}{2}},\) gives

$$\begin{aligned} {} V(t) \le V(0)\exp \Big ( \delta _8\int _0^t \theta (s)ds \Big ) \le D_2, \end{aligned}$$
(4.8)

where \(D_2\) is a positive constant. From inequalities (4.8) and the left hand side of (4.2) it is clear that,

$$\begin{aligned} {} \Vert X(t)\Vert ^2 + \Vert Y(t)\Vert ^2 \le 2 \delta _1^{-1}D_2 = D_*^2. \end{aligned}$$
(4.9)

It follows from (4.9) that,

$$\begin{aligned} {} \Vert X(t)\Vert \le D_* ~\text{ and } ~ \Vert Y(t)\Vert \le D_*. \end{aligned}$$
(4.10)

This ends the proof of the theorem. \(\square \)

Remark 4.5

This result was established without using the popular Gronwall-Bellman inequality.

Remark 4.6

We have been able to establish the boundedness results of Eq. (1.1) or system (1.2) without using the signum function as in the case of the boundedness results of Omeike et al. [23] obtained for this same equation.

5 Examples

Example 5.1

We consider the following special cases of system (1.2) for \(n = 2\) when \(P(t, X, Y) \equiv 0\) and when \(P(t, X, Y) \ne 0.\)

Let

$$\begin{aligned} F(X,Y) = \left[ \begin{array}{cc} 2 + \frac{1}{1 + x^2_1 + y^2_1} &{} 1 \\ 1 &{} 2 + \frac{1}{1 +x^2_2 + y^2_2} \end{array} \right] \text{ and }~~ H(X) = \left[ \begin{array}{c} 4x_1 + \sin x_1 \\ 2x_2 + \sin x_2 \end{array} \right] . \end{aligned}$$

After some calculations we obtain the following as the eigenvalues of matrix F(X, Y).

$$ \lambda _1 = 4 + \frac{1}{1 + x_1^2 + y_1^2} + \frac{1}{1 + x_2^2 + y_2^2} + \sqrt{\Big ( \frac{1}{1 + x_1^2 + y_1^2} + \frac{1}{1 + x_2^2 + y_2^2} \Big )^2 + 4},$$

and

$$ \lambda _1 = 4 + \frac{1}{1 + x_1^2 + y_1^2} + \frac{1}{1 + x_2^2 + y_2^2} - \sqrt{\Big ( \frac{1}{1 + x_1^2 + y_1^2} + \frac{1}{1 + x_2^2 + y_2^2} \Big )^2 + 4},$$

so that,

$$ 2 \le \lambda _i(F(X,Y)) \le 6 + 2\sqrt{2}, ~ (i = 1,2,3...).$$

The Jacobian matrix of vector H(X) is given by

$$\begin{aligned} J_H(X) = \left[ \begin{array}{cc} 4 + \cos x_1 &{} 0 \\ 0 &{} 2 + \cos x_2 \end{array} \right] . \end{aligned}$$

Then, we obtain the bounds for the eigenvalues of this matrix as \(1 \le \lambda _i(J_H(X)) \le 5, ~(i = 1, 2, 3,...)\).

In addition, let

$$\begin{aligned}\ P(t, X, Y) = (1 + t)^{-2}\left[ \begin{array}{c} 1 + x_1 + y_1 \\ 1 + x_2 + y_2 \end{array} \right] . \end{aligned}$$

Then,

$$\begin{aligned} \parallel P(t, X, Y) \parallel\le & {} \sqrt{5} (1 + t)^{-2}(1 + \parallel X \parallel + \parallel Y \parallel )\\\le & {} \theta (t)(1 + \parallel X \parallel + \parallel Y \parallel ), \end{aligned}$$

where

$$\begin{aligned} \int _{0}^{\infty } \theta (s) ds = \sqrt{5}\int _{0}^{\infty } (1 + s)^{-2} ds = \sqrt{5}. \end{aligned}$$

Therefore, all the conditions of Theorem 4.1 and Theorem 4.2 are satisfied.

Example 5.2

Suppose in the Example 5.1 above, we have

$$\begin{aligned} P(t, X, Y) = (1 + t)^{-2}\left[ \begin{array}{c} \frac{1}{3 + \sin x_1 + \cos y_1} \\ \frac{1}{3 + \sin x_2 + \cos y_2} \end{array} \right] . \end{aligned}$$

Then,

$$\begin{aligned} \parallel P(t, X, Y)\parallel \le \sqrt{2}(1 + t)^{-2} = \theta (t), \\ \int _{0}^{\infty } \theta (s) ds = \sqrt{2}\int _{0}^{\infty }\frac{ds}{(1 + s)^2} = \sqrt{2}. \end{aligned}$$

Again, all the conditions of Theorem 4.4 are satisfied.

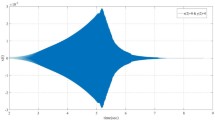
Figure 1 below shows that the trivial solution of the example constructed is stable, asymptotically stable and uniformly stable when \(P(t, X, Y) \equiv 0.\)

Fig. 1
figure 1

Shows the stability of the trivial solution of the example constructed.

Full size image
Fig. 2
figure 2

Shows the boundedness of solutions of example constructed.

Full size image

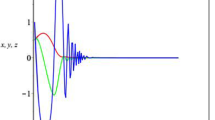
Figure 2 shows the boundedness of solutions of the example constructed when \(P(t, X, Y) \ne 0.\)

6 Conclusion

In this paper, a certain second order vector differential equation is considered. By constructing a new complete Lyapunov function, we established results on the stability, asymptotic stability, uniform stability, boundedness and uniform boundedness of solutions of the equation considered. The results of this paper complement and improve on some established results found in the literature. Examples are given to illustrate the correctness of main results.