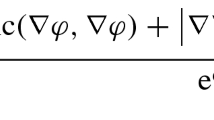Abstract
We prove height estimates concerning compact hypersurfaces with nonzero constant weighted mean curvature and whose boundary is contained into a slice of a weighted product space of nonnegative Bakry–Émery–Ricci curvature. As applications of our estimates, we obtain half-space type results related to complete noncompact hypersurfaces properly immersed in such an ambient space.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In 1969, Heinz [17] showed that a compact graph of positive constant mean curvature H in the 3-dimensional Euclidean space \({\mathbb {R}}^3\) with boundary on a plane can reach at most height \(\frac{1}{H}\) from this plane. A hemisphere in \({\mathbb {R}}^3\) of radius \(\frac{1}{H}\) shows that this estimate is optimal. In particular, Heinz’s result motivated several authors to approach the problem of obtaining a priori estimates for the height function of a compact hypersurface whose boundary is contained into a slice of a Riemannian product space (see, for instance, [2, 3, 8, 13, 18, 23]). More recently, extending the ideas of Alías and Dajczer [4], García-Martínez, Impera and Rigoli [15] proved sharp height estimates concerning compact hypersurfaces immersed in certain types of warped product spaces, with some constant higher order mean curvature and whose boundary is contained into a slice.
Concerning the Lorentzian setting, López [22] obtained a sharp estimate for the height of compact constant mean curvature spacelike surfaces with boundary contained in a spacelike plane of the 3-dimensional Lorentz–Minkowski space \({\mathbb {L}}^3\). Later on, the first author [10] established a height estimate for compact spacelike hypersurfaces with some positive constant higher order mean curvature and whose boundary is contained in a spacelike hyperplane of the \((n+1)\)-dimensional Lorentz–Minkowski space \({\mathbb {L}}^{n+1}\). As in [22], through the computation of the height of the hyperbolic caps of \({\mathbb {L}}^{n+1}\), he showed that his estimate is sharp. Afterwards, this same author jointly with Colares [9] generalized the results of [10] to the context of Lorentzian product spaces of the type \(-{\mathbb {R}}\times {{\mathbb {P}}}^n\), where the fiber \({{\mathbb {P}}}^n\) is supposed to have nonnegative sectional curvature. Proceeding with this picture, García-Martínez and Impera [14] extended the results of [9] to the so-called generalized Robertson–Walker spacetimes.
On the other hand, into the branch of the geometric analysis, many problems lead us to consider Riemannian manifolds endowed with a measure that has a smooth positive density with respect to the Riemannian one. This turns out to be compatible with the metric structure of the manifold and the resulting spaces are the weighted manifolds, which are also called manifolds with density or smooth metric measure spaces in the literature.
More precisely, given a complete n-dimensional Riemannian manifold \((M^n,g)\) and a smooth function \(f:M^n\rightarrow {\mathbb {R}}\), the weighted manifold \(M^n_f\) associated to \(M^n\) and f is the triple \((M^n, g, d\mu =e^{-f}dM)\), where dM denotes the standard volume element of \(M^n\). Appearing naturally in the study of self-shrinkers, Ricci solitons, harmonic heat flows and many other objects, weighted manifolds are proved to be important nontrivial generalizations of Riemannian manifolds and, nowadays, there are several geometric investigations concerning them. For a brief overview of results in this scope, we refer to the articles of Morgan [24] and Wei-Wylie [27].
We point out that a theory of Ricci curvature for weighted manifolds goes back to Lichnerowicz [20, 21] and it was later developed by Bakry and Émery in the seminal work [6], where they introduced the Bakry–Émery–Ricci tensor \(\mathrm{Ric}_f\) of a weighted manifold \(M^n_f\) as being the following extension of the standard Ricci tensor \(\mathrm{Ric}\) of \(M^n\):
So, it is natural to try to extend results stated in terms of the Ricci curvature to analogous results for the Bakry–Émery–Ricci tensor.
Here, our purpose is to revisit the problem of measure the vertical height of a compact hypersurface with nonzero constant weighted mean curvature and whose boundary is supposed, now, to be contained into a slice of a weighted product space. In this setting, under the assumption that the ambient space has nonnegative Bakry–Émery–Ricci curvature, we are able to establish optimal height estimates (see Theorems 1 and 3). As application of these estimates, we extend the ideas of [10, 14] and [15] in order to prove half-space type theorems (see Theorems 2 and 4).
2 Preliminaries
In what follows, let us consider an \((n+1)\)-dimensional product space \({\overline{M}}^{n+1}\) of the form \(I\times {{\mathbb {P}}}^n\), where \(I\subset {\mathbb {R}}\) is an open interval, \({\mathbb {P}}^n\) is an n-dimensional connected Riemannian manifold and \({\overline{M}}^{n+1}\) is endowed with the standard product metric
where \(\epsilon =\pm 1\), \(\pi _{I}\) and \(\pi _{{\mathbb {P}}}\) denote the canonical projections from \(I\times {\mathbb {P}}^n\) onto each factor, and \(\langle ,\rangle _{{\mathbb {P}}}\) is the Riemannian metric on \({\mathbb {P}}^n\). For simplicity, we will just write \({\overline{M}}^{n+1}=\epsilon I\times {\mathbb {P}}^n\) and \(\langle ,\rangle =\epsilon dt^2+\langle ,\rangle _{{\mathbb {P}}}\). In this setting, for a fixed \(t_0\in I\), we say that \({\mathbb {P}}^n_{t_0}=\{t_0\}\times {\mathbb {P}}^n\) is a slice of \({\overline{M}}^{n+1}\).
Throughout this paper, we will consider \(\Sigma ^n\) a connected hypersurface immersed into \({\overline{M}}^{n+1}\). In the case where \({\overline{M}}^{n+1}\) is Lorentzian (that is, when \(\epsilon =-1\)) we will assume that \(\Sigma ^n\) is a spacelike hypersurface, that is, the metric induced on \(\Sigma ^n\) via the immersion is a Riemannian metric. Since \(\partial _t\) is a globally defined timelike vector field on \(-I\times {\mathbb {P}}^n\), it follows that there exists a unique unitary timelike normal field N globally defined on \(\Sigma ^n\) which is in the same time-orientation as \(\partial _t\), so that its corresponding angle function \(\Theta =\langle N,\partial _t\rangle \) satisfies \(\Theta \le -1\). In that case, we will refer to N as the future-pointing Gauss map of \(\Sigma ^n\). When \({\overline{M}}^{n+1}\) is a Riemannian product space (that is, when \(\epsilon =1\)), \(\Sigma ^n\) will be assumed to be a two-sided hypersurface in \({\overline{M}}^{n+1}\). This condition means that there is a globally defined unit normal vector field N.
Denoting by \({\overline{\nabla }}\), \(\nabla \) and \({\widetilde{\nabla }}\) the gradients with respect to the metrics of \(\epsilon I\times _{\rho }{\mathbb {P}}^n\), \(\Sigma ^n\) and \({\mathbb {P}}\), respectively, a simple computation shows that the gradient of \(\pi _{I}\) on \({\overline{M}}^{n+1}\) is given by
So, from (2.1) we conclude that the gradient of the (vertical) height function \(h=(\pi _{I})|_{\Sigma }\) of \(\Sigma ^n\) is given by
where \((\ )^{\top }\) denotes the tangential component of a vector field in \({{\mathfrak {X}}}({\overline{M}}^{n+1})\) along \(\Sigma ^n\). Thus, we get the following relation
where \(|\ |\) denotes the norm of a vector field on \(\Sigma ^n\).
Now, let \(\epsilon I\times {\mathbb {P}}^n\) be a semi-Riemannian product space endowed with a weighted function f. For a Riemannian hypersurface \(\Sigma ^n\) immersed in \(\epsilon I\times {\mathbb {P}}^n\), the f-divergence operator on \(\Sigma ^n\) is defined by
for all tangent vector field X on \(\Sigma ^n\) and, for a smooth function \(u:\Sigma ^n\rightarrow {\mathbb {R}}\), its drifting Laplacian is given by
According to Gromov [16], the weighted mean curvature, or simply f-mean curvature, \(H_f\) of \(\Sigma ^n\) is given by
where H denotes its standard mean curvature function of \(\Sigma ^n\) with respect to its orientation N.
3 The Riemannian setting
It follows from a splitting theorem due to Fang, Li and Zhang (see [12, Theorem 1.1]) that if a weighted product space \(I\times {\mathbb {P}}^n\) with bounded weighted function f is such that \({\overline{\mathrm{Ric}}}_f\ge 0\), then f must be constant along I. So, motivated by this result, along this section we will consider weighted product spaces \(I\times {\mathbb {P}}^n\) whose weighted function f does not depend on the parameter \(t\in I\), that is, \(\langle {\overline{\nabla }} f,\partial _t\rangle =0\) and, for the sake of simplicity, we will denote them by \(I\times {\mathbb {P}}^n_f\).
Now, we present our first height estimate.
Theorem 1
Let \(I\times {\mathbb {P}}^n_f\) be a weighted Riemannian product space with \({\overline{\mathrm{Ric}}}_f\ge 0\) and let \(\Sigma ^n\) be a compact hypersurface with boundary contained into the slice \(\{s\}\times {{\mathbb {P}}}^n\), for some \(s\in I\), and whose angle function \(\Theta \) does not change sign. If \(\Sigma ^n\) has nonzero constant f-mean curvature such that \(nH_f^2\le |A|^2\), where A denotes the Weingarten operator of \(\Sigma ^n\) with respect to its unit normal vector field N, then the height function h of \(\Sigma ^n\) satisfies
Proof
Initially, we will show that
where \({\widetilde{\mathrm{Ric}}}_f\) stands for the Bakry–Émery–Ricci tensor of \({{\mathbb {P}}}^n\) and \(N^*=N-\Theta \partial _t\) is the projection of N onto \({{\mathbb {P}}}^n\).
Indeed, from Proposition 6 of [5] (see also Proposition 1 of [1]) we have that
where \(\partial _t^\top \) stands for the tangential component of \(\partial _t\) along \(\Sigma ^n\) and \({\widetilde{\mathrm{Ric}}}\) is the Ricci tensor of \({{\mathbb {P}}}^n\).
On the other hand, using our assumption that \(\langle {\overline{\nabla }}f,\partial _t\rangle =0\) and that \(H_f\) is constant, from (1.1) and (2.5) we get
Moreover, taking into account once more that \(\langle {\overline{\nabla }}f,\partial _t\rangle =0\), it is not difficult to verify that
where \({\widetilde{\mathrm{Hess}}} f\) stands for the Hessian of f on \({{\mathbb {P}}}^n\).
Consequently, since
So, from the Eqs. (3.3) and (3.6) we deduce (3.3).
Moreover, since f is constant along \(\mathbb {R}\), from (2.1) we get that
But, from Proposition 7.35 of [25] we have that
for every \(X\in {\mathfrak {X}}(\Sigma )\). Thus, from (2.2) and (3.8), we get
Hence, from (3.9) we have
Therefore, from (2.4), (2.5), (3.7) and (3.10) we obtain
Now, we define on \(\Sigma ^n\) the function
Consequently, since \({\widetilde{\mathrm{Ric}}}_f(N^{*},N^{*})={\overline{\mathrm{Ric}}}_f(N,N)\ge 0\), \(nH_f^2\le |A|^2\) and choosing N such that \(-1\le \Theta \le 0\), from (3.13) we get that \(\Delta _f\varphi \ge 0\). Thus, we conclude from the maximum principle that \(\varphi \le \varphi _{|\partial \Sigma }\) and, hence, from (3.12) we have that
We then consider the two possible cases. In the case that \(H_f>0\), from (3.11) we have \(\Delta _fh\le 0\) and, from the maximum principle, \(h\ge s\) on \(\Sigma ^n\). Thus, from (3.14) we conclude that
Finally, in the case that \(H_f<0\), from (3.11) we have \(\Delta _fh\ge 0\) and, again from the maximum principle, \(h\le s\) on \(\Sigma ^n\). Thus, from (3.14) we must have
Therefore, estimate (3.1) follows from (3.15) and (3.16). \(\square \)
Remark 1
Concerning Theorem 1, we note that if \(\Sigma ^n\) is locally a graph over \({\mathbb {P}}^n\), then its angle function \(\Theta \) is either \(\Theta <0\) or \(\Theta >0\) along \(\Sigma ^n\). Hence, the assumption that \(\Theta \) does not change sign is generally weaker than that of \(\Sigma ^n\) being a local graph. Moreover, as it was already observed by Espinar and Rosenberg [11] when they made allusion to immersions into the Euclidean space, the condition that \(\Theta \) does not change sign can also be regarded as the image of the Gauss map of the hypersurface lying in a closed hemisphere of the Euclidean sphere.
On the other hand, we also observe that the hypothesis \(nH_f^2\le |A|^2\) is automatically satisfied in the case that the weighted function f is constant. Furthermore, taking into account Heinz’s estimate [17] previously commented in the introduction, we see that our estimate (3.1) is optimal.
From Theorem 1, and according to the ideas of [10, 14, 15], we obtain the following half-space type result.
Theorem 2
Let \({\mathbb {R}}\times {\mathbb {P}}^n_f\) be a weighted Riemannian product space with \({\overline{\mathrm{Ric}}}_f\ge 0\) and \({{\mathbb {P}}}^n\) compact. Let \(\Sigma ^n\) be a complete noncompact two-sided hypersurface properly immersed in \({\mathbb {R}}\times {\mathbb {P}}^n_f\), whose angle function \(\Theta \) does not change sign. If \(\Sigma ^n\) has nonzero constant f-mean curvature such that \(nH_f^2\le |A|^2\), then \(\Sigma ^n\) cannot lie in a half-space of \({\mathbb {R}}\times {\mathbb {P}}\). In particular, \(\Sigma ^n\) must have at least one top and one bottom end.
Proof
Suppose by contradiction that, for instance, \(\Sigma ^n\subset (-\infty ,\tau ]\times {\mathbb {P}}\), for some \(\tau \in {\mathbb {R}}\). Thus, for each \(s<\tau \) we define
Since \({\mathbb {P}}\) is compact and \(\Sigma ^n\) is properly immersed in \({\mathbb {R}}\times {\mathbb {P}}^n_f\), we have that \(\Sigma _s^{+}\) is a compact hypersurface contained in a slab of width \(\tau -s\) and with boundary in \(\left\{ s\right\} \times {\mathbb {P}}\). Thus, we can apply Theorem 1 to get that \(\Sigma _s^{+}\) is contained in a slab of width \(\frac{1}{|H_f|}\), so that it must be \(\tau -s\le \frac{1}{|H_f|}\). Consequently, choosing s sufficiently small we violate this estimate, reaching a contradiction.
Analogously, if we suppose that \(\Sigma ^n\subset [\tau ,+\infty )\times {\mathbb {P}}\) with \(\tau \in {\mathbb {R}}\), for each \(s>\tau \) we define \(\Sigma _s^{-}\) by
Hence, since \(\Sigma _s^{-}\) is a compact hypersurface with boundary in \(\left\{ s\right\} \times {\mathbb {P}}\), we can reason as in the previous case and obtain another contradiction. \(\square \)
4 The Lorentzian setting
As a consequence of a splitting theorem due to Case (see [7, Theorem 1.2]), if a weighted Lorentzian product space \(-{\mathbb {R}}\times {\mathbb {P}}\) is endowed with a bounded weighted function f and if \({\overline{\mathrm{Ric}}}_f(V,V)\ge 0\), for all timelike vector field V on \(-I\times {\mathbb {P}}\), then f must be constant along \(\mathbb {R}\). Motivated by this result, in what follows we will consider weighted Lorentzian product spaces \(-I\times {\mathbb {P}}^n\) whose weighted function f does not depend on the parameter \(t\in I\), that is, \(\langle {\overline{\nabla }} f,\partial _t\rangle =0\) and we will denote them by \(-I\times {\mathbb {P}}^n_f\).
We proceeding with our second height estimate.
Theorem 3
Let \(-I\times {\mathbb {P}}^n_f\) be a weighted Lorentzian product space with \({\overline{\mathrm{Ric}}}_f\ge 0\) and let \(\Sigma ^n\) be a compact spacelike hypersurface with boundary contained into the slice \(\{s\}\times {{\mathbb {P}}}^n\), for some \(s\in I\). If \(\Sigma ^n\) has nonzero constant f-mean curvature such that \(nH_f^2\le |A|^2\), where A denotes the Weingarten operator of \(\Sigma ^n\) with respect to its future-pointing unit normal vector field N, then the height function h of \(\Sigma ^n\) satisfies
Proof
Since from Proposition 1 of [1] gives us
in a similar way of the proof of Theorem 1 we get that
Moreover, also analogously as in the proof of Theorem 1, we have that
So, we define on \(\Sigma ^n\) the function
Consequently, since \({\widetilde{\mathrm{Ric}}}_f(N^{*},N^{*})={\overline{\mathrm{Ric}}}_f(N,N)\ge 0\), \(nH_f^2\le |A|^2\) and choosing N future-pointing (that is, \(\Theta \le -1\)), we get that \(\Delta _f\varphi \ge 0\). Thus, we conclude from the maximum principle that \(\varphi \le \varphi _{|\partial \Sigma }\) and, hence, from (4.4) we have that
We then consider the two possible cases. In the case that \(H_f>0\), from (4.3) we have \(\Delta _fh\ge 0\) and, from the maximum principle, \(h\le s\) on \(\Sigma ^n\). Thus, from (4.5) we conclude that
In the case that \(H_f<0\), from (4.3) we have \(\Delta _fh\le 0\) and, again from the maximum principle, \(h\ge s\) on \(\Sigma ^n\). Thus, from (4.5) we must have
Therefore, estimate (4.1) follows from (4.6) and (4.7). \(\square \)
Remark 2
Taking into account the height estimate of [10] mentioned in the introduction, we see that our estimate (4.1) is also sharp.
Finally, reasoning as in the proof of Theorem 2, from Theorem 3 we get the following
Theorem 4
Let \(-{\mathbb {R}}\times {\mathbb {P}}^n_f\) be a weighted Lorentzian product space with \({\overline{\mathrm{Ric}}}_f\ge 0\) and \({{\mathbb {P}}}^n\) compact. Let \(\Sigma ^n\) be a complete noncompact spacelike hypersurface properly immersed in \(-{\mathbb {R}}\times {\mathbb {P}}^n_f\), with bounded angle function \(\Theta \). If \(\Sigma ^n\) has nonzero constant f-mean curvature such that \(nH_f^2\le |A|^2\), then \(\Sigma ^n\) cannot lie in a half-space of \(-{\mathbb {R}}\times {\mathbb {P}}\). In particular, \(\Sigma ^n\) must have at least one top and one bottom end.
Remark 3
We recall that an integral curve of the unit timelike vector field \(\partial _t\) is called a comoving observer and, for a fixed point \(p\in \Sigma ^n\), \(\partial _t(p)\) is called an instantaneous comoving observer. In this setting, among the instantaneous observers at p, \(\partial _t(p)\) and N(p) appear naturally. From the orthogonal decomposition \(N(p)=N^*(p)-\Theta (p)\partial _t(p)\), we have that \(|\Theta (p)|\) corresponds to the energy E(p) that \(\partial _t(p)\) measures for the normal observer N(p). Furthermore, the speed \(|\upsilon (p)|\) of the Newtonian velocity \(\upsilon (p):=E^{-1}(p)N^*(p)\) that \(\partial _t(p)\) measures for N(p) satisfies the equation \(|\upsilon (p)|^2=\tanh (\cosh ^{-1}|\Theta (p)|)\). Hence, the boundedness of the angle function \(\Theta \) of the spacelike hypersurface \(\Sigma ^n\) means, physically, that the speed of the Newtonian velocity that the instantaneous comoving observer measures for the normal observer do not approach the speed of light 1 on \(\Sigma ^n\) (cf. [26, Sections 2.1 and 3.1]). In this direction, as it was already observed by Latorre and Romero [19], the assumption of \(\Theta \) be bounded on a complete spacelike hypersurface is a mild hypothesis to supply the noncompactness of it.
References
Albujer, A.L., Aledo, J.A., Alías, L.J.: On the scalar curvature of hypersurfaces in spaces with a Killing field. Adv. Geom. 10, 487–503 (2010)
Aledo, J.A., Espinar, J.M., Gálvez, J.A.: Surfaces with constant curvature in \({\mathbb{S}}^2\times {\mathbb{R}}\) and \({\mathbb{H}}^2\times {\mathbb{R}}\). Height estimates and representation. Bull. Braz. Math. Soc. 38, 533–554 (2007)
Aledo, J.A., Espinar, J.M., Gálvez, J.A.: Height estimates for surfaces with positive constant mean curvature in \(M^2\times {\mathbb{R}}\). Ill. J. Math. 52, 203–211 (2008)
Alías, L.J., Dajczer, M.: Constant mean curvature hypersurfaces in warped product spaces. Proc. Edinb. Math. Soc. 50, 511–526 (2007)
Alías, L.J., Dajczer, M., Ripoll, J.: A Bernstein-type theorem for Riemannian manifolds with a Killing field. Ann. Glob. Anal. Geom 31, 363–373 (2007)
Bakry, D., Émery, M.: Diffusions hypercontractives. In: Azéma, J., Yor, M. (eds.) Séminaire de Probabilités XIX, 1983/84. Lecture Notes in Mathematics, vol. 1123, pp. 177–206. Springer, Berlin (1985)
Case, J.S.: Singularity theorems and the Lorentzian splitting theorem for the Bakry–Émery–Ricci tensor. J. Geom. Phys. 60, 477–490 (2010)
Cheng, X., Rosenberg, H.: Embedded positive constant \(r\)-mean curvature hypersurfaces in \(M^m\times {\mathbb{R}} \). Ann. Braz. Acad. Sci 77, 183–199 (2005)
Colares, A.G., de Lima, H.F.: Space-like hypersurfaces with positive constant \(r\)-mean curvature in Lorentzian product spaces. Gen. Relativ. Gravity 40, 2131–2147 (2008)
de Lima, H.F.: A sharp height estimate for compact spacelike hypersurfaces with constant \(r\)-mean curvature in the Lorentz–Minkowski space and application. Differ. Geom. Appl. 26, 445–455 (2008)
Espinar, J.M., Rosenberg, H.: Complete constant mean curvaturesurfaces and Bernstein type theorems in \(M^2\times {\mathbb{R}}\). J. Differ. Geom 82, 611–628 (2009)
Fang, F., Li, X.-D., Zhang, Z.: Two generalizations of Cheeger–Gromoll splitting theorem via Bakry–Émery–Ricci curvature. Ann. Inst. Fourier 59, 563–573 (2009)
Gálvez, J.A., Martínez, A.: Estimates in surfaces with positive constant Gauss Curvature. Proc. Am. Math. Soc. 128, 3655–3660 (2000)
García-Martínez, S.C., Impera, D.: Height estimates and half-space theorems for spacelike hypersurfaces in generalized Robertson–Walker spacetimes. Differ. Geom. Appl. 32, 46–67 (2014)
García-Martínez, S.C., Impera, D., Rigoli, M.: A sharp height estimates for compact hypersurfaces with constant \(k\)-mean curvature in warped product spaces. Proc. Edinb. Math. Soc. 58, 403–419 (2015)
Gromov, M.: Isoperimetry of waists and concentration of maps. Geom. Funct. Anal. 13, 178–215 (2003)
Heinz, E.: On the nonexistence of a surface of constant mean curvature with finite area and prescribed rectificable boundary. Arch. Ration. Mech. Anal. 35, 249–252 (1969)
Hoffman, D., de Lira, J.H., Rosenberg, H.: Constant mean curvature surfaces in \(M^2\times \mathbb{R}\). Trans. Am. Math. Soc. 358, 491–507 (2006)
Latorre, J.M., Romero, A.: Uniqueness of noncompact spacelike hypersurfaces of constant mean curvature in generalized Robertson–Walker spacetimes. Geom. Dedic. 93, 1–10 (2002)
Lichnerowicz, A.: Variétés Riemanniennes à tenseur C non négatif. C. R. Acad. Sci. Paris Sér. A-B 271, A650–A653 (1970)
Lichnerowicz, A.: Variétés Kählériennes à première classe de Chern non negative et variétés Riemanniennes à courbure de Ricci généralisée non negative. J. Differ. Geom. 6, 47–94 (1971)
López, R.: Area monotonicity for spacelike surfaces with constant mean curvature. J. Geom. Phys. 52, 353–363 (2004)
Manzano, J.M.: Estimates for constant mean curvature graphs in \(M\times {\mathbb{R}}\). Rev. Mat. Iberoam. 29, 1263–1281 (2013)
Morgan, F.: Manifolds with density. Not. Am. Math. Soc. 52, 853–858 (2005)
O’Neill, B.: Semi-Riemannian Geometry with Applications to Relativity. Academic Press, London (1983)
Sachs, R.K., Wu, H.: General Relativity for Mathematicians, Graduate Texts in Mathematics. Springer, New York (1977)
Wei, G., Willie, W.: Comparison Geometry for the Bakry–Emery–Ricci Tensor. J. Differ. Geom. 83, 377–405 (2009)
Acknowledgements
The first author is partially supported by CNPq, Brazil, Grant 303977/2015-9. The authors would like to thank the referee for giving valuable suggestions and comments which improved the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
de Lima, H.F., Santos, M.S. Height estimates and half-space type theorems in weighted product spaces with nonnegative Bakry–Émery–Ricci curvature. Ann Univ Ferrara 63, 323–332 (2017). https://doi.org/10.1007/s11565-016-0268-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11565-016-0268-5
Keywords
- Weighted product spaces
- Bakry–Émery–Ricci tensor
- Compact hypersurfaces
- Height estimates
- Half-space type theorems