Parallel fractal image compression using quadtree partition with task and dynamic parallelism

Abstract

Fractal image compression is a lossy compression technique based on the iterative function system, which can be used to reduce the storage space and increase the speed of data transmission. The main disadvantage of fractal image compression is the high computational cost of the encoding step, compared with the popular image compression based on discrete cosine transform. The aim of this paper is the development of parallel implementations of fractal image compression using quadtree partition. We develop two parallel implementations: the first one uses task parallelism over a multi-core system and the second uses dynamic parallelism over a GPU architecture. We show performance comparisons of the parallel implementations using standard images to compare the capabilities of these parallel architectures. The proposed parallel implementations achieve speedups over the serial implementation of approximately $15 \times$ using the multi-core CPU and $25 \times$ using the GPU.

1 Introduction

In the field of information technology, a huge amount of data has been generated. The data growth rate is much higher than the growth rate of technologies [1]. Digital image compression has generated different techniques to this challenge of having efficient ways to store and transmit information. These techniques are essential in most real-time applications like television broadcasting, satellite imagery, geographical information systems, flight simulators, video conferencing, graphics, digital libraries, among others [1,2,3].

The compression techniques can be divided into two groups: preserving or lossless, which permits error-free data reconstruction in the decompress step, and lossy compression, which does not preserve information completely [4]. The fractal image compression is classified into lossy compression techniques. The first practical fractal image compression algorithm based on a partitioned iterated function system (PIFS) was reported by A. Jacquin in 1992 [5]. Fractal image compression is an active area of research due to high compression ratios and high quality in the decompressed image. The main disadvantage is the high computational cost on the encoding step, which has a complexity order $\mathcal {O}(M^4)$ for an image of size $M\times M$ pixels [6]. Thus, the development of parallel implementations has been interesting, where it is possible to use different architectures such as multi-core CPU, FPGAs, and GPUs [7,8,9].

In [10], a parallel algorithm for the fractal compression using quadtree is proposed, following a master–slave strategy and reaching a speedup of $1.80 \times$ with input images of size $512\times 512$ pixels in a multi-core system. The four partitions of the input image are assigned to the available slave processors. A range is compared with a set of non-overlapping domains for each processor to find the least root-mean-square error. If this least error is less than certain tolerance, the range block returns to the master processor to compute the fractal transform and store the compression data. Elsewhere, the recursive partition and assignment of blocks to available processors is performed.

In [11], a parallelization algorithm using OpenMP is proposed, considering the Jacquin’s fractal compression scheme. The input image is partitioned in a fixed number of non-overlapping range blocks. Therefore, two loops go through the partitions. They parallelize the first for loop that runs through the partitions horizontally. For each partition, a domain block is found that is very similar to the range block. Finally, when all threads have finished, the best-matched mapping parameters are saved. Their parallel implementation reached a speedup of almost $6 \times$ using a multi-core system with four physical cores at 2.33 GHz, for an image of size $512\times 512$ pixels.

In [12], an approach to parallelize the Jacquin’s fractal compression scheme over GPU using CUDA is proposed. They consider each range and domain block as corresponding to a block of threads on the CUDA model. Thus, they parallelize the for loops that go through the range blocks launching a set of thread blocks, the computations inside the for loops that go through the domain blocks are executed in parallel for each pixel value, and the reduction instructions like summation and averaging are done using a standard parallel reduction of CUDA programming. Their parallel implementation reaches a speedup of $10.75 \times$ using an image of size $512\times 512$ pixels.

In [2], a fractal compression algorithm is implemented using a GPU cluster. They perform the fractal compression at different quadtree levels, using the fixed sizes of $4\times 4$, $8\times 8$, $16\times 16$, and $32\times 32$ pixels for the range blocks. The program is executed on a GPU cluster with 24 GPUs, using the dynamic allocation with circulating pipeline processing as topology, where one of the GPUs is the master and the rest are slaves. The master sends the range blocks in a circulated way through a pipeline that traverses through the slave nodes. Each slave node contains a set of domain blocks, and thus, each range is matched with the domains. Once a match is found, the range leaves the pipeline. If no match is obtained, the master node subdivides the range into four sub-blocks, these sub-blocks are sent to the slave nodes, and the process of matching continues through the pipeline. This approach reaches a speedup of almost $14 \times$.

Recently, in [9], a parallel version of the Fisher classification scheme using CUDA is proposed. They linearize the quadtree structure to launch kernels for nodes of the quadtree at the same time. Unlike the sequential algorithm where the decision of dividing the range block into sub-blocks is given by the comparison of the root-mean-square error with tolerance, in this parallel implementation, all range blocks at each level of the quadtree are taken into account to compute the best matching with the domain blocks. Thus, all results of the range blocks are stored in the memory, subsequently parsed, and saved in the compression data. The parallel implementation reaches a speedup of $4.9 \times$ with images of size $1024\times 1024$ pixels.

In this work, we propose the use of task and dynamic parallelism to build parallel implementations of fractal image compression using quadtree partition. To the best of our knowledge, these strategies have not been taken into account in the previous works. We use OpenMP for multi-thread programming on the multi-core CPU, while we use CUDA programming on the GPU. Unlike the multi-core implementations reported in [10, 11], we use the $\texttt {task}$ directive of OpenMP for parallelizing the units of work that are dynamically generated through the quadtree structure. Unlike the GPU implementations reported in [2, 9, 12], we use the dynamic parallelism extension of CUDA programming with streams to parallelize the recursive quadtree procedure.

This paper aims to compare the capabilities of the task parallelism in a multi-core CPU and the dynamic parallelism in a GPU. The outline of this paper is as follows. In Sect. 2, we present the mathematical background of fractal image compression. In Sect. 3, we describe the fractal image compression algorithm. In Sect. 4, we present the parallel implementations for multi-core CPU and GPU architectures. The experimental results are present in Sect. 5, and our conclusions are given in Sect. 6.

2 Mathematical background

The fractal image compression consists in repeating the method of the iterated function system that defines the Hutchinson operator, which is used to generate fractals (see [13]), but in a more general setting, using now a partitioned iterated function system. Let $I=[0,1]$ and let us denote $I^2=I \times I$, $I^3=I \times I \times I$. An image can be modeled as a function $z=f(x,y)$ that gives the grey level at each point (x, y). Because real images are finite in extent, we take the domain of f as $I^2$ and its range as I. On the other hand, a function $f:I^2 \rightarrow I$ can be considered an image of infinite resolution. The graph of a function $f:I^2 \rightarrow I$ is the subset of $\mathbb {R}^3$ given by $gra(f)=\{ (x,y,f(x,y)) : (x,y) \in I^2 \}$.

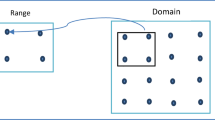
Formally, the function is different from its graph, but both contain the same information; thus, we will not distinguish between the function and its graph. Consider the space $F:=\{ f:I^2 \rightarrow I \}$ of images defined as the graphs of measurable functions over $I^2$ with values in I. Let $R_1,...,R_N$, $D_1,...,D_N$ be subsets of $I^2$, which we call ranges and domains, respectively, consider a familiy of mappings $v_i: I^3 \rightarrow I^3$, $i=1,...,N$, and define $w_i : D_i \times I \rightarrow I^3$ as the restriction of $v_i$ on $D_i \times I$, i.e., $w_i=v_i|_{D_i \times I}$. Suppose that $w_i$ takes values in $R_i \times I$. Since each mapping $w_i$ sends subsets of $D_i \times I$ into subsets of $R_i \times I$ and $gra(g|_{D_i}) \subset D_i \times I$ for each $g \in F$, then we can define $w_i(g)(x,y):=w_i \bigl ( x,y, g(x,y) \bigr )$, for each $g \in F$ and $(x,y) \in D_i$. Thus, $w_i(g)$ turns out to be an image in F restricted to the range $R_i$. We say that the collection $w_1,...,w_N$ tile $I^2$ if it satisfies that $\bigcup _{i=1}^N w_i(g) \in F$, for each $g \in F$. From now on, we suppose that the collection $w_i$, $i=1,..,N$, tile $I^2$, which implies that $\bigcup _{i=1}^{N} R_i =I^2$ and $R_i \cap R_j = \emptyset$, for $i \ne j$.

Given a metric space X, a mapping $W:X \rightarrow X$ is contractive if there exists $s \in [0,1)$, such that $d(W(f),W(g)) \le s (f,g)$ for every $f,g \in X$. The number s is called the Lipschitz constant of W. The Banach Contraction Principle states that if X is complete and W is contractive, then there exists a unique $x_W \in X$, such that $W(x_W)=x_W$. The element $x_W$ is called the fixed point or the attractor of W. Furthermore, for any $g \in X$, the sequence $(W^{(n)}(g))_{n=1}^{\infty }$ formed by the iterations of g under W converges to $x_W$. Finally, under the hypothesis of the Banach Contraction Principle, the Collage Theorem states that $d(f,x_W) \le (1-s)^{-1} \, d(f,W(f))$, for every $f \in X$.

A mapping $w:\mathbb {R}^3 \rightarrow \mathbb {R}^3$ is called z-contractive if there exists $s \in (0,1)$ satisfying the following condition: for every $x,y,z_1,z_2 \in \mathbb {R}$, with $w(x,y,z_1)=(x',y',z_1')$ and $w(x,y,z_2)=(x',y',z_2')$, we have that

$$d(z_1',z_2') \le s \, d(z_1,z_2),$$

and, furthermore, $x'$ and $y'$ are independent of $z_1$ and $z_2$. Now, we will define the operator that will encode our image. For each $i=1,...,N$, suppose that $w_i : D_i \times I \rightarrow I^3$ is z-contractive and define the operator $W : F \rightarrow F$ by

$$W(g)= \bigcup _{i=1}^N w_i(g), \text {for each} \ g \in F.$$

Since $w_1,...,w_N$ tile $I^2$, we have that the operator W is well defined. Since $w_i : D_i \times I \rightarrow I^3$ is z-contractive, then W is a contractive operator defined in the metric space $\bigl ( F, d_{\sup } \bigr )$, where $d_{\sup } (f,g)= \sup _{(x,y) \in I^2} |f(x,y)-g(x,y)|$. On the other hand, it is well known that the metric space $\bigl ( F, d_{\sup } \bigr )$ is complete. Therefore, by the Banach Contraction Principle, we have that there exists a unique fixed point $x_W \in F$ of W, i.e., $W(x_W)=x_W$. Moreover, if we iterate any image $g \in F$ by W, we have that the sequence $\bigl ( W^{(n)}(g) \bigr )_{n=1}^\infty$ formed by the iterates converges to $x_W$.

The operator W is inspired by the Hutchinson operator used to generate fractals. What if $w_i$ is not z-contractive for some i? To answer this question, recall that a generalization of the Banach Contraction Principle states that if W is eventually contractive, i.e., if for some $M \in \mathbb {N}$, the Mth iterate $W^{(M)}$ is contractive, then W has a unique fixed point and $W^{(n)}(g) \rightarrow x_W$ for every $g \in F$. Notice that $W^{(M)}$ is composed of a union of compositions of the form $w_{i_1} \circ \cdots \circ w_{i_M}$; thus, if there are enough contractive functions $w_{i_j}$, then the compositions will also be contractive, since the contractive mappings eventually dominate the non-contractive ones, and thus, W will be eventually contractive.

Let f be a fixed image; according to Fisher’s work [13], the compression problem is to find a collection of maps $w_1$, $w_2$, ..., $w_N$, with $W=\cup _{i=1}^N w_i$ and $f=x_W$. The transformations $w_i$ are of the form

$$\begin{aligned} w_i\left[ \begin{array}{c} x \\ y \\ z \end{array} \right] = \left[ \begin{array}{ccc} a_i &{} b_i &{} 0 \\ c_i &{} d_i &{} 0 \\ 0 &{} 0 &{} s_i \end{array} \right] \left[ \begin{array}{c} x \\ y \\ z \end{array} \right] + \left[ \begin{array}{c} e_i \\ f_i \\ o_i \end{array} \right] . \end{aligned}$$

(1)

We seek a partition of f into pieces, to which the transformations w are applied to obtain f.

If we take $a_i, b_i, c_i, d_i, s_i \in (0,1)$, then the functions $w_i : D_i \times I \rightarrow I^3$, $1=1,...,N$ fulfill the hypotheses mentioned above and form a partitioned iterated function system. Recall that given a metric space X and $E_i \subset X$, $i=1,...,N$, a partitioned iterated function system (PIFS) is a finite collection of contractive mappings $u_i : E_i \rightarrow X$, for each $i=1,...,N$.

In general, the images do not contain parts that can be transformed to fit exactly somewhere else in the original image. What is expected is to find another image $f'=x_W$ with a root-mean-square distance $d_{rms}(f',f)$ small. Then, we seek a transformation W whose fixed point is closed to f

$$\begin{aligned} f\approx f'=W(f')=W(f)=w_1(f) \cup w_2(f) \cup ... w_N(f). \end{aligned}$$

(2)

Thus, it is sufficient to minimize

$$\begin{aligned} d_{rms}(f \cap (R_i \times I),w_i(f)) \;\; i=1,...,N, \end{aligned}$$

(3)

which means to find the ranges $R_i$ and corresponding domains $D_i$ with maps $w_i$.

To compare $R_i$ with $D_i$, $D_i$ is subsampled to create a square $\tilde{D}_i$ with the same size as $R_i$. Given two squares containing m pixel intensities, $a_1,...,a_m$ from $\tilde{D}_i$ and $b_1,...,b_m$ from $R_i$, the contrast s and brightness o parameters are computed minimizing the following error function:

$$\begin{aligned} \varepsilon =\frac{1}{m}\sum _{j}^{m}(sa_j+o-b_j)^2. \end{aligned}$$

(4)

The minimum of $\varepsilon$ is obtained when the partial derivatives with respect to s and o are zero; this generates the following system of two equations with two unknowns:

$$\begin{aligned} \left( \begin{array}{cc} {\Gamma} _2^D {}\;\; {\Gamma} _1^D \\ {\Gamma} _1^D {}\;\; m \end{array} \right) \left( \begin{array}{c} s \\ o \end{array} \right) = \left( \begin{array}{c} {\Gamma} ^{RD} \\ {\Gamma} _1^R \end{array} \right) , \end{aligned}$$

(5)

where ${\Gamma} _1^D=\sum _{j=1}^{m}a_j$, ${\Gamma} _2^D=\sum _{j=1}^{m}a_j^2$, ${\Gamma} _1^R=\sum _{j=1}^{m}b_j$ and ${\Gamma} ^{DR}=\sum _{j=1}^{m}a_jb_j$. Solving this system of equations, we have that

$$\begin{aligned} s=\frac{m{\Gamma} ^{DR}-{\Gamma} _1^D{\Gamma} _1^R}{m{\Gamma} _2^D-({\Gamma} _1^D)^2} \end{aligned}$$

(6)

and

$$\begin{aligned} o=\frac{1}{m}({\Gamma} _1^R-s{\Gamma} _1^D). \end{aligned}$$

(7)

Then, the error function can be computed as follows:

$$\begin{aligned} \varepsilon=\frac{1}{m}[{\Gamma} _2^R + s(s{\Gamma} _2^D-2{\Gamma} ^{DR}+2o{\Gamma} _1^D)\nonumber \\+o(mo-2{\Gamma} _1^D)], \end{aligned}$$

(8)

with ${\Gamma} _2^R=\sum _{j=1}^{m}b_j^2$ and the $\text {rms}$ error is equal to $\sqrt{\varepsilon }$. If the determinant of the system matrix is zero, then $s=0$ and $o=\frac{1}{m}{\Gamma} _1^R$.

According to the above, if $s_i<1$ for every i, then each $w_i$ is z-contractive and, therefore, there exists a unique $x_W \in F$, such that $W(x_W)=x_W$ and $W^{(n)}(g) \rightarrow x_W$, $n \rightarrow \infty$, for every $g \in F$. By construction, $f \approx W(f)$, and the Collage Theorem guarantees that $f \approx x_W$. On the other hand, if $s_i \ge 1$ for some i, but there are enough numbers $s_j<1$, then W may be eventually contractive, and thus, we would also have the existence of a fixed point $x_W$ and the convergence of the iterates to $x_W$. As we mentioned, it is safer to take $s_i<1$ to ensure contractivity of W, but experiments show that taking $s_i<1.2$ is safe and results in encodings as good as those of taking $s_i<1$. Therefore, we will not impose conditions on $s_i$.

There are three types of domain libraries $D_1$, $D_2$, and $D_3$. These are selected as sub-squares of the image, equally spaced vertically and horizontally, depending on parameter l. $D_1$ has a lattice whose spacing is the domain size divided by l, i.e., it has more small domains than large, this is the domain library used by Jacquin in [5]. $D_2$ has a lattice as $D_1$ but with the opposite spacing-size relationship, i.e., it has more large domains than small. $D_3$ has a lattice with fixed spacing equal l, i.e., it has approximately the same number of domains in each level of the quadtree, where R is compared.

The domain-range comparison step is very computationally intensive. Fisher in [13] uses a classification scheme to minimize the number of domains compared with a range. Before the quadtree procedure, all the domains in some domain libraries are classified, and only domains with the same classification are compared with the range. The idea of using a classification scheme was developed independently in [5, 14]. The Fisher classification scheme divides a square sub-image into upper left, upper right, lower left, and lower right quadrants numbered sequentially. On each quadrant, values proportional to the average and variance are computed as follows:

$$\begin{aligned} A_i=\sum _{j=1}^n r_j^i, \;\; V_i=\sum _{j=1}^n (r_j^i)^2-A_i^2, \end{aligned}$$

(9)

where $r_1^i,...,r_n^i$ are the pixel values in the quadrants $i=1,2,3,4$. The $A_i$ are ordered in one of the following three major classes:

$$\begin{aligned} A_1\ge {} A_2 \ge A_3 \ge A_4,\nonumber \\ A_1\ge {} A_2 \ge A_4 \ge A_3,\nonumber \\ A_1\ge {} A_4 \ge A_2 \ge A_3. \end{aligned}$$

(10)

Next, there are 24 ways to order the values $V_i$ in each major class; thus, there are $3 \times 24 = 72$ classes in all. If the scaling value $s_i$ is negative, the orderings in the classes are rearranged. Therefore, each domain is classified in two orientations: positive $s_i$ and negative $s_i$.

3 Fractal image compression algorithm using quadtree partition

Algorithms 1 and 2 show the main procedures of the fractal image compression method reported in [13], which uses a quadtree structure. A quadtree is a hierarchical spatial tree data structure based on the principle of recursive decomposition of space [15]. In an image, each node of the tree represents a partition of the image and contains four children or sub-squares, corresponding to the four quadrants of the partition. The root of the tree is the input image, and the leaves are the sub-squares constructed before a condition is reached through the tree, such as the minimum size of the sub-square.

First, the input image f of size $M \times M$ is downsampling with the average of $2 \times 2$ pixel groups (see Algorithm 1), considering four locations which are the combination of odd and even addresses (x, y). Thus, four domain images $g=\{g_1,g_2,g_3,g_4\}$ of size $M/2 \times M/2$ are obtained. The downsampling procedure avoids the repeated computation of averaging $2 \times 2$ pixel groups from the image f.

Next, for each level i in the quadtree from $\texttt {min\_d}$ to $\texttt {max\_d}$, and for each domain location (x, y) from a domain pool $D_p$ corresponding to the level i, a sub-square D of size $M'$ from the domain images g at corresponding position (x, y) is obtained, where $M'$ is the size of the sub-squares at level $i-1$. D is classified in some of the 72 classes, obtaining also the ${\Gamma} _1^D$ and ${\Gamma} _2^D$ values, which are added to a list $L_D$ in the corresponding class c.

The following step is the quadtree recursive procedure (see Algorithm 2), which considers the whole image as a partition the first time that is called. If the depth level d of the quadtree is less than $\texttt {min\_d}$, then the quadtree procedure is called itself in four different ways, corresponding to the four equal-sized sub-squares in which the partition can be divided. It is done recursively until d is equal to the $\texttt {min\_d}$. Then, a sub-square R is obtained from the image f at position (x, y) with size $M \times M$; note that x, y, and M values depend on the level d of the quadtree. Next, R is classified and compared with domains that belong to the same class, computing the best root-mean-square error ($\texttt {best\_rms}$).

If the $\texttt {best\_rms}$ is greater than a tolerance $\texttt {tol}$ and d is less than the maximum level $\texttt {max\_d}$, then R is subdivided into four quadrants, calling four times the recursive quadtree procedure. In another case, there are two possibilities. In the first one, there is a domain D which is similar to R with a $\texttt {best\_rms}$ less than or equal to $\texttt {tol}$. In the second one, the level d has reached the maximum level $\texttt {max\_d}$, and therefore, it is no longer possible to divide R. In both possibilities, R is covered by D, and the compression data are saved.

To increase the compression, Fisher uses the following bit allocation scheme. One bit is used at each quadtree level to denote a further recursion ($save(C_d,1)$) or not ($save(C_d,0)$). At the maximum depth ($d=\texttt {max\_d}$), this bit is not used, since no further partitions are possible. Five bits are used to store the scaling and seven for the offset ($save(C_d,s,o)$). The number of bits needed to store the domain index $\texttt {idx\_D}$ depends on the number of domains of each level, while only three bits are used to store the orientation or symmetric operation $\texttt {s\_op}$ of the domain-range mapping ($save(C_d,\texttt {s\_op},\texttt {idx\_D})$). However, when the scaling value is zero, the domain index is irrelevant, and therefore the orientation information.

4 Parallel implementation

We develop two implementations in C/C++ of the sequential fractal image compression algorithm. The first one uses a multi-core CPU and the second one uses a GPU. We use OpenMP for multi-thread programming on the multi-core CPU system, while on the GPU architecture, we use CUDA programming version 11.2. We also use the open computer vision library OpenCV version 4.5 [16] only for reading and writing images. We compile our programs using $\texttt {g++}$ for the sequential and multi-core versions and using $\texttt {nvcc}$ for the GPU version. In both cases, we add the flag $\texttt {-O2}$ to the compiler, which enables optimizations for speed, including automatic vectorization using the CPU processors [17].

In both implementations, we use OpenMP with loop-level parallelism for the downsampling of the input image f and the classification of the domains (see Algorithm 1). On the other hand, for the quadtree procedure (see Algorithm 2), which is the computationally heaviest part of the fractal image compression, we use OpenMP with task parallelism and CUDA with dynamic parallelism. In the following subsections, we describe the implementation of these procedures.

4.1 OpenMP with loop-level parallelism

OpenMP is an application programming interface (API) for shared memory parallel programming in a multi-core CPU architecture [18]. Thus, OpenMP is suitable for systems in which each thread or process can access all available memory. OpenMP provides a set of directives or pragmas used to specify parallel regions. Among other things, these directives efficiently manage threads inside parallel regions and distribute for loops in parallel.

We parallelize the downsampling of the input image f and the classification of the domains using the directives shown in the Listing 1.

The directive $\texttt {\#pragma}$ $\texttt {omp}$ $\texttt {parallel}$ opens a parallel region and, with the $\texttt {for}$ directive, parallelizes the for loop. The use of this directive is limited to those kinds of loops where the number of iterations can be determined. The loop must have an integer counter variable whose value is incremented (or decremented) by a fixed amount at each iteration until some bound is reached [19]. Thus, OpenMP can distribute the iterations to the team of threads launched and produces a result consistent with the corresponding sequential for loop [20].

In shared-memory programs, the individual threads have private and shared memory. Communication is accomplished through shared variables. Inside the parallel region, all variables are shared by default for all threads; then, we use only the $\texttt {private}$ directive to declare private variables for each thread. We also use the $\texttt {firstprivate}$ directive to declare private variables for each thread, which are initialized with the value that they have before entering the parallel region. Additionally, we use the directive $\texttt {num\_threads(N\_T)}$ to specify the number of threads $\texttt {N\_T}$ to be launched in our program.

4.2 OpenMP with task parallelism

OpenMP may execute the different tasks at different points in time, based on the availability of cores and their execution. The $\texttt {task}$ directive was initially introduced in OpenMP standard version 3.0 for expressing irregular parallelism and for parallelizing units of work that are dynamically generated [21]. OpenMP performs two activities related to tasks, the packing to create a structure that describes a task entity and the execution to assign a task to a thread. The task directive allows the decoupling of these activities; thus, the tasks can be dynamically created, nested, and queued for later execution [20].

We add the directives shown in the Listing 2 to the first call of the quadtree procedure (see Algorithm 1). The first directive opens a parallel region launching N_T threads. The single directive specifies that the quadtree procedure is executed by one thread only. The $\texttt {taskwait}$ directive is a barrier, which ensures that the tasks inside the quadtree procedure have been completed.

We parallelize the recursive calls of the quadtree procedure using the $\texttt {task}$ directive as shown in the Listing 3. With the $\texttt {task}$ directive, we assign to each available thread a task or quadtree procedure corresponding to one of the four quadrants of the partition. In this way, each task will have four child tasks. By default, when a task is created, this is tied to one thread, and the same thread will execute that task from the beginning to the end. Due to the number of comparisons between a range and the domains can be different for each task, some threads will finish their task faster than others. Thus, we add the $\texttt {untied}$ clause, which allows that idle threads to continue creating new tasks within tasks started by other threads obtaining a better load balancing.

4.3 CUDA with dynamic parallelism

CUDA (compute unified device architecture) is an extension to the C language that contains a set of instructions for parallel computing in a GPU. The host processor spawns multi-thread tasks (kernels) onto the GPU device, which has its internal scheduler that allocates the kernels to whatever available GPU hardware [22]. The GPU is used for general-purpose computation; it contains multiple transistors for the arithmetic logic unit, based on the single instruction and multiple threads (SIMT) programming model, which is exploited when multiple data are managed from a single parallel instruction, similar to the single instruction multiple data (SIMD) model [23].

Dynamic parallelism extends the CUDA programming model, which allows a kernel to create a new grid of thread blocks launching new kernels. It is only supported by GPUs of compute capability of 3.5 and higher [24]. With a single level of parallelism, the recursive algorithms needed to be implemented with multiple kernel launches, increasing the burden on the host, amount of host–device communication, and total execution time. However, with the dynamic parallelism support, the algorithms that dynamically discover new work can launch new kernels without burdening the host [25].

We create a kernel quadtree procedure using dynamic parallelism. This kernel is called at the first time as shown in Listing 4, launching only a thread-block with a thread $\texttt {<<<1,1>>>}$, without dynamic shared memory and using the NULL stream. When a stream is not specified in the call to a kernel function, the default NULL stream in the block is used by all threads. Thus, all kernels launched in the same block will be serialized even if different threads launched them [25].

Inside this kernel quadtree procedure, four child kernels are called in a recursive way, as shown in Listing 5 using four streams. Both named and unnamed (NULL) streams can be used in dynamic parallelism. The scope of a stream is private to the block in which the stream was created. Streams created on the host have undefined behavior when used within any kernel, just as streams created by a parent grid have undefined behavior if used within a child grid. An unlimited number of named streams are supported per block, but the maximum concurrency supported by the GPU is limited. If more streams are created than can support concurrent execution, some of these may serialize [25].

With the $\texttt {cudaStreamCreateWithFlags()}$ API and the $\texttt {cudaStreamNonBlocking}$ flag, we create the four streams that can run concurrently and perform no implicit synchronization with the NULL stream. Each level of the kernel quadtree procedure can be considered as a new nesting level. The maximum nesting depth is limited in hardware to 24 [25].

To improve the performance of the kernel quadtree procedure, we launch a fixed number of threads per block ($\texttt {TPB}$) for all kernel children as shown in Listing 6. In this way, the number of comparisons between a range and the domains is divided by the $\texttt {TPB}$, and each thread performs its comparison set in parallel. The rest of the instructions shown in the Algorithm 2 are assigned only to one thread.

5 Experimental results

The experiments were executed on an Alienware laptop and a server. The laptop has an Intel(R) Core(TM) i7-4720HQ CPU with a clock speed of 2.60 GHz, Windows 10 Pro (64-bits), 8 hyper-threading cores, 16 GB RAM; and a video card Nvidia GeForce GTX 980M with a clock speed of 1.13 GHz, and compute capability of 5.2. On the other hand, the server has an Intel(R) Core(TM) i9-9920X CPU with a clock speed of 3.50 GHz, Ubuntu 20.04 (64-bits), 24 hyper-threading cores, 64 GB RAM; and a video card Nvidia TITAN RTX with a clock speed of 1.77 GHz, and compute capability of 7.5. We develop our sequential and parallel implementations using 32-bit floating-point data (float precision). The standard images used in our experiments are available in [26, 27]. In all of our experiments, we execute the sequential and parallel implementations 20 times, reporting the mean of the processing time.

The program returns a compressed file that contains the necessary information to decompress the image. We compute the number of bits of information stored per pixel (bpp), dividing the size of the compressed file in bits by the size of the image. The lower the value of bpp, the better the compression ratio. With the decompressed image, we compute the peak signal-to-noise ratio (PSNR), and structural similarity (SSIM) quality measures [28]. PSNR is expressed in a logarithmic decibel scale (dB), while the SSIM is a decimal value in the range $[-1,1]$. The higher the value of both measures, the better the quality of the decompressed image.

We compare our results with those reported in other works to evaluate the consistency of our implementation. Table 1 shows the results of some implementations of the fractal image compression (FIC) based on quadtree partition (QP), using four standard images of size $256\times 256$ pixels. The results of the FIC with Fisher’s classification (FICQP), nonlinear affine map-based on FIC (FICQP-NAM), FIC using upper bound on scaling parameter (FICQP-UBSP), FIC with adaptive QP and nonlinear affine map (FIC-AQP-NAM), and the fast affine transform-based FIC (FICQP-FAT) were reported in recent work in [29]. For our FICQP implementations, we show the result obtained using the three types of domain libraries and fixing $l=1$ in the Alienware laptop. To obtain results similar to those of the other implementations, we fix the parameters $\texttt {min\_d}=5$ and $\texttt {max\_d}=7$ that correspond to compare domains with ranges of size from $8\times 8$ to $2\times 2$ pixels, while we use a different value of the parameter $\texttt {tol}$ for each image, $\texttt {tol}=15$ for Peppers, $\texttt {tol}=24$ for Boat, $\texttt {tol}=18$ for Cameraman, and $\texttt {tol}=27$ for Baboon. Both in our sequential version and our parallel versions, we obtain the same results.

Table 1 Number of bits of information stored per pixel (bpp), and quality measures for fractal image compression methods based on quadtree partition, using images of size $256\times 256$ pixels

In general, the best results in our implementations are obtained with the $D_3$ library; however, the processing time is higher than with the other two libraries. Note that with $l=1$, the domains in the sets $D_1$ and $D_2$ consist of non-overlapping sub-squares of the image, while the domains in the set $D_3$ are overlapping sub-squares which have a stride of a pixel between them. Thus, the $D_3$ library has more domains than the other libraries, allowing to obtain a better result in exchange for a longer processing time. Table 2 shows the processing time in seconds and speedup of our sequential and parallel implementations using the $D_3$ library and the images of size $256\times 256$ pixels with the same parameters used above. The speedup is computed by dividing the sequential or serial program’s processing time by the parallel program’s processing time [18]. For our multi-core implementation, we launch $\texttt {N\_T}=\{2,4,8\}$ threads, since the Alienware laptop has 8 hyper-threading cores available. For our GPU implementation, we have two versions. The first one uses streams (ST), and the second uses ST and 32 threads per block (ST-32). We consider the times of memory copies between the CPU and the GPU to compute the processing time. Note that the multi-core implementation has the best performance obtaining speedups from $2.25 \times$ with two cores (2C) to $6.06 \times$ with eight cores (8C), while with the GPU, although there is an improvement using the ST-32 with respect to the ST version, the processing time is higher than the serial execution.

Table 2 Processing time (seconds) and speedup of our sequential and parallel implementations in the Alienware laptop, using the $D_3$ library and images of size $256\times 256$ pixels

In a computer like the Alienware laptop, the operative system frequently uses the GPU for rendering the graphical user interface (GUI) to the display. If a GPU application has a large processing time, the GUI can become unresponsive, resulting in a “freeze”. Thus, the operative system has a GPU watchdog daemon, which kills GPU activities that run for longer than a certain time limit (around 3 s in our Alienware laptop) [30]. On the other hand, the server has no GUI; thus, the kernel functions can take a large processing time in the GPU. In this way, we perform experiments in the server using images of $512\times 512$ and $1024\times 1024$ pixels to show the performance of the parallel implementations in large images.

Figure 1 shows the resultant quadtree partitions and the decompressed images of our FICQP implementation using the $D_3$ library. The first row shows the original images: Boat and Baboon of $512\times 512$ pixels; Male and Airport of $1024\times 1024$ pixels. We fix the parameters $\texttt {min\_d}=4$ and $\texttt {max\_d}=8$ that correspond to compare domains with ranges of size from $32\times 32$ to $2\times 2$ pixels for Boat and Baboon images; and ranges of size from $64\times 64$ to $4\times 4$ pixels for Male and Airport images. The second and third rows show the resultant quadtree partitions and decompressed images fixing the parameter $\texttt {tol}=20$, while the fourth and fifth rows show the resultant quadtree partitions and decompressed images fixing the parameter $\texttt {tol}=5$. The processing time of the sequential implementation, bpp, PSNR, and SSIM are shown in Table 3. We obtain the same results of the bpp, PSNR, and SSIM for our parallel implementations. Note that with a small value of parameter $\texttt {tol}$, the quadtree partition has more small squares than bigger, which causes that the processing time, bpp, PSNR, and SSIM are higher. Furthermore, the processing time between images with the same size for a fixed $\texttt {tol}$ can be different; for example, in the Baboon and Airport images, there are more textured regions than in the Boat and Man images, respectively, which causes that there are more small squares in the Baboon and Airport images and the processing time is higher than in the Boat and Man images. Although the compression ratio is higher when we use $\texttt {tol}=20$, there are some details of the original images that are missing in the decompressed images, such as the sea region of the Boat image, the Baboon whiskers, the Man’s hat, and some lines in the ground of the Airport image. Therefore, depending on the application, there must be a trade-off between the desired compression ratio and the quality of the resultant decompressed image.

Fig. 1

Fractal image compression with quadtree partition using large images. Original images (first row). Resultant quadtree partitions and decompressed images with $\texttt {tol}=20$ (second and third rows). Resultant quadtree partitions and decompressed images with $\texttt {tol}=5$ (fourth and fifth rows)

Table 3 Processing time (seconds), number of bits of information stored per pixel (bpp), and quality measures for our FICQP implementation using the $D_3$ library and large images in the server

Table 4 shows the processing time in seconds of our sequential and parallel implementations using the multi-core CPU (from 2C to 24C), and the GPU with ST and a different number of TPB (from 32 to 512) for large images, with $\texttt {tol}=20$ and $\texttt {tol}=5$. We fix the parameters $\texttt {min\_d}=4$, $\texttt {max\_d}=8$, and we use the $D_3$ library. With these processing times, we compute the speedups shown in Fig. 2. The processing times with $\texttt {tol}=20$ are smaller than with $\texttt {tol}=5$ due to that there are a fewer number of ranges in the quadtree partition (see Fig. 1). Note that the speedup is higher when there are a bigger number of ranges in the quadtree partition. When $\texttt {tol}=20$, the processing times and speedups using the multi-core CPU with 24C are better than those obtained using GPU with ST, ST-32, and ST-128. However, when we use the GPU with ST-512 for the Airport image, we obtain a speedup of $10.43 \times$, which is better than the speedup of $9.53 \times$ obtained by the multi-core CPU. On the other hand, when $\texttt {tol}=5$, the processing times and speedups using the GPU with ST are better than those obtained using multi-core CPU with 2C; this behavior is noted with the processing times of ST-32, ST-128, and ST-512 compared with the 8C, 12C, and 24C, respectively. The best processing times and speedups are reached with the GPU ST-512, obtaining a speedup of $24.45 \times$ for the Baboon image.

Table 4 Processing time in seconds of our sequential and parallel implementations in the server, using the $D_3$ library for large images

Fig. 2

Evaluation of speedups of our FICQP implementation, using the multi-core CPU (from 2C to 24C), and the GPU with streams and a different number of TPB (from 32 to 512) in the server: a with $\texttt {tol}=20$; b with $\texttt {tol}=5$

6 Conclusions

In this paper, we presented new parallel implementations of fractal image compression using quadtree partition, with task parallelism over a multi-core CPU and dynamic parallelism over a GPU. We presented the compression and decompression results from standard images of $256\times 256$, $512\times 512$, and $1024\times 1024$ pixels, considering the processing time, number of bits of information stored per pixel, and two quality measures.

The parallel implementation based on dynamic parallelism outperforms the speedup of the task parallelism, reaching the best speedups with our GPU ST-512 version. The best speedup with multi-core is approximately $15 \times$, while with the GPU, the best speedup is approximately $25 \times$. We observed that the speedup of our parallel implementations is higher when the quadtree partition has more small squares than bigger. The GPU implementation was improved by launching a set of threads per block inside each stream assigned to a recursive kernel function to parallelize the comparisons between a range and a set of domains.

We plan to apply and adapt these parallel implementations to compress color images and video as future work.