Introduction

The application of the RMIS greatly improves the surgical OR efficiency, enabling minimally invasive surgery to be more dexterous and beneficial for improving surgeon performance [1]. Future research will focus on the semi-autonomous and autonomous surgery [2, 3], and the surgical intelligence is still a challenging problem in surgical OR, especially for some critical sub-tasks such as suturing and cutting [4,5,6]. Normally, the hand–eye calibration links the kinematics information and the vision information between robot slave arm and the laparoscope system. This relationship forms the basis for incorporating more significant components such as multi-model data to enhance the surgical intelligence and improve the surgical OR efficiency [7,8,9].

In the typical hand–eye calibration problem, conventional solution estimates the hand–eye relationship by using a calibration object. The geometry parameters of calibration object are taken as known conditions to solve hand–eye calibration equation. Mathematically speaking, the hand–eye calibration problem can be represented as AX = XB [10]. There are extensive solutions to solve the hand–eye calibration separately, and the rotation and translation components are estimated individually [11, 12]. For another approach, there are some studies to solve the AX = XB problem simultaneously [13, 14]. Some recent works further study the hand–eye calibration algorithms for the RMIS scenario [15,16,17,18]. However, for the typical configuration of the minimally invasive surgical robot system, the hand–eye calibration for RMIS is still a challenging problem, the traditional hand–eye calibration methods directly applied to the RMIS are not applicable in practice, the hand–eye calibration must be carried out before the surgery, and placing external calibration object is not possible in the abdominal environment. In addition, due to the movement of robot slave arm, the hand–eye calibration must be executed to adapt to the changes of hand–eye transformation. This progress will disturb the normal surgical workflow and reduce the efficiency of surgical OR. Furthermore, the typically RCM constraint of minimally invasive surgical robot limits the motion range of the hand–eye calibration, which lower the calibration accuracy [19]. To cope this problem, some researchers study the structure-from-motion (SFM) method to realize the hand–eye calibration, and this approach may be appropriate for this requirement [20]. However, the typical configuration of surgical robot will lead to insufficient viewpoints. According to the literature [10, 21], hand–eye calibration without the calibration object relies purely on surgical instrument already in the RMIS scenario is attractive, the method can solve this problem efficiently. In [21], the authors estimate the hand–eye transformation by surgical instrument tracking. However, this approach requires accurate 3D surgical instrument pose tracking to form the basis for accurate hand–eye calibration. It may be difficult to obtain the appropriate surgical instrument detection and pose estimation.

To cope this challenge, in this paper, we demonstrate a novel hand–eye calibration algorithm to link the laparoscope information and the kinematics information. The proposed method does not need accurate high-level 3D pose surgical tracking. We acquire the line feature of the surgical instrument to realize the hand–eye calibration. We enhance the calibration algorithm through stereo laparoscope system [22,23,24]. Our hand–eye calibration algorithm is inspired by [16, 25]. In view of the surgical intelligence, the proposed method explores the minimal and practical minimally invasive surgical robot system in the surgical OR. Promising evaluations are conducted through simulation and experimental surgical robot system.

Method

Consider the RMIS configuration shown in Fig. 1, the mission is to estimate the transformation from the laparoscope frame \( F_{\text{Camera}} \) to robot laparoscope slave arm end-effector frame \( F_{\text{arm}} \). The minimally invasive surgical robot system mainly contains robot instrument slave arm and robot laparoscope slave arm. In our case, the base frames of two slave arms locate at one base, and the base frame is set as \( F_{\text{base}} \). The RCM point frame on the robot instrument arm is set as \( F_{\text{RCM}} \). Typically speaking, the slave arms are all moved with RCM constraint. The RCM point is located at trocar point on the abdomen of patient.

Fig. 1
figure 1

Geometric schematic for proposed hand–eye calibration algorithm. a The relative transformation of each frame. b Geometric model of right camera for hand–eye calibration

Full size image

We set the reference plane according to the optic origin point and the surgical instrument axis. A novel redundant constraint based on the stereo laparoscope configuration is proposed to enhance the algorithm. The normal vector of the reference plane can be calculated as Eqs. 1 and 2, \( V_{\text{l}} (i) \) and \( V_{\text{r}} (i) \) denote the left and right reference plane, respectively, and i denotes the number of motion, as shown in Fig. 1.

$$ V_{\text{l}} (i) = P_{{M\_{\text{l}}}} (i) \times P_{{N\_{\text{l}}}} (i) $$
(1)
$$ V_{\text{r}} (i) = P_{{M\_{\text{r}}}} (i) \times P_{{N\_{\text{r}}}} (i) $$
(2)

In Eqs. 1 and 2, we set the projection points in the image plane of stereo laparoscope from arbitrary points on the surgical instrument. \( P_{{M\_{\text{l}}}} = \left[ {M_{{{\text{l}}x}} ,M_{{{\text{l}}y}} ,M_{{{\text{l}}z}} } \right]^{T} \) and \( P_{{N\_{\text{l}}}} = \left[ {N_{{{\text{l}}x}} ,N_{{{\text{l}}y}} ,N_{{{\text{l}}z}} } \right]^{T} \) denote the projection points on the left camera, and \( P_{{M\_{\text{r}}}} = \left[ {M_{{{\text{r}}x}} ,M_{{{\text{r}}y}} ,M_{{{\text{r}}z}} } \right]^{T} \), \( P_{{N\_{\text{r}}}} = \left[ {N_{{{\text{r}}x}} ,N_{{{\text{r}}y}} ,N_{{{\text{r}}z}} } \right]^{T} \) denote the projection points on the right camera. Geometrically speaking, we can conclude that \( M_{{{\text{l}}z}} = N_{{{\text{l}}z}} = f_{\text{l}} \), \( M_{{{\text{r}}z}} = N_{{{\text{r}}z}} = f_{\text{r}} \), and fl and fr are the focal length of two cameras.

The target estimated right camera hand–eye calibration transformation is set as X, as shown in Eq. 3. The target estimated right camera hand–eye calibration transformation with redundant constraint based on left camera is set as Y. In this paper, in view of the stereo laparoscope, we take the right camera’s hand–eye calibration process as an example to illustrate algorithm.

$$ X = {}_{\text{arm}}^{{{\text{Camera}}R}} T = \left[ {\begin{array}{*{20}l} {R_{X} } \hfill &\quad {t_{X} } \hfill \\ 0 \hfill &\quad 1 \hfill \\ \end{array} } \right],\quad Y = {}_{\text{arm}}^{{{\text{Camera}}R}} T_{Y} = \left[ {\begin{array}{*{20}l} {R_{Y} } \hfill &\quad {t_{Y} } \hfill \\ 0 \hfill &\quad 1 \hfill \\ \end{array} } \right] $$
(3)

The transformation between robot laparoscope slave arm and RCM point on the robot instrument slave arm is shown as Eq. 4. Here, thanks to the typical structure of minimally invasive surgical robot and the minimally invasive surgery scenario, RCM point is fixed at the trocar point on the abdomen of patient. We set RCM frame on the RCM point, and the instrument always goes through this RCM point. The transformation is set as N motions, the relationship can be obtained from the forward kinematics provided by the joint encoders and DH parameters, and the joint positions of robot instrument arm and robot laparoscope arm are set as N motions, respectively.

$$ T_{A} (i) = {}_{\text{base}}^{\text{arm}} T(i){}_{\text{RCM}}^{\text{base}} T(i) = \left[ {\begin{array}{*{20}l} {R_{A} (i)} \hfill & \quad{R_{A} (i)} \hfill \\ 0 \hfill & \quad 1 \hfill \\ \end{array} } \right] $$
(4)

The transformation relationship between left and right camera of laparoscope is shown as Eq. 5. The relationship can be determined by a pre-calibration procedure.

$$ {}_{\text{r}}^{\text{l}} T = \left[ {\begin{array}{*{20}l} {R_{Z} } \hfill &\quad {t_{Z} } \hfill \\ 0 \hfill & \quad1 \hfill \\ \end{array} } \right] $$
(5)

In view of the configuration of surgical instrument, the instrument always goes through the RCM point. Geometrically speaking, the surgical instrument axis is always located on the reference plane, and the direction vector of the surgical instrument axis is always perpendicular to the normal vector of reference plane. We model the relationship as shown in Eq. 6:

$$ V_{\text{r}}^{T} (i)R_{X} R_{A} (i)V_{S} (i) = 0 $$
(6)

where \( V_{S} (i) \) denotes the direction of surgical instrument axis. Then, we add the redundant constraint to enhance the calibration accuracy. The stereo laparoscope has two cameras with rigidly transformation. The hand–eye transformation of right camera can be represented by the left camera projection model, as shown in Eq. 7:

$$ V_{\text{l}}^{T} (i)R_{Z} R_{Y} R_{A} (i)V_{S} (i) = 0 $$
(7)

We set the relationship as shown in Eq. 8. Equation 7 can be rearranged to Eq. 9. Two equations can be solved with the same method. We propose a two-step method for right camera as follows:

$$ V_{\text{lr}}^{T} (i) = V_{\text{l}}^{T} (i)R_{Z} $$
(8)
$$ V_{\text{lr}}^{T} (i)R_{Y} R_{A} (i)V_{S} (i) = 0 $$
(9)

For the first step, we can obtain the estimated rotation component of right camera hand–eye transformation for initialization. In this case, to solve Eqs. 6 and 9, according to [12], we introduce the Kronecker product to rearrange the equation as:

$$ \left( {\left( {R_{A} (i)V_{S} (i)} \right)^{T} \otimes V_{\text{r}}^{T} (i)} \right){\text{vec}}R_{X} = 0 $$
(10)
$$ \left( {\left( {R_{A} (i)V_{S} (i)} \right)^{T} \otimes V_{\text{lr}}^{T} (i)} \right){\text{vec}}R_{Y} = 0 $$
(11)

Then, we can solve Eqs. 10 and 11 through Eqs. 12 and 13 [12, 26]. Equation 12 denotes the estimated value according to the right camera, and Eq. 13 denotes the redundant constraint estimated value according to the left camera.

$$ \mathop {\arg \hbox{min} }\limits_{{{\text{vec}}V_{X} \in {\mathbb{R}}^{9} }} \sum\limits_{i} {\left\| {\left( {\left( {R_{A} (i)V_{S} (i)} \right)^{T} \otimes V_{r}^{T} (i)} \right){\text{vec}}V_{X} } \right\|_{2}^{2} } ,\quad R_{X} = \frac{{{\text{sign}}\left( {\det (V_{X} )} \right)}}{{\left| {\det (V_{X} )} \right|^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} }}V_{X} $$
(12)
$$ \mathop {\arg \hbox{min} }\limits_{{{\text{vec}}V_{Y} \in {\mathbb{R}}^{9} }} \sum\limits_{i} {\left\| {\left( {\left( {R_{A} (i)V_{S} (i)} \right)^{T} \otimes V_{\text{lr}}^{T} (i)} \right){\text{vec}}V_{Y} } \right\|_{2}^{2} } ,\quad R_{Y} = \frac{{{\text{sign}}\left( {\det (V_{Y} )} \right)}}{{\left| {\det (V_{Y} )} \right|^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} }}V_{Y} $$
(13)

After the first step initialization, we adopt the nonlinear optimization method to refine the rotation component. According to [13, 25], the unit quaternion q and q0 correspond to RX and RY, respectively. \( \tilde{q} \) and \( \tilde{q}_{0} \) denote the conjugate of q and q0. We can arrange Eqs. 7 and 9 as:

$$ \begin{aligned} \left\| {V_{\text{r}}^{T} (i)R_{X} R_{A} (i)V_{S} (i)} \right\|_{2}^{2} & = \left\| {v_{{{\text{r}}i}} \cdot \left( {qv_{Si} \tilde{q}} \right)} \right\|_{2}^{2} \left\| q \right\|_{2}^{2} \\ & = \left\| {\left( {v_{{{\text{r}}i}} q} \right) \cdot \left( {qv_{Si} } \right)} \right\|_{2}^{2} = \left\| {q^{T} V_{{{\text{r}}i}}^{T} V_{Si} q} \right\|_{2}^{2} \\&= \left\| {q^{T} K_{X} q} \right\|_{2}^{2} \end{aligned} $$
(14)
$$ \begin{aligned} \left\| {V_{\text{lr}}^{T} (i)R_{Y} R_{A} (i)V_{S} (i)} \right\|_{2}^{2} & = \left\| {v_{{{\text{lr}}i}} \cdot \left( {q_{0} v_{Si} \tilde{q}_{0} } \right)} \right\|_{2}^{2} \left\| {q_{0} } \right\|_{2}^{2} \\ & = \left\| {\left( {v_{{{\text{lr}}i}} q_{0} } \right) \cdot \left( {q_{0} v_{Si} } \right)} \right\|_{2}^{2} = \left\| {q_{0}^{T} V_{{{\text{lr}}i}}^{T} V_{Si} q_{0} } \right\|_{2}^{2} \\&= \left\| {q_{0}^{T} K_{Y} q_{0} } \right\|_{2}^{2} \end{aligned} $$
(15)

Here, the definition of Vri, Vlri and VSi can be found in [13]. In addition, we can define the parameters in the equations as:

$$ v_{{{\text{r}}i}} = \left( {0,V_{\text{r}}^{T} (i)} \right),\;v_{Si} = \left( {0,R_{A} (i)V_{S} (i)} \right),\;v_{{{\text{lr}}i}} = \left( {0,V_{\text{lr}}^{T} (i)} \right),\;K_{X} = V_{\text{ri}}^{T} V_{Si} ,\;K_{Y} = V_{{{\text{lr}}i}}^{T} V_{Si} $$

Then, we can obtain rotation component of right camera hand–eye transformation by solving Eqs. 16 and 17. Equation 16 denotes the estimated value according to the right camera, and Eq. 17 denotes the redundant constraint estimated value according to the left camera.

$$ \mathop {\arg \hbox{min} }\limits_{{R_{X} \in {\text{SO}}(3)}} \sum\limits_{i} {\left\| {V_{\text{r}} (i)R_{X} R_{A} (i)V_{S} (i)} \right\|_{2}^{2} } = \mathop {\arg \hbox{min} }\limits_{{q \in {\text{SU}}(2)}} \sum\limits_{i} {\left\| {q^{T} K_{X} q} \right\|_{2}^{2} } $$
(16)
$$ \mathop {\arg \hbox{min} }\limits_{{R_{Y} \in {\text{SO}}(3)}} \sum\limits_{i} {\left\| {V_{\text{lr}} (i)R_{Y} R_{A} (i)V_{S} (i)} \right\|_{2}^{2} } = \mathop {\arg \hbox{min} }\limits_{{q_{0} \in {\text{SU}}(2)}} \sum\limits_{i} {\left\| {q_{0}^{T} K_{Y} q_{0} } \right\|_{2}^{2} } $$
(17)

As for the translation component of hand–eye transformation, we also construct the geometric model as follows. Geometrically speaking, the surgical instrument axis is always located on the reference plane, even though the RCM point is not visible in the laparoscope image plane, the origin of the RCM frame is always in the reference plane. Thanks to this geometry relationship, we can model the relationship as shown in Eqs. 18 and 19:

$$ \left[ \begin{aligned} V_{\text{r}} (i) \hfill \\ 1 \hfill \\ \end{aligned} \right]^{T} X\left[ \begin{aligned} t_{A} (i) \hfill \\ 1 \hfill \\ \end{aligned} \right] = 1 $$
(18)
$$ \left[ \begin{aligned} V_{\text{l}} (i) \hfill \\ 1 \hfill \\ \end{aligned} \right]^{T} {}_{\text{r}}^{\text{l}} TX\left[ \begin{aligned} t_{A} (i) \hfill \\ 1 \hfill \\ \end{aligned} \right] = 1 $$
(19)

Then, the hand–eye transformation of right camera can be represented by the left camera projection model, as shown in Eqs. 20 and 21:

$$ V_{\text{r}}^{T} (i)R_{X} t_{A} (i) + V_{\text{r}}^{T} (i)t_{X} = 0 $$
(20)
$$ V_{\text{l}}^{T} (i)R_{Z} R_{Y} t_{A} (i) + V_{\text{l}}^{T} (i)R_{Z} t_{Y} + V_{\text{l}}^{T} (i)t_{Z} = 0 $$
(21)

Then, we can obtain the translation component of right camera hand–eye transformation by solving Eqs. 22 and 23. Equation 22 denotes the estimated value according to the right camera, and Eq. 23 denotes the redundant constraint estimated value according to the left camera.

$$ \mathop {\arg \hbox{min} }\limits_{{t_{X} \in {\mathbb{R}}^{3} }} \sum\limits_{i} {\left\| {V_{i} R_{X} t_{A} (i) + V_{i} t_{X} } \right\|_{2}^{2} } $$
(22)
$$ \mathop {\arg \hbox{min} }\limits_{{t_{Y} \in {\mathbb{R}}^{3} }} \sum\limits_{i} {\left\| {V_{\text{l}}^{T} (i)R_{Z} R_{Y} t_{A} (i) + V_{\text{l}}^{T} (i)R_{Z} t_{Y} + V_{\text{l}}^{T} (i)t_{Z} } \right\|_{2}^{2} } $$
(23)

The final stage in estimating hand–eye transformation is to average the left and right camera calibration results according to [21]. To sum up, the algorithm is shown in Algorithm 1.

figure a

Experimental and simulation results

Simulation study

In this section, synthetic data are generated by MATLAB (MathWorks Inc.). The experiments are run on a 4.2 GHz Intel Core i7-7700 k workstation with 32 GB RAM. The overall algorithm takes the processor around 1 s with 343 motion configurations. The minimally invasive surgical robot developed by our laboratory is used to construct the simulated robot model [27], as shown in Fig. 4. Inspired by [25], we use the 3D visualizer Rviz to make scenario visualization. The method guarantees that the surgical instrument is always visible in the laparoscope image plane. The motion of minimally invasive surgical robot, the reference axis of surgical instrument and the RCM point can be linked to the Rviz environment. The motion range is around 20 mm in translation and the 10 degree in rotation. In this simulation, we generate the ground truth of hand–eye transformation according to the simulated robot model along with random robot pose of two slave arms. Then, we can calculate the reference plane and the reference axis from the robot pose transformation and the ground-truth transformation. Before the transformations are input to hand–eye calibration algorithm, they are corrupted by the noise according to [26]. Finally, the estimated hand–eye transformation can be calculated and compared with the ground truth. We define the error of translation and rotation components in hand–eye transformation. The translation error is defined as the norm of the difference between calculated value and ground-truth value \( \theta_{t} = \left\| {t_{G} - t_{X} } \right\| \). The rotation error is defined as \( \theta_{\omega } = \left\| {{\text{Ro}}\left( {\omega_{G} \omega_{X}^{ - 1} } \right)} \right\| \), and \( {\text{Ro}}\left( {} \right) \) denotes the Rodrigues' function. The code and the robot model of our implementation for the work will naturally be made available in the future for further research (https://github.com/hitersyw/hand-eye).

The performance of the algorithm with synthetic data is shown in Fig. 2. We start by displaying the comparison between using monocular information and stereoscopic constraint. Later, we use the synthetic simulation to explore how increasing Gaussian noise affects the performance of algorithm. We first evaluate the noise with a constant step size added to the robot kinematics, and then, we add the noise to both the laparoscope and the robot kinematics. Last, we add the noise to the laparoscope, kinematics and the transformation between left and right camera of stereo laparoscope system. The noise is the zero-mean Gaussian noise, and the value of abscissa in Fig. 2 denotes the noise coefficients. In the RMIS hand–eye calibration scenario, the noise in laparoscope, kinematics and extrinsic stereo laparoscope calibration is the most fit condition. Furthermore, we set the motion configurations as large as possible to lower the influence of motion configuration, and the number of motions is set as 1728. We repeat each synthetic parameter for 100 trials. The results we display show that the estimated error increases with increasing Gaussian noise. Moreover, we can conclude that the proposed redundant stereo laparoscope constraint is efficient in view of improving the calibration accuracy and stability against error with respect to the same simulation conditions.

Fig. 2
figure 2

Performance of the algorithm with synthetic data. a, b The rotation and translation error with increasing noise in robot motion. c, d The rotation and translation error with increasing noise in robot motion and laparoscope. e, f The rotation and translation error with increasing noise in robot motion, laparoscope and stereo configuration

Full size image

Finally, the simulation is done by checking how algorithm performs under varying number of motions, and the performance of algorithm with synthetic data is shown in Fig. 3. In our minimally invasive surgical robot model, the active joints of surgical instruments and laparoscope are used to realize the RCM constraint and perform intra-operative task, and there are three joints for two types of slave arm. Thus, the motion configurations can be obtained as \( M_{L}^{3} \times M_{I}^{3} \) [25], and the \( M_{L} \) and \( M_{I} \) are set as the position conditions for each joint. Later, we can obtain varying motion configurations as shown in the abscissa values of Fig. 3. In the simulation, we inject the noise to robot motion, laparoscope and the stereo configuration as a constant value, including noise coefficients 1 mm in translation and 1 degree in rotation, and these values are the middle value of previous experiment. The simulation results output that calibration error decreases with increasing motion configurations. After the motion configurations are increased to a certain degree, the accuracy no longer refines significantly, and the curve tends to be flat. Obviously, the motion configurations workload of this method is larger compared to the state-of-art method. But from the perspective of the RMIS scenario, this way of sacrificing workload to remove the dependency on the calibration object is somewhat desirable. It is true that future work in this article can be studied from this perspective.

Fig. 3
figure 3

Performance of the algorithm with synthetic data with increasing motion configurations. a Estimated rotation error. b Estimated translation error

Full size image

Experimental results

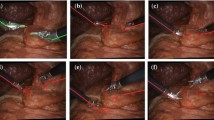
In this section, the minimally invasive surgical robot system developed by our laboratory is used to implement the evaluation, as shown in Fig. 4. The Storz 3D laparoscope system is attached to end-effector of robot laparoscope slave arm. The minimally invasive surgical robot system has two slave arms to hold the surgical instrument, and we only use one robot instrument slave arm to realize the hand–eye calibration. In the robot experiments, ground truth cannot be accurately obtained. We evaluate the performance of hand–eye calibration by measuring the reprojection error of a known point inspired by [15, 16]. The head point [7, 9] on the surgical instrument is chosen as the tracked point, in this case, in view of the instrument structure and the literature, the claspers rotate together around the same axis, we set the point on this axis as head point, and the forward kinematics of head point can be calculated according to the DH parameters. Then, the head point is projected to the image plane of laparoscope with the estimated hand–eye transformation. The reprojection error in pixels can be obtained according to the projected image coordinate and on-screen locations. The computation time is not explored as the calibration can be executed offline in the preoperative procedure of surgical OR. The calibration is executed before the surgical operation, but in this case, surgical instrument and laparoscope have been placed in the abdomen of patient. According to Refs. [15, 21], the challenging problem of hand–eye calibration in the RMIS scenario is to prevent affecting the normal workflow while in view of changing the laparoscope and surgical instrument. The proposed method removes the need that pull out the laparoscope from abdomen to conduct hand–eye calibration. The proposed method without conventional calibration target also provides potential for autonomous hand–eye calibration [21].

Fig. 4
figure 4

a Experimental setup. b Example scenario of the laparoscope. The blue line demonstrates the detection axis of surgical instrument

Full size image

As the focus of this paper is not to develop surgical instrument line feature detection algorithms, we do not explore the line detection algorithm deeply. We employ the simple method to verify our idea that implements hand–eye calibration with the surgical tool axis line feature. The detection method is applied according to the computer vision technology [29, 30]. In the simulation RMIS scenario and vivo environment, the background mainly consists of the tissue and organ, and the main color of the scene is red. On the contrast, the surgical instrument of our robot system is made by carbon fiber, and the main color is black. The area of the surgical instrument can be segmented between the two colors [28]. The line feature information of the surgical instrument can be obtained by feature extraction of the region after segmentation. The experimental scenario is shown in Fig. 4b.

We evaluate our approach with increasing number of motions to test the performance. We execute the experiment with the 1728 motions to get as more data as possible only used for indicating the trend, and this value may not be reached in practical applications. During the experiment, we move the robots randomly within robot work space to obtain the relative surgical instrument positions and orientations, and record the joint encoder data to obtain the kinematics. Meanwhile, the surgical instrument information in the camera coordinate was also derived from the stereo image. We repeat each motion configuration for 20 trials. To calculate the pixel error for each trial, 15 data sets with different motions of surgical instrument are captured, and the average pixel error of head point is acquired as the pixel error for each trial. The experimental performance is outlined in Fig. 5. The results demonstrate that projection error decreases with increasing motion configurations, which is in line with simulation results. Analysis of the experimental results shows that calibration error mainly contains the following components. To evaluate the hand–eye calibration, we construct the relationship between camera and the target point, and the inaccurate laparoscope intrinsic calibration and the inaccuracy of forward kinematics will output an inaccurate image coordinate projection. The measured on-screen locations may also contain the error. Obviously, the system model error is the same as the simulation conditions, and the noise in robot model and camera model and camera calibration, lead to the calibration error. Furthermore, the line feature projection error of surgical instrument axis may also contribute to the calibration inaccuracy.

Fig. 5
figure 5

Performance of the re-projection error with increasing motion configurations

Full size image

We compare the estimated results between our proposed method and the ATA hand–eye approach with custom sterile calibration grid [26]. From the previous study, we can see that the curve tends to be flat with increasing motions, and we try to choose a small number when the curve becomes flat to reduce the workload of the experimental process. Therefore, the number of motion configurations is set as 343. For the ATA method, we choose 12 motions according to the literature. The proposed method and state-of-the-art method are validated by measuring the reprojection error. We totally carry out 6 experiments and report the quantitative analysis in Fig. 6. In each experiment, we repeat 10 trials for each method. To calculate the reprojection error, 15 data sets with different motions of surgical instrument are captured, and the average pixel error of head point is acquired as the pixel error for each trial. The error of our algorithm is set as Error 1, and the state-of-art method reprojection error is set as Error 2. We can find that the reprojection error of proposed method is a little lower than the traditional hand–eye calibration method, and the gap between two methods is small. The results agree with [21, 26]. The performance of comparative experiment demonstrates the efficiency of our method, while removing the need for calibration grid, providing the practical application in RMIS scenario. Furthermore, the proposed method using line feature lowers the requirement of surgical instrument tracking of the literature. Normally, the method in [21] requires accurate 3D pose tracking using priori knowledge of 3D model to form the basis for accurate hand–eye calibration. In our proposed method, we just use the line feature as calibration object. In the future, it will be significant to explore the reliability and accuracy of surgical instrument axis line detection algorithm. The robust and accurate detection algorithms can make our proposed algorithm resilient to the RMIS scenario clutters.

Fig. 6
figure 6

Comparative experiment results

Full size image

Conclusion

In this paper, we have proposed a vision-based hand–eye calibration for minimally invasive surgical robot. This work, to the best of our knowledge, represents a novel attempt to perform a practical hand–eye calibration without the custom calibration grid based on the geometry model in the RMIS scenario. This level of hand–eye calibration for the RMIS is broadly unexplored, and the approach and the proposed method can be extended to handle even more accurate hand–eye calibration by incorporating additional mathematically model. In our algorithm, the geometry model of surgical instrument is first adopted to construct the reference plane and the reference axis, and typically, RCM configuration of the minimally invasive surgical robot is used as the geometry constraint. Moreover, a novel redundant constraint based on the stereo laparoscope configuration is adopted to improve the calibration accuracy and stability against error. The proposed approach has been evaluated by the simulation and robot experiments. The performance of our experiments demonstrates that our approach can exhibit hand–eye calibration without calibration object.