Introduction

Precise detection and identification of individual spine structures, e.g., the vertebrae and inter-vertebral discs, provide anatomical benchmarks that facilitate the evaluation and reporting of frequent inter-vertebral disc deformities such as protrusion [1]. Performing spine labeling manually is tedious and time-consuming, more so when the number of images in a spine series is large as is the case in magnetic resonance imaging (MRI),Footnote 1 which is the best modality to assess disc disorders [1]. MRI scans depict soft-tissue structures, thereby allowing characterization/quantification of disc bulges and protrusions. Automating or semi-automating spine labeling in MRI can reduce significantly the amount of user inputs, allowing thorough, reproducible and fast diagnosis of various spine diseases. This computational problem has recently attracted significant research attention [2,3,4,5,6,7,8,9,10,11,12,13,14]. In addition to their usefulness in spine diagnosis, such anatomical labels yield a natural patient-specific coordinate system that can be very useful in (i) mapping radiology reports to the corresponding image segments, (ii) building semantic inspection tools, and (iii) facilitating significantly other difficult spine image processing tasks. Indeed, such labeling techniques can guide image registration and fusion [15], and provide priors/constraints for image segmentation, retrieval, as well as shape and population analysis. For instance, several recent spine segmentation methods rely on a given labeling as input [16], or add a labeling process as a part of a segmentation algorithm [3]. Unfortunately, and as acknowledged by several studies [7, 8, 10], automating spine labeling is a difficult computational problem for several reasons:

  • The intensity appearances of the structures of interest change significantly with the modality and acquisition protocol;

  • There are wide variations in the positions, sizes and shapes of the spine, vertebrae and discs;

  • The number of visible vertebrae and discs can vary from one image to another; and

  • It is difficult to distinguish between individual spine structures because of their repetitive nature and similar appearances/shapes.

Prior art

Most of the existing algorithms require intensive and time consuming training from a large, manually-labeled data set (e.g., [5, 7,8,9,10,11]), with the results often being dependent on (i) the choice of a specific training set and (ii) the choice of modality, image type and acquisition protocol. The purpose of such training phase is to build priors on the shapes/appearances of spine structures and their interconnections. These priors are subsequently embedded within a classification or regression technique using, for instance, deep convolution networks [5], graphical models [7, 13, 17], adaptive-boosting learning [8, 14], support vector machines [11], random forest regression [9], or generative probabilistic models [10], among others. Although they can yield exceptional performance in cases similar to the training set, training-based algorithms may have difficulty in capturing the substantial variations encountered in a clinical context. For instance, the existing excellent algorithms that were recently designed for CT (e.g., [7, 12, 13]) are not directly applicable to MRI [8], mainly because of the significant differences in appearances between these two modalities. In MRI, the difficulties are compounded by the intensity similarities and weak edges between different structures in the same spine image, abundant noise and significant variations in appearances and resolutions from one image to another. Such large variability also results from numerous types of MRI sequences (e.g., T1-weighted, T2-weighted, PD, etc.) and acquisition protocols. For instance, an algorithm designed and trained on T2-weighted MR data (e.g., [10]) may not be applicable to T1-weighted MR images. Moreover, training-based geometric models may not properly capture unseen (or pathological) cases outside the range of geometric characteristics learned from the training set. For instance, in [10], the authors embedded training-based information on the geometric interactions between pairs of discs, enforcing the distance between neighboring discs to fall within a range learned a priori from the training set. Therefore, a pathological case, which does not necessarily conform to these learned distances, may not be labeled correctly.

Summary of contributions

In this study, we propose an efficient (nearly real-time) two-stage spine MRI labeling algorithm that removes the need for an external training while being applicable to different types of MRI data. Based solely on the current image data, the first stage aims at detecting potential vertebra candidates following the optimization of a segmentation functional containing two terms: (i) a distribution-matching term encoding contextual information about the vertebrae via a density model learned from a very simple user input, which amounts to a point (mouse click) on a predefined vertebra; and (ii) a regularization constraint, which penalizes isolated candidates in the solution. The second stage removes false positives and identifies all vertebra and discs by optimizing a geometric constraint, which embeds generic anatomical information on the interconnections between neighboring spine structures. Based on generic knowledge, our geometric constraint does not require external training. We performed quantitative evaluations of the algorithm over a data set of 90 mid-sagittal MRI images of the lumbar spine acquired from 45 different subjects. To assess the flexibility of the algorithm, we used both T1- and T2-weighted images for each subject. A total number of 990 structures were automatically detected/labeled and compared to ground-truth annotations by a radiology expert. On the T2-weighted data, we obtained an accuracy of \(91.6\%\) for the vertebrae and \(89.2\%\) for the discs. On the T1-weighted data, we obtained an accuracy of \(90.7\%\) for the vertebrae and \(88.1\%\) for the discs.

Formulation

Regularized distribution matching functional

Let \(\mathbf {D}: \varOmega \subset \mathbb {R}^2 \rightarrow {\mathcal {F}} \subset \mathbb {R}^k\) be a function defined over spatial image domain \(\varOmega \), and whose values are in a finite set \({\mathcal {F}}\) containing k-dimensional features (or bins). For each point \(\mathbf {x}\in \varOmega \), we build a feature vector \(\mathbf {D}(\mathbf {x}) = [D_1(\mathbf {x}) \ldots D_k(\mathbf {x})]\) that contains image statistics within several box-shaped image patches of different orientations/scales. Such patch-based features can encode contextual information about the vertebrae and their neighboring structures, e.g., size, shape, orientation and geometric relationships with neighboring structures. The purpose of this stage of our method is to detect potential vertebra candidates via a regularized distribution matching approach. Let \(u: \varOmega \rightarrow \{0,1\}\) denotes a binary pixel classifier function, which defines a variable partition of \(\varOmega \): \(\{\mathbf {x}\in \varOmega / u(\mathbf {x})=1 \}\), corresponding to the classification (or segmentation) region containing the vertebra candidates, and its complement \(\{\mathbf {x}\in \varOmega / u(\mathbf {x})=0 \}\), corresponding to non-vertebra pixels in \(\varOmega \). We optimize the following functional with respect to u, which yields an initial two-region classification of the image domain:

$$\begin{aligned} E(u) = \underbrace{-\sum _{f \in {\mathcal {F}}} \sqrt{\mathbf {P}_{u}(f){\mathcal {M}}(f)}}_\mathrm{Contextual~Distribution~matching} + \underbrace{\lambda \int _{\varOmega } \Vert \nabla u\Vert d\mathbf {x}}_\mathrm{Regularization} \end{aligned}$$
(1)

In the following, we describe each of the variables and notations that appear in the regularized classification problem in (1):

  • The regularization term is a standard total-variation (TV) penalty [18], which encourages the solution to be smooth. In the case of a discrete characteristic function u of a given set, the total variation of u is the perimeter of the set [18]. This term penalizes solutions with a large number of very small isolated regions. This facilitates inference in the next step, and keeps only strong vertebral candidates in the solution.

  • \(\mathbf {P}_{u}\) is the kernel density estimate (KDE) of the distribution of features \(\mathbf {D}\) within the vertebral class (region) defined by \(\{\mathbf {x}\in \varOmega / u(\mathbf {x})=1 \}\):

    $$\begin{aligned} \mathbf {P}_{u}(f) = \frac{\int _{\varOmega }u K(\mathbf {D}-f) d\mathbf {x}}{\int _{\varOmega } u \hbox {d}\mathbf {x}} \end{aligned}$$
    (2)

    and K is the Gaussian kernel given by:

    $$\begin{aligned} K(t)=\frac{1}{(2\pi \sigma ^{2})^{\frac{k}{2}}} \exp ^{-\frac{\Vert t\Vert ^{2}}{2\sigma ^{2}}} \end{aligned}$$
    (3)

    with \(\sigma \) the width of the kernel.

  • The first term in (1) is the negative Bhattacharyya coefficient, which evaluates the similarity (or affinity) between two distributions (or densities). The lower the value of this coefficient, the better the affinity between the distributions: the range of the distribution matching term is \([-1, 0]\), with \(-1\) indicating a perfect match between the densities and 0 corresponding to a total mismatch. The Bhattacharyya coefficient is very popular in statistics for evaluating the affinity between densities, and it has the following geometric interpretation: it corresponds to the cosine of the angle between the unit vectors \((\sqrt{\mathbf {P}_{u} (f)}, f \in {\mathcal {F}})^T\) and \((\sqrt{{\mathcal {M}}(f)}, f \in {\mathcal {F}})^T\). Therefore, it considers explicitly \(\mathbf {P}_{u}\) and \({\mathcal {M}}\) as distributions by representing them on the unit hypersphere.

    Minimization of this term aims at finding a classification region whose contextual-feature distribution most closely matches a model distribution \({\mathcal {M}}\). The latter can be either estimated interactively from a very simple user input placed on one of the images within a spine MRI series, or learned a priori from training data (i.e., a set of expert-labeled images different from the testing data set). In particular, our model is convenient in practice when we do not have a large set of relevant training images. As we will see later in the experiments, regularized classifier (1) does not require an intensive external learning of \({\mathcal {M}}\) to yield satisfying performances. We can estimate \({\mathcal {M}}\) from the feature vectors within a small region centered at a one-click user input (e.g., a point within a predefined vertebra such as L5).

  • \(\lambda \) is a positive constant that balances the contribution of each term.

Optimization

Optimizing directly the high-order functional in (1) is a difficult problem because of (i) the high non-convexity (and non-linearity) of the distribution matching term in (1) and (ii) the integer-value constraint imposed on classification variable u. To obtain a solution efficiently, we split the problem into a sequence of sub-problems, each optimizing a bound (or auxiliary function) of (1) via a convex relaxation and the augmented Lagrangian method. An auxiliary function is an upper bound on the original energy, which verifies a certain condition. Optimizing an auxiliary function iteratively guarantees that the original energy decreases at each iteration (“Bound optimization and auxiliary function” section). The auxiliary function in this work is a sum of a linear function and a total-variation (TV) term. Therefore, unlike the original difficult functional, it can be optimized efficiently via a convex-relaxation (i.e., we relax the integer constraint) and an efficient multiplier-based algorithm. Specifically, for computing a global minimum of our relaxed auxiliary function, we solve an equivalent constrained problem via the standard augmented Lagrangian method [19,20,21], which embeds the constraint as a convex term (“Equivalent constrained problems and augmented Lagrangian method” section).

Bound optimization and auxiliary function

Bound optimization has recently led to competitive algorithms in the computer vision community, including efficient solutions to several difficult (high-order and integer-valued) segmentation functions, e.g., entropy [22], non-submodular pairwise terms [23] and distribution-matching constraints [24]. Rather than optimizing directly E, we optimize a sequence of auxiliary functions (bounds on E), denoted \(A(u|u^i)\), \(i \ge 1\) (i is the iteration number), whose optimization is easier than E:

$$\begin{aligned}&u^{i+1} = \, \min _{u} \; A(u|u^i), \quad i \ge 1 \quad \text{ s.t. } \end{aligned}$$
(4a)
$$\begin{aligned}&E(u) \le \, A(u|u^i) , \quad i \ge 1 \end{aligned}$$
(4b)
$$\begin{aligned}&E(u^i) = A(u^i|u^i) \end{aligned}$$
(4c)

An auxiliary function of E is a function that verifies the constraints in (4b) and (4c). Using these constraints, and by definition of minimum in (4a), one can show that the sequence of solutions in (4a) yields a decreasing sequence of E:

$$\begin{aligned} E(u^i) = A(u^i, u^i) \ge A(u^{i+1}, u^i) \ge E(u^{i+1}) \end{aligned}$$
(5)

Furthermore, \(E(u^i)\) is lower bounded and, therefore, converges to a minimum of E. In this work, we consider the following bound on the negative Bhattacharyya coefficient, which we recently derived in [24].

Bound on the negative Bhattacharyya coefficient

Given a fixed \(u^i\), for any \(u:\varOmega \rightarrow \{0,1\}\) verifying \(\{\mathbf {x}\in \varOmega / u(\mathbf {x})=1 \} \subset \{\mathbf {x}\in \varOmega / u^i(\mathbf {x})=1 \}\) and \(\forall \alpha \in [0, \frac{1}{2}]\), we have the following bound (auxiliary function) on the negative Bhattacharyya coefficient [24]:

$$\begin{aligned}&-\sum _{f \in {\mathcal {F}}} \sqrt{\mathbf {P}_{u}(f){\mathcal {M}}(f)} \le B_{\alpha }(u|u^i) \nonumber \\&-\sum _{f \in {\mathcal {F}}} \sqrt{\mathbf {P}_{u^i}(f){\mathcal {M}}(f)} = B_{\alpha }(u^i|u^i) \end{aligned}$$
(6)

with \(B_\alpha \) given by:

$$\begin{aligned} B_{\alpha }(u|u^i)&= -(1+\alpha ) \sum _{f \in {\mathcal {F}}} \sqrt{\mathbf {P}_{u^i}(f){\mathcal {M}}(f)}\\&\quad + \int _{\varOmega } \left\{ \alpha u g^i + (1+\alpha )(1-u)h^i \right\} d\mathbf {x}\end{aligned}$$

where

$$\begin{aligned}&g^i = \frac{\sum _{f \in {\mathcal {F}}} \sqrt{\mathbf {P}_{u^i}(f){\mathcal {M}}(f)}}{\int _{\varOmega }u^i d\mathbf {x}}; \nonumber \\&h^i(\mathbf {x}) = \frac{u^i(\mathbf {x})}{\int _{\varOmega }u^i d\mathbf {x}} \sum _{f \in {\mathcal {F}}}K(\mathbf {D}(\mathbf {x}) - f)\sqrt{\frac{{\mathcal {M}}(f)}{\mathbf {P}_{u^i}(f)}} \end{aligned}$$
(7)

It is easy to see that, using the result in (6), we have the following auxiliary function for our TV-regularized distribution matching functional in (1):

$$\begin{aligned} A_{\alpha }(u|u^i) = B_{\alpha }(u|u^i) + \lambda \int _{\varOmega } \Vert \nabla u\Vert \hbox {d}\mathbf {x}\end{aligned}$$
(8)

Convex relaxation of the auxiliary functions

The auxiliary function in (8) is the sum of a linear function \(B_{\alpha }\) and a total-variation (TV) term. Therefore, it can be optimized efficiently via powerful convex-relaxation techniques, e.g., [20, 21, 25, 26]. In fact, \(\min _{u \in \{0,1\}} A_{\alpha }\) is still a non-convex problem due to the integer-valued constraint \(u \in \{0,1\}\). However, relaxing such constraint to interval [0, 1] yields the following convex problem:

$$\begin{aligned} \min _{u \in [0,1]} A_{\alpha }(u|u^i) \end{aligned}$$
(9)

Furthermore, we can use a standard and powerful result in the total-variation literature [18, 20, 21, 25], which states that, for problems of the same form as our auxiliary function (i.e., a total-variation term combined with a linear term), simply thresholding the optimum \(u^* \in [0, 1]\) of the relaxed convex problem yields a global optimum of the non-convex discrete problem over \(u \in \{0,1\}\).

Now, the following equivalence allows us to compute an exact and global optimum of \(A_{\alpha }\) over \(u \in \{0, 1\}\) using a multiplier-based augmented Lagrangian method [20, 21, 25].

Equivalent constrained problems and augmented Lagrangian method

The convex problem in (9) is equivalent to the following constrained problem (The proof follows the ideas of [21]):

$$\begin{aligned}&\max _{p_h, p_g, p} \min _u \; \int _{\varOmega } \left\{ p_h + u({{\mathrm{div}}}p-p_h+p_g) \right\} d\mathbf {x}\quad \hbox {s.t}. \nonumber \\&p_h(\mathbf {x}) \le (1+\alpha ) h^i(\mathbf {x}); \nonumber \\&p_g(\mathbf {x}) \le \alpha g^i(\mathbf {x}); \quad \text{ and }\quad \left|p(\mathbf {x})\right| \le \lambda ~\text {a.e.}~ \mathbf {x}\in \varOmega \end{aligned}$$
(10)

where u is viewed as the multiplier to constraint \({{\mathrm{div}}}p-p_h+p_g=0\). \(p: \varOmega \rightarrow {\mathbb R}\), \(p_h: \varOmega \rightarrow {\mathbb R}\) and \(p_g: \varOmega \rightarrow {\mathbb R}\) are variables in the form of scalar functions. Furthermore, by simply thresholding the optimum \(u^* \in [0, 1]\) of (10), we obtain an exact and global optimum of the non-convex problem \(min_{u \in \{0,1\}} A_{\alpha }(u|u^i)\). From the equivalence between (9) and (10), one can use an efficient multiplier-based algorithm for computing a local optimum of E(u). The algorithm follows the standard augmented Lagrangian method [19,20,21]. This amounts to optimizing the following augmented Lagrangian function, which corresponds to our problem in (10) (Multiplier u is replaced here by v to avoid confusion between inner and outer iterations in the algorithm presented next):

$$\begin{aligned} L_c(p_h,p_g, p, v)= & {} \int _{\varOmega } \left\{ p_h + v({{\mathrm{div}}}p- p_h +p_g) -\frac{c}{2}\right. \nonumber \\&\left. \left||{{\mathrm{div}}}p-p_h+p_g\right||^2 \right\} \hbox {d}\mathbf {x}\end{aligned}$$
(11)

where c is a positive constant. A summary of the algorithm is given in Algorithm 1 (i and j are the numbers of inner end outer iterations respectively).

figure a

The scheme is amenable to parallel implementations on graphics processing units (GPU), and yields nearly real-time solutions (\({<}1\) s) for labeling a typical 2D spine MRI of size \(512 \times 512\). This is an important advantage over graph-cut solutions for distribution matching [24], which do not accommodate parallel implementations. Also, it is worth noting that our optimization scheme can be extended to 3D. In our experiments, however, we focused on 2D evaluations because, from a clinical-application perspective, spine labeling in MRI is typically required on 2D mid-sagittal slices. One of the main applications is to use such mid-sagittal labels to facilitate navigation through axial slices via cross-reference features. Our 2D evaluations are consistent with previous works on labeling spine MRI, e.g., [10, 28] (where the focus is also on 2D mid-sagittal slices).

Fig. 1
figure 1

Illustration of the geometric scores. Left plausible distances and angles between neighboring vertebrae; middle unlikely distance setting; right unlikely angle setting

Full size image
Table 1 Details of the T1-weighted and T2-weighted MR datasets. Pixel resolution and slice thickness are given in mm
Full size table

Embedding high-level anatomic constraints

This second stage of our method removes the false positives obtained at the previous step, and identifies all the vertebrae and discs in the image. It consists of optimizing a geometric score (or constraint), which embeds anatomical information on the interconnections between neighboring spine structures. Based on anatomical knowledge, the proposed geometric score does not require any additional training effort. Let K denotes the number of connected regions obtained from the previous pixel-level classification step; see the examples in Fig. 4. Let \([z_1, \ldots , z_K] \in \varOmega ^K\) be the centroids of these regions, and \(y_\mathrm{input}\) the user-provided point. This step consists of finding an optimal set of N points \([\hat{y}_1, \ldots , \hat{y}_N] \in \varOmega ^N\) among all the possible combinations of N points in \([z_1, \ldots , z_K\)] (\(N<K\)). We propose to optimize the following constraint, which, as illustrated in Fig. 1, embeds priors on the geometric relationships between spine structures:

$$\begin{aligned}{}[\hat{y}_1, \ldots , \hat{y}_N]= & {} \max _{[y_1, \ldots , y_N] \subset [z_1, \ldots , z_K]} G (y_1, \ldots , y_N) \nonumber \\&\text{ s.t. }\, y_1 = y_\mathrm{input} \quad \text{ with } \nonumber \\ G (y_1, \ldots , y_N)= & {} \underbrace{\sum _{i=1}^{N-1} \cos ({\mathbf {V}}_i, {\mathbf {V}}_{i+1})}_\mathrm{Angles}\nonumber \\&+ \underbrace{\sum _{i=1}^{N-1} \min \left( \frac{\left||{\mathbf {V}}_i\right||}{\left||{\mathbf {V}}_{i+1}\right||}, \frac{\left||{\mathbf {V}}_{i+1}\right||}{\left||{\mathbf {V}}_i\right||} \right) }_\mathrm{Distances} \end{aligned}$$
(12)

where \({\mathbf {V}}_i\) is the vector pointing from \(y_i\) to \(y_{i+1}\), \(i=1, \dots , N-1\): \({\mathbf {V}}_i = y_{i+1} - y_i\). The function in (12) enforces the following anatomical constraints (see Fig. 1 for an illustration):

  • The distance constraint ensures that the distances between neighboring vertebrae are not significantly different. For instance, the geometry of the labeling in the middle of Fig. 1 is not likely: the distance between vertebrae \((y_i, y_{i+1})\) is much smaller than the distance between vertebrae \((y_{i+1}, y_{i+2})\).

  • The angle constraint ensures that each three successive vertebrae correspond to a plausible (not excessive) bending of the spine. For instance, the geometry of the the three successive vertebrae in the right-hand side of Fig. 1 corresponds to a very sharp angle (or a high curvature), which is not consistent with the geometry of human spines (not even those showing significant deformities/abnormalities).

We find the optimum of (12) with an exhaustive search. We can vary N from 1 to K in the exhaustive search, and choose the combination that yields the highest value of G in Eq. (12). In our implementation, we start with a plausible minimum number of N, e.g., \(N=5\) (because, typically, a lumbar spine image contains at least the five vertebrae from L1 to L5). Then, we increase N gradually by searching for candidate points that yield the best possible increase of criterion G. For our problem, such an exhaustive search can be performed in real-time because our regularized distribution matching does not result in a very large number of connected regions (refer to the examples in Fig. 4). In our implementation, it took about \(10^{-3} s\) for a typical 2D spine MRI scans of size \(512 \times 512\). The optimal set \([\hat{y}_1, \ldots , \hat{y}_N]\) yields the target vertebrae. The target discs are computed from the optimum as follows: \(t_i = \frac{\hat{y}_i + \hat{y}_{i+1}}{2} \quad \forall i \in [1, \dots , N-1]~ \text{ and }~ t_0 = \frac{3\hat{y}_1}{2}-\frac{\hat{y}_2}{2}\). The individual labels of the structures follow directly from the detected structures by using the known spatial organization of the structures, e.g., L1 below T12, L2 below L1, etc.

Experiments

Data set, model parameters and features

We performed quantitative evaluations of the algorithm over a data set of 90 mid-sagittal MRI images of the lumbar spine acquired from 45 different subjects (45 images of the type T2-weighted and 45 of the type T1-weighted). The purpose of using both the T1- and T2-weighted images of each subject is to assess the ability of the algorithm to handle different types of MRI data, with significant changes in appearances and various levels of resolution and noise. For the T1-weighted data, the slice thickness is in the range [3, 4 mm], and the pixel spacing is in the range [0.47, 0.57 mm]. For the T2-weighted data, the slice thickness is in the range [0.88, 4 mm], and the pixel spacing is in the range [0.41, 0.90 mm]. The details of the datasets are presented in Table 1. A total of number of 990 structures were automatically detected and labeled: in our evaluations, we focused on 11 lumbar structures/labels per image: 5 vertebra labels (T12, L1, L2, L3 and L4) and 6 disc labels (T12-L1, L1-L2, L2-L3, L3-L4, L4-L5 and L5-S1). Model \({\mathcal {M}}\) is estimated from the feature vectors within a disc centered at a very simple user input: a mouse click placed within the L5 vertebra for each subject. The parameters of the model were invariant for all the test images in the data set, and were fixed as follows: \(\lambda =1\) and \(N=6\). The contextual-feature function \(\mathbf {D}\) is computed from the input image as follows. For each point \(\mathbf {x}\in \varOmega \), we built a feature vector of dimension 3: \(\mathbf {D}(\mathbf {x})=[D_1(\mathbf {x}), D_2(\mathbf {x}), D_3(\mathbf {x})]\), with \(D_1\) the mean of intensity within a \(3 \times 10\) rectangular-shaped, vertically-oriented patch, \(D_2\) the mean of intensity within a \(10~\times ~3\) rectangular-shaped, horizontally-oriented patch, both centered at point \(\mathbf {x}\), and \(D_3\) the intensity of \(\mathbf {x}\). Note that other features based on image gradients or textures can be used within the same framework. Finally, the radius of the disc for estimating model \({\mathcal {M}}\) is fixed equal to 5 pixels.

Fig. 2
figure 2

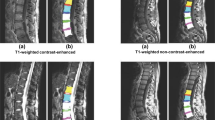
Typical results obtained with the proposed algorithm on T1-weighted and T2-weighted images with significant changes in appearances and geometric characteristics such as the degree of bending of the spine and the shapes/sizes of individual vertebrae and discs. These examples show that the proposed algorithm handles effectively these variations, without the need for external training

Full size image
Fig. 3
figure 3

A typical T1-weighted MR example, which shows that the choice of the initial label (red) does not have a significant impact on the results

Full size image
Fig. 4
figure 4

Examples of regularized distribution matching and the corresponding evolutions of the distribution matching term as a function of the iteration number. First and second row T2-weighted examples; third and fourth row T1-weighted examples

Full size image
Fig. 5
figure 5

Performance evaluations for each structure of the lumbar spine: percentage of correctly detected and labelled vertebrae/discs for the T1-weighted images (left) and T2-weighted images (right)

Full size image

Typical examples and computational time

Figure 2 depicts typical results obtained with the proposed algorithm on T1-weighted and T2-weighted images with significant changes in appearances and geometric characteristics such as the degree of bending of the spine and the shapes/sizes of individual vertebrae/discs. These examples show that the proposed algorithm effectively handles these variations, without the need for intensive external training. For each of these examples, the user click is placed at the L5 vertebra, and the solutions were obtained in near real-time: for a typical MRI scan of size \(512 \times 512\), the first stage took less than 1s, and the second took about \(10^{-3} s\). Figure 3 depicts experiments with 5 different choices of the initial label. One can see from these typical examples that the choice of the initial label does not have a significant impact on the results. This makes sense because the feature distributions of the vertebrae are quite close. It is worth noting that from user perspective, L5 might be the easiest and fastest to identify. The convex relaxation optimizer was run in parallel on a graphics processing unit (GPU) of the type NVIDIA Quadro FX3700, with 112 Cuda cores.

Fig. 6
figure 6

The median, 5th percentile and 95th percentile values of Euclidean distances (in mm) between the automatically obtained annotations and ground-truth annotations for different pixel resolutions. Comparisons over 990 annotations showed that the performance of the algorithm did not vary significantly with pixel resolution

Full size image

Examples of intermediate segmentation results

Figure 4 depicts typical examples of the regularized distribution matching segmentation results we obtained using images from six different subjects (three T2-weighted in the first row of the figure and three T1-weighted in the third row). Below each image, we plot the corresponding evolution of the distribution matching term (the negative Bhattacharyya coefficient) as a function of the iteration number. Notice that, for each example, this segmentation step yielded a single connected region for each vertebral structure. Also, the number of the remaining irrelevant regions (i.e., the false positives that do not correspond to vertebral structures) is, typically, of the same order as the number of true positives (or even smaller in some cases). This shows how our regularized distribution matching discriminates well between the target structures and the rest of the image, significantly facilitating subsequent detection/annotation steps. Finally, it is worth noting that our distribution matching converges within a few iterations (typically less than 10 iterations); see the plots in Fig. 4.

Quantitative evaluations

We evaluated two performance measures: (i) the Euclidean distances (in mm) between the automatically obtained annotations and ground-truth annotations (Ground-truth labels are manually placed by a radiology expert at about the center of mass of each structure) and (ii) the detection accuracy given by the percentage of correctly detected and labeled vertebrae/discs. Similar to the study in [10], a structure (vertebra or disc) is considered correctly detected and labelled if (a) the detected point is within the structure and (b) the automatic label is consistent with the ground-truth label. Table 3 reports the percentages of correctly detected and labeled vertebrae/discs over all the data set, and the Euclidean distances (expressed in mean ± standard deviation) between the automatically obtained annotations and ground-truth annotations. Figures 5 and 7 plot the detailed performances of our method for each individual structure of the lumbar spine. Figure 6 depicts the Euclidean distances (in mm) between the automatically obtained annotations and ground-truth annotations for the different pixel resolutions in our data set. This plot illustrates how the performance of the algorithm did not vary significantly with pixel spacing.

Fig. 7
figure 7

The median, 5th percentile and 95th percentile values of Euclidean distances (in mm) between the automatically obtained annotations and ground-truth annotations for the T1-weighted images (left) and the T2-weighted images (right)

Full size image
Table 2 A meta-analysis of accuracies for several state-of-the-art spine labeling techniques
Full size table
Table 3 The overall labeling performances and Euclidean distances (in mm) with respect to ground-truth labels
Full size table

Comparison with prior work

Table 2 reports a meta-analysis of accuracyFootnote 2 for several state-of-the-art spine labeling techniques, including: the training-based method in [28], which proposed a deformable part model object detector combined with dynamic programming; the probabilistic model in [10], which integrates both pixel-level (appearance and shape) and context; the deep learning technique in [29], which combines image-to-image network, message passing and sparsity regularity; the method in [30], which uses supervised classification forests; and the deep convolutional neural network method in [31]. The performance of these techniques are reported in term of the percentage of correctly labeled structures. For each method, we report a range of accuracies as the authors of these studies report several performances, each corresponding to a different proportion of testing/training data, a different imaging protocol, or a differnt part of the spine (lumbar, thoracic or cervical). Notice that, for each of the methods (including ours), the best performance is close to \(90\%\) accuracy. Of course, we do not expect our algorithm to outperform training-based techniques because our algorithm uses much less information. However, the results (Table 3) suggest that the proposed algorithm can reach a performance comparable to training-based algorithms, although it does not use any external training data (i.e., model learning in our case is subject-specific and is based on a very simple user input). The study in [10] reported a performance comparable to us over an MRI data set of about the same size (105 subjects, with about half of the population for testing and the rest for training): the accuracy [10] is in the range \([87.7, 89.1\%]\). However, the method in [10] is based on intensive training information from annotated data sets of over 50 subjects. It is worth noting that a systematic comparison between our interactive method and such training-based methods on the same data is not possible because our algorithm does not use any external training information. In fact, our method is not in direct competition with these learning-based techniques. It can be used when training information is not available, or as a tool that can efficiently build large annotated data sets for learning-based algorithms (e.g., convolutional neural networks)

Discussion

We proposed a fast (nearly real-time) spine MRI labeling algorithm that removes the need for external training while being applicable to different types of MRI data and acquisition protocols. The algorithm was based solely on the current testing image and a subject-specific model density, which is learned from a very simple user input. When applied to T1- and T2-weighted MRI images, our regularized distribution-matching formulation, followed by a simple geometric filtering step, achieved performances comparable to state-of-the-art training-based techniques. Such comparisons are based on a meta-analysis of accuracies. In fact, our method is not in direct competition with these learning-based techniques: a systematic comparison on the same data (including training images) is not possible because our algorithm does not use any external training information. Our interactive method can be used when training information is not available or, also, to rapidly build massive annotated data sets, which can boost the performances of learning-based algorithms (e.g., convolutional neural networks).

The fact that our algorithm does not use external training information is a practical advantage over the existing methods. However, it comes at the price of a user input (a mouse click). Such an input makes the problem easier because off-by-one errors are less likely to occur. Also, learning a distribution from the testing image makes the algorithm flexible: it can be readily applied to different types of MRI data and acquisition protocols without re-training.

Our method was evaluated on patient data, but we did not focus on a specific pathology or injury. Our goal was to design a system that performs well for the majority of patient data sets that are collected from clinical routine MRIs of the spine, with no exclusion criteria. Our data involved spine patients with typical disorders such as herniation or degenerative disc disease (DDD).

One of the limitations of the method is that the geometric refinement step does not account for missing structures. Another limitation is that the image features that we used for building the distribution-matching term are hand-crafted. There are several possible extensions to address these limitations. As our algorithm runs in nearly real-time, an interesting and practical extension would be to embed minimal user interactions in the form of constraints so as to rapidly correct possible errors in the results. Such an extension would prompt the user to add interactively new clicks, which the algorithm account for in a subsequent result-improvement step. For instance, interactive manual corrections would be useful when the method fails in labeling some parts of the spine, particularly in cases of atypical images such as those of patients with spine injuries. Another extension would be to learn the range of our geometric features (e.g., the angles) from a few annotated examples, or to learn a set of image features in order to build the distribution matching term. Also, there are several possible evaluations of the proposed method and its extensions, which we intend to investigate in the future. For instance, it would be interesting to evaluate the algorithm in the context of other modalities, e.g., computed tomography (CT), or on Thoracic and Cervical spine. We anticipate that our method works reasonably on these parts of the spine as well. Similarly to the lumbar spine, the Thoracic/Cervical features should not change significantly from one vertebra to another and the geometric prior seems to be plausible.