Query-by-example surgical activity detection

Abstract

Purpose

Easy acquisition of surgical data opens many opportunities to automate skill evaluation and teaching. Current technology to search tool motion data for surgical activity segments of interest is limited by the need for manual pre-processing, which can be prohibitive at scale. We developed a content-based information retrieval method, query-by-example (QBE), to automatically detect activity segments within surgical data recordings of long duration that match a query.

Methods

The example segment of interest (query) and the surgical data recording (target trial) are time series of kinematics. Our approach includes an unsupervised feature learning module using a stacked denoising autoencoder (SDAE), two scoring modules based on asymmetric subsequence dynamic time warping (AS-DTW) and template matching, respectively, and a detection module. A distance matrix of the query against the trial is computed using the SDAE features, followed by AS-DTW combined with template scoring, to generate a ranked list of candidate subsequences (substrings). To evaluate the quality of the ranked list against the ground-truth, thresholding conventional DTW distances and bipartite matching are applied. We computed the recall, precision, F1-score, and a Jaccard index-based score on three experimental setups. We evaluated our QBE method using a suture throw maneuver as the query, on two tool motion datasets (JIGSAWS and MISTIC-SL) captured in a training laboratory.

Results

We observed a recall of 93, 90 and 87 % and a precision of 93, 91, and 88 % with same surgeon same trial (SSST), same surgeon different trial (SSDT) and different surgeon (DS) experiment setups on JIGSAWS, and a recall of 87, 81 and 75 % and a precision of 72, 61, and 53 % with SSST, SSDT and DS experiment setups on MISTIC-SL, respectively.

Conclusion

We developed a novel, content-based information retrieval method to automatically detect multiple instances of an activity within long surgical recordings. Our method demonstrated adequate recall across different complexity datasets and experimental conditions.

Introduction

Surgical procedures are performed as a sequential composition of activity segments. These segments are useful for evaluation and teaching [10], and may differ in difficulty to learn and execute them [19]. Advances in techniques such as laparoscopy or robotic surgery and access to sensor technology in the training laboratory and in the operating room have led to availability of large amounts of tool motion and video data on surgical performance. Manual parsing of these data to provide targeted feedback and build useful indexed surgical performance catalogs requires a prohibitive amount of resources. Automated detection of activity segments of interest enables effective use of the data through technology for efficient training of surgeons. For example, automated activity detection within surgical performances in the training laboratory and in the operating room can enable learning through well-indexed libraries and data-driven feedback.

Several techniques have been proposed to automatically classify (i.e., assign labels to segments with known boundaries) and recognize (i.e., identify boundaries and assign labels) surgical activity segments. The segments are usually specified based on a semantic understanding of the surgical activity (e.g., gestures, maneuvers, tasks). Currently available methods to classify or recognize semantically meaningful activity segments such as gestures include variants of hidden Markov models [15, 18], conditional random fields [8, 16], linear dynamical systems [2, 21], and different forms of dictionary learning [1, 14]. Applications using these methods to automatically classify or recognize semantically meaningful activity segments are limited by the need for extensive manual curation and pre-processing. All such methods are supervised and rely upon learning parameters for particular models (with necessary assumptions, which may not be suitable for longer and more complex activity segments), sometimes using data from the entire signal.

In this paper we describe a novel content-based information retrieval method called query-by-example (QBE) and apply it to automatically detect and retrieve surgical activities of interest from a database of recordings. QBE has been applied to zero-resource spoken term detection [7] where the query (example) is a short acoustic utterance of a word, and to laparoscopic video indexing [17] where the query is a video snippet. Our proposed QBE method simultaneously detects multiple segments within the long recordings (trials), whereas traditional QBE detects a single best segment. Figure 1 illustrates the concept of our QBE approach to surgical activity detection, where we demonstrate the case that there are multiple segments within the trial that resemble the input query. We will show that all the segments that resemble the input query within the long trial can be simultaneously detected. In this paper, we applied a nonlinear feature learning method to obtain a succinct and informative representation of kinematic data in surgical recordings. The proposed method may be generalized to other time series data such as video, with automatically learnt or hand-crafted features such as HOG [17].

Fig. 1

Query-by-example for surgical activity detection. Top row shows one dimension of the kinematic data as a time series, and the bottom row shows the surgical activities, of the query and the target trial, respectively

Our contributions in this work include: (1) a QBE approach to simultaneously detect all segments of interest within long surgical data recordings; (2) a novel method called asymmetric subsequence dynamic time warping (AS-DTW) to enable detection of multiple instances of a query; and (3) a method to evaluate performance of techniques to detect multiple instances of a query based on DTW distance thresholding and bipartite matching.

Methodology

Problem formulation

In the QBE context, data for the query and the target trial are represented in the same format, for example, via the same data capture mechanism. Let $X\in {\mathcal {R}}^{m\times d}$ denote the query, and let $Y\in {\mathcal {R}}^{n\times d}$ be the target trial, where d is the dimensionality of the features and m, n denote the number of temporal frames in X and Y, respectively. The basic QBE problem can be formulated as:

$$\begin{aligned} (a^*, b^*) = {\mathop {{{\mathrm{\hbox {argmax}}}}}\limits _{{(a,b)\in {\mathcal {N}}, 1\le a < b\le n}}} S(X, Y_{a:b}) \end{aligned}$$

(1)

where $Y_{a:b}$ denotes a substring of Y composed of frames between time-indices a and b, and $S(\cdot , \cdot )$ is a similarity metric. (1) aims to find the unique substring in the target trial that is most similar to the query.

In a more generic formulation of the QBE problem, detecting multiple substrings in the target trial that resemble the query may be achieved by either applying a threshold on the similarity between the candidate substrings and the query, or by constraining the cardinality of set of end points $(a_i,b_i)$, or by applying both constraints. Let $s_\mathrm {thr}$ denote the similarity threshold, and let N denote the number of subsequences to be found. The QBE problem to detect multiple substrings in the target trial can be formulated as:

$$\begin{aligned} \bigcup _i (a_i^*, b_i^*) =\bigcup _{i\in \{1, 2, \ldots , N\}^{(\#1)}} {\mathop {{{\mathrm{\hbox {argmax}}}}}\limits _{{\begin{array}{c} (a_i,b_i)\in {\mathcal {N}},\\ 1\le a_i< b_i\le n\\ b_i<a_{i+1}\\ S(X, Y_{a_i:b_i}) \ge s_\mathrm {thr}^{(\#2)} \end{array}}}} S(X, Y_{a_i:b_i}) \end{aligned}$$

(2)

where the condition $b_i< a_{i+1}$ ensures no overlap between the multiple substrings that are detected. Note that in (2) the conditions ${(\#1)}$ and ${(\#2)}$ correspond to the cardinality and the threshold constraints, respectively.

Pipeline

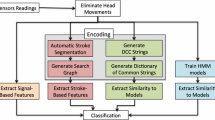
Figure 2 shows the pipeline of our QBE surgical activity detection, which includes four modules:

• 1. Feature learning, where we used a stacked denoising autoencoder (SDAE) [20] to learn nonlinear features from the kinematic data;

  Fig. 2

  

  The pipeline for our QBE framework

• 2. AS-DTW scoring, where we compute a distance matrix for query against trial and apply a novel algorithm called asymmetric subsequence dynamic time warping (AS-DTW)¹ to get a score function for possible substrings of the trial;

• 3. Template scoring, where a template generated from the query is used to score the distance matrix;

• 4. Subsequence detection, where we determine substrings by peak detection on a fused score function followed by backtracking and further refinement.

We will introduce each module in detail in the following subsections.

Nonlinear feature learning

In this study, the query and target trials are surgical tool motion or kinematic data, which are composed of positions, velocities, rotation matrices, angular velocities, and gripper angles within a coordinate frame attached to the tip of the manipulators of the da Vinci Surgical System (dVSS, Intuitive Surgical Inc, Sunnyvale, CA) [5]. The kinematic data contain pose (orientations) and velocity information which are nonlinearly dependent. Therefore, we need a nonlinear feature extraction method to extract succinct and useful information from the kinematic data.

We used a stacked denoising autoencoder (SDAE) [20] to learn nonlinear features from the kinematic data. An autoencoder (AE) is a type of artificial neural network that transforms inputs into outputs with the least possible reconstruction error. By incorporating nonlinear activation functions, AEs decompose the nonlinear dependency between features and reorganize them to produce a useful representation. The AEs can be stacked into a deep structure and trained efficiently using the layer-wise pre-training strategy [3]. If the last layer of the network has fewer nodes than the input layer, then the network serves to reduce dimensionality as well. SDAE is a variation of a stacked AE where the input is first partially corrupted and the network is trained to reconstruct a clean repaired input. SDAE features are more robust since they preserve the underlying manifold of the data [20].

Let $\tilde{\mathbf {x}}$ denote the corrupted version of input $\mathbf {x}$, and let $W \in {\mathcal {R}}^{n\times m}$ denote the weight matrix and $\mathbf {b} \in {\mathcal {R}}^{m}$ be the offset, where n, m are the number of nodes in the input layer and the hidden layer, respectively. Let f denote the forward mapping and g denote the reconstruction mapping, i.e. $f(\mathbf {x}) =\mathbf {s}(W^T\mathbf {x}+\mathbf {b})$ and $g(\mathbf {h}) =\mathbf {s}(W\mathbf {h}+\mathbf {b'})$, where $\mathbf {s}(\cdot )$ can be chosen as the sigmoid function (nonlinearity). The objective function for training a DAE is written as

$$\begin{aligned} J_\mathrm{DAE} = L(\mathbf {x}, g\circ f (\tilde{\mathbf {x}}))+ \frac{\lambda }{2} \Vert W\Vert _F^2 \end{aligned}$$

(3)

where $L(\cdot , \cdot )$ is a loss function, and the second term serves to regularize the weights. In this study we used a sigmoid activation and squared error loss.

The SDAE used in this study has a 3-layer topology with [836-256-15] number of nodes. We used the implementation of SDAE in the DeepLearnToolbox [12]. According to [1], the unit time that the change in human motion can be observed is approximately 200 ms. Thus for the signal sampled at 50 Hz, we constructed the input frame as a concatenation of successive kinematic frames within a sliding window of 11 frames to incorporate temporal context in the data, and a sliding step of five frames to allow 50 % overlap between consecutive input frames. Our initial experiments with 2, 3, 4 and 5 layers indicate that reconstruction error was higher with 2 layers; however, there was minimal advantage of using more than three layers. We thus used a 3-layer topology. The output dimension was predetermined since the total degree of freedom of two hands are 14, and we allowed 1 more dimension to help reorganize the features. Figure 3 depicts our SDAE feature extraction procedure.

Fig. 3

Stacked denoising autoencoder for feature learning

AS-DTW scoring

Distance matrix computation

Our QBE method is a content-based information retrieval approach to surgical activity detection, which utilizes the similarity between a query and a target trial. Given the query $X\in {\mathcal {R}}^{m\times d}$ and the target trial $Y\in {\mathcal {R}}^{n\times d}$, the similarity can be reflected by a distance matrix $D(X, Y)\in {\mathcal {R}}^{m\times n}$ such that $D(i,j) = d(\mathbf {x}_i, \mathbf {y}_j)$, where $\mathbf {x}_i$ and $\mathbf {y}_j$ denote the i-th and j-th frames of X and Y, respectively, and $d(\cdot , \cdot )$ is a distance metric. We used a cosine distance in this study:

$$\begin{aligned} d(\mathbf {x}, \mathbf {y}) = \frac{1}{2}\left( 1-\frac{\langle \mathbf {x}, \mathbf {y}\rangle }{\Vert \mathbf {x}\Vert \cdot \Vert \mathbf {y}\Vert }\right) . \end{aligned}$$

(4)

Note that the distance matrix appears “wide” in shape because the query X is usually much shorter than the trial Y. To prevent zero distance that may bias the distance accumulation in later modules, a small amount of noise is added to the query before computing the distance matrix.

Asymmetric subsequence dynamic time warping (AS-DTW)

We developed a novel method called asymmetric subsequence dynamic time warping (AS-DTW), which is applied on the distance matrix in order to generate a score function that indicates the multiple candidate substrings of the target trial that resemble the query. Before we introduce AS-DTW, we briefly review dynamic time warping (DTW) and subsequence-DTW.

DTW [13] is an algorithm to find the optimal match between two sequences. Given two sequences X and Y with length m and n, respectively, DTW aims to minimize the overall distance between all frames that are warped onto each other:

$$\begin{aligned} \min _{[p^x, p^y]^T\in {\varPhi }} J_\mathrm {dtw} =\sum _{i=1}^l d(\mathbf {x}_{p^x_i},\mathbf {y}_{p^y_i} ) \end{aligned}$$

(5)

where ${\varPhi }$ is the space of the warping path that satisfies three constraints: (1) boundary $[p^x_1, p^y_1] = [1,1] \text{ and } [p^x_l, p^y_l] = [m, n]$; (2) monotonicity $i_1< i_2\Rightarrow p_{i_1} \le p_{i_2}$; (3) continuity $[p^x_{i+1}, p^y_{i+1}] - [p^x_i, p^y_i] \in \{ [0,1],~[1,0],~ [1,1]\}$.

Let $D_C\in {\mathcal {R}}^{m\times n}$ denote the accumulated distance matrix. DTW can be implemented by dynamic programming:

$$\begin{aligned} D_C(i,j)= & {} \min \{ D_C(i-1, j-1), D_C(i, j-1),\nonumber \\&D_C(i-1, j)\}+D(i,j) \end{aligned}$$

(6)

with the base case $D_C(0,0) =0$. The optimal warping path is found by backtracking [13]. Note that the boundary constraints tie together the start frames (and end frames) of X and Y; therefore, the algorithm matches the two sequences in their entirety.

In order to obtain an optimal substring, a variation called subsequence-DTW [11] was introduced by initializing the first row of $D_C$ to be same the as the first row of D, instead of accumulation. The initialization can be formally described as:

$$\begin{aligned} D_C(1, 1:n) =0, ~~~ D_C(1:m, 1) = \sum _{i = 1}^m d(\mathbf {x}_i, \mathbf {y}_1) \end{aligned}$$

(7)

Using subsequence-DTW, a scoring function ${\Delta }$ is defined as the last row of $D_C$:

$$\begin{aligned} {\Delta }{:}\; [1, n] \rightarrow {\mathcal {R}}, ~~~{\Delta }(b) := D_C(m, b) \end{aligned}$$

(8)

${\Delta } (b)$ is the minimum warped distance between X and some substrings of Y ending at the b-th frame. The global minimum of ${\Delta }(b)$ indicates the optimal substring and the local minima of ${\Delta }(b)$ suggest candidates for locally optimal matches. Thus subsequence-DTW provides a convenient tool to find multiple substrings, which fits our goal.

However, without boundary constraints, the progression of the warping path in subsequence-DTW is biased by the length of the path such that a short path is always preferred. For example, at the location (i, j), according to (6) the progression of the warping path is determined by the smallest among $\{D_C(i-1, j-1), D_C(i-1, j), D_C(i, j-1)\}$, corresponding to three directions: diagonal, downwards, and rightwards. Since both $(i-1, j-1)$ and $(i-1, j)$ may be achieved from the top row within $i-1$ steps, it is possible that $D_C(i-1, j-1)$ and $D_C(i-1, j)$ are the sum of $i-1$ distance values. Conversely, the warping path must traverse at least i steps to reach $(i, j-1)$, resulting in $D_C(i, j-1)$ being the sum of at least i distance values. Consequently, the warping path favors downward and diagonal progression, which leads to a biased warping path.

The reason behind this problematic property of length bias with subsequence-DTW is because the vertical and the horizontal directions are not treated the same. The accumulation of distance stops at the vertical critical point of $i=m$, but there is no such stopping rule for j; thus, the subsequence-DTW breaks the assumption that the two warped (sub)strings are similar to each other except some local delay as the warping path usually deviates locally from the diagonal line.

We propose an asymmetric progression method to remove the length bias in subsequence-DTW; thus, our algorithm is referred as asymmetric subsequence dynamic time warping (AS-DTW). Consider two warping paths $p_1$ and $p_2$, where $p_1$ contains rightwards progression steps and $p_2$ is composed of only downwards and diagonal progression steps. It is obvious that the difference between the lengths of $p_1$ and $p_2$ is the number of rightwards steps. Hence we need a way to reconcile the extra length introduced by rightwards progression, and this needs to be treated locally in a dynamic programming framework. Note that whenever there is a rightwards progression, the length of the warping path will be increased by 1. Thus we adjust the accumulated distance to be a sum of equivalent i distance values via multiplying by a factor of $i/i+1$ after taking a rightward step, where i is the current row. Formally, the proposed recursive formula of AS-DTW is

$$\begin{aligned} \begin{aligned} D_C(i,j) = \min \{&D_C(i-1, j-1)+D(i,j),\\&D_C(i-1, j)+D(i,j)\\&\frac{i}{i+1}(D_C(i, j-1)+D(i,j)) \} \end{aligned} \end{aligned}$$

(9)

Figure 4 shows a toy example to compare AS-DTW and subsequence-DTW.

Fig. 4

An example of showing that asymmetric progression finds the correct warping where subsequence-DTW fails. a Distance matrix D overlaid with the true path. b Accumulated distance matrix $D_C$ and paths obtained by subsequence-DTW. Multiple paths found but none are correct. c $D_C$ and the path obtained by AS-DTW. Arrows in b and c indicate back-tracking. Note: the computation retains more significant digits to preserve precision; only two are shown in the figure

In our AS-DTW scoring module, we use a two-way AS-DTW to smooth the distance matrix D and combine the smoothed and original distance matrices together for further AS-DTW. The output of AS-DTW includes a score function ${\Delta }(b)$ as defined in (8), and an accumulated distance matrix with paths information for substrings end at each frame of Y.

Distance matrix template scoring

In addition to the similarity on the warping path obtained by AS-DTW, we considered the similarity of the local structure by studying the distance matrix. Given the query and a substring of the target trial, let us first define three local distance matrices: self-distance matrix of the query, denoted by $D_Q$, self-distance matrix of a substring of the trial, denoted by $D_S$, and the cross-distance matrix between the query and the substring, denoted by $D_X$, respectively. Figure 5 shows the three distance matrices.

Fig. 5

Self-distance matrix of the query (left), of a substring (right), and the cross-distance matrix between those two (middle)

A desired property is that both $D_S$ and $D_X$ be similar to $D_Q$. We use the normalized inner product as the metric to evaluate the similarity between distance matrices. In other words, we can take $D_Q$ as a template distance matrix, and score each substring. Although the substrings may be of different lengths, using AS-DTW we can obtain the warping path for each substring to warp them into the same length as the query. Let $D_S'$ and $D_X'$ denote the self- and cross-distance using the warped substring, then the similarity is computed as

$$\begin{aligned} S(D_Q, D_S') = \frac{\langle D_Q, D_S'\rangle }{\Vert D_Q\Vert _F\Vert D_S'\Vert _F}\,. \end{aligned}$$

(10)

$S(D_Q, D_X')$ is defined in the same way.

For each frame b of the trial, there exists an optimal substring (beginning at some frame $a<b$) that ends at b. Therefore, we define a score function ${\varGamma }$ as

$$\begin{aligned} {\varGamma }: [1, n]\rightarrow R, ~~ {\varGamma }(b):= & {} \alpha S(D_Q, D_S'(b)) \nonumber \\&+ \beta S(D_Q, D_X'(b)) \end{aligned}$$

(11)

where $D_S'(b)$ and $D_X'(b)$ denote the corresponding distance matrices of the substring that ends at frame b. $\alpha$ and $\beta$ are hyperparameters satisfying $\alpha +\beta =1$. An approximation of ${\varGamma }(b)$ can be computed by taking a fixed length substring ending at frame b. The rationale behind this approximation is that the length $b-a+1$ of the optimal substring is close to the length of the query. With this assumption, ${\varGamma }(b)$ may be computed (approximately) simply by sliding a fixed window of length $\Vert D_Q\Vert$ along D, and calculating the score between $D_Q$ and the part of D covered by the window, avoiding the back-tracking needed to find a. In our experiments, we use this approximation for computational efficiency, with $\alpha =0$ and $\beta = 1$.

Substring detection

Given the two score functions ${\Delta }(b)$ and ${\varGamma }(b)$, we select candidate endpoints by applying a peak detection algorithm on the average of the two functions, which finds out the local maxima of the signal with the constraints of dominance and separation. These peaks $\{b_i\}$ indicate high similarity both along the warping path and in local structure. The warping path, and starting point $a_i$ corresponding to each $b_i$, are determined by back-tracking. The set of substrings $\{(a_i,b_i)\}$ is further refined to eliminate overlapping substrings. Figure 6 shows the evolution of the distance matrices and the scoring functions along a single trial.

Fig. 6

From top to bottom original distance matrix D; merged distance matrix for the final AS-DTW; accumulated distance matrix $D_C$ overlapped with found warping paths; scoring functions and the detected peaks

Experiments

Datasets

We used two datasets captured in the surgical training laboratory in this study: the JHU-ISI Gesture and Skill Assessment Working Set (JIGSAWS) [5] and the JHU Minimally Invasive Surgical Training and Innovation Center—Science of Learning (MISTIC-SL) datasets [6]. In both cases, data were captured as surgeons performed on bench-top models on the da Vinci Surgical System (dVSS; Intuitive Surgical, Inc., Sunnyvale, CA) in the laboratory. From both datasets, we used the tool-tip position, orientation, velocities, and gripper angles from the surgeon-side and patient-side manipulators of the dVSS.

JIGSAWS included 39 instances (trials) of a continuous suturing task performed by eight subjects. Each trial consisted of four suture throws (passing needle across an incision). MISTIC-SL included 72 trials (49 right-handed trials used in this study, and 23 left-handed not used in this study) performed by 15 trainee surgeons. Each surgeon performed an average of five trials (range = 1–15). Each trial in MISTIC-SL consisted of a suture throw followed by a surgeon’s knot, eight more suture throws, and another surgeon’s knot. Figure 7 illustrates the bench-top models for tasks in JIGSAWS and MISTIC-SL. The task composition in MISTIC-SL is more complex than that in JIGSAWS because it involved tying a surgeons knot before and after multiple suture throws. Surgeons in MISTIC-SL also were required to manage longer lengths of suture than in JIGSAWS.

Fig. 7

Bench-top models used in JIGSAWS (left) and MISTIC-SL (right)

We evaluated our method using a suture throw maneuver as the query. The suture throw maneuver begins when the needle is inserted into the tissue and ends when the needle is rotated or pulled out of the tissue. A suture throw is a fundamental activity that can be observed within most surgical procedures and is an essential component of most surgical skills training curricula.

Evaluation method and metrics

The QBE method involves detecting segments in a trial that are similar to a query. Thus the unit experiment is composed of a suture throw exemplar X and a target trial Y, and an output of predicted substrings $P = \{P_j=(a_j, b_j), j = 1, 2,\ldots , |P|\}$, plus the set of ground-truth suture throws $G = \{G_i=(a_i, b_i), i = 1, 2,\ldots , |G|\}$. A unit experiment E is therefore a 4-tuple:

$$\begin{aligned} E = (X, Y, G, P ) \end{aligned}$$

(12)

The evaluation for E is not straightforward since the correspondence between G and P are undetermined. In addition, the lengths of the detected substrings vary, which also affect performance of the method. Inspired by [4], we developed a two-step approach to create a one-to-one correspondence between P and G that involves DTW-thresholding and bipartite matching.

We regarded substrings of Y denoted by the predicted and ground-truth labels as nodes of a graph and thus specified two sets of nodes by P and G. To determine the edges, we first computed the DTW distance between each pair of overlapping substrings $(Y_{G_i}, Y_{P_j})$, then applied a threshold $d_\mathrm {thr}$ on the DTW distances to construct an adjacency matrix. A large threshold admits more matches (high recall), while a small threshold permits fewer, more accurate matches (high precision).

The graph is bipartite since all connections are across the two sets G and P. However, a node in one set may be connected with two or more nodes from the other set. We used the maximum flow algorithm to find the maximum bipartite match in the graph. Let $G'$ and $P'$ denote the resulting bipartite match where $P'_i$ exclusively corresponds to $G'_i$. Given the one-to-one correspondence of $G'$ and $P'$ from bipartite matching, we defined $hit = |P'| = |G'|$. We computed recall, precision, F1 score to evaluate performance of the QBE method at the segment level.²

For evaluation at the frame level, we defined an evaluation metric called J-score which is based on the Jaccard Index [9]:

$$\begin{aligned} J(P, G) = \sqrt{\sum _{i=1}^{|G|}\max _j\frac{G_i\cap P_j}{G_i\cup P_j}} \end{aligned}$$

(13)

The J-score reflects the extent of overlap between the prediction and ground-truth. The square root rescales the value so that it is comparable with the metrics we used for evaluation at the segment level.

Experimental setup

We anticipated that the performance of the QBE method would be influenced by two factors: (1) whether the query and target trial were performed by the same surgeon (proxy for surgeon-specific style variations and technical skill/expertise), and (2) whether the query and target trial were performed on the same day/session or on different days (proxy for surgeons’ level of exhaustion/alertness and learning effect). Therefore, to evaluate the performance of the method and to study how the performance will be affected by the above-mentioned factors, we designed three different experiment setups: (1) same surgeon same trial (SSST), where the query originates from the target trial; (2) same surgeon different trial (SSDT), where the query originates from a different trial performed by the same surgeon that performed the trial being searched; and (3) different surgeon (DS), where the query and the target trial were performed by different surgeons.

In SSST, we adopted a viewpoint of a one-way analysis of variance (ANOVA) and assumed that the surgeon-specific factor is reflected by the mean of each surgeon. Given a trial containing q queries, we conducted q unit experiments as defined in (12) and averaged the evaluation metrics for the trial. We reported the global mean and variance for each evaluation metric.

In SSDT, we designed a leave-one-trial-out cross validation for each surgeon. For surgeon i who performed $n_i$ trials, we sampled a query from a left-out trial j and used trial k ($k\ne j$) as a target. We created a matrix (for each evaluation metric) $M^i$ of size $n_i\times n_i$ to denote all the experiments for surgeon i, where $M^i_{jk}$ denotes a unit experiment if $j\ne k$, and $M^i_{jj}$ (diagonal element) is empty. The average of j-th row (excluding the diagonal) indicates performance of the QBE method with queries derived from trial j. The average of k-th column indicates performance of the QBE method with trial k as the target. We reported the overall performance in SSDT by averaging across surgeons.

In DS, we designed a leave-one-surgeon-out cross validation experiment. A matrix M of size $u\times u$ was created for the cross validation experiment, where $M_{ij}$ denotes the experiment of a query from one surgeon i applied to a target trial from surgeon j. In each experiment, we sampled q queries from surgeon i, and t trials from surgeon j. The metrics for $M_{ij}$ are averaged over all the $q\times t$ experiments. We reported the performance for each surgeon as the target, and the overall performance in DS by averaging across surgeons.

Results and discussion

Table 1 shows the overall performance of our QBE method on JIGSAWS and MISITC-SL. On both datasets, the QBE method demonstrates a high recall (87–93 % on JIGSAWS, 75–87 % on MISTIC-SL), which is a more important evaluation metric in the surgical teaching context because false negatives or misses are more consequential than false alarms. The recall is robust to experimental settings on both datasets, indicating that it is less sensitive to the surgeon-specific style variations and day/session variations. Precision drops (72–53 %) as experimental settings changes from SSST to DS on the MISTIC-SL dataset, indicating that our method is sensitive to surgeon-specific style variations in a way that it may introduce extraneous segments matching the query.

Table 1 Overall performance of QBE method on JIGSAWS (a) and MISTIC-SL (b)

The performance of our QBE method on JIGSAWS is better than its performance on MISTIC-SL, which may be explained by differences in task complexity and annotation protocols. The task in JIGSAWS included only suture throws, whereas the task in MISTIC-SL included both suture throws and knot-tying. In addition, subjects in the MISTIC-SL dataset were free to manipulate the camera. The task complexity and camera movement resulted in a greater variation in motion in MISTIC-SL compared with JIGSAWS. Furthermore, the ground-truth in MISTIC-SL sometimes had missing annotations when a surgeon made an error in performance and repeated a maneuver; any suture throw detected in the unannotated region was deemed a false alarm by default in our evaluation.

Consistent with observations in previous research on surgical activity detection [2, 8, 15, 16, 18, 21], surgeon-specific style variations affected performance of our QBE method. This is evident from the somewhat lower recall and precision in DS than in SSST and SSDT for both datasets. The drop in performance under the DS setup was larger in MISTIC-SL than in JIGSAWS, perhaps because greater task complexity in MISTIC-SL led to more surgeon-specific style variations. Finally, our estimates of evaluation metrics in MISTIC-SL are less robust because the number of trials per surgeon was more variable than in JIGSAWS.

Conclusion

In this paper, we described a query-by-example approach to detect activity segments of interest in surgical motion data and evaluated its performance. Our QBE method does not require intensive manual annotation for training the system, nor does it apply strong modeling assumptions. Thus it is a flexible tool to efficiently chapter and index activity segments within long surgical data recordings. We also proposed a novel algorithm for substring search called asymmetric subsequence dynamic time warping. Our experiments on surgical maneuver detection on two robotic surgical training datasets showed that the QBE method has good recall, moderate precision. Performance of our QBE method is sensitive to the complexity of task composition and surgeon-specific style variations.

Our QBE method may be applied to search for queries other than surgical maneuvers. It may be applied to other types of queries such as gestures or tasks, and with queries and target trials derived from different datasets. In future work, we will evaluate performance of our QBE method on different types of queries that may or may not be semantically meaningful. Future work will also include evaluating performance of our QBE method on data captured in the operating room, and other types of data such as video images or events.