Computing Weakly Reversible Deficiency Zero Network Translations Using Elementary Flux Modes

Abstract

We present a computational method for performing structural translation, which has been studied recently in the context of analyzing the steady states and dynamical behavior of mass-action systems derived from biochemical reaction networks. Our procedure involves solving a binary linear programming problem where the decision variables correspond to interactions between the reactions of the original network. We call the resulting network a reaction-to-reaction graph and formalize how such a construction relates to the original reaction network and the structural translation. We demonstrate the efficacy and efficiency of the algorithm by running it on 508 networks from the European Bioinformatics Institutes’ BioModels database. We also summarize how this work can be incorporated into recently proposed algorithms for establishing mono- and multistationarity in biochemical reaction systems.

1 Introduction

A chemical reaction network (CRN) is given by a directed graph where the vertices are complexes (i.e., linear combinations of the interacting species) and the edges are reactions (i.e., interactions between species). Under appropriate physical assumptions, such as spatial homogeneity and abundant molecularity, the system is often modeled by an autonomous system of ordinary differential equations in the concentrations of the chemical species. The use of such dynamical models is widespread in systems biology (Alon 2007; Ingalls 2013).

The relationship between the structural properties of a CRN and the dynamical and steady-state behavior of the resulting dynamical systems has been studied from a variety of perspectives, including flux balance analysis (Orth et al. 2010), extreme pathway analysis (Wiback and Palsson 2002), and stoichiometric network analysis (Clarke 1980, 1988). Recent study has focused on a structural parameter known as the deficiency. It was shown by Feinberg (1972, 1972) that, if a mass-action system is weakly reversible and has a deficiency of zero, then it necessarily has complex-balanced steady states (deficiency zero theorem). Complex balancing guarantees uniqueness and stability of steady states for all parameter values and initial conditions and also affords a simple monomial parametrization of the steady-state set (Horn and Jackson 1972; Craciun et al. 2009). Further connections between the deficiency and the steady states of mass-action systems have also been established (Feinberg 1987, 1988, 1989, 1995a, b; Craciun et al. 2009; Dickenstein and Pérez Millán 2011).

The study of the deficiency was recently initiated in generalized chemical reaction networks (GCRNs) by Müller and Regensburger (2012, 2014). In a GCRN, each vertex in the reaction graph is associated with two potentially distinct complexes, one for the stoichiometry and one for the kinetic rate of the reaction. Surprisingly, for weakly reversible generalized mass-action systems which have a stoichiometric and kinetic-order deficiency of zero, we still obtain a simple monomial parametrization of the steady-state set. A process for relating CRNs and GCRNs, called network translation, was furthermore established by Johnston (2014). Network translation consists of restructuring a given CRN in such a way that the resulting network (a GCRN) can be used to guarantee dynamical and steady-state properties of the original CRN. The process has been utilized to establish connections between chemical reaction network theory (Feinberg 1979), the algebraic study of toric varieties (Craciun et al. 2009; Pérez Millán et al. 2012; Dickenstein and Pérez Millán 2018), and biochemical reaction modeling (Conradi and Shiu 2015; Tonello and Johnston 2018). Recent work has also established a deficiency-based method for constructing rational parametrizations of steady-state sets for a broad class of mass-action systems (Johnston et al. 2018).

In this paper, we focus on computational methods for performing the structural component of network translation, which we call structural translation. In general, given a biochemical reaction network of realistic scale, it is challenging to determine a suitable (e.g., weakly reversible, deficiency zero) structural translation. We extend the recent computational work of Johnston (2015) and Tonello and Johnston (2018) by introducing an elementary flux mode-based approach for performing structural translation. To accomplish this, we introduce a directed graph (called a reaction-to-reaction graph) which treats the reactions of a network as vertices and uses the elementary modes to form directed cycles. Under certain rules on the connections on this graph, a weakly reversible and deficiency zero structural translation of the original network can then be constructed. We formulate the construction of this reaction-to-reaction graph as a binary linear programming problem. Such problems can be solved in polynomial time in the number of constraints by Lenstra’s algorithm (1983).

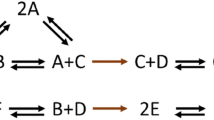
Consider the histidine kinase system given in Fig. 1a, which is modified from an example by Conradi et al. (2017) and reproduced by Johnston et al. (2018). This network has two elementary flux modes (sets of reactions which balance the net stoichiometry change), namely, $e_1 = \{ r_1, r_2, r_4\}$ and $e_2 = \{ r_2, r_3 \}$. Consistent with these elementary flux modes, we can construct the reaction-to-reaction graph given in Fig. 1b where the reactions are treated as vertices and there is a minimal cycle on each elementary flux mode of the original network. From this reaction-to-reaction graph, we can then construct the structural translation of the original network given in Fig. 1c. Notably, the structural translation is weakly reversible and deficiency zero, while the original network is neither.

The paper is organized as follows. In Sect. 2, we introduce the terminology and background results relevant to chemical reaction networks and structural translation. In Sect. 3, we introduce the notion of a reaction-to-reaction graph, demonstrate how it is related to the structure of a chemical reaction network, and introduce a binary linear programming framework for constructing them. In Sect. 4, we present the output of a run of the algorithm on the European Bioinformatics’ BioModels database (Li et al. 2010) and detail a few biochemical examples. In Sect. 5, we summarize the results of the paper. In “Appendix A,” we demonstrate how the results of our algorithm may be utilized to construct steady-state parametrizations of mass-action systems according to Lemma 12 and Theorem 14 of Johnston et al. (2018) and, when possible, establish mono- or multistationarity according to Corollary 2 of Conradi et al. (2017).

Fig. 1

A chemical reaction network (a) corresponding to a histidine kinase network where X and Y are two signaling proteins and p is a phosphate group (Conradi et al. 2017). This CRN has elementary flux modes $\{r_1, r_2, r_4\}$ and $\{r_2, r_3\}$ which correspond to the directed cycles in the reaction-to-reaction graph (b). The structural translation c has the same elementary flux modes and stoichiometric vectors as the CRN, but the elementary flux modes correspond to cycles

We use the following notation throughout:

• ${\mathbb {R}}_{> 0}^n = \{ (x_1, \ldots , x_n) \mid x_i > 0, \; i = 1, \ldots , n\}$

• ${\mathbb {R}}_{\ge 0}^n = \{ (x_1, \ldots , x_n) \mid x_i \ge 0, \; i = 1, \ldots , n\}$

• ${\mathbf {0}}^{m \times n}$ is the $m \times n$ matrix with ${\mathbf {0}}_{i,j} = 0$ for all $i = 1, \ldots , m$ and $j = 1, \ldots , n$

• $I^{m \times m}$ is the m-dimensional identity matrix

• For an indexed set ${\mathcal {X}} \subseteq \{ X_1, \ldots , X_n \}$, $\text{ supp }({\mathcal {X}}) = \{ i \in \{1, \ldots , n \} \mid X_i \in {\mathcal {X}}\}$.

• For a vector ${\mathbf {v}} \in {\mathbb {R}}_{\ge 0}^n$, $\text{ supp }({\mathbf {v}}) = \{ i \in \{ 1, \ldots , n \} \mid v_i > 0 \}$

2 Background

In this section, we present the terminology relevant to chemical reaction networks, structural translation, and elementary flux modes. Note that we only introduce the terminology required to establish the computational program presented in Sect. 3.3. In particular, we do not use the full generality of generalized chemical reaction networks as given by Müller and Regensburger (2012, 2014).

2.1 Chemical Reaction Networks

We define a species set$\mathcal {S}= \{ X_1, \ldots , X_m\}$ and a complex set$\mathcal {C}= \{ y_1, \ldots , y_n\}$ whose elements (complexes) are linear combinations of the species, i.e.,

$$\begin{aligned} y_i = \sum _{j=1}^m y_{ij} X_j, \quad i=1,\ldots , n. \end{aligned}$$

The coefficients $y_{ij} \in {\mathbb {Z}}_{\ge 0}$ are called stoichiometric coefficients. Allowing a slight abuse of notation, we let $y_i$ denote both the complex itself and the corresponding complex vector$y_i = (y_{i1}, \ldots , y_{im}) \in {\mathbb {Z}}_{\ge 0}^m$. The reaction set is given by $\mathcal {R}= \{ r_1, \ldots , r_r \} \subseteq \mathcal {C}\times \mathcal {C}$ where we represent individual reactions as either ordered pairs of complexes (i.e., $r_k = (y_i,y_j)$) or directed edges (i.e., $r_k = y_i \rightarrow y_j$). It will occasionally be convenient to use mappings $s, p: \text{ supp }(\mathcal {R}) \mapsto \text{ supp }(\mathcal {C})$ such that s (respectively, p) maps the source (respectively, product) of each reaction to the corresponding complex, i.e., $r_k = y_{s(k)} \rightarrow y_{p(k)}$. A chemical reaction network (CRN) is given by the triple $(\mathcal {S}, \mathcal {C}, \mathcal {R})$.

The reaction graph of a CRN is the directed graph $G = (V,E)$ where the vertices are the complexes (i.e., $V = \mathcal {C}$) and the edges are the reactions (i.e., $E = \mathcal {R}$). The connected components of the reaction graph of a CRN are called linkage classes, while the strongly connected components are called strong linkage classes. We will let $\ell$ denote the number of linkage classes in a CRN. A CRN is said to be weakly reversible if its linkage classes and strong linkage classes coincide. To each reaction $r_k = y_{s(k)} \rightarrow y_{p(k)} \in {\mathcal {R}}$ we may associate a reaction vector$y_{p(k)} - y_{s(k)} \in {\mathbb {Z}}^{m}$. The stoichiometric matrix of a CRN is given by the matrix $\varGamma \in {\mathbb {Z}}^{m \times r}$ with columns defined by $\varGamma _{\cdot , k} = y_{p(k)} - y_{s(k)}$. The stoichiometric subspace of a CRN is given by $S = \text{ im }(\varGamma )$.

Consider a time-dependent vector of nonnegative chemical concentrations ${\mathbf {x}}(t) = (x_1(t), \ldots , x_m(t)) \in {\mathbb {R}}_{\ge 0}^m$. Assuming sufficient molecularity of chemical species and mass-action kinetics, it is common to assign each reaction $r_i \in \mathcal {R}$ a rate constant $k_i \in {\mathbb {R}}_{> 0}$ and model the evolution of ${\mathbf {x}}(t)$ via the mass-action system

$$\begin{aligned} \frac{{\mathrm{d}{\mathbf {x}}}}{{\mathrm{d}t}} = \varGamma R({\mathbf {x}}) \end{aligned}$$

(1)

where $R({\mathbf {x}}) \in {\mathbb {R}}_{\ge 0}^r$ has entries $R_i({\mathbf {x}}) = \prod _{j=1}^m x_j^{[y_{s(i)}]_j}$ (Guldberg and Waage 1864). Other widely used kinetic choices for $R({\mathbf {x}})$ include Michaelis–Menten and Hill kinetics (Hill 1910; Michaelis and Menten 1913). Note that $d{\mathbf {x}}/dt \in S$ for all $t \ge 0$ and consequently solutions are restricted to stoichiometric compatibility classes, i.e., ${\mathbf {x}}(t) \in (S+ {\mathbf {x}}_0) \cap {\mathbb {R}}_{\ge 0}^m$ for $t \ge 0$. The analysis we perform in this paper will focus largely on the structural aspects of CRNs rather than dynamical equations (1). That is, we focus on $\varGamma$ rather than $R({\mathbf {x}})$.

We may further factor the stoichiometric matrix $\varGamma$ by introducing a complex matrix$Y \in {\mathbb {Z}}_{\ge 0}^{m \times n}$ with columns $Y_{\cdot ,i} = y_i$ and an incidence matrix$I_a \in \{ -1,0,1 \}^{n \times r}$ with entries $[I_a]_{ik} = -1$ if $s(k) = i$, $[I_a]_{ik} = 1$ if $p(k) = i$, and $[I_a]_{ik} = 0$ otherwise. It can be easily verified that $\varGamma = YI_a$. The deficiency of a CRN is a nonnegative parameter defined by $\delta = \text{ dim }(\text{ ker } (Y) \cap \text{ im } (I_a))$. Alternatively, the deficiency can be computed by the formula $\delta = n - \ell - \text{ dim }(S)$ (Johnston 2014). The deficiency was first introduced by Feinberg (1979, 1972) and has been used extensively since in the context of steady states of mass-action systems (Feinberg 1987, 1988, 1989, 1995a, b; Müller and Regensburger 2012; Müller et al. 2014; Johnston 2014).

Consider the following example.

Example 1

Reconsider the histidine kinase network from Fig. 1a.

We have the following sets:

$$\begin{aligned} \mathcal {S}= & {} \{ X, X_p, Y, Y_p \}\nonumber \\ \mathcal {C}= & {} \{ X, X_p, X_p + Y, X+Y_p, Y_p, Y \}\nonumber \\ \mathcal {R}= & {} \{ X \rightarrow X_p, X_p + Y \rightarrow X + Y_p, X + Y_p \rightarrow X_p + Y, Y_p \rightarrow Y\}. \end{aligned}$$

(2)

The network has six complexes ($n = 6$) and three linkage classes ($\ell = 3$). The second linkage class is strongly connected, while the first and third are not. It follows that the network is not weakly reversible. Using the ordering of species and reactions given above, we can compute that the network has the following structural matrices

$$\begin{aligned} \varGamma = \left[ \begin{array}{cccc} -\,1 &{} 1 &{} -\,1 &{} 0\\ 1 &{} -\,1 &{} 1 &{} 0 \\ 0 &{} -\,1 &{} 1 &{} 1 \\ 0 &{} 1 &{} -\,1 &{} -\,1 \end{array}\right] = \left[ \begin{array}{cccccc} 1 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} 1 &{} 1 &{} 0 \end{array}\right] \left[ \begin{array}{cccc} -\,1 &{} 0 &{} 0 &{} 0 \\ 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} -\,1 &{} 1 &{} 0 \\ 0 &{} 1 &{} -\,1 &{} 0 \\ 0 &{} 0 &{} 0 &{} -\,1 \\ 0 &{} 0 &{} 0 &{} 1 \end{array}\right] = Y I_a. \end{aligned}$$

(3)

We have that $\text{ dim }(S) = 2$ so that the deficiency is $\delta = n - \ell - \text{ dim }(S) = 6 - 3 - 2 = 1$. Alternatively, we can compute that $\delta = \text{ dim }(\text{ ker } (Y) \cap \text{ im } (I_a)) = 1$.

2.2 Structural Translation

We introduce the following structural notion of network translation, which is weaker than those presented by Johnston (2014, 2015), Tonello and Johnston (2018), and Johnston et al. (2018).

Definition 1

Consider two CRNs $(\mathcal {S},\mathcal {C},\mathcal {R})$ and $(\mathcal {S},\mathcal {C}',\mathcal {R}')$ with corresponding complex, incidence, and stoichiometric matrices Y, $I_a$, $\varGamma$, $Y'$, $I_a'$, and $\varGamma '$ as defined in Sect. 2.1. We say that $(\mathcal {S},\mathcal {C},\mathcal {R})$ and $(\mathcal {S},\mathcal {C}',\mathcal {R}')$ are structural translations of one another if $\varGamma = YI_a = Y'I_a' = \varGamma '$.

Intuitively, two CRNs are structural translations of one another if, despite potentially different complexes and reactions (i.e., the Y and $I_a$), they have the same reaction vectors (i.e., columns of $\varGamma$). In practice, we will typically have a CRN $(\mathcal {S},\mathcal {C},\mathcal {R})$ given to us and want to construct a CRN $(\mathcal {S},\mathcal {C}',\mathcal {R}')$ which has specific structure properties. Consequently, we will typically refer to $(\mathcal {S},\mathcal {C},\mathcal {R})$ as the original network and $(\mathcal {S},\mathcal {C}',\mathcal {R}')$ as the structural translation.

Network translation can be visualized by the operation of adding or subtracting linear combinations of species, known as translation complexes, from individual reactions. The summation of the original network’s complexes and corresponding translation complexes then produces the translated network’s complexes. Formally, we let $\varLambda = \{ \alpha _1, \ldots , \alpha _r \}$ where $\alpha _i \in {\mathbb {R}}^m$, $i = 1, \ldots , r$, denote a set of translation complexes. We represent the operation of translating the reaction $r_k = y_{s(k)} \rightarrow y_{p(k)} \in \mathcal {R}$ by the translation complex $\alpha _k$ as

for $k = 1,\ldots , r$. This operation produces the translated reactions $y_{s(k)} + \alpha _k \rightarrow y_{p(k)} + \alpha _k \in {\mathcal {R}}'$ and translated complexes $y_{s(k)} + \alpha _k, y_{p(k)} + \alpha _k \in \mathcal {C}'$. Note that this may produce repeated complexes and therefore new connections in the corresponding reaction graph. Since the net stoichiometric change across each reaction is unaltered by this operation (i.e., $y_{p(k)} - y_{s(k)} = (y_{p(k)} + \alpha _k) - (y_{s(k)} + \alpha _k) = y'_{p(k)} - y'_{s(k)}$) we have that $\varGamma = \varGamma '$ and the networks are structural translations of one another.

Consider the following example.

Example 2

Reconsider the histidine kinase network from Fig. 1a taken with the following translation scheme

That is, we translate $r_1$ by $\alpha _1 = Y$, translate $r_2$ and $r_3$ by $\alpha _2 = \alpha _3 = \emptyset$, and translate $r_4$ by $\alpha _4 = X$. This produces the structural translation in Fig. 1c.

Notably, the stoichiometric changes across each reaction in the two networks are identical. Formally, for the network in Fig. 1c, we have the sets

$$\begin{aligned} \mathcal {S}= & {} \{X, X_p, Y, Y_p \} \\ \mathcal {C}= & {} \{X+Y, X_p + Y, X+Y_p\}. \end{aligned}$$

Using this ordering of species and complexes, we can determine the following structural matrices:

$$\begin{aligned} \varGamma ' = \left[ \begin{array}{cccc} -\,1 &{} 1 &{} -\,1 &{} 0 \\ 1 &{} -\,1 &{} 1 &{} 0 \\ 0 &{} -\,1 &{} 1 &{} 1 \\ 0 &{} 1 &{} -\,1 &{} -\,1 \end{array}\right] = \left[ \begin{array}{ccc} 1 &{} 0 &{} 1 \\ 0 &{} 1 &{} 0 \\ 1 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right] \left[ \begin{array}{cccc} -\,1 &{} 0 &{} 0 &{} 1 \\ 1 &{} -\,1 &{} 1 &{} 0 \\ 0 &{} 1 &{} -\,1 &{} -\,1 \end{array} \right] = Y' I_a' \end{aligned}$$

(5)

Since $\varGamma = \varGamma '$ where $\varGamma$ is from (3), we have that the networks in Fig. 1a, c are structural translations of one another by Definition 1.

It is notable that the CRN in Fig. 1c is weakly reversible and deficiency zero, while the original CRN in Fig. 1a is not weakly reversible and has a deficiency of one. The structure of the CRN in Fig. 1c can be used to establish properties about the steady-state set of mass-action system (1) corresponding to the network in Fig. 1a by the results of Johnston et al. (2018) and Conradi et al. (2017). We outline some of these methods in “Appendix A.”

2.3 Elementary Flux Modes

The following structural property of CRNs will factor significantly in our construction of structural translations in Sect. 3.

Definition 2

Consider a CRN $(\mathcal {S},\mathcal {C},\mathcal {R})$ with stoichiometric matrix $\varGamma$ and incidence matrix $I_a$. Then:

• 1. A vector $e_i \in {\mathbb {R}}_{\ge 0}^r$ is an elementary flux mode of the CRN if $e_i \in \text{ ker }(\varGamma )$ and $e_i$ is not a convex combination of any other $e_j, e_k \in \text{ ker }(\varGamma ) \cap {\mathbb {R}}_{\ge 0}^r$. The set of elementary flux modes of a CRN will be denoted ${\mathcal {E}} = \{e_1, \ldots , e_p \}$.

• 2. The elementary flux cone is defined as $\text{ cone }({\mathcal {E}}) = \text{ ker }(\varGamma ) \cap {\mathbb {R}}_{\ge 0}^r$.

• 3. An elementary flux mode $e_i \in {\mathcal {E}}$ is called a cyclic generator of the CRN if $e_i \in \text{ ker }(I_a)$.

• 4. An elementary flux mode $e_i \in {\mathcal {E}}$ is called a stoichiometric generator of the CRN if $e_i \not \in \text{ ker }(I_a)$.

• 5. The set of elementary flux modes ${\mathcal {E}}$ is unitary if every entry of every $e_i \in {\mathcal {E}}$ is a one or a zero.

• 6. The set of elementary flux modes ${\mathcal {E}}$covers the reaction set $\mathcal {R}$ if $\text{ cone }({\mathcal {E}})\,\cap \,{\mathbb {R}}_{> 0}^r \not = \emptyset$.

Note that the set of elementary modes ${\mathcal {E}} = \{ e_1, \ldots , e_p \}$ consists of the extremal generators of the elementary flux cone, $\text{ cone }({\mathcal {E}})$.

In this paper, we only consider networks whose elementary flux modes are all unitary. In such cases, we have that $e_i$ is completely determined by $\text{ supp }(e_i)$ and, consequently, we will allow $e_i$ to correspond to both the elementary flux mode and its support, e.g., we will use $e_i = (1, 0, 1, 1, \ldots )$ and $e_i = \{ r_1, r_3, r_4, \ldots \}$ interchangeably. We may interpret unitary elementary flux modes as sets of reactions which, if taken in any order, would result in no net gain or loss of any species. A cyclic generator furthermore has the property that this sequence of reactions corresponds to a directed cycle in the reaction graph of the CRN. Elementary flux modes have played a significant role recently in metabolic engineering, although efficient computation of the set ${\mathcal {E}}$ remains challenging (Zanghellini et al. 2013).

Consider the following example.

Example 3

Reconsider the histidine kinase example given in Fig. 1a and the structural translation given in Fig. 1c. Also consider the corresponding matrices Y and $I_a$ given in (3) and $Y'$ and $I_a'$ given in (5). Since $\varGamma = \varGamma '$, we have that the elementary modes of the two CRNs coincide. We can compute that $e_1 = (1,1,0,1)$ and $e_2 = (0,1,1,0)$. Since $e_1$ and $e_2$ only consist of zeros and ones, we have that the CRNs have unitary elementary modes. We therefore write $e_1 = \{ r_1, r_2, r_4\}$ and $e_2 = \{ r_2, r_3\}$. Furthermore, since $\text{ ker }(\varGamma ) \cap {\mathbb {R}}_{> 0}^r \not = \emptyset$, we have that ${\mathcal {E}}$ covers $\mathcal {R}$.

For the CRN in Fig. 1a $e_1$ does not correspond to a cycle but $e_2$ does so that $e_1$ is a stoichiometric generator of the CRN, while $e_2$ is a cyclic generator. For the CRN in Fig. 1c, we have that both $e_1$ and $e_2$ correspond to cycles so that $e_1$ and $e_2$ are both cyclic generators of the CRN. Structural translation scheme () therefore converted the stoichiometric generator $e_1$ into a cyclic generator. The primary objective of the methods presented in Sect. 3 will be to use structural translation to convert stoichiometric generators into a cyclic generator. Notably, if all of the stoichiometric generators are converted into cyclic generators, then the deficiency of the resulting network is zero.

3 Main Results

In general, given a CRN $(\mathcal {S},\mathcal {C},\mathcal {R})$, a structural translation $(\mathcal {S},\mathcal {C}',\mathcal {R}')$ with desirable properties (e.g., weak reversibility, deficiency zero) is not known and therefore must be constructed. For biochemical reaction networks of realistic size, computational implementation is necessary.

Computational algorithms using mixed-integer linear programming (MILP) have been explored recently by Johnston (2015) and Tonello and Johnston (2018). Johnston (2015) presented a MILP program for performing network translation by reconstructing the reaction graph of the original network. The method, however, depended upon the translated network’s complexes and the network’s rate constants, both of which are typically not a priori known. The method introduced by Tonello and Johnston (2018), by contrast, relies only upon knowledge of the network’s elementary flux modes and attempts to convert the network’s stoichiometric generators into cyclic generators. The method, however, requires a large number of decision variables and relies sensitively on the ordering of the reactions. For example, using the method presented in this paper, entry biomd0000000653 in the European Bioinformatics Institute’s BioModels database, which has 124 reactions, computes in 4 minutes and 37 seconds on the primary author’s professional use laptop but would not load using the method of Tonello and Johnston (2018).

In this section, we present a novel computational method by which to compute structural translations. Our method depends upon a new CRN object which we call a reaction-to-reaction graph. We show how this object relates to the underlying CRN and then introduce a binary linear programming (BLP) problem on this graph which can be used to establish structural translations. This represents a significant improvement over existing methods since BLP problems can be solved in polynomial time in the number of constraints by Lenstra’s algorithm (1983).

3.1 Reaction-to-Reaction Graph

We introduce the following.

Definition 3

A directed graph $G^\mathcal {R}= (V^\mathcal {R}, E^\mathcal {R})$ is a reaction-to-reaction graph of a CRN $(\mathcal {S},\mathcal {C},\mathcal {R})$ if $V^\mathcal {R}= \mathcal {R}$ and $E^\mathcal {R}\subset \mathcal {R}\times \mathcal {R}$. Furthermore, we say that $(\mathcal {S},\mathcal {C},\mathcal {R})$ and $G^\mathcal {R}$ are:

• 1. product-to-source compatible (PS-compatible) if, for any $r_i = y_{s(i)} \rightarrow y_{p(i)}$ and $r_j = y_{s(j)} \rightarrow y_{p(j)}$, $(r_i,r_j) \in E^\mathcal {R}$ if and only if $y_{p(i)} = y_{s(j)}$.

• 2. common source compatible (CS-compatible) if $y_{s(i)} = y_{s(j)}$ and $(r_k,r_i) \in E^\mathcal {R}$ implies $(r_k,r_j) \in E^\mathcal {R}$, i.e., if $r_i$ and $r_j$ have a common source complex, then every reaction $r_k$ with an edge to $r_i$ has an edge to $r_j$.

• 3. elementary flux mode compatible (EM-compatible) if every elementary flux mode of the CRN corresponds to the vertices of a minimal directed cycle in $G^\mathcal {R}$, and vice versa.

A reaction-to-reaction graph treats the reactions of a network as its vertices, while the edges enforce additional conditions on the relationship with the underlying CRN (PS-, CS-, or EM-compatibility). The condition of PS-compatibility makes a correspondence between edges $(r_i, r_j) \in E^\mathcal {R}$ in the reaction-to-reaction graph and junctions of the following form in the reaction graph of the CRN:

$$\begin{aligned} \cdots {\mathop {\longrightarrow }\limits ^{r_i}} y {\mathop {\longrightarrow }\limits ^{r_j}} \cdots \end{aligned}$$

The condition of CS-compatibility joins reactions from common source complexes, e.g.,

$$\begin{aligned} \cdots {\mathop {\longrightarrow }\limits ^{r_k}} y \begin{array}{c} {}^{r_i} \\ {}_{r_j} \end{array} \begin{array}{c} \nearrow \\ \searrow \end{array} \end{aligned}$$

forces $(r_k,r_i) \in E^\mathcal {R}$ iff $(r_k,r_j) \in E^\mathcal {R}$. Note that a reaction-to-reaction graph is trivially CS-compatible with a CRN if there are no reactions with a common source (see Fig. 2a). The condition of EM-compatibility forces a correspondence between elementary flux modes in the CRN and directed cycles in the reaction-to-reaction graph.

Our goal is to construct reaction-to-reaction graphs which are CS- and EM-compatible with a given CRN $(\mathcal {S},\mathcal {C},\mathcal {R})$ and then enforce PS-compatibility to construct a network translation $(\mathcal {S},\mathcal {C}',\mathcal {R}')$. Consider the following examples.

Fig. 2

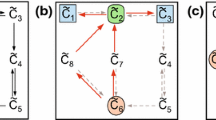
Two reaction-to-reaction graphs of four reactions, labeled $\{ r_1, r_2, r_3, r_4\}$. The reaction-to-reaction graph on the left is PS- and CS-compatible with the CRN in Fig. 1a, while the reaction-to-reaction graph on the right is EM- and CS-compatible with the CRN in Fig. 1a and PS-, CS-, and EM-compatible with the CRN in Fig. 1c.

Example 4

Reconsider the histidine network given in Fig. 1a. We can construct a reaction-to-reaction graph which is PS- and CS-compatible, but not EM-compatible, with this CRN by selecting the edges $E^\mathcal {R}= \{ (r_2,r_3),$$(r_3,r_2) \}$. This gives the reaction-to-reaction graph in Fig. 2a. Note that we do not include any interactions involving $r_1$ and $r_4$ since these reactions do not connect with any others in the reaction graph of the CRN.

Alternatively, we may construct a reaction-to-reaction graph which is EM- and CS-compatible but not PS-compatible to the CRN in Fig. 1a. We select edges such that there are minimal cycles on $e_1 = \{ r_1, r_2, r_4\}$ and $e_2 = \{ r_2, r_3\}$. Selecting $E^\mathcal {R}= \{ (r_1,r_2),(r_2,r_4),(r_4,r_1),(r_2,r_3),(r_3,r_2)\}$ gives the reaction-to-reaction graph given in Fig. 2b. It can be checked exhaustively that there is no reaction-to-reaction graph which is all of PS-, CS-, and EM-compatible with this CRN.

Example 5

Consider the CRN in Fig. 1a. We may construct a reaction-to-reaction graph which is PS-, CS-, and EM-compatible with the CRN in Fig. 1c by taking $E^\mathcal {R}= \{ (r_1,r_2),(r_2,r_4),(r_4,r_1),(r_2,r_3),(r_3,r_2)\}$. Notably, this edge set coincides with the edge set for the reaction-to-reaction graph which was CS- and EM-compatible to the CRN in Fig. 1a.

Remark 1

Notice that there are no implications of the reaction-to-reaction graph on the source complexes of the corresponding CRN. In particular, a single vertex (reaction) may have multiple source complexes. For example, consider the reaction-to-reaction graph in Fig. 2b as it relates to the CRN in Fig. 1a. We have that $(r_1,r_2) \in E^\mathcal {R}$ and $(r_3,r_2) \in E^\mathcal {R}$; however, we have $y_{s(1)} = X \not = X + Y_p = y_{s(3)}$.

3.2 Main Theory

In order to state our objectives in Sect. 3.3, we need to further understand the relationship between CRNs and PS-, CS-, and/or EM-compatibility of reaction-to-reaction graphs.

We have the following results.

Lemma 1

Consider a CRN $(\mathcal {S},\mathcal {C},\mathcal {R})$ and a reaction-to-reaction graph $G^\mathcal {R}= (V^\mathcal {R}, E^\mathcal {R})$ which is PS-compatible with $(\mathcal {S},\mathcal {C},\mathcal {R})$. Then $G^\mathcal {R}$ is CS-compatible with $(\mathcal {S},\mathcal {C},\mathcal {R})$.

Proof

Consider a CRN $(\mathcal {S},\mathcal {C},\mathcal {R})$ and let $G^\mathcal {R}= (V^\mathcal {R}, E^\mathcal {R})$ be a reaction-to-reaction graph which is PS-compatible with $(\mathcal {S},\mathcal {C},\mathcal {R})$. Suppose that $(r_k,r_i) \in E^\mathcal {R}$ and $y_{s(i)} = y_{s(j)}$ for some $r_j \in \mathcal {R}$. Since $G^\mathcal {R}$ is PS-compatible with $(\mathcal {S},\mathcal {C},\mathcal {R})$, we have $y_{p(k)} = y_{s(i)} = y_{s(j)}$. It follows from PS-compatibility that $(r_k,r_j) \in E^\mathcal {R}$ and therefore CS-compatibility is attained. $\square$

Lemma 2

Consider a CRN $(\mathcal {S},\mathcal {C},\mathcal {R})$ and a reaction-to-reaction graph $G^\mathcal {R}= (V^\mathcal {R}, E^\mathcal {R})$ which is PS-compatible with $(\mathcal {S},\mathcal {C},\mathcal {R})$. Suppose $(\mathcal {S},\mathcal {C},\mathcal {R})$ has a set of elementary modes ${\mathcal {E}} = \{e_1, \ldots , e_p \}$ which is unitary and covers $\mathcal {R}$. Then $G^\mathcal {R}$ is EM-compatible with $(\mathcal {S},\mathcal {C},\mathcal {R})$ if and only if $(\mathcal {S},\mathcal {C},\mathcal {R})$ is weakly reversible and deficiency zero.

Proof

Consider a CRN $(\mathcal {S},\mathcal {C},\mathcal {R})$ and let $G^\mathcal {R}= (V^\mathcal {R}, E^\mathcal {R})$ be a reaction-to-reaction graph which is PS-compatible with $(\mathcal {S},\mathcal {C},\mathcal {R})$ and note that PS-compatibility implies CS-compatibility by Lemma 1. We prove the forward and backward implications separately.

($\Longrightarrow$) Suppose $G^\mathcal {R}$ is EM-compatible with $(\mathcal {S},\mathcal {C},\mathcal {R})$. Since the elementary modes of $(\mathcal {S},\mathcal {C},\mathcal {R})$ cover $\mathcal {R}$, we have by EM-compatibility that every reaction (vertex) in $G^\mathcal {R}$ is a part of a cycle. It follows immediately that $(\mathcal {S},\mathcal {C},\mathcal {R})$ is weakly reversible.

Now suppose that $(\mathcal {S},\mathcal {C},\mathcal {R})$ is not deficiency zero. It follows that $\delta = \text{ dim }(\text{ ker }(Y) \cap \text{ im } (I_a)) > 0$ so that there is a vector ${\mathbf {v}} \in {\mathbb {R}}^r$ such that $I_a {\mathbf {v}} \not = {\mathbf {0}}$, but $Y I_a {\mathbf {v}} = {\mathbf {0}}$. If ${\mathbf {v}} \in {\mathbb {R}}_{\ge 0}^r$, since $\varGamma {\mathbf {v}} = {\mathbf {0}}$, we have that ${\mathbf {v}} \in \text{ cone }({\mathcal {E}})$, i.e., ${\mathbf {v}}$ is in the elementary flux cone. Since the elementary modes are unitary and the reaction-to-reaction graph and CRN are PS- and EM-compatible, we have that ${\mathbf {v}}$ corresponds to a summation of cycles in $(\mathcal {S},\mathcal {C},\mathcal {R})$ so that $I_a {\mathbf {v}} = {\mathbf {0}}$, which is a contradiction.

Now suppose that ${\mathbf {v}} \not \in {\mathbb {R}}_{\ge 0}^r$, i.e., at least two components have opposite signs. Then, since ${\mathcal {E}}$ covers $\mathcal {R}$, we have that there are $\lambda _i \ge 0$, $i = 1, \ldots , p,$ such that ${\mathbf {w}} = {\mathbf {v}} + \sum _{i=1}^p \lambda _i e_i \in {\mathbb {R}}_{\ge 0}^r$. Furthermore, we have $\varGamma {\mathbf {w}} = \varGamma {\mathbf {v}} + \sum _{i=1}^p \lambda _i \varGamma e_i = {\mathbf {0}}$ so that ${\mathbf {w}} \in \text{ cone }({\mathcal {E}})$. Since the elementary flux modes are unitary, it follows that ${\mathbf {w}}$ corresponds to a summation of weighted cycles in $(\mathcal {S},\mathcal {C},\mathcal {R})$ so that $I_a {\mathbf {w}} = {\mathbf {0}}$. Note that $I_a {\mathbf {v}} = I_a {\mathbf {w}} - \sum _{i=1}^r \lambda _i I_a e_i = {\mathbf {0}}$. This contradicts our assumptions and completes the forward direction of the proof.

($\Longleftarrow$) Now suppose that $(\mathcal {S},\mathcal {C},\mathcal {R})$ is weakly reversible and deficiency zero. It follows from $\delta = 0$ that $\varGamma {\mathbf {v}} = {\mathbf {0}}$ implies $I_a {\mathbf {v}} = {\mathbf {0}}$, i.e., if ${\mathbf {v}} \in \text{ cone }({\mathcal {E}})$, then ${\mathbf {v}}$ is a cyclic generator of the CRN. It follows from PS-compatibility that every elementary flux mode is a cycle in the reaction graph of the CRN and therefore a cycle in $G^\mathcal {R}$. It follows that $G^\mathcal {R}$ is EM-compatible, and we are done. $\square$

We now want to relate the properties of PS-, CS-, and EM-compatibility to structural translation (Definition 1). We have the following result.

Theorem 1

Consider a CRN $(\mathcal {S},\mathcal {C},\mathcal {R})$ with a set of elementary flux modes ${\mathcal {E}} = \{e_1, \ldots , e_p\}$ which is unitary and covers $\mathcal {R}$. If there is a reaction-to-reaction graph $G^\mathcal {R}= (V^\mathcal {R}, E^\mathcal {R})$ which is CS- and EM-compatible to $(\mathcal {S},\mathcal {C},\mathcal {R})$, then there is a CRN $(\mathcal {S},\mathcal {C}',\mathcal {R}')$ which is PS-, CS-, and EM-compatible with $G^\mathcal {R}$. Furthermore, $(\mathcal {S},\mathcal {C}',\mathcal {R}')$ is a weakly reversible, zero deficiency structural translation of $(\mathcal {S},\mathcal {C},\mathcal {R})$. In particular, the translation complexes $\alpha _i \in {\mathbb {R}}_{\ge 0}^m$, $i=1,\ldots , r$, required to produce such a translation satisfy the following linear system, which is necessarily consistent:

$$\begin{aligned} \alpha _i - \alpha _j = y_{s(j)} - y_{p(i)}, \quad (r_i,r_j) \in E^\mathcal {R}. \end{aligned}$$

(6)

Proof

Consider a reaction-to-reaction graph $G^\mathcal {R}= (V^\mathcal {R}, E^\mathcal {R})$ which is CS- and EM-compatible with $(\mathcal {S},\mathcal {C},\mathcal {R})$. We show that it is possible to construct a CRN $(\mathcal {S},\mathcal {C}',\mathcal {R}')$ which is EM-, CS-, and PS-compatible to $G^\mathcal {R}$ by setting up and solving corresponding linear system (6) in the translation complexes $\varLambda = \{ \alpha _1, \ldots , \alpha _r \}$.

In order for $(\mathcal {S}, \mathcal {C}', \mathcal {R}')$ to be PS-compatible to $G^\mathcal {R}$, we require that

$$\begin{aligned} y'_{p(i)} = y'_{s(j)}, \quad \text{ for } (r_i,r_j) \in E^\mathcal {R}. \end{aligned}$$

(7)

Note that we can satisfy this set of equations if there is a set of translation complexes $\varLambda = \{ \alpha _1, \ldots , \alpha _r \}$ where $\alpha _i \in {\mathbb {R}}^m$, $i =1, \ldots , r$, such that $y'_{p(i)} = y_{p(i)} + \alpha _i$ and $y'_{s(j)} = y_{s(j)} + \alpha _j$, i.e., each complex in $\mathcal {C}'$ results from translating a complex in $\mathcal {C}$ by the corresponding translation complex $\alpha _i \in \varLambda$. From (7), this gives the system

$$\begin{aligned} y_{p(i)} + \alpha _i = y_{s(j)} + \alpha _j, \quad (r_i,r_j) \in E^\mathcal {R}\end{aligned}$$

(8)

which can be rearranged to give (6) in the unknown vectors $\alpha _i \in {\mathbb {R}}^{m}$, $i = 1, \ldots , r$. We now show that, since $G^\mathcal {R}$ is CS- and EM-compatible with $(\mathcal {S},\mathcal {C},\mathcal {R})$, that (6) is necessarily consistent.

For ease of notation, we let $q = |E^\mathcal {R}|$ and suppose the edges $(r_i,r_j) \in E^\mathcal {R}$ are ordered $1, \ldots , q$, i.e., $E^\mathcal {R}= \{ v_1, \ldots , v_q \} \subseteq \mathcal {R}\times \mathcal {R}$ where $v_k = (r_i, r_j)$. We can then write (6) as the linear system $A \alpha = {\mathbf {b}}$ where $\alpha = ( \alpha _1, \ldots , \alpha _r) \in {\mathbb {R}}^{mr}$ is a vector of unknowns, ${\mathbf {b}} = (b_1, \ldots , b_q) \in {\mathbb {R}}^{mq}$ has entries $b_k = (y_{s(j)} - y_{p(i)}) \in {\mathbb {R}}^m$ if $v_k = (r_i,r_j) \in E^\mathcal {R}$, and $A \in {\mathbb {R}}^{mq \times mr}$ has the block structure

$$\begin{aligned} A = \left[ \begin{array}{cccc} A_{11} &{} A_{12} &{} \cdots &{} A_{1r} \\ A_{21} &{} A_{22} &{} \cdots &{} A_{2r} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ A_{q1} &{} A_{q2} &{} \cdots &{} A_{qr} \end{array}\right] \end{aligned}$$

(9)

where, given $v_k = (r_i, r_j) \in E^\mathcal {R}$, we set $A_{ki} = I^{m \times m}$, $A_{kj} = -I^{m \times m}$, and $A_{kl} = {\mathbf {0}}^{m \times m}$ for all $l \not = i$ or $l \not = j$.

In order to show the linear system $A \alpha = {\mathbf {b}}$ is consistent, it is sufficient to show that ${\mathbf {c}} \in \text{ ker }(A^{\mathrm{T}})$ implies that ${\mathbf {c}}^{\mathrm{T}} {\mathbf {b}} = 0$. To characterize $\text{ ker }(A^{\mathrm{T}})$, notice that the block structure of $A^{\mathrm{T}}$ corresponds to the incidence matrix of $G^\mathcal {R}$ (interpreting the identity blocks $I^{m \times m}$ as 1 and the $0^{m \times m}$ blocks as 0). It follows that $\text{ ker }(A^{\mathrm{T}})$ has support on the minimal cycles of $G^\mathcal {R}$ which correspond by EM-compatibility to the elementary modes ${\mathcal {E}} = \{ e_1, \ldots , e_p \}$ of $(\mathcal {S},\mathcal {C},\mathcal {R})$. We can extend this to the block structure of $A^{\mathrm{T}}$ in the following way: to each elementary mode $e_k \in {\mathcal {E}}$, we introduce an arbitrary vector ${\bar{\beta }}_k \in {\mathbb {R}}^m$ and define $\beta ^k = (\beta _1^k, \ldots , \beta _q^k) \in {\mathbb {R}}^{mq}$ such that, if $\{ v_{\mu (1)},\ldots , v_{\mu (l)}\}$ the minimal cycle in $G^\mathcal {R}$ corresponding to the elementary mode $e_k$, we have $\beta _{\mu (i)}^k = {\bar{\beta }}_k$ for all $i = 1, \ldots , l$. We have that $\{ \beta ^1, \ldots , \beta ^p \}\subseteq {\mathbb {R}}^{mq}$ forms a basis of $\text{ ker }(A^{\mathrm{T}})$. Furthermore, it follows that for $k \in \{ 1, \ldots , p \}$,

$$\begin{aligned} (\beta ^k)^{\mathrm{T}} {\mathbf {b}} = {\bar{\beta }}_k^{\mathrm{T}} \sum _{i=1}^l (y_{s(\mu (i))} - y_{p(\mu (j))}) = -{\bar{\beta }}_k^{\mathrm{T}} \sum _{i=1}^l (y_{p(\mu (i))} - y_{s(\mu (i))}) = 0 \end{aligned}$$

since $e_k = \{r_{\mu (1)} , \ldots , r_{\mu (l)}\}$ is an elementary flux mode of $(\mathcal {S},\mathcal {C},\mathcal {R})$.

It follows that the system $A \alpha = {\mathbf {b}}$ is consistent so that we may solve system (6) for the translation complexes $\varLambda = \{ \alpha _1, \ldots , \alpha _r\}$. By construction, the resulting network $(\mathcal {S},\mathcal {C}',\mathcal {R}')$ is PS-, CS-, and EM-compatible with $G^\mathcal {R}$. Furthermore, we have $\varGamma = \varGamma '$ so that $(\mathcal {S},\mathcal {C},\mathcal {R})$ and $(\mathcal {S},\mathcal {C}',\mathcal {R}')$ are structural translations of one another, and $(\mathcal {S},\mathcal {C}',\mathcal {R}')$ is weakly reversible and deficiency zero by Lemma 2, and we are done.$\square$

Example 6

Reconsider the reaction-to-reaction graph in Fig. 2b. This graph is both CS- and EM-compatible with the CRN in Fig. 1a. It follows from Theorem 1 that there is a CRN $(\mathcal {S},\mathcal {C}',\mathcal {R}')$ which is PS-, CS-, and EM-compatible with the reaction-to-reaction graph in Fig. 2b. Furthermore, this CRN is a weakly reversible, deficiency zero structural translation of the original CRN. We can quickly verify that these properties are satisfied by the CRN in Fig. 1c.

Remark 2

Note that having a structural translation with a deficiency of zero corresponds to a stoichiometric deficiency of zero in the corresponding generalized chemical reaction network (Müller and Regensburger 2012, 2014). It is still possible, however, that the kinetic-order deficiency is nonzero (see “Appendix A.4”).

3.3 Computing Structural Translations

Theorem 1 and the networks in Fig. 1 suggest a process by which to construct structural translations. We perform the following steps:

• 1. From the given CRN $(\mathcal {S},\mathcal {C},\mathcal {R}$), we compute the set of elementary flux modes ${\mathcal {E}} = \{e_1, \ldots , e_p \}$ and the set of sets of reactions with shared source complexes, i.e., ${\mathcal {F}} = \{ f_1, \ldots , f_q\}$ where $r_i, r_j \in f_k$, $i \not = j$, for some k if $y_{s(i)} = y_{s(j)}$.

• 2. From the sets ${\mathcal {E}}$ and ${\mathcal {F}}$, we determine a reaction-to-reaction graph $G^\mathcal {R}= (V^\mathcal {R}, E^\mathcal {R})$ which is CS- and EM-compatible with $(\mathcal {S},\mathcal {C},\mathcal {R})$.

• 3. From this reaction-to-reaction graph $G^\mathcal {R}$, we construct a CRN $(\mathcal {S},\mathcal {C}',\mathcal {R}')$ which is PS-, CS-, and EM-compatible with $G^\mathcal {R}$ by solving (6).

Note that, if successful, this algorithm produces a weakly reversible, deficiency zero structural translation of $(\mathcal {S},\mathcal {C},\mathcal {R})$ by Theorem 1. In what follows we describe the approaches taken to these three steps.

Step 1: Computing Elementary Flux Modes

Consider a CRN $(\mathcal {S},\mathcal {C},\mathcal {R})$. To determine the set of elementary flux modes ${\mathcal {E}}$ of $(\mathcal {S},\mathcal {C},\mathcal {R})$, we use the crnpy Python package developed by Tonello (2016). In accordance with Theorem 1, we do not consider the network if the set ${\mathcal {E}}$ is not unitary (i.e., some elementary flux modes $e_i \in {\mathcal {E}}$ with entries other than zeros and ones) or does not cover $\mathcal {R}$ (i.e., there is a reaction which does not have support on any elementary mode $e_i \in {\mathcal {E}}$).

We also collect sets of reactions with shared source complexes into a set ${\mathcal {F}} = \{ f_1, \ldots , f_q \}$ where q is the number of source complexes which are the source for at least two reactions. This set can be constructed by direct analysis of the incidence matrix $I_a$ of the CRN.

Throughout this section, we consider elementary flux modes according to their supports, i.e., $e_i \subseteq \mathcal {R}$.

Step 2: Computing the Reaction-to-Reaction Graph

Recall that a binary linear programming (BLP) problem can be stated in the general form

$$\begin{aligned} \begin{array}{ll} \text{ maximize } &{} {\mathbf {c}}^{\mathrm{T}} {\mathbf {x}}\\ \text{ subject } \text{ to } &{} A {\mathbf {x}} \le {\mathbf {b}} \end{array} \end{aligned}$$

(10)

where $A \in {\mathbb {R}}^{n \times m}$, ${\mathbf {b}} \in {\mathbb {R}}^n$, and ${\mathbf {c}} \in {\mathbb {R}}^m$ are matrices and vectors of parameters, and ${\mathbf {x}} \in \{0, 1\}^m$ is a vector of binary decision variables.

We formulate the problem of determining a reaction-to-reaction graph $G^\mathcal {R}= (V^\mathcal {R}, E^\mathcal {R})$ which is CS- and EM-compatible with $(\mathcal {S},\mathcal {C},\mathcal {R})$ as a BLP problem. We introduce binary decision variables $x_{ij} \in \{ 0, 1 \}$, $i, j = 1, \ldots , r$, $i \not = j$, with the following logical requirement:

$$\begin{aligned} x_{ij} = 1 \; \Longleftrightarrow \; (r_i, r_j) \in E^\mathcal {R}\end{aligned}$$

where $E^\mathcal {R}$ is the edge set of our reaction-to-reaction graph $G^\mathcal {R}= (V^\mathcal {R}, E^\mathcal {R})$. We now seek to set up constraints sufficient to guarantee the reaction-to-reaction graph $G^\mathcal {R}$ is CS- and EM-compatible with $(\mathcal {S},\mathcal {C},\mathcal {R})$. For this purpose, it is sufficient to consider the sets ${\mathcal {E}}$ and ${\mathcal {F}}$ determined in Step 1.

Elimination of unnecessary edges: It is often apparent from the structure of ${\mathcal {E}}$ and ${\mathcal {F}}$ that the reactions may be partitioned into nonintersecting sets of reactions. We define the binary relation ‘$\equiv$’ to be the transitive closure of the following properties:

• 1. $e_i \equiv e_j$ if $e_i \cap e_j \not = \emptyset$, and

• 2. $e_i \equiv e_j$ if there are $r_k \in e_i$ and $r_l \in e_j$ such that $r_k, r_l \in f_{u}$ for some $f_{u} \in {\mathcal {F}}$.

That is, two elementary modes are connected by the relation ‘$\equiv$’ if they share a reaction (condition 1) or possess reactions which have a common source complex (condition 2). We then impose the following partition rule:

$$\begin{aligned} \qquad \qquad x_{ij} = 0, \quad \text{ if } r_i \in e_k \text{ and } r_j \in e_l \text{ where } e_k \not \equiv e_l. \qquad \qquad \qquad \qquad \qquad \qquad ({\mathrm{Par}}) \end{aligned}$$

CS-compatibility: To guarantee $G^\mathcal {R}= (V^\mathcal {R}, E^\mathcal {R})$ is CS-compatible with $(\mathcal {S},\mathcal {C},\mathcal {R})$, we impose that, if $r_i, r_j \in f_l$ for some $f_l \in {\mathcal {F}}$, then

$$\begin{aligned} x_{ki} - x_{kj}&= 0, \quad&k = 1, \ldots , r.\qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad ({\mathrm{CS}}) \end{aligned}$$

The constraint set (CS) guarantees that either $(r_k, r_i) \in E^\mathcal {R}$ and $(r_k, r_j) \in E^\mathcal {R}$, or $(r_k, r_i) \not \in E^\mathcal {R}$ and $(r_k, r_j) \not \in E^\mathcal {R}$.

EM-compatibility: Consider an elementary flux mode $e_k \in {\mathcal {E}}$. We introduce the following constraint set:

$$\begin{aligned} \left\{ \begin{array}{ll} \sum _{r_i \in e_k} x_{ij} = 1,&{}\quad r_j \in e_k \\ \sum _{r_j \in e_k} x_{ij} = 1,&{}\quad r_i \in e_k. \end{array}\right. \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad ({\mathrm{EM1}}) \end{aligned}$$

The first constraint set in (EM1) guarantees that the number of edges on a component corresponding to the support of an elementary flux mode contains exactly the number of edges contained in the elementary flux mode. The second constraint set in (EM1) guarantees that each vertex of the component has exactly one outgoing edge, while the third constraint set guarantees that each such vertex has exactly one incoming edge.

The constraint set (EM1) guarantees that every vertex (reaction) belonging to an elementary mode is a part of exactly one cycle on the support of that elementary mode. It does not, however, guarantee that these cycles are maximal with respect to the support of the elementary mode. For example, an elementary mode consisting of 6 reactions may be split into a 2-cycle and a 4-cycle, or two 3-cycles. We furthermore impose that elementary flux modes may not be decomposed into subcycles. We guarantee this by imposing that, for every elementary mode $e_k \in {\mathcal {E}}$ with $l(k) = |e_k| \ge 4$, every combination $e'_k = \{ r_{\mu (1)}, \ldots , r_{\mu (l(k'))} \} \subset e_k$ with $2 \le |e'_k| \le \lfloor \frac{|e_k|}{2} \rfloor$ satisfies:

$$\begin{aligned} \left\{ \sum _{r_i, r_j \in e'_k} x_{ij} \le |e_{k'}| - 1 \right. \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad ({\mathrm{EM2}}) \end{aligned}$$

Since a cycle on a component of size $|e_{k'}|$ is required to have $|e_{k'}|$ edges, the constraint set (EM2) guarantees that no subcycles exist on the support of an elementary flux mode. Notice that we do not need to apply this condition for components $|e_{k'}| > \lfloor \frac{|e_k|}{2} \rfloor$ since a subcycle of such size necessitates a subcycle of size $|e_{k'}| \le \lfloor \frac{|e_k|}{2} \rfloor$ by (EM1).

Objective function: We impose the following objective function

$$\begin{aligned} \text{ minimize } \quad \mathop {\sum _{i,j=1}^r}_{i \not = j} x_{ij}.\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad ({\mathrm{Obj}}) \end{aligned}$$

That is, we minimize the number of edges in $(r_i,r_j) \in E^\mathcal {R}$. This prohibits the procedure from adding unnecessary edges $(r_i,r_j) \in E^\mathcal {R}$. We produce a reaction-to-reaction graph by optimizing (Obj) over the constraint sets (Par), (EM1), (EM2), and (CS).

Remark 3

Although (EM2) guarantees that there are no subcycles on a given elementary flux mode, it is possible that the optimization procedure will create cycles which do not correspond to minimal elementary flux modes (for example, consider entry biomd0000000008 in the European Bioinformatics Institute’s BioModels database). The resulting reaction-to-reaction graph will then fail to be EM-compatible with $(\mathcal {S},\mathcal {C},\mathcal {R})$. Rather than implementing further constraints like (EM2) to eliminate this possibility, we note that such a network will fail to have consistent system (6). Consistency of a linear system $A {\mathbf {x}} = {\mathbf {b}}$ is simple to check computationally by checking $\text{ rank }(A) = \text{ rank }(B)$ where B is the augmented matrix $B = [A \mid {\mathbf {b}}]$. If $\text{ rank }(A) \not = \text{ rank }(B)$, we do not proceed to Step 3.

Step 3: Construct Structural Translation $(\mathcal {S},\mathcal {C}',\mathcal {R}')$

To construct a structural translation $(\mathcal {S},\mathcal {C}',\mathcal {R}')$ from the reaction-to-reaction graph produced in Step 2, we need to solve linear system (6). As a preprocessing step, we check whether (6) is consistent by computing the rank of the associated matrices. If the system is not consistent, the network does not admit a structural translation by Lemma 2. If the system is consistent, we may construct a structural translation $(\mathcal {S},\mathcal {C}',\mathcal {R}')$ by solving (6) for the set of translation complexes $\varLambda = \{ \alpha _1, \ldots , \alpha _r\}$.

Rather than solving (6) directly, we use the observation that, for a known $\alpha _i$, we have

$$\begin{aligned} \alpha _j = y_{p(i)} - y_{s(j)} + \alpha _i \end{aligned}$$

for every $r_j \in \mathcal {R}$ such that $(r_i, r_j) \in E^\mathcal {R}$. Consequently, we may use the following algorithm to solve (6):

• 1. Initialize the sets ${\mathcal {P}} = \mathcal {R}$, ${\mathcal {P}}' = \emptyset$, and ${\mathcal {P}}'' = \emptyset$.

• 2. Select an arbitrary $r_i \in {\mathcal {P}}$ and then:

  • (a) set $\alpha _i = {\mathbf {0}}$ and

  • (b) set ${\mathcal {P}}' = \{ r_i\}$ and ${\mathcal {P}} = {\mathcal {P}} \setminus \{r_i \}$.

• 3. Choose a $r_j \in {\mathcal {P}}$ such that $r_i \in {\mathcal {P}}'$ and $(r_i, r_j) \in E^\mathcal {R}$, and then do the following:

  • (a) set $\alpha _j = y_{p(i)}-y_{s(j)}+\alpha _i$ and

  • (b) set ${\mathcal {P}}'' = ({\mathcal {P}}'' \cup \{r_j\}) \setminus {\mathcal {P}}'$.

• 4. If ${\mathcal {P}}'' \not = \emptyset$, then:

  • (a) set ${\mathcal {P}}' = {\mathcal {P}}''$, ${\mathcal {P}} = {\mathcal {P}} \setminus {\mathcal {P}}'$, and ${\mathcal {P}}'' = \emptyset$ and

  • (b) repeat from step 3.

• 1. If ${\mathcal {P}}'' = \emptyset$ and ${\mathcal {P}} \not = \emptyset$ then repeat from step 2.

• 2. If ${\mathcal {P}}'' = \emptyset$ and ${\mathcal {P}} = \emptyset$, we are done.

This algorithm solves for each translation complex in (6) successively and can in general be solved more efficiently than the corresponding system in matrix form. We subsequently adjust translation complexes so that the resulting complexes are nonnegative by adding nonnegative complexes to entire linkage classes where needed.

4 Examples

In this section, we apply the algorithm presented in Sect. 3.3 to 508 curated models from the European Bioinformatics’ BioModels database and summarize the output. We also expand upon two models the algorithm determined to have a weakly reversible, zero deficiency structural translation: a zigzag model of plant–pathogen interactions (Jones and Dangl 2006; Pritchard and Birch 2014) and a MAPK cascade model (Markevich et al. 2004). In “Appendix A,” we outline how the outcome of the algorithm in Sect. 3.3 can be utilized to construct steady-state parametrizations according to the results of Johnston et al. (2018) and establish mono- or multistationarity within stoichiometric compatibility classes according to the results of Conradi et al. (2017).

4.1 BioModels Database

We implemented the algorithm outlined in Sect. 3.3 in Python and tested it on 508 curated networks from the European Bioinformatics Institute’s BioModels database (Li et al. 2010). We imposed a twenty-minute timeout per model. The algorithm found 176 models which permitted a weakly reversible, deficiency zero structural translation to be computed. Of those models, 34 were not originally weakly reversible, deficiency zero networks.

Of the models for which the program did not succeed in finding a weakly reversible, deficiency zero structural translation, 239 failed because the network had an elementary flux mode set ${\mathcal {E}}$ which either was not unitary or did not cover $\mathcal {R}$, 60 failed because a EM- and CS-compatible reaction-to-reaction graph could not be constructed, and 27 failed due to computational time out. The mean size of the networks which failed to compute due to computational timeout was 387 reactions, and the median was 144 reactions.

4.2 Example: Zigzag Model

Consider the following network of the zigzag model of plant–pathogen interactions (Jones and Dangl 2006; Pritchard and Birch 2014) which corresponds to network biomd0000000563 in the BioModels database (Li et al. 2010):

where $X_1 = \text{ PAMP }$, $X_2 = \text{ PRR }$, $X_3 = \text{ PRR }^*$, $X_4 = \text{ Callose }$, $X_5 = \text{ E }_{\text{ int }}$, $X_6 = \text{ R }$, $X_7 = \text{ R }^*$, $X_8 = \text{ Pathogen }_{\text{ bulk }}$, $X_9 = \text{ Pathogen }$, $X_{10} = \text{ E }$, $X_{11} = \text{ F }$, $X_{12} = \text{ EF }$, and $X_{13} = \text{ FCallose }$. All interactions given by Pritchard and Birch (2014) are assumed to be mass-action except for $X_{10} \rightarrow X_{5}$ which is inhibited by $X_4$ according to the competitive inhibition reaction rate

$$\begin{aligned} \frac{V_{\mathrm{max}}x_{10}}{ \frac{K_m}{K_i}x_4 + x_{10} + K_m} \end{aligned}$$

(12)

where $V_{\mathrm{max}}, K_i, K_m > 0$ are parameters. We have replaced the reaction $X_{10} \rightarrow X_5$ with the reaction set $r_{17}$ through $r_{21}$ in () to reflect the activity of an unseen activator ($X_{11} = \text{ F }$) and inhibition of $X_{11}$ by $X_4$. The quasi-steady-state approximation for the production of $X_5$ is given by (12) with $V_{\mathrm{max}} = k_{20} (x_{11}(0) + x_{12}(0))$, $K_i = \frac{k_{23}}{k_{22}}$, and $K_m = \frac{k_{19}+k_{20}}{k_{18}}$ (Ingalls 2013). Consequently, the steady states of the mass-action system we use and the original system of ordinary differential equations studied by Pritchard and Birch (2014) coincide.

The program outlined in Sect. 3.3 Step 2 constructs the reaction-to-reaction graph given in Fig. 3a, which is CS- and EM-compatible with (). The process outlined in Sect. 3.3 Step 3 yields the following network, which is a weakly reversible, deficiency zero structural translation of (), and is PS-, CS-, and EM-compatible with the reaction-to-reaction graph in Fig. 3a:

In “Appendix A.3,” we show how structural translation () can be used to construct a steady-state parametrization of corresponding mass-action system (1).

Fig. 3

Two reaction-to-reaction graphs determined by the BLP outlined in Sect. 3.3. In a, the reaction-to-reaction graph is CS- and EM-compatible with () and PS-, CS-, and EM-compatible with (). In b, the reaction-to-reaction graph is CS- and EM-compatible with () and PS-, CS-, and EM-compatible with ()

4.3 Example: MAPK Model

Consider the following model of a mitogen-activated protein kinase (MAPK) cycle studied by Markevich et al. (2004), which corresponds to biomd0000000026 in the BioModels database (Li et al. 2010):

The program outlined in Sect. 3.3 Step 2 constructs the reaction-to-reaction graph given in Fig. 3b. The following weakly reversible, deficiency zero structural translation can then be constructed by the procedure outlined in Sect. 3.3 Step 3:

In “Appendix A.4,” we show how structural translation () can be used to construct a steady-state parametrization of corresponding mass-action system (1) and guarantee the capacity for multistationarity according to Corollary 2 of Conradi et al. (2017).

5 Conclusions

We have presented a procedure for constructing structural translations which are weakly reversible and deficiency zero. The backbone of the algorithm is binary linear programming (BLP) problem for determining a suitable reaction-to-reaction graph. This graph treats the reactions of the given CRN as vertices in a new graph. We show that constructing a reaction-to-reaction graph satisfying two conditions on the edges (CS- and EM-compatibility) guarantees that a weakly reversible, deficiency zero structural translation may be constructed by imposing one further condition on the reaction-to-reaction graph (PS-compatibility). Crucially, BLP problems can be solved in polynomial time in the number of constraints by Lenstra’s algorithm (1983) so that this represents a significant improvement in scalability compared to existing methods for constructing weakly reversible, deficiency zero translations.

This work presents several avenues for future work.

• 1. The procedure outlined in Sect. 3.3 is only able to produce weakly reversible, deficiency zero structural translations, which corresponds to translating all stoichiometric generators in the set of elementary flux modes into cyclic generators. Applications exist, however, for translations which are not necessarily weakly reversible or deficiency zero (e.g., absolute concentration robustness as studied by Shinar and Feinberg 2010; Tonello and Johnston 2018). Future work will focus on adapting the procedure outlined in Sect. 3.3 to account for CRNs where some stoichiometric generators are not translated into cyclic generators.

• 2. Recent results of Johnston et al. (2018) give sufficient conditions for the parametrization of the steady-state set of a generalized chemical reaction network which is weakly reversible and has a structural deficiency of zero [this is called the effective deficiency by Johnston et al. (2018)]. Results have also recently been established regarding mono- and multistationarity within stoichiometric compatibility classes by Conradi et al. (2017). Integrating the structural translation procedure introduced in Sect. 3.3 into a unified program for applying these results is ongoing. In “Appendix A,” we outline the steps involved in this approach on the examples contained in Sects. 4.2 and 4.3.

A: Appendix—Parametrization Method

While two structural translations have the same stoichiometric matrices $\varGamma$ and $\varGamma '$, they may nevertheless have different mass-action systems (1) due to differences in $R({\mathbf {x}})$. In this Appendix, we outline the method by which a steady-state parametrization may be constructed from a structural parametrization as constructed by the algorithm presented in Sect. 3.3.

For ease of notation and continuity, rather than repeating the technical definitions and Theorems introduced by Müller and Regensberger (2012, 2014) and Johnston et al. (2018), we outline the parametrization procedure through examples.

1.1 A.1: Histidine Kinase Model

We use the histidine kinase network in Fig. 1a as a motivating example. Through application of the algorithm presented in Sect. 3.3, we were able to correspond the following CRN (left) with the indicated structural translation (right):

Although these two networks have the same reaction vectors (i.e., $\varGamma = \varGamma '$), the governing system of differential equations (1) does not coincide due to differences in $R({\mathbf {x}})$. Specifically, the source complex of $r_1$ and $r_4$ differs in Network 1 from Network 2. To accommodate this difference, we map the source complexes from Network 1 into a secondary set of complexes known as kinetic-order complexes in Network 2. We can represent this with the following network:

Network () is an example of a generalized chemical reaction network (GCRN) (Müller and Regensburger 2012, 2014). In a GCRN, each vertex is assigned two complexes: a stoichiometric complex (unbracketed) and a kinetic-order complex (bracketed). In the corresponding generalized mass-action system

$$\begin{aligned} \frac{d{\mathbf {x}}}{dt} = \varGamma \tilde{R}({\mathbf {x}}) \end{aligned}$$

(17)

the reaction vectors forming $\varGamma$ are determined by the differences of the stoichiometric complexes, while the monomials in $\tilde{R}({\mathbf {x}})$ are determined by the kinetic-order complexes. Denote the ith kinetic-order complex by $\tilde{y}_i$, we have that $\tilde{R}({\mathbf {x}})$ has entries $\tilde{R}_i({\mathbf {x}}) = \prod _{j=1}^m x_j^{[\tilde{y}_{s(i)}]_j}$. For example, the term in $\tilde{R}({\mathbf {x}})$ corresponding to $r_1$ in () is $k_1 x$ rather than $k_1 x y$. It can be easily checked that dynamical equations (17) corresponding to () coincide with dynamical equations (1) corresponding to Network 1.

Note that when converting from Network 2 to (), we split the vertex $X+Y_p$. Consequently, the stoichiometric complex $X+Y_p$ is repeated at vertices 3 and 4 in () (indicted with $\dag$). This is allowed by Johnston et al. (2018) and, in fact, required since $r_3$ and $r_4$ would otherwise have multiple kinetic-order complexes at a single vertex [although, with some supplemental conditions, this is allowed by Johnston (2015) and Tonello and Johnston (2018)]. In order to regain weak reversibility, Johnston et al. (2018) introduce a new set of edges (called “phantom reactions") which connect stoichiometrically identical complexes. Notice that introducing such reactions introduces zero columns in $\varGamma$ and therefore does not alter the corresponding system of differential equations (17).

For technical reasons, Johnston et al. (2018) imposed further rules upon the splitting of stoichiometric complexes and the introduction of phantom reactions. They define equivalence classes of stoichiometrically identical complexes and select from within each such class a distinguished vertex (indicated with a $\star$). The set of phantom reactions is then introduced such that:

• 1. All “true reactions” (i.e., from the set $\mathcal {R}$) which have their product at any vertex in this equivalence class have the distinguished vertex as its product.

• 2. The phantom reactions between vertices on this equivalence class consist only of reactions with the distinguished complex as its source and the remaining complexes as the product.

We may interpret the distinguished vertices as hubs through which are all paths through an equivalence class of stoichiometrically identical complexes must pass. Such a construction produces a $V^{\star }$-directed GCRN which is important in the construction of positive parametrizations.

For network (), we select vertex 3 as the distinguish vertex (indicated with $\star$) and label the phantom edge with a free parameter $\sigma$:

Notice that only $r_2$ has a product in the equivalence class of vertices $\{3, 4\}$ and its product is the distinguished complex 3 (condition 1), and the only reaction on vertices $\{3, 4 \}$ goes from the distinguished vertex 3 to the remaining vertex 4 (condition 2). GCRN () is therefore $V^{\star }$-directed. Notice that the rate constant $\sigma$ corresponding to the phantom edge $3 \rightarrow 4$ joins stoichiometrically identical complexes and consequently does not appear in the system of differential equations (1).

Johnston et al. (2018) showed that, if the deficiency of the structural translation (called the effective deficiency) is zero and the corresponding GCRN is $V^{\star }$-directed, then the positive steady-state set of original dynamical system (1) can be characterized by the complex-balanced steady states of dynamical system (17), namely, the equation

$$\begin{aligned} A_k \tilde{R}({\mathbf {x}}) = 0 \end{aligned}$$

(19)

where $A_k \in {\mathbb {R}}^{n \times n}$ is the Laplacian of the reaction graph of the GCRN. For network (), this corresponds to the system:

$$\begin{aligned} \left[ \begin{array}{cccc} -k_1 &{} 0 &{} 0 &{} k_4 \\ k_1 &{} - k_2 &{} k_3 &{} 0 \\ 0 &{} k_2 &{} -k_3 - \sigma &{} 0 \\ 0 &{} 0 &{} \sigma &{} - k_4 \end{array} \right] \left[ \begin{array}{c} x \\ x_py \\ xy_p \\ y_p \end{array} \right] = \left[ \begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \end{array} \right] \end{aligned}$$

Relationships between $\text{ ker }(A_k)$ and the steady-state set of mass-action systems have been studied extensively in recent years. It is known that, for weakly reversible networks, $\text{ ker }(A_k)$ can be characterized by algebraic combinations of the rate constants of a network known as “tree constants” (Johnston 2014; Johnston et al. 2018) which we summarize in “Appendix A.2.” For this network, we can directly compute that $\text{ ker }(A_k) = \text{ span } \{( K_1, K_2, K_3, K_4 )\}$ where

$$\begin{aligned} \begin{aligned} K_1&= k_2k_4\sigma ,&K_2&= k_1(k_3 + \sigma )k_4,&K_3&= k_1k_2k_4,&K_4&= k_1k_2 \sigma \end{aligned} \end{aligned}$$

are the tree constants. The steady-state condition $(x, x_py,xy_p,y_p) \in \text{ ker }(A_k)$ gives the implicit equations

$$\begin{aligned} \frac{x}{k_2k_4\sigma } = \frac{x_py}{k_1(k_3+\sigma )k_4} = \frac{xy_p}{k_1k_2k_4} = \frac{y_p}{k_1k_2\sigma }. \end{aligned}$$

Taking pairwise differences, this gives the following log-linear system of equations:

$$\begin{aligned} \left[ \begin{array}{cccc} -\,1 &{} 1 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \\ -\,1 &{} 0 &{} 0 &{} 1 \end{array} \right] \left[ \begin{array}{c} \ln (x) \\ \ln (x_p) \\ \ln (y) \\ \ln (y_p) \end{array} \right] = \left[ \begin{array}{c} \frac{k_1(k_3 + \sigma )}{k_2\sigma } \\ \frac{k_1}{\sigma } \\ \frac{k_1}{k_4} \end{array} \right] \end{aligned}$$

(20)

Surprisingly, the solvability of system (20) depends on the deficiency of network () taken with only the kinetic-order complexes:

The deficiency of network () is known as the kinetic-order deficiency (Müller and Regensburger 2012, 2014). We can compute that the deficiency of () is zero so that the kinetic-order deficiency of () is zero. Consequently, log-linear system (20) is guaranteed to be consistent and therefore have a solution for all values of rate constants (including $\sigma$) Johnston et al. (2018). For this example, (20) can be solved for the log concentrations, which can then be exponentiated to give the following parametrization:

$$\begin{aligned}\left\{ \begin{aligned} x&= \frac{k_4}{\sigma } ,&y&= \tau , \\ x_p&= \frac{k_1(k_3+\sigma )k_4}{k_2\sigma ^2\tau }, \; \; \; \; \;&y_p&= \frac{k_1}{\sigma }, \end{aligned} \right. \end{aligned}$$

where $\sigma , \tau > 0$ are positive parameters. Notice that the parameter $\tau$ has arisen from parametrizing the null space of the coefficient matrix in (20), which is the span of the vector $(0,-\,1,1,0)$.

1.2 A.2: General Procedure for Parametrizations

For a given GCRN, we let $\tilde{y}_i$ denote the kinetic-order complex at the vertex labeled i and define ${\mathcal {T}} \subseteq \mathcal {R}$ to be the set of all trees which span the linkage class containing the vertex i and have vertex i as a unique sink. The tree constants $K_i$ corresponding to the vertex labeled i are given by

$$\begin{aligned} K_i = \sum _{T \in {\mathcal {T}}} \prod _{r_j \in T} k_j. \end{aligned}$$

(22)

By Lemma 12 of Johnston et al. (2018), if the GCRN has an effective deficiency of zero, we have the following representations of the steady-state set of the corresponding generalized mass-action system:

$$\begin{aligned} \frac{{\mathbf {x}}^{\tilde{y}_i}}{K_i} = \frac{{\mathbf {x}}^{\tilde{y}_j}}{K_j} \; \; \; \Longleftrightarrow \; \; \; (\tilde{y}_j - \tilde{y}_i)^{\mathrm{T}} \ln ({\mathbf {x}}) = \ln \left( \frac{K_j}{K_i} \right) \end{aligned}$$

(23)

for all vertices i and j belonging to the same linkage class. We can use the log-linear equation on the right of (23) to construct a linear system in the log concentrations. We define a matrix M such columns $M_{\cdot , k} = \tilde{y}_j - \tilde{y_i}$ and a vector b with entries $b_k = \ln (K_j/K_i)$ where the pairs (i, j) are chosen to be a maximal set of colorredvertices such that the resulting set spans the vertices of the underlying GCRN and does not have any nontrivial cycles. This process produces the following log-linear system

$$\begin{aligned} M^{\mathrm{T}} \ln ({\mathbf {x}}) = b. \end{aligned}$$

(24)

An effective deficiency of zero guarantees all steady states can be found by solving (24) (Lemma 12, Johnston et al. 2018). A kinetic-order deficiency of zero guarantees the solvability of this system for all values of the rate constants (Theorem 14 part 1, Johnston et al. 2018). A GCRN with a nonzero kinetic-order deficiency, however, may still produce solvable system (24) provided certain supplemental conditions on the rate parameters are satisfied (Theorem 14 part 2, Johnston et al. 2018).

The example in “Appendix A.1” suggests the following general procedure for determining a positive steady-state parametrization for mass-action systems (1):

• Step 1: Construct a weakly reversible, deficiency zero structural translation by the algorithm presented in Sect. 3.3.

• Step 2: Transfer source complexes from the original CRN as kinetic-order complexes in the network GCRN, splitting stoichiometric complexes as necessary.

• Step 3: Within each equivalence class of stoichiometrically identical complexes, select distinguished vertices and phantom edges so that the resulting GCRN is $V^{\star }$-directed. Note that the choice of distinguished vertices may be made arbitrarily.

• Step 4: Compute the kinetic-order deficiency. (The deficiency of the network with only the kinetic-order complexes from the $V^{\star }$-directed network found in Step 3.) If the kinetic-order deficiency is zero, skip to Step 5; otherwise proceed to Step 4*.

• Step 4*: Determine a basis $\{ c_1, \ldots , c_{\tilde{\delta }} \}$ of $\text{ ker }(M)$ and for every vector $c_i$ attempt to solve the system $c_i^{\mathrm{T}} b = 0$ for the phantom edge parameters $\sigma _j$ according to Theorem 15 of Johnston et al. (2018). If these conditions cannot be satisfied, the procedure fails. Otherwise, substitute the solved parameters $\sigma _j$ into the GCRN constructed in Step 3 and proceed to Step 5.

• Step 5: Compute the “tree constants” at each vertex of this $V^{\star }$-directed GCRN.

• Step 6: Set up and solve log-linear system (24) for the concentrations.

1.3 A.3: ZigZag Model Example

Reconsider the zigzag model of plant–pathogen interactions (). We now outline how the steps described in “Appendix A.2” apply to this network.

Step 1: We were able to use the algorithm described in Sect. 3.3 to determine the following structural translation:

As expected by the algorithm, this network is weakly reversible and deficiency zero. It follows from Lemma 12 of Johnston et al. (2018) that all of the steady states can be found by setting up and solving log-linear system (24).

Steps 2 & 3: Notice that the complexes $X_3 + X_4$, $X_9 + X_{10} + X_{11}$, and $X_9 + X_{11}$ have multiple source complexes which are translated to them from (). We therefore split these vertices in () when assigning kinetic-order complexes. We also need to select distinguish complexes and add phantom edges to satisfy the conditions of being $V^\star$-directed given in “Appendix A.1.” This can be accomplished by the following network, where the phantom edges are labeled with $\sigma _i$, $i=1, \ldots , 4$, the equivalence classes of stoichiometrically identical complexes are indicated with the symbols $\S$, $\dag$, and $\ddag$, and the distinguished vertices are indicated with $\star$.

Step 4: The kinetic-order deficiency is the deficiency of the CRN produced by considering only the kinetic-order (bracketed) complexes in (). It can be quickly computed that the deficiency is $\delta = n - \ell - s = 17-4-13 = 0$. It follows from Theorem 14 of Johnston et al. (2018) that the remainder of the steps may be performed to yield a steady-state parametrization.

Step 5: From (), we compute the following tree constants:

$$\begin{aligned} \begin{aligned} K_1&= k_2k_5(k_4+\sigma _1)&K_{10}&= k_8k_{10}k_{11}k_{12}k_{14}k_{15}k_{16}(k_{18}+k_{19})\\ K_2&= k_1(k_4+\sigma _1)k_5&K_{11}&= k_8k_{11}k_{12}k_{14}k_{15}k_{16}(k_{17}k_{19}+(k_{18}+k_{19})\sigma _2)\\ K_3&= k_1k_3k_5&K_{12}&= k_{11}k_{12}(\sigma _3+\sigma _4+k_{13})k_{14}k_{15}k_{16}((\sigma _2+k_{17})k_{19}+k_{18}\sigma _2)\\ K_4&= k_1k_3\sigma _1&K_{13}&= k_8k_{10}k_{11}k_{12}k_{14}k_{15}k_{16}k_{17}\\ K_5&= k_7&K_{14}&= k_8k_{10}k_{11}k_{14}k_{15}k_{16}k_{17}k_{19}\\ K_6&= k_6&K_{15}&= k_8k_9k_{12}k_{14}k_{15}k_{16}(k_{17}k_{19}+(k_{18}+k_{19})\sigma _2)\\ K_7&= k_8k_{10}k_{11}k_{12}k_{15}k_{16}(k_{18}+k_{19})\sigma _2&K_{16}&= k_{21}\\ K_8&= k_8k_{11}k_{12}k_{14}k_{16}((\sigma _2+k_{17})k_{19}+k_{18}\sigma _2)\sigma _3&K_{17}&= k_{20}\\ K_9&= k_8k_{11}k_{12}k_{14}k_{15}((\sigma _2+k_{17})k_{19}+k_{18}\sigma _2)\sigma _4\\ \end{aligned} \end{aligned}$$

Step 6: Log-linear system (24) can be set up for any maximal set of pairs of vertices lying in the same linkage class. We take the pairs

$$\begin{aligned}&\{ 1, 2\}, \{1, 3\}, \{1, 4\}, \{5, 6\}, \{7, 8\}, \{7, 9\}, \{7, 10\}, \{7, 11\},\\&\quad \{7, 12\}, \{7, 13\}, \{7, 14\}, \{7, 15\}, \{16, 17\}. \end{aligned}$$

This gives the following linear system in log concentrations (24):

$$\begin{aligned} \left[ \begin{array}{ccccccccccccc}-\,1&{}-\,1&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ -\,1&{}-\,1&{}0&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ -\,1&{}-\,1&{}0&{}1&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}-\,1&{}-\,1&{}1&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}1&{}-\,1&{}0&{}0&{}0\\ 0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}1&{}-\,1&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}1&{}-\,1&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}1&{}0&{}-\,1&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}-\,1&{}0&{}1&{}0\\ 0&{}0&{}0&{}0&{}1&{}0&{}0&{}0&{}0&{}-\,1&{}0&{}0&{}0\\ 1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}-\,1&{}0&{}0&{}0\\ 0&{}0&{}0&{}-\,1&{}0&{}0&{}0&{}0&{}0&{}0&{}-\,1&{}0&{}1\end{array} \right] \left[ \begin{array}{c} \ln (x_1) \\ \ln (x_2) \\ \ln (x_3) \\ \ln (x_4) \\ \ln (x_5) \\ \ln (x_6) \\ \ln (x_7) \\ \ln (x_8) \\ \ln (x_9) \\ \ln (x_{10}) \\ \ln (x_{11}) \\ \ln (x_{12}) \\ \ln (x_{13}) \end{array} \right] = \left[ \begin{array}{c} \ln \left( K_2/K_1 \right) \\ \ln \left( K_3/K_1 \right) \\ \ln \left( K_4/K_1 \right) \\ \ln \left( K_6/K_5 \right) \\ \ln \left( K_8/K_7 \right) \\ \ln \left( K_9/K_7 \right) \\ \ln \left( K_{10}/K_7 \right) \\ \ln \left( K_{11}/K_7 \right) \\ \ln \left( K_{12}/K_7 \right) \\ \ln \left( K_{13}/K_7 \right) \\ \ln \left( K_{14}/K_7 \right) \\ \ln \left( K_{15}/K_7 \right) \\ \ln \left( K_{17}/K_{16} \right) \end{array} \right] \end{aligned}$$

Since the kinetic-order deficiency is zero, this is a consistent system and therefore guaranteed to have a solution for all rate constants (Theorem 14, Johnston et al. 2018). Solving the system for $\ln (x_i)$ and then exponentiating gives the following solution, which is a rational parametrization of the steady-state set of mass-action system (1) corresponding to () in the parameters $\sigma _1, \sigma _2, \sigma _3, \sigma _4 \in {\mathbb {R}}y_{> 0}$:

$$\begin{aligned} \begin{aligned} x_1&= \frac{ k_9 k_{12}(k_{17} k_{19}+(k_{18}+k_{19})\sigma _2)\sigma _1}{k_5k_8k_{10}k_{17}k_{19}}&x_8&= \frac{k_{12}(k_{13}+\sigma _3+\sigma _4)((k_{17}+\sigma _2)k_{19}+k_{18}\sigma _2) \sigma _1}{ k_5k_{10}k_{11} k_{17} k_{19}}\\ x_2&= \frac{k_2 (k_4+\sigma _1)k_5 k_{10} k_{11} k_{17}k_{19} \sigma _4 }{ k_1 k_3 k_9k_{12}k_{16} (k_{17} k_{19}+(k_{18} + k_{19}) \sigma _2) \sigma _1}&x_9&= \frac{ k_{12}(k_{17} k_{19}+(k_{18}+k_{19}) \sigma _2)\sigma _1 }{k_5 k_{10} k_{17} k_{19}}\\ x_3&= \frac{(k_4+\sigma _1)\sigma _4 }{ k_3k_{16}}&x_{10}&= \frac{k_{12} (k_{18}+k_{19})\sigma _1 \sigma _2 }{k_5 k_{14}k_{17} k_{19}}\\ x_4&= \frac{\sigma _4}{k_{16}}&x_{11}&= \frac{k_{14}}{\sigma _2}\\ x_5&= \frac{\sigma _1}{k_5}&x_{12}&= \frac{ k_{12}\sigma _1}{k_5 k_{19}}\\ x_6&= \frac{ k_5 k_7\sigma _3}{k_6k_{15} \sigma _1 }&x_{13}&= \frac{ k_{14} k_{20}\sigma _4}{k_{16} k_{21}\sigma _2}\\ x_7&= \frac{\sigma _3}{k_{15}}\\ \end{aligned} \end{aligned}$$

(27)

Notice that this parametrization does not guarantee that for a given initial condition ${\mathbf {x}}(0) \in {\mathbb {R}}_{\ge 0}^m$ the parametrization intersects the relevant compatibility class $({\mathbf {x}}(0) + S) \cap {\mathbb {R}}_{\ge 0}^m$. For this example, we can observe that $x_8$ experiences no stoichiometric change in any of the system’s interactions and therefore we have $x_8(t)=x_8(0)$ for all $t \ge 0$. This requirement combined with (27) imposes further conditions on the rate constants which must be satisfied for a positive steady state to exist.

1.4 A.4: MAPK Model Example

Reconsider MAPK model ().

Step 1: We were able to use the algorithm described in Sect. 3.3 to determine the following structural translation:

Steps 2 & 3: The complexes $X+K+M$ and $X_p + K +M$ are both assigned multiple kinetic complexes and therefore must be split. Setting 1 and 3 as the distinguished complexes and introducing phantom edges gives the following $V^{\star }$-directed GCRN:

where $\sigma _1$ and $\sigma _2$ indicate the phantom edges, $\dag$ and $\ddag$ indicate equivalence classes of stoichiometrically identical complexes, and $\star$ indicates the distinguished vertex within each class.

Step 4: We can compute that the kinetic-order deficiency is one. We therefore have one condition of the form $c^{\mathrm{T}} b = 0$ where $c \in \text{ ker }(M)$ to satisfy on the rate constants in order to apply the method prescribed by Theorem 14 of Johnston et al. (2018). We suspend discussion of the construction of the matrix M to Step 6, but note that the required condition is

$$\begin{aligned} \frac{(k_{11}+k_{12})\sigma _2}{k_{16}\sigma _1} = 1 \; \Longrightarrow \; \sigma _2 = \frac{k_{11}+k_{12}}{k_{16}} \sigma _1. \end{aligned}$$

(29)

That is, we eliminate one of our free parameters to satisfy the condition. Since this result is positive, we may proceed.

Step 5: After substituting (29) into (), we can compute the following tree constants

$$\begin{aligned} \begin{aligned} K_1&= (k_2+k_3)(k_5+k_6)k_7k_{9}k_{10}(k_{11}+k_{12})k_{12}k_{14}k_{15}\sigma _1\\ K_2&= k_1(k_5+k_6)k_7k_{9}k_{10}(k_{11}+k_{12})k_{12}k_{14}k_{15}\sigma _1 \\ K_3&= k_1k_3 (k_5 + k_6) k_7 k_{9} k_{10}(k_{11} + k_{12}) (k_{13} + k_{14}) k_{15} k_{16} \\ K_4&= k_1k_3k_4k_7k_{9}k_{10}(k_{11}k_{13}+k_{11}k_{14}+k_{12}k_{13}+k_{12}k_{14})k_{15}k_{16}\\ K_5&= k_1 k_3 k_4 k_6(k_8 + k_{9}) k_{10} (k_{11} k_{13} + k_{11} k_{14} + k_{12} k_{13}+ k_{12} k_{14})k_{15} k_{16} \\ K_6&= k_1k_3k_4k_6k_7k_{10}(k_{11}k_{13}+k_{11}k_{14}+k_{12}k_{13}+k_{12}k_{14})k_{15}k_{16}\\ K_7&= k_1k_3(\sigma _1(k_5+k_6)k_{11}+k_{16}k_4k_6)k_7k_9(k_{11}+k_{12})(k_{13}+k_{14})k_{15}\\ K_8&= k_1k_3(k_5 + k_6)k_7 k_{9} k_{10} (k_{11}+k_{12})(k_{13} + k_{14}) k_{15} \sigma _1 \\ K_9&= k_1k_3(k_5+k_6)k_7k_{9}k_{10}(k_{11}+k_{12})k_{12}k_{15}\sigma _1\\ K_{10}&= (k_2\sigma _1+k_3\sigma _1+k_1k_3)(k_5+k_6)k_7k_{9}k_{10}(k_{11}+k_{12})k_{12}k_{14}\sigma _1\\ K_{11}&= (k_2k_5+k_2k_6+k_3k_5+k_3k_6)k_7k_{9}k_{10}(k_{11}+k_{12})k_{12}k_{14}k_{15}\sigma _1^2/k_{16} \end{aligned} \end{aligned}$$

Step 6: Log-linear system (24) can be set up for any maximal set of pairs of vertices lying in the same linkage class. We take the pairs

$$\begin{aligned} \{ 1, 2\}, \{1, 3\}, \{1, 4\}, \{1, 5\}, \{1, 6\}, \{1, 7\}, \{1, 8\}, \{1, 9\}, \{1, 10\}, \{1, 11\}. \end{aligned}$$

This gives the following log-linear system (24):

$$\begin{aligned} \left[ \begin{array}{ccccccccccc}-\,1&{}0&{}0&{}0&{}-\,1&{}1&{}0&{}0&{}0&{}0&{}0\\ -\,1&{}1&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ -\,1&{}0&{}0&{}0&{}-\,1&{}0&{}1&{}0&{}0&{}0&{}0\\ -\,1&{}0&{}1&{}1&{}-\,1&{}0&{}0&{}0&{}0&{}0&{}0\\ -\,1&{}0&{}0&{}0&{}-\,1&{}0&{}0&{}1&{}0&{}0&{}0\\ -\,1&{}0&{}0&{}0&{}-\,1&{}0&{}0&{}0&{}1&{}0&{}0\\ -\,1&{}1&{}0&{}1&{}-\,1&{}0&{}0&{}0&{}0&{}0&{}0\\ -\,1&{}0&{}0&{}0&{}-\,1&{}0&{}0&{}0&{}0&{}1&{}0\\ -\,1&{}0&{}0&{}0&{}-\,1&{}0&{}0&{}0&{}0&{}0&{}1\\ 0&{}0&{}0&{}1&{}-\,1&{}0&{}0&{}0&{}0&{}0&{}0\end{array} \right] \left[ \begin{array}{c} \ln (X) \\ \ln (X_p) \\ \ln (X_{pp}) \\ \ln (M) \\ \ln (K) \\ \ln (XK) \\ \ln (X_pK) \\ \ln (X_{pp}M) \\ \ln (X_pM) \\ \ln (X^*_pM) \\ \ln (XM) \end{array} \right] = \left[ \begin{array}{c} \ln \left( K_2/K_1 \right) \\ \ln \left( K_3/K_1 \right) \\ \ln \left( K_4/K_1 \right) \\ \ln \left( K_5/K_1 \right) \\ \ln \left( K_6/K_1 \right) \\ \ln \left( K_7/K_1 \right) \\ \ln \left( K_8/K_1 \right) \\ \ln \left( K_9/K_1 \right) \\ \ln \left( K_{10}/K_1 \right) \\ \ln \left( K_{11}/K_1 \right) \end{array} \right] \end{aligned}$$

(30)

Note that, in Step 4, we used the left kernel vector $c = (0,1,0,0,0,0,-\,1,0,0,1)$ of the coefficient matrix $M^{\mathrm{T}}$ of (30). Since we have satisfied the condition $c^{\mathrm{T}} b = 0$ with (29), this is a consistent system. We can solve this system and exponentiate to obtain the following steady-state parametrization:

$$\begin{aligned} \begin{aligned} X&= \frac{(k_2+k_3)k_{15}\tau _1}{(k_2+k_3)\sigma _1+k_1k_3}&X_pK&= \frac{k_1k_3k_4(k_{13}+k_{14})k_{15}k_{16}\tau _1\tau _2}{((k_2+k_3)\sigma _1+k_1k_3)(k_5+k_6)k_{12}k_{14}\sigma _1}\\ X_p&= \frac{k_1k_3(k_{13}+k_{14})k_{15}k_{16}\tau _1}{((k_2+k_3)\sigma _1+k_1k_3)k_{12}k_{14}\sigma _1}&X_{pp}K&= \frac{k_1k_3k_4k_6(k_{13}+k_{14})k_{15}k_{16}\tau _1\tau _2}{((k_2+k_3)\sigma _1+k_1k_3)(k_5+k_6)k_9k_{12}k_{14}\sigma _1}\\ X_{pp}&= \frac{k_1k_3k_4k_6(k_8+k_9)(k_{13}+k_{14})k_{15}k_{16}^2\tau _1}{((k_2+k_3)\sigma _1+k_1k_3)(k_5+k_6)k_7k_9k_{12}k_{14}\sigma _1^2}&X_pM&= \frac{k_1k_3(\sigma _1(k_5+k_6)k_{11}+k_4k_6k_{16})(k_{13}+k_{14})k_{15}\tau _1\tau _2}{((k_2+k_3)\sigma _1+k_1k_3)(k_5+k_6)k_{10}k_{12}k_{14}\sigma _1}\\ M&= \frac{\sigma _1\tau _2}{k_{16}}&X^*_pM&= \frac{k_1k_3k_{15}\tau _1\tau _2}{((k_2+k_3)\sigma _1+k_1k_3)k_{14}}\\ K&= \tau _2&XM&= \tau _1\tau _2\\ XK&= \frac{k_1k_{15}\tau _1\tau _2}{(k_2+k_3)\sigma _1+k_1k_3}&\end{aligned} \end{aligned}$$

(31)

in the parameters $\sigma _1, \tau _1, \tau _2 \in {\mathbb {R}}_{>0}$.

Parametrization (31) is quite useful in the context of determining the capacity for mono- and multistationarity within stoichiometric compatibility classes of mass-action system (1) corresponding to MAPK network (). The steady states are not toric so that the results of Pérez Millán et al. (2012) and Müller et al. (2016) cannot be applied. We can, however, apply the computational procedure of Corollary 2 of Conradi et al. (2017). To satisfy the assumptions, we note that the network has the following conservation laws and is therefore dissipative:

$$\begin{aligned} X_{\mathrm{tot}}= & {} X + X_p + X_{pp} + XK + X_pK + XM + X_pM + X_p^*M + X_{pp}M\\ K_{\mathrm{tot}}= & {} K + XK + X_pK \\ M_{\mathrm{tot}}= & {} M + XM + X_pM + X_p^*M + X_{pp}M. \end{aligned}$$

It also has no critical siphons so that there are no boundary equilibria Angeli et al. (2007). Computing the determinant of the Jacobian $a({\hat{x}})$ evaluated along parametrization (31) yields a rational function in the three parameters $\sigma _1, \tau _1,$ and $\tau _2$ with a strictly positive denominator. It can be checked that, in the numerator of $a({\hat{x}})$, $\tau _1^2 \tau _2^2$ and $\sigma _1^2 \tau _1 \tau _2^3$ are extremal with respect to the corresponding Newton polytope and that the coefficients have mixed sign in $a({\hat{x}})$. It follows that the mechanism exhibits multistationarity for some choices of rate constants and initial conditions. It should be noted that parametrization (31) reduces the dimension of the system from 11 variables to 3 which allows significantly faster computation and analysis of $a({\hat{x}})$.