1 Introduction

Radiation is commonly used in cancer treatment, either as monotherapy or as combination treatment with surgery and chemotherapy. Radiation is a DNA damaging agent, and radiation as cancer therapy benefits from cancer cells being less efficient in repairing radiation-induced damage than normal cells. Total radiation dose is divided into small frequent fractions to provide temporal windows for normal tissue recovery. Treatment schedules (fractionation) are predominantly based on evolved empirical knowledge and wisdom, but greatly constrained by logistical considerations. Recent developments include hypo- and hyperfractionation for various cancer types, that is delivery of either larger doses temporally further separated or smaller doses more frequently.

Despite many technical improvements in the efficiency of radiotherapy, many tumors are refractory to irradiation. Various clinical and biological factors explain such complications, including DNA damage repair (Hall and Giaccia 2006; Mathews et al. 2013), prevalence of hypoxia, and tumor heterogeneity and plasticity. Recently, the presence of cancer stem cells and a tumor hierarchy has been discussed as source of intratumoral heterogeneity and therapy response (Marjanovic et al. 2013; Shackleton et al. 2009). The cancer stem cell hypothesis proposes that the small subpopulation of so-called cancer stem cells (CSCs) is critically important for the initiation and maintenance of the tumor. These CSCs are able to self-renew indefinitely and undergo symmetric and asymmetric divisions to retrospectively increase the CSC population and produce progenitor cells that will make up the bulk of the tumor (Reya et al. 2001). Recent evidence suggests plasticity between non-CSC and CSC states (Gupta et al. 2011), due to genetic or microenvironmental perturbations. CSCs have been shown to utilize superior radiation-induced DNA damage repair mechanisms to prevent cell death (Bao et al. 2006). After radiation exposure, cells with damaged DNA attempt different pathways of repair, and the repair time is likely dependent on the delivered radiation dose (Lagadec et al. 2010; Sarcar et al. 2011).

The conventional radiotherapy protocol for most tumors delivers a total dose of 50–70 Gy in 2 Gy fractions on each weekday, with no treatment given on weekends. To reduce toxicity and increase efficiency, alternative treatments have been considered, including a hyperfractionated protocol with 1 Gy per fraction twice a day; an accelerated regimen of 1.2 Gy per fraction twice daily; and hypofractionation with 5 Gy twice-a-week fractions. Here, we develop a minimal mathematical model to study the effect of tumor heterogeneity and repair in tumors exposed to theses different radiation treatment schedules.

Several mathematical models have been developed to simulate the effects of radiotherapy. Most models utilize the so-called linear quadratic (LQ) model and its various extensions (Hall and Giaccia 2006). In the original LQ model, cell survival probability S after acute doses of radiation d can be estimated with

$$\begin{aligned} S(d)=\exp (-\alpha d - \beta d^2), \end{aligned}$$
(1)

where \(\alpha \) (Gy\(^{-1}\)) and \(\beta \) (Gy\(^{-2}\)) are tissue-specific radiosensitivity parameters that are usually derived from fitting the LQ model to clonogenic survival data (Hall and Giaccia 2006). More recently, mathematical frameworks have been combined with experimental data to investigate the different responses to clinically available radiation protocols (Dhawan et al. 2014; Dionysiou et al. 2004; Enderling et al. 2009; Stamatakos et al. 2014). Recently, Leder et al. (2014) proposed an optimized radiation dosing schedule for PDGF-driven glioblastoma. The model, however, is dependent on a large number of parameters and, with limited biological data, some parameters are far from biological realism. In particular, tissue-specific radiosenstivity parameters \(\alpha \) and \(\beta \) are derived such that the derived ratio of \(\alpha /\beta =865,789\) Gy is five orders of magnitude larger than frequently derived \(\alpha /\beta =3-10\) Gy (Leder et al. 2014). Nevertheless, the model-predicted optimal dose fractionation showed prolonged survival in subsequent mouse experiments, emphasizing that the currently applied standard-of-care radiation fractionation may not yield optimal outcomes. Mathematical models may help decipher the complex biology underlying cancer cell response to irradiation, with the ultimate aim to improve clinical application of radiotherapy.

Herein we propose a simple mathematical model of breast cancer cell dynamics under fractionated radiation exposure. The model includes phenotypic cell heterogeneity and plasticity, as well as radiation-induced cell cycle arrest, which may play a pivotal role in analyzing radiation protocols with multiple doses per day. The effect of different model parameters and repair mechanisms on heterogeneity are studied for different clinically feasible radiotherapy treatments.

2 Method

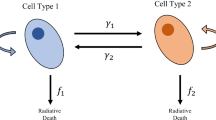
We developed a two-compartment mathematical model to analyze the effect of radiation therapy on the two phenotypically distinct subpopulations of radioresistant and radiosensitive cancer cells. In breast cancer, these populations have been identified by, respectively, CD44highCD24low (\(CD^{+}\); biomarker positive) and CD44lowCD24high (\(CD^{-}\); biomarker negative), which are also markers of cancer stemness (Al-Hajj et al. 2003; Fillmore and Kuperwasser 2008). Both subpopulations are capable of self-renewal, albeit with lower rates for biomarker negative CD\(^-\) cells that also feature higher death rates. We discuss the balance of self-renewal and cell death as the net population growth rate, which does not affect the behavior of the system. As a visualization of phenotypic plasticity, cells can switch from one phenotype to the other (Marjanovic et al. 2013). After exposure to radiation, cells in each compartment are forced into cell cycle arrest to attempt repair from radiation-induced DNA damage. Biomarker positive cells have been shown to have better repair mechanisms (Bao et al. 2006; Baumann et al. 2008) and, thus, a larger fraction of growth-arrested biomarker positive CD\(^+\) (calculated by the LQ model with phenotype-specific \(\alpha _S\) and \(\beta _S\) parameters) returns into the viable population after successful repair. Figure 1 shows a schematic diagram of the proposed model, and model parameters are summarized in Table 1.

Fig. 1
figure 1

(Color figure online) Schematic diagram of the model

Full size image
Table 1 Description of the model parameters
Full size table

We denote by \(N_{S}\), \(N_{RS}\), \(N_{P}\), and \(N_{RP}\) the population of resistant cells, resistant repairing cells, sensitive cells, and sensitive repairing cells, respectively. The model can be mathematically represented by the following system of equations

$$\begin{aligned} \begin{aligned} \frac{\hbox {d}N_{S}}{\hbox {d}t}&=\rho _{S}N_{S}+\rho _{PS}N_{P}+g(d)e^{(-\alpha _{S}d-\beta _{S}d^{2})}N_\mathrm{RS}-\rho _\mathrm{SP}N_{S}-\delta _{S}fN_{S},\\ \frac{\hbox {d}N_\mathrm{RS}}{\hbox {d}t}&=\delta _{S}fN_{S}-g(d)N_\mathrm{RS},\\ \frac{\hbox {d}N_{P}}{\hbox {d}t}&=\rho _{P}N_{P}+\rho _\mathrm{SP}N_{S}+g(d)e^{(-\alpha _{P}d-\beta _{P}d^{2})}N_\mathrm{RP}-\rho _\mathrm{PS}N_{P}-\delta _{P}fN_{P},\\ \frac{\hbox {d}N_\mathrm{RP}}{\hbox {d}t}&=\delta _{P}fN_{P}-g(d)N_\mathrm{RP}.\\ \end{aligned} \end{aligned}$$
(2)

Cells acquire on average one DNA double strand break after exposure to 1 Gy of radiation. Therefore, we assume that each cell will enter cell cycle arrest and attempt repair after each radiation fraction, but no new damage arises in the interval between radiation treatments. Hence, \(f=1\) at discrete times when radiation is given, and \(f=0\) otherwise. Dependent on radiosensitivity parameters \(\alpha _{i}\) and \(\beta _{i}\) with \(i\in \{S, P\}\), cells will either die due to radiation-induced DNA damage with probability \(1-S_{i}(d)\) or return to the viable non-repairing population S or P with probability \(S_{i}(d)\) at dose-dependent rate g(d). We assume the function g(d) to be of the order of inverse square of the dose (Lagadec et al. 2010; Sarcar et al. 2011), such that cells irradiated with a dose of 1 Gy spend on average 1 h attempting repair, and 4 h after exposure to 2 Gy.

2.1 Parameter estimation

Stochastic and deterministic simulations have been compared to two sets of experimental data to derive suitable values for model parameters. The experimental study on breast cancer initiating cells (i.e., CSCs) and mammosphere formation assay (MFA) data calibrates the fraction of biomarker positive CSCs (Lagadec et al. 2010). In this study, the breast cancer cell line is irradiated with a single dose or daily doses of 2 Gy. After 48 hours, single cells are seeded to form spheres for 20 days. The fraction of CSCs and mammosphere formation capacity are reported in Table 2 (Lagadec et al. 2010).

Table 2 Fractionated irradition effect on CSC population and mammosphere formation capacity (Lagadec et al. 2010)
Full size table

As the MFA experiment was initiated from a single cell (Lagadec et al. 2010), stochastic effects are important. We apply the Gillespie algorithm to compare model sphere forming capacity predictions with the experimental data in Table 2. Since running the Gillespie algorithm is computationally expensive, it is only used to fit the parameters of the model when \(\delta {s}=\delta _{p}=g=0\). We vary model parameters without repair to obtain the best fit to the experimental data. At the same time, we use the deterministic Eq. 2 to compare the theoretical results of average CSC fraction to experimental data. The estimated model parameters are summarized in Table 3, alongside the fraction of CSCs and sphere forming capacity using those values, which show good agreement with the experimental results in Table 2. Of note is that the reported parameter value combinations are not unique and, thus, we will perform a sensitivity analysis to investigate the impact of each parameter on model outcome.

Table 3 Estimated model parameters when \(\delta _{S}=\delta _{P}=g=0\)
Full size table
Fig. 2
figure 2

(Color figure online) Fitting the modified linear quadratic model to the experimental data of (Phillips et al. 2006). The black points are the extracted experimental data. The solid curve is the model result using the estimated radiosensitivity parameters \(\alpha _{S}=0.14\) Gy\(^{-1}\), \(\beta _{S}=0.048\) Gy\(^{-2}\), \(\alpha _{P}=0.41\) Gy\(^{-1}\) and \(\beta _{P}=0.17\) Gy\(^{-2}\)

Full size image

Herein, resistant and sensitive tumor cells are considered to have different radiosensitivities. Thus, the total population of cells at time t is given by \(N(t)=N_{S}(t)+N_{P}(t)\) (hereafter, \(N_{S}\equiv N_{S}+N_\mathrm{RS}\) and \(N_{P}\equiv N_{P}+N_\mathrm{RP}\) unless stated otherwise); the population of cells after exposure to treatment for the period of time \(\tau \) can be calculated as

$$\begin{aligned} \begin{aligned} \frac{N(t+\tau )}{N(t)}&=\frac{N_{S}(t)}{N(t)}e^{(-\alpha _{S}d-\beta _{S}d^{2})}+\frac{N_{P}(t)}{N(t)}e^{(-\alpha _{P}d-\beta _{P}d^{2})}. \end{aligned} \end{aligned}$$
(3)

Assuming that the fraction of CSCs is at its steady-state value before the radiation, and using the experimental data of (Lagadec et al. 2010), we set \(\frac{N_{S}(t)}{N(t)}=0.076\) (and \(\frac{N_{P}(t)}{N(t)}=0.924\)). Then, the modified linear quadratic model (Eq. 3) is used to fit model results to the experimental data of (Phillips et al. 2006), which yields \(\alpha _{S}=0.14\) Gy\(^{-1}\), \(\beta _{S}=0.048\) Gy\(^{-2}\) (\(\alpha _S/\beta _S\)=2.9 Gy), \(\alpha _{P}=0.41\) Gy\(^{-1}\) and \(\beta _{P}=0.17\) Gy\(^{-2}\) (\(\alpha _S/\beta _S\)=2.4 Gy) (Fig. 2). Since at each radiation fraction the majority of damaged cells undergo repair mechanisms, we assume that \(90\%\) of cells will be arrested (Withers 1992). However, sensitivity analysis shows that reducing this fraction as low as to \(40\%\) does not qualitatively change the results (see Figure S1 and Figure S2 in supplementary materials). The list of all model parameters and their estimated values are reported in Table 4.

3 Results

We consider different clinical radiotherapy treatment protocols for one week including standard of care (SoC; daily doses of 2 Gy), hyperfractionated (HR; two daily doses of 1 Gy), accelerated hyperfractionation (AC; two daily doses of 1.2 Gy), and hypofractionated (HO; twice-a-week doses of 5 Gy). Additionally, we simulate the recently suggested optimal protocol for PDGF-driven glioblastoma by Leder (Leder et al. 2014) (Optimum-1, OP; see Table 5). All protocols deliver a total dose of \(D=10\) Gy per week, except accelerated hyperfractionated with a total dose of \(D=12\) Gy. However, the accelerated hyperfractionated protocol has the same biologically effective dose (BED) as SoC (see Table 6). BED is used to describe the biological effect of dose fractionation and is defined as

$$\begin{aligned} \begin{aligned} \text {BED}= \frac{-\ln (SF(d))}{\alpha }=D\left( 1+\frac{d}{\alpha /\beta }\right) , \end{aligned} \end{aligned}$$
(4)
Table 4 Model parameter values
Full size table

where SF(d) is the LQ model derived single dose d-dependent survival fraction with radiobiological parameters \(\alpha \) and \(\beta \) (compare Eq. 1). Due to the linear quadratic relationship of dose and survival, total dose can be increased when smaller doses are given in each fraction (Fowler 1989). The model introduced in Sect. 2 considered two subgroups of cancer cells (resistant cells and sensitive cells) with different radiosensitivities. Thus, following the survival fraction of cancer cells in Eq. 3, the BED is given by

$$\begin{aligned} \begin{aligned} \text {BED}= \frac{-\ln (mSF_{S}+(1-m)SF_{P})}{m \alpha _{S}+(1-m) \alpha _{P}}, \end{aligned} \end{aligned}$$
(5)

where \(SF_{S}\) and \(SF_{P}\) are survival fractions for resistant cells and sensitive cells, respectively. The constant m represents the proportion of resistant cells in the tumor prior to irradiation. Table 6 shows the BED for the standard of care (SoC), hyperfractionated (HR), and accelerated hyperfractionated (AC) protocols with different initial fractions of resistant cells: tumors containing only resistant cells (\(m=1\)), tumors containing only sensitive cells (\(m=0\)), and heterogeneous tumors with a small subpopulation of resistant cells (\(m=0.076\)) as estimated. The BED is almost identical for standard-of-care and accelerated hyperfractionation, but significantly smaller for hyperfractionation.

Table 5 Radiotherapy schedules for one week of treatment. Different colors are used for corresponding colors in the figures
Full size table
Table 6 Biological effective dose for hyperfractionation, standard of care, and accelerated hyperfractionated protocols
Full size table

Figure 3 shows the number of cancer cells \(N_{S}+N_{P}\) and fraction of resistant cells \(N_{S}/(N_{S}+N_{P})\) for all considered radiation schedules (compare Table 5). Simulations show that protocols with larger number of fractions leads to more cell kill, with accelerated hyperfractionation yielding the smallest number of cells after one week of therapy. However, the fraction of stem cells is largest compared to the other radiotherapy protocols. Hypofractionation with smallest overall cell kill leads also to least competitive release of the most resistant stem cell subpopulation (Enderling et al. 2009).

Fig. 3
figure 3

(Color figure online) Number of cancer cells \(N_{S}+N_{P}\) and the fraction of resistant cells \(N_{S}/(N_{S}+N_{P})\) for radiotherapy protocols reported in Table 5

Full size image
Table 7 Sensitivity analysis for different parameters of the model
Full size table
Fig. 4
figure 4

(Color figure online) Number of cancer cells \(N_{S}+N_{P}\) and the fraction of resistant cells \(N_{S}/(N_{S}+N_{P})\) when \(\alpha _{P}\) and \(\beta _{P}\) are changed to \(\alpha _{P}-0.5\alpha _{P}\) and \(\beta _{P}-0.5\beta _{P}\) for radiotherapy protocols reported in Table 7

Full size image

For the chosen parameter combinations (Table 4), accelerated hyperfractionation and SoC schedules yield the lowest number of cancer cells after one week of treatment (Fig. 3). Sensitivity analysis showed that the results are robust to changes in the parameter values (Table 7), with the exception that decreasing \(\alpha _{P}\) and \(\beta _{P}\) by \(50\%\) produces hypofractionated and accelerated hyperfractionated as best protocols (Fig. 4).

Heretofore we assumed that \(90\%\) of cells undergo arrest to attempt repair, and the parameter values for \(\delta _{S}\) and \(\delta _{P}\) were chosen large enough to satisfy this assumption. However, decreasing the values for these parameters so that less than \(40\%\) of cells attempt repair suggests accelerated hyperfractionated as the best schedule (see Figure S1 and Figure S2 in supplementary materials). Furthermore, the model considers that cells leave arrest with rate g(d), which is assumed to be on the order of \(1/\hbox {dose}^2\). If g(d) was proportional to \(1/\hbox {dose}\) the number of cancer cells at the end of the course of radiation therapy decreases significantly; however, the accelerated hyperfractionated schedule remains the best treatment protocol followed by SoC. Moreover, if \(g(d)=1\), the order of the best treatment regimens remains (see Figures S3, S4, and S5 in supplementary materials).

4 Conclusion

In this paper, a two-compartment mathematical model has been developed to assess the effect of tumor heterogeneity and radiotherapy fractionation on treatment response. Model simulations suggest that radiotherapy can alter tumor heterogeneity and elevates the fraction of resistant cells. Future studies may further increase biological complexity by considering increased self-renewal of the resistant population in response to radiation (Gao et al. 2013). If the total radiation dose is insufficient to eradicate the tumor, enrichment in cancer stem cells may lead to tumor relapse and recurrence. Therefore, if total tumor control cannot be achieved optimal therapies should balance decreases in tumor burden and prevention of outgrowth of the most resistant subpopulation. Interestingly, none of our simulations suggested standard-of-care fractionation as the best therapeutic approach, further emphasizing the need to prospectively evaluate alternative fractionation protocols in the clinic. Furthermore, our model calibrated for breast cancer was unable to confirm the optimum treatment schedule for PDGF-driven glioblastoma (as in Leder et al. 2014). This suggests that treatment optimization may be highly tumor biology, mathematical model, and model parameter dependent, and utmost importance must be paid to identifying underlying biological mechanisms. Hence, a general optimal radiation schedule as suggested in (Conforti et al. 2008; Leder et al. 2014; Wein et al. 2000) may not be feasible and designing an efficient protocol may be required for each type of cancer, and even each individual patient.

At the moment, the study is hypothesis generating, and we sincerely hope that the presented results are exciting and encouraging for experimentalists and clinicians to test the presented model predictions.