1 Introduction

With the development of computer vision counting and artificial intelligence counting, machine learning methods should generally be used to count objects in digital images. The counting problem is the estimation of the number of objects in a still image or video frame. It arises in many applications, including cell counting in microscopic images [1], estimating the scale of social events [2], and estimating animal crowds for ecological surveys [3], to name a few.

Cell counting based on microscopic images is a fundamental part of medical diagnosis and biology. Doctors and researchers encounter the problem of quantitatively processing a large number of medical images; if the data is effectively quantified, the efficiency of doctors’ disease diagnosis can be improved. Therefore, it makes sense to conduct statistics and analysis of quantitative results through scientific research [4] to obtain more accurate and valid findings. Many works in biology and medicine require counting or detecting the localization of cells in cell images to help diagnose diseases and select the appropriate treatments. For example, a patient’s health status can be inferred from the number of red blood cells and white blood cells; in clinical pathology, cell counting can be used to investigate hypotheses about developmental or pathological processes; in molecular biology, the cell concentration can be used to regulate the number of chemicals used in an experiment.

Fig. 1
figure 1

The working process of the density regression microscopic cell counting method is represented visually. a A Gaussian function is used to generate the ground-truth density map, and the difference between the prediction count map generated by the density map estimator and the ground-truth density map is measured using L2 loss. b The generated predictive output uses the optimal transport method to directly compute the error between the predicted counts and annotations and employs VGG19 as the network backbone to construct the density map estimator

Full size image

Counting the number of cells in microscopic cell images is a tedious task. Manual counting consumes considerable manpower and material resources. In addition, due to fatigue and other reasons, workers are prone to errors when manually calculating the number of cells in hundreds of microscopic cell images, and the calculated number of cells is also affected by subjective reasons. Because the cell density in the cell images is relatively high, cells often block and adhere to one another, while the microscopic image resolution is low, the quality of the cell images cannot be well guaranteed, and blurring or low contrast may occur. All of these factors can negatively affect the accuracy of the counting work. In addition, for medical images, the limited number of trainable images must be considered in medical image processing. To solve these problems, we can use machine learning methods to automatically estimate the number of cells from microscopic images. Considering the limited trainable data, the data processing adopts data enhancement methods such as random clipping and flipping to enhance the robustness of the method and prevent the training results from overfitting.

In our work, the labels in the dataset to train the neural network are annotated so that there is a single point annotation at the center of the cell in the image. The model training is difficult due to the sparse binarized form of the point annotations in the dataset. Therefore, to facilitate model training, the format of the data is converted to a smoother format. The prediction count map that should match the ground-truth density map is calculated by padding and convolving the input microscopic cell images. Since the annotations in the annotated map consist of binary matrices, while the generated prediction count map consists of smooth real-valued matrices, it is difficult to measure the difference between annotated map and prediction count map in a uniform format. Using various methods, the input annotation map can be transformed into a ground-truth density map that can be computed as a difference with the prediction count map generated by the neural network. The current popular generation method uses a Gaussian function to blur the annotation points and converts the annotation points into a Gaussian blob to obtain a ground-truth density map [5, 6].

The L2 loss is a pixel-to-pixel computational procedure that trains the density map estimator between pixels as a regression problem (Fig. 1). Many works use the L2 loss to measure the gap between prediction count map and ground-truth density map and use the difference that it calculates to train the model [7, 8]. Thus, the accuracy of the ground-truth density map greatly affects the accuracy of the counting work, and most methods to generate the ground-truth density map use a Gaussian function to convert each cell marked by a point into a label range that the Gaussian function generates [9]. In fact, this method relies too much on the size selection of the Gaussian kernel, so it affects the accuracy of the model. Moreover, the L2 loss, which is a pixel-to-pixel loss calculation method, is not conducive to the attention of cells in the image during training. The density change of a unit in the background area is equivalent to the density change of a unit near the cell annotated by a point. Methods that pay more attention to the changes in the pixel units of annotated cells will result in more accurate numbers. With these problems, this work uses a loss function that is not limited to the pixel difference metric. In brief, our contributions in this paper can be summarized as follows:

  • We propose a new cell counting method based on deep learning to accurately count cells by directly learning the mapping from the prediction count map to the annotation map.

  • We propose a loss function based on an optimal transport algorithm that treats cell counting as a probability distribution problem, converts a map of density values and binary dot annotation into probability density functions, and measures the gap between them to reliably supervise the counter. The introduction of this loss function eliminates the need for dot annotation to construct the likelihood function through the Gaussian function to generate the ground-truth density map. It also eliminates the negative impact of the determination of the width of the Gaussian kernel in the Gaussian function on the accuracy of the ground-truth.

  • We add an entropy regularization constraint term to the loss function to improve the stability of the training process and make the prediction count map closer to the ground-truth density map.

  • We conducted experiments on the public datasets VGG, MBM, and ADI, which were given labels with point annotations at the center of each cell. Our method was experimentally validated for its effectiveness and better performance than other automated cell counting methods.

2 Related works

Current automatic cell counting methods can be categorized into detection-based methods [10,11,12,13] and regression-based methods [7, 14,15,16,17].

Most of the early works adopted the direct detection method. The detection-based automated cell counting methods generally use a sliding window [18], an SVM framework [11], and extremal region trees [13]. Detection-based methods generally directly detect or segment cells in images, which encounter two main challenges. First, automated cell counting methods require lower cost consumption than manual counting while ensuring accuracy. Second, training object detectors requires bounding-box or instance mask annotations, which is much more labor-intensive in dense-cell microscopic images. In particular, this detection-based approach has limitations, and for very dense cells, mutual occlusion among the cells can negatively affect the results.

Another method based on density estimation does not need to detect or segment the cells in the image in advance but calculates the number of cells by generating a density map and integrating the estimated density map. Cell counting and density estimation in this method avoid the difficult detection and segmentation of individual cells, which makes it more effective for tasks that require only the number of cells in any region. Lempitsky and Zisserman first proposed the method of density map estimation [14]. They used dense SIFT features from the images as a linear regression to predict the density map, which avoids location-based detection of individual cells. Later, Fiaschi et al. [19] integrated the predictive density graph generated by input images to count according to the work of Lempitsky et al. The linear regression was changed to random forest to calculate the object density, which improved the training efficiency. With the development of methods based on density regression. Arteta [20] proposed an interactive counting method, which can quickly feedback and display annotation dots. This work also proves that the ridge regression method can be used to simply, accurately, and effectively estimate object density.

In recent years, deep learning methods have been widely used in various research fields. The excellent performance of neural networks in many computer vision tasks has inspired researchers to calculate the nonlinear relationship between images and density maps and apply neural networks to generate predicted density maps for regression calculations in the area of cell counting. Interestingly, deep convolutional neural networks have been shown to outperform the latest techniques in many computer vision tasks. Xie et al. [5] used a convolutional neural network [21] to regressively calculate the density map generated after Gaussian function processing. Cohen et al. [16] incorporated the methods of Segui et al. [22] to predict counts in a redundant manner and generate a predictive density map using a smaller network running on the image that was trained to count the number of objects in its rectangular sense field of a particular size. The U-Net network model [23] designed by Ronneberger et al. has achieved very good performance in different biomedical image segmentation tasks.

Many counting works use the L1 loss and L2 loss to balance the gap between prediction and ground truth. However, experiments show that such pixel-level loss calculation is greatly affected by the selection of the Gaussian kernel size [24]. Recent work has been devoted to reducing the influence of Gaussian kernel selection on model accuracy. Therefore, several methods that are not limited to pixel-level loss have been proposed in several works. Ma et al. [25] proposed a different loss function from the previous method of converting point annotations into predicted density maps using the Gaussian kernel. The loss function in this work calculates the expected count at each annotation point by summating the posterior probability of target occurrence at each pixel and the density predicted by the neural network, which shows better results on several common reference datasets.

Inspired by several computational methods [26, 27], we realized that the method of converting the dot annotation map to the ground-truth density map using a Gaussian function would generate errors in generating the ground-truth density map due to the difficulty of adapting the size of Gaussian kernel. In many works, this size was manually determined, which reduced the accuracy of the counting work. Then, these works discarded the use of the Gaussian function, treated the counting work as a probability distribution problem, and measured the difference between the prediction count map generated by the counter and the annotated true value as a probability distribution problem.

3 Method

In our work, we utilize the neural network model VGG19 [28] to analyze microscopic cell images. Specifically, we input these images into the model to regress density maps, which are subsequently used to generate accurate cell counts. To ensure the accuracy of our approach, we employ a straightforward loss function to supervise the regression process. In this section, we will provide a detailed description of our method for defining the loss function. Additionally, we will explain the expected error bounds and demonstrate the theoretical validity of our approach.

3.1 Loss based on optimal transmission

The optimal transport [29] distance is the minimum transmission mass required to convert one probability distribution to another. Optimal transport is widely used in industry, economics, and other fields. It is also increasingly used to solve various problems such as color or texture processing in imaging science, shape manipulation of images, and in machine learning for regression, classification, and generative modeling. The shortest path principle employed by optimal transport can guide the generation of most decisions in application areas such as planning traffic and sending information to several fixed points. Based on its core method, theory, and the mathematical form in which it applies to population distribution, we believe that optimal transport theory is equally applicable to analyzing the distribution of cells in microscopic cell images and predicting the number of cells.

The Earth Mover’s distance [30], Monge-Kantorovich distance [31], and Wasserstein distance [32] are commonly used in various fields of machine learning. In this work, we regard the direct gap between the dot annotation map and the prediction count map as a probability problem and use the Monge-Kantorovich distance to measure the gap between probability measures.

Let \(\mathcal {X}\) and \(\mathcal {Y}\) be two sets of points, and let \(\mathcal {X}=\{x_i \vert i\in \{1,\ldots , n\}\}\), \(\mathcal {Y}=\{y_j \vert j\in \{1,\ldots , n\}\}\). Let c(x, y) be the cost function from set of points x to set of points y. Let \(\mu \) and \(\nu \) be two probability measures defined on \(\mathcal {X}\) and \(\mathcal {Y}\), The Monge-Kantorovich distance is defined as

$$\begin{aligned} \mathcal {W}=\min _{\phi \in \Phi (\mu ,\nu )} \langle {C},\phi \rangle , \end{aligned}$$
(1)

where C is the cost matrix corresponding to two sets of points \(\mathcal {X}\) and \(\mathcal {Y}\), \(C_{ij}=c(x_i,y_j)\). \(\mu \) and \(\nu \) are the probability measures defined on \(\mathcal {X}\) and \(\mathcal {Y}\). We define \(\phi \) as the transmission mode from one probability measure \(\mu \) to another probability measure \(\nu \). \(\Phi (\mu ,\nu ):=\{\phi \in \mathbb {R}_{+} ^{n\times n}:\phi \textbf{1}=\mu ,\phi ^{T}\textbf{1}=\nu \}\) represents the set of all possible ways to transport a probabilistic mass from point set \(\mathcal {X}\) to \(\mathcal {Y}\), i.e., the transmission scheme space of two probability measures \(\mu \) and \(\nu \).

Kantorovich optimal transport is a specialized linear programming problem designed for discrete probability vectors [33]. Its objective is to extend the transport mapping to a transport scheme, which allows for the probabilistic transport of mass from one source to multiple targets. Kantorovich’s key idea is to relax the deterministic nature of transport, which assumes that the source can only be assigned to a single point or location. Instead, he proposes the concept of probabilistic transport, recognizing that mass at any point may be dispersed to several places. Advanced linear programming algorithms can be used to solve this problem.

Linear programming algorithms, such as the simplex method, interior point method, and ellipsoid method, can encounter limitations when faced with many existing problems. In such cases, entropy regularization is often employed to overcome these challenges. By limiting the complexity of the optimal transport problem solution, entropy regularization can significantly reduce problem complexity and yield an approximate solution to the problem at hand.

The optimal transmission problem of entropy regularization is defined as

$$\begin{aligned} \mathcal {W}=\min _{\phi \in \Phi (\mu ,\nu )} \langle {C},\phi \rangle - \varepsilon H(\phi ), \end{aligned}$$
(2)

where \(H(\phi )\) is the entropy regularization function, and we define \(\varepsilon \) as the entropy regularization parameter. Entropy regularization remains a concept that requires effective algorithms to unlock its potential, and the particular structure of the problem allows the use of balancing algorithms [34], which are also known as Sinkhorn algorithms [35] and RAS [36]. The images in our dataset contain an irregular point set of cells, requiring a convergent solution from the transfer matrix approach. Therefore, we use the Sinkhorn algorithm in each training iteration to generate predicted count maps at minimal cost. As \(\varepsilon \) approaches 0, the optimal solution of the approximate optimal transport problem theoretically converges to the optimal solution with maximum entropy in the Kantorovich optimal transport problem. By definition, this predicted cell distribution can converge to a near-optimal solution, allowing for more accurate cell location predictions.

Furthermore, based on the existence of dyadic forms in Monge-Kantorovitch problem, the Monge-Kantorovitch distance can be expressed as

$$\begin{aligned} \mathcal {W}=\min _{\phi \in \Phi (\mu ,\nu )} \langle {C},\phi \rangle =\max _{k,v\in {\mathbb {R}}^n}\langle k,\mu \rangle +\langle v,\nu \rangle , \end{aligned}$$
(3)

where (k, v) is the solution to the dual problem, and \(k_{i} + v_{j} \leqslant {c(x_{i},y_{j})}\). For this approach, the best-known complexity bound in the literature is \(\tilde{O}\left( \frac{n^2}{\varepsilon ^3}\right) \) to obtain Eq. (2). They also show that the regularization parameters should be proportionally chosen to \(\varepsilon \), which requires the use of matrix \(\exp (-C/\varepsilon )\) and leads to the problem of numerical stability of the algorithm, i.e., the approximate optimal solution obtained by algorithm [37] is set as \(\Phi = \textit{k}_i \textit{v}_j \exp (-C_{ij}/\varepsilon )\).

We denote \(a_i\) as the binary vectorization mapping function of point annotation and \(\hat{a}_i\) as the vectorization function mapping of the intermediate prediction density graph generated by the neural network. Let \({\Vert a\Vert }_1\) and \({\Vert \hat{a}\Vert }_1\) be the L1 norm of a and \(\hat{a}\). Let \(A(a)=\frac{a}{{\Vert a\Vert }_1}\) be the probability density functions of a. Naturally, the loss function based on the Monge-Kantorovich distance can be described as

$$\begin{aligned} \mathcal {L}_{mk}(a,\hat{a})=\min \langle {A(a)},{A(\hat{a})}\rangle =\langle k,{\frac{a}{{\Vert a\Vert }_1}} \rangle + \langle v,{\frac{\hat{a}}{{\Vert \hat{a}\Vert }_1}} \rangle . \end{aligned}$$
(4)

The gradient of Eq. (4) with respect to \(\hat{a}\) is

$$\begin{aligned} \frac{\partial \mathcal {L}_{mk}}{\partial \hat{a}} = \frac{v}{{\Vert \hat{a}\Vert }_1} - \frac{\langle v,{\hat{a}}\rangle }{{{\Vert \hat{a}\Vert }_1^2}}. \end{aligned}$$
(5)

Let \(\mathcal {I}\) denote the set of microscopic cell images and \(\mathcal {A}\) denote the set of dot annotation maps. Suppose that \(\{\mathcal {H}_i\}\) are hypothesis spaces, each \(i=1,\ldots ,m\). Let \(\mathcal {G}=\mathcal {H}_1 \times \ldots \times \mathcal {H}_i \), each \(g\in \mathcal {G}\) maps \(I\in \mathcal {I}\) to each dimension of \(a\in \mathcal {A}\). Let \(\mathcal {Z}\) denote the i.i.d. sample of (I, a) in the hypothesis space. Let \(S=((I_1,a_1),\ldots ,(I_m,a_m))\) be the sampling of the joint distribution of M image sets and dot annotation maps.

To prove the effectiveness of the algorithm, we use the empirical Radmacher complexity to express the bounds to compute the optimal transport loss. According to [38], the empirical teacher complexity of \(\mathcal {G}\) is

$$\begin{aligned} {R}_S(\mathcal {G}) = \mathbb {E}[\sup _{g\in \mathcal {G}} \frac{1}{M}\sum _{i=1}^{m}{\sigma }_i g({{I}_i})], \end{aligned}$$
(6)

where variables \(\sigma _m\) in \(\{\sigma \}\) are distributed i.i.d. according to \(\mathbb {P}[\sigma = +1] = \mathbb {P}[\sigma =-1] = \frac{1}{2}\), \(\{\sigma \}=({\sigma }_1,\ldots ,{\sigma }_m)\in \{\pm 1\}^m\).

Let \(\Gamma =\mathcal {H}_1 \times \ldots \times \mathcal {H}_i \times \mathcal {F}^m\) be the space mapping; each \(\gamma \in \Gamma \) can be considered a mapping from (I, a) to \((\hat{a},a)\), where \(\mathcal {F}\) is a single function space. \(R(S,\gamma ,\ell )={{\mathbb {E}}_{(I,S)}}[\ell (S,\gamma (I))]\) is the expected risk. Assume that for all \(x\sim \mathcal {Z}\), we have \(\ell (x,x') \le c\). Based on McDiarmid inequality, the expression inequality for the extension bound can be obtained as follows:

$$\begin{aligned} R_{\mathcal {S}}(E,g,\ell )-R_{\mathcal {Z}}(\mathcal {Z},g,\ell ) \le 2R(\ell \circ \Gamma )+5c\sqrt{\frac{2\log (8/\delta )}{m}}, \end{aligned}$$
(7)

E is the Empirical Risk Minimization (ERM) rule, which finds a hypothesis that is close to the optimal hypothesis in S, and c is a Lipschitz constant based on 1-Lipschitz. Lipschitz optimization [39] is based on the assumption that the slope of the objective function is bounded.

The Lipschitz constant in the Monge-Kantorovich distance can be obtained as follows:

$$\begin{aligned} \mathcal {L}_{mk}=\sum _{ij}C_{ij}\phi _{ij} \le \sum _{ij}C_{\max }\phi _{ij}=C_{\max }, \end{aligned}$$
(8)

where \(C_{\max }\) is the maximum value in C. Assume that \(\ell (x,x')={\left\| \frac{x}{\Vert x\Vert }_1-\frac{x'}{\Vert x'\Vert }_1\right\| }_1\); then, \(\ell (x,x')\) is 2n-Lipschitz. For \(\forall p,p',q,q' \in {\mathbb {R}}_+^n\), we have

$$\begin{aligned} \vert \ell (p,p')-\ell (q,q') \vert \le 2n({\Vert p-q\Vert }_1+{\Vert p'-q'\Vert }_1). \end{aligned}$$
(9)

3.2 Loss of total variation distance

When Sinkhorn is used as the entropy regularization algorithm, only the optimal approximate solution can be obtained [40]. Therefore, the density map of the cell image predicted by the intermediate predicted cell density map generator can only be close to the ground-truth density map but cannot be consistent. The total variation (TV) distance [41] can be used to measure the gap between two probability distributions to optimize our loss function. The TV distance is defined as

$$\begin{aligned} \begin{aligned} \mathcal {L}_{tv}({a},\hat{a})&=\sup \left| {A(a)}-{A(\hat{a})}\right| _1 \\ {}&=\frac{1}{2} \left\| {\frac{a}{{\Vert a\Vert }_1}}-{\frac{\hat{a}}{{\Vert \hat{a}\Vert }_1}} \right\| _1. \end{aligned} \end{aligned}$$
(10)

To simplify the description, we define \(o ={\frac{a}{{\Vert a\Vert }_1}}-{\frac{\hat{a}}{{\Vert \hat{a}\Vert }_1}}\). The gradient of Eq. (10) with respect to \(\hat{a}\) is

$$\begin{aligned} \frac{\partial {\mathcal {L}_{tv}}({a},\hat{a})}{\partial \hat{a}} = -\frac{1}{2}\left( \frac{sign(={o})}{{\Vert \hat{a}\Vert }_1} - \frac{\langle sign(={o}), \hat{a}\rangle }{{{\Vert \hat{a}\Vert }_1^2}} \right) . \end{aligned}$$
(11)
Fig. 2
figure 2

Examples of images in three datasets

Full size image

The slope in the TV loss function is calculated to obtain the constant in Lipschitz optimization, which is

$$\begin{aligned} \begin{aligned} \mathcal {L}_{tv}&=\frac{1}{2} \left\| {\frac{a}{{\Vert a\Vert }_1}}-{\frac{\hat{a}}{{\Vert \hat{a}\Vert }_1}} \right\| _1 \\&\le \frac{1}{2}\left( {\left\| \frac{a}{\Vert a\Vert }_1\right\| }_1+{\left\| \frac{\hat{a}}{\Vert \hat{a}\Vert }_1\right\| }_1\right) \\&=1. \end{aligned} \end{aligned}$$
(12)

3.3 Count loss of cell number

Sparse features are extracted by the L1 norm to optimize the learning process, which is also an effective regularization method in common machine learning. The loss function is used to compute the cost so that the generation forecasting density figure approaches the real groud-truth density map to make us count the cell image closer to the point with the real value.

Thus, we must directly calculate to limit the counting gap between their differences. Their counting gap is directly defined as

$$\begin{aligned} \mathcal {L}_{ct}(a,\hat{a})=\vert {{\Vert a\Vert }_1}-{{\Vert \hat{a}\Vert }_1}\vert . \end{aligned}$$
(13)

Similar to Eq. (9), the 1-Lipschitz constant for \(\forall p,p',q,\) \(q' \in {\mathbb {R}}_+^n\) can be calculated as follows:

$$\begin{aligned} \vert \ell (p,p')-\ell (q,q') \vert \le {\Vert p-q\Vert }_1+{\Vert p'-q'\Vert }_1. \end{aligned}$$
(14)

Given our assumption that the function on the mapping space is bounded by a constant c, we calculate the Lipschitz constant in \(\mathcal {L}{ct}\) as \(\mathcal {L}{ct}\le c\).

To enhance the accuracy of the predicted cell image density map, we propose a loss function for the optimized training process. This loss function is defined by combining Eqs  (4), (10), and (13) as follows:

$$\begin{aligned} \mathcal {L}(a,\hat{a})=\alpha \mathcal {L}_{mk}(a,\hat{a}) + \beta {\Vert a\Vert }_1\mathcal {L}_{tv}(a,\hat{a})+\mathcal {L}_{ct}(a,\hat{a}), \end{aligned}$$
(15)

where \(\alpha , \beta \) are adjustable hyperparameters, but the TV distance loss term is multiplied by \({{\Vert a\Vert }_1}\) so that \(\mathcal {L}_{tv}\) and \(\mathcal {L}_{ct}\) are in the same proportion.

Point annotations in microscopic cell image datasets provide information about the location of cells. However, most density estimation algorithms require regions of varying sizes in the background corresponding to the pixel location of each cell. Therefore, diffusion parameters need to be determined based on the size of each cell in the image. In dense cell counting images, cell size is usually related to the distance between the centers of neighboring cells. To generate ground-truth density maps that are adaptive to determine the diffusion parameters of each cell based on the average distance from each cell to its neighboring cells, many studies utilize Gaussian functions.

The ground-truth density map \(a'\), which is traditionally generated by a Gaussian function, is generated here by convolving the ground-truth dot annotation map \(\hat{a}\) with the position of each cell marked as 1 with the Gaussian kernel \(k_\sigma \):

$$\begin{aligned} a' = \hat{a} *k_\sigma . \end{aligned}$$
(16)

Previous studies that use Gaussian kernels to generate ground-truth density maps have shown some error in both the density and point annotation maps. This error is due to the selection of Gaussian kernel size and can impact the accuracy of cell prediction density map generation. The error caused by using the Gaussian method is even more significant when the cell distribution is irregular and dense in the images of the dataset. To demonstrate the theoretical superiority of our method, we calculated error bounds for these methods using the same theoretical analysis we used to calculate error bounds for our approach based on the generalized Gaussian method.

Table 1 Comparison of our results with previous work on the VGG dataset
Full size table
Table 2 Comparison of our results with previous work on the MBM dataset
Full size table

Assume that g is the kernel function on \(\mathcal {G}\) with \(k_\sigma \) as the Gaussian kernel; then, let \(\mathcal {A'}\) be the set of predicted density maps generated by the Gaussian function. Let \(\mathcal {Z'}\) denote the i.i.d. sample of \({(I,a')}\) in the hypothesis space. According to the definitions of the empirical Radmacher complexity and Gaussian Blur function [42], we can obtain the upper bound on the generalization error in the process of generating the ground-truth density map for a kernel function with Gaussian kernel \(\sigma \) as follows: \( R_\mathcal {Z'}(\mathcal {Z'},g',\mathcal {L}') + 2nR(\mathcal {H})+5c\sqrt{\frac{2\log (8/\delta )}{m}}+ {\mathbb {E}_{(I,a)\thicksim \mathcal {Z}}{\Vert a-a'\Vert }_1}, \) where \(\mathcal {L}'\) is the loss function.

Similarly, the upper bound on the generalization error of this work can be obtained by substituting the Lipschitz constants of each partial loss function: \( R_\mathcal {Z}(\mathcal {Z}, g,\mathcal {L}) +(\alpha 4{n}^{2}C_{\max }+\beta N{n^2}+2n)R(\mathcal {H})+5(\alpha C_{\max }+{\beta }{N}+c)\sqrt{\frac{2\log (8/\delta )}{m}}\), where N is the maximum cell count in the dot annotation maps.

In the above analysis of the upper exact bound on the generalization error, we observe that \(R(\mathcal {H})\) and \(\sqrt{\frac{2\log (8/\delta )}{m}}\) gradually converge to 0 as m increases. This implies that, in the training process using Gaussian smoothed ground-truth density maps, the upper bound on the generalization error converges to \(R_\mathcal {Z'}(\mathcal {Z'},g',\mathcal {L}') +{\mathbb {E}_{(I,a)\thicksim \mathcal {Z}}{\Vert a-a'\Vert }_1}\), while in the optimal transportation method, the upper bound on the generalization error tends to \( R_\mathcal {Z}(\mathcal {Z}, g,\mathcal {L})\). By contrast, our method, which uses direct computation of the point annotation map and prediction count map gap, has a more compact upper bound on the generalization error.

The use of theoretical proof provides a more intuitive understanding of our method’s effectiveness, as measured by the empirical Rademacher complexity measures and the rate of uniform convergence. This demonstrates the theoretical accuracy of our approach.

4 Experimental

Table 3 Comparison of our results with previous work on the ADI dataset
Full size table

4.1 Datasets

We evaluate the proposed method on three public cell counting benchmarks: the synthetic fluorescence microscopy (VGG) dataset, Modified Bone Marrow (MBM) dataset, and human subcutaneous adipose tissue (ADI) dataset [16].

  1. (1)

    There are 200 images with a 256\(\times \)256 resolution, which contain simulated bacterial cells from fluorescence-light misroscopy in the VGG dataset. Lempitsky and Zisserman [14] used the method in [43] to create this dataset. Each image contained \(174 \pm 64\) overlapping cells at different focal distances.

  2. (2)

    The MBM dataset consisted of 11 bone marrow images of height healthy individuals based on the 1200\(\times \)1200 resolution introduced by Kainz et al. [44], where the nuclei of various cell types were marked blue using standard procedures. In [16], each 1200\(\times \)1200 resolution source data image was cropped into four 600\(\times \)600 resolution images, i.e., a total of 44 images in the dataset. There were \(126 \pm 33\) cells in each image.

  3. (3)

    The source data of the ADI dataset is a human subsutaneous adipose tissue dataset obtained by the Genotype-Tissue Expression Consortium (GTEx) [45]. There are 200 images with a 150\(\times \)150 resolution. On average, there are \(165 \pm 44.2\) cells per image.

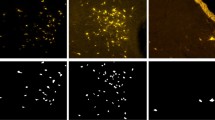
Due to the small size of the dataset, to train a better neural network model and avoid problems such as overfitting, we performed mirror flipping on the data to amplify the data volume and randomly clipped each image in the dataset for training. The clipping size of the VGG and ADI datasets is 112\(\times \)112, and that of the MBM dataset is 224\(\times \)224. Figure 2 shows the image examples of the three datasets used in this paper and their corresponding annotated visualizations.

Fig. 3
figure 3

Visualization of the predicted count maps generated with different loss functions. The first column shows the input cell image, and the second column shows the corresponding count target. Each white annotated point represents a cell to be counted in the input image. The third column displays the prediction count map of the corresponding input image generated by the neural network under the L2 loss function, while the fourth column displays the predicted count map of the same input image generated by the neural network under our proposed loss function. As seen in the visualization, our proposed loss function yields prediction counts that are closer to the true counts compared to the L2 loss function

Full size image
Fig. 4
figure 4

Experimental results for multiple methods with different N. N refers to the number of images used for training in the dataset. The left panel displays the results on the VGG dataset, the middle panel shows the experimental results on the MBM dataset, and the right panel shows the experimental results on the ADI dataset. The horizontal axis indicates the number of images N used for training, and the vertical axis represents the MAE results on the test data

Full size image

4.2 Evaluation metric

Based on previous work, we randomly selected images from the test set and used these images to evaluate the performance of the proposed model. We use the mean absolute error (MAE) of cell counts between the prediction and the ground-truth of each test image as the evaluation criterion, which is formulated as follows:

$$\begin{aligned} MAE=\frac{1}{N}\sum _{i=1}^{N}\vert {\hat{{y}}_i}-{{{y}}_i}\vert , \end{aligned}$$
(17)

where N is the total number of test images, i denotes the image index, \({{y}}_i\) is the ground-truth value of the number of cells in the current ith image, and \({\hat{{y}}_i}\) is the number of cells predicted by the current i-th image.

4.3 Optimization

In our experiment, we optimized the neural network parameters using the Adam optimizer. We addressed the issue of moment estimators in the adaptive gradient descent algorithm of Adam by computing the gradient using a moment and second-moment estimation, and designing parameters for different independent vector adaptabilities. We set the weight decay value to 0.0001 and the initial learning rate to 0.00001. Throughout all experiments, we used parameter values of 0.1 for \(\alpha \) and 0.01 for \(\beta \). To regularize our results, we utilized the Sinkhorn algorithm, setting the regularization parameter of the Sinkhorn entropy to 10, and running 100 iterations.

4.4 Results and discussion

We divided the training set and test set for each dataset according to the evaluation criteria proposed in previous works [5, 14, 16]. The number of images used for training, denoted as \({N}_{train}\), was kept consistent across all experiments to ensure the fairness and credibility of our results. We used the same parameter settings as those in the comparison work. The experimental results for the VGG, MBM, and ADI datasets are presented in Tables 1, 2, and 3, respectively. The second column of each table indicates the segmentation methods for the number of training set images in the datasets of different methods, and the third column shows the mean absolute error (MAE) values of the experimental results. To facilitate the comparison of different methods, we only present the best results obtained for different N train divisions in each table. Specifically, for the VGG dataset, we obtained the best results when N train was set to 64, while for MBM and ADI, the values of \({N}_{train}\) were 15 and 50, respectively. Our method performed similarly to the existing best-performing methods on the VGG and ADI datasets, while outperforming them in terms of accuracy.

We conducted 10 experiments with different training set size divisions in various datasets using the same configuration environment. We calculated the mean values of the results and compared them with those of previous works. The prediction count maps using different training losses are shown in Fig. 3. Our method produced more accurate predictions and localizations compared to the previous works. Figure 4 provides a comparison of our method with the previous work in several aspects, demonstrating that our approach outperforms the previous work.

Table 4 Different combinations of loss functions
Full size table
Fig. 5
figure 5

Comparing the results of setting different experimental parameters

Full size image

4.5 Ablation study

In our work, the loss function is comprised of three components: the loss of counts (\(\mathcal {L}{ct}\)), which directly measures the difference between predicted and actual counts; the total variance distance (\(\mathcal {L}{tv}\)), which acts as a regularization to smoothen the density map predictions; and the Monge-Kantorovitch distance loss (\(\mathcal {L}_{mk}\)), which matches the predicted and true images through distribution matching. To evaluate the effectiveness of our proposed loss function, we conducted ablation experiments on the VGG dataset using different combinations of these three components during training. The experimental results are shown in Table 4, which demonstrate that our proposed loss function improves the accuracy of the prediction count map generated by the model. By incorporating the loss of counts, we are able to directly measure the difference between predicted and actual counts, resulting in more accurate predictions. Additionally, the total variance distance acts as a regularization to prevent overfitting and smoothen the density map predictions, while the Monge-Kantorovitch distance loss matches the predicted and true images through distribution matching, further improving the accuracy of our predictions.

In the loss function, \(\alpha \) and \(\beta \) are adjustable parameters, and we adjust the parameter values on the VGG dataset. We fix the value of \(\alpha \) to 0.1 and adjust \(\beta \) to 0.001, 0.01, 0.03, 0.05, and 0.07. The model results performed best when \(\beta \) was 0.01, so we set \(\beta \) to 0.01. Additionally, the value of \(\alpha \) was adjusted to 0.01, 0.1, 0.3, 0.5, and 0.7, and the model results showed the best performance when \(\alpha \) was 0.1. Therefore, we set \(\alpha =0.1\) and \(\beta =0.01\) in all datasets. The comparison results are shown in Fig. 5.

We set different numbers of Sinkhorn iterations. The experimental results show that after the number of iterations has been set to 100, the experimental results gradually tend to be stable. Table 5 shows the experimental results on the VGG dataset with different numbers of Sinkhorn iterations. When the Sinkhorn value is set to 100, the counting results in the dataset are the most accurate.

Table 5 Set different numbers of Sinkhorn iterations
Full size table

5 Conclusion

In this paper, we propose to use an optimal transport theory approach to supervise density regression for cell counting and demonstrate its effectiveness on public microscopic cell datasets. A neural network model is utilized to generate prediction count maps, and the difference between the generated predictions and annotated data is treated as a distribution matching problem, which optimizes the predicted count result. This approach weakens the negative impact on the count results caused by issues such as mutual occlusion of cells in the cell images and low quantity of training data. Our distribution matching approach demonstrates strong generalization power in counting work with different datasets. The visualization figures and results across three datasets show that compared with commonly used loss functions such as L2 loss, the prediction count maps obtained by our proposed method based on the loss function constructed by optimal transport theory have more compact prediction maps and better quantification results. In conclusion, our proposed approach based on optimal transport theory provides a powerful tool for supervising density regression in cell counting tasks. Our results demonstrate the superiority of our approach over commonly used loss functions, showing that it is effective in handling mutual occlusion of cells and low quantity of training data.