Abstract
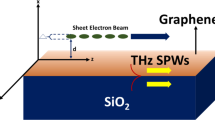
Resonant excitation of terahertz surface plasmons by optical rectification over rippled graphene surface, deposited on \(\text {SiO}_{2}\) using a mode conversion of amplitude modulated p-polarized laser beam. A pump surface plasmons exert a ponderomotive force on the free electrons of the graphene surface and impart a linear oscillatory velocity at the modulation frequency. The current density develops by coupling the linear oscillatory velocity with modulated electron density and resonantly excites the terahertz surface plasmons at the modulation frequency. The amplitude of terahertz surface plasmons can be tunable by Fermi energy of graphene surface \(\text {E}_\text {F}\). There is a possibility that the current study will be used to utilize THz detectors and sensors.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Terahertz (THz) technology has garnered significant academic attention in recent years owing to its expanding range of applications in fields such as sensing [1,2,3], medical imaging [4, 5], and communications [6, 7]. THz radiation is generated by various processes, such as the nonlinear mixing of two lasers [8, 9], optical rectification (OR) [10, 11], laser (or electron beam)-plasma interaction [12, 13], and photoconductive antennas [14, 15].
There is presently a significant focus on the investigation of graphene’s potential applications, driven by its remarkable electronic, mechanical, and optical characteristics [16]. In particular, the development of graphene-based devices in the terahertz (THz) regime has garnered attention due to recent discoveries regarding the tunability of surface plasmons (SPs) supported by graphene sheets. This tunability can be achieved by adjusting the external gate voltage or through chemical doping [17, 18]. THz SPs generation over a rippled graphene surface studied using linear mode conversion and second harmonic by Srivastav and Panwar [19, 20]. Li et al. [21] investigated harmonic THz SPs generation by electron beam over a uniform graphene surface. Bhasin and Tripathi [22] reported excitation of THz SPs on metallic surfaces by OR. Bhasin and Tripathi [23] investigated THz radiation generation by OR in magnetized rippled density plasma using an x-mode laser. Also, Singh et al. [24] theoretically studied the excitation of THz radiation by OR in transversely magnetized rippled density plasma using a hyperbolic-secant laser pulse. Generation of THz radiation over carbon nanotubes can be achieved using various laser profiles, such as self-focusing lasers and cross-focused Gaussian lasers, both in the presence and absence of a magnetic field [25,26,27,28,29,30]. Unadkat and Kumar [31] reported the generation of sub-THz radiation by an electron beam within the drift space of a plasma-assisted slow wave structure using particle-in-cell simulation.
This paper presents an analytical and numerical study of the excitation of THz SPs over a rippled graphene surface using a modulated amplitude of a p-polarized laser beam by OR (see Fig. 1). The excitation of SPs may be accomplished by the utilization of an amplitude-modulated p-polarized laser, obliquely incident at an angle on the interface between graphene and free space. This objective may be accomplished through two methods: the attenuated total reflection configuration or by directly irradiating the laser onto a rippled graphene surface that possesses a certain wave number. SPs wave, which is modulated amplitude exerts a ponderomotive force on free electrons in graphene. This ponderomotive force imparts oscillatory velocity to free electrons at the modulation frequency. The current density is produced by coupling oscillatory velocity with modulated electron density and resonant excitation of THz SPs at the modulation frequency. The linear current density is represented in “Linear Current Density” section. The expression of THz SPs is represented in “Terahertz Graphene Surface Plasmons Amplitude” section. Results and discussion in “Results and Discussion” section and conclusion in “Conclusion” section.
Linear Current Density
The electric field of SPs wave is given as follows [22]:
where \(E=E_{0}(1+\mu \cos \Omega (t-z/v_{g}))\), \(\alpha ^2_1 = \left( k_{z}^2 - ({\omega ^2}/{c^2}) \right)\), \(\alpha _2^2 = k_{z}^2 - ({\omega ^2}/({c^2} \epsilon _{eff}))\), \(\gamma _{1} = -(i k_{z}/\alpha _{1})\), \(\gamma _{2} =-\left( { i k_{z}}/{ \alpha _{2} }\right)\), \(\epsilon _{eff}^{\Omega } = \epsilon _{\text {SiO}_2} + (i \sigma _{g})/(\Omega \epsilon _{0})\), \(\sigma _{g} = (i e^{2} \text {E}_\text {F})/(\pi \hbar ^{2}(\omega +i\nu ))\) is conductivity of graphene, e is electron charge and \(\hbar\) is Plank constant, \(\text {E}_\text {F}\) is Fermi energy of graphene, \(\nu\) is collision frequency, \(k_{z}\) is propagation constant of SPs wave in direction of \(\hat{z}\), \(\mu\) is modulation index, \(\Omega\) is modulation frequency and \(v_{g}\) is group velocity of SPs wave.
The SPs electric field imparts oscillatory velocity \(\vec {v}_{\omega }\) to the electrons of the graphene surface, may be written as follows:
where \(m_{e}^{*}\) is the effective mass, \(m_{e}^{*} = E_{F}/v_{F}^{2}\) [32] and \(v_{F}\) is Fermi velocity.
The SPs wave exerts ponderomotive force \(\vec {F}_p =- (m_e^{*}/4) (\vec {v}_s \cdot \nabla \vec {v}_s^{*} + \vec {v}_s^{*} \cdot \nabla \vec {v}_s) - (e/4) (\vec {v}_s \times \vec {B}_s^{*} + \vec {v}_s^{*} \times \vec {B}_s)\) on free electrons and it represented as follows:
where \(F_{P x} = (\tilde{v}_{\omega }^x \alpha ^{*}_2 \tilde{v}^{*x}_{\omega } - \tilde{v}_{\omega }^z i k_z \tilde{v}^{*x}_{\omega }) + \left( {{v^{*x}_{\omega }} } \alpha _2 \tilde{v}_{\omega }^x {{+ v^{*z}_{\omega }} } i k_z \tilde{v}_{\omega }^x \right) + (1 / i \omega ) \left( \tilde{v}_{\omega }^{*z} \left( \alpha _2 - i k_z {\beta _2} \right) + \tilde{v}_{\omega }^z (\alpha ^{*}_2 + i k_z \beta _2^{*}) \right)\) and
\(F_{P z} = (1 / i \omega ) \left( \tilde{v}_{\omega }^{*x} \left( \alpha _2 - i k_z {\beta _2} \right) + \tilde{v}_{\omega }^x (\alpha ^{*}_2 + i k_z \beta _2^{*}) \right) - \left( (\tilde{v}_{\omega }^x \alpha ^{*}_2 \tilde{v}^{*z}_{\omega } - \tilde{v}_{\omega }^z i k_z \tilde{v}^{*z}_{\omega }) + \left( {{v^{*x}_{\omega }} } \alpha _2 \tilde{v}_{\omega }^z +{{ v^{*z}_{\omega }} } i k_z \tilde{v}_{\omega }^z \right) \right)\)
Considering the ponderomotive force at modulation frequency \(\Omega\) can be written as follows:
Now, the oscillatory velocity components of free electrons at modulation frequency \(\Omega\) is given as follows:
and
where \(\tilde{v}_{\Omega }^x = i F_{P x} / (\Omega + i \nu )\).
The oscillatory velocity couples with modulated electron density to produce current density \(\vec {J}_{\Omega }\) at modulation frequency \(\Omega\) and it is given as follows:
Terahertz Graphene Surface Plasmons Amplitude
By using Maxwell’s equation, \(\Omega\) modulation frequency SPs wave field can be expressed as follows:
and
where \(\epsilon _{eff}^{\Omega } = \epsilon _{\text {SiO}_2} + (i \sigma _{g})/(\Omega \epsilon _{0}) \text { for x} \le 0\) and \(\varepsilon _{eff}^{\Omega } = 1 \text { for x} > 0\), and s represents the SPs.
The wave equation may be written as follows:
Here, \(\epsilon _{eff}^{\Omega }\) is graphene effective permittivity at frequency \(\Omega\). When r.h.s term of Eq. (11) is zero that is \(\vec {J}_{\Omega }\) is absence then SPs eigen mode structure with
where \(\vec {E}_{s,0}\) and \(\vec {B}_{s,0}\) is given as follows:
and
The SPs electric field can be represented as follows:
where \(\gamma _{1}^{\Omega } = -(i k_{z}^{\Omega }/ \alpha _{1}^{\Omega })\), \(\gamma _{2}^{\Omega } = -i k_{z}^{\Omega }/\alpha _{2}^{\Omega }\), \((\alpha _{2}k_z^{\Omega })^2 = (k_z^{\Omega })^2 -(\Omega ^2/c^2) \epsilon _{eff}^{\Omega }\), \((\alpha _{1}^{\Omega })^2 = (k_z^{\Omega })^2 -(\Omega ^2/c^2)\), \(k_{z}^{\Omega } = q + \Omega /v_{g}\) and q provides the extra wave number for phase matching condition.
Figure 2 represents the variation of q with THz frequency \(\omega\) for different values of graphene Fermi energy \(E_{F}= 0.35\)eV (green line), \(E_{F}= 0.40\)eV (blue dashed line) and \(E_{F}= 0.45\)eV (red dotted line) at \(\Omega =1\) THz.
If the current density \(\vec {J}_{\Omega }\) is present, then the electric and magnetic fields of the THz SPs wave can be expressed as follows:
Solving Eqs. (10) and (11) with Eq. (16), and using Eq. (13), we get
and
Using Eq. (17) in Eq. (18) and taking \(\partial a /\partial t \approx \partial b /\partial t\), we get
Multiplying Eq. (19) by \(\vec {E}_{s,0}^{*} d x\) and integrate \(- \infty\) to \(\infty\), we obtained
where \(I_{1} = \int ^{\infty }_{- \infty } \vec {E}_{s,0} \cdot \vec {E}_{s,0}^{*} d x\) and \(I_{2} = \int ^{\infty }_{- \infty } \vec {J}_{\Omega } \cdot \vec {E}_{s,0}^{*} d x\).
Solving Eq. (20), one may obtained
Let \(\partial /\partial t = - i \Omega\), we obtain
Equation (22) represents the THz SPs amplitude ratio \(\mid {a/A_{0}}\mid\). It depends upon the ripple height h, modulation index \(\mu\), and Fermi energy of graphene surface \(\text {E}_{\text {F}}\).
(Color Online) THz SPs amplitude ratio \(\mid {a/A_{0}}\mid\) verses THz frequency \(\omega\) for three values of graphene Fermi energy \(E_{F}= 0.35\)eV (green line), \(E_{F}= 0.40\)eV (red dashed line) and \(E_{F}= 0.45\)eV (blue dotted line). Other parameters are \(\mu = 0.3\), \(h=50 \mu m\) and \(\epsilon _{\text {SiO}_{2}} = 3.9\)
Results and Discussion
The ripple wave number q increases with an increase in Fermi energy of graphene surface \(E_{F}\) at particular values of THz frequency \(\omega\). Also, the Ripple wave number q increases with an increase in THz frequency \(\omega\) at particular values of Fermi energy of graphene surface \(E_{F}\). Ripple wave number q gives the extra wave number to resonantly excite the THz SPs wave. THz SPs amplitude ratio \(\mid {a/A_{0}}\mid\) verses THz frequency \(\omega\) is plotted in Fig. 3 for three values of graphene Fermi energy \(E_{F}= 0.35\)eV (green line), \(E_{F}= 0.40\)eV (red dashed line) and \(E_{F}= 0.45\)eV (blue dotted line) at \(\mu = 0.3\), \(h=50 \mu m\), \(\Omega =2\) THz and \(\epsilon _{\text {SiO}_{2}} = 3.9\). THz SPs amplitude increases with a decrease in THz frequency \(\omega\). Also, it increases with a decrease in Fermi energy of graphene surface \(\text {E}_{\text {F}}\).
Conclusion
In the present paper, theoretically and numerically examined the generation of THz SPs over a rippled graphene surface through OR of an amplitude-modulated p-polarized laser. The generation of THz SPs was examined within the frequency range of 1 to 3 THz, with the Fermi energy of graphene \(E_{F}\) vary from 0.35 to 0.45 eV. The amplitude of THz SPs was found to increase as the THz frequency and Fermi energy of graphene decreased. Additionally, the amplitude of THz SPs increased with an increase in the modulation index, ripple height, and laser amplitude. This work explores the potential use of the Fermi energy of graphene to control the excitation of THz waves at specific frequencies, thereby enabling the development of THz devices [33,34,35].
Data Availability
No datasets were generated or analyzed during the current study.
References
Gezimati M, Singh G (2023) Terahertz imaging and sensing for healthcare: current status and future perspectives. IEEE Access 11:18590–18619
Hillger P, Grzyb J, Jain R, Pfeiffer UR (2019) Terahertz imaging and sensing applications with silicon-based technologies. IEEE Trans Terahertz Sci Technol 9(1):1–19
Bogue R (2018) Sensing with terahertz radiation: a review of recent progress. Sens Rev 38(2):216–222
Castro-Camus E, Koch M, Mittleman DM (2022) Recent advances in terahertz imaging: 1999 to 2021. Appl Phys B 128(1):12
Yang X, Zhao X, Yang K, Liu Y, Liu Y, Fu W, Luo Y (2016) Biomedical applications of terahertz spectroscopy and imaging. Trends Biotechnol 34(10):810–824
Huang Y, Shen Y, Wang J (2023) From terahertz imaging to terahertz wireless communications. Engineering 22:106–124
Banafaa M, Shayea I, Din J, Azmi MH, Alashbi A, Daradkeh YI, Alhammadi A (2023) 6g mobile communication technology: requirements, targets, applications, challenges, advantages, and opportunities. Alex Eng J 64:245–274
Kumar M, Lee K, Hee Park S, Uk Jeong Y, Vinokurov N (2017) Terahertz radiation generation by nonlinear mixing of two lasers in a plasma with density hill. Phys Plasmas 24(3):033104
Chauhan S, Parashar J (2014) Laser beat wave excitation of terahertz radiation in a plasma slab. Phys Plasmas 21(10):103113
Singh RK, Singh M, Rajouria SK, Sharma R (2017) High power terahertz radiation generation by optical rectification of a shaped pulse laser in axially magnetized plasma. Phys Plasmas 24(10):103103
Kumar S, Singh RK, Sharma R (2016) Strong terahertz generation by optical rectification of a super-gaussian laser beam. Europhys Phys Rev Lett 114(5):55003
Gupta D, Jain A, Kulagin V, Hur MS, Suk H (2022) Coherent terahertz radiation generation by a flattened gaussian laser beam at a plasma-vacuum interface. Appl Phys B 128(3):50
Yang S, Wang S, Wang Z, Zhang P, Xia Y, Tang C, Gong Y (2022) Terahertz radiation generated by electron-beam-driven plasma waves in a transverse external magnetic field. Phys Plasmas 29(5):053106
Shalini M, Madhan MG (2022) Photoconductive bowtie dipole antenna incorporating photonic crystal substrate for terahertz radiation. Opt Commun 517:128327
Boby ENF, Prajapati J, Rathinasamy V, Rao TR, Mondal S (2022) 6g and beyond: investigation of broadband terahertz interdigitated photoconductive antenna by exploiting laser parameters. Microw Opt Technol Phys Rev Lett 64(12):2197–2206
Novoselov KS, Geim AK, Morozov SV, Jiang DE, Zhang Y, Dubonos SV, Grigorieva IV, Firsov AA (2004) Electric field effect in atomically thin carbon films. Science 306(5696):666–669
Yarahmadi M, Moravvej-Farshi MK, Yousefi L (2015) Subwavelength graphene-based plasmonic thz switches and logic gates. IEEE Trans Terahertz Sci Technol 5(5):725–731
Liu M, Yin X, Ulin-Avila E, Geng B, Zentgraf T, Ju L, Wang F, Zhang X (2011) A graphene-based broadband optical modulator. Nature 474(7349):64–67
Srivastav RK, Panwar A (2023) Linear mode conversion of terahertz radiation into terahertz surface plasmon wave over a graphene-free space interface. Int J Mater Res 114(7–8):572–578
Srivastav RK, Panwar A (2023) Generation of second harmonic terahertz surface plasmon wave over a rippled graphene surface. Int J Mater Res 114(7–8):579–585
Li D, Wang Y, Nakajima M, Hashida M, Wei Y, Miyamoto S (2016) Harmonics radiation of graphene surface plasmon polaritons in terahertz regime. Phys Phys Rev Lett A 380(25–26):2181–2184
Bhasin L, Tripathi VK (2010) Resonant terahertz generation by optical rectification of an amplitude modulated surface plasma wave. IEEE J Quantum Electron 46(6):965–969
Bhasin L, Tripathi VK (2009) Terahertz generation via optical rectification of x-mode laser in a rippled density magnetized plasma. Phys Plasmas 16(10):103105
Singh RK, Singh M, Rajouria SK, Sharma R (2017) Strong terahertz emission by optical rectification of shaped laser pulse in transversely magnetized plasma. Phys Plasmas 24(7):073114
Kumar S, Vij S, Kant N (2022) Combined effect of transverse electric and magnetic fields on THz generation by beating of two amplitude-modulated laser beams in the collisional plasma. J Astrophys Astron 43:30
Kumar S, Vij S, Kant N (2022) Interaction of obliquely incident lasers with anharmonic CNTs acting as dipole antenna to generate resonant THz radiation. Waves in Random and Complex Media 1-13
Kumar S, Vij S, Kant N (2022) Resonant terahertz generation by the interaction of laser beams with magnetized anharmonic carbon nanotube array. Plasmonics 17:381–388
Kumar S, Vij S, Kant N, Thakur V (2022) Resonant terahertz generation by cross-focusing of Gaussian laser beams in the array of vertically aligned anharmonic and magnetized CNTs. Opt Commun 513:128112
Thakur V, Kant N, Kumar S (2023) THz field enhancement under the influence of cross-focused laser beams in the m-CNTs. Trends Sci 20(6):5284
Kumar S, Kant N, Thakur V (2023) THz generation by self-focused Gaussian laser beam in the array of anharmonic VA-CNTs. Opt Quant Electron 55:281
Unadkat P, Kumar N (2024) Study of space charge potential for propagation of plasma-assisted electron beam. In: IEEE Transactions on Plasma Science 1-7
Verma N, Govindan A, Kumar P (2021) Terahertz plasmon excitation by nonlinear mixing of two laser beams in graphene sheet. Plasmonics 16(3):711–716
Sandeep HK (2023) Malik, enhancement of terahertz radiation due to excitation of spw on graphene strip coated on GaAs structure. Results Opt 13:100538
Shur M (2024) Sensing using terahertz radiation. Int J High Speed Electron Syst 2440022
Islam M, Bhardwaj A, Kumar G (2024) Planar terahertz multi-resonator meta-waveguide based upon strongly coupled nested split-ring resonator. Optik 302:171712
Funding
The authors have not disclosed any funding.
Author information
Authors and Affiliations
Contributions
Rohit Kumar Srivastav developed the formulation of the manuscript. Rohit Kumar Srivastav prepared Figs. 1–3.
Corresponding author
Ethics declarations
Ethical Approval
This declarations is “not applicable.”
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Srivastav, R.K. Resonant Excitation of Terahertz Surface Plasmons by Optical Rectification Over a Rippled Graphene Surface. Plasmonics (2024). https://doi.org/10.1007/s11468-024-02437-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11468-024-02437-8