Introduction

Terahertz (THz) radiation frequency lies in the range of 0.1–10 THz and known as THz Gap [1, 2]. THz radiation is novel type radiation and has several unique properties like as quantum and electronic properties of materials, non-ionizing properties, easily penetrates through most polymeric materials and which are often opaque at visible frequencies and also easily absorb in water. Since more than two decades, the Terahertz radiation generation and detection became a fascinating and forefront research area due to large number of diversified applications [2,3,4,5,6,7,8,9,10]. THz radiation also used as an important tool for studying the benign and malignant brain tumours [11, 12]. Strong field THz radiation is also used to explore the new phenomena including high harmonics generation, and relativistic charged particle acceleration at very high energy (THz-based compact particle accelerators-THz radiation has strong electric field gradient which are beneficial for ultrashort compact and x-ray sources) [13, 14].

Currently, there are many schemes of high-power THz radiation generation with high field, among them high-power laser interaction with solids (metal/semiconductors/dielectrics) and plasmas are widely used [15,16,17]. Another alternative and important scheme for terahertz radiation generation is based on electron beam. A high energy electron beam moves through a magnetic wiggler/undulator or two different dielectrics materials; it generates the synchrotron/transition THz radiation [18,19,20]. In current applications, the confined and guided electromagnetic modes are required; these modes are known surface plasma waves (SPWs) or surface plasmons (SPs) [21,22,23]. These modes are collective oscillations of electrons that propagate at interfaces of conductor or plasma and confined near the interface of different media, their amplitude attenuates in perpendicular direction of propagation. These highly confined modes or SPs have large number of applications including extraordinary transmission, THz plasmonics, plasmonic laser, plasmonic sensors, high harmonics generation, magnetoplasmonics (ultrafast switch), surface-enhanced Raman scattering (SERS), and laser ablation of materials for thin film deposition [24,25,26,27,28].

An electron beam or laser beam is widely used for resonant excitation of THz- SPs in various structures including in thin metallic films, graphene, and structured surfaces. The resonant frequency of these SPs can be tuned by the thickness of the film and changing the scale of structured surfaces [29,30,31,32]. The alternative approach for electron beam propagation without any divergence is based on conductor-dielectric-conductor or conductor-free space-conductor structure. The SPs have negative refraction at optical frequency in metal-dielectric-metal structure; this structure can control the propagations of surface plasmons, which can manipulate the light at nanoscale [33] and also shows the omnidirectional resonance, at the SPs frequency of the conductor–dielectric interface [34]. A slab-symmetric structure is also used for relativistic electron acceleration and Cherenkov THz radiation generation [35]. The microwave pulse shortening occurs in Cherenkov devices based on slow-wave structures; this is due to the transformation of kinetic energy of relativistic electrons beam into microwave energy [36]. The high-power microwave (HPM) sources based on plasma filled backward oscillators have high efficiency as compared to other backward oscillators, because the plasma in an HPM source is the charge neutralizing effect of positively charged plasma on electron beams [37]. Metallic mesostructured or periodic structures of very thin wires also support the SP modes in infrared or GHz frequency range [38].

In this manuscript, we study the properties of plasmons in THz frequency range that arise when a beam passes through the gap between two metallic plates. The structure supports the field of guided electromagnetic modes or SPs and have minimum value at the middle of the gap, so the electron beam passing through this air gap, experiences a converging force and this electron beam can propagate without any divergence through this gap. These SPs have lower phase velocity than the free space velocity of photon, so SPs can be excited by a moving relativistic electron beam via Cherenkov interaction. A relativistic electron beam moving through this air gap, it resonantly excites the SPs in THz frequency and these THz-SPs are transformed into Coherent THz radiation, when they passing over a periodic structure. In “Mode Structure and Dispersion Relation of Surface Plasmons” section, we derived the modes’ structure and dispersion relation; in “Terahertz Surface Plasmons Excitation by a Relativistic Electron Beam” section, the excitation and the growth rate of THz SPs are discussed; and in “Conclusion” section, the result is discussed.

Mode Structure and Dispersion Relation of Surface Plasmons

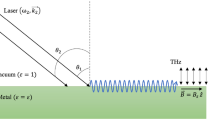
Consider a symmetrical structure (metal-air-metal) of two parallel metallic (gold) plates, which are separated by finite air gap; this structure supports the surface plasma waves (SPWs) or surface plasmons (SPs) that are propagating on the metal-air interface, which is shown in Fig. 1. The dispersion relation and modes structure of SPs are obtained by using the following Maxwell’s equations,

$$\nabla \times \overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}=+i\omega {\mu }_{0}\overrightarrow{H,}$$
(1)
$$\nabla \times \overrightarrow{H}=\overrightarrow{J}+{\varepsilon }_{0}\frac{\partial \overrightarrow{E}}{\partial t}=\sigma \overrightarrow{E}+{\varepsilon }_{0}\left(-i\omega \overrightarrow{E}\right)=i\omega {\varepsilon }_{eff}^{\prime}\overrightarrow{E},$$
(2)

where the total effective permittivity of metal is given by \({\varepsilon }_{eff}^{\prime}={\varepsilon }_{eff}={\epsilon }_{L}-{\omega }_{p}^{2}/{\omega }^{2}\) for x < -a and x > a, and \({\varepsilon }_{eff}^{\prime}=1\) for -a < x < a. From Eqs. (1) and (2), one may get \({\nabla }^{2}\overrightarrow{E}-\nabla \left(\nabla .\overrightarrow{E}\right)+\frac{{\omega }^{2}}{{c}^{2}}{\varepsilon }_{eff}\overrightarrow{E}=0\), and taking the divergence of this equation in media, using the Gauss’s law in these two media, i.e., \({\varepsilon }_{eff}^{\prime}\nabla .\overrightarrow{E}=0\) i.e. \(\nabla .\overrightarrow{E}=0\), this gives equation of surface plasmons

Fig. 1
figure 1

SPs modes propagation in metal-air-metal symmetrical structure

Full size image
$${\nabla }^{2}\overrightarrow{E}+\frac{{\omega }^{2}}{{c}^{2}}{\varepsilon }_{eff}^{\prime}\overrightarrow{E}=0.$$
(3)

In terms of x and z components, the wave Eq. (3) can be written as \(\frac{{\partial }^{2}{E}_{z}}{\partial {x}^{2}}+\frac{{\partial }^{2}{E}_{z}}{\partial {z}^{2}}+\frac{{\omega }^{2}}{{c}^{2}}{\varepsilon }_{eff}^{\prime}{\overrightarrow{E}}_{z}=0\), and differential operator is replaced like as \(\frac{{\partial }^{2}}{\partial {z}^{2}}\to -{k}_{z}^{2}\), one may get

$$\frac{{\partial }^{2}{E}_{z}}{\partial {x}^{2}}-{\alpha }^{2}{E}_{z}=0,$$
(4)

where \({\alpha }^{2}={\alpha }_{I}^{2}={k}_{z}^{2}-\frac{{\omega }^{2}}{{c}^{2}}{\varepsilon }_{eff}\) for x > a and x < -a and \({\alpha }^{2}={\alpha }_{II}^{2}={k}_{z}^{2}-\frac{{\omega }^{2}}{{c}^{2}}\) for -a < x < a. The modes of different components of mode structure of SPs in different medium can be obtained by solving the Eq. (4) in these different media. In medium x < -a, the solutions of Eq. (4) for z and x components (using \(\nabla .\overrightarrow{E}=0,\) for x component of electric field) can be written as

$$\begin{aligned}&{E}_{z}={A}_{I}\text{exp}\left({\alpha }_{I}x\right)exp\left[-i\left(\omega t-{k}_{z}z\right)\right],\\&{E}_{x}=-{A}_{I}\frac{i{k}_{z}}{{\alpha }_{I}}\text{exp}\left({\alpha }_{I}x\right)exp\left[-i\left(\omega t-{k}_{z}z\right)\right].\end{aligned}$$
(5)

In medium -a < x < a (air gap), the solutions of Eq. (4) can for z and x components (using \(\nabla .\overrightarrow{E}=0,\) for x component of electric field) be written as

$$\begin{aligned}&{E}_{z}=\left({A}_{II}\text{exp}\left({\alpha }_{II}x\right)+{A}_{II}^{\prime}exp\left({\alpha }_{II}x\right)\right)exp\left[-i\left(\omega t-{k}_{z}z\right)\right],\\&{E}_{x}=-\frac{i{k}_{z}}{{\alpha }_{II}}\left[{A}_{II}\text{exp}\left({\alpha }_{II}x\right)+{A}_{II}^{\prime}exp\left(-{\alpha }_{II}x\right)\right]exp\left[-i\left(\omega t-{k}_{z}z\right)\right].\end{aligned}$$
(6)

In Medium x > a, the solutions of Eq. (4) can for z and x components (using \(\nabla .\overrightarrow{E}=0,\) for x component of electric field) be written as

$$\begin{aligned}&{E}_{z}={A}_{III}exp\left({-\alpha }_{III}x\right)exp\left[-i\left(\omega t-{k}_{z}z\right)\right],\\&{E}_{x}={A}_{III}\frac{i{k}_{z}}{{\alpha }_{I}}exp\left({-\alpha }_{III}x\right)exp\left[-i\left(\omega t-{k}_{z}z\right)\right].\end{aligned}$$
(7)

At boundaries x = -a and x = a, Eqs. (5)–(7) demand that

$$\begin{aligned}&{A}_{I}exp\left(-{\alpha }_{I}a\right)={A}_{II}exp\left(-{\alpha }_{II}a\right)+{A}_{II}^{\prime}exp\left({\alpha }_{II}a\right),\\&{\varepsilon }_{m}\frac{{\alpha }_{II}}{{\alpha }_{I}}{A}_{I}={A}_{II}exp\left(-{\alpha }_{II}a\right)+{A}_{II}^{\prime}exp\left({\alpha }_{II}a\right),\end{aligned}$$
(8)
$$\begin{aligned}&{A}_{II}exp\left({\alpha }_{II}a\right)+exp\left({-\alpha }_{II}a\right){A}_{II}^{\prime}={A}_{III}exp\left({-\alpha }_{I}a\right),\\&{A}_{II}exp\left({\alpha }_{II}a\right)-{A}_{II}^{\prime}exp\left(-{\alpha }_{II}a\right)=-\frac{{\alpha }_{I}{\varepsilon }_{m}}{{\alpha }_{I}}{A}_{III}exp\left({-\alpha }_{I}a\right).\end{aligned}$$
(9)

For symmetrical mode (\({E}_{z}\) is symmetric about x = 0), i.e., \({A}_{II}^{\prime}={A}_{II}\) and \({A}_{III}={A}_{I}\), hence Eq. (9) gives the dispersion relation of SPs propagating in metal-air-metal symmetrical structure, i.e.,

$$\text{tanh}\left({\alpha }_{II}a\right)=-\frac{{\alpha }_{II}{\varepsilon }_{m}}{{\alpha }_{I}}.$$
(10)

The dispersion relation of Eq. (10) and mode structure of SPs Eqs. (5–7) are plotted in Figs. 2 and 3 for different normalized values of \(a{\omega }_{p}/c=\text{5, 10, 15}\) of the air gap between the metallic plates. Figure 2 shows that up to upper limit of SPs frequency, the frequency has linear behavior. For higher value of wavenumber, the curve has same behavior as that of single conductor surface. At the inter metallic surfaces of metal-air-metal structure, the SPs have maximum value and have zero inside the conductors (metallic plates) is shown in Fig. 3.

Fig. 2
figure 2

Dispersion relation of surface plasmons in for metal-air-metal symmetrical structure for different values of air gap \(a{\omega }_{p}/c=\text{5, 10, 15}\) between metallic plates

Full size image
Fig. 3
figure 3

Mode structure of SPs in metal-air-metal symmetrical structure for different values of air gap \(a{\omega }_{p}/c=\text{5, 10, 15}\) between metallic plates

Full size image

Terahertz Surface Plasmons Excitation by a Relativistic Electron Beam

Consider an electron beam of density \({n}_{0b}\) and moving with relativistic velocity \({v}_{0b}\widehat{z}\), through the air gap between two metallic plates (Fig. 4); the electron beam density is given by

$${n}_{0b}={N}_{0}exp\left(-{x}^{2}/{r}_{b}^{2}\right),$$
(11)

where rb is the radius of beam. The electron beam has a current is given by \({I}_{b}=\surd \pi {N}_{0}abe{v}_{0b}\), where b is the width of the electron beam. When this beam moves through the gap, it couples with the SPs. The response of electron beam in presence of SPs fields is given by the equation of motion

Fig. 4
figure 4

THz surface plasmons excitation by a relativistic electron beam passing through the gap

Full size image
$$\left(\frac{\partial }{\partial t}\left(\gamma \overrightarrow{v}\right)+\overrightarrow{v}\cdot \nabla \left(\gamma \overrightarrow{v}\right)\right)=\frac{-e}{m}\left(\overrightarrow{E}+\frac{\overrightarrow{v}\times \overrightarrow{B}}{c}\right).$$
(12)

The electric and magnetic fields of SPs the air gap -a < x < a are given by

$$\begin{aligned}&\overrightarrow{E}=\left({A}_{II}\left(\widehat{z}-\frac{i{k}_{z}}{{\alpha }_{II}}\widehat{x}\right)exp\Bigg({\alpha }_{II}x\right)\\&\quad\quad+{A}_{II}^{\prime}\left(\widehat{z}+\frac{i{k}_{z}}{{\alpha }_{II}}\widehat{x}\Bigg)exp\left(-{\alpha }_{II}x\right)\right)exp\left[-i\left(\omega t-{k}_{z}z\right)\right],\\&\overrightarrow{B}=\widehat{y}\frac{c}{i\omega }\frac{{\omega }^{2}}{{c}^{2}{\alpha }_{II}}({A}_{II}\text{exp}\left({\alpha }_{II}x\right)\\&\quad\quad+{A}_{II}^{\prime}exp\left({\alpha }_{II}x\right))exp\left[-i\left(\omega t-{k}_{z}z\right)\right].\end{aligned}$$
(13)

The velocity of electron beam in the presence of SPs is given by \(\overrightarrow{v}={v}_{0b}\overrightarrow{z}+{\overrightarrow{v}}_{1}\) (beam velocity and perturbed velocity) and the Lorentz factor γ of the moving electron beam is given by \(\gamma ={\left(1-\frac{{v}^{2}}{{c}^{2}}\right)}^{-1/2}\) or \(\gamma ={\gamma }_{0}+{\gamma }_{0}^{3}\frac{{v}_{0b}\overrightarrow{{v}_{1z}}}{{c}^{2}}\). In terms of components and linearizing the Eq. (12), we have

$$\begin{aligned}&\frac{\partial }{\partial t}\left({\gamma }_{0}{v}_{1x}\widehat{x}+{\gamma }_{0}^{3}{v}_{1z}\widehat{z}\right)+i{k}_{z}{v}_{0b}\left({\gamma }_{0}{v}_{1x}\widehat{x}+{\gamma }_{0}^{3}{v}_{1z}\widehat{z}\right) \\&\quad=\frac{-e}{m}\left[\widehat{x}\left(\left(1-\frac{{k}_{z}{v}_{0b}}{\omega }\right){E}_{x}+\frac{{v}_{0b}}{i\omega }\frac{\partial }{\partial x}{E}_{z}\right)+\widehat{z}{E}_{z}\right].\end{aligned}$$
(14)

The x and z components of velocity of Eq. (14) can be written as \({v}_{1z}=\frac{e{E}_{z}}{im{\gamma }_{0}^{3}\left(\omega -{k}_{z}{v}_{0b}\right)}\),

\({v}_{1x}=\frac{e{E}_{x}}{mi\omega {\gamma }_{0}}-\frac{e{v}_{0b}}{m\omega \left(\omega -{k}_{z}{v}_{0b}\right){\gamma }_{0}}\frac{\partial }{\partial x}{E}_{z}\). The equation of continuity is \(\frac{\partial n}{\partial t}+\nabla \cdot \left(n\overrightarrow{v}\right)=0\) where \(n={n}_{0b}+{n}_{1};\) this gives the perturbed density

$${n}_{1=}\frac{\partial {n}_{0b}}{\partial x}\frac{{v}_{1x}}{i\left(\omega -{k}_{z}{v}_{0b}\right)}{E}_{z}+\frac{{n}_{0b}\nabla \cdot \overrightarrow{{v}_{1}}}{i\left(\omega -{k}_{z}{v}_{0b}\right)}.$$
(15)

The total perturbed current density is given by \(\overrightarrow{{J}_{1}}=-{n}_{0b}e\overrightarrow{{v}_{1}}+{n}_{1}{ev}_{0b}\widehat{z}\). For purely growing instability, we look the terms that have \({\left(\omega -{k}_{z}{v}_{0b}\right)}^{2}\) in denominator and other terms may be discarded it. So, the total perturbed current density is given by

$$\begin{aligned}\overrightarrow{{J}_{1}}=&-\frac{\widehat{z}{ev}_{0b}}{i{\left(\omega -{k}_{z}{v}_{0b}\right)}^{2}}\\&\Bigg[-\frac{\partial {n}_{0b}}{\partial x}\frac{{ev}_{0b}}{m\omega {\gamma }_{0}}\frac{\partial }{\partial x}{E}_{z}-\frac{{ev}_{0b}{n}_{0b}}{m\omega {\gamma }_{0}}\frac{{\partial }^{2}}{\partial {x}^{2}}{E}_{z}+\frac{{n}_{0b}{{k}_{z}eE}_{z}}{m{\gamma }_{0}^{3}}\Bigg],\end{aligned}$$
(16)

The Cherenkov condition demands that \({k}_{z}\approx \omega /{v}_{0b}\). In Eq. (16), the last two terms cancel out each other and one may get

$$\overrightarrow{{J}_{1}}=\frac{\widehat{z}{{e}^{2}v}_{0b}}{im\omega {{\gamma }_{0}\left(\omega -{k}_{z}{v}_{0b}\right)}^{2}}\frac{\partial {n}_{0b}}{\partial x}\frac{\partial {E}_{z}}{\partial x}.$$
(17)

At boundaries x = -a and x = a of interfaces in metal-air metal structure, the field of SPs satisfying the Maxwell’s equations \(\nabla \times {\overrightarrow{E}}_{s}=\frac{i\omega }{c}{\overrightarrow{H}}_{s},\)  \(\nabla \times {\overrightarrow{H}}_{s}=-\frac{i\omega }{c}{\varepsilon }^{\prime}{\overrightarrow{E}}_{s}\), in the absence of electron beam. The permittivity has value \({\varepsilon }^{\prime}={\varepsilon }_{m}={\epsilon }_{L}-{\omega }_{p}^{2}/{\omega }^{2}\) in I (-a < x) and III (a > x). In the presence of moving electron beam, the new electric and magnetic fields of SPs are given by.

$$\overrightarrow{E}=A(t){\overrightarrow{E}}_{s},\;\overrightarrow{H}=B(t){\overrightarrow{H}}_{s}.$$
(18)

The fields \(\overrightarrow{E} \;\text{and}\; \overrightarrow{H}\) of SPs both satisfy the Maxwell’s equations inside the metals, which are given by \(\nabla \times \overrightarrow{E}=-\frac{1}{c}\frac{\partial \overrightarrow{H}}{\partial t},\) \(\nabla \times \overrightarrow{H}=\frac{4\pi }{c}\left( \overrightarrow{{J}_{1b}}+\overrightarrow{{J}_{1p}}\right)=\frac{{\varepsilon }_{L}}{c}\frac{\partial \overrightarrow{E}}{\partial t}\), where \(\overrightarrow{{J}_{ip}}={\sigma }_{m}A{\overrightarrow{E}}_{s}+i\frac{{\partial \sigma }_{m}}{\partial \omega }\frac{\partial A}{\partial t}{\overrightarrow{E}}_{s},\) \({\varepsilon }_{m}={\varepsilon }_{L}+i\frac{4\pi {\sigma }_{m}}{i\omega }\) and outside the metals \({\varepsilon }_{L}=1, \sigma =0,\) using Eq. (18). We have

$$\frac{\partial B}{\partial t}=-i\omega \left(A-B\right),$$
(19)
$$\left[\frac{\partial A}{\partial t}\frac{\partial }{\partial \omega }{\varepsilon }^{\prime}\left(\omega \right)-i\omega {\varepsilon }^{\prime}\left(A-B\right)\right]{\overrightarrow{E}}_{s}=-4\pi \overrightarrow{{J}_{1b}.}$$
(20)

Putting Eq. (19) into Eq. (20) and assuming that \(\partial B/\partial t\cong \partial A/\partial t\), the resulting equation is multiplying by \({E}_{s}^{*}\) and integrating over the limit \(-\infty to+\infty ,\) we have

$$\frac{\partial A}{\partial t}=\Gamma A=-2\pi \frac{\int_{-\infty }^{\infty }{J}_{1z}\cdot {E}_{sz}^{*}dz}{\int_{-\infty }^{\infty }\overrightarrow{{E}_{s}}\cdot\overrightarrow{{E}_{s}^{*}}dx}=R\left(A\right),$$
(21)

where \(R(A)=-\frac{2\pi {\int_{-a}^{a}}\frac{\partial {n}_{0b}}{\partial x} \frac{\partial {E}_{sz}}{\partial x}{E}_{sz}^{*}dz\frac{{e}^{2}{v}_{0b}^{2}}{im\omega {{\gamma }_{0}\left(\omega -{k}_{z}{v}_{0b}\right)}^{2}}}{{\int_{-\infty }^{-a}}{\overrightarrow{E}}_{s}\cdot \overrightarrow{{E}_{s}^{*}}dx+{\int_{-a}^{a}}\overrightarrow{{E}_{s}}\cdot \overrightarrow{{E}_{s}^{*}}dx+{\int_{a}^{\infty}}\overrightarrow{{E}_{s}}\cdot \overrightarrow{{E}_{s}^{*}}dx}\). In air gap -a < x < a, between metallic plates the electric field \(\overrightarrow{{\text{E}}_{\text{s}}}\) of SPs is given by \({\overrightarrow{E}}_{s}=2{A}_{II}\left(\mathit{cos}h\left({\alpha }_{II}x\right)\widehat{z}-\frac{i{k}_{z}}{{\alpha }_{II}}\mathit{sin}h\left({\alpha }_{II}x\right)\widehat{x}\right)exp\left[-i\left(\omega t-{k}_{z}z\right)\right]\) and using \(\frac{\partial {n}_{0b}}{\partial x}=-\frac{2{N}_{0}x}{{r}_{b}^{2}}exp\left(-{x}^{2}/{r}_{b}^{2}\right)\), \(\frac{\partial {E}_{sz}}{\partial x}=2{A}_{II}{\alpha }_{II}s\mathit{in}h\left({\alpha }_{II}x\right)exp\left[-i\left(\omega t-{k}_{z}z\right)\right]A\), the values of following terms are \({\int_{-a}^{a}}\frac{\partial {n}_{0b}}{\partial x} \frac{\partial {E}_{sz}}{\partial x}{E}_{sz}^{*}dz=-\frac{8{N}_{0}}{{r}_{b}^{2}}{ A}_{II }^{2}{ \alpha }_{II }^{2}{r}_{b}^{3}\surd \pi /2\), \({\int_{-a}^{a}}\overrightarrow{{E}_{s}}\cdot \overrightarrow{{E}_{s}^{*}}dx=={A}_{II }^{2}\left(\frac{2}{{\alpha }_{\mathit{II}}}\mathit{sin}h\left(2{\alpha }_{II}a\right)+4a\left(1-\frac{{k}_{z}^{2}}{{ \alpha }_{II }^{2}}\right)\right)\) and \({\int_{a}^{\infty}}\overrightarrow{{E}_{s}}\cdot \overrightarrow{{E}_{s}^{*}}dx={A}_{I }^{2}\left(1+\frac{{k}_{z}^{2}}{{ \alpha }_{I }^{2}}\right){\int_{a}^{\infty}}exp\left({-2\alpha }_{I}x\right)dx={A}_{I }^{2}\left(1+\frac{{k}_{z}^{2}}{{ \alpha }_{I }^{2}}\right)\frac{1}{2{\alpha }_{I}}exp\left({-2\alpha }_{I}a\right)\), hence the RHS of Eq. (21) becomes \(\frac{2\pi {e}^{2}{v}_{0b}^{2}}{im\omega {{\gamma }_{0}\left(\omega -{k}_{z}{v}_{0b}\right)}^{2}}\frac{4{N}_{0}{ \alpha }_{II }^{2}{r}_{0b}\surd \pi }{\left(\frac{2}{{\alpha }_{\mathit{II}}}\mathit{sin}h\left(2{\alpha }_{II}a\right)+4a\left(1-\frac{{k}_{z}^{2}}{{ \alpha }_{II }^{2}}\right)+\frac{{A}_{I }^{2}}{{A}_{II }^{2}}\left(1+\frac{{k}_{z}^{2}}{{ \alpha }_{I }^{2}}\right)\frac{1}{{\alpha }_{I}}exp\left({-2\alpha }_{I}a\right)\right)}\). Using \(\frac{{A}_{I }^{2}}{{A}_{II }^{2}}=4 exp\left({2\alpha }_{I}a\right)c{\mathit{os}h}^{2}\left({\alpha }_{II}a\right)=2 exp\left({2\alpha }_{I}a\right)\left(1+\mathit{cos}h\left(2{\alpha }_{II}a\right)\right)\), the RHS gives \(\frac{2\pi {e}^{2}{v}_{0b}^{2}2{N}_{0}{ \alpha }_{II }^{3}{r}_{0b}\surd \pi }{im\omega {{\gamma }_{0}\left(\omega -{k}_{z}{v}_{0b}\right)}^{2}D}\), where \(D=\mathit{sin}h\left(2{\alpha }_{II}a\right)+\frac{{\alpha }_{II}}{{\alpha }_{I}}\left(1+\frac{{k}_{z}^{2}}{{ \alpha }_{I }^{2}}\right)\left(1+\mathit{cos}h\left(2{\alpha }_{II}a\right)\right)+2{\alpha }_{II}a\left(1-\frac{{k}_{z}^{2}}{{ \alpha }_{II }^{2}}\right)\), hence the Eq. (21) gives.

$$\frac{\partial A}{\partial t}=\frac{4{\pi }^{3/2}{e}^{2}{v}_{0b}^{2}{N}_{0}{r}_{0b}{ \alpha }_{II }^{3}}{m{\gamma }_{0}\omega \left(\omega -{k}_{z}{v}_{0b}\right)D}$$
(22)

Taking \(\partial A/ \partial t=-i\delta , \omega ={k}_{z}{v}_{0b}+\delta\), one may obtain the \({\delta }^{3}=R\; exp\left(2il\pi \right)\), where \(R=\frac{4{\pi }^{3/2}{e}^{2}{v}_{0b}^{2}{N}_{0}{r}_{0b}{ \alpha }_{II }^{3}}{m{\gamma }_{0}\omega D}\). Hence, the growth rate turns out to be, \(\Gamma =im\delta= {R}^{1/3}\frac{\surd 3}{2}\) and it gives

$$\Gamma =\frac{\sqrt{3}}{2}{\left(\frac{{\omega }_{pb}^{2}{v}_{0b}^{2}{r}_{0b}{ \alpha }_{II }^{3}}{{\gamma }_{0}\omega D}\right)}^{1/3}.$$
(23)

The Eq. (23) gives the growth rate of THz SPs generation. The normalized growth rates versus normalized frequency of THz SPs for different energy values (\({\gamma }_{0}\)) of an electron beam and different normalized values of air gap (\({a\omega }_{p/c}\)) between metallic plates is plotted in Figs. 5, 6, 7, and 8. We plotted the normalized growth rates for following parameters: \({\omega }_{\text{pb}}/{\omega }_{p}=1{0}^{-3}\); \({v}_{0b}/c=1{0}^{-2}\); \({{r}_{0b}\omega }_{p/c}=1{0}^{-5}\); \({\varepsilon }_{L}=9\); for different energy values of electron beam \({\gamma }_{0}=\text{1, 2, 3, 4, 5}\) and air gap between metallic plates \({a\omega }_{p/c}=\text{5, 10, 15, 20}\). Figures 5, 6, 7 and 8 show that there is board spectrum of THz radiation. The growth rate of THz radiation is lower for high energy electron beam as compared to low energy electron beam, because at low energy the electron beam has strong interaction with highly localized and propagating SPs. In Figs. 6, 7, and 8, it is shown that as increasing the air gap between the metallic plates, the growth rate is decreased. Figures 5, 6, 7 and 8 also show that the growth rate decreases with increases in the beam energy, frequency, and air gap between the plates.

Fig. 5
figure 5

Normalized growth rate \(\Gamma /{\omega }_{p}\) as a function of normalized frequency \(\omega /{\omega }_{p}\) for the following parameters: \({\omega }_{\text{pb}}/{\omega }_{p}=1{0}^{-3}\); \({v}_{0b}/c=1{0}^{-2}\); \({r}_{0b}{\omega }_{p}/c=1{0}^{-5}\); \({\varepsilon }_{L}=9\); for different relativistic energy \({\gamma }_{0}=\text{1, 2, 3, 4, 5}\) and normalized gap \(a{\omega }_{p}/c=5\)

Full size image
Fig. 6
figure 6

Normalized growth rate \(\Gamma /{\omega }_{p}\) as a function of normalized frequency \(\omega /{\omega }_{p}\) for the following parameters: \({\omega }_{\text{pb}}/{\omega }_{p}=1{0}^{-3}\); \({v}_{0b}/c=1{0}^{-2}\); \({r}_{0b}{\omega }_{p}/c=1{0}^{-5}\); \({\varepsilon }_{L}=9\); for different relativistic energy \({\gamma }_{0}=\text{1, 2, 3, 4, 5}\) and normalized gap \(a{\omega }_{p}/c=10\)

Full size image
Fig. 7
figure 7

Normalized growth rate \(\Gamma /{\omega }_{p}\) as a function of normalized frequency \(\omega /{\omega }_{p}\) for the following parameters: \({\omega }_{\text{pb}}/{\omega }_{p}=1{0}^{-3}\); \({v}_{0b}/c=1{0}^{-2}\); \({r}_{0b}{\omega }_{p}/c=1{0}^{-5}\); \({\varepsilon }_{L}=9\); for different relativistic energy \({\gamma }_{0}=\text{1, 2, 3, 4, 5}\) and normalized gap \(a{\omega }_{p}/c=15\)

Full size image
Fig. 8
figure 8

Normalized growth rate \(\Gamma /{\omega }_{p}\) as a function of normalized frequency \(\omega /{\omega }_{p}\) for the following parameters: \({\omega }_{\text{pb}}/{\omega }_{p}=1{0}^{-3}\); \({v}_{0b}/c=1{0}^{-2}\); \({r}_{0b}{\omega }_{p}/c=1{0}^{-5}\); \({\varepsilon }_{L}=9\); for different values of normalized gap \(a{\omega }_{p}/c=\text{5, 10, 15, 20}\) and fixed energy of electron beam \({\gamma }_{0}=1\)

Full size image

Conclusion

In conclusion, the metal-air-metal symmetrical structure is a favorable structure for broadband THz radiation generation by relativistic electron beam (MeV). These beams are easily generated from plasma-based charged particle accelerators [39]. The growth rate and frequency have large value for low energy electron beam. The growth rate of generated THz radiation is varying with one third power of beam current density and peak of the growth rate at particular value of frequency is decided by the energy of electron beam and an air gap between the plates (few micron). The radiation frequency about 0.50 THz can be generated by an electron beam have current about 170 A and energy nearly about 3 MeV and has growth time is few ns. The highly confined and propagating THz SPs can be transformed into THz radiation by a suitable surface grating that are commonly used at present days. The beam current has value nearly about 170 A. Hence, the proposed structure will open the possibility to design a compact source for coherent and tuneable THz radiation generation in broad spectrum regime. When a background plasma is created by the beam, the mode structure is considerably modified, leading to a reduction in the growth rate, hence to the efficiency of the device. In addition, this proposed structure also provides a new way of controlling the propagation of THz-SPs, which are important for manipulation of optical waves. The feasible applications of this device will be useful for medical diagnostics and treatments with considerable advantages, etc.