Introduction

Radiating structures based on gratings embedded into a dielectric waveguide transforming eigenwaves to free space waves are promising as low-cost, low-profile, and easy-to-fabricate elements of millimetre-wave devices such as filters or antennas with frequency scanning ability [1, 2].

New materials are available today, such as graphene. Graphene can be considered as 2d plane of carbon atoms, ideally 1 atom thick. It is famous for being electrically conductive, mechanically strong, and optically transparent. Graphene strips can support plasmon polariton surface waves and corresponding plasmon resonances at THz. The resonant frequency can be tuned by applying electrostatic or magnetostatic doping [3, 4]. This feature makes graphene perspective in designing of tunable THz devices. For example, one can adjust the equivalent impedance of the structure and reduce the reflection. Together with the ability of graphene to absorb the electromagnetic field, it becomes a very promising element of absorbers [5,6,7]. The use of graphene for sensing application is also possible [8,9,10]. For the THz range, a numerical analysis of the plasmon resonances on a single graphene strip and corresponding sensing properties in the case of variation of the refractive-index of the host medium is given in Shapoval and Nosich [11], and for several strips with substrate is given in Nejat and Nozhat [12].

The mutual interaction of graphene strips in the array is smaller than metallic ones because of the short surface plasmon polariton wavelength [13, 14]. This effect can be used in antennas to reduce their size. The configuration of tunable leaky-wave antenna with graphene strips embedded into or placed on dielectric slab is discussed in previous studies [15,16,17].

Graphene strips may be considered as zero thickness resistive surfaces with the restriction that the strip width is > 100 nm. Here one can assume that the edge effect on the graphene conductivity is negligible, and the electrical conductivity model developed for infinite graphene surfaces can be used. For the considered frequency range 1…4 THz, permittivity, and chemical potential values, the spatial dispersion can be neglected [18]. In the absence of spatial dispersion and magnetostatic bias field, the conductivity of graphene is a scalar function \(\sigma=\sigma(f,\mu_c,\tau,\;T)\) of frequency f, chemical potential \(\mu_c\) electron relaxation time \(\tau\) and temperature T. It can be obtained from the Kubo formalism [19, 20].

Finite-difference time-domain method is one of possible computation instruments for graphene structures [5, 21,22,23,24]. However, as in the case of commercial packages based on the finite-elements method [25], it leads to the huge system of equations due to the large domain of discretization. In addition, the time step is defined by the thickness of graphene which is only one-atom. Another disadvantage is inability to analytically satisfy the radiation conditions that limits the accuracy of the results to several digits. Approximate techniques, which work much faster, can give reliable results and describe physical effects [17, 26].

Another alternative is meshless rigorous techniques such as methods of singular integral equations (SIEs) with Nystrom discretization [27,28,29,30,31] or method of analytical regularization [32]. They provide controlled accuracy within a reasonable computation time.

In previous studies [27, 28, 32], several types of resonances are discussed which graphene strip grating embedded into dielectric slab can support. Near the plasmon resonances, an increase in the total scattering and absorption cross section is observed. Except the plasmon resonances, which can arise on a single graphene strip, the grating inside the dielectric slab can support the grating-mode resonances. It is shown that in the case of plane wave incidence, near these resonances significant increase in scattering and absorption is also observed.

In the present work, we study how the radiation from the dielectric waveguide with finite graphene strip grating can be controlled in the THz range. For the solution, we use the method of SIEs with discretization based on the Nystrom-type method of discrete singularities [33, 34]. Preliminary results were presented in the conference papers [35, 36]; here, results are significantly extended.

Singular Integral Equation

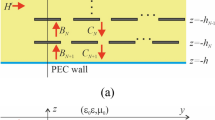
Let us consider planar dielectric waveguide with coplanar graphene strips placed as shown in Fig.1. We denote the set of strips as \(L=\underset{n=1}{\overset{N}{\cup }}{L}_{n}\), where \({L}_{n}\) is the n th strip. The width of the waveguide is 2 h; its permittivity is \({\varepsilon }_{0}\varepsilon\).

Fig. 1
figure 1

Structure geometry (created in CorelDRAW X5)

Full size image

We will assume that the field is independent of x and consider only the H-polarized waves. Hence, the electromagnetic field has the following components: \((0, E_{y}, E_{z}), (H_{x},0,0)\), which satisfy the Helmholtz equation, the boundary conditions at the dielectric-vacuum interface

$${H}_{x}^{+}={H}_{x}^{-}, {E}_{y}^{+}={E}_{y}^{-}, if\;z=h\;or\;z=-h$$
(1)

the boundary conditions on graphene strips and outside the strips

$${E}_{y}^{+}=\frac{1}{\sigma }{(H}_{x}^{+}-{H}_{x}^{-}), z=0,y\in L$$
(2)
$${H}_{x}^{+}={H}_{x}^{-}, z=0,y\notin L$$
(3)
$${E}_{y}^{+}={E}_{y}^{-},z=0$$
(4)

the radiation and the edge conditions. The signs “ ± ” indicate the limit values of the field components from above (below) the interfaces.

Outside the dielectric waveguide, the radiated field is the field of cylindrical waves which propagate to the infinity. The amplitude of this field decreases as \(1/\sqrt{k\rho }\), if \(k\rho \to \infty\), where \(\rho\) is the distance. However, inside the dielectric waveguide, \(-h<z<h\), the scattered field can be represented as a sum of the evanescent and propagating eigenwaves. The amplitude of the propagating eigenwaves is non-decreasing function, if \(k\rho \to \infty\). Here, we should use the radiation condition in a special form [37, 38].

The incident eigenwave \(H_{p}\) of the planar dielectric waveguide with number p propagates from the negative direction of the y-axis. The total field can be represented as a sum of the incident and scattered field, \({H}^{\text{total}}={H}^{p}+{H}^{s}\).

The scattered field can be expanded in terms of Fourier integral in each domain as follows: \(H^{s}(y,z)=\)

$$\left\{\begin{array}{c}\int\limits_{-\infty}^\infty a(\xi)\frac{b(\xi/\sqrt\varepsilon)}{1-g(\xi\sqrt\varepsilon)}exp(ik\xi y+ik\gamma(\xi)z)d\xi,z > h\\\int\limits_{-\infty}^\infty(c(\xi)\;exp(ik_1\xi y+ik_1\gamma(\xi)z)+exp(ik_1\xi y+ik_1\gamma(\xi)z))\frac{b(\xi)}{1-g(\xi)}d\xi,\\0 < z < h,\\\int\limits_{-\infty}^\infty(f(\xi)\;exp(ik_1\xi y-ik_1\gamma(\xi)z)+g(\xi)exp(ik_1\xi y+ik_1\gamma(\xi)z))\frac{b(\xi)}{1-g(\xi)}d\xi,\\-h < z < 0,\\\int\limits_{-\infty}^\infty d(\xi)\frac{b(\xi/\sqrt\varepsilon)}{1-g(\xi\sqrt\varepsilon)}exp(ik\xi-ik\gamma(\xi)z)d\xi,z < -h,\end{array}\right.$$
(5)

where \(k=\omega\sqrt{\varepsilon_0\mu_0} , k_{1}=\omega\sqrt{\varepsilon_0\varepsilon\mu_0}\)  and are wavenumbers in vacuum and in the dielectric waveguide, \(\gamma(\xi)=\sqrt{1-\xi^2}\) with non-negative real and imaginary parts,

$$\begin{aligned}a(\xi )& =2\gamma (\xi )\left(\mathrm{exp}(-ikh\gamma (\xi /\sqrt{\varepsilon }))(\gamma (\xi /\sqrt{\varepsilon })\sqrt{\varepsilon }+\gamma (\xi ))\right.\\ &+exp(-ih(-2{k}_{1}\gamma (\xi )+k\gamma (\xi /\sqrt{\varepsilon })))(\gamma (\xi /\sqrt{\varepsilon })\sqrt{\varepsilon }\\ &-\left.\gamma (\xi ))\right)/G(\xi )/\sqrt{\varepsilon },\end{aligned}$$
(6)
$$c(\xi )=\mathrm{exp}(i{k}_{1}h\gamma (\xi ))\left(-{\gamma }^{2}(\xi /\sqrt{\varepsilon })\varepsilon +{\gamma }^{2}(\xi )-\mathrm{exp}(2i{k}_{1}h\gamma (\xi ))(\gamma (\xi /\sqrt{\varepsilon })\sqrt{\varepsilon }-\right.\left.\gamma \left(\xi \right){)}^{2}\right)/G(\xi ),$$
(7)
$$\begin{aligned}f(\xi )& =-\left(\gamma (\xi /\sqrt{\varepsilon })\sqrt{\varepsilon }+\gamma (\xi )\right)\left(\mathrm{exp}(-i{k}_{1}h\gamma (\xi ))(\gamma (\xi /\sqrt{\varepsilon })\sqrt{\varepsilon }+\gamma (\xi ))\right.\\ &+exp(-ih{k}_{1}\gamma (\xi ))(\gamma (\xi /\sqrt{\varepsilon })\sqrt{\varepsilon }-\left.\gamma (\xi ))\right)/G(\xi ),\end{aligned}$$
(8)
$$\begin{array}{c}g(\xi )=\left(\gamma (\xi /\sqrt{\varepsilon })\sqrt{\varepsilon }-\gamma (\xi )\right)exp(i{k}_{1}h\gamma (\xi ))\left(\gamma (\xi /\sqrt{\varepsilon })\sqrt{\varepsilon }+\gamma (\xi )\right.\\ +exp(2ih{k}_{1}\gamma (\xi ))(\gamma (\xi /\sqrt{\varepsilon })\sqrt{\varepsilon }-\left.\gamma (\xi ))\right)/G(\xi ),\end{array}$$
(9)
$$d(\xi )=-a(\xi ),$$
(10)
$$G(\xi )=\mathrm{exp}(i{k}_{1}h\gamma (\xi ))\left({\gamma }^{2}(\xi /\sqrt{\varepsilon })\varepsilon -{\gamma }^{2}(\xi )+\mathrm{exp}(-2i{k}_{1}h\gamma (\xi ))(\gamma (\xi /\sqrt{\varepsilon })\sqrt{\varepsilon }+\right.\left.\gamma (\xi ){)}^{2}\right),$$
(11)

\(b(\xi)\) is unknown function. In fact, (5) is the field expansion in terms of plane waves which propagate in the positive and negative directions of the \(z\)-axis. In (5), taking into account (6)–(11), the boundary conditions (1) and (4) and radiation conditions in the domain \(|z|>h\) are satisfied automatically.

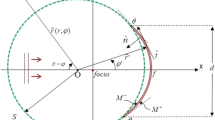
Let us consider the radiation conditions inside the waveguide, \(-h<z<h\) Function \(1-g(\xi)\) has zeros at the points\(\beta_{m},\; m=1,2,\dots ,\)  which correspond to the propagation constants of the eigenwaves of the dielectric waveguide. For the evanescent waves, points \({\beta }_{m}\) are complex numbers with \(\text {Im} \ \beta_m\neq0\). For the propagating waves, points \(\beta_m\) are real numbers, \(\text {Im} \ \beta_m=0\). Points \({\beta }_{m}>0\) (\({\beta }_{m}<0\)) correspond to the waves which propagate to the positive (negative) direction of the y-axis. As a result, integrands in (5) have singularities on the integration path. They can be treated as poles. After that the Cauchy integral formula or residue theorem can be used. To calculate these integrals, the integration path should be transformed. First of all, we should note that integrands in (5) are meromorphic functions which satisfy the asymptotic relation

$${\text{integrand}}\sim |\xi {|}^{-\frac{3}{2}}\mathrm{exp}\left(-ky\mathrm{Im}\xi \right), when|\xi |\to \infty, |y|>>1.$$
(12)

Then, for \(y\rightarrow+\infty(y\rightarrow-\infty)\) inside the waveguide, if \(-h < z < h\) expression (5) should give us waves that propagate to the positive (negative) direction of the y-axis or decay exponentially. The integration over the real axis can be exchanged by the integration over the contour in the form of semicircle in the upper or lower half-space that will enclose our initial path. From (12) it follows that to obtain convergent integral for \(y>0(y<0)\) we should take semicircle in the upper \(\mathrm {Im}\xi> 0(\mathrm {lower}\;\mathrm {Im}\xi< 0)\)  half-space. For \(y > 0(y <0),\) points\(\beta_{m}> 0\;(\beta_{m}< 0)\)  must be inside the contour and points \(\beta_{m}< 0(\beta_{m}> 0)\) must be outside the contour. Thus, the integration path should be transformed so it coincides with the real axis everywhere except points \(\beta_{m}\). Negative points \(\beta_{m}\)  should be bypassed from above, and positive points \(\beta_{m}\) should be bypassed from below (see Fig. 2). In this case, the radiation condition is satisfied.

Fig. 2
figure 2

Integration path (created in CorelDRAW X5)

Full size image

Finally, the scattered field inside the waveguide, if \(y\to \pm \infty\), is

$$\begin{array}{c}H^s(y,z)=4\pi\sum_{m=0}^\infty\alpha_m\sin\left(k_1\gamma(\beta_m)z\right)exp(ik\vert\beta_my\vert),-h < z < h,\\\alpha_m=\lim_{\xi\rightarrow sgn(y)\xi_m}b(\xi)(\xi-sgn(y)\xi_m).\end{array}$$
(13)

The enforcement of the remaining boundary conditions (2) and (3) gives us dual integral equations relatively unknown function \(b(\xi )\):

$$\int\limits_{{-}\infty}^\infty b(\xi)\exp(ik_1\xi y)d\xi=0,y\not\in L$$
(14)
$$\begin{array}{c}ik_1\int\limits_{{-}\infty}^\infty\gamma(\xi)(1-c(\xi))\frac{b(\xi)}{1-g(\xi)}exp(ik_1\xi y)d\xi\\+\frac{2ik_1\sqrt\varepsilon}{\sigma Z_0}\int\limits_{{-}\infty}^\infty b(\xi)\exp(ik_1\xi y)d\xi=-\frac\partial{\partial z}H^p(y,0),y\in L,\end{array}$$
(15)

where \({Z}_{0}=120\pi\) Ohm.

The application of Hilbert transform [39] allows us to reduce the dual integral equations (14) and (15) to SIE over the set of strips

$$\frac{1}{\pi }PV\underset{L}{\overset{}{\int }}\frac{F(\eta )}{\eta -y}d\eta +\frac{1}{\pi }\underset{L}{\overset{}{\int }}Q(y,\eta )F(\eta )d\eta =-\frac{\partial }{\partial z}{H}^{p}\left(y,0\right), y\in L.$$
(16)
$$\frac{1}{\pi }\underset{{L}_{n}}{\overset{}{\int }}F\left(\xi \right)d\xi =0,n=1,2\dots,N,$$
(17)

where \(Q(y,\eta)\) is the kernel function,

$$\begin{aligned}Q(y,\eta) = &k_1 \int\limits_0^\infty \left(1+i\frac{\gamma(\xi)}{\xi}\frac{1-c(\xi)}{1-g(\xi)}\right)\sin(k_1\xi(y-\eta))d\xi \\ &+ \begin{cases}2ik\pi (\sigma Z)^{-1},\; if \; \eta \leq y, \\ 0, \; if \; \eta > y,\end{cases} \end{aligned}$$
(18)

F(y) can be expressed in terms of \(b(\xi)\) with the help of Fourier transform, \(F(y)=ik_1\int\limits_{-\infty}^\infty\xi b(\xi)exp(ik_1\xi y)d\xi\).

The first integral in (16) is understood as Cauchy principal value integral. The kernel-function \(Q(y,\eta)\) (18) in the second integral in (16) contains poles. The integration contour is shown in Fig. 2. However, the integral over infinite semicircle vanishes. Thus, the integration path in the kernel-function coincides with the real axis everywhere, except the poles \(\beta_{m}\) , and the poles are bypassed from below. After application of the regularization procedure and Cauchy integral formula, the kernel-function becomes the regular integral. It can be calculated numerically with the use of the quadrature formula such as the Simpson’s or Gaussian rules.

For discretization of SIE, the quadrature rule for the Cauchy principal value singular integrals is used [34, 35]. Taking into account the edge condition and representing unknown function as a product of new unknown regular function n \(u_{n}(t)\) and function with the inverse square root singularity on every strip, \(F(\Psi_n(t))=u_n(t)/\sqrt{1-t^2}\), we can obtain system of SIEs on the standard interval (-1;1). Here Ψn(t) is linear transformation function of (-1,1) to the segment which corresponds to the n th strip Ln. After that, integrands are replaced with interpolating polynomials. The nodes coincide with the zeros of the Chebyshev polynomials of the first kind. The values of y, co-called collocation points, are taken from the set of zeros of the Chebyshev polynomials of the second kind. As a result, the set of algebraic equations can be obtained.

Numerical Results

Convergence

The solution of (16)–(18) is unique and convergence is based on the theorems [40, 41]. To control the error of numerical results, we used the error-function defined as err(M)=|S(M)-S(2M)|/|S(2M)|, where S is equal to the radiated power and M is the order of the Chebyshev polynomial. Numerical results are obtained using C +  + .

Let us consider the system of identical strips of a width 2d placed equidistantly. The period is l.

Figure 3 shows dependences of \(\text{err(}M)\). The results are presented for several values of width of strips and frequency. The convergence in monotone and the error vanishes if M becomes larger than a certain value. With the normalized width of the strip kd is increased, we should take larger value of M.

Fig. 3
figure 3

Dependences of the error-function on the order of the Chebyshev polynomial \(\varepsilon=2.25\), \(\mu_{c}=1eV, T=300K, \tau=1\) ps (created in Origin 6.1)

Full size image

Notice that (12) is valid for y >  > 1. To calculate the near field, we regularize integrals in (5) in the same way as in (17) and used composed Gaussian quadrature for integrals without singularities. Firstly, it follows from  (12) that values \(T^{ampl}=1-4\pi{a}_{1}\;\mathrm{and}\;R^{ampl}=-4\pi{a}_{-1}\) are reflection and transmission coefficients (amplitude) of the dominant eigenwave of the waveguide. Secondly, amplitude of the field inside the waveguide also equals to the reflection (or transmission) coefficient. Thus,

$$H^s(y,z_0)\rightarrow-4{{\pi}{a}}_{\pm1}, \mathrm{if}\; y\rightarrow+\infty.$$
(19)

We checked (19) numerically by increasing |y|. Equation (19) is satisfied at the level of machine accuracy. This allows to validate our home-made program block connected with the elimination of singularities in (5) and (17).

In Kaliberda et al. [34, 35], we demonstrate that the results of commercial software HFSS agreed well with our results. At the same time, the radiation patterns calculated with the help of HFSS show slight instability: the width and the angle of the main lobe vary in the interval \(\pm {2}^{0}{...3}^{0}\); the angle and magnitude of the side-lobes significantly depend on the size of the “vacuum box”.

Scattering Characteristics

Figures 4, 5 and 6 show dependences of the radiation, Rad absorption A, reflection R, and transmission T coefficients (power) as functions of frequency in the case of the dominant eigenwave of the dielectric waveguide excitation. The following relation is satisfied: Rad+A+R+T = 1.The behaviour of the curves can be explained in terms of the resonances that the structure under study can support. The maxima of the radiation coefficient correspond to the plasmon resonances (marked as \(P_{i}\)). They depend on the parameters of individual graphene strip. The position of these resonances on the frequency axis can be controlled by variation of the chemical potential. The most effective radiation is observed for \(\mu_{c}=1eV\). For \(\mu_{c}=0.3eV\) near the first plasmon resonance, the radiation efficiency is poor, < 20%. With an increase of the chemical potential, the radiated power also increases near the first plasmon resonance and reaches its maximum value of about 79% for \(\mu_{c}=1eV\). For greater number of strips N we do not obtain better radiation, if \(d=10\mu m\). Almost all non-radiated power is absorbed by the graphene strips, so the radiation efficiency is also about 79%. For \(\mu_{c}=1eV\) near the first plasmon resonance frequency, the reflected and transmitted power does not exceed 2%.

Fig. 4
figure 4

Dependences of the a radiation, b absorption, c reflection, and d transmission coefficient on the frequency for  \(h=50\;\mu{m}, d=10\;\mu{m}, \mu_{c}=0.3\;eV\) (solid lines), \(\mu_{c}=0.5\;eV\) (dashed lines), \(\mu_{c}=0.6\;eV\) (dotted lines), \(\mu_{c}=1\;eV\) (shot-dotted lines), \(l=70\;\mu{m},\,\varepsilon=2.25,\;T=300\;K\;,\tau=1\)ps, N = 10, dominant mode, and p = 1 (created in Origin   6.1)

Full size image
Fig. 5
figure 5

Dependences of the a radiation, b  absorption, c reflection, and d transmission coefficient on the frequency for \(h=70\mu{m},\;d=10\mu{m}\). Other parameters are the same as in Fig. 4 (created in  Origin 6.1)

Full size image
Fig. 6
figure 6

Dependences of the a radiation, b absorption, c reflection, and d transmission coefficient on the frequency for \(h=70\mu{m},\;d=7\mu{m}\). Other parameters are the same as in Fig. 4 (created in  Origin 6.1)

Full size image

As one can know, the natural waves and corresponding resonances can be excited in periodic structures. Except the plasmon resonances, the structure under study can support resonances, which are caused by the periodicity of the displacement of the strips. Such resonances are marked as  \(N_{qi}\) . The position of these resonances mostly depends on the parameters of the dielectric slab and the period and is slightly perturbed by the parameters of graphene strips. Thus, it cannot be controlled by variation of the chemical potential. To identify these resonances, we considered two values of the waveguide width \(h=50\mu{m}\) and \(h=70\mu{m}\). These resonances give maxima in the dependences of R and minima in the dependences of Rad. In the case of the plane wave incidence from domain z > 0, resonance N12 is identified as grating-mode resonance [27, 32]. Near the grating-mode resonances, in extremely narrow frequency band, almost total absorption is observed in the infinite graphene grating. These resonances do not arise in the free space. They are also observed in the case of the perfectly electric conducting gratings inside the dielectric slab [42]. The propagation constant χ of natural waves of periodic structure can be obtained from the following equation [43]:

$$\mathrm{det}\left(I-\mathrm{exp}\left(-i\chi l\right)te-erer{\left(I-\mathrm{exp}\left(i\chi l\right)et\right)}^{-1}\right)=0$$
(20)

where t and r are reflection and transmission matrixes of a single strip, I is the identity matrix, and diagonal matrix e has elements \(\mathrm{exp}(ik_{1}l\beta_{m})\) . Fig. 7 shows dependences of Im χ as a function of period l. Extremes of Im χ correspond to the resonances of the natural waves of the periodic part of the structure.

Fig. 7
figure 7

Dependences of Im χ on the period l for f=2THz (solid line), f=3.34THz (dashed line) \(\begin{aligned}h & =50\;\mu{m}, d=10\;\mu{m}, l=70\mu{m},\varepsilon\ =2.25,\;\mu_{c}=1 eV,\;T=300K,\tau=1\end{aligned}\)ps, N = 10, dominant mode, p = 1 (created in  Origin 6.1)

Full size image

Near Field

Figure 8 shows the total field distribution near the plasmon resonances Pi. Field has maxima along the strip. The number of maxima is equal to the number of resonance i. As a rule, the first plasmon resonance is much more pronounced. One can observe much more pronounced maxima near P1 in Figs. 4-6 as well as a high field concentration near the graphene strips.

Fig. 8
figure 8

Field distribution near the plasmon resonances for \(\begin{aligned}h & =70\;\mu{m}, d=10\;\mu{m}, l=70\mu{m},\varepsilon =2.25,\;\mu_{c}=0.3 eV,\;T=300K,\tau=1\end{aligned}\)ps, dominant mode p = 1. a First plasmon resonance, f = 1.5 THz; b second plasmon resonance, f  = 2.5 THz (Created in OriginPro 2015)

Full size image

Figure 9 shows the total field distribution near the resonances of the natural waves of periodic part of the structure. Nqi The field distribution near the resonances Nqi significantly differs from that near the plasmon resonances. It is clearly seen that the field near resonances Nqi has different number of variations along the y and z axes inside the waveguide. The total field has q maxima of the amplitude on a single period \((l \cdot n;l \cdot (n+1))\)  and i maxima on the interval 0 < z < h.

Fig. 9
figure 9

Field distribution near the resonances of the natural waves of periodic structure for h = 70 μm, d = 10 μm, l = 70 μm, ε = 2.25, μc = 1 eV, T = 300 K, τ = 1 ps, N = 10, dominant mode, p=1. a Resonance, N11  f  = 1.85 THz; b resonance N12,  f  = 3.14 THz; c resonance N22, f  = 3.5 THz (created in OriginPro 2015)

Full size image

Far Field

Let us study the far radiated field for various parameters. Fig. 10 shows the radiation patterns (power) near the first plasmon resonance P1 and near the resonance of natural wave of periodic structure N12. The patterns are normalized by the global maximum which corresponds to the first plasmon resonance, f = 2.46 THz, \(\mu_{c}=1eV\). We take the parameters of the structure so that only one dominant eigenwave of dielectric waveguide can propagate. The results are presented for the first plasmon resonance P1 for \(\mu_{c}=0.3eV\) and \(\mu_{c}=1eV\) as well as for the resonance N12. If the parameters of the structure correspond to the plasmon resonance, amplitude of the main lobe reaches its maximum. The strong dependence of the graphene conductivity on the chemical potential allows to tune the antenna resonant frequency and the main lobe magnitude.

Fig. 10
figure 10

Normalized radiation patterns for various values of the chemical potential and frequency, \(\mu_{c}=0.1\)eV (shot-dotted lines), \(\mu_{c}=0.3\)eV (dashed lines), \(\mu_{c}=0.6\)eV (solid lines), \(\mu_{c}=1\)eV (dotted lines), \(\begin{aligned}h & =50\;\mu{m}, d=10\;\mu{m}, l=70\mu{m},\varepsilon =2.25,\;T=300K,\tau=1\end{aligned}\)ps, dominant mode, p = 1. a Plasmon resonance frequency f = 1.5 THz for \(\mu_{c}=0.3\)eV; b plasmon resonance frequency f = 2.46 THz for \(\mu_{c}=1\)eV; c  N12 resonance frequency f = 3.34THz  (Created in OriginPro 2015)

Full size image

Despite the large reflection near the resonances of natural waves of periodic structure Nqi for practical applications, resonances with even indexes can be interesting. Near N12, in-phase excitation of currents on strips is observed. As a result, the angle of the main lobe of the radiations pattern is 90°. As we mentioned above, the position of resonances Nqi does not depend on the parameters of graphene strips. However, the amplitude of the main lobe here can be controlled by variation of the chemical potential.

As it is usual for the radiating periodic structures, the considered structure shows the frequency-scanning ability. The angle of the main lobe mostly depends on the normalized period kl. Fig. 11 demonstrates the diffraction patterns with the frequency-dependent main lobe angle for the same value of the chemical potential \(\mu_{c}=1eV\).

Fig. 11
figure 11

Normalized radiation patterns for various values of the frequency, f = 2.3THz (shot-dotted lines), f = 2.46 THz (dashed lines), f = 2.7 THz (solid lines), f = 3.2 THz (dotted lines) \(\mu_{c}=1\) eV;\(\begin{aligned}h & =50\;\mu{m}, d=10\;{um}, l=70\mu{m},\varepsilon =2.25,\;T=300K,\tau=1\end{aligned}\)ps, N = 10 , dominant mode, p = 1  (Created in OriginPro 2015)

Full size image

The possibility of independent biasing each strip gives additional degrees of freedom. In antenna design, it is required that the radiation pattern has the lowest side-lobe level. By variation of the chemical potential of every individual strip in the array, we are going to reduce the side-lobe level. The results are presented in Figs. 12 and 13 for two values of frequency, f = 2.7THz and f = 3 THz. The values of the strip width and period are the same. Our purpose is to obtain the side-lobe level less that -20 dB. As seen, the actual side-lobe level is in good agreement with the desired one. The values of the chemical potential are given in Table 1. We used the gradient descent algorithm, 150 iterations. A total of -20 dB angular width of the main lobe of the obtained radiation pattern is about 25° for f = 2.7 THz and about 20° for f = 3 THz. The radiation pattern for constant value of the chemical potential \(\mu_{c}=1eV\) is also presented for comparison.

Fig. 12
figure 12

Normalized radiation patterns for constant value of the chemical potential on every strip \(\mu_{c}=1\)eV (solid line) and for different values of the chemical potential on every strip (dotted line), f = 2.7 THz,\(\begin{aligned}h & =50\;\mu{m}, d=10\;\mu{m}, l=70\mu{m},\varepsilon =2.25,\;T=300K,\tau=1\end{aligned}\) ps, N = 10, dominant mode, p = 1  (Created in OriginPro 2015)

Full size image
Fig. 13
figure 13

Normalized radiation patterns for constant value of the chemical potential on every strip μc=1eV (solid line) and for different values of the chemical potential on every strip (dotted line), f = 3 THz, \(\begin{aligned}h & =50\;\mu{m}, d=10\;\mu{m}, l=70\mu{m},\varepsilon=2.25,\;T=300K,\tau=1\end{aligned}\)ps, N = 10, dominant mode, p = 1  (Created in OriginPro 2015)

Full size image
Table 1 Values of the chemical potential of graphene strips
Full size table

Conclusion

We have studied the scattering of eigenwaves of the planar dielectric waveguide by graphene strip grating in the range from 1 to 4 THz. The scheme of solution is based on the mathematically grounded and effective method of singular integral equations with the discretization by the Nystrom-type algorithm. It provides the controllable accuracy of the solution. The calculation time of one curve in Figs.10-12 is about 10 s.

The behaviour of the scattering characteristics of the structure has clear resonant nature. The radiated power and main lobe magnitude is maximal near the plasmon resonances. Variation of the chemical potential allows to tune the resonant frequency and radiated power. Near the resonance of natural waves of periodic part of the structure, the main lobe is perpendicular, but the reflection is high. Every individual graphene strip in the array can be biased separately. In this way, we reduce the side-lobe level.

We believe that presented results can be potentially used in designing of leaky-wave graphene antennas.