Introduction

Graphene has become the most fascinating research area in science and technology in present days because of its several unique properties [1,2,3] and potential applications [4,5,6,7]. One important property of graphene is that all its Dirac electrons, irrespective of their energy, have same speed, as energy versus momentum relation is linear. Graphene localizes electron motion in a plane with very small electron effective mass giving rise to high in-plane conductivity. The special spectrum of the charge carriers leads to a number of interesting transport properties.

In many cases it is desirable to tightly confine the probing radiation like as surface plasmons (SPs). SPs are guided electromagnetic modes, propagate along the surface between a conductor and a dielectric or conductor and air with their field amplitude peaking at the interface and falling off exponentially away from it in either medium [8,9,10,11]. It also has been shown that in a noble metal film, SPs can be used to generate light radiation [12].

Moreover, graphene surface plasmons (GPs) have many advantages over metal film SPPs because the conductivity and permittivity of graphene can be controlled by adjusting external gate voltage, chemical doping, etc. The graphene GPs have the properties of extremely high confinement and low Ohmic loss because of their high carrier mobility at room temperature [13,14,15]. The 2D nature of graphene also gives rise to plasmons with wavelengths that are substantially smaller than free-space electromagnetic radiation of the same frequency by approximately two orders of magnitude, generating large non-local effects. Graphene plasmon is used for making the radiation source with two infrared–visible–ultraviolet range, by using low-energy electrons that may conceivably be generated in an on-chip device [16].

The difference frequency generation (DFG) at mid-infrared in graphene is enhanced due to the presence of plasmon resonance [17,18,19]. Such an all-optical coupling scheme for plasmon generation in graphene holds great promise, for example, in the design of plasmon sensors or new THz sources. The generation of THz SPs via the nonlinear mixing of lasers in planar structure comprises a dielectric plate coated on top with an ultrathin metal film with suitable ripple is also studied [16]. The metal has larger loss and low confinement of SPs due to low carrier mobilities, surface roughness, grain microstructure and impurities [20], and the large electronic density of states compared with GPs at THz frequencies [13, 14].

The most important topics in graphene applications is to generate terahertz (THz) radiation, for that the plasmon frequency in graphene lies in the 1–50 THz frequency regime 21. The coherent and tunable THz radiation can be generated from SPs excited by a moving electron beam atop multilayer graphene deposited on a substrate [21]. Various approaches have been proposed and investigated to generate THz radiation [22, 23]. However, developing high powered and tunable THz radiation sources remains a significant challenge. Several works demonstrated that graphene plasmonics could be a promising candidate for developing coherent and tunable THz sources with high power density.

In this paper, we proposed a scheme of THz SP generation via the nonlinear mixing of lasers in the graphene sheet which is deposited on glass substrate. The structure supports highly confined THz SPs with weak attenuation. Two laser beams obliquely incident, from free space on the graphene sheet. These laser beams impart oscillatory velocities to electrons and exert a difference frequency ponderomotive force on the free electrons of the graphene film, the latter beats with the carrier density to produce a nonlinear current that excites THz GSPs at difference frequency in graphene. The novelty of this scheme is that this structure is ripple free structure and phase matching condition is satisfied automatically.

In “Surface Plasmon Dispersion Relation in Graphene,” we derive the dispersion relation for graphene plasmons. The “Non-linear  Mixing of Two Laser Beams and THz GSP Excitation in Graphene” section is devoted to THz GP excitation by nonlinear mixing, and the “Discussion” section discussed the results.

Surface Plasmon Dispersion Relation in Graphene

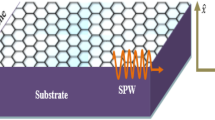
Consider a glass substrate of relative permittivity \({\varepsilon }_{d}\) occupying half space \(x \le 0\) (cf. Fig. 1). The region \({\text{x}} > {\text{d}}\)is free space. A monolayer graphene of conductivity \(\sigma_{g}\) is deposited on it. The conductivity is a function of thickness and given by

$$\sigma = \sigma_{{\text{g}}} \delta \left( x \right)$$
(1)
Fig. 1
figure 1

A monolayer of graphene is deposited on glass substrate

Full size image

and the current density in graphene layer may be defined as

$$J_{z} = \sigma \,E_{z}$$
(2)

Consider a SPs propagate (Fig. 1) along \(\hat{z}\) as with t-z variations as \({\text{exp[ - }}i{(}\omega \,t{ - }k_{z} z{)}]\). The electric and magnetic fields of the SPs in different regions can be written as

x > 0 (Vacuum)

$${\vec{\text{E}}}\left( {x{,}z{,}t} \right) = A_{{}} {(}\hat{z} + \frac{{ik_{z} }}{{\alpha_{I} }}\hat{x}{\text{)exp( - }}\alpha_{{\text{I}}} x)\exp \left[ { - i\left( {\omega t - k_{z} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z} } \right)} \right]$$
(3)
$$\vec{H}_{{y{\text{I}}}} = \frac{{i\omega \varepsilon_{0} }}{{\alpha_{{\text{I}}} }}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} {\text{ A exp( - }}\alpha_{{\text{I}}} x)\exp \left[ { - i\left( {\omega t - k_{z} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z} } \right)} \right]$$

x < 0 (dielectric)

$$\vec{E}\left( {x,z,t} \right) = A_{{}} {(}\hat{z} - \frac{{ik_{z} }}{{\alpha_{{{\text{II}}}} }}\hat{x}{\text{)exp(}}\alpha_{{{\text{II}}}} x{)}\exp \left[ { - i\left( {\omega t - k_{z} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z} } \right)} \right]$$
(4)
$$\vec{H}_{{y{\text{II}}}} = - \frac{{i\omega \varepsilon_{0} \varepsilon_{d} }}{{\alpha_{{{\text{II}}}} }}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y}{{\text A exp}}\left( {\alpha_{{{\text{II}}}} x} \right)\exp \left[ { - i\left( {\omega t - k_{z} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z} } \right)} \right]$$

where \(a_{{\text{I}}} = {(}k_{z}^{{2}} - \omega^{{2}} {/}c^{{2}} {)}^{{1/2}}\) and \(a_{{{\text{II}}}} = {(}k_{z}^{2} - {(}\omega^{{2}} {/}c^{{2}} {)}\varepsilon_{d} {)}^{{1/2}}\) are known as the decay constants in free space and dielectric, respectively, [7,8,9] and \(k_{z}\) is propagation constant of SPs. Using jump condition on \({\vec{\text{H}}}_{{}}\)at x = 0), \(\oint {\vec{H} \times \vec{d}l} = \int {\vec{J} \times d\vec{s} + \int {\frac{{\partial \vec{D}}}{\partial t}} } \times d\vec{s}\) one may get

$$\vec{H}_{{{\text{yI}}}} - H_{yII} = \sigma_{g} \int {\delta (x)} E_{z} dx$$
$${\vec{\text{H}}}_{{{\text{yI}}}} - {\rm H}_{yII} = \sigma_{g} \left. {{\rm E}_{z} } \right|_{x = 0}$$
(5)

Putting Eqs. (3) and (4) into Eq. (5), one may get

$$\frac{1}{{\left( {k_{z}^{2} - \frac{{\omega^{2} }}{{c^{2} }}} \right)^{1/2} }} + \frac{{\varepsilon_{d} }}{{\left( {k_{z}^{2} - \frac{{\omega^{2} }}{{c^{2} }}\varepsilon_{d} } \right)^{1/2} }} = \frac{{N_{0} e^{2} }}{{\omega^{2} \varepsilon_{0} m^{*} }}$$
(6)

Eq. (8) gives the SP dispersion relation in graphene, where \(m^{*}\) is the effective mass of electron and is given by \({\text{m}}^{*} = \varepsilon_{F} {/}v_{F}^{{2}}\), \(v_{F}\) is the Fermi velocity of electron \(( \approx {10}^{{8}} {\text{cm/sec)}}\), and \(N_{0}\) is the free electrons surface density in graphene. In Fig. 2, we have plotted normalized \(\left( {\omega /\omega_{p} } \right)\) versus normalized (\(k_{z} c/\omega_{p}\)) for the SPs for typical parameters: \(v_{F} /c = 1/300\), \(\varepsilon_{d} = 2.5\). The figure shows that at low frequency \(\omega\) varies linearly with \(k_{z}\). However, at higher frequencies it varies gradually, because there is a week coupling between lasers and graphene plasmons.

Fig. 2
figure 2

Dispersion relation of graphene plasmons

Full size image

Non-linear Mixining of Two Laser Beams and THz GSPs Excitation in Graphene

Consider two lasers which are y-polarized and incident on a graphene sheet deposited on a dielectric substrate (cf. Fig. 3), the laser beams may be written as

$$\vec{E}_{{1}} = \hat{y}A_{{1}} {\text{exp[}} - i\,(\omega_{{1}} t - k_{{{1}x}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} - k_{{{1}z}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z} {)]}$$
(7)
$$\vec{E}_{{2}} = \hat{y}A_{{2}} {\text{exp[}} - i{(}\,\omega_{{2}} t - k_{{{2}x}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} - k_{{{2}z}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{z} {)]}$$
(8)
Fig. 3
figure 3

Two laser beams obliquely incident from free space on the graphene sheet

Full size image

The phase matching conditions demands that

$${\omega }_{\mathrm{SPTHz}}={\omega }_{1}-{\omega }_{1} , {k}_{\mathrm{SPTHz}}={k}_{1}-{k}_{2}$$
(9)

The lasers impart oscillatory velocities to the electrons, given as

$${\overrightarrow{v}}_{1}=\frac{e{\overrightarrow{E}}_{1}}{mi{\omega }_{1}}{T}_{A} , { \overrightarrow{v}}_{2}=\frac{e{\overrightarrow{E}}_{2}}{mi{\omega }_{2}}{T}_{A}$$
(10)

Here, we consider the transmission coefficient of two laser beams being same and taking into account the transmission effect. These laser beams also impart a ponderomotive force on electrons at beat frequency, so the force is given by

$${\vec{{F}}}_{{{p}}} = - \frac{{{e}}}{{2}}{{(\vec{v}}}_{{1}} \times {\vec{{B}}}_{{2}}^{ * } + {\vec{{v}}}_{{2}}^{ * } \times {\vec{{B}}}_{1} )$$
(11)

The z component of Eq. (11) may be written as

$$F_{pz} = - \frac{m}{{2}}i {(}k_{iz} - k_{{{2}z}} {) }\vec{v}_{{1}} .\vec{v}_{{2}}^{*}$$
(12)

The ponderomotive force also imparts oscillatory velocity to electrons at frequency \(\left( {\omega_{{1}} - \omega_{{2}} } \right)\)and may be written as

$$\vec{v}_{{\left( {\omega_{{1}} - \omega_{2} } \right)}} = \frac{{ - \vec{F}_{p} }}{{mi{ (}\omega_{{1}} - \omega_{{2}} {)}}}$$
(13)

the nonlinear current may be written as

$$\vec{J}_{\omega }^{{{\text{NL}}}} = - \hat{z}n_{{0}} e\frac{{{(}k_{{{1}z}} - k_{{{2}z}} {)}}}{{{2(}\omega_{{1}} - \omega_{{2}} {)}}}\vec{v}_{{1}} {.}\vec{v}_{{2}}^{ * } \cong \hat{z}\:F d{\text{ exp[ - }}i{(}\omega t{ - }k_{{{\text{TH}}}} z)]\delta (x)$$
(14)

where

$$F = - \, n_{{0}}^{{0}} \, e\frac{{{(}k_{{{1}z}} - k_{{{2}z}} {)}}}{4\omega } \, \frac{{e^{{2}} A_{1} A_{2} }}{{m^{{2}} \omega_{1} \omega_{2} }}\left| {T_{A} } \right|^{2}$$
(15)

where \(T_{A} = 2/{1} + \frac{{\varepsilon_{g} (\omega /c)\cos \theta_{i} }}{{k_{{{1}\;{\text{THz}}}} }}\) is transmission coefficient, \({\text{k}}_{{{1}\;{\text{THz}}}} = \sqrt {\frac{{\omega^{2} }}{{c^{2} }}\varepsilon_{g} - \frac{{\omega^{2} }}{{c^{2} }}\sin^{2} \theta_{i} }\). The nonlinear current density manifests itself in the jump condition on \(\vec{H}_{y}\) of the SPs, i.e.,

$$\left. {H_{y} } \right|_{{x = {0}^{ + } }} - \left. {H_{y} } \right|_{{x = {0}^{ - } }} = \sigma_{g} d\left. {E_{z} } \right|_{{x = {0}}} + Fd{\text{ exp[}} - i{(}\omega \,t - k_{{{\text{THz}}}} z{)]}$$
(16)

Substituting Eqs. (3) and (4) into Eq. (16), we get

$$\left\{ {\frac{1}{{\alpha_{I} }} + \frac{{\varepsilon_{d} }}{{\alpha_{II} }} + \frac{{\sigma_{g} d}}{{i\omega \varepsilon_{0} }}} \right\}A = \frac{Fd}{{i\omega \varepsilon_{0} }} \cong - i\frac{Fd}{{\omega \varepsilon_{0} }}$$
(17)

Equation (17) can be written as

$$DA = - i\frac{Fd}{{\omega \varepsilon_{0} }}$$
(18)

where

$$\frac{1}{{\alpha_{I} }} + \frac{{\varepsilon_{d} }}{{\alpha_{II} }} + \frac{{\sigma_{g} d}}{{i\omega \varepsilon_{0} }} = D$$
(19)

At exact phase matching D vanishes. However, due to finite length of interaction \(L = 2r_{0}\) where \(r_{0}\) = laser spot size so D can be replaced by region \(D \cong - i(\partial D/\partial k_{z} )(\partial /\partial z)\), Eq. (19) can be written as

$$\frac{\partial D}{{\partial k_{z} }} = - k_{z} \left( {\frac{1}{{\left( {k_{z}^{2} - \frac{{\omega^{2} }}{{c^{2} }}} \right)^{3/2} }} + \frac{{\varepsilon_{d} }}{{\left( {k_{z}^{2} - \frac{{\omega^{2} }}{{c^{2} }}\varepsilon_{d} } \right)^{3/2} }}} \right)$$
(20)

If there is free electron collision, the SP has a finite imaginary part in \(k_{z}\),\(k_{z} = k_{zr} + ik_{zi}\), and \(D \cong - i(\partial D/\partial k_{z} )\left( {\partial /\partial z + k_{i} } \right)\), putting in Eq. (18), one may get

$$\frac{{\partial A_{0} }}{\partial z} + k_{i} A_{0} = \frac{{Fd/\omega \varepsilon_{0} }}{{\partial D/\partial k_{z} }}$$
(21)

For interaction length \(L \approx 2r_{0} > 1/k_{i}\) (attenuation length), \(A_{0} = \left( {Fd/\omega \varepsilon_{0} } \right)/k{}_{i}\left( {\partial D/\partial k_{z} } \right)\) and for interaction length \(L < 1/k_{i}\) (attenuation length) \(A_{0} = \left( {FdL/\omega \varepsilon_{0} } \right)/\left( {\partial D/\partial k_{z} } \right)\), we get

$$A_{0} = \frac{{n_{0}^{0} e}}{4\omega }(k_{1z} - k_{2z} )\frac{{e^{2} A_{1} A_{2} }}{{m^{2} \omega_{1} \omega_{2} }}\left| {T_{A} } \right|^{2} \frac{dL}{{\omega \varepsilon_{0} \left\{ {k_{z} \left( {1/\alpha_{I}^{3/2} + \varepsilon_{d} /\alpha_{II}^{3/2} } \right)} \right\}}}$$
(22)

Solving and rearranging the terms in Eq. (22), we get

$$\frac{{A_{0} }}{{A_{1} }} = \frac{1}{{\left( {\omega /\omega_{p} } \right)}}\left( {\frac{\omega }{{4\omega_{1} }}} \right)(\frac{{k_{1z} - k_{2z} }}{{k_{Z} }})\frac{{\left| {v_{2} } \right|}}{c}\left| {T_{A} } \right|^{2} \frac{{(d\omega_{p} /c)(L\omega /c)}}{{1/(k_{z}^{2} c^{2} /\omega^{2} - 1)^{3/2} + \varepsilon_{d} /(k_{z}^{2} c^{2} /\omega^{2} - \varepsilon_{d} )^{3/2} }}$$
(23)

Equation (23) gives the ratio of terahertz graphene plasmons to the amplitude of laser beam, where \(\nu_{2}\) is the oscillatory velocity of electron, c is the speed of light, \(\omega\) and \(\omega_{1}\) are the frequencies of incident laser beams, \(d\omega_{p} /c\) is the normalized thickness, and \(L\omega /c\) is the normalized length of interaction. We have plotted Eq. (23) for the following parameters corresponding to modest laser intensity ~ 1012 W/cm2 at \({1}{\mu m}\) wavelength [19]:\(\nu_{2} = 10^{6} \;{\text{m/s}}\), \(c = 3 \times 10^{8} \;{\text{m/s}}\), \(\varepsilon_{d} = 2.5\), \(k_{z}^{2} c^{2} /\omega^{2} = 2.6\), \(\omega \approx 10^{13} \;rad/s\), \(\omega_{1} \approx 2 \times 10^{12} \;rad/s\), \(\omega_{p} \approx 2.5 \times 10^{12} \;rad/s\),\(d\omega_{p} /c \approx 10^{ - 2}\), \(L\omega /c \approx 10\), and \(\left| {T_{A} } \right| \approx 97\%\). As the terahertz frequency and thickness are raised, the amplitude falls monotonically (cf. Fig. 4) because at higher frequency and large thickness, the coupling between graphene SPs and laser is weak.

Fig. 4
figure 4

Normalized THz SP amplitude variation with normalized frequency for two different normalized thickness

Full size image

Discussion

In the conclusion, we studied the promise of producing THz SPs at difference frequency in graphene sheet by using nonlinear mixing of two laser beams, which have frequency difference in THz range at modest power lasers. The nonlinearity arises through the ponderomotive force. The THz SPs are strongly localized near around the graphene sheet and propagate at long distance along the interface. The attenuation of THz SP in graphene is weak because they are highly localized and efficiently excited by modest laser power ~ 1012 W/cm2. The ratio of THz SP field amplitude and laser amplitude is of the order ~ 10–4 at laser intensity ~ 1012 W/cm2 at \(1\sim\mu \mathrm{m}\) wavelength. The efficiency has been upper bound given by Manley -Rowe relations. This scheme will be useful for making the THz radiation source for future applications.