Resonant Enhancement of THz Radiation Through Vertically Aligned Carbon Nanotubes Array by Applying Wiggler Magnetic Field

Abstract

The present analysis develops a novel theory of terahertz radiation generation by beating of two laser beams, incident obliquely on the array of vertically aligned carbon nanotubes (CNTs) in the presence of an external wiggler magnetic field. The array of CNTs behaves as nanoantenna to generate THz radiations. The incident lasers exert a ponderomotive force on the electrons of the CNTs to produce nonlinear oscillatory velocity, which beats with the applied wiggler magnetic field. This beating produces a nonlinear current at (ω₂ − ω₁, k₂ − k₁ + k₀) which acts as an antenna to produce the THz radiation. We observe that when the beat frequency (ω₂ − ω₁) lies near the effective plasmon frequency of the CNTs, strong THz radiation is produced due to a resonant interaction of the laser with CNT electrons. The externally applied wiggler magnetic field enhances the efficiency of THz radiation of nanoantenna by providing the necessary momentum to the generated THz radiation. We explore the impact of radius and length of nanotubes on the efficiency of THz generation. The generated THz power is enhanced at an optimum angle of incidence of lasers with an array of CNTs.

Introduction

One of the most challenging tasks of researchers of nanoelectronics is to create a compact and efficient source of terahertz (THz) radiation due to its wide-ranging applications in science and technology. Among the various recent techniques of THz technology, the use of carbon nanotubes (CNTs) as the THz radiation source is very effective and reliable due to their nanoscale dimensions. CNTs are cylindrical carbon molecules having diameter in nanometers and length in micrometers [1, 2]. Due to their compact size and exceptional combination of transverse and longitudinal dimensions, CNTs gain popularity in the field of nanoelectronics for the development of sensors, electronic components, THz optoelectronics devices, and THz antennas, etc. Among these, THz radiation sources have a number of applications in remote sensing, biomedical imaging and tomography, defense, semiconductors characterization, material detection, high-field condensed matter studies, short-distance wireless communications and sensing, and explosives detections [3,4,5,6,7].

Researchers have proposed a variety of schemes to generate THz radiations by employing carbon nanotubes and nanostructures. A metallic nanostructured surface was employed by Welsh and Wyne [8] to generate ultrafast THz radiations with the help of excitation of surface plasmon. THz radiations on either side of a gold-coated nanograting of nanometer dimensions, using a 785-mm, 150-ps, 1-kHz Ti:sapphire laser, have been successfully reported by Garwe et al. [9]. Dragomon and Dragomon [10] have proposed a technique to produce THz radiation from a resonant tunneling diode based on semiconducting CNTs. Their simulation results show that the output power generated from semiconducting CNTs is greater by one order of magnitude than that of emitted using semiconductor heterostructures. The optical rectification of laser in an array of carbon nanotubes has been introduced in order to study THz radiation generation by Parashar and Sharma [11]. THz generation during laser interaction with an array of cylindrical carbon nanotubes, lying on a metallic surface under the effect of static magnetic field was analyzed by Jain et al. [12]. In the presence of laser a ponderomotive force is experienced by the free electrons of the nanotubes, which results in introducing a current density at twice the modulation frequency. These oscillating nanotube arrays play the role of antennas to generate THz radiation. THz generation by the beating of two Gaussian laser beams, in a medium containing conducting nanoparticles, was studied by Javan and Erdi [13]. They came to conclusion that composite of graphite nanoparticles is good for the generation of THz radiations, as one of plasmon resonance frequencies lies in the THz range. THz generation via laser coupling to the anharmonic carbon nanotube array was studied by Sharma and Vijay [14]. They introduce a model for nonlinear absorption and THz generation of the laser embedded with hollow CNT electrons and is treated as a nonlinear function of displacement and collisions. Large resonance absorption is shown during CNT response to the laser as the execution of restoration force on electron decreases.

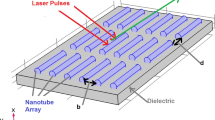
In the present analysis, we propose a model for THz radiation generation by the interaction of intense laser beams with a vertically aligned array of carbon nanotubes grown on metal surface. Laser absorption is strongly enhanced due to the presence of nanoparticles or nanoscaled carbon tubes on metallic surface [15]. The periodic and random arrays of single-walled carbon nanotubes (SWCNTs) are synthesized on metal substrate by employing plasma-enhanced chemical vapor deposition (PECVD) technique. Two similar laser beams with slightly different frequencies of ω₁ and ω₂ are obliquely incident on the array of CNTs. Electric fields of the incident lasers exert ponderomotive force on the free electrons of the nanotubes which produces a nonlinear oscillatory velocity. This oscillatory velocity beats with an applied wiggler magnetic field to produce a macroscopic electron current at the beat frequency (ω₂ − ω₁), which generates THz radiation.

The theoretical considerations of nonlinear current density and the THz radiation generation are presented in “Theoretical Consideration.” The observations are discussed in “Observations and Discussion.” The last section is devoted to the conclusion of the present scheme.

Theoretical Consideration

Consider a metal surface over which vertical array of single-walled carbon nanotubes (SWCNTs) of radius r_c, length l_c, is mounted. Vertically aligned array means that the nanotubes are grown along z-direction, perpendicular on the metallic surface in the x-y plane (refer to Fig. 1). There are N tubes per unit area and a = 1/N² is the inter-tube separation. Two plane-polarized lasers of frequencies ω₁ and ω₂ are obliquely incident on nanotubes at an angle θ. The electric and magnetic fields of these lasers can be represented as follows:

$$ {\displaystyle \begin{array}{l}{\overrightarrow{E}}_j=\left(\widehat{z}\cos \theta -\widehat{x}\sin \theta \right){A}_j{e}^{-i\left[{\omega}_jt-{k}_j\right(z\sin \theta +x\cos \theta \Big]},\\ {}\end{array}} $$

(1)

$$ {\overrightarrow{B}}_j=\frac{c\;\left({\overrightarrow{k}}_j\times {\overrightarrow{E}}_j\right)}{\omega_j} $$

(2)

where ${A}_j={A}_{j0}{e}^{-\left(y-{l}_c\right)/{r}_{jo}}$ is the amplitude of laser, ${k}_j={\omega}_j/c\sqrt{\varepsilon_l-{\omega}_p^2/{\omega}_j^2}$ is the propagation constant, ω_p = (4πn₀e²/m)^1/2 is the plasma frequency of electrons inside a nanotube, n₀ is the free electron density inside a nanotube, ε_l is relative permittivity of the lattice, c is the velocity of light in free space, r_jois the initial beam radius, e and m are the electronic charge and mass respectively. A wiggler magnetic field ${\overrightarrow{B}}_W={B}_0\;{e}^{{\mathrm{ik}}_0\left(z\sin \theta +x\cos \theta \right)}\widehat{y},$ is applied on the array of CNTs along y-direction, where k₀ is the wave number of the wiggler magnetic field.

Fig. 1

Schematic representation for THz radiation generation from the array of vertically aligned carbon nanotubes (CNTs) in the presence of an external wiggler magnetic field

The lasers ionize the atoms of nanotubes to provide oscillatory velocity ${\overrightarrow{v}}_j$ to the electrons of nanotubes, which is governed by the following equation of motion:

$$ m\frac{d{\overrightarrow{v}}_j}{\mathrm{dt}}=-e{\overrightarrow{E}}_j-\frac{e}{c}\left({\overrightarrow{v}}_j\times {\overrightarrow{B}}_W\right)-\frac{m{\omega}_p^2\widehat{z}}{2{\varepsilon}_l}\int {v}_{\mathrm{jz}}\mathrm{dt}. $$

(3)

The x- and z-components of this oscillatory velocity ${\overrightarrow{v}}_j$can be obtained as follows:

$$ {v}_{jx}=-\frac{ie{A}_j}{m}\left[\frac{-\sin \theta }{\omega_j}+\frac{i\cos \theta {\omega}_c-\sin \theta {\omega}_c^2/{\omega}_j}{\omega_j^2-{\omega}_c^2-{\omega}_p^2/2{\varepsilon}_l}\right] $$

(4)

$$ {v}_{jz}=\frac{e{A}_j}{m}\left[\frac{\sin \theta {\omega}_c-i\cos \theta {\omega}_j}{\omega_j^2-{\omega}_c^2-{\omega}_p^2/2{\varepsilon}_l}\right] $$

(5)

where ω_c = eB₀/mc is the cyclotron frequency. The above velocity beats with wiggler magnetic field to apply ponderomotive force on the electrons of a CNT, which can be written as follows:

$$ {\displaystyle \begin{array}{l}{\overrightarrow{F}}_{\mathrm{pj}}=\frac{-e}{2c}\left({\overrightarrow{v}}_j\times {\overrightarrow{B}}_w\right)=\frac{-{e}^2{B}_0{A}_j{e}^{{\mathrm{ik}}_0\left[z\sin \theta +x\cos \theta \right]}{e}^{-i\left[{\omega}_jt-{k}_j\left(z\sin \theta +x\cos \theta \right)\right]}}{2\;\mathrm{cm}}\times \\ {}\left[\frac{\left(i\sin \theta {\omega}_j^2-i\sin \theta {\omega}_p^2/2{\varepsilon}_l+\cos \theta {\omega}_j{\omega}_c\right)\widehat{z}}{\omega_j\left({\omega}_j^2-{\omega}_c^2-{\omega}_p^2/2{\varepsilon}_l\right)}+\frac{\widehat{x}\left(-\sin \theta {\omega}_c+i\cos \theta {\omega}_j\right)}{\left({\omega}_j^2-{\omega}_c^2-{\omega}_p^2/2{\varepsilon}_l\right)}\right].\end{array}} $$

(6)

The oscillatory velocity due to this ponderomotive force at (ω_j, k_j + k₀) is as follows:

$$ {\overrightarrow{v}}_{\omega j}^{\prime }=\frac{i{\overrightarrow{F}}_{\mathrm{pj}}{\omega}_j}{m\left({\omega}_j^2-{\omega}_p^2/2{\varepsilon}_l\right)} $$

(7)

The ponderomotive force on the electrons of a CNT at (ω₂ − ω₁) and (k₂ − k₁ + k₀) is as follows:

$$ {\overrightarrow{F}}_{p\left({\omega}_2-{\omega}_1\right)}=\frac{-e}{2c}\left[{\overrightarrow{v}}_{\omega 2}^{\prime}\times {\overrightarrow{B}}_{\omega_1}^{\ast }+{\overrightarrow{v}}_{\omega_1}^{\prime \ast}\times {\overrightarrow{B}}_{\omega_2}\right]=-\frac{{\mathrm{iek}}_1{\omega}_2{E}_1^{\ast}\left({F}_{p2x}\hat{z}-{F}_{p2z}\hat{x}\right)}{2{\omega}_1m\left({\omega}_2^2-{\omega}_p^2/2{\varepsilon}_l\right)}-\frac{{\mathrm{iek}}_2{\omega}_1{E}_2\left({F}_{p1x}^{\ast}\hat{z}-{F}_{p1z}^{\ast}\hat{x}\right)}{2{\omega}_2m\left({\omega}_1^2-{\omega}_p^2/2{\varepsilon}_l\right)}. $$

(8)

The nonlinear velocity ${v}_{\left({\omega}_2-{\omega}_1\right)}^{\mathrm{NL}}$ due to this ponderomotive force at (ω₂ − ω₁, k₂ − k₁ + k₀) is as follows:

$$ {\overrightarrow{v}}_{\left({\omega}_2-{\omega}_1\right)}^{\mathrm{NL}}=\frac{i{\overrightarrow{F}}_{p\left({\omega}_2-{\omega}_1\right)}\left({\omega}_2-{\omega}_1\right)}{m\left({\left({\omega}_2-{\omega}_1\right)}^2-{\omega}_p^2/2{\varepsilon}_l\right)}. $$

(9)

The nonlinear current density on the electrons of a CNT at (ω₂ − ω₁)is as follows:

$$ {\overrightarrow{J}}_{\omega}^{\mathrm{NL}}=-{n}_0e{\overrightarrow{v}}_{\left({\omega}_2-{\omega}_1\right)}^{\mathrm{NL}}=\frac{\omega_c{\omega}_p^2 e\omega {A}_1^{\ast }{A}_2{e}^{-i\left[\omega t-k\left(z\sin \theta +x\cos \theta \right)\right]}\left({\alpha}_1\widehat{x}+{\alpha}_2\widehat{z}\right)}{16 m\pi \left({\omega}^2-{\omega}_p^2/2{\varepsilon}_l\right)} $$

(10)

where ω = ω₂ − ω₁, $k={k}_2-{k}_1+{k}_0,{\displaystyle \begin{array}{l}{\alpha}_1=\frac{-i\sin \theta {\omega}_2^2{k}_1+i{k}_1\sin \theta {\omega}_p^2/2{\varepsilon}_l-\cos \theta {\omega}_c{\omega}_2{k}_1}{\omega_1\left({\omega}_2^2-{\omega}_p^2/2{\varepsilon}_l\right)\left({\omega}_2^2-{\omega}_c^2-{\omega}_p^2/2{\varepsilon}_l\right)}+\frac{-i\sin \theta {\omega}_1^2{k}_2+i\sin \theta {\omega}_p^2{k}_2/2{\varepsilon}_l-{\omega}_1{\omega}_c{k}_2\cos \theta }{\omega_2\left({\omega}_1^2-{\omega}_p^2/2{\varepsilon}_l\right)\left({\omega}_1^2-{\omega}_c^2-{\omega}_p^2/2{\varepsilon}_l\right)},\\ {}{\alpha}_2=\frac{i\cos \theta {\omega}_2^2{k}_1-\sin \theta {\omega}_c{\omega}_2{k}_1}{\omega_1\left({\omega}_2^2-{\omega}_p^2/2{\varepsilon}_l\right)\left({\omega}_2^2-{\omega}_c^2-{\omega}_p^2/2{\varepsilon}_l\right)}+\frac{i\cos \theta {\omega}_1^2{k}_2-{\omega}_1{\omega}_c{k}_2\sin \theta }{\omega_2\left({\omega}_1^2-{\omega}_p^2/2{\varepsilon}_l\right)\left({\omega}_1^2-{\omega}_c^2-{\omega}_p^2/2{\varepsilon}_l\right)}.\end{array}}$

The nonlinear current density is finite over the cross-sectional area of a CNT and zero for the area between the tubes, (which is a²). So, the average THz current density due to the array of CNTs can be written as follows:

$$ {\overrightarrow{J}}_{\omega_{\mathrm{av}.}}^{\mathrm{NL}}=\frac{\omega_c{\omega}_p^2 e\omega {r}_c^2{\mathrm{NA}}_{10}^{\ast }{A}_{20}{e}^{-i\left[\omega t-k\left(z\sin \theta +x\cos \theta \right)\right]}{e}^{-{\left(y-{l}_c\right)}^2/{r}_0^2}}{16m\left({\omega}^2-{\omega}_p^2/2{\varepsilon}_l\right)}\left({\alpha}_1\widehat{x}+{\alpha}_2\widehat{z}\right) $$

(11)

Since the CNTs are fabricated on the metallic surface, so there will be an image current density below the metallic surface, which can be denoted as ${\overrightarrow{J}}_{\omega_{av.}}^{N{L}^{\prime }}$ and is equal and opposite to ${\overrightarrow{J}}_{\omega_{\mathrm{av}.}}^{\mathrm{NL}}$ .

The vector potential at a far point $\overrightarrow{r}\left(r,{\theta}^{\prime },\phi \right)$because of the current distribution of the array of x and z dimensions of l × l is as follows:

$$ \overrightarrow{A}\left(r,t\right)=\frac{\mu_0}{4\pi}\left[\int \frac{{\overrightarrow{J}}_{w_{\mathrm{av}.}}^{\mathrm{NL}}\left({\overrightarrow{r}}^{\prime },t-R/c\right)d{V}^{\prime }}{R}+\int \frac{{\overrightarrow{J}}_{w_{\mathrm{av}.}}^{{\mathrm{NL}}^{\prime }}\left({\overrightarrow{r}}^{\prime },t-R/c\right)d{V}^{\prime }}{R}\right] $$

(12)

where $R=\mid \overrightarrow{r}-{\overrightarrow{r}}^{\prime}\mid \approx r\left(1-\overrightarrow{r}.{\overrightarrow{r}}^{\prime }/{r}^2\right)=r-\sin\;{\theta}^{\prime}\cos\;\phi {x}^{\prime }-\sin\;{\theta}^{\prime}\sin\;\phi {y}^{\prime }-\cos\;{\theta}^{\prime }{z}^{\prime }$. r, θ^', and ϕ are the spherical coordinates of the point of observation. Putting the value of R, Eq. (12) can be written as follows:

$$ \overrightarrow{A}\left(\overrightarrow{r},t\right)={C}_1{e}^{-i\left[\omega \left(t-r/c\right)\right]}\left({I}_1-{I}_2\right) $$

(13)

where, ${C}_1=\frac{\mu_o{\omega}_c{\omega}_p^2 e\omega {r}_c^2N{A}_{10}^{\ast }{A}_{20}}{64\pi mr\left({\omega}^2-{\omega}_p^2/2{\varepsilon}_l\right)}\left({\alpha}_1\widehat{x}+{\alpha}_2\widehat{z}\right),$

$$ {I}_1=\underset{\frac{-l}{2}}{\overset{\frac{l}{2}}{\int }}\underset{-\infty }{\overset{\infty }{\int }}\underset{\frac{-l}{2}}{\overset{\frac{l}{2}}{\int }}{e}^{i\beta}{e}^{-{\left({y}^{\prime }-{l}_c\right)}^2/{r}_0^2}{\mathrm{dx}}^{\prime }{\mathrm{dy}}^{\prime }{\mathrm{dz}}^{\prime },{I}_2=\underset{\frac{-l}{2}}{\overset{\frac{l}{2}}{\int }}\underset{-\infty }{\overset{\infty }{\int }}\underset{\frac{-l}{2}}{\overset{\frac{l}{2}}{\int }}{e}^{i\beta}{e}^{-{\left({y}^{\prime }+{l}_c\right)}^2/{r}_0^2}{\mathrm{dx}}^{\prime }{\mathrm{dy}}^{\prime }{\mathrm{dz}}^{\prime } $$

and $\beta =\frac{\omega }{c}\left[{x}^{\prime}\left(\cos\;\theta -\sin\;{\theta}^{\prime}\cos\;\phi \right)-\sin\;{\theta}^{\prime}\sin\;\phi {y}^{\prime }+{z}^{\prime}\left(\sin\;\theta -\cos\;{\theta}^{\prime}\right)\right].$

On solving I₁ and I₂, we obtain the following:

$$ {I}_1=\frac{4{c}^2\sqrt{\pi }{r}_0}{\omega^2}\frac{\sin\;\left[\frac{\omega l}{2c}\left(\cos\;\theta -\sin\;{\theta}^{\prime}\cos\;\phi \right)\right]\sin\;\left[\frac{\omega l}{2c}\left(\sin\;\theta -\cos\;{\theta}^{\prime}\right)\right]{e}^{-\frac{i\omega {l}_c\sin\;{\theta}^{\prime}\sin\;\phi }{c}}{e}^{-\frac{r_0^2{\omega}^2{\sin}^2{\theta}^{\prime }{\sin}^2\phi }{4{c}^2}}}{\left(\cos\;\theta -\sin\;{\theta}^{\prime}\cos\;\phi \right)\left(\sin\;\theta -\cos\;{\theta}^{\prime}\right)} $$

(14)

$$ {I}_2=\frac{4{c}^2\sqrt{\pi }{r}_0}{\omega^2}\frac{\sin\;\left[\frac{\omega l}{2c}\left(\cos\;\theta -\sin\;{\theta}^{\prime}\cos\;\phi \right)\right]\kern0.28em \sin\;\left[\frac{\omega l}{2c}\left(\sin\;\theta -\cos\;{\theta}^{\prime}\right)\right]{e}^{\frac{i\omega {l}_c\sin\;{\theta}^{\prime}\sin\;\phi }{c}}{e}^{-\frac{r_0^2{\omega}^2{\sin}^2{\theta}^{\prime }{\sin}^2\phi }{4{c}^2}}}{\left(\cos\;\theta -\sin\;{\theta}^{\prime}\cos\;\phi \right)\left(\sin\;\theta -\cos\;{\theta}^{\prime}\right)} $$

(15)

Magnetic field at far distance $\overrightarrow{r}\left(r,{\theta}^{\prime },\phi \right)$is as follows:

$$ {\displaystyle \begin{array}{l}\overrightarrow{B}=\overrightarrow{\nabla}\times \overrightarrow{A}= i\omega /c\left(\hat{r}\times \overrightarrow{A}\right)\\ {}=\sqrt{\alpha_1^2\left({\sin}^2{\theta}^{\prime }{\sin}^2\phi +{\cos}^2{\theta}^{\prime}\right)+{\alpha}_2^2{\sin}^2{\theta}^{\prime }-2{\alpha}_1{\alpha}_2\sin\;{\theta}^{\prime}\cos\;{\theta}^{\prime}\cos\;\phi }=\sqrt{Y}\end{array}} $$

(16)

Time average Poynting vector is ${\overrightarrow{S}}_{\mathrm{av}}=c{\left|\overrightarrow{B}\right|}^2/2{\mu}_0\hat{r}$. If we normalize it with the peak power of one of the lasers, (which is ${P}_1=c{B}_1^2\pi {r}_0^2/2{\mu}_0$), then the normalized radiated terahertz power is as follows:

$$ \frac{{\overrightarrow{S}}_{\mathrm{av}}{r}^2}{P_1}=\frac{\widehat{r}{\left({\mu}_0{c}^2\right)}^2}{64{\pi}^2}{\left(\frac{\omega_c}{\omega}\right)}^2{a}_2^2{\left({\mathrm{Nr}}_c^2\right)}^2\frac{1}{\left(\frac{\omega^2}{\omega_p^2}-\frac{1}{2{\varepsilon}_l}\right)}X\;\left({\omega}^4{c}^2Y\right) $$

(17)

where, $X=\frac{\sin^2\;\left[\frac{\omega l\left(\cos\;\theta -\sin\;{\theta}^{\prime}\cos\;\phi \right)}{2c}\right]{\sin}^2\left[\frac{\omega l\left(\sin\;\theta -\cos\;{\theta}^{\prime}\right)}{2c}\right]{\sin}^2\left[\frac{\omega {l}_c\sin\;{\theta}^{\prime}\sin\;\phi }{c}\right]{e}^{-\frac{r_0^2{\omega}^2{\sin}^2{\theta}^{\prime }{\sin}^2\phi }{2{c}^2}}}{{\left(\cos\;\theta -\sin\;{\theta}^{\prime}\cos\;\phi \right)}^2{\left(\sin\;\theta -\cos\;{\theta}^{\prime}\right)}^2}.$

Observations and Discussion

We have carried out numerical simulations for the following set of laser, plasma, and CNTs parameters: CO₂ laser of frequencies ω₁ = 1.85 × 10¹⁴ rad/s and ω₂ = 2 × 10¹⁴ rad/s is chosen such that difference ω₂ − ω₁ lies in THz range. Corresponding wavelengths of two beams are λ₁ = 10.2 μm, λ₂ = 9.44 μm with peak intensity I ≈ 10¹⁵ W/cm² and spot size r₀ = 1 μm. The length (l_c) and diameter of an armchair CNT used for the analysis is 1 μm × 30 nm. The inter-tube separation is a = 30 nm. The relative permittivity of Si substrate is ε_l = 12. The externally applied wiggler magnetic field B₀ = 200 kG, plasma frequency ω_p = 7.3 × 10¹³rad/s and the angle of incidence θ = 28.6^o.

In Fig. 2, the variation of the normalized THz power ${\overrightarrow{S}}_{\mathrm{av}}{r}^2/{P}_1$ with normalized THz frequency ω/ω_p is shown. It can be clearly observed from this plot that, the THz power is resonantly enhanced at plasmon frequency (ω_p/2ε_l) of CNTs. This is due to the reason that, when the plasma density is near to $4{\varepsilon}_l^2$ times the critical density corresponding to THz frequencyω, the resonance absorption of laser energy by the electrons of the CNTs takes place and THz power shows the prominent maxima.

Fig. 2

Variation of the normalized THz power ${\overrightarrow{S}}_{\mathrm{av}}{r}^2/{P}_1$ with normalized terahertz frequency ω/ω_p at θ = 28.6^o, θ^′ = 61.3^o, ϕ = 17.2^o, a₂ = 0.25, ω_c = 3.5 × 10¹²rad/s, r_c = 15 nm and l_c = 1 μm

Figure 3 is a 3D plot, in which the conical profile of the THz emission from the array of CNTs is presented. The THz power radiated from CNT antenna is observed to have an oscillatory behavior withϕ. The values of θ^′ = 61.3^o and ϕ = 17.2^o are chosen from the plot, for which maximum THz power is observed.

Fig. 3

Variation of the normalized THz power ${\overrightarrow{S}}_{\mathrm{av}}{r}^2/{P}_1$ with spherical coordinates θ^′ and ϕ at ω_p = 7.3 × 10¹³rad/s. The rest of the parameters are same as taken in Fig. 2

In Fig. 4, the plot of the normalized THz power ${\overrightarrow{S}}_{\mathrm{av}}{r}^2/{P}_1$ with angle of incidence θ is presented. One may clearly observe from this figure that, the THz power attains maximum at θ = 28.6^o. So, this is the optimized value of angle of incidence at which the lasers should be incident on vertically aligned CNTs so that the maximum conversion efficiency of THz wave can be achieved. In order to analyze the impact of radius and length of CNTs, the plots of THz power are shown for different values of radius, r_c, and length, l_c, of nanotubes in Figs. 4 and 5 respectively. Such tubes of different radius and length can be synthesized on various substrates, using plasma-enhanced chemical vapor deposition process by controlling the growth parameters and the geometry of the bias voltage electrodes. Our results show the direct dependence of THz power on CNTs radius and length.

Fig. 4

Variation of the normalized THz power ${\overrightarrow{S}}_{\mathrm{av}}{r}^2/{P}_1$ with angle of incidence θ for different values of radius r_c of nanotubes at ω_p = 7.3 × 10¹³rad/s. The rest of the parameters are same as taken in Fig. 2

Fig. 5

Variation of the normalized THz power ${\overrightarrow{S}}_{\mathrm{av}}{r}^2/{P}_1$ with angle of incidence θ for different values of l_cof nanotubes at ω_p = 7.3 × 10¹³rad/s.The rest of the parameters are same as taken in Fig. 2

In order to study the effect of external magnetic field on generated THz power, the variation of normalized THz power ${\overrightarrow{S}}_{\mathrm{av}}{r}^2/{P}_1$ with normalized wiggler magnetic field ω_c/ω_p is plotted in Fig. 6. The wiggler magnetic field supports the THz generation by producing a THz current and providing the necessary momentum required for phase matching in THz generation.

Fig. 6

Variation of the normalized THz power ${\overrightarrow{S}}_{\mathrm{av}}{r}^2/{P}_1$ with normalized wiggler magnetic field for the same set of parameters as taken in Fig. 2

Conclusion

The array of carbon nanotubes embedded on metallic surface acts as an antenna to produce THz radiation by the interaction of two similar laser beams of slightly different frequency. The incident laser beams exert a ponderomotive force on the electrons of CNTs which on beating with applied and laser magnetic field produces transverse nonlinear current at (ω₂ − ω₁) to generate THz radiation. The plasmon resonance of CNTs significantly enhances the efficiency of THz generation. The wiggler magnetic field provides requisite phase matching and gives rise to high values of THz conversion efficiency. The direct dependence of THz power on CNTs dimensions is observed. The model presented in the analysis is important from a technical point of view, because the development of THz radiator from CNTs can be practically useful due to its compactness.