Modeling of the creep and nonlinear damage effects of rocks and its application in tunnels

Abstract

The creep and nonlinear damage behavior of rocks are two main factors that can cause large deformations and instability in tunnels. In this paper, uniaxial compression creep and triaxial compression tests were conducted to analyze the time-dependent and damage-induced strain-softening response of sandstone obtained from a water-conveyance tunnel in China. Using the test results, a new constitutive model was developed by coupling damage mechanics, Maxwell and Kelvin viscoelastic models, and the Mohr–Coulomb failure criterion. The model is formulated to describe both the full creep process (including the three stages of transient, steady, and accelerated creep) and the damaged-induced strain-softening behavior of the sandstone. The proposed model was validated against experimental data and was adopted to investigate the long-term safety of the segmental liner of the water-conveyance tunnel. The results showed that the differences between the rock peak and residual strength or between the initial and residual stiffness of sandstone increased as the confining pressure increased. In addition, the ratio between the crack damage stress and the peak strength increased initially with the increase in confining pressure and then decreased with a further increase in confining pressure. The ratio between creep deformation and total deformation increased with the increase in applied stress, and the specimen exhibited significant creep behavior at the final loading stage. Furthermore, the steady creep rate increased, and the viscosity coefficient decreased with the increase in loading stress. Good agreement was found between the values of failure strengths and shapes of stress–stain curves between the numerical simulation and experimental results under the uniaxial unconfined compressive creep test or triaxial compressive test. The axial load and bending moment of the tunnel segmental liner increased with the increase in the yield strength of concrete. The plot of axial force along the entire segmental liner ring varied greatly with time, while the plot of bending moment was less affected by time.

1 Introduction

Tunnel instabilities such as squeezing, bursting, and collapse are major issues for underground engineering. Instabilities bring great challenges to the design of tunnels and the short-term to long-term safety of supporting structures. Examples are rock collapse [13], shield jamming [22, 42], failure of primary support [6, 19], and cracking of secondary lining [12]. Unstable rock deformation is often time-dependent and associated with the post-peak and creep features of rocks [2]. Thus, it is of vital importance to investigate these two features of rocks to ensure the stability and safety of tunnels.

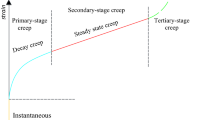
Many experiments were conducted to study the post-peak and creep behavior of rocks. For the post-peak behavior, experimental results [10, 21, 25, 30, 33, 39] show that there are five types of stress–strain curves in post-peak stage, i.e., self-sustaining (type I [34]), perfectly brittle-plastic (type II), strain-softening (type III), perfectly plastic (type IV), and strain-hardening (type V) (Fig. 1). In addition, with the increase in confining pressure, the stress–strain curves show three features, namely, (1) the peak and residual strengths increase; (2) the strength loss in the post-peak stage reduces; and (3) there is a transition from brittle to fully ductile behavior. As for the creep behavior, experimental results [18, 24, 32, 37, 38, 41, 43, 44] indicate that the creep deformation of rocks under constant stress has three creep stages, i.e., (1) primary, (2) secondary, and (3) tertiary. Moreover, the creep rate and creep stages are related to the damage caused by the initiation and propagation of micro-cracks.

Fig. 1

Rock mechanics characteristic: a typical post-peak behavior [10]; b typical creep stages under constant stress

Among the five typical post-peak behaviors mentioned above, strain-softening behavior is often observed in underground rock engineering [9, 35]. Thus, numerous models have been proposed to describe the strength-weakening effect in the strain-softening process. These models can be mainly divided into two categories. One is that the strength parameters are assumed to reduce linearly with the growth of strain in the softening stage and remain constant in the residual stage [7, 17, 31]. The other is the use of the damage evolution function to describe the deterioration process of strength parameters due to micro-fracture propagation [16, 25, 36]. As for the creep behavior, many models have been put forward to describe the three creep stages. Yang et al. [40] proposed a nonlinear creep model to describe the tertiary creep behavior of diabase. Barla et al. [3] proposed a creep model combining a Burger’s body and a stress-hardened viscoplastic body to study the time-dependent deformation of surrounding rocks. Tao et al. [29] developed a new creep model based on variable-order fractional derivatives and continuum damage mechanics to describe the tertiary creep behavior of rocks. Liao et al. [20] adopted a fractional order creep element to simulate the creep behavior of frozen silt. Many of these models require several curve-fitting parameters that lack physical significance.

This paper aims to put forward a nonlinear damage creep model that can describe the strain-softening behavior and all the creep stages of rocks by adopting a statistical damage evolution rule. The proposed model is validated against experimental data and then used to investigate the long-term safety of segmental liners in a water-conveyance tunnel in sandstone.

2 Experimental tests

2.1 Preparation of the experiment

The rock specimens were obtained from a water-conveyance tunnel in China (Fig. 2). The tunnel mainly passes through the sandstone strata, and three excavating methods are used to ensure the safety of the tunnel construction under different geological conditions, namely, (1) open type TBM for the tuff sandstone strata, (2) drilling and blasting method for the fault fracture zone, and (3) shield TBM for the weak sandstone and mudstone.

Fig. 2

Geologic profile of the background engineering

Cores of the gray-green sandstone were firstly obtained through drilling to a depth of about 100 m, and then cylindrical specimens with a diameter of 50 mm and length of 100 mm were prepared for the experimental tests. Uniaxial unconfined compression with creep was conducted using a servo-controlled rock triaxial rheological apparatus able to apply a constant load to the sample with time. Triaxial compression tests with constant confining pressures of 5, 8, and 11 MPa under drained conditions were conducted using an MTS 815 Rock Mechanics Test System.

2.2 Test results

The stress–strain curves of the sandstone with different confining pressures are presented in Fig. 3a. The initial axial strain ε₁ vs. deviatoric stress σ = (σ₁ − σ₃) curves show that, due to the closure of pre-existing microcracks, the specimens initially undergo a nonlinear deformation process where the curves are concave up. The confining pressure has an evident influence on the microcrack closure in this stage; that is, the microcrack closure process is more distinct at lower confining pressure than at higher confining pressure. This phenomenon can be attributed to the closure of pre-existing microcracks under the action of higher confining pressure before axial deformation occurs. After the closure of pre-existing microcracks, the specimens undergo elastic deformation, where the axial strain–stress curve is linear. Then, the stress–strain curve becomes nonlinear, and the specimens undergo inelastic deformation. There is no distinct yield stage for the specimens under uniaxial compression, while the pre-peak yield feature of confined specimens gradually increased with the increase in confining pressure. Once the peak stress is reached, strain-softening follows. Further increase in axial strain resulted in unstable behavior, leading to a complete collapse of the samples.

Fig. 3

Short-term mechanical behavior of sandstone: a strain–stress curves (dash-curves are volumetric plots); b microscopic structural characteristics of the rock; c compression tests; d fracture pattern of failed samples

Also shown in Fig. 3a are plots of the lateral strain ε₃ vs. deviatoric stress σ = (σ₁ − σ₃). Unlike the axial strain, the lateral strain vs. stress curves do not show the initial concave-up response but are initially linear. With increasing stress, the samples expand laterally until the lateral strain dominates the axial strain, and the samples start to dilate. In terms of the volumetric strain ε_v = (ε₁ + 2ε₃) (dashed lines in Fig. 3a), the samples initially contract, then clearly dilate. The contraction-dilation response is evidently stress-dependent, with maximum volumetric contraction increasing with an increase of confining pressure σ₃ = 0, 5, 8, and 11 MPa. It can be seen from the failure pattern (Fig. 3d) that a single compression-shear fracture surface formed when the specimens failed.

The strain-softening feature can be decomposed into brittle and ductile components (as shown in Fig. 4a), in which the brittle part results in a reduction of the stiffness and strength, while the ductile part causes an increase in plastic strain [10]. Three parameters are introduced to characterize the ductility/brittleness of the test specimens (Fig. 4a): (1) the plastic strain δ_εp during the drop in the stress from peak to residual state (δ_ε1p and δ_ε3p represents axial plastic strain and lateral plastic strain, respectively), (2) the drop in the stress from peak to residual state δ_σ, and (3) the change in stiffness δ_E (δ_E = E − E_r), where E is initial secant stiffness, and E_r is residual secant stiffness). As shown in Fig. 4b and Table 1, all these parameters increase as the confining pressure increases.

Fig. 4

Idealized strain-softening behavior of test specimens: a illustration of parameters to characterize ductility/brittleness; b values of ductility/brittleness parameters as function of confining pressure

Table 1 Parameters regarding to the strain-softening behavior of sandstone

As discussed above, the volumetric strain vs. stress curves show that the specimens under triaxial compression initially undergo compression/compaction, followed by dilation (Fig. 5a). Firstly, the relationship between volumetric strain and stress is linear (OA). Deformation is contractive until the maximum compressive strain is reached at point B, where an inflection occurs, after which the specimen dilates. The stress at points A, B, and C are designated as crack initiation stress (σ_a), crack damage stress (σ_cd), and threshold stress (σ_vo), respectively. Table 2 displays the key parameters regarding the volumetric behavior of the sandstone, while Fig. 5b–d displays the ratio of stress, axial strain, and circumferential strain between points A, B, C, and the point of peak strength. The stress ratios, axial strain ratios, and circumferential strain ratios at point A remain almost unchanged for different confining pressures, while the ratios at points B and C exhibit an inversed V-shaped distribution as the confining pressure increases. For stress ratio, the peak value at point B or C occurs at σ₃ = 11 MPa, while for axial or circumferential strain ratios, the maximum values at points B and C occur at σ₃ = 8 MPa and 11 MPa, respectively.

Fig. 5

Behavior of volumetric deformation: a illustration of the key parameters; b the ratio between stress at points A, B, C and the peak strength; c the ratio between axial strain at points A, B, C and the point of peak strength; and d the ratio between lateral strain at points A, B, C and the point of peak strength

Table 2 Parameters regarding to the volumetric behavior of sandstone

It can be inferred from the above findings that the changing trends of the strain-softening feature of sandstone in terms of δ_σ and δ_E do not follow the typical rule, that is, the difference between the peak and residual strength or the difference between the initial and the residual stiffness decreases as the confining pressure increases. In addition, the ratios between the crack damage stress, threshold stress, and peak strength increase with the increase in confining pressure, then decrease with the further increase in confining pressure. These phenomena can be attributed to the reason that, as the original in situ stress in the sandstone stratum is small, a lower confining pressure can weaken the strain-softening effect in the post–peak stage and increase the stress level of the crack damage stress threshold. On the other hand, higher confining pressure will damage the rock structure to some extent, which can strengthen the strain-softening effect and decrease the stress level of the crack damage stress threshold.

Six different stress levels at which the creep tests are to be carried out were selected in accordance with the uniaxial compressive strength of sandstone. Figure 6 shows the creep curves and fracture pattern of sandstone. Table 3 lists the creep strains, steady creep rates, and viscosity coefficients of sandstone at different stress levels. In Table 3, t_c represents the creep time, ε_i, ε_c, and ε_t are the instantaneous, creep, and total strains of the rock, respectively, and $\dot{\varepsilon }_{{\text{cs}}}$ refers to the steady creep rate of rock, which is the slope of strain curve versus time as shown in Fig. 7. The viscosity coefficient η based on the Burger’s creep model can be calculated using the following equation [28]:

$$\eta = \frac{\sigma_1 - \sigma_3 }{{3\dot{\varepsilon }_{{\text{cs}}} }}$$

(1)

Fig. 6

Uniaxial compressive creep feature of sandstone

Table 3 Parameters regarding to the creep behavior of sandstone

Fig. 7

Typical creep stages of specimen under different loading stress level: a two creep stages for stress level of 10.5 MPa; b three creep stages for stress level of 15 MPa

It can be seen from Figs. 6 and 7 that, at the lower loading stress level, the creep curves show two stages: a primary creep stage with a decreasing strain rate and a steady-state creep stage with a constant strain rate. For the final stress level, the creep curve shows three stages, and the tertiary creep stage leads to rock failure. It can be concluded from Table 3 and Fig. 8 that the ratio ε_c/ε_t between creep deformation and total deformation increases with an increase in loading stress level, and the specimen exhibits significant creep behavior at the final loading stress level. At the final loading stress level, the creep strain reaches up to 0.69 × 10⁻³, which is more than the sum of the creep strain at the former loading stage. In addition, the steady creep rate increases with the increase in loading stress level at the former four loading levels, and then it exhibits a significant linear increase. As for the viscosity coefficient, it decreases with the increase in the loading level. The phenomenon indicates that the higher the stress level, the more evident the creep deformation. When the stress level reaches some extent, the creep deformation in the steady creep stage keeps increasing for the constant steady creep rate, which may also lead to the delayed failure of the rock.

Fig. 8

Creep strain, steady creep rate and viscosity coefficient of sandstone under different confining pressure

3 A nonlinear damage creep model for sandstone

3.1 Constitutive model

The creep and strain-softening behavior of rock surrounding a tunnel are the two main factors that cause large deformation and instability (e.g., squeezing) in a tunnel. Thus, a constitutive model to describe both the creep and strain-softening response of rocks is proposed. In the creep model (Fig. 9), the Maxwell-damage body, Kelvin-damage body, and plastic-damage body are connected in series. For the convenience of the following description, the creep model is referred to as “DCVISC”. In terms of damage, it is assumed that all the elastic, viscous, and plastic parameters follow the same damage rule, and the damage evolution law can be obtained through Eq. (2) [16]:

$$D = 1 - \exp \left( { - \left( {\frac{\varepsilon }{\lambda }} \right)^m } \right)$$

(2)

where λ and m are the material parameters, ε is the plastic strain related to failure pattern of rocks.

Fig. 9

The component of DCVISC model

Rocks may fail in tension when the confining pressure is zero or low, while they may undergo shear failure when the confining pressure is high. Thus, ε is determined as follows:

$$\varepsilon = \left\{ {\begin{array}{*{20}l} {\frac{2}{3}\sqrt {{\left[ {(\varepsilon_1^p - \varepsilon_2^p )^2 + (\varepsilon_2^p - \varepsilon_3^p )^2 + (\varepsilon_3^p - \varepsilon_1^p )^2 } \right]}} } \hfill & {({\text{shear failure}})} \hfill \\ {\varepsilon_3^p } \hfill & {({\text{tensile failure}})} \hfill \\ \end{array} } \right.$$

(3)

For σ < σ_s, no damage occurs in each body. Thus, the creep equation is:

$$\varepsilon = \frac{\sigma }{E_m } + \frac{\sigma }{\eta_m }t + \frac{\sigma }{E_k }\left( {1 - e^{ - \frac{E_k }{{\eta_k }}t} } \right)$$

(4)

where E_m, E_k are the elastic modulus of Maxwell-damage and Kelvin-damage body, respectively. η_m, η_k are the viscosity coefficient of Maxwell-damage and Kelvin-damage body, respectively.

For σ > σ_s, deviatoric strain rate partitioning is:

$$\dot{e}_{ij} = \dot{e}_{ij}^k + \dot{e}_{ij}^m + \dot{e}_{ij}^p$$

(5)

where $\dot{e}_{ij}^k$, $\dot{e}_{ij}^m$ and $\dot{e}_{ij}^p$ are the deviatoric strain rate of the Kelvin-damage body, Maxwell-damage body, and plastic-damage body, respectively.

The Kelvin-damage body is given by:

$$S_{ij} = 2\eta_k (1 - D)\dot{e}_{ij}^k + 2G_k (1 - D)e_{ij}^k$$

(6)

where S_ij is the devatoric stress, G_k is the shear modulus of Kelvin-damage body.

The Maxwell-damage body is formulated as:

$$\dot{e}_{ij}^m = \frac{{\dot{S}_{ij} }}{2G_m (1 - D)} + \frac{{S_{ij} }}{2\eta_m (1 - D)}$$

(7)

where G_m is shear modulus of Maxwell damage body.

The plastic behavior of rocks is described by the Mohr–Coulomb criterion, and the yield envelope of the Mohr–Coulomb-damage body is given:

$$f_{\text{s}} = \sigma_1 - \sigma_3 N_\varphi + 2c(1 - D)\sqrt {N_\varphi }$$

(8)

$$f_{\text{t}} = \sigma_3 - (1 - D)\sigma_t$$

(9)

where f_s is shear yield criterion, f_t is tensile yield criterion,$N_\varphi = \frac{1 + \sin [(1 - D)\varphi ]}{{1 - \sin [(1 - D)\varphi ]}}$, c, φ and σ_t are the cohesion, friction angle and tensile strength of the rock, respectively. From the flow rule, the deviatoric plastic strain increment can be calculated as:

$$\dot{e}^p_{ij} = \lambda \frac{\partial g}{{\partial \sigma_{ij} }} - \frac{1}{3}\dot{e}_v^p \delta_{ij}$$

(10)

where δ_ij is Kronecker delta, λ is plastic index, $\dot{\varepsilon }_v^p$ is shear volumetric strain:

$$\dot{e}_v^p = \lambda \left( {\frac{\partial g}{{\partial \sigma_1 }} + \frac{\partial g}{{\partial \sigma_2 }} + \frac{\partial g}{{\partial \sigma_3 }}} \right)$$

(11)

where σ₁ is the first principal stress, which is distributed along the loading direction, and σ₂ and σ₃ is the second and third principal stresses, respectively, which are both distributed along the circumferential direction. The above assumptions are mainly consistent with the stress state of surrounding rock after tunnel excavation, without considering different combinations of principal stresses.

The non-associative plastic potential functions g corresponding to the failure criteria have the form:

$$g_s = \sigma_1 - \sigma_3 N_\psi$$

(12)

$$g_t = - \sigma_3$$

(13)

where g_s and g_t are the plastic potential functions related to f_s and f_t, respectively, $N_\psi = \frac{1 + \sin ((1 - D)\psi )}{{1 - \sin ((1 - D)\psi )}}$, and ψ is the dilation angle.

The volumetric behavior is given by:

$$\dot{\sigma }_v = K(1 - D)(\dot{e}_v - \dot{e}^p_v )$$

(14)

where $\sigma_v$ and $\dot{e}^p_v$ are volumetric stress and strain.

The implementation of the creep model in the commercially available computer code FLAC 3D (Fast Lagrangian Analysis of Continua 3D) developed by Itasca [15] is described in “Appendix I”.

3.2 Model calibration

Numerical uniaxial compressive creep test and triaxial compressive test were used to validate the proposed model. A cylindrical specimen with a diameter of 50 mm and a height of 100 mm was built, as shown in Fig. 10. The vertical deformation at the bottom of the specimen was fixed. Uniformly distributed pressure was applied at the top of the specimen during each loading stress level for the creep test, while constant vertical speed at 1 × 10^–6 m/step was applied at the top of the specimen for the triaxial compression test. The vertical deformation at point A was recorded during the loading to monitor the response of the model.

Fig. 10

FLAC3D mesh for calibration of constitutive model

The short-term mechanical parameters (Table 4) of sandstone were calibrated based on the compressive experimental results. It should be noted that the softening reaction of rocks may be the result of failure along a shear band or failure plane, but only the deformation response of rocks is considered in parameter calibration. It can be seen from Fig. 11 that good agreements in the values of failure strengths, the shape of stress–strain curves, and the fracture patterns were found between the numerical and experimental results, indicating that the Mohr–Coulomb damage body can describe the strain-softening behavior of rocks. The influence of damage parameters on the short-term mechanical behavior of rocks is displayed in Fig. 12. It shows that the peak and residual strength increased with the increasing m, while the damage parameter η only affects the post-peak features of rocks, and the residual strength increased with the increasing η. As for the fracture patterns, two shearing zones with an ‘X’ shape and a ‘V’ shape and one oblique shearing zone occurred for specimens with m = 0.1, 0.4, and 1 under uniaxial compression test, respectively. Two shearing zones with an ‘X’ shape appeared for specimens with η = 0.05, 1, and 5 under the uniaxial compression test. For specimens with a confining pressure of 8 MPa, two shearing zones with a ‘V’ shape emerged for each case.

Table 4 Short-term parameters of sandstone

Fig. 11

Comparison of the short-term mechanical behavior of sandstone between numerical simulation and experimental results: a stress–strain curves; b damage patterns (the dashed lines are the numerical simulation results and the solid lines represent the experimental results)

Fig. 12

The influence of damage parameters on the short-term mechanical behavior of sandstone: a uniaxial compression; b axial compression with confining pressure of 8 MPa

The creep parameters of the DCVISC model were calibrated to reproduce the behavior of sandstone during the uniaxial compressive creep test. The model parameters used are shown in Table 5. As shown in Fig. 13, good agreement was found between the failure strength and the trends of the creep curves between the numerical simulation and the experimental results. Figure 14 also shows that the simulation result of the DCVISC model was similar to that of the CVISC model that is built-in in FLAC 3D when the applied axial stress was less than 15 MPa. When the applied stress reached 15 MPa, the deformation of the CVISC model cannot describe the tertiary creep stage. In comparison, for the DCVISC model, the creep deformation at 15 MPa could be divided into three distinct stages, i.e., OA was the transient creep stage, AB was the steady creep stage, and BC was the accelerated creep stage. Thus, the DCVISC model performed well in representing all the creep stages of the rock.

Table 5 Creep parameters of sandstone

Fig.13

Creep behavior: a Comparison between the numerical results of FLAC3D CVISC MODEL and experimental results; b Comparison between the numerical results of the proposed DCVISC and the experimental results

Fig. 14

The influence of damage parameters on the creep behavior of sandstone: a the influence of m; b the influence of λ

The influence of damage parameters on the creep behavior of rocks is shown in Fig. 13. It reveals that the value of m has no influence on the creep strength of sandstone, while it has a huge effect on the tertiary creep stage of rocks, that is, the occurrence of the tertiary creep stage delayed from point A to point B with the increase in m from 0.2 to 1. With the further increase in m from 1 to 3, the creep rate underwent an evident decrease. The value of η also has no influence on the creep strength of rocks, while the occurrence of the tertiary creep stage is delayed with the increasing η. In addition, an oblique fracture zone occurred when the rock failed in each case.

4 Application to tunneling

The models developed above and implemented in FLAC3D are used to simulate the response of a water-conveyance tunnel in China. The shield-TBM excavated tunnel is reinforced using a concrete (RC) segment, and the concrete type is C50. Figure 15 shows the layout of the segmental ring. The outer and inner diameters are 2.6 and 2.3 m, respectively, and the thickness is 0.3 m. The segmental ring is assembled by four universal wedge-shaped segments with a width of 1.2 m, using eight M36 circumferential bolts in the segmental joints. The experimental results in Sect. 2 show that sandstone has a distinct strain-softening feature and shows evident creep behavior in low in situ stress. In addition, the segment is installed soon after excavation, leaving hardly any time for ground relaxation. Thus, the segment may bear large earth pressure, resulting in structural instability with great possibility during the operation time.

Fig. 15

Layout of segment

To overcome this problem, the segmental liner should have the ability to accommodate deformation to some extent [5]. Liners with this feature are called yielding support and are mainly implemented in two ways: one is arranging a compressible layer in the overcut behind the liner, and the other is installing a compressible layer along the circumferential direction of the liner [1]. In many cases, the first option is preferable. The material of the compressible layer has various types, such as polyurethane foam, lightweight concrete, and compressible mortar, which is made of expanded polystyrene [4, 26, 27]. For the water-conveyance tunnel, a segment with a compressible concrete layer in the overcut is chosen as the supporting structure. Thus, its long-term safety under the action of creep and strain-softening effect of surrounding rock is studied in this section.

4.1 Numerical simulation

Figure 16 shows the numerical model used to simulate the section of the water-conveyance tunnel. The distances between the center of the tunnel to the x- and z-boundaries are both 40 m. The tunnel lining segments are modeled using the liner element in FLAC3D, which can resist shear and bending forces and simulate the frictional interactions between segments and surrounding rock. As shown in Fig. 16, a segmental liner is divided into four liner elements in the longitudinal direction, and nodes at joint positions are coincident (that is, the coordinates of nodes n and n' are equal, n = 1, 2, 3, 4, 5). The springs at nodes 2 and 2', 4 and 4' are set to simulate the joint, and the springs at the remaining nodes are set to simulate the interactions between the segment and surrounding rock.

Fig. 16

Numerical models

The bending stiffness of the joint is obtained through numerical simulation put forward by Feng et al. [11], and the results are shown in Fig. 17. The shear and compressive stiffness of the joint were set as 200 M/m [8]. The mechanical parameters of the joint are listed in Table 6.

Fig. 17

Plots between k_R0 with bending moment and axial force: a bending stiffness for positive moment; b bending stiffness for negative moment

Table 6 Mechanical parameters of joint

The double-yield constitutive model can represent the behavior of materials that undergo shear or tensile yielding and produce significant irreversible compaction by including strain-softening shear and tensile failure envelopes in addition to the volumetric yield surface [15]. Thus, in this study, the model was used to simulate the behavior of compressible concrete [14], and its parameters are listed in Table 7.

Table 7 Mechanical parameters of compressible concrete for p₁ = 0.3MPa

The following three cases are selected to investigate the mechanical response of segmental liner: (1) In-situ stress field with the lateral pressure coefficient ϕ = 1, σ_x = σ_y = 4 MPa; ϕ = 2, σ_x = 2.5 MPa, σ_y = 5 MPa; ϕ = 0.5, σ_x = 5 MPa, σ_y = 2.5 MPa. (2) Yield strength of compressible concrete: p₁ = 0.3 MPa, 0.8 MPa, 1.5 MPa, and 2 MPa, and (3) Thickness of yielding layer: h = 10 mm, 15 mm, and 20 mm.

4.2 Analysis of the results

The long-term mechanical behavior of segmental liner at ϕ = 0.5 and h = 20 cm with different yield strengths of the compressible concrete p₁ are shown in Fig. 18. The following conclusions are based on the results from this figure:

Fig. 18

Long-term mechanical behavior of segment for φ = 0.5: a the damage of surrounding rock at t = 0; b the damage of surrounding rock at t = 60; c the deformation of yielding layer at t = 0; d the deformation of yielding layer at t = 60; e the inner force and safety factor at t = 0; f the inner force and safety factor at t = 60; g the inner force and safety factor of vault versus time

• 1. The damage zone of the surrounding rock mainly appeared at the crown and inverted region. In addition, the area of the damage zone and its corresponding damage degree and the deformation of the yielding layer decreases with the increase in yielding strength, indicating that the yielding layer with lower strength has a stronger yielding capability.

• 2. The axial force and bending moment of the lining segment increases with the increase in p₁. Taking t = 0 (t is the tunnel operation time, and its unit is year) for an example, the maximum positive moments are 19.6, 29.3, 30.7 and 40.5 kN·m, the maximum negative moments are − 25.3, − 37.6, − 41.2 and − 54.2 kN·m, and the maximum axial forces are 86.1, 140.1, 144.9 and 199.45 kN for p₁ = 0.3, 0.8, 1.5 and 2 MPa, respectively.

• 3. The distribution of axial force shows an evident change with the increase in time, while the distribution of moment is barely affected by time. Specifically, the axial force is unevenly distributed along the entire ring with an ellipse shape, that is, it is small near the left and right arch waists, while it is large near the arch and the bottom at t = 0. For t = 60, the axial force is evenly distributed along the entire ring with a circle shape. As for the bending moment, the positive moment is distributed near the left and right arch waists, and the negative moment is distributed near the arch and the bottom for both t = 0 and t = 60.

• 4. The factor of safety (the method used to determine the safety factor is provided in “Appendix II”) for the same section of segmental liner decreases with the increase in p₁. In addition, the factor of safety near the joint is the highest, and the factor of safety of each section is larger than one at t = 0. For t = 60, the critical sections of the structure are near the vault and arch waist. The factors of safety for p₁ = 0.3 MPa are larger than 1.0, for p₁ = 0.8 or 1.5 MPa are around 1.0, and for p₁ = 2 MPa are less than 1.0 in these critical sections.

• 5. The bending moment of the vault increases as time increases, and then it decreases with a further increase in time. The turning point is between 20 and 30 years. The axial force increases through the whole operation period, and the turning point from rapid growth to low growth is also between 20 and 30 years.

The mechanical behavior of segments with different failure strengths of the compressible concrete for ϕ = 1 and 2 (h = 20 cm) are shown in Figs. 19 and 20. It can be concluded that:

Fig. 19

Mechanical behavior of segment at φ = 1: a the damage of surrounding rock at t = 0; b the damage of surrounding rock at t = 60; c the deformation of yielding layer at t = 0; d the deformation of yielding layer at t = 60; e the inner force and safety factor at t = 0; f the inner force and safety factor at t = 60

Fig. 20

Mechanical behavior of segment for φ = 2: a the damage of surrounding rock at t = 0; b the damage of surrounding rock at t = 60; c the deformation of yielding layer at t = 0; d the deformation of yielding layer at t = 60; e the inner force and safety factor at t = 0; f the inner force and safety factor at t = 60

• 1. In the case of ϕ = 0.5, the region of the damage zone and its damage degree of surrounding rock and the deformation of the yielding layer decreases with the increase in yielding strength. For ϕ = 1, the damage zones occurred around the tunnel perimeter at t = 0, and it emerged with an ‘X’ shape at t = 60. For ϕ = 2, the damage zones are mainly distributed near the haunch regions. In addition, the deformation of the yielding layer has its maximum value at the sections adjacent to the joints of the lining due to the lower stiffness of the lining at these locations.

• 2. For ϕ = 1, the axial force is evenly distributed along the entire ring with a circular plot. As for the bending moment, the positive moment is distributed near the left and right arch waists and the negative moment is distributed near the arch, and the bottom for both t = 0 and t = 60. For t = 0, the safety factor of the segment at p₁ = 0.8 MPa is the lowest, while for t = 60, the safety factor of the segment at p₁ = 2 MPa is the lowest.

• 3. For ϕ = 2, the distribution of axial force and moment shows an evident change with the increase in time. Specifically, the axial force is unevenly distributed along the entire ring with an ellipse-shaped ploy at t = 0, that is, it is large near the left and right arch waists, while it is small near the arch and the bottom. Meanwhile, for t = 60, the axial force is evenly distributed along the entire ring with a circular plot. As for the bending moment, the negative moment is distributed near the left and right arch waists, and the positive moment is concentrated near the arch and the bottom at t = 0. While for t = 60, the positive moment is only distributed in the vault region at p₁ = 0.3 or 0.8 MPa. The maximum positive, negative, and axial forces increase with the increase in p₁, which results in the decrease in the safety factor with the increase in p₁.

• 4. At the same time, as time goes on, the internal force also increases. Taking the bending moment as an example, as time increases, the positive bending moment near the haunch and the negative bending moment near the vault and bottom both significantly increase. Specifically, it manifests as the expansion of the arc at the haunch and the contraction of the arc at the vault and bottom.

Taking p₁ = 0.8 MPa (ϕ = 0.5, h = 20 cm) as an example, the mechanical behavior of the segment with different heights of compressible concrete are displayed in Fig. 21. The figure shows that:

Fig. 21

Mechanical behavior of segment with different height of the compressible layer for φ = 0.5: a the damage of surrounding rock at t = 0; b the damage of surrounding rock at t = 60; c the deformation of yielding layer at t = 0; d the deformation of yielding layer at t = 60; e the inner force and safety factor at t = 0; f the inner force and safety factor at t = 60

• 1. For the surrounding rocks, the area of the damage zone and its corresponding damage degree and the deformation of the yielding layer increase with the increase in the height of the yielding layer from h = 10 cm to h = 15 cm, then they decrease with a further increase in h.

• 2. At t = 0, the inner force at h = 10 mm is the largest, and the inner force at h = 15 mm is the smallest among the three heights. For h = 20 mm, the safety factor near the joint is the highest. For h = 15 mm, the safety factor evenly distributes along the entire ring with a circle shape. It can be concluded that the segmental liner with compressible concrete of 15 mm has an optimal performance.

• 3. At t = 60, the maximum and minimum bending moments occur at h = 10 and 15 mm, respectively. Meanwhile, the maximum and minimum axial forces occur at h = 10 and 20 mm, respectively. It can be seen from the distribution of safety factors that the safety factors at h = 10 mm are the smallest, with values less than one in most sections. The safety factors at h = 15 mm are evenly distributed along the entire ring, with values larger than one in each section. The safety factors at h = 20 mm are larger than h = 15 mm in most sections, while they are less than one in the vault region. Thus, a segmental liner with compressible concrete of 15 mm has an optimal performance.

5 Summary and conclusions

The creep and strain-softening behavior of sandstone were studied through experimental tests. A combined nonlinear damage and creep model, which can describe the strain-softening behavior and complete creep stages of sandstone, was put forward by adopting a statistical damage evolution rule. The proposed model was validated against experimental data and was used to investigate the long-term safety of the segment of a water-conveyance tunnel in a sandstone stratum. The main conclusions of this study are summarized as follows:

• 1. The difference between the peak and residual strength or the difference between the initial and residual stiffness of sandstone increases as the confining pressure increases. In addition, the ratio between the crack damage stress threshold and the peak strength increases with the increase in confining pressure, and then it decreases with the further increase in confining pressure.

• 2. The ratio between creep deformation and total deformation increases with the increase in loading stress, and the specimen exhibits significant creep behavior at the final loading stress level. In addition, the steady creep rate increases with the increase in loading stress, while the viscosity coefficient decreases with the increase in the loading stress, indicating that the higher the stress level, the more evident the creep deformation.

• 3. Good agreement was found between the values of failure strengths and shapes of the curves between the numerical simulation and the experimental results under the uniaxial compressive creep test or triaxial compressive test, indicating that the proposed DCVISC model did a satisfactory job in representing the whole creep stages and strain-softening features of sandstones.

• 4. The axial force and bending moment of the segmental liner increases with the increase in the yield strength of compressible concrete. The distributed shape of axial force along the entire ring varies greatly with time, while the distributed shape of the bending moment is less affected by time. In addition, the segment with compressible concrete of 15 mm has an optimal performance among the several common thicknesses (10, 15, and 20 mm).

Appendices

Appendix I: Implementation of the DCVISC in FLAC3D

The incremental expression of Eq. (5) has the form:

$$\Delta e_{ij} = \Delta e_{ij}^k + \Delta e_{ij}^m + \Delta e_{ij}^p$$

(15)

$$\Delta e_{ij}^m = \frac{{\Delta S_{ij} }}{2G_m (1 - D)} + \frac{{\overline{S}_{ij} }}{2\eta_m (1 - D)}\Delta t$$

(16)

$$\overline{S}_{ij} = 2\eta_k (1 - D)\Delta e_{ij}^k + 2G_k (1 - D)\overline{e}_{ij}^k \Delta t$$

(17)

where

$$\overline{S}_{ij} = \frac{{\overline{S}_{ij}^{\text{N}} + \overline{S}_{ij}^{\text{O}} }}{2}$$

(18)

$$\overline{e}_{ij}^2 = \frac{{e_{ij}^{2,{\text{N}}} + e_{ij}^{2,{\text{O}}} }}{2}$$

(19)

The superscripts N and O denote new and old values during a time step, respectively. $\overline{S}_{ij}^{\text{O}}$ and $\overline{S}_{ij}^{\text{N}}$ are the new and old deviatoric stress tensors, respectively. $e_{ij}^{2,{\text{N}}}$ and $e_{ij}^{2,{\text{O}}}$ are the new and old deviatoric strain tensors, respectively.

Substituting Eqs. (18) and (19) into Eq. (17) yields:

$$e_{ij}^{k,{\text{N}}} = \frac{1}{A}\left[ {Be_{ij}^{k,{\text{O}}} + \frac{\Delta t}{{4\eta_k (1 - D)}}(S_{ij}^{\text{N}} + S_{ij}^{\text{O}} )} \right]$$

(20)

where

$$A = 1 + \frac{G_k \Delta t}{{2\eta_k }},\quad B = 1 - \frac{G_k \Delta t}{{2\eta_k }},$$

(21)

Substituting Eqs. (16) and (20) into Eq. (15) yields:

$$S_{ij}^{\text{N}} = \frac{1}{a}\left[ {\Delta e_{ij} - \Delta e_{ij}^P + bS_{ij}^{\text{O}} - \left( {\frac{B}{A} - 1} \right)e_{ij}^{k,{\text{O}}} } \right]$$

(22)

where

$$a = \frac{1}{2G_m (1 - D)} + \frac{\Delta t}{{4(1 - D)}}\left( {\frac{1}{\eta_m } + \frac{1}{A\eta_k }} \right),\quad \;b = \frac{1}{2G_m (1 - D)} - \frac{\Delta t}{{4(1 - D)}}\left( {\frac{1}{\eta_m } + \frac{1}{A\eta_k }} \right)$$

(23)

The volumetric strain is:

$$\sigma_0^{\text{N}} = \sigma_0^{\text{O}} + K(1 - D)(\Delta e_{{\text{vol}}} - \Delta e_{{\text{vol}}}^p )$$

(24)

The function h(σ₁, σ₃) = 0, which is represented by the diagonal between the strength envelope of f_s = 0 and f_t = 0 in the principal stress plane (see Fig. 22),

Fig. 22

Definition of h and the domains used in determining yield mode of the rock [35]

is defined to determine the yield type of rock matrix:

$$h = \sigma_3 - \sigma_t + \alpha^p (\sigma_1 - \sigma^p )$$

(25)

where

$$\alpha^p = \sqrt {1 + N_\varphi^2 } + N_\varphi$$

(26)

$$\sigma^p = \sigma^t N_\varphi - 2c\sqrt {N_\varphi }$$

(27)

If the stress falls within domain 1, then shear failure occurs, and the new stress is revised using the flow rule derived from g_s. If the stress falls within domain 2, then tensile failure occurs, and the new stress is re-calculated adopting the flow rule derived from g_t.

Expressing Eqs. (20) and (24) in the principal axes, the definition of the trial stresses can be written as follows:

$$S_i^N = \hat{S}_i^N - \frac{1}{a}\Delta e_i^3$$

(28)

$$\sigma_0^N = \hat{\sigma }_0^N - K\Delta \varepsilon_{{\text{vol}}}^3$$

(29)

Adding (28) and (29) and expressing the result in principal axes yields:

$$\left\{ \begin{gathered} \sigma_1^N = \hat{\sigma }_1^N - [\alpha_1 \Delta \varepsilon_1^3 + \alpha_2 (\Delta \varepsilon_2^3 + \Delta \varepsilon_3^3 )] \hfill \\ \sigma_2^N = \hat{\sigma }_2^N - [\alpha_1 \Delta \varepsilon_2^3 + \alpha_2 (\Delta \varepsilon_1^3 + \Delta \varepsilon_3^3 )] \hfill \\ \sigma_3^N = \hat{\sigma }_3^N - [\alpha_1 \Delta \varepsilon_3^3 + \alpha_2 (\Delta \varepsilon_1^3 + \Delta \varepsilon_2^3 )] \hfill \\ \end{gathered} \right.$$

(30)

where

$$\alpha_1 = K + \frac{2}{3a}$$

(31)

$$\alpha_2 = K - \frac{1}{3a}$$

(32)

For shear failure, partial differentiation of Eq. (12):

$$\left\{ {\begin{array}{l} {\frac{{\partial g^s }}{{\partial \sigma _1 }} = 1}\\ {\frac{{\partial g^s }}{{\partial \sigma _2 }} = 0} \\ {\frac{{\partial g^s }}{{\partial \sigma _3 }} = - N_\psi } \\ \end{array} } \right.$$

(33)

Substituting Eq. (33) into Eq. (30) yields:

$$\left\{ \begin{gathered} \sigma_1^N = \hat{\sigma }_1^N - \lambda^* [\alpha_1 - \alpha_2 N_\psi ] \hfill \\ \sigma_2^N = \hat{\sigma }_2^N - \lambda^* \alpha_2 (1 - N_\psi ) \hfill \\ \sigma_3^N = \hat{\sigma }_3^N - \lambda^* (\alpha_2 - \alpha_1 N_\psi ) \hfill \\ \end{gathered} \right.$$

(34)

where

$$\lambda^* = \frac{f^s }{{(\alpha_1 - \alpha_2 N_\psi ) - ( - \alpha_1 N_\psi + \alpha_2 )N_\varphi }}$$

(35)

For tensile failure, partial differentiation of Eq. 13:

$$\left\{ {\begin{array}{l} {\frac{{\partial g^t }}{{\partial \sigma _1 }} = 0} \\ {\frac{{\partial g^t }}{{\partial \sigma _2 }} = 0} \\ {\frac{{\partial g^t }}{{\partial \sigma _3 }} = - 1} \\ \end{array} } \right.$$

(36)

Substituting Eq. (36) into Eq. (30) yields:

$$\left\{ \begin{gathered} \sigma_1^N = \hat{\sigma }_1^N - \lambda^* \alpha_2 \hfill \\ \sigma_2^N = \hat{\sigma }_2^N - \lambda^* \alpha_2 \hfill \\ \sigma_3^N = \hat{\sigma }_3^N - \lambda^* \alpha_1 \hfill \\ \end{gathered} \right.$$

(37)

where

$$\lambda^* = \frac{\sigma_3 - \sigma_t }{{\alpha_1 }}$$

(38)

The flow chart of the implementation of DCVISC in FLAC3D is shown in Fig. 23.

Fig. 23

Flow chart of the implementation of DCVISC in FLAC3D

Appendix II: Determination of the factor safety of a segmental liner

The factor of safety is the most intuitive index to evaluate the safety of segment. We adopted the calculation method recommended in the design specification of highway tunnel [23]:

• 1. For e₀ ≤ 0.2 h, the load-bearing capacity of lining is controlled by the compressive strength of concrete. Thus, its safety factor can be calculated using Eq. (39).

  $$K = \frac{\phi \alpha R_a bh}{N}$$

  (39)

  where K is safety factor, R_a is the compressive strength, N is axial force, b is the width of section, h is the height of section, φ is longitudinal bending coefficient of lining, α is eccentricity influence coefficient of axial force:

  $$\alpha = 1 + 0.648(e_0 {/}h) - 12.569(e_0 {/}h)^2 + 15.444(e_0 {/}h)^3$$

  (40)

  where

  $$e_0 = N{/}M$$

  (41)

  where e₀ is eccentricity of axial force and M is the bending moment.

• 2. For e₀ > 0.2 h, the load-bearing capacity of lining is controlled by the tensile strength of concrete. Thus, its safety factor can be calculated using Eq. (II.4):

  $$K = \varphi \frac{1.75R_l bh}{{\frac{6e_0 }{h} - 1}} \times \frac{1}{N}$$

  (42)

  where R_l is the tensile strength of concrete.