1 Introduction

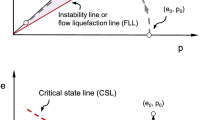
Flow liquefaction, also known as static liquefaction or flow slide, is a phenomenon that a granular soil mass, when subjected to a perturbance, undergoes a sudden loss of strength and a rapid development of deformation, accompanied by a quick buildup of pore water pressure. The consequences of flow liquefaction are often dramatic and devastating. Notable cases include the collapse of Fort Peck Dam [6], the flow slides of a submarine berm [31] and the failure of Stava tailings dams [7]. Over the past decades, a great deal of efforts has been made to investigate the mechanisms of flow liquefaction [3, 6, 9, 21, 23, 26, 31, 32, 36, 37, 39], leading to a framework of understanding and analysis that is now widely accepted. The key concepts of the framework include (a) the existence of a critical state line in the stress space (Fig. 1), which is the locus of ultimate states of shear failure, termed as steady state or critical state and (b) the existence of a flow liquefaction line or instability line, which links the peak in the stress path and the origin. The two lines in the stress space define a zone of potential instability in which loose granular soil tends to become unstable when a perturbation is imposed. It is worth noting that the instability line is not an intrinsic property but depends on both void ratio and mean effective stress, and its gradient can be related to the initial state parameter (ψ0) of the soil as follows [37]:

$$ \eta _{{{\text{IL}}}} = \left( {\frac{q}{{p^{\prime } }}} \right)_{{{\text{IL}}}} = \frac{{M_{{\text{c}}} }}{B}\, \exp \left( {A \phi_{0} } \right) $$
(1)

where Mc is the gradient of the critical state locus; A and B are two soil-specific parameters. As shown in Fig. 1, the state parameter is a measure of how far the initial state is from the critical state in terms of density [3]. The implication of Eq. (1) is that a granular soil mass at a medium dense state may also have the potential for liquefaction as long as the confining stress is sufficiently high.

Fig. 1
figure 1

Undrained monotonic loading of loose sand leading to flow liquefaction in the context of critical state concepts (after [39]): a q–p′ plane and b e–p′ plane

Full size image

Most of the studies on flow liquefaction have tended to focus on isotropically consolidated specimens subjected to undrained shear. This condition, however, does not properly replicate in situ stress conditions typical for slopes and dams—in which a static, driving shear stress exists in the element of soil prior to external loading (Fig. 2a). There have been concerns about the potential effect of the initial shear stress. For example Fourie and Tshabalala [18] reported an investigation of a tailings dam failure in South Africa, arguing that the use of the friction angle corresponding to the instability line determined from isotropically consolidated specimens would lead to unreasonably low values of factor of safety. They carried out undrained triaxial tests on isotropically and K0 consolidated specimens of tailings material, concluding that the instability line determined from K0 consolidated specimens is positioned steeper in the stress space, thus giving a larger friction angle and a higher factor of safety. This conclusion appears to be counterintuitive, since it suggests that the presence of initial shear stress is beneficial to the safety of slopes. More recently, Yang et al. [39] reported new data sets obtained from a specifically designed experimental programme, showing that no notable difference exists between the stress ratios at the onset of instability for isotropically and anisotropically consolidated specimens, as long as their post-consolidation states are similar, and that the critical state concepts are applicable.

Fig. 2
figure 2

Schematic illustration of stress state changes induced by pore water pressure rise in association with rainfall: a field condition and b laboratory simulation using constant shear drained (CSD) test

Full size image

Adding to the complexity is that flow liquefaction can also be initiated under drained conditions, as evidenced by a number of rainfall-induced slope failures. Among the tragic case histories are the collapse of a coal waste tip in Aberfan (South Wales) in 1966, which killed 144 people including 116 schoolchildren, and the massive slides of a large fill slope in Sau Mau Ping (Hong Kong) in 1972, which claimed 76 lives. There is now a general agreement that a perched water table as a result of rainfall infiltration can be a critical cause for flow slides [8, 35]. In laboratory experiment, the field stress path can be replicated using the so-called constant shear drained (CSD) test in which rise in pore water pressure, due to water infiltration, causes a decrease in mean effective stress at an almost constant shear stress [5, 29]. Since the stress path is largely different from that in conventional undrained triaxial tests, there is growing interest in the mechanical behaviour of soils in the CSD tests [1, 2, 10, 12, 15, 22, 25, 34]. These studies have created valuable data that contribute to the development of fundamental understanding of the problem. Nevertheless, existing views on several critical issues remain rather diverse or controversy. It is noticed that theoretical prediction of the condition for instability using advanced constitutive laws or the notion of loss of controllability [20, 28] is not in agreement with experimental results. Adding to this complexity, several researchers reported that for loose sandy soil specimens, where the state parameter (ψ) is positive, contraction will not occur along the CSD stress path but can occur on the conventional undrained triaxial stress path [22]. Also, the final states of the specimens in many of the reported experiments did not fall close to the corresponding critical state loci established from the conventional triaxial compression tests.

These observed discrepancies are not trivial but bring about significant conceptual difficulties, since they indicate that both instability line and critical state line are stress path dependent. The implication is that the existing analysis framework, established from extensive undrained triaxial tests in conjunction with the critical state concepts, is of little use in the evaluation of flow liquefaction associated with the CSD stress path. In this paper, an attempt is made to address the concerns arising from these discrepancies, by combining theoretical and experimental considerations and paying attention to several fundamental questions: (a) How the mechanisms of flow liquefaction under drained conditions differ from that under conventional undrained conditions? (b) Whether the instability line determined from the CSD tests differs from that determined from the anisotropic or isotropic undrained triaxial tests? (c) Whether the instability line from the CSD tests is dependent on void ratio and effective confining stress? and (d) If yes, can this state dependence be collectively accounted for using the critical state concepts?

2 Theoretical and experimental considerations

For the sake of simplicity, discussion is limited to the triaxial setting commonly used in soil mechanics, but it can be generalised to multiaxial conditions without difficulty. In elastoplasticity, the relationship between stress and strain increments can be established for triaxial setting as follows [38]:

$$ \left\{ {\begin{array}{*{20}c} {dp^{\prime } } \\ {dq} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {C_{pp} } & {C_{pq} } \\ {C_{qp} } & {C_{qq} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {d\varepsilon_{{\text{v}}}^{{\text{e}}} + d\varepsilon_{{\text{v}}}^{{\text{p}}} } \\ {d\varepsilon_{q}^{{\text{e}}} + d\varepsilon_{q}^{{\text{p}}} } \\ \end{array} } \right\} = \left[ C \right]\left\{ {\begin{array}{*{20}c} {d\varepsilon_{{\text{v}}} } \\ {d\varepsilon_{q} } \\ \end{array} } \right\} $$
(2)

where p′ is mean effective stress, and q is deviatoric stress; \(\varepsilon_{{\text{v}}}\) is volumetric strain, and \(\varepsilon_{q} \) is deviatoric strain; the superscripts e and p denote elastic and plastic strain components, respectively. The four components of the elastoplastic stiffness matrix [C] can be determined for a given constitutive model. For stress-controlled tests in laboratory, dp and dq are considered control variables; for example dq = 0 and dp′ < 0 are prescribed in CSD tests (Fig. 2). If onset of instability is regarded as loss of controllability or uniqueness in the test [20], mathematically, this requires vanishing determinant of the stiffness matrix in Eq. (2), i.e. det[C] = 0. This is exactly the derivation used in several studies [28] to generate the theoretical prediction. One may note that the condition of det[C] = 0 is equivalent to Kp = 0, where Kp is known as plastic hardening modulus in elastoplasticity [38]. Therefore, the condition leading to instability along the CSD stress path is coincident with the condition leading to failure in conventional drained triaxial tests [38]; that is for loose sand, the onset of instability occurs at the critical state, whereas for dense sand, the onset of instability occurs at the peak state.

While the above derivation appears to be theoretically sound, it fails to yield correct prediction for the experimental observation. The reason is that the derivation overlooks an important fact of the CSD tests, that is the test is not a conventional stress-controlled test. In conducting CSD tests on triaxial apparatus, two methods are generally adopted: One is to reduce the confining pressure at a given rate while maintaining the shear stress constant, and the other method is to maintain the confining pressure unchanged while increasing the back pressure. In both methods, the pore water pressure in the specimen is under control such that the volume change of the specimen is not entirely free.

Another line of analysing flow liquefaction is to treat it as an instability behaviour and employ the classic Hill’s stability criterion [4, 13]. In accordance with Hill’s criterion [19] and for triaxial setting, the condition for a material being stable is given as follows:

$$ d^{2} W = \left( {dp^{\prime } d\varepsilon_{{\text{v}}} + dq\, d\varepsilon_{q} } \right) > 0 $$
(3)

where \(d^{2} W\) is the second-order work per unit volume of the material. For a perfect CSD test in which dq = 0, the condition leading to instability becomes \(d\varepsilon_{{\text{v}}} = 0\). However, it has been frequently observed in CSD tests that a strictly constant shear stress cannot be achieved [10, 25, 30], due to inherent difficulty. This implies that instability can be initiated under conditions other than \(d\varepsilon_{{\text{v}}} = 0\). Depending on the sign of dq, the volumetric strain increment (\(d\varepsilon_{{\text{v}}}\)) at onset of instability can be positive or negative in accordance with Eq. (3). Owing to this difficulty and other uncertainty, different criteria have been put forward to detect the onset of instability in CSD tests [10, 22, 25]. As a consequence, diverse views and confusion arise.

It is also noted that in the investigation of the instability behaviour along the CSD stress paths, one often chooses to compare the result with that from isotropically consolidated undrained tests (i.e. ICU tests) and assumes that these ICU tests give a unique instability line. This is not considered reasonable since there is now solid evidence that the instability line from ICU tests is not unique but depends on the post-consolidation state, as discussed earlier. A small change in void ratio can lead to a marked change in liquefaction potential of sand specimens in undrained tests [33, 41]. Furthermore, isotropic consolidation does not replicate the anisotropic stress state in a slope (Fig. 2). A rational and desirable comparison is that the CSD test and the anisotropic consolidation undrained test (ACU test) share a similar post-consolidation state in terms of void ratio, mean effective stress and deviatoric stress prior to shearing. From the experimental point of view, however, it is difficult to obtain systematic data sets that fulfil this requirement, as the behaviour of sandy soils is sensitive to void ratio. In the present study, an alternative strategy is used, which involves systematic simulations of the CSD, ACU and ICU stress paths in the framework of anisotropic critical state plasticity and Hill’s stability criterion.

3 Critical state plasticity modelling and calibration

A robust critical state-based modelling platform [11, 38] is modified in relation to the effect of fabric anisotropy [24, 42] to improve its predictive capability for a range of responses. The model formulations are briefly presented below for completeness. More details can be found in the relevant references. The yield surface of the model is a wedge in the q–p′ plot, and kinematic hardening law is assumed:

$$ f = \left\{ {\begin{array}{*{20}l} {\eta - \alpha - m = 0 \;\;\left( {\eta > \alpha } \right)} \hfill \\ {\eta - \alpha + m = 0\;\;\left( {\eta < \alpha } \right)} \hfill \\ \end{array} } \right. $$
(4)

where η is the stress ratio defined as q/p′, α is back stress and m is a constant defining the width of the wedge. The evolution of dilatancy is assumed to depend on state parameter, stress ratio and fabric anisotropic variable as follows:

$$ d = d_{0} \left[ {M_{{\text{c}}} \exp \left( {n^{d} \zeta } \right) - \eta } \right] $$
(5)

where Mc is the critical state stress ratio, d0 and \(n^{d}\) are material constants to be calibrated from experimental data. \(\zeta\) is dilatancy state parameter and is defined as\(\zeta = \psi - e_{A} \left( {A_{{\text{F}}} - 1} \right)\); here, \(e_{A}\) is a material constant, and \(A_{{\text{F}}}\) is a fabric anisotropy variable accounting for the combined effect of loading direction and deviatoric part of the fabric tensor:

$$ A_{{\text{F}}} = F_{ij }^{d} n_{ij} $$
(6)

The plastic hardening modulus is defined as follows:

$$ K_{p} = \frac{{G_{0} h_{0} \left( {1 - c_{h} e} \right)}}{{\left| {\eta - \eta_{in} } \right|}}\left( {\frac{{p^{\prime } }}{{p_{{{\text{at}}}} }}} \right)^{ - 1/2} \left[ {M_{{\text{c}}} \exp \left( { - n^{b} \zeta } \right) - \eta } \right] $$
(7)

where ηin is the stress ratio, and it is updated at loading reversal state, G0 is elastic modulus constant, h0, ch and \(n^{b} \) are material constants. The critical state locus in e–p′ plane is defined as follows:

$$ e_{{\text{c}}} = e_{\Gamma } - \lambda_{{\text{c}}} \left( {\frac{{p^{\prime } }}{{p_{{{\text{at}}}} }}} \right)^{\xi } $$
(8)

where \(e_{\Gamma }\), \(\lambda_{{\text{c}}} \) and \(\xi\) are critical state parameters, and they are related to particle characteristics [40]. The degree of fabric anisotropy is assumed to be controlled by the norm of the deviatoric part of fabric tensor (\(F^{d}\)), with initial value of Fin, and the fabric evolution law is described by

$$ dF^{d} = c_{f} \left( {1 - F^{d} } \right)\left| {d\varepsilon_{q}^{p} } \right| $$
(9)

where \(c_{f}\) controls the magnitude of evolution, and \(d\varepsilon_{q}^{p}\) is plastic deviatoric strain increment.

To calibrate the model parameters, a set of undrained triaxial tests was conducted on Toyoura sand, a uniform quartz sand that has been widely used in the laboratory for various purposes. Its mean particle size (D50) is 0.203 mm, and the coefficient of uniformity (Cu) is 1.474, with 0% fines content; its particles are subrounded to subangular. All the specimens were prepared by the moist tamping method and were carefully saturated. Figure 3a and b shows the results of four triaxial tests in terms of stress path and stress–strain curve; the four specimens were isotropically consolidated to the same stress level but differing void ratios.

Fig. 3
figure 3

Undrained shear behaviour of isotropically consolidated sand specimens at varying void ratios: a and b test results; c and d model simulations

Full size image

It can be seen that under otherwise identical conditions, a small variation in void ratio leads to a markedly different response, from non-liquefiable (e0 = 0.878) to highly liquefiable (e0 = 0.946). The behaviour in between these two cases (e0 = 0.894) is known as limited flow or partial liquefaction, being characterised by a peak strength followed by a limited period of strain softening and then a continuous dilation to high strength. The state corresponding to the local minimum strength, known as the quasi-steady state, is well captured. Using the results of the four triaxial tests, the model is calibrated, and the resulting parameters are given in Table 1. For comparison, the model responses are shown in Fig. 3c and d. Clearly, a good agreement is achieved for the range of responses. Figure 4 shows the critical state locus along with the experimental data in q–p′ plane and e–p′ plane. Note that all the simulations for the CSD, ACU and ICU stress paths in the present study are produced using the same set of model parameters, without any additional calibration or adjustment.

Table 1 Model parameters calibrated from experimental data
Full size table
Fig. 4
figure 4

Critical state locus (CSL) in a q–p’ plane and b e–p′ plane

Full size image

4 Behaviour under CSD and ACU stress paths

4.1 Influence of void ratio under CSD stress path

Figure 5 shows the simulation result for a very loose specimen of Toyoura sand. The specimen is subjected to isotropic consolidation to p0′ = 200 kPa and e0 = 0.960 (stage O to A), followed by standard drained triaxial compression to the anisotropic state where q = 200 kPa (stage of A to B), and then subjected to a constant q path by decreasing p′. It is noted that the pattern of axial strain response (Fig. 5c) is quite similar to that observed in experiments. A marked feature of Fig. 5 is that q is perfectly maintained constant throughout the test (Fig. 5a and b). Using Hill’s criterion, the state corresponding to vanishing second-order work is marked by triangles in the four plots. Clearly, large axial strain is about to accelerate at this state where the volumetric strain increment achieves zero (i.e. \(d\varepsilon_{{\text{v}}} = 0\)). Note that this state is not at the point where the curvature of the axial strain curve is maximum but appears a bit earlier. The instability line in the q–p′ plane (Fig. 5a) is markedly below the critical state line, confirming that the onset of instability is well inside the plastic limit.

Fig. 5
figure 5

CSD behaviour of sand at very loose state (e0 = 0.960, p0′ = 200 kPa): a stress path; b stress–strain relation; c evolution of axial strain and d volumetric strain–axial strain relation

Full size image

Figure 6 shows the simulation result for a medium loose specimen (e0 = 0.920) under otherwise identical conditions. While the overall response is similar to that of the very loose specimen, the specimen exhibits a prolonged stage of dilative response upon decreasing the confinement (Fig. 6d), and the onset of instability is closer to the point where the curvature is maximum (Fig. 6c). The instability line in the stress space is also located closer to the critical state locus, lending clear evidence for its state dependence. The results in Figs. 5 and 6 suggest that the resistance to flow failure can be significantly enhanced by decreasing a small amount of void ratio, and the behind mechanism is the dilatancy potential of the sand. To make the point clearer, Fig. 7 compares the evolution of volumetric strain and second-order work with mean effective stress of the two specimens. Although the two specimens share the same q and p′ prior to applying the constant q stress path, the very loose specimen undergoes a shorter and slighter dilation than the medium loose specimen and achieves zero second-order work at a smaller axial strain.

Fig. 6
figure 6

CSD behaviour of sand at medium loose state (e0 = 0.920, p0′ = 200 kPa): a effective stress path; b stress–strain relation; c evolution of axial strain and d volumetric strain–axial strain relation

Full size image
Fig. 7
figure 7

State dependence of CSD behaviour: a volumetric strain evolution and b second-order work evolution

Full size image

4.2 Influence of void ratio under ACU stress path

For better comparison, a pair of ACU tests is simulated for the two specimens as well, and the results are shown in Figs. 8 and 9, respectively. For the very loose specimen (e0 = 0.960), complete liquefaction is achieved, and its peak strength state exactly corresponds to vanishing second-order work. The axial strain level at the onset of instability is very small due to the presence of an initial shear stress of as high as 200 kPa, confirming the experimental observations of Yang et al. [39]. By comparison, the medium loose specimen (e0 = 0.920) displays the phenomenon of partial liquefaction or limited flow (Fig. 9), being characterised by a limited period of strain softening and then continuous dilation to higher strength. The quasi-steady state or phase transformation state under anisotropic consolidation is well captured here, see Fig. 9b and c. Furthermore, the gradient of the instability line is found to be largely increased in the case of lower void ratio, meaning that the instability line under the ACU conditions is not unique either, but is also state dependent.

Fig. 8
figure 8

ACU behaviour of sand at very loose state (e0 = 0.960, p0′ = 200 kPa): a stress path; b stress–strain relation; c evolution of axial strain and d volumetric strain–axial strain relationship

Full size image
Fig. 9
figure 9

ACU behaviour of sand at medium loose state (e0 = 0.920, p0′ = 200 kPa): a stress path; b stress–strain relation; c evolution of axial strain and d volumetric strain–axial strain relationship

Full size image

4.3 CSD stress path versus ACU stress path

Comparing the results in Figs. 8a and 9a with that in Figs. 5a and 6a, respectively, one may note that the gradient of the instability line under the ACU stress path is nearly the same with its counterpart under the CSD stress path. To confirm this finding, Fig. 10 presents results for two additional specimens which are isotropically consolidated to e0 = 0.960 and p0′ = 200 kPa, brought to the same anisotropic condition (q = 150 kPa) and then subjected to the CSD and ACU stress path, respectively. The state corresponding to vanishing second-order work is marked by triangles for the CSD test and by circles for the ACU test. It becomes evident that the two points for vanishing second-order work lie on the same line passing through the stress origin (Fig. 10a). Nevertheless, it should be noted that the two specimens display different patterns of second-order work evolution (Fig. 10c), and the specimen under the ACU stress path tends to lose stability earlier.

Fig. 10
figure 10

Model simulations of CSD and ACU tests at very loose state (e0 = 0.960, p0′ = 200 kPa, q = 150 kPa): a stress path; b stress–strain relation; c evolution of axial strain and d evolution of second-order work

Full size image

In Fig. 11, the responses under the CSD and ACU stress paths are compared in e–p′ plane with reference to the critical state locus, for the case of very loose specimen (e0 = 0.960, q = 200 kPa) and the case of medium loose specimen (e0 = 0.920, q = 200 kPa). For the former, the specimen undergoes slight dilation in the initial stage as the result of decreasing confining stress, which is followed by a strong contractive response towards the critical state locus. When the specimen is subjected to the ACU stress path, the effective confining stress decreases all the way to the fully liquefied state under the constraint of constant volume. For the medium loose specimen under the constant q path, it undergoes a moderate contractive response upon the initiation of instability, arriving at a state below the critical state locus in the e–p′ plane, and then displays a dilative response towards the critical state locus. Under the ACU stress path, the medium loose specimen follows a constant volume path to the left of the critical state locus, and the path then reverses towards the critical state locus. The reversal point corresponds to the phase transformation state. The results shown in Fig. 11 lend support that the critical state concepts work well for both CSD and ACU stress paths and for a range of loose states.

Fig. 11
figure 11

Comparison of CSD and ACU behaviour in e–p′ plane with reference of critical state line: a very loose state (e0 = 0.960, q = 200 kPa) and b medium loose state (e0 = 0.920, q = 200 kPa)

Full size image

So far, the simulations are for specimens looser than critical state. It is of interest to further explore the response characteristics of specimens denser than critical state in the CSD and ACU stress paths. In doing that, two additional specimens are isotropically consolidated to e0 = 0.910 and p0′ = 100 kPa and then brought to the same anisotropic condition (q = 100 kPa). The results are generated using the same set of parameters and are shown in Fig. 12. Along the ACU stress path, the specimen exhibits the limited flow behaviour, characterised by a limited strength reduction and subsequently a strong dilative response towards the critical state. For the CSD stress path, the specimen undergoes three stages of response in the e–p′ plane, all in the zone below the critical state locus: The first is a dilative response caused by reducing the confining stress, then a very brief and slight contractive response and finally a strong dilation to the critical state with a nearly constant p′. In the q–p′ plane, the two specimens share the same instability line which is located very close to the critical state line. Comparing Fig. 12a with Fig. 10a, the influence of density on the location of the instability line is evident. One can expect that when the post-consolidation void ratio is further reduced, the instability line will tend to emerge to the left of the critical state line in the q–p′ plane. In such case, there would be no strength reduction or strain softening under the ACU stress path. This implies that the instability of sufficiently dense soils is the mode of dilative failure rather than the diffuse mode for loose soils. In other words, the flow-type failure would not be possible for dense soils. Further discussion of the instability of dilative mode is worthwhile but is outside the scope of this study. Results will be presented in future.

Fig. 12
figure 12

CSD and ACU behaviour of sand at medium dense state (e0 = 0.910, p0′ = 100 kPa): a q–p’ plane; b stress–strain relation; c e–p′ plane and d volumetric strain–axial strain relation

Full size image

4.4 State parameter-dependent instability line

It is now interesting to examine whether the relationship in Eq. (1), derived from isotropic consolidation undrained tests, is valid regardless of stress paths applied. In doing so, a series of ICU tests is simulated along with the series of CSD and ACU tests. Two examples are shown in Fig. 13: One case is for complete liquefaction and the other for partial liquefaction. The results well confirm that the instability line varies with the post-consolidation state, although the difference in void ratio of the two specimens is only 0.04. In Fig. 14a, the stress ratio at onset of instability is plotted against initial state parameter (ψ0) for all CSD, ACU and ICU simulations (Table 2). Here, the initial state refers to the point after anisotropic consolidation and prior to shearing. It is clear that a unique relationship in the form of Eq. (1) fits the data points quite well, resulting in parameters A and B of − 4.85 and 1.08, respectively. If the state parameter corresponding to the onset of instability is used, the goodness of fit can be further improved, as shown in Fig. 14b. The significance of the finding in Fig. 14 is that the state dependence of the instability line is not affected by stress path, and the critical state concepts work consistently well. For practical applications, one can use conventional undrained triaxial tests on isotropically consolidated specimens to determine the relationship in Eq. (1) and then apply it to the CSD and ACU stress paths. Moreover, it is worth mentioning that the instability line so determined can also be applied to cyclic loading conditions because of the correspondence between monotonic and cyclic loading behaviours. An excellent example is provided in Fig. 15 where results of two specially designed tests on Toyoura sand are put together: One specimen was subjected to isotropic consolidation and then undrained monotonic loading to flow failure, and the other was anisotropically consolidated to a similar state in terms of void ratio and mean effective stress and then subjected to cyclic loading. One can see that when the cyclic stress path touched on the instability line (i.e. flow liquefaction line) determined from the monotonic loading test, flow failure was initiated in the form of abrupt runaway deformation. It should be noted that the undrained cyclic tests are often conducted under stress controlled, whereas the monotonic loading tests are often conducted under strain controlled to obtain reliable data after the onset of instability. For stress-controlled tests, the measurements after the onset of instability may not be reliable and thus should be used with caution in the evaluation of critical states.

Fig. 13
figure 13

State-dependent behaviour of sand in ICU test: a stress path and b stress–strain relation

Full size image
Fig. 14
figure 14

Unique relationship between stress ratio at onset of instability and state parameter: a initial state parameter and b current state parameter

Full size image
Table 2 Series of CSD, ACU and ICU stress path simulations
Full size table
Fig. 15
figure 15

Experimental evidence for linkage of monotonic and cyclic loading-induced flow liquefaction: a stress path and b stress–strain relation

Full size image

5 Discussion

Several studies in the literature have concluded that the onset of instability under drained constant shear conditions does not coincide with that under undrained conditions. While the possible reasons for the disagreement have been discussed in the preceding sections, further clarification and verification are desirable. Recalling the incremental stress–strain relationship in Eq. (2), one can readily obtain the following relation for the CSD stress path:

$$ \frac{{d\varepsilon_{{\text{v}}} }}{{d\varepsilon_{q} }} = - \frac{{C_{qq} }}{{C_{qp} }} = \omega $$
(10)

Apparently, vanishing second-order work requires \(C_{qq} = 0\).

On the other hand, the incremental stress–strain relationship in Eq. (2) can be written in an alternative form as follows:

$$ \left\{ {\begin{array}{*{20}c} {d\varepsilon_{{\text{v}}} } \\ {dq} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}l} {C_{pp}^{ - 1} } \hfill & {\quad - C_{pq} C_{pp}^{ - 1} } \hfill \\ {C_{qp} C_{pp}^{ - 1} } \hfill & {\quad C_{qq} - C_{pq} C_{qp} C_{pp}^{ - 1} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {dp} \\ {d\varepsilon_{q} } \\ \end{array} } \right\} $$
(11)

For undrained conditions, the loss of stability is equivalent to the loss of uniqueness, which requires:

$$ \det \left[ {\begin{array}{*{20}l} {C_{pp}^{ - 1} } \hfill & {\quad - C_{pq} C_{pp}^{ - 1} } \hfill \\ {C_{qp} C_{pp}^{ - 1} } \hfill & {\quad C_{qq} - C_{pq} C_{qp} C_{pp}^{ - 1} } \hfill \\ \end{array} } \right] = 0 $$
(12)

From Eq. (11), one can obtain \(C_{qq} = 0\). Hence, the condition leading to instability under drained conditions is exactly the same with that under undrained conditions, regardless of the constitutive model chosen. Following the procedure of Yang and Li [38] and for the plasticity model used here, the condition for onset of instability can further be derived as follows:

$$ \frac{{3GK_{p} p^{\prime } - 3KG\eta d\, {\text{sgn}} \left( {d\varepsilon_{q}^{p} } \right)}}{{3G + K_{p} p^{\prime } - dK\eta \, {\text{sgn}} \left( {d\varepsilon_{q}^{p} } \right)}} = 0 $$
(13)

where G and K are elastic shear modulus and bulk modulus, respectively, and both depend on the density and confining stress of the soil. This implies the onset of instability is state dependent, which is well consistent with experimental findings [37, 39].

It should be mentioned that the present study has been limited to the triaxial space. This is because most of the experimental data on soil behaviour have been obtained from triaxial tests, primarily triaxial compression tests. To study instability behaviour under more complex stress paths beyond the conventional triaxial space, the formulations need to be generalised to multiaxial conditions. This can be done without much difficulty. Nevertheless, the lack of quality experimental data under such general stress paths for model calibration and for validation of simulations is always a concern. Other interesting issues related to instability include, for example the effect of pre-shearing history [14], the effect of fines [27, 41] and the effect of anisotropy [16, 17]. Further research in both experimental and numerical aspects is needed.

6 Summary and conclusions

The diverse views in relation to the initiation of instability and flow failure in granular soils under drained and undrained conditions and the conceptual difficulties brought by the discrepancies have been discussed from theoretical and experimental points of view. The main results and findings of the study are summarised as follows:

  1. (a)

    The constant shear drained (CSD) stress path is not a conventional stress-controlled test where dq and dp′ are prescribed, but is a special one with the volume change under certain control. Overlooking this fact in theoretical analysis may result in the conclusion that loss of instability along the CSD stress path occurs when the plastic hardening modulus becomes zero during loading. This conclusion is misleading and is not supported by the experimental observation that the loss of instability in loose granular soils occurs well within the plastic limit and is a diffuse mode.

  2. (b)

    The CSD stress path in laboratory experiments involves several inherent difficulties and uncertainties such that a strictly constant shear stress often cannot be achieved, and the experimental data are often noisy. This is considered the main reason why different criteria were put forward to determine the onset of instability in experimental studies, and why diverse views arose. Owing to the nature of the CSD tests, the response recorded after the onset of instability in experiments may not be reliable and thus should be used with caution in the evaluation of critical states.

  3. (c)

    The specifically designed simulations for CSD and ACU stress paths under a range of initial states indicate that the condition leading to instability along the CSD stress path is coincident with that for the ACU stress path, provided that they share the same initial state prior to shearing. While sharing the same instability line in the stress space, they, however, display different evolution patterns of the second-order work, and loss of instability tends to occur earlier under the ACU stress path.

  4. (d)

    For very loose sand that exhibits complete liquefaction under undrained shear conditions, its response to the CSD stress path is characterised by two stages: Initial dilation caused by reducing the confining stress and subsequent contraction following the onset of instability. For medium loose to medium dense sand that exbibits partial liquefaction or partial strain softening under undrained conditions, the response along the CSD stress path consists of three stages: first dilation, then contraction and finally dilation again towards the critical state.

  5. (e)

    The state dependence of the instability line is confirmed for CSD, ACU and ICU stress paths using systematic simulations for a range of initial states. This state dependence can be characterised using the initial state parameter defined with reference to the critical state locus. The relationship between the gradient of the instability line and the state parameter can be well described by an exponential function, which is nearly unique for a given soil regardless of the CSD, ACU or ICU stress path. Theoretically, it has shown that the conditions for instability under these different stress paths are exactly the same, regardless of the constitutive models chosen.

Further validation of the above findings using experimental data of both drained and undrained stress paths and extending the study from the compressional regime to the extensional regime are worthwhile. The uncertainty and difficulty involved in the laboratory CSD test, however, needs to be carefully addressed.