1 Introduction

It has been demonstrated through long-term observations that the rockfill dams and high filled ground in mountainous areas show significant time-dependent post-construction settlement, which has become a major threat to the serviceability and safety of these structures and deserves much concern [55, 56]. The time-dependent breakage behavior of rockfill material that is attributed to the large size and angular shape of particles is the major cause of this phenomenon [43, 47]. The particle breakage and creep behavior of rockfill materials have been widely studied in terms of laboratory test, constitutive modeling and numerical simulation [10, 36, 50, 51]. Among these studies, the DEM simulation has gained more and more attention because it is capable of modeling the discrete structures of granular materials and particle breakage by considering the interaction of separate elements [13, 15]. Prominent advantages of DEM models have been demonstrated in the studies of laboratory test simulation, microscopic mechanism analysis, size effects and so on [1, 4, 13, 17, 25, 26, 32, 34, 51, 54, 58].

Several methods for considering the particle breakage phenomenon in PFC2D/3D models can be found from the literature review: (1) the breakage of clusters which are formed by attaching some disks/spheres together with deformable and breakable bonds. If the shear or tensile force reaches the corresponding strength, the bond will break and the disk/sphere will depart from the cluster. Robertson and Bolton [51] and Cheng et al. [13] develop a cluster model in PFC3D for simulating the crushing behavior of sand particles. Shao et al. [54] and Jiang and Xu [25] adopt clusters to model the breakage of rockfill particles as well; (2) the breakage of clumps: Lobo-Guerrero and Vallejo [32], Lobo-Guerrero et al. [34], Deluzarche and Cambou [17] and Alaei and Mahboubi [1] use clumps formed by attaching several disks or spheres that cannot have any relative displacement during cycling, to simulate the rockfill particle. The clump will be replaced by predefined finer grains if the tensile stress calculated from the loading conditions of the clump exceeds the predefined tensile strength. This model cannot simulate the various breakage patterns owing to the stress concentration of irregular particles, despite its higher efficiency than the cluster models; (3) particle removal: Couroyer et al. [16] proposed that if the maximum normal contact force of a particle reaches its crushing strength value, the particle is considered as broken and is removed from the assembly. Particle removal is thought to represent cases where the parent grain crushes into dust that falls into the large inter-particle void space; and (4) reducing the contact stiffness of a grain: Marketos and Bolton [39] introduced the stiffness reduction to simulate the situation where the fragments can still carry some force immediately after breakage, with deformation of inter-fragment voids making the local response less stiff.

Compared to the modeling of particle breakage, the simulation of creep gained relatively less attention. Soil creep may be caused by delayed grain breakage [4, 28, 49] and reorientation or time-delayed sliding of particles [27]. For rockfill materials, particle breakage is more pronounced. Therefore, in this paper, the main focus is on creep due to delayed particle breakage, which is also widely suggested for rockfill material. Tran et al. [58] made the strength of the bond decay with time in PFC2D based on the time-independent model proposed by Deluzarche and Cambou [17] so that the delayed failure of particles and creep can be simulated. The parameters related to the time-dependent strength decay need to be calibrated according to creep tests which are performed up to failure on rock blocks. However, the calibration is quite difficult due to the limited amount of test data. Alonso et al. [4] developed a useful and novel DEM model in PFC3D based on the creep theory of rockfill proposed by Oldecop and Alonso [47, 49]. This DEM model can consider the delayed particle breakage phenomenon on the micro level by incorporating the theory of subcritical crack propagation into the model. The particle was modeled as a pyramid clump consisting of 14 elementary spherical particles. Only one crack was placed at a fixed position in each clump, where the maximum tensile stress was obtained by assimilating the clump to spheres of equivalent radius. The maximum length was limited to half of the particle’s size and was assumed to simply follow a distribution with uniform probability density function. The tensile stress and stress intensity factor of the cracks were then calculated, and the crack propagation velocity could be determined directly. When the crack length reached the mean dimension of the particle, the particle was assumed to be broken into two new particles of approximately equal shape and size (14 → 8+6; 8 → 4+4; 6 → 3+3; 4 → 2+2; 2 → 1+1). The model was used to simulate the oedometric creep behavior including the stress–strain relationship and the evolution of particle size distribution. In addition, the evolution of the short-term compressibility and creep indexes was studied in terms of the particle size.

Actually, the particles of rockfill material are often of angular shape and may result in complex breakage patterns including the global breakage of particles, the local breakage of vertices and various mixed breakage patterns, which cannot yet be fully considered by the model proposed by Alonso et al. [4]. The length of defects attributed to the particles is a key parameter and should be carefully studied and determined. In addition, the detailed creep mechanism of rockfill material still needs to be carefully studied. One important problem related to the creep mechanism of rockfill material is the size scale effect on the creep [3, 37, 40, 41]. Without knowing clearly the scale effect, creep tests in laboratory, where test samples with much reduced size particles have to be used due to the limitation of test equipments, cannot be used for practical engineering projects, such as rockfill dams and foundations where rockfill material with much larger particles is usually used.

Therefore, this paper proposes a further improved DEM model for the complex breakage and creep behavior of rockfill, by using the bonded clusters and introducing virtual cracks with random lengths. The model is able to simulate the complex breakage pattern including the breakage of the main body of the particles and angularity abrasion, as well as to reflect the scale effects on the breakage and creep behavior. Numerical single particle crushing tests are first conducted to carefully determine the statistical distribution of crack lengths according to Weibull’s statistical model of brittle failure and corresponding rules describing the size effects. Oedometric creep tests for rockfill are simulated by using this proposed model, and the results are compared to test data. The effects of stress levels are revealed, and the scale effects on the creep behavior are analyzed through the calculations of 35 specimens. Based on these analyses, preliminary formulas reflecting the effects of scales and stress levels are tentatively proposed.

2 Creep mechanism

2.1 Breakage of rockfill particles

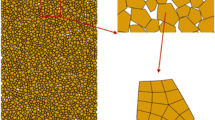
The mechanical behavior of rockfill is affected by particle breakage because of the relatively large particle size and angular particle shape [1, 4, 17, 21, 23, 25, 31, 35, 41, 49, 54, 58]. Larger particles usually possess more defects and faults than smaller particles and are often subjected to higher contact forces as well [1, 9, 29, 33]. Angular particles are found to experience more breakage than rounded particles because angular particles suffer stress concentration at their vertices [1, 20, 29, 30]. As shown by the photograph of breakage of the rockfill particle [2] in Fig. 1, two types of fragmentation can be commonly observed, including the local breakage, i.e., crushing of particle vertices or angularity abrasion, and the global breakage, i.e., cracking across a particle that divides it into several pieces [52, 53]. Nakata et al. [46] and Altuhafi and Coop [5] found that different gradings result in different types of particle breakage and compressive behavior. For uniformly graded samples, the particles mainly suffer abrupt splitting. For well-graded sand, there is a distinct difference in the crushing behavior. The larger particles will mainly suffer from asperity breakage, and there will be little particle splitting. Even in the single particle crushing test, due to the irregular shape, the particle breakage can be very complicated, which has been summarized by Cavarretta and O’Sullivan [11] as initial rotation, damage related to the asperity breakage, elastic response, fragmentation caused by the missing of parts of the bulk and the final crushing. It is therefore believed that in the case of rockfill that is characterized with particles of large size and irregular shape, the complex breakage patterns are very significant, which should be carefully considered in the simulation of creep behaviors related to particle breakage.

Fig. 1
figure 1

Stress corrosion, subcritical crack propagation and breakage patterns in rockfill [2, 28, 49]

Full size image

2.2 Stress corrosion and subcritical crack propagation

The general creep mechanism of rockfill and the detailed definition and calculation method, such as the definition of stress intensity factor, the judgement of subcritical cracks and the crack propagation velocity based on the stress corrosion mechanism, are introduced here as the most important theoretical basis of the proposed model, which can also be found in Oldecop and Alonso [48, 49]. As illustrated in Fig. 1, it is assumed by the general mechanism for the creep behavior of rockfill that the broken fragments generated by the time-dependent breakage of particles can fill the voids more efficiently, causing densification and settlement. The delayed breakage is found to be closely related to the crack growth in the particles, which is induced by the combined action of the applied stresses and water at the crack tip, known as the stress corrosion mechanism.

In stress corrosion, the chemical reaction between the rock and the water filling the crack is determined by the stress state at the crack tip. In linear elastic fracture mechanics [9], the stress intensity factor K is generally used to characterize the stress concentration in the vicinity of the crack tip. According to the stress intensity factor K as well as the fracture toughness K c and stress corrosion limit K 0, the state of a crack can be divided into three cases: (1) The crack does not develop at all if K < K 0 because stress corrosion is prevented; (2) the crack propagates at a velocity V if K 0 ≤ K < K c, which is also called the subcritical crack propagation; and (3) the crack fails and the particle breaks suddenly if K ≥ K c. For case 2, the velocity V can be calculated by the following phenomenological model proposed by Charles [12]:

$$ V = V_{0} \left( {\frac{K}{{K_{\text{c}} }}} \right)^{n} $$
(1)

where K c and K 0 can be considered as material properties. V 0 and n are the parameters of the equation, usually obtained by fitting experimental data. Experimental data reported by Wiederhorn et al. [60] suggested that the parameter n is not affected by the air relative humidity (RH) for a usual range of values (say 20–100 %). In addition, Freiman [19] suggested that V is almost positively linearly correlated with RH based on the test data, that is, the parameter V 0 includes the effect of RH. Therefore, when the rockfill material and relative humidity change, the corresponding effects can be considered by changing the two parameters in Eq. (1). Based on the propagation velocity of subcritical crack, the lifespan of the crack, i.e., the time elapsed between the instant of load application and the final breakage of the crack, can be derived as follows [49]:

$$ t = \frac{2}{n - 2}\frac{a}{V} $$
(2)

2.3 Statistical variation and size effect of particle crushing strength

As is well known, the crushing strength or the characteristic tensile strength of particles with the same diameter shows significant statistical variability due to the effect of flaws or weak zones [1, 13, 33, 42, 44, 45]. Since every specimen is unique with specific crack distribution including the crack location, direction, number and length, the tensile strength varies obviously, which leads to the survival probability for materials subjected to a specific tensile stress σ. The Weibull’s distribution function is proved to be able to describe this phenomenon mathematically [13, 33, 44, 45]. Weibull [59] proposed that for a block of a material under a uniform tensile stress σ, the probability of survival P s for the block is given by Eq. (3).

$$ \begin{aligned} P_{\text{s}} = \exp \left[ { - \left( {\frac{\sigma }{{\sigma_{0} }}} \right)^{m} } \right] \hfill \\ \ln [\ln (1/P_{\text{s}} )] = m\ln \left( {\frac{\sigma }{{\sigma_{0} }}} \right) \hfill \\ \end{aligned} $$
(3)

where σ 0 is the characteristic stress in which 1/e (37 %) of the samples survive; m is the Weibull modulus, which quantifies the scatter of strength values (i.e., high values of m indicate low scatter), as shown in Fig. 2. When σ/σ 0 = 0, all particles surely survive and thus P s is 1. When σ/σ 0 increases, more and more particles will fail, and P s decreases.

Fig. 2
figure 2

Weibull’s distribution function for tensile strength

Full size image

On the other hand, the larger the particle is, the higher will be the probability of having more and large-size cracks within the particle [6, 33]. In macroscopic view, larger particles may crush more easily under the same stress. Based on the weakest link proposition, Weibull [59] proposed that for a block of a material of volume V under a uniform tensile stress σ, the probability of survival P s is given by Eq. (4).

$$ P_{\text{s}} (V) = \exp \left[ { - \frac{V}{{V_{0} }}\left( {\frac{\sigma }{{\sigma_{0} }}} \right)^{m} } \right] $$
(4)

Here V 0 is the characteristic volume. Mcdowell and Amon [42] further proposed the following relationship between characteristic tensile strength σ 0 and particle diameter d,

$$ \sigma_{0,d} = \left( {\sigma_{0} d_{0}^{3/m} } \right)d^{ - 3/m} $$
(5)

where σ 0,d is the characteristic tensile strength of particle with volume V. It is indicated from this formula that the logarithm tensile strength has a negative linear relationship with the logarithm particle size with slope 3/m. This relationship has been validated by Lobo-Guerrero and Vallejo [33], who conducted more than 390 point load tests on samples made from two different rocks: a red Biotite Gneiss and a gray Quartzite.

3 Model proposed

According to the above analysis of the creep mechanism, the time-dependent breakage of rockfill particles can be easily considered by incorporating the subcritical crack propagation theory into the DEM model [2, 53]. Based on the theory, the cracks and their growth in the particle can be calculated and the delayed particle breakage is thus simulated. On the other hand, the complicated breakage phenomenon of the rockfill particle can be comprehensively simulated by the cluster model [13, 25, 26, 51, 54]. Therefore, it is proposed in this study to combine the cluster model with the subcritical crack propagation theory, which finally leads to a new DEM model with random virtual cracks to fully consider the angular shape, the complex breakage pattern and subcritical crack propagation in rockfill particles.

3.1 DEM model with random virtual cracks

As shown in Fig. 3, four typical shapes are chosen based on the observation of actual rockfill particles and corresponding clusters are adopted to model the particles to reflect its irregular shape in PFC2D [24]. It should be noted that the number of disks formulating the cluster determines the resolution of the model and has significant influences on the computational time for large-specimen DEM simulation. Because one of the objectives of this paper is to investigate the creep behavior of laboratory specimen in DEM and the virtual cracks that are introduced into the model will cause a large amount of additional calculation time, the number of particles that constitutes clusters must be small to run simulations in a reasonable time. In the model proposed by Cheng et al. [13] and Cil and Alshibli [14], totally 57 and 69 sub-particles are adopted to form an agglomerate, which is found to be sufficient to simulate the breakage behavior reasonably. In this study, the initial cluster is first created by bonding 61 individual disks together to form a regular assembly in hexagonal close packing (HCP). The final four kinds of clusters reflecting the different shapes are generated by removing some disks from the initial cluster, and in each of these clusters, there will be 29–53 disks.

Fig. 3
figure 3

Four different clusters for rockfill particles

Full size image

The contact bond in PFC2D is adopted in the proposed model for simplicity. Although this type of bond is point contact, it represents actually an adhesion surface of finite size between different parts within a particle. It can also be conceived as a parallel bond with the bending moments being neglected, which is reasonable when the disk diameter is relatively small. Then it is proposed here that the stress in the bonds can be calculated from the normal and tangential contact forces:

$$ \sigma_{n} = F_{n} /2r;{\kern 1pt} \quad \tau_{\text{s}} = F_{\text{s}} /2r $$
(6)

where r is the radius of the disks that form the clusters; σ n and τ s are, respectively, the normal and shear stresses acting at the bond in the plane tangential to the contact point; F n and F s are, respectively, the normal and tangential forces in the contact bonds.

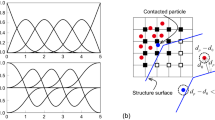
To simulate time-dependent breakage of particles, virtual cracks are randomly placed at the bonds within the clusters (particles) according to the characteristics of the rockfill as well as the disk size. The initial directions of the cracks are assumed to be perpendicular to the normal direction of the bonds, which is illustrated in Fig. 4. In the numerical example presented in Sect. 5, all the bonds are assumed to contain an initial crack. For general practical simulation, a probability value can be given for any bonds within a particle to contain an initial virtual crack. Then for each type of particles, all the bonds are numbered sequentially, and a proportion of these numbers are randomly generated according to the equal-probability principle that determines which bonds should contain an initial crack. For a bond with initial cracks, the stress intensity factor at the crack tip can be calculated by using the stresses calculated above when the normal stress is in tension:

$$ \begin{aligned} K_{\text{I}} = \beta_{\text{I}} \sigma_{n} \sqrt {\pi a} \hfill \\ K_{\text{II}} = \beta_{\text{II}} \tau_{\text{s}} \sqrt {\pi a} \hfill \\ \end{aligned} $$
(7)

where a equals half the length of the crack; β is a non-dimensional factor that reflects the influence of the position and the relative size of the crack in the particle, the geometry of the grain and the direction and position of the applied loads; and σ n and τ s are, respectively, the calculated normal and shear stresses across the crack without considering the cracks in the particle, which is in accordance with the theory in linear elastic fracture mechanics (see for instance Ref. [9]).

Fig. 4
figure 4

DEM model with virtual cracks

Full size image

It is worth noting that the coefficient β varies with different particle shapes and crack locations and is usually very difficult to find [57]. However, it can be found that in cases where the length of cracks is relatively small compared to the particle size, β usually approaches one. So in this model, it is assumed that β always equals to one for simplicity.

3.2 The maximum tangential stress theory

Cracks in rockfill particles are usually subjected to combined shear and tension, which is different from the assumption of simple tension state made by Alonso et al. [4] and Shao [53]. In addition, Kwok and Bolton [28] emphasized that crack growth in rocks is influenced by both the tensile force and the shear force. In this study, the maximum tangential stress theory proposed by Erdogan and Sih [18] is adopted as the failure criteria, which assumes that a crack propagates perpendicular to the direction of the maximum tangential tensile stress based on experimental observations. In 2D models, the stress at the crack tip can be expressed in polar coordinates:

$$ \begin{aligned} \sigma_{\text {rr}} &= \frac{1}{{2\sqrt {2\pi r} }}\left[ {K_{\text{I}} (3 - \cos \theta )\cos \frac{\theta }{2} + K_{\text{II}} (3\cos \theta - 1)\sin \frac{\theta }{2}} \right] \hfill \\ \sigma_{\uptheta \uptheta } &= \frac{1}{{2\sqrt {2\pi r} }}\cos \frac{\theta }{2}[K_{\text{I}} (1 + \cos \theta ) - 3K_{\text{II}} \sin \theta ] \hfill \\ \sigma_{{\rm r}\uptheta } &= \frac{1}{{2\sqrt {2\pi r} }}\cos \frac{\theta }{2}[K_{\text{I}} \sin \theta + K_{\text{II}} (3\cos \theta - 1)] \hfill \\ \end{aligned} $$
(8)

where σ rr, σ θθ and σ rθ are, respectively, the radial, tangential and shear stress component; K I and K II are, respectively, the stress intensity factor of cracks of mode I and II; r and θ are the polar coordinates.

The theory stipulates that: (1) The crack propagates along the direction θ 0 perpendicular to the direction of σ θθmax. For cracks of mode I, K II = 0 and θ 0 = 0, the crack will propagate along its own direction; for cracks of mode II, K I = 0 and θ 0 = −70°32′ and for cracks of mixed type,

$$ \theta_{0} = 2{\text{arctg}}\frac{{(K_{\text{I}} /K_{\text{II}} \pm \sqrt {(K_{\text{I}} /K_{\text{II}} )^{2} + 8} )}}{4} $$
(9)

(2) The crack will fail when the equivalent stress intensity factor K e reaches K IC.

$$ K_{\text{e}} = \frac{1}{2}\cos \frac{{\theta_{0} }}{2}[K_{\text{I}} (1 + \cos \theta_{0} ) - 3K_{\text{II}} \sin \theta_{0} ] $$
(10)

The tensile and shear strength of contact bonds within a particle should be set as very large numbers, even when virtual cracks are placed there, so that the bond will not break until the crack is judged to be broken according to the maximum tangential stress theory. When the stress intensity factor exceeds the limit, the direction of the crack propagation can be judged approximately by using Eq. (9) with consideration of the distribution of the adjacent bonds. Figure 4 illustrates so-determined breakage line for an initial crack where the stress intensity factor exceeds the limit. The cluster is then divided by the line into two parts, and the bonds lying between the two parts are all removed, i.e., the strengths are set to zero. As a result, the cluster is broken into two sub-clusters. If more than one crack in a cluster fails, the treatment is the same as above for each of the cracks; thus, complex breakage patterns can be realized.

One should notice that the breakage pattern in the proposed model may result in very angular sub-clusters that would be locked in space and lead to a high apparent friction. This may cause increased friction angle of the specimen, increased dilation, etc. The phenomenon is unavoidable in modeling particle breakage by clusters, because the angularity of the fragments is controlled by the size of disks/balls that formulate the cluster, except that the disks/balls are small enough. But in actual tests as shown in Fig. 1c, saw teeth or angularity can be observed on the fracture surface of fragments. Therefore, it seems that this high apparent friction is not too artificial.

3.3 Cracks in the model

As is stated in Sect. 2.3, the particle crushing strength shows significant statistical variability with the same diameter and obvious size effect with different diameters, due to the complex distribution of cracks. However, it is very difficult and unnecessary to fully consider all the factors reflecting the statistical variability of the crushing strength. In this study, the location and direction of cracks are set to be closely related to those of the bonds, and the number of cracks is determined by a certain proportion of the bond number, and then, the crack length is the only parameter that controls the crushing strength for simplicity. The ratio of the virtual crack length to particle diameter α = l/d (l = 2a) is attributed randomly between 0 and Α with a Gaussian distribution in which the mean value is 0.5Α and the standard deviation is s. To reflect the size effect, l max should be larger when the particle size increases.

$$ l_{\hbox{max} } = Ad $$
(11)

The crack lengths in a specific particle are thus controlled by parameters A and s.

It should be mentioned that by adopting the Gaussian distribution for the crack length ratio α = l/d unacceptable values, i.e., values larger than l max or less than zero, may be taken for the crack length. In the simulation model that will be directly prohibited. The error due to this treatment is believed to be negligible, as the probability for taking those unreasonable values is obviously very low.

Based on the crack length, which will be determined by numerical single particle crushing test in the next section, the crushing and time-dependent breakage of the rockfill particles can then be directly simulated with some additional basic property constants of rocks (i.e., V 0, n, K 0, K c).

4 Behavior of single particle crushing

The model developed above is now used to conduct the single particle crushing test to show the complex breakage pattern, the crushing strength that follows the Weibull statistics (Eq. 3) and corresponding size rules (Eq. 4) and to propose a routine method for determining the crack parameters.

4.1 Simulation of single particle crushing test

Single particle compression tests, in which just one particle is compressed between two rigid horizontal platens, are widely used as an index test to examine the susceptibility of a given rockfill particle to breakage. These tests can also help calibrate the DEM models that can capture the crushing and size–strength relationships [1, 5, 11, 13, 46]. In this study, the clusters are crushed between two smooth and stiff platens under displacement-controlled compression. Due to the variability of crack lengths, different peak stresses can be obtained.

Figure 5 presents typical results of the crushing tests for four different particle shapes (D = 1.8 cm). The normal and tangential stiffness are set to 1.5 × 108 N/m, and the local friction coefficient is set to 0.7. K c is set to 1 MPa m0.5 according to Oldecop and Alonso [49]. It is observed from the DEM results that different breakage patterns can be simulated. The different peaks on the force–displacement relationships are attributed to the particle rotation, vertex breakage, global breakage of clusters and secondary breakage of sub-clusters.

Fig. 5
figure 5

DEM simulation of single particle crushing test

Full size image

4.2 Determination of crack parameters

In the crushing test of single rockfill particle, the crushing strength is found to match the Weibull’s distribution [1, 13, 33], which can be achieved by changing the crack length of the particle model proposed above. In 2D cases, the maximum tensile stress (crushing strength) in the particle is assessed as [1]:

$$ \sigma = P/(\bar{d} \times 1) $$
(12)

where P is the peak load that is applied to the block by the loading plate; \( \bar{d} \) is the distance between two loading plates; and the thickness is equal to unity due to the model’s 2D background.

The survival probability of a batch of clusters can be calculated using the mean rank position [1, 13].

$$ P_{\text{s}} = 1 - i/(N + 1) $$
(13)

where i is the rank position of a grain when the grains are sorted into increasing order of peak stress and N is the number of tests (here N = 30). The survival probabilities under increasing stresses are N/(N + 1), (N − 1)/(N + 1), …, 1/(N + 1). The characteristic stress σ 0 can then be determined, and the Weibull modulus can be obtained by carrying out a least-squares regression according to the second formula in Eq. (3).

Figure 6 illustrates the relationship between the crack parameters A and s and the Weibull distribution parameter σ 0. It can be found that σ 0 decreases obviously with the increase in A, while s has very little effects on σ 0. In addition, the correlation between crack parameters A and s and the Weibull modulus m is shown in Fig. 7, where the particle with shape c (see Fig. 3) is considered. The correlations for clusters of the other shapes are very similar. It is found that the Weibull modulus m is directly influenced by both A and s, that is, m will increase with the increase in A and decrease in s. Based on the above analysis, the following method for determining the crack parameters can be drawn: The characteristic stress σ 0 and Weibull modulus m are obtained by fitting the test data; then, the parameter of mean crack length A can be determined by the characteristic stress σ 0, and finally, the standard deviation s can be obtained according to the Weibull modulus m.

Fig. 6
figure 6

Relationship between crack parameter A, s and characteristic strength σ 0

Full size image
Fig. 7
figure 7

Relationship between crack parameter A, s and Weibull modulus m

Full size image

4.3 Size effect of the crushing strength

Numerical single particle crushing tests for different particle size are also conducted and the results are shown in Fig. 8, where shape c is selected for the particle with A and s equal to 0.5 and 0.1, respectively. An obvious linear decrease tendency of the logarithm crushing strength σ with the increase in logarithm particle diameters can be found. The regression formula is also plotted in Fig. 8. The value of m is found to be 5.7, which is just the same as that obtained by calculation of the survival probabilities (Fig. 7). Therefore, it is indicated that the introduction of the Gauss distribution of crack length can reflect not only the Weibull distribution of single particle strength with similar sizes, but also the quantitative size effect of single particle strength with different sizes.

Fig. 8
figure 8

Crushing strength σ crush with different particle sizes

Full size image

5 Simulation of creep tests under oedometric condition

The model developed is now applied to simulate the oedometric creep tests, and the results are compared to test data. The effects of stress levels are revealed. The microscopic behavior, such as the evolution of particle breakage and load chains, is also analyzed.

5.1 Experimental information

Confined compressive creep tests were conducted on the broken limestone from the construction site of the Kunming New Airport [10, 61]. In this high filled ground project, the maximum altitude difference is about 210 m and the maximum filled height is about 54 m. The gravel coarse aggregate used in the high filled ground includes clastic rock and carbonatite rock. The construction method for the rockfill includes hierarchical dynamic compaction and rolling compaction. Due to the dimension limitation of the test equipment, the maximum particle size of the prototype specimen has to be reduced from 600 to 40 mm and the grading of the material is thus changed, which are presented in Fig. 9. Both the height and the diameter of the specimen for the oedometric creep tests are 200 mm. The ratio between the specimen size and maximum grain diameter is 5, which just satisfies the limit suggested by Head [22]. The dry density is 1.98 g/cm3 and the void ratio is 0.33. The load is applied step by step, and the loading levels are, respectively, 0.14, 0.34, 0.54, 0.74, 0.94 and 1.14 MPa. The load lasts for 1–2 h for 0.14 and 0.54 MPa, while 6–7 days for 0.34, 0.74, 0.94 and 1.14 MPa. The measured creep strain versus log time curves are shown in Fig. 10, which indicates that the initial strain rate and creep strain become larger with the increase in stress level generally, except stress level 0.94 MPa. In addition, the creep strain increases almost linearly with log time.

Fig. 9
figure 9

Particle grading of the prototype specimen and scaled test specimen

Full size image
Fig. 10
figure 10

Measured creep results by Cao [10]

Full size image

5.2 Sample creation

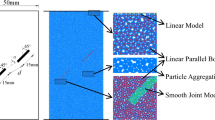
Now, test simulation by the proposed DEM model is conducted. In generating numerical test samples, the grading curve is truncated at a particle diameter of 5 mm to avoid small particles, as they may cause a large augmentation of the number of particles and consequently the computation time. The sample is created by following the steps: (1) The initial disks that match the particle grading are generated by using the radius expansion method (Fig. 11a); (2) these disks are randomly replaced by four kinds of clusters as shown in Fig. 3 (Fig. 11b). The number proportion for each of the four shapes is set to be equal in this simulation; (3) the sample was compacted by moving the upper and lower plates until the sample’s void ratio reached the desired value (Fig. 11c). In Fig. 11c, the particles, which are in contact and with the same color, are in the same cluster. In addition, a few small grains are seen floating. This is because it takes a long time to deposit the small grains completely. Considering that these small grains stay in the void between large particles and usually have little influence on the load distribution and transfer of the sample, this deposition process is not fully complemented so that the DEM simulation can be faster. When the sample is prepared, a random crack length is given to each of the bonds in all clusters. The crack length follows a normal distribution determined by the parameters A and s. During all the stages of sample preparation, crushing is prohibited according to the simulation method.

Fig. 11
figure 11

Numerical sample preparation

Full size image

In addition, two more different samples are generated according to the same principle (Fig. 12) in order to check whether simulations by using such generated model can give representative results.

Fig. 12
figure 12

Two additional random samples

Full size image

The parameters in the DEM model can be divided into three categories: (1) rock property parameters which can be determined by corresponding tests, including the fracture toughness K c, stress corrosion limit K 0 and the parameters in Charles law V 0 and n; (2) particle contact parameters in DEM, including the normal and tangential stiffness and the friction coefficient; and (3) crack parameters, A and s, which can be determined according to some single particle crushing tests. Here, the parameters of the Charles law V 0 = 0.1 m/s, n = 25, are chosen, being well within the range of the experimental data summarized by Oldecop and Alonso [49]. A fracture toughness K c = 1.0 MPa m0.5 is used, which is within the range of values reported (0.78–2.06 MPa m0.5) in the literature for limestones [7]. The stress corrosion limit is assumed to be K 0 = 0.3 K c as proposed by Atkinson and Meredith based on some theoretical considerations [8]. Since no single particle crushing tests have been conducted for similar limestones, and some typical values of m reported in the literature are 2.75 and 4.23 for the red Biotite Gneiss and the gray Quartzsite, respectively [33], the value of A and s is chosen to make the Weibull modulus equal to 3.7, as shown in Fig. 7. Table 1 lists all the parameters in this DEM simulation.

Table 1 Parameters used in the DEM model
Full size table

In the present study, two-dimensional models are used. In fact, simulations by using three-dimensional models should be more realistic. Comparing a two-dimensional model with a three-dimensional model, we may mention the following differences: (1) In 2D models, the particles are treated as plane strain disks, which cannot consider the actually existing particle interaction out of the plane. Then, the force transmission in a two-dimensional model will be also different from reality, whereas a 3D model may provide more possibility for a better simulation of the particle interaction and inter-particle force transmission; (2) 3D models may better simulate the actual complex particle breakage pattern than 2D models; and (3) the calculated specimen behavior at particle crushing may be also of some difference. Since broken particles will be subjected to more constraints from surrounding particles in 3D models than in 2D models, the creep strain caused by breakage may be less. Despite these shortcomings, it is believed that two-dimensional analysis is at least of qualitative values. Based on these considerations, two-dimensional model is used as a first step of creep simulation for the time being.

5.3 Discussion of time step and calculation procedure of the model

In a creep simulation, two independent times can be defined, i.e., numerical time and creep time [58]. Numerical time is the time consumed to make the system reach the balanced state after some particles break and can be evaluated by multiplying the number of calculation cycles by the time steps. In PFC2D, the time step is chosen carefully based on an estimation of the critical time step, which is related to the period of the system and usually is very small (10−7 s in this study) to ensure the computational stability because the motion equations are solved by an explicit time-stepping scheme [24]. On the other hand, creep time is the real time during which the propagation of each subcritical crack is predicted. The timescale of critical crack growth, i.e., the life of the subcritical crack, ranges from several seconds to hundreds of years, much larger than the numerical time step.

The simulation of creep consists of the two types of time steps alternately: (i) When breakage occurs, numerical time is needed to make the new system with broken clusters come to a new balanced state, and the macroscopic deformation is calculated. As this calculation is a process approaching gradually to the new stable deformation state, a convergence criterion is needed, and the tolerated error is set to be 0.001 (the ratio between strain increment in the current step to the accumulated strain till the last step) based on a compromise between efficiency and accuracy, and (ii) after the system balance calculation, creep time is applied to calculate the crack growth until the next breakage appears. To improve the calculation efficiency, the life spans of all the subcritical cracks are obtained at this step according to Eq. (2) and the minimum life t min is determined as the creep time step. During this stage, no numerical calculation is conducted and no change occurs in the system. All these calculations are purely mathematical for the virtual cracks: (1) The type of crack is judged according to the obtained stress conditions; (2) for each subcritical crack, the life span is calculated; (3) for all these life spans, the minimum is selected as t min; (4) the corresponding crack is set to be broken and corresponding bonds in the cluster are removed according to the position of the crack; (5) t min is added into the total creep time. That is, the whole simulation will proceed by a jump of time to time + t min after a subcritical crack break; and (6) numerical calculation begins, that is, all the particles begin to move, and the force distribution in the system changes.

Figure 13 shows the whole procedure for the calculation with this model. The calculation of stress, stress intensity factors and the failure criteria for particles have been all implemented into the program PFC2D via the FISH language [24].

Fig. 13
figure 13

The whole procedure of the proposed virtual crack DEM model

Full size image

5.4 Simulation results and verification

Before the creep simulation, a predefined pressure is applied on the sample by moving the top and the bottom platens. During all testing stages, the velocities of the top and bottom platens are controlled automatically by a numerical servo-mechanism to maintain a constant pressure on the sample, and the left and right walls are kept fixed. The loading scheme follows the experiment by Cao [10]. Figure 14 shows the deformation–time records for the load levels of 0.34, 0.74, 0.94 and 1.14 MPa, for which the laboratory tests lasted for 6–7 days. The simulated creep curves by using the generated samples are compared with the test data by Cao [10]. It can be seen from the comparison that the creep strain correlates reasonably with the test results in general. The creep curves calculated by using the three different randomly generated samples are also compared in Fig. 14, which shows that relatively large difference exists among these calculated creep curves for three samples, although the general shape and the final creep strain are similar. That may indicate more particles are required for generating the sample, and the particle shape as well as its size gradation should be also modeled more close to reality. For the time being we just used the first sample for the subsequent calculation to illustrate the proposed procedure.

Fig. 14
figure 14

Comparison of creep curves between test and DEM with different random samples

Full size image

5.5 Analysis of stress level influence and mesoscopic creep mechanism

Now, the same test specimen is simulated to creep under different vertical stress levels, respectively, including 0.54, 0.74, 1.14, 1.34, 1.54, 1.74 and 1.94 MPa. The creep simulation is assumed to be finished when no subcritical cracks exist or the creep time reaches 1 × 1010 s (about 300 years). As shown in Fig. 15, all the time history records show a similar pattern—an instantaneous deformation is followed by a delayed accumulation of strains. The number of broken particles and vertical strain during the instantaneous strain phase for each stress level is plotted in Fig. 16. It can be found that generally the higher the stress level is, the larger are the number of broken particles and the instantaneous strain. This figure shows that the instantaneous deformation of rock fills is usually much larger than the later developed creep deformation even after a relatively long time period, which agrees with the test results. Here it has been checked that there is no overlap of particles, which should be prevented by the computation procedure as well as the very large stiffness of the bonds.

Fig. 15
figure 15

Relationship between vertical deformation and time records under different stress levels

Full size image
Fig. 16
figure 16

Number of broken particles and vertical strain during the instantaneous strain phase. a Number of broken clusters. b Vertical strain

Full size image

To investigate the grading variation of the sample due to particle breakage, the particle grading of the sample before the test and after the creep simulation is presented in Fig. 17a. To verify this particle grading variation, the grain size change of the test by Cao [10] is also plotted in Fig. 17b. It can be seen from the figure that the simulated results have a similar evolution of grain size distribution with the test results. An increase in the fines content and a decrease in its average size can be observed from both experimental results and model prediction. Because the load lasts only 1–2 h in the experiment, which is obviously less than the simulated time, the grain size distribution in the test is found to have a less significant variation than that in the simulation. The comparison between the tests with different vertical stress levels demonstrates that a larger stress level results in higher particle breakage and increased variation in particle grading.

Fig. 17
figure 17

Particle grading before and after test for specimens with different vertical stresses. a Test results. b DEM results

Full size image

Long-term deformations are found (Fig. 15) to be almost linearly related to log(time). The long-term compressibility index is therefore calculated and compared with the test results reported by Cao [10], Ortega [50] and Oldecop and Alonso [49] and simulation results by Alonso et al. [4], as shown in Fig. 18.

$$ v_{t} = \Delta \varepsilon /\ln (t_{2} /t_{1} ) $$
(14)

where t 1 is the time value corresponding to the point on the strain–time curve that denotes the start of creep strain after the instantaneous deformation and t 2 is the total simulation period.

Fig. 18
figure 18

Long-term compressibility index for test specimens with different vertical stresses and comparison with other tests and DEM simulation

Full size image

It is found that the simulated and test results correlate well and the long-term compressibility index generally increases with the stress level, which can be explained from the microscopic behavior of the specimen, as illustrated in Fig. 19. The behavior of specimens under vertical stresses of 1.14 and 1.94 MPa is compared and analyzed. It can be found that more subcritical cracks appear under 1.94 MPa, which leads to more breakage in the sample and larger number of sub-clusters in the same simulation period. Therefore, the macro-strain and the long-term compressibility index of the specimen subjected to vertical stress of 1.94 MPa are larger.

Fig. 19
figure 19

Analysis of microscopic behavior of specimens under stress levels of 1.14 and 1.94 MPa. a Number of sub-clusters. b Number of subcritical cracks

Full size image

In Fig. 20, the creep behavior under stress level of 1.94 MPa is intensively analyzed to investigate the creep mechanism. The load chains in the sample before and after the creep simulation are compared in Fig. 20a, b. It can be found that particle breakage has influences on the load chains and thus leads to some changes of the load transfer. The load chains can be more dispersed, and the corresponding contact forces are reduced due to breakage. In addition, the detailed breakage pattern can be observed in Fig. 20c. Thanks to the application of clusters to model the particle breakage, the complex breakage pattern is well simulated. It is demonstrated in Fig. 20c that particles can develop various breakage patterns (Particle 1 and 2), including global breakage, local breakage and even complex mixed breakage.

Fig. 20
figure 20

Analysis of load chains and breakage pattern. a Load chains before creep. b Load chains after creep. c Broken clusters after creep

Full size image

As is well known, the sliding movement of sub-clusters after breakage is the main cause of macro-strains of the specimen. It can be observed from Fig. 20c that some of the sub-clusters cannot slide after breakage. Therefore, the breakage of these clusters cannot contribute to the macro-strain (Particle 1). Only those clusters that break and develop obvious sliding can lead to significant macro-strain, which is closely related to the pore structure of the sample (Particle 2). This mechanism can be further demonstrated from the comparison between the evolution of number of sub-clusters and strain magnitudes shown in Figs. 15 and 19. The steps on the creep strain–time curves (t ≈ 3 s and 5000 s) that show large increase in strain are corresponding to the breakage of only one or two clusters. On the other hand, a large number of breakage (t ≈ 104 s) may cause less obvious strain increase. It should be noted that the reason that the sub-clusters cannot slide is not only the constraint from adjacent particles but also the very angular fragments that may lock in space. This may cause increased friction angle of the specimen, increased dilation, etc. This phenomenon cannot be avoided in modeling particle breakage by clusters, because the angularity of the fragments is controlled by the size of disks/balls that formulate the cluster. In order to reduce this effect, the disks/balls need to be small enough, especially for large clusters. Therefore, to improve the model, it is suggested to use the same disks to generate the clusters with different sizes, i.e., the large clusters should consist of more disks/balls.

6 Scaling effects of rockfill creep

Rockfill is often used in the construction of large infrastructures such as embankments, dams and high filled ground of airports. The particle size in the rockfill can be over a meter. Common D 50 size in rockfill dams is in the range 10–40 cm. However, the largest testing apparatus reported [37, 38, 40, 41, 47] is only capable of testing aggregates with maximum particle size of 15–20 cm. Therefore, published experimental data for the mechanical behavior of rockfill are based on tests on scaled grain size distributions.

It has been proved by tests conducted on rockfill material with ‘similar’ grain size distributions but a varying mean grain size that the rockfill behavior is significantly influenced by particle size scale [3, 37, 40, 41]. Therefore, in this section, the proposed DEM model is used to simulate and discuss the important scale effect and to demonstrate the advantage of the model, which is a direct result coming from the application of the subcritical crack propagation theory in DEM.

In order to investigate the scale effect, the size of the specimen and all particles for sample 1 in Sect. 5.2 is increased with the same scale (2, 3, 6 and 12) to compare their creep behavior qualitatively (stress levels = 0.54, 0.74, 1.14, 1.34, 1.54, 1.74 and 1.94 MPa). The differences between the samples are the size of the specimen and all particles and the crack length. As the grain size changes, the crack parameters A and s remain the same, but the crack length (=Ad) will be larger for increased grain size.

The results of specimens with different scales (stress levels = 1.14 MPa) are compared in Figs. 21 and 22. It is found that the creep strain, the long-term compressibility index and the number of sub-clusters increase with the scale. As is emphasized in Sect. 2.3, specimen with larger size has larger particles and longer cracks in the particle, making the particle break more easily under the same stress level. So the number of sub-clusters increases, causing larger creep strain and long-term compressibility index.

Fig. 21
figure 21

Deformation–time curves of specimens with different sizes

Full size image
Fig. 22
figure 22

Breakage and particle grading of specimens with different particle sizes. a Number of sub-clusters. b Particle grading

Full size image

The creep velocities of all the 35 samples with different scales (1, 2, 3, 6 and 12) and stress levels are plotted in Fig. 23. The effect of stress levels has been demonstrated in Sect. 5.5 for scale 1 and is further verified for larger scales in this section. On the other hand, the larger the scale is, the higher is the creep rate. Two formulas can be developed to calculate the effect of stress levels and size scale on the creep rate. First, a formula that only includes the stress effect is proposed by using the regression method:

$$ v = a\sigma^{b} $$
(15)

where a and b are parameters related to the particle size, and σ is the stress level (MPa). The DEM results in Fig. 23 and test data from Ortega [50] in Fig. 17 are fitted by Eq. (15). The regression results are listed in Table 2. Then, the two coefficients a and b are further fitted with the maximum particle size d max:

$$ \begin{aligned} a &= 8.192d_{\hbox{max} }^{1.1794} \times 10^{ - 7} \hfill \\ b &= - 0.875\ln d_{\hbox{max} } + 5.56 \hfill \\ \end{aligned} $$
(16)

The accuracy of the proposed formulas for the long-term compressibility index for different stress levels and particle sizes is illustrated in Fig. 24. As can be seen, the formula can give reasonable prediction for the long-term compressibility index of rockfill under oedometric and dry conditions.

Fig. 23
figure 23

Long-term compressibility index for different sample scales and stress levels

Full size image
Table 2 Regression results for Eq. (15)
Full size table
Fig. 24
figure 24

Accuracy of Eqs. (15) and (16)

Full size image

7 Conclusions

This paper proposes a random virtual crack DEM model for rockfill creep in PFC2D, which is used to simulate the oedometric creep tests of rockfill material. The creep behavior and mechanism are investigated. In addition, the effects of scaling are analyzed. The following conclusions can be drawn from this study:

  1. 1.

    To simulate the irregular shape and complex breakage pattern of rockfill particles more accurately, the bonded clusters can be adopted to represent the rockfill particles. Time effects can be considered by placing virtual cracks with random lengths that are closely related to the particle size in the bonds of the clusters. The maximum tangential stress criterion can be employed to calculate the propagation direction of cracks under combined tension and shear.

  2. 2.

    The statistical distribution of crack lengths can be determined by numerical single particle crushing tests according to Weibull’s statistical model of brittle failure and corresponding size rules. It is shown that the complex breakage pattern, statistical variation and size effects of crushing strength of a single particle can be reflected quantitatively by the proposed model.

  3. 3.

    The model is used to simulate the oedometric creep tests of rockfill material and is validated by some test data. The analysis of stress effects on the oedometric creep behavior indicates that the long-term compressibility index, creep strain and particle breakage generally increase with the stress level. The mesoscopic analysis reveals that particles can develop various breakage patterns, including global breakage, local breakage and even complex mixed breakage.

  4. 4.

    The study of the effects of scaling on the oedometric creep behavior indicates that the creep strain, long-term compressibility index and the number of sub-clusters increase with the scale of the samples. Formulas are developed to estimate the effect of stress levels and size scale on the long-term compressibility index, which can give a reasonable and practical prediction of the creep rate of rockfill under oedometric and dry conditions.

However, it should be noted that the study is an initial step for the simulation of creep by using the discrete element method. The main points of this paper are given to illustrate the proposed simulation procedure, and the conclusions are mainly of qualitative value. For more refined analysis, three-dimensional models with much more particles should be used, and at the same time, the particle size gradation of the rockfill and the proper sliding along cracks are all need to be considered carefully. Besides, the effects of water, which are proved to be quite significant in engineering, should be carefully studied and incorporated in the model to simulate practical engineering problems.