1 Introduction

In numerical analysis of structures, soil–pile interaction can be modelled by means of linear spring elements [13, 15,16,17, 30, 31, 38, 39], neglecting the nonlinear behaviour of the soil–piles system. Nonetheless, during seismic loading a controlled yielding of the piles may produce favourable effects, dissipating seismic energy and limiting the seismic actions transferred to the superstructure [5]. In these cases, the capacity of piled foundations assumes a central role in evaluating the seismic performance of the superstructure. The nonlinear response of single piles subjected to vertical and horizontal loads can be accounted for in an uncoupled manner by assigning an elastic–plastic constitutive law to the springs placed along the shaft and at the pile tip [2, 40]. However, the global nonlinear response of pile groups is still affected by numerous uncertainties, such as the evaluation of the ultimate capacity under multi-axial loading. In engineering practice, the ultimate capacity of a pile group is typically evaluated independently for vertical and horizontal loads, assuming that the horizontal capacity is not influenced by the presence of external vertical forces and vice versa. By contrast, it is well known that the interaction between the loads acting on a geotechnical system can alter profoundly its overall resistance for the highly asymmetry in the soil behaviour, as it was demonstrated for the case of shallow foundations [1, 4, 6, 9, 24, 25, 28, 29, 34,35,36, 41] and bridge abutments [21,22,23]. In the context of a macroelement approach [12, 20, 41, 43], the effect of the interaction between the external loads on failure is represented by an ultimate limit state surface in the force space, associated with the activation of global plastic mechanisms of the system. In this regard, some formulations were proposed for foundation piles considering a three-axial load pattern including a vertical load, a horizontal load and a moment acting in a vertical plane of the foundation (in-plane load path). These studies, primarily based on pushover numerical analyses of specific soil–piles systems [10, 11, 18, 19], demonstrated the dependence of the ultimate capacity of the group on the direction of the resultant load and the essential role played by the inelastic response of the piles. Afterwards, Di Laora et al. [33] proposed an analytical solution for the bearing capacity of pile groups under vertical eccentric loads able to describe the in-plane failure surface.

In this study, we propose a generalised, analytical model of ultimate surface accounting for a full transmission of forces between the superstructure and the foundation piles. The ultimate loads of pile groups under multi-axial conditions are analysed through the development of a simplified numerical procedure based on the lower bound theorem of plastic limit analysis. The importance of considering the multi-axial capacity in the design of piled foundations is finally critically assessed by comparing the proposed approach with the classical standard design criterion.

2 Problem definition

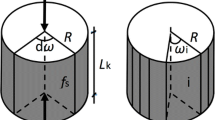
In this section, the proposed numerical procedure to determine the ultimate loads of a pile group under multi-axial loading is presented. Figure 1 depicts an illustrative layout of the piled foundation analysed in this study: it is composed of N piles connected to a rigid, suspended raft (not interacting with the soil) which the external generalised forces Qi = {Q1, Q2, Q3, QR1, QR2} are applied to. The contribution of the moment QR3 around the vertical axis is neglected. As a further simplifying hypothesis, the moments at the pile–raft connections are not included in the global balance equations of the foundation, since they do not affect significantly the ultimate conditions of the group [33], but are considered in the evaluation of the horizontal limit loads of the piles. Since the present study is aimed at evaluating the ultimate conditions of a pile group, only the strength of the individual components needs to be characterised. Therefore, both soil and pile behaviours are regarded as perfectly plastic, while the dependence of the yield moment Mn,y of the pile cross-section on the axial force Nn is explicitly considered. The interaction among the piles at failure is taken into account by efficiency coefficients, excluding a full block-type failure mode. This assumption can be deemed reasonable for a pile spacing larger than three diameters.

Fig. 1
figure 1

Schematic layout of the reference piled foundation (dimensions of the foundation in metres), with representation of the positive directions of the external forces Qi

Full size image

Failure of the pile group can be caused by two different global plastic mechanisms:

  • a vertical load mechanism caused by the attainment of the vertical limit load (compression or tensile capacity) in all piles;

  • a horizontal load mechanism due to the mobilisation of the horizontal limit load in all piles according to a long-pile failure mode; this is the case of piled foundations designed to carry significant vertical loads, which in most cases have a length larger than 10–15 diameters.

In the numerical procedure, the ultimate condition of the group for a prescribed load path is detected as the plastic mechanism that activates first, representing the weakest plastic mode, which varies with the load direction.

The vertical and horizontal limit loads of the single pile represent the input quantities for the numerical procedure, and several methodologies are available in the literature for their evaluation. In particular, the horizontal limit load of the group depends on the available yield moment in each pile, which is in turn a function of the respective axial force. In the presence of an external moment, the axial force is not uniform among the piles and is bounded by the axial capacity in compression and tension. Accordingly, the axial forces are determined by the following procedure to reproduce the progressive attainment of the strength among the piles as the external forces rise.

2.1 Incremental numerical procedure

The axial force \(N_{\text{n}}\) in the nth pile varies linearly with the vertical load Q3 up to the attainment of the respective compressive or tensile capacity, as follows:

$$N_{n} = \left\{ {\begin{array}{*{20}c} {\frac{{Q_{3} }}{N} + Q_{{\text{Ri}}} \cdot J_{{\text{ij}}}^{ - 1} \cdot x_{{\text{j},\text{n}}} ,N_{\lim }^{( - )} \le N_{\text{n}} \le N_{\lim }^{( + )} \quad 1(\text{a})} \\ {N_{\lim }^{( \pm )} ,N_{\text{n}} > N_{\lim }^{( + )} \,\text{or}\,N_{\text{n}} < N_{\lim }^{( - )} \quad \quad \quad \quad\,\,\,\, 1(\text{b})} \\ \end{array} } \right.$$

in which N(m) = Q3/N represents the mean axial force among the piles, the vector QRi = {QR2, QR1} lists the moment components around the horizontal axes and Jij is the inertia matrix of the pile group in the horizontal plane, which reads:

$$J_{{\text{ij}}} = \left[ {\begin{array}{*{20}c} {\sum\limits_{{\text{n} = 1}}^{\text{N}} {x_{{\text{n,2}}}^{2} } } & {\sum\limits_{{\text{n} = 1}}^{\text{N}} {x_{{\text{n,2}}} \cdot x_{{\text{n,1}}} } } \\ {\sum\limits_{{\text{n} = 1}}^{\text{N}} {x_{{\text{n,1}}} \cdot x_{{\text{n,2}}} } } & {\sum\limits_{{\text{n} = 1}}^{\text{N}} {x_{{\text{n,1}}}^{2} } } \\ \end{array} } \right]$$
(2)

where \(x_{{\text{n,i}}}\) is the coordinate of the nth pile in the i-direction.

In principle, if the piles had an infinite capacity, Eq. 1a would give directly the respective axial forces for any combination of the generalised loads. Instead, in the present study the soil–pile system exhibits more realistically a dissymmetric plastic behaviour that required the implementation of the following incremental procedure to properly compute the axial force at each load increment.

In the numerical procedure, the loads Qi are incremented gradually according to prescribed ratios between the load components. Then, an internal iterative calculation determines the axial forces in the piles: a trial, elastic distribution of \(N_{\text{n}}\) is initially computed through Eq. 1a, with a consequent check on the attainment of the axial capacity of the piles. If no pile has reached its vertical capacity, the trial axial forces satisfy both the equilibrium and the compatibility with the strength criterion in the vertical direction and the internal iteration stops. If the nth axial force is greater than the vertical capacity in compression or tension (\(N_{\lim }^{( \pm )}\)), an unbalanced axial force \(\Delta N\) and two unbalanced moments \(\Delta Q_{{\text{R1}}} = \Delta N \cdot x_{{\text{n,2}}}\) and \(\Delta Q_{{\text{R2}}} = \Delta N \cdot x_{{\text{n,1}}}\) generate, which must be balanced by the piles that have not reached their capacity yet. Accordingly, the terms of the inertia matrix are updated considering only the piles not yielded and the consequent roto-translation of the principal axes of inertia is computed by diagonalising Jij. (the principal axes of inertia are coincident with the physical 1- and 2-directions of the foundation only when the response of all piles is not plastic). Thus, a new distribution of the axial forces is computed through Eq. 1 considering also \(\Delta N\)–\(\Delta Q_{{\text{R1}}}\)–\(\Delta Q_{{\text{R2}}}\), and a new check follows on the compatibility of \(N_{\text{n}}\) with the axial capacity \(N_{\lim }^{( \pm )}\). This procedure iterates until balance and compatibility are satisfied. A vertical load mechanism is detected when all the piles reach the axial capacity.

The yield moment Mn,y of the pile cross-section is a function of the axial force \(N_{\text{n}}\) computed above, that is taken constant along the uppermost pile portion which is involved in the long-pile failure mechanism (typically five to ten diameters [32]). For compatibility with the strength criterion, the shear force \(H_{\text{n}}\) in the nth pile cannot be greater than its horizontal limit load \(H_{{\text{n,}\,\text{lim}}}\) and a horizontal plastic mechanism occurs when \(H_{\text{n}} = H_{{\text{lim}}}\) for n = 1,…,N. An equal lateral capacity is considered for each pile, as this may be deemed acceptable for foundations with a limited number of piles. The incremental calculation terminates when a failure mode (against vertical or horizontal loads) activates.

The proposed procedure respects the assumptions of the lower bound theorem of plastic limit analysis (perfectly plastic behaviour, equilibrium and compatibility with the strength criterion), and therefore, it can be thought to provide a conservative solution for the limit loads of the group.

2.2 Case study

The numerical procedure described above is applied to the soil–pile system depicted in Fig. 1. It is composed of N = 12 piles, of diameter D = 0.8 m, length L = 26 m and arranged in n1 = 4 rows in the 1-direction and n2 = 3 rows in the 2-direction. The same spacing i1 = i2 = 4D = 3.2 m is assumed in the two coordinate horizontal directions. The piles are reinforced concrete elements with a cross-section including 9 longitudinal 12-mm-diameter steel rebars spaced by 0.3 m, whose strength envelope is depicted in Fig. 2. In this manner, the yield moment Mn,y of the pile is a function of the respective axial force Nn. The subsoil is composed of a sandy soil with a ground water table located at zw = 2.0 m. The unit weight of the soil is equal to 16 kN/m3 and 17 kN/m3 above and below the ground water table, respectively.

Fig. 2
figure 2

Axial force–moment (N–M) strength envelope of the pile cross-section

Full size image

For simplicity, but without loss of generality of the procedure, in this study the compressive axial capacity of the single pile is computed in a decoupled manner as \(N_{{\text{lim}}}^{{\text{( + )}}} =\upeta _{\text{v}} \cdot \left( {N_{{\text{lim}}}^{{(\text{B})}} + N_{{\text{lim}}}^{{(\text{L})}} } \right)\), where \(N_{{\text{lim}}}^{{(\text{B})}}\) is the bearing capacity of the pile tip and \(N_{{\text{lim}}}^{{(\text{L})}}\) the shaft resistance, evaluated according to the expressions listed in Viggiani et al. [47]; \(\upeta _{\text{v}}\) is an equivalent efficiency of the pile group for vertical loads accounting for the mutual interaction among the piles, evaluated according to [27]. The tensile capacity \(N_{{\text{lim}}}^{( - )}\) of the single pile is equal to the lateral resistance \(N_{{\text{lim}}}^{{\text{(L)}}}\) only. The horizontal limit load \(H_{{\text{n,}\,\text{lim}}}\) of each pile is computed using the Broms method [3], considering an equivalent efficiency, \(\upeta _{\text{h}}\), of the group for horizontal loads evaluated through the solution proposed by Mokwa [37]. Of course, different solutions for the limit loads and for the equivalent efficiencies of the piles could be introduced in the proposed framework without altering the validity of the procedure.

3 In-plane failure mechanisms

In this section, we analyse the failure conditions of the reference pile group loaded separately by two force combinations \(Q_{\text{1}}\)–\(Q_{\text{3}}\)–\(Q_{{\text{R2}}}\), acting in the 1–3 vertical plane, and \(Q_{\text{2}}\)–\(Q_{\text{3}}\)–\(Q_{{\text{R1}}}\), relative to the 2–3 vertical plane (Fig. 1). Within the framework described in the previous section, the ultimate loads of a pile group are qualitatively identical for coarse- or fine-grained soils since the only difference consists in different expressions for the vertical and horizontal limit loads of the single pile. Therefore, only the case of a homogeneous sandy soil is tackled for brevity. A purely frictional strength criterion was assumed (c’ = 0 kPa) with an angle of shearing resistance φ′ = 35°.

In the incremental numerical procedure, the loads were progressively increased following a variety of loading paths. In order to represent the failure points in a homogeneous force space, the moment components were divided by the length B1 = 12.6 m of the raft, such that \(Q_{{\text{R1}}}^{*} = Q_{{\text{R1}}} /B_{\text{1}}\) and \(Q_{{\text{R2}}}^{*} = Q_{{\text{R2}}} /B_{1}\).

Figure 3 shows, in a deformed scale, the force combinations acting in the two coordinate vertical planes of the foundation that activate global plastic mechanisms of the group. Let us focus initially on the failure envelopes \(Q_{\text{1}}\)–\(Q_{\text{3}}\) and \(Q_{2}\)–\(Q_{\text{3}}\) in the absence of moment (\(Q_{{\text{R1}}}\) = \(Q_{{\text{R2}}}\) = 0). In the case of a sole vertical load, the positive and negative vertical limit loads, \(Q_{3,\,\lim }^{( + )}\) and \(Q_{3,\,\lim }^{( - )}\), are associated with the mobilisation of the bearing and tensile capacity in all piles, respectively. In this case, \(Q_{3,\,\lim }^{( + )} > > Q_{3,\,\lim }^{( - )}\) because the tensile capacity of the group is due to the attainment of the tensile capacity in the pile cross-section, which is lower than the tensile capacity \(N_{{\text{lim}}}^{( - )}\) of the soil–pile system. The horizontal limit loads \(Q_{1,\,\lim }\) and \(Q_{2,\,\lim }\) (\(Q_{\text{3}} = 0\)), more simply indicated as \(Q_{1 - 2,\,\lim }\), are identical because the horizontal efficiency adopted in this study does not vary with the load direction.

Fig. 3
figure 3

Force combinations Q2–Q3 and Q1–Q3 causing failure of the reference pile group, for different levels of the respective normalised moment QR1/QR1(max) and QR2/QR2(max) from 0 to 1.0, obtained with the proposed simplified framework (circles) and through advanced numerical analyses (triangles)

Full size image

The coupled limit load \(Q_{1 - 2,\,3}^{(\lim )} = \sqrt {Q_{1 - 2}^{2} + Q_{3}^{2} }\) increases when \(Q_{\text{3}}\) is directed downwards (\(Q_{\text{3}} > 0\)) because it increases the yield moment \(M_{{\text{n,}\,\text{y}}}\) of the piles and vice versa when \(Q_{\text{3}}\) is directed upwards (\(Q_{\text{3}} < 0\)). The direct proportionality between \(Q_{\text{3}}\) and \(M_{{\text{n,}\,\text{y}}}\) is due to the fact that in this case the maximum axial forces in the piles are equal to \(N^{(\max )}\) = \(Q_{{\text{3,}\,\text{lim}}}^{( + )} /N\) = 4.2 MN, involving the region of the strength envelope of the pile cross-section in which the variation of the yield moment agrees with the variation of the axial force, excluding the possibility to have fragile plastic mechanisms. Notwithstanding, it was seen that if the axial force \(N_{\text{n}}\) is larger than 4.2 MN the limit domain in Fig. 3 contracts keeping its shape unchanged.

In the present case, the failure mode is driven by the attainment of the vertical limit load if \(Q_{1 - 2} < 0.1 \times Q_{3}\) while a horizontal plastic mechanism activates otherwise. Hence the simultaneous application of the horizontal and vertical loads can lead to a substantial reduction of the available vertical capacity of the group and also to a significant modification of the horizontal limit load as a function of the load ratio \(Q_{3} /Q_{1 - 2}\).

Figure 3 shows also the effect of the external moment on the combined limit load \(Q_{1 - 2,\,3}^{(\lim )}\). The activation of a failure mode is not influenced by the direction of the moments \(Q_{{\text{R1}}}\) and \(Q_{{\text{R2}}}\) because in the proposed framework this leads only to a specular distribution of the axial forces in the piles without altering the vertical and horizontal limit loads. The presence of an external moment always reduces \(Q_{1 - 2,\,3}^{(\lim )}\) for every load path followed, since the external moment leads to a different distribution of the axial forces among the piles altering the respective vertical and horizontal limit loads. The ultimate locus contracts as the moment rises until degenerating in a point when the external moments are equal to the respective maximum values \(Q_{{\text{R1}}}^{(\max )} /B_{1} =4.8\) MN and \(Q_{{\text{R2}}}^{(\max )} /B_{1} = 6.9\) MN (trends at \(Q_{{\text{R1 - R2}}} /Q_{{\text{R1 - R2}}}^{(\max )} = 1\) in Fig. 3). In the proposed simplified framework, this condition corresponds to an opposite attainment of the axial capacity in the piles with respect to the central vertical axis of the foundation. This is evident in Fig. 4 in which the failure envelopes in the \(Q_{{\text{R2}}} /B_{1}\)–\(Q_{3}\) and \(Q_{{\text{R1}}} /B_{1}\)–\(Q_{3}\) spaces are represented together with the mechanisms characterising failure for \(Q_{1}\) = 0. For a sufficiently low vertical force, the horizontal loads reduce the domain of the admissible forces due to the activation of a horizontal load mechanism, as an equivalent interpretation of the failure locus in Fig. 3. The ultimate loci for \(Q_{1 - 2} /Q_{1 - 2,\,\lim } = 0\) (Fig. 4) are in perfect agreement with the strength envelope proposed by Di Laora et al. [33] relative to the combined effect of the vertical force and the external moment.

Fig. 4
figure 4

Force combinations QR1/B1–Q3 and QR2/B1–Q3 causing failure of the reference pile group, for different levels of the respective normalised horizontal load Q2/Q2(max) and Q1/Q1(max) from 0 to 0.9

Full size image

Several three-dimensional numerical analyses were carried out to support the results obtained with the proposed procedure. Specifically, independent estimates of the ultimate load of the pile group along selected loading paths were obtained through the application of the theorems of limit analysis in finite element simulations [44,45,46] using the code OPTUM G3 [42]. The numerical model reproduced the geometry and mechanical properties of the reference soil–pile system (Sect. 2). Fixed restrained were applied along the boundaries of the soil domain. Both the soil domain and the piles were modelled by means of solid elements with a rigid-perfectly plastic behaviour described by the Mohr–Coulomb failure criterion with an associated flow rule. In detail, a cohesion cp = 3400 kPa and a friction angle φp′ = 37 kPa for the elements of the piles were calibrated by trial and error in order to reproduce the strength envelope of Fig. 2. The numerical simulations computed the magnitude of the horizontal load Q1 applied to the slab that cause failure of the system, considering four vertical force levels \(Q_{3} /Q_{3,\,\lim }^{( + )}\) = 0, 0.1, 0.3, 0.6. Each analysis is composed of several iterations with mesh adaptivity: the calculation stops when upper and lower bound solutions become close to each other and do not vary significantly with the number of iterations. The resulting limit loads are shown in Fig. 3 (triangular symbols). The portion of the failure envelope obtained with OPTUM G3 should be compared with that calculated with the simplified procedure for QR2/QR2(max) = 0: it yields larger values of the horizontal limit loads, as an effect of the conservatism introduced in the use of the Broms solution and in the choice of the horizontal efficiency factors, but it follows quite closely the shape of the failure envelope obtained with the simplified procedure. The plastic mechanisms associated with the upper bound solution, shown in Fig. 5, indicate that only a limited portion of the foundation soil is involved in the mechanisms, within a maximum depth of 5.5–7 diameters.

Fig. 5
figure 5

Central section view of the kinematic failure mechanisms of the reference pile group and contours of the relative shear dissipation (from 0 kJ in blue to 1 kJ in red) obtained through the advanced numerical analyses in OPTUM G3 in the case of a combined load Q1-Q3 with Q3 = 0, 0.1, 0.3, 0.6 × Q3,lim(+) (a, b, c, d, respectively)

Full size image

Coming back to the results of the simplified procedure, the effect of the co-presence of a horizontal load and an external moment is illustrated in Fig. 6, considering different levels of the vertical force \(Q_{3} /Q_{3,\,\lim }^{( + )}\). The shape of the failure locus changes from \(Q_{3} /Q_{3,\,\lim }^{( + )}\) = 0 to 0.9 with a progressively lower interaction between the two load components. The maximum horizontal limit forces are attained for \(Q_{3} /Q_{3,\,\lim }^{( + )}\) = 0.75 and remain essentially constant for greater values in virtue of the ductile behaviour of the piles.

Fig. 6
figure 6

Force combinations Q1–QR2/B1 and Q2–QR1/B1 causing failure of the reference pile group, for different levels of the vertical load Q3/Q3(max) = 0–0.9

Full size image

4 Out-of-plane failure mechanisms

A superstructure likely transfers to the foundation all the generalised external forces \(Q_{\text{i}} = \left\{ {Q_{1} ,\,Q_{2} ,\,Q_{3} ,\,Q_{{\text{R1}}} ,\,Q_{{\text{R2}}} } \right\}\). In this section, we analyse the interaction between the horizontal loads and between the moments acting in the two orthogonal vertical planes 1–3 and 2–3 (Fig. 1).

4.1 Q 1–Q 2 interaction

Consider the reference pile group loaded by both the horizontal loads \(Q_{1}\) and \(Q_{2}\) in the absence of external moment, taking advantage of the slight interaction between them on the resultant limit load (Fig. 6). The norm \(Q_{{\text{h,}\,\text{lim}}} = \sqrt {Q_{1,\,\lim }^{2} + Q_{2,\,\lim }^{2} }\) and the direction of the resultant limit load in the horizontal plane are controlled by the horizontal efficiency \(\upeta _{\text{h}}\) among the piles. The latter was evaluated through Mokwa’s solution [3] so that the limit load \(Q_{{\text{h,}\,\text{lim}}}\) does not change with the direction of the resultant horizontal load \(Q_{\text{h}} = \sqrt {Q_{1}^{2} + Q_{2}^{2} }\) because the reference pile group has the same spacing in both the horizontal directions. As a result, by using the proposed numerical procedure the ultimate locus in the \(Q_{1}\)–\(Q_{2}\) space is represented by a circumference, whose radius is strongly influenced by the presence of the vertical force, as shown in Fig. 7. The vertical force produces an expansion of the admissible domain up to a level \(Q_{3} /Q_{3,\,\lim }^{( + )}\) of about 0.6, beyond which the horizontal limit load remains unchanged in virtue of the ductile behaviour exhibited by the piles (Sect. 3).

Fig. 7
figure 7

Force combinations Q1–Q2 causing failure of the reference pile group, for different levels of the vertical load Q3/Q3(max) = 0–0.95, obtained with the proposed simplified framework (circles) and through advanced numerical analyses (triangles)

Full size image

The proposed framework could be easily improved by the introduction of a more sophisticated model for the horizontal efficiency, which would reasonably lead to an elliptical shape of the limit locus in the \(Q_{1}\)–\(Q_{2}\) space. This is demonstrated by the values of \(Q_{{\text{h,}\,\text{lim}}}\) obtained through the advanced numerical analyses performed in OPTUM G3, represented in Fig. 7 (triangular symbols), varying the ratio \(Q_{1}\)/\(Q_{2}\) and for a vertical force level \(Q_{3} /Q_{3,\,\lim }^{( + )}\) = 0.6. The comparison between the numerical analyses and the proposed simplified procedure reveals that for the case at hand the latter underestimates \(Q_{{\text{h,}\,\text{lim}}}\) by 20–30% and that the limit loads in 1- and 2-directions differ by about 10%.

4.2 Q R1–Q R2 interaction

The effect of the bi-directionality of the external moment is analysed considering only the co-presence of the vertical force \(Q_{3}\). Figure 8 shows the moment combinations, \(Q_{{\text{R1}}}^{(\lim )}\) and \(Q_{{\text{R2}}}^{(\lim )}\), producing failure of the pile group \(Q_{{\text{Rh}}}^{(\lim )} = \sqrt {Q_{{\text{R1}}}^{(\lim )2} + Q_{{\text{R2}}}^{(\lim )2} }\), computed for \(Q_{3} /Q_{3,\,\lim }^{( + )}\) = 0–0.95. When the vertical force is equal to zero, the interaction between \(Q_{{\text{R1}}}\) and \(Q_{{\text{R2}}}\) is negligible. As the vertical force rises, this interaction becomes increasingly more pronounced, leading to an elliptical relationship between \(Q_{{\text{R1}}}^{(\lim )}\) and \(Q_{{\text{R2}}}^{(\lim )}\) for \(Q_{3} /Q_{3,\,\lim }^{( + )}\) > 0.6. More in detail, the size of the admissible domain increases with the vertical force as long as \(Q_{3} /Q_{3,\,\lim }^{( + )}\) < 0.5, while it reduces for \(Q_{3} /Q_{3,\,\lim }^{( + )}\) > 0.5; the case \(Q_{3} /Q_{3,\,\lim }^{( + )}\) = 0.5 is the condition in which the ultimate locus reaches its maximum dimension, as it appears evident from the results in Fig. 4. This non-monotonic variation of the strength envelope from small to large values of \(Q_{3} /Q_{3,\,\lim }^{( + )}\) predicted by the proposed framework is due to a different mobilisation of the axial capacity among the piles. Figure 9 shows the progressive mobilisation of the axial capacity of the piles for some significant loading paths: cases (a) and (b) consider the sole application of the moment \(Q_{{\text{R1}}}\) and \(Q_{{\text{R2}}}\), respectively, while cases (c) and (d) refer to the concomitant application of the two external moments \(Q_{{\text{R1}}}\) = \(Q_{{\text{R2}}}\) considering a normalised vertical force \(Q_{3} /Q_{3,\,\lim }^{( + )}\) = 0 and 0.8, respectively. The number associated with each pile indicates the order with which the relative axial capacity is attained. In case (a), the piles in the row 1 reach simultaneously the tensile capacity, with a redistribution of the internal forces among the other piles at the subsequent load increment. A similar sequence occurs in case (b), with a progressive mobilisation of the tensile capacity in three rows and a sole lateral row in which the piles fail in compression. A different mobilisation of the overall resistance occurs in the case of a bi-component moment \(Q_{{\text{R1}}}\) = \(Q_{{\text{R2}}}\) with \(Q_{3} /Q_{3,\,\lim }^{( + )}\) = 0 (case c), with a non-symmetric mobilisation of the axial capacity.

Fig. 8
figure 8

Force combinations QR1/B1–QR2/B1 causing failure of the reference pile group, for different levels of the vertical load Q3/Q3(max) = 0–0.95

Full size image
Fig. 9
figure 9

Progressive attainment of the axial capacity in the piles considering a load pattern Q3-QR1/B1-QR2/B1

Full size image

5 Equation of the ultimate limit state surface

In this section, an analytical formulation for the ultimate limit state surface \(y = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} \left( {Q_{\text{i}} } \right)\) of pile groups is developed, referring to the trends of the generalised limit load found through the proposed numerical procedure (Sect. 4). The importance of an analytical description of the ultimate conditions is related to its application in (1) plasticity-based macroelement representations for piled foundations and (2) a more rational design of piled foundations accounting for the interaction between all the loads transferred by the superstructure.

5.1 In-plane mechanisms

In the light of the results shown in Sect. 3, the relationship between the vertical force \(Q_{3}\) and the horizontal forces \(Q_{1}\) and \(Q_{2}\) (\(Q_{{\text{R1}}} = Q_{{\text{R2}}} = 0\)) should include the following features:

  • the highly dissymmetric effect of \(Q_{3}\) (Fig. 3);

  • the marked nonlinear interaction between \(Q_{3}\) and \(Q_{1 - 2}\) (Fig. 3);

  • a variable size and shape of the ultimate locus in the \(Q_{1}\)–\(Q_{{\text{R2}}}\) and \(Q_{2}\)–\(Q_{{\text{R1}}}\) spaces as a function of the mobilised vertical resistance \(Q_{3} /Q_{3,\,\lim }^{( + )}\) (Fig. 4).

To use the ultimate surface in numerical computations (macroelement modelling), it is also convenient that its shape be convex, needed to have consistent plastic deformations [14], and smooth (no angular points).

We propose to describe the ultimate surface in the \(Q_{1}\)–\(Q_{3}\) and \(Q_{2}\)–\(Q_{3}\) spaces through the following modified expression of the Granville’s egg [26]:

$$\begin{aligned} \left( {Q_{1 - 2} \cdot Q_{3} + Q_{1 - 2} \cdot Q_{3,1 - 2}^{(0)} } \right)^{2} & = \frac{{A_{3} }}{2} \cdot S_{1 - 2}^{2} \cdot \Gamma_{1 - 2}^{2} \cdot \left( {c_{3} + Q_{3,1 - 2}^{(0)} } \right) \cdot \left( {Q_{3} - c_{3} + \frac{{A_{3} }}{2}} \right) \cdot \\ & \quad \cdot \left( { - Q_{3} + c_{3} + \frac{{A_{3} }}{2}} \right) \\ \end{aligned}$$
(3)

which is a quartic ovoidal curve, completely defined by the constitutive parameters \(c_{3}\), \(Q_{3,1 - 2}^{(0)}\), \(A_{3}\), \(S_{{\text{F,}1 - 2}}\) and \(\Gamma_{1 - 2}\). Figure 10 depicts the ultimate locus in the \(Q_{1}\)–\(Q_{3}\) space for the reference pile group. The size of the Granville’s egg along the \(Q_{3}\)-axis is controlled by \(A_{3} = Q_{3,\,\lim }^{( + )} - Q_{3,\,\lim }^{( - )}\), while its position by \(c_{3} = \left( {Q_{3,\,\lim }^{( + )} + Q_{3,\,\lim }^{( - )} } \right)/2\), representing the \(Q_{3}\)-coordinate of the centre of the ultimate locus (the translation is needed to reproduce the asymmetric response of the piles). The ultimate locus is symmetric with respect to the \(Q_{3}\)-axis and its dimensions along the \(Q_{1 - 2}\)-axes are controlled by the interaction parameters \(Q_{3,\,1 - 2}^{(0)}\), the scale factors \(S_{{\text{F,}\,1 - 2}}\), scaling the size of the ultimate locus, and the shape ratios \(\Gamma_{1 - 2}\).

Fig. 10
figure 10

Representation of the physical meaning of the constitutive parameters of the modified Granville’s egg [26] in the Q1–Q3 space

Full size image

5.1.1 Effect of the moment

The external moment always causes a contraction of the limit locus in the \(Q_{1}\)–\(Q_{3}\) and \(Q_{2}\)–\(Q_{3}\) spaces. This effect was included into the parameters \(I_{\text{i}} = \left\{ {c_{3} ,\,Q_{3,1 - 2}^{(0)} ,\,A_{3} ,\,S_{{\text{F,}1 - 2}} ,\,\Gamma_{1 - 2} } \right\}\) of the modified Granville’s egg (Eq. 3): the generic evolution law \(I_{\text{i}} = \hat{I}_{\text{i}} \left( {Q_{{\text{R2 - R1}}} /Q_{{\text{R2 - R1}}}^{(\max )} } \right)\) (the symbol \(\hat{I}_{\text{i}}\) indicates the body of the function) relates the parameter \(I_{\text{i}}\) to the corresponding mobilised moment \(Q_{{\text{R2 - R1}}} /Q_{{\text{R2 - R1}}}^{(\max )}\) in order to reproduce the desired translation and changes in size and shape of the ultimate locus as the moment rises (Figs. 3, 4 and 6). Through a systematic comparison with the results obtained by the numerical procedure, the functions \(\hat{I}_{\text{i}} \left( {Q_{{\text{R2 - R1}}} /Q_{{\text{R2 - R1}}}^{(\max )} } \right)\) are here described by super-ellipses, such as:

$$c_{\text{3}} \left( {Q_{{\text{R2 - R1}}} } \right) = c_{3}^{(0)} + a_{{\text{c,3}}} \cdot \left[ {1 - \left( {\frac{{\left| {Q_{{\text{R2 - R1}}} } \right|}}{{Q_{{\text{R2 - R1}}}^{(\max )} \cdot b_{{\text{c,3}}} }}} \right)^{{n_{{\text{c,3}}} }} } \right]^{{{1 \mathord{\left/ {\vphantom {1 {n_{{\text{c,3}}} }}} \right. \kern-\nulldelimiterspace} {n_{{\text{c,3}}} }}}}$$
(4)
$$Q_{{\text{3,1 - 2}}}^{(0)} \left( {Q_{{\text{R2 - R1}}} } \right) = a_{{\text{Q3,1 - 2}}} \cdot \left[ {1 - \left( {\frac{{\left| {Q_{{\text{R2 - R1}}} } \right|}}{{Q_{{\text{R2 - R1}}}^{(\max )} \cdot b_{{\text{Q3,1 - 2}}} }}} \right)^{{n_{{\text{Q3,1 - 2}}} }} } \right]^{{{1 \mathord{\left/ {\vphantom {1 {n_{{\text{Q3,1 - 2}}} }}} \right. \kern-\nulldelimiterspace} {n_{{\text{Q3,1 - 2}}} }}}}$$
(5)
$$A_{3} \left( {Q_{{\text{R2 - R1}}} } \right) = a_{{\text{A,3}}} \cdot \left[ {1 - \left( {\frac{{\left| {Q_{{\text{R2 - R1}}} } \right|}}{{Q_{{\text{R2 - R1}}}^{(\max )} \cdot b_{{\text{A,3}}} }}} \right)^{{n_{{\text{A,3}}} }} } \right]^{{{1 \mathord{\left/ {\vphantom {1 {n_{{\text{A,3}}} }}} \right. \kern-\nulldelimiterspace} {n_{{\text{A,3}}} }}}}$$
(6)
$$S_{{\text{F,1 - 2}}} \left( {Q_{{\text{R2 - R1}}} } \right) = S_{{\text{F,1 - 2}}}^{(0)} + a_{{\text{Sf,1 - 2}}} \cdot \left[ {1 - \left( {\frac{{\left| {Q_{{\text{R2 - R1}}} } \right|}}{{Q_{{\text{R2 - R1}}}^{(\max )} \cdot b_{{\text{Sf,1 - 2}}} }}} \right)^{{n_{{\text{Sf,1 - 2}}} }} } \right]^{{{1 \mathord{\left/ {\vphantom {1 {n_{{\text{Sf,1 - 2}}} }}} \right. \kern-\nulldelimiterspace} {n_{{\text{Sf,1 - 2}}} }}}}$$
(7)
$$\Gamma_{{\text{1 - 2}}} \left( {Q_{{\text{R2 - R1}}} } \right) = a_{{\Gamma \text{,1 - 2}}} \cdot \left[ {1 - \left( {\frac{{\left| {Q_{{\text{R2 - R1}}} } \right|}}{{Q_{{\text{R2 - R1}}}^{(\max )} \cdot b_{{\Gamma \text{,1 - 2}}} }}} \right)^{{n_{{\Gamma \text{,1 - 2}}} }} } \right]^{{{1 \mathord{\left/ {\vphantom {1 {n_{{\Gamma \text{,1 - 2}}} }}} \right. \kern-\nulldelimiterspace} {n_{{\Gamma \text{,1 - 2}}} }}}}$$
(8)

in which the moment components vary in the range [− \(Q_{{\text{R1 - R2}}}^{(\max )}\), \(Q_{{\text{R1 - R2}}}^{(\max )}\)]. Note that the parameters \(\left\{ {c_{3} ,Q_{3,1 - 2}^{(0)} ,A_{3} ,S_{{\text{F,}1 - 2}} ,\Gamma_{1 - 2} } \right\}\) are a function of the absolute value of the respective external moment because in the proposed numerical procedure the horizontal limit load does not depend on the direction of the external moment. The resulting generalised surface of ultimate loads in the Q1–Q3–QR2/Bx and Q2–Q3–QR1/Bx spaces can be therefore obtained by simply introducing Eqs. 4–8 into Eq. 3 (Appendix).

5.2 Five-dimensional ultimate limit state surface

The ultimate surface described by Eqs. 3–8 identifies the admissible force states in the two orthogonal vertical planes, 1–3 and 2–3, of the foundation (Fig. 1), considering the respective load patterns Q1–Q3–QR2/Bx and Q2–Q3–QR1/Bx applied separately. To describe failure conditions induced by a generic five-dimensional load path, we need to introduce into Eqs. 3–8 the effect on the limit load of the reciprocal interaction between the horizontal forces, \(Q_{\text{1}}\) and \(Q_{\text{2}}\), and between the moment components, \(Q_{{\text{R1}}}\) and \(Q_{{\text{R2}}}\) (Figs. 7 and 8). The shape of the ultimate locus in the Q1–Q2 space depends on the horizontal efficiency \(\upeta _{\text{h}}\) of the piles. In the reference case (Fig. 7), the isotropic model proposed by Mokwa [37] was employed so that the ultimate locus presents a circular shape. More in general, a super-elliptical relationship is here proposed between the horizontal limit loads \(Q_{1,\,\lim }\) and \(Q_{2,\,\lim }\), whose Cartesian equation reads:

$$\left( {\frac{{Q_{{\text{1,}\,\text{lim}}} }}{{a_{{\text{Q1}}} }}} \right)^{{n_{{\text{12}}} }} + \left( {\frac{{Q_{2,\,\lim } }}{{a_{{\text{Q2}}} }}} \right)^{{n_{{\text{12}}} }} = 1$$
(9)

in which the exponent n12 determines the shape of the locus: n12 < 1 gives a hypo-ellipse, characterised by a concave shape, n12 = 1 represents a linear relationship between \(Q_{1,\,\lim }\) and \(Q_{2,\,\lim }\), while n12 > 1 confers the desired convex shape to the locus; more in detail, n12 = 2 is an ellipse and n12 > 2 describes a super-elliptical relationship in which the curvature of the locus is minimum for \(Q_{{\text{1,}\,\text{lim}}}\) = 0 or \(Q_{2,\,\lim }\) = 0 and increases progressively towards \({{Q_{{\text{1,lim}}} } \mathord{\left/ {\vphantom {{Q_{{\text{1,lim}}} } {Q_{{\text{2,lim}}} }}} \right. \kern-\nulldelimiterspace} {Q_{{\text{2,lim}}} }}\) = 1. The terms \(a_{{\text{Q1}}}\) and \(a_{{\text{Q2}}}\) are the semi-axes of the super-ellipse and represent the horizontal limit forces \(Q_{{\text{1,lim}}}\) and \(Q_{{\text{2,lim}}}\) when \(Q_{2}\) = 0 and \(Q_{1}\) = 0, respectively. When \(a_{{\text{Q1}}}\) and \(a_{{\text{Q2}}}\) are identical, Eq. 9 degenerates into a circumference. The dependence of \(a_{{\text{Q1}}} = Q_{\text{1}} \left( {Q_{2} = 0,\,Q_{3} ,\,Q_{{\text{R1}}} ,\,Q_{{\text{R2}}} } \right)\) and \(a_{{\text{Q2}}} = Q_{2} \left( {Q_{1} = 0,\,Q_{3} ,\,Q_{{\text{R1}}} ,\,Q_{{\text{R2}}} } \right)\) on the other force components is described by Eqs. 3–8, while their dependence on the external moment is reproduced by the relationship between \(Q_{{\text{R1}}}^{(\lim )}\) and \(Q_{{\text{R2}}}^{(\lim )}\).

To reproduce analytically the numerical results shown in Fig. 8 a super-elliptical model is again adopted to describe the interaction between \(Q_{{\text{R1}}}^{(\lim )}\) and \(Q_{{\text{R2}}}^{(\lim )}\):

$$\left( {\frac{{Q_{{\text{R1}}}^{(\lim )} }}{{a_{{\text{QR1}}} }}} \right)^{{n_{{\text{R1R2}}} }} + \left( {\frac{{Q_{R2}^{(\lim )} }}{{a_{{\text{QR2}}} }}} \right)^{{n_{{\text{R1R2}}} }} = 1$$
(10)

in which \(a_{{\text{QR1}}} = Q_{{\text{R1}}} \left( {Q_{2} ,\,Q_{3} ,\,Q_{{\text{R1}}} ,\,Q_{{\text{R2}}} = 0} \right)\) and \(a_{{\text{QR2}}} = Q_{{\text{R2}}} \left( {Q_{2} ,\,Q_{3} ,\,Q_{{\text{R1}}} = 0,\,Q_{{\text{R2}}} } \right)\) vary according to Eqs. 3–8. The shape of the ultimate locus in the \(Q_{{\text{R1}}}\)–\(Q_{{\text{R2}}}\) space changes with the level of the vertical force \(Q_{3} /Q_{3,\,\lim }^{( + )}\) (Fig. 8). This effect is simulated by assuming a super-elliptical variation of the exponent \(n_{{\text{R1R2}}}\) with \(Q_{3} /Q_{3,\lim }^{( + )}\):

$$n_{{\text{R1R2}}} \left( {\frac{{Q_{\text{3}} }}{{Q_{{\text{3,}\,\text{lim}}}^{{\text{( + )}}} }}} \right) = a_{{\text{R1R2}}} \cdot \left[ {1 - \left( {\frac{{Q_{\text{3}} }}{{Q_{{\text{3,}\,\text{lim}}}^{{\text{( + )}}} \cdot b_{{\text{R1R2}}} }}} \right)^{{n_{{\text{R1R2}}}^{{\text{(Q3)}}} }} } \right]^{{{1 \mathord{\left/ {\vphantom {1 {n_{{\text{R1R2}}}^{{\text{(Q3)}}} }}} \right. \kern-\nulldelimiterspace} {n_{{\text{R1R2}}}^{{\text{(Q3)}}} }}}}$$
(11)

in which \(a_{{\text{R1R2}}}\), \(b_{{\text{R1R2}}}\) and \(n_{{\text{R1R2}}}^{{\text{(Q3)}}}\) are constant parameters to be calibrated. For the pile group under examination, a linear variation of \(n_{{\text{R1R2}}}\) with \(Q_{3} /Q_{3,\lim }^{( + )}\) was found to provide the best fitting with the numerical results of Fig. 8, so that \(n_{{\text{R1R2}}}^{{\text{(Q3)}}}\) = 1.

The ultimate surface in the \(Q_{1}\)–\(Q_{2}\)–\(Q_{3}\)–\(Q_{{\text{R1}}}\)–\(Q_{{\text{R2}}}\) space can be now derived by introducing the parametric form of Eqs. 9–11 into Eq. 3. After some manipulation, the Cartesian equation of the ultimate surface can be written as:

$$\begin{aligned} y\left( {Q_{1} ,Q_{2} ,Q_{3} ,Q_{{R1}} ,Q_{{R2}} } \right) & = 2 \cdot \left[ {Q_{1} \cdot Q_{3} + Q_{1} \cdot \hat{Q}_{{3,1}}^{{(0)}} \left( {Q_{{R2}} } \right)} \right]^{2} \cdot \left\{ {\hat{A}_{3} \left( {Q_{{R2}} } \right) \cdot \hat{S}_{{F,1}}^{2} \left( {Q_{{R2}} } \right) \cdot \hat{\Gamma }_{1}^{2} \left( {Q_{{R2}} } \right)} \right. \\ & \quad \left. { \cdot \left[ {\hat{c}_{3} \left( {Q_{{R2}} } \right) + \hat{Q}_{{3,1}}^{{(0)}} \left( {Q_{{R2}} } \right)} \right]^{2} \cdot \left[ { - Q_{3} + \frac{{\hat{A}_{3}^{{(0)}} \left( {Q_{{R2}} } \right)}}{2} + \hat{c}_{3} \left( {Q_{{R2}} } \right)} \right] \cdot \left[ {Q_{3} + \frac{{\hat{A}_{3}^{{(0)}} \left( {Q_{{R2}} } \right)}}{2} - \hat{c}_{3} \left( {Q_{{R2}} } \right)} \right]} \right\}^{{ - 1}} \\ & \quad + 2 \cdot \left[ {Q_{2} \cdot Q_{3} + Q_{2} \cdot \hat{Q}_{{3,2}}^{{(0)}} \left( {Q_{{R1}} } \right)} \right]^{2} \cdot \left\{ {\hat{A}_{3} \left( {Q_{{R1}} } \right) \cdot \hat{S}_{{F,2}}^{2} \left( {Q_{{R1}} } \right) \cdot \hat{\Gamma }_{2}^{2} \left( {Q_{{R1}} } \right)} \right. \\ & \quad \left. { \cdot \left[ {\hat{c}_{3} \left( {Q_{{R1}} } \right) + \hat{Q}_{{3,2}}^{{(0)}} \left( {Q_{{R1}} } \right)} \right]^{2} \cdot \left[ { - Q_{3} + \frac{{\hat{A}_{3}^{{(0)}} \left( {Q_{{R1}} } \right)}}{2} + \hat{c}_{3} \left( {Q_{{R1}} } \right)} \right] \cdot \left[ {Q_{3} + \frac{{\hat{A}_{3}^{{(0)}} \left( {Q_{{R1}} } \right)}}{2} - \hat{c}_{3} \left( {Q_{{R1}} } \right)} \right]} \right\}^{{ - 1}} - 1 = 0 \\ \end{aligned}$$
(12)

in which the two moment components QR1 and QR2 are included in the evolution functions \(\hat{I}_{\text{i}} \left( {Q_{{\text{Rj}}} } \right)\) (Eqs. 3–8). Equation 12 represents a hyper-ovoidal surface with super-elliptical generatrices, and the relative parametric equations are reported in Appendix.

The formulation described above was used to determine the ultimate surface for the reference pile group, calibrating the evolution laws \(I_{\text{i}}\) to reproduce the failure points obtained by the numerical procedure. Limiting the representation to the Q1–Q3–QR2/B1 space, Fig. 11 shows that the proposed analytical model is able to simulate quite satisfactorily the progressive contraction of the ultimate locus, with an ultimate surface that remains convex for every force combination. (The projections of the surface on all the coordinate force planes are convex and do not intersect with each other.) The maximum differences between the numerical and analytical solutions are \(\Delta\) = 22–23% and occur for high values of the external moment (QR2/QR2(max) > 0.5 in the Q1–Q3 space in Fig. 11) and of the vertical force (Q3/Q3,lim(+) > 0.5 in the Q1–QR2/B1 space in Fig. 11).

Fig. 11
figure 11

Fitting of the numerical results (filled circles) with the proposed analytical model of ultimate surface with representation of the relative maximum differences \(\Delta\)

Full size image

The entire set of parameters used to describe the ultimate surface is reported in Table 1, which were chosen according to the following calibration procedure.

Table 1 Parameters of the ultimate limit state surface
Full size table

6 Calibration of the ultimate limit state surface

The proposed five-dimensional ultimate surface for a pile group, Eq. 12, is defined by the 33 parameters listed in Table 1, which, however, can be considerably reduced by identifying the most significant input quantities (in bold in Table 1) from which all the others can be derived.

The vertical limit loads \(Q_{3,\lim }^{( - )}\) and \(Q_{3,\lim }^{( + )}\) can be evaluated by referring to many solutions available in the literature. By virtue of the shape of the ultimate locus in the \(Q_{1 - 2}\)–\(Q_{3}\) spaces, \(Q_{1}^{(\max )}\) and \(Q_{2}^{(\max )}\) can be evaluated, for example, by Brom’s theory [27] considering a yield moment of the piles corresponding to \(Q_{3,\lim }^{( + )}\). The maximum moments \(Q_{{\text{R}1}}^{(\max )}\) and \(Q_{{\text{R2}}}^{(\max )}\) occur when

$$Q_{3} = {{\left( {N_{{\text{lim}}}^{( + )} + \left| {N_{{\text{lim}}}^{( - )} } \right|} \right)} \mathord{\left/ {\vphantom {{\left( {N_{{\text{lim}}}^{( + )} + \left| {N_{{\text{lim}}}^{( - )} } \right|} \right)} 2}} \right. \kern-\nulldelimiterspace} 2}$$
(13)

and correspond to a symmetric failure mode: half of the pile rows mobilise the axial capacity in compression and the remaining half the capacity in tension (Sect. 3). Under this condition, the maximum external moment \(Q_{{\text{Rk}}}^{(\max )}\) around direction k can be computed as:

$$Q_{{\text{Rk}}}^{(\max )} = \frac{{N_{{\text{lim}}}^{( + )} + \left| {N_{{\text{lim}}}^{( - )} } \right|}}{2} \cdot i_{\text{h}} \cdot \sum\limits_{{\text{j = 1}}}^{\text{N}} {\left< {n_{\text{h}} - \left( {2j - 1} \right)} \right>} \cdot n_{\text{k}}$$
(14)

in which < > represent the Macaulay brackets and the subscript h denotes the horizontal direction orthogonal to direction k.

In order to define a form of general validity for the super-elliptical evolution laws in Eqs. 4–8, it is convenient to introduce the following normalisation scheme for the ultimate surface: the vertical force \(Q_{\text{3}}\) and the evolution parameters \(\hat{c}_{3} \left( {Q_{{\text{R2 - R1}}} } \right)\), \(\hat{Q}_{3,1 - 2}^{(0)} \left( {Q_{{\text{R2 - R1}}} } \right)\) and \(\hat{A}_{3} \left( {Q_{{\text{R2 - R1}}} } \right)\), which control the size and translation of the ultimate locus along the \(Q_{\text{3}}\)-axis, are normalised with respect to \(Q_{3,\lim }^{( + )}\); the horizontal forces \(Q_{1}\) and \(Q_{2}\) are divided by the corresponding limit values, \(Q_{{1,\text{lim}}}^{{(\text{1D})}}\) and \(Q_{{2,\text{lim}}}^{{(\text{1D})}}\), under uniaxial loading conditions; the two moment components \(Q_{{\text{R1}}}\) and \(Q_{{\text{R2}}}\) have been already normalised by \(Q_{{\text{R}1}}^{(\max )}\) and \(Q_{{\text{R2}}}^{(\max )}\); finally the scale factor \(\hat{S}_{{\text{F,1 - 2}}} \left( {Q_{{\text{R2 - R1}}} } \right)\) and the shape ratio \(\hat{\Gamma }_{{\text{1 - 2}}} \left( {Q_{{\text{R2 - R1}}} } \right)\) are non-dimensional by definition. The resulting non-dimensional expressions for \(c_{3}\), \(Q_{3,1 - 2}^{(0)}\) and \(A_{\text{3}}\) are:

$$\frac{{c_{\text{3}} }}{{Q_{{\text{3,lim}}}^{( + )} }} = \frac{{c_{3}^{(0)} }}{{Q_{{\text{3,lim}}}^{( + )} }} + \frac{{a_{{\text{c,3}}} }}{{Q_{{\text{3,lim}}}^{( + )} }} \cdot \left[ {1 - \left( {\frac{{\left| {Q_{{\text{R2 - R1}}} } \right|}}{{Q_{{\text{R2 - R1}}}^{(\max )} \cdot b_{{\text{c,3}}} }}} \right)^{{n_{{\text{c,3}}} }} } \right]^{{{1 \mathord{\left/ {\vphantom {1 {n_{{\text{c,3}}} }}} \right. \kern-\nulldelimiterspace} {n_{{\text{c,3}}} }}}}$$
(15)
$$\frac{{Q_{{\text{3,1 - 2}}}^{(0)} }}{{Q_{{\text{3,lim}}}^{( + )} }} = \frac{{a_{{\text{Q3,1 - 2}}} }}{{Q_{{\text{3,lim}}}^{( + )} }} \cdot \left[ {1 - \left( {\frac{{\left| {Q_{{\text{R2 - R1}}} } \right|}}{{Q_{{\text{R2 - R1}}}^{(\max )} \cdot b_{{\text{Q3,1 - 2}}} }}} \right)^{{n_{{\text{Q3,1 - 2}}} }} } \right]^{{{1 \mathord{\left/ {\vphantom {1 {n_{{\text{Q3,1 - 2}}} }}} \right. \kern-\nulldelimiterspace} {n_{{\text{Q3,1 - 2}}} }}}}$$
(16)
$$\frac{{A_{\text{3}} }}{{Q_{{\text{3,lim}}}^{( + )} }} = \frac{{a_{{\text{A,3}}} }}{{Q_{{\text{3,lim}}}^{( + )} }} \cdot \left[ {1 - \left( {\frac{{\left| {Q_{{\text{R2 - R1}}} } \right|}}{{Q_{{\text{R2 - R1}}}^{(\max )} \cdot b_{{\text{A,3}}} }}} \right)^{{n_{{\text{A,3}}} }} } \right]^{{{1 \mathord{\left/ {\vphantom {1 {n_{{\text{A,3}}} }}} \right. \kern-\nulldelimiterspace} {n_{{\text{A,3}}} }}}}$$
(17)

Figure 12 shows the non-dimensional evolution laws, obtained considering the values assigned to the parameters of the ultimate surface for the reference pile group (Table 1), and the relative effects on the shape of the ultimate surface in the \(Q_{1}\)–\(Q_{3}\) space. By virtue of the non-dimensional form, the evolution functions in Fig. 12 can be considered as a general result for rectangular piled foundations and accordingly the input parameters reduce drastically.

Fig. 12
figure 12

Non-dimensional representation and effect of the evolution parameters c1-2/Q3(max) (a, b), Q3,1–2/Q3(max) (c, d), A1-2/Q3(max) (e, f), SF,1–2/Q3(max) (g, h), Г1–2/Q3(max) (i, j)

Full size image

The evolution function \(\hat{c}_{3} \left( {Q_{{\text{R2 - R1}}} } \right)\) (Fig. 12a) is completely defined by the initial value \(\hat{c}_{3} \left( {Q_{{\text{R2 - R1}}} = 0} \right) = c_{3}^{(0)}\) (translation of the ultimate surface along the \(Q_{\text{3}}\)-axis), which can be written as a function of the vertical limit loads \(Q_{3,\lim }^{( + )}\) and \(Q_{3,\lim }^{( - )}\):

$$c_{3}^{(0)} = a_{{\text{c,3}}} + \frac{{\left( {Q_{{\text{3,lim}}}^{( + )} - Q_{{\text{3,lim}}}^{( - )} } \right)}}{2} + Q_{{\text{3,lim}}}^{( - )}$$
(18)

in which the parameter \(a_{{\text{c,3}}}\) is taken as 0.5 \(Q_{3,\lim }^{( + )}\) to reproduce the non-dimensional curve in Fig. 12a. If the capacity in compression is comparable with the tensile capacity, \(c_{3}^{(0)}\) = 0, while for a marked dissymmetric behaviour of the group (\(Q_{{\text{3,lim}}}^{( + )} > > Q_{{\text{3,lim}}}^{( - )}\)) the ultimate locus is highly decentred with respect to the axis origin, \(c_{3}^{(0)}\) > 0, as illustrated in Fig. 12b. When the external moment \(Q_{{\text{R2 - R1}}} /Q_{{\text{R2 - R1}}}^{(\max )}\) rises the centre \(c_{3}\) moves progressively to greater values of \(Q_{\text{3}}\), reproducing the numerical results in Fig. 11.

The interaction parameter \(\hat{Q}_{3,1 - 2}^{(0)} \left( {Q_{{\text{R2 - R1}}} } \right)\) modifies the shape of the ultimate surface in the \(Q_{1}\)-\(Q_{3}\) space, as shown in Fig. 12c, d: it can be proved that the ultimate surface is convex if and only if \(\hat{Q}_{3,1 - 2}^{(0)} \left( {Q_{{\text{R2 - R1}}} } \right) \ge Q_{3,\lim }^{( + )}\), ∀ \(Q_{{\text{R2 - R1}}} \le Q_{{\text{R2 - R1}}}^{(\max )}\). In particular, large values of \(Q_{3,1 - 2}^{(0)}\) lead to a spherical surface in the \(Q_{1}\)–\(Q_{3}\) space, while it assumes an ovoidal shape as \(Q_{3,1 - 2}^{(0)}\) tends to \(Q_{3,\lim }^{( + )}\). Accordingly, by imposing the condition \(\hat{Q}_{{\text{3,1 - 2}}}^{(0)} \left( {Q_{{\text{R2 - R1}}} } \right) = Q_{{\text{3,lim}}}^{( + )}\) when \(Q_{\text{R}2 - \text{R}1} = Q_{\text{R}2 - \text{R}1}^{(\max )}\) into Eq. 16 the following analytical expression for \(a_{Q3,1 - 2}\) is obtained as:

$$a_{{\text{Q3,1 - 2}}} = - \frac{{Q_{{\text{3,lim}}}^{( + )} }}{{\left( {1 - \frac{1}{{b_{{\text{Q3,1 - 2}}}^{{n_{{\text{Q3,1 - 2}}} }} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {n_{{\text{Q3,1 - 2}}} }}} \right. \kern-\nulldelimiterspace} {n_{{\text{Q3,1 - 2}}} }}}} }}$$
(19)

which guarantees that the ultimate surface is convex. Then, according to Eq. 16 the shape of the ultimate locus becomes progressively more spherical as the external moment rises, reproducing the effect shown in Fig. 11.

The function \(\hat{A}_{3} \left( {Q_{{\text{R2 - R1}}} } \right)\) represents the size of the ultimate locus along the \(Q_{\text{3}}\)-axis, which decreases less than linearly with the external moment, Fig. 12e, until becoming equal to zero when \(Q_{\text{R}2 - \text{R}1} = Q_{\text{R}2 - \text{R}1} ^{(\max )}\) (in this condition, the projection of the ultimate surface in the \(Q_{1}\)–\(Q_{3}\) space degenerates into a point aligned with the \(Q_{\text{3}}\)-axis). The initial value \(a_{A,3}\) can be simply determined using the vertical limit loads \(Q_{3,\lim }^{( + )}\) and \(Q_{3,\lim }^{( - )}\) as:

$$a_{{\text{A,3}}} = Q_{3,\lim }^{( + )} - Q_{3,\lim }^{( - )}$$
(20)

The size of the ultimate locus along the \(Q_{1}\)-axis is controlled by the scale factor \(\hat{S}_{{\text{F,1 - 2}}} \left( {Q_{{\text{R2 - R1}}} } \right)\) and the shape ratio \(\hat{\Gamma }_{{\text{1 - 2}}} \left( {Q_{{\text{R2 - R1}}} } \right)\). The horizontal limit loads increase linearly with \(\hat{S}_{{\text{F,1 - 2}}} \left( {Q_{{\text{R2 - R1}}} } \right)\) and \(\hat{\Gamma }_{{\text{1 - 2}}} \left( {Q_{{\text{R2 - R1}}} } \right)\), as illustrated in Fig. 12h, j. The scale factor increases more than linearly with the normalised moment (Fig. 12g) so that the major axis of the locus in the \(Q_{1}\)–\(Q_{3}\) space is aligned with the \(Q_{3}\)-axis for \(Q_{{\text{R2 - R1}}} /Q_{{\text{R2 - R1}}}^{(\max )}\) less than about 0.5, while it is aligned with the \(Q_{1}\)-axis for greater values of \(Q_{{\text{R2 - R1}}} /Q_{{\text{R2 - R1}}}^{(\max )}\). Hence, the input parameter for the function \(\hat{S}_{{\text{F,1 - 2}}} \left( {Q_{{\text{R2 - R1}}} } \right)\) is the initial value \(S_{F,1 - 2}^{(0)}\), which, by definition, is given by:

$$S_{{\text{F,}1 - 2}}^{(0)} = S_{{\text{F,}1 - 2}} \left( {Q_{{\text{R2 - R1}}} = 0} \right) - a_{{\text{Sf,1 - 2}}} = \frac{{Q_{1 - 2}^{(\max )} }}{{Q_{{1 - 2\text{,ref}}}^{(\max )} }} - a_{{\text{Sf,1 - 2}}}$$
(21)

The maximum horizontal load \(Q_{1 - 2}^{(\max )}\) can be evaluated as described at the beginning of this section, while \(Q_{{1 - 2\text{,ref}}}^{(\max )}\) can be computed through the parametric expression of the horizontal limit load in Eq. 25, reported in Appendix, in which \(\hat{S}_{{\text{F,1 - 2}}} \left( {Q_{{\text{R2 - R1}}} } \right) = 1\) and \(\hat{\Gamma }_{{\text{1 - 2}}} \left( {Q_{{\text{R2 - R1}}} } \right) = 1\).

Finally, the initial value \(a_{{\Gamma \text{,1 - 2}}} = \hat{\Gamma }_{{\text{1 - 2}}} \left( {Q_{{\text{R2 - R1}}} = 0} \right)\) can be computed as:

$$a_{{\Gamma \text{,1 - 2}}} = \hat{\Gamma }_{{\text{1 - 2}}} \left( {Q_{{\text{R2 - R1}}} = 0} \right) = \frac{{Q_{1 - 2}^{(\max )} }}{{Q_{{1 - 2\text{,ref}}}^{(\max )} }}$$
(22)

The good match between the numerical results and the ultimate surface in Fig. 11 refers to an exponent \(n_{{\Gamma ,\text{1 - 2}}}\) (Eq. 8) equal to 1, describing a linear decrease of \(\Gamma_{{\text{1 - 2}}}\) with the normalised moment. This choice was dictated by the fact that the ultimate locus must be convex: Figure 12j shows indeed that the traces of the ultimate surface for different levels of \(Q_{{\text{R2 - R1}}} /Q_{{\text{R2 - R1}}}^{(\max )}\) intersect with each other when \(n_{{\Gamma ,\text{1 - 2}}}\) = 2.0, implying a loss of convexity of the ultimate surface in the \(Q_{{\text{R1 - R2}}}\)-\(Q_{3}\) spaces. To keep the ultimate surface convex, it was seen that \(n_{{\Gamma ,\text{1 - 2}}}\) has to be close to unity and, at the same time, not too low in order to avoid a too rapid contraction of the locus as the normalised moment rises (case with \(n_{{\Gamma ,\text{1 - 2}}}\) = 0.5 in Fig. 12j).

7 Towards an improved design criterion for piled foundations

The proposed expression for the ultimate limit state surface of piled foundations may be used in the formulation of a macroelement representation of the overall behaviour of the foundation. The same limit surface can also be employed for a direct assessment of the safety of the foundation, within a traditional force-based design approach. To illustrate this, the limit surface found for the case study of Fig. 1 was used to carry out force-based verifications in which the safety with respect to an ultimate limit state is expressed by a factor reducing the overall resistance [7, 8]. A value of the factor equal to 2.5 was selected, lumping uncertainties on loads, characteristic resistance and design resistance in a single parameter, but the present discussion is not affected by a particular choice of the partial factors, since these produce only a contraction of the limit surface.

In the standard design approach of a pile group, loaded simultaneously in different directions, it is difficult to evaluate a priori the yield bending moment of the pile sections, as this depends on the axial force acting on each pile. In the example illustrated in this section, we assume that the loading path is made of two different loading stages. In a first stage, which may represent a permanent situation, the foundation is loaded by a vertical force, which is either centred, or applied with a fixed eccentricity e, and no horizontal load. In a second stage, which may represent a transient situation, the vertical and horizontal forces \(Q_{\text{3}}\) and \(Q_{\text{1}}\) are varied proportionally, maintaining a constant eccentricity.

Figure 13 depicts two sections of the design limit surface in the \(Q_{\text{1}}\)–\(Q_{\text{3}}\) plane evaluated for two different values of the eccentricity \(e = {{Q_{{\text{R2}}} } \mathord{\left/ {\vphantom {{Q_{{\text{R2}}} } {Q_{\text{1}} }}} \right. \kern-\nulldelimiterspace} {Q_{\text{1}} }}\), equal to zero (Fig. 13a) and to 0.15 \(B_{\text{1}}\) (Fig. 13b), where \(B_{\text{1}}\) is the width of the pile cap in the direction-1. The vector in these figures, of norm \(Q_{\text{3}} = Q_{\text{3}}^{{\text{(ref)}}}\), represents the initial loading condition. In order to evaluate the limit domain that would result from a standard design approach, the hypothesis is made that in such approach the same yield bending moment \(M_{\text{y}}\) is assumed in all piles and that it corresponds to the mean axial force \(N_{{}}^{{(\text{mean})}}\) evaluated at the end of the initial loading stage.

Fig. 13
figure 13

Comparison between the failure force combinations Q1–Q3–QR2 for the reference pile group, provided by the proposed hyper-egg ultimate surface and the standard design, considering an initial external moment QR2(ini) equal to (a) 0.0 × and (b) 0.5 × SF × QR2(max) (SF = safety factor)

Full size image

As shown in Fig. 13, for a given value of e the limit domain obtained with a standard approach is rectangular: the maximum and minimum values of the vertical force \(Q_{\text{3}}\) depend on the compressive and tensile resistance of the piles, while the maximum value of the horizontal force \(Q_{\text{1}}\) depends on \(M_{\text{y}}\), which is the same for all piles and in turn depends on \(Q_{\text{3}}^{{\text{(ref)}}}\) and e. As expected, the standard design approach predicts a limit load, which is in agreement with the proposed limit surface for near-vertical loading paths, that is, for limit conditions related to the attainment of the vertical bearing capacity of the pile group. For loading paths with a significant horizontal component, \(Q_{\text{1}}\), the adequacy of the standard approach depends crucially on the selection of the effective yield bending moments in the piles. If, as in Fig. 13, \(M_{\text{y}}\) is calculated for \(N = N_{{}}^{{(\text{mean})}}\), then the standard and the proposed procedures are nearly coincident for loading paths with minor changes in the vertical load component \(Q_{\text{3}}\). On the contrary, when changes in \(Q_{\text{3}}\) are significant but the limit conditions are still dominated by the horizontal limit load in the piles, the discrepancies between the two design approaches are significant and, in the example of Fig. 13, the standard approach produces a very large overestimation of the resistance for loading paths characterised by an increment of \(Q_{\text{1}}\) and a decrement of \(Q_{\text{3}}\).

Figure 14 refers to different loading paths that, starting from the same initial loading stage of Fig. 13, entail proportional increments of the horizontal load \(Q_{\text{1}}\) and the moment \(Q_{{\text{R2}}}\). This could represent, for instance, the effect of seismic loading on a bridge pier of height \(h = {{Q_{{\text{R2}}} } \mathord{\left/ {\vphantom {{Q_{{\text{R2}}} } {Q_{\text{1}} }}} \right. \kern-\nulldelimiterspace} {Q_{\text{1}} }}\). Figure 14 shows for the case study of Fig. 1 the section of the design limit surface for \(Q_{\text{3}} = Q_{\text{3}}^{{\text{(ref)}}}\) = 10 MN. The three loading paths depicted in this figure are relative to three different pier heights, equal to 0.75, 1.3 and 2.5 times the width \(B_{\text{1}}\) of the pile cap. It can be seen that in all cases a standard approach that considers a constant yield moment in all piles produces a significant overestimation of the resistance of the pile group.

Fig. 14
figure 14

Comparison between the proposed hyper-egg ultimate surface and the standard design: representation in the Q1–QR2/B1 space of the admissible force states for the reference pile group, considering a safety factor SF = 2.5 and a vertical load Q3 (ref) = 10 MN

Full size image

8 Conclusions

In this study, we developed an efficient, simplified numerical procedure to analyse the ultimate conditions of deep foundations under multi-axial loading. The procedure is compatible with the lower bound theorem of plastic limit analysis and provides the combinations of the generalised external forces activating global plastic mechanisms of the soil–pile system. The proposed procedure was validated comparing the response along selected loading paths with that obtained with a series of three-dimensional numerical analyses that implement iteratively the limit analysis theorems (OPTUM G3). The principal effects of the interaction between the external forces at failure can be summarised as follows:

  • the interaction of the vertical and horizontal loads has a strong influence on the resistance of the foundation because of the important effect of the axial forces on the yield moment of each pile;

  • the external moments cause a progressive attainment of the axial pile capacities, and a global plastic mechanism occurs for a much larger load than that needed to yield the most loaded pile;

  • the directions of the resultant load and moment in the horizontal plane can modify significantly the available resistance of the pile group, to an extent that is a function of the mobilised vertical resistance of the group, \(Q_{\text{3}} /Q_{{\text{3,lim}}}^{{\text{( + )}}}\);

  • the interaction between the resultant horizontal load and moment has instead a minor influence on the limit load of the group for high vertical loads, \(Q_{\text{3}} > 0.75Q_{{\text{3,lim}}}^{{\text{( + )}}}\).

On the basis of the results of the numerical procedure, an analytical expression was developed to describe the ultimate limit state surface of a piled foundation, formulated as a hyper-egg with super-elliptical generatrices in the five-dimensional force space. This expression for the ultimate surface can be regarded as a yield surface of a plasticity-based macroelement. To this end, a calibration procedure was devised in which the ultimate surface can be completely defined by the vertical and horizontal limit loads of the pile group. However, the same expression for the ultimate surface can also be employed for the direct verification of the ultimate limit state of a piled foundation, taking implicitly into consideration the interaction between the different load components, as demonstrated in the previous section.