1 Introduction

Classical plasticity theory assumes the direction of plastic flow is colinear with the normal of a plastic potential usually defined in the space of principal stresses. Consequently, the directions of principal plastic strain rates coincide with those of the principal stresses, (i.e., the so-called coaxiality). On the other hand, the non-coaxiality of inelastic strain rate has been extensively observed in experiments on soils under stress rotations [4, 11, 17, 26, 28, 31, 33, 34, 38, 40, 44, 45]. These experimental works generally suggest that the direction of plastic strain rate not only depends on the current state of stress but also the stress rate.

In accordance with soil behavior revealed from laboratory investigations, attentions have been given to incorporating the non-coaxial plastic flow into the constitutive models for soils. To model the strain localization of brittle rock mass, Rudnicki and Rice [35] employed a yield surface with a vertex-like structure, which leads directly to a non-coaxial plastic flow rule. In such framework, the plastic strain rate can be decomposed into coaxial and non-coaxial components, where the latter is colinear with the non-coaxial stress rate. Qian et al. [32] completed this non-coaxial flow theory by considering the influence of the third stress invariant and consequently extending the original theory to three-dimensional stress space. Such general model framework (hereafter referred to as tangential loading approach) has successfully replicated many non-coaxial responses of soils including those observed in simple shear [5, 13, 25, 50, 56, 61] and pure principal stress rotation [21, 22, 41, 46, 52, 55].

The plastic theory based on assuming non-coaxial plastic flow colinear with the non-coaxial stress rate encounters difficulties in describing the non-coaxiality in soils under monotonic loading with fixed principal stress directions [26, 31, 51], where the stress increment is also colinear with the current stress direction; hence, the non-coaxial stress rate is zero. On the other hand, non-coaxial plastic deformations of soils under monotonic loading with fixed principal stress directions are extensively reported for fine-grained soils [4, 11, 26, 31, 33, 47, 51]. To simulate non-coaxial behavior under monotonic loading with fixed principal stress directions, Gutierrez et al. [12] define a flow rule including the radial component and the tangential component in a special stress space. The tangential component plays a crucial role in dictating the non-coaxial flow and is associated with the radial one, which represents the coaxial flow, by means of the non-coaxial function. Subsequently, the anisotropic transformed stress method [57], which defines an anisotropic transformed stress tensor with different principal directions from the ordinary stress tensor, was introduced and the non-coaxiality of sand was modeled from the view of cross-anisotropy [42]. Also, the plastic potential in terms of fabric anisotropy was introduced to describe the non-coaxiality in sand under loading with fixed principal stress direction [10]. Alternatively, the non-coaxial flow direction can be redefined as the orthogonal direction of the current principal stresses, as proposed by Chen and Huang [6]. The above approaches for modeling non-coaxial plastic flow have mainly been applied to sand, whereas its counterpart for clays is largely underdeveloped. Given that the non-coaxiality of sand and clay is often governed by different factors (e.g., state dependence, particle gradation and fabrics are the main factors for sand [4, 58], while structuration, anisotropy and stress histories are the main factors for clay [31, 62]), the non-coaxial models reviewed above generally cannot be directly applied to clay.

The goal of this work is to propose a critical state-based elastoplastic constitutive model to represent the non-coaxial plastic responses of saturated clays under monotonic loading with fixed principal stress directions. For this purpose, a novel non-coaxial approach is introduced by modifying Qian et al.’s [32] non-coaxial plastic flow rule. A comprehensive HCA (hollow cylinder apparatus) testing program is performed on saturated Shanghai soft clay to assess the proposed non-coaxial model. Also, the presented model is verified against the published results of laboratory tests on saturated Wenzhou soft clay.

2 Non-coaxial flow rule

The non-coaxial plastic theory additively decomposes the total strain rate into elastic, coaxial plastic and non-coaxial plastic parts:

$$\dot{\varepsilon }_{ij} { = }\dot{\varepsilon }_{ij}^{e} + \dot{\varepsilon }_{ij}^{pc} + \dot{\varepsilon }_{ij}^{pn}$$
(1)

where a superposed dot indicates a time derivative, and the superscripts e, pc and pn denote elastic, coaxial plastic and non-coaxial plastic, respectively. The coaxial plastic strain rate \(\dot{\varepsilon }_{ij}^{pc}\) can be conventionally defined by a plastic potential, i.e.,

$$\dot{\varepsilon }_{ij}^{pc} = \dot{\Lambda }\frac{\partial Q}{{\partial \sigma_{ij} }}$$
(2)

where \(\dot{\Lambda }\), \(Q\) and \(\sigma_{ij}\) denote the plastic scalar factor, the plastic potential and the effective stress tensor, respectively.

According to the non-coaxial flow theory proposed by Qian et al. [32], the non-coaxial plastic strain rate \(\dot{\varepsilon }_{ij}^{pn}\) is colinear with the non-coaxial stress rate, which in generalized stress space is given by

$$\dot{s}_{ij}^{n} { = }\dot{s}_{ij} - \frac{{\dot{s}_{kl} s_{kl} }}{{s_{mn} s_{mn} }}s_{ij} - \frac{{\dot{s}_{kl} S_{kl} }}{{S_{mn} S_{mn} }}S_{ij}$$
(3)

where \(s_{ij}\) is the deviatoric stress tensor; the superscript n denotes non-coaxiality; and \(S_{ij}\) is given by

$$S_{ij} = s_{ik} s_{kj} - \frac{2}{3}J_{2} \delta_{ij} - \frac{3}{2}\frac{{J_{3} }}{{J_{2} }}s_{ij}$$
(4)

where \(\delta_{ij}\) = Kronecker delta; and \(J_{2}\), \(J_{3}\) = second and third invariants of the deviatoric stress tensor, \(s_{ij}\). The two invariants are given as follows:

$$J_{2} = s_{ij} s_{ij} /2,\;J_{3} = s_{ij} s_{jk} s_{ki} /3$$
(5)

Equation (4) can introduce the influence of the third stress invariant and define a three-dimensional stress space \(\delta_{ij}\)–\(s_{ij}\)–\(S_{ij}\) and consequently formulate non-coaxial stress rate. Hence, the corresponding non-coaxial strain rate is defined as

$$\dot{\varepsilon }_{ij}^{pn} = \frac{1}{{H_{t} }}\dot{s}_{ij}^{n}$$
(6)

where \(H_{t}\) denotes the plastic modulus governing the response related to the stress rate tangential to the yield surface.

In the works by Qian et al. [32], the Gram–Schmidt orthogonal projection of \(\dot{s}_{ij}\) with respect to the reference stress tensor \(s_{ij}\) was conducted and \(s_{ij}\) was regarded as the reference stress tensor. In this process, the influence of the third stress invariant of \(s_{ij}\) was taken into consideration. Then, the stress rate decomposition \(\dot{s}_{ij}^{n}\) was obtained and the corresponding non-coaxial strain rate was defined. Equation (6) can be rewritten in the following form

$$\dot{\varepsilon }_{ij}^{pn} = C_{ijkl}^{np} \dot{\sigma }_{kl}$$
(7)

where \(\dot{\sigma }_{kl}\) = effective stress rate; and \(C_{ijkl}^{np}\) = non-coaxial compliance tensor given by

$$C_{ijkl}^{np} = \frac{1}{{H_{{\text{t}}} }}\left( {\frac{{\delta_{ik} \delta_{jl} + \delta_{il} \delta_{jk} }}{2} - \frac{{\delta_{kl} \delta_{ij} }}{{\delta_{mn} \delta_{mn} }} - \frac{{s_{ij} s_{kl} }}{{s_{mn} s_{mn} }} - \frac{{S_{ij} S_{kl} }}{{S_{mn} S_{mn} }}} \right)$$
(8)

Equation (6) implies that the non-coaxial plastic strain rate direction is actually coincident with the non-coaxial stress rate direction, and Eqs. (3) and (7) imply that both of these two directions are orthogonal to the current stress direction. Equation (7) essentially defines a relaxed plastic loading condition compared with the classical plasticity. In this way, the plastic responses for stress path tangential to the yield surface (i.e., the neutral loading in classical plasticity) can be considered.

As mentioned earlier, when the stress rate direction coincides with that of the current stress (for instance, under monotonic shearing with fixed principal stress directions), i.e.,

$$\frac{{s_{ij} \dot{s}_{ij} }}{{\sqrt {s_{kl} s_{kl} } \sqrt {\dot{s}_{mn} \dot{s}_{mn} } }} = 1$$
(9)

then Eq. (7) will lead to

$$\dot{\varepsilon }_{ij}^{pn} = C_{ijkl}^{np} \dot{\sigma }_{kl} = 0$$
(10)

Equation (10) implies that all plastic strains will be coaxial under monotonic shearing with fixed principal stress directions. This, however, contradicts experimental observations [26, 31, 51]. To resolve this issue, the previous non-coaxial theory should be revised to describe the non-coaxiality under monotonic shear loading. It had been proved by Li and Dafalias [23] that the coaxial stress rate is a simple and reasonable form and is in agreement with their definition form. They also stated that the non-coaxial stress rate should be obtained in regard to the principal axes of the reference tensor. Motivated by Qian et al. [32] and Li and Dafalias [23], the principal stress tensor \(s_{ij}^{p}\) is used to replace \(s_{ij}\) in the non-coaxial stress rate by Qian et al. [32] and defined as

$$s_{ij}^{p} = \frac{2}{3}q\left[ {\begin{array}{*{20}c} {\sin \left( {\theta - \frac{2}{3}\pi } \right)} & 0 & 0 \\ 0 & {\sin \theta } & 0 \\ 0 & 0 & {\sin \left( {\theta + \frac{2}{3}\pi } \right)} \\ \end{array} } \right]$$
(11)

where \(\theta = \frac{1}{3}\sin^{ - 1} \left[ { - \frac{3\sqrt 3 }{2}\frac{{J_{3} }}{{J_{2}^{3/2} }}} \right]\) and \(q = \sqrt {3J_{2} }\) are the Lode angle and the equivalent deviatoric stress computed with reference to the current stress states. In addition, \(S_{ij}^{p}\) is used to replace \(S_{ij}\) and the normalized unit tensor \(n_{ij}^{{\dot{\sigma }}}\) is used to replace \(\dot{s}_{ij}^{{}}\). Eventually, the non-coaxial stress part \(n_{ij}^{non}\) is obtained:

$$n_{ij}^{non} = n_{ij}^{{\dot{\sigma }}} - \frac{{n_{kl}^{{\dot{\sigma }}} s_{kl}^{p} }}{{s_{mn}^{p} s_{mn}^{p} }}s_{ij}^{p} - \frac{{n_{kl}^{{\dot{\sigma }}} S_{kl}^{p} }}{{S_{mn}^{p} S_{mn}^{p} }}S_{ij}^{p}$$
(12)

where \(n_{ij}^{{\dot{\sigma }}} = \frac{{\dot{\sigma }_{ij} }}{{\left\| {{\dot{\mathbf{\sigma }}}} \right\|}}\) denotes the unit stress rate. The tensor \(S_{ij}^{p}\) in Eq. (12) is related to the second and third invariants of the tensor \(s_{ij}^{p}\):

$$S_{ij}^{p} = s_{ik}^{p} s_{kj}^{p} - \frac{2}{3}J_{2} \delta_{ij} - \frac{3}{2}\frac{{J_{3} }}{{J_{2} }}s_{ij}^{p}$$
(13)

Equations (11), (12) and (13) imply that the direction of the non-coaxial plastic flow is defined by conducting a Gram–Schmit orthogonal projection of the current stress rate with respect to the reference stress tensor \(s_{ij}^{p}\). From a view of the mechanism, \(s_{ij}^{p}\) represents a stress state equivalent to the current stress \(s_{ij}\) in terms of the intensity of shear stress and the intermediate principal stress ratio (i.e., the same deviatoric stress \(q\) and Lode angle \(\theta\)), yet its principal directions coincide with the material axes of anisotropy defined by the direction of initial deposition and the two mutually orthogonal directions along the bedding plane (note that these three mutually orthogonal directions are coincident with the base vectors used to define all second-order tensors throughout this work). So it is related to material axes of anisotropy defined by the direction of initial deposition of natural clay and its fabric. Taking the tensor \(s_{ij}^{p}\) as a reference tensor, the normalized unit tensor \(n_{ij}^{{\dot{\sigma }}}\) can be decomposed into the coaxial and non-coaxial parts. The reference tensor \(s_{ij}^{p}\) and the non-coaxial stress rate \(n_{ij}^{non}\) are consistent with the general non-coaxiality mechanism between two tensors by Li and Dafalias [23]. Lastly, it should be noted that in Eq. (12) \(s_{mn}^{p} s_{mn}^{p}\) and \(S_{mn}^{p} S_{mn}^{p}\) are the second invariant of \(s_{ij}^{p}\) and \(S_{ij}^{p}\), while \(n_{kl}^{{\dot{\sigma }}} s_{kl}^{p}\) and \(n_{kl}^{{\dot{\sigma }}} S_{kl}^{p}\) are the second joint invariant of between tensors \(n_{ij}^{{\dot{\sigma }}}\) and \(s_{ij}^{p}\), and between \(n_{ij}^{{\dot{\sigma }}}\) and \(S_{ij}^{p}\). Accordingly, the non-coaxial flow direction is a linear combination of the second-order symmetric tensors \(n_{ij}^{{\dot{\sigma }}}\), \(s_{ij}^{p}\), \(S_{ij}^{p}\) and their invariants and joint invariants; hence, the objectivity of the flow direction can be ensured. Given the direction of the non-coaxial plastic strain rate specified by Eq. (12), we postulate that the rate of such plastic strain can be expressed by

$$\dot{\varepsilon }_{ij}^{pn} = \dot{\Lambda }\left\langle {1 - \frac{\eta }{M}} \right\rangle^{\gamma } k_{n} n_{ij}^{non}$$
(14)

where 〈 〉 is the symbol of Macaulay brackets; \(\eta\) and \(M\) denote the current stress ratio and the critical state stress ratio, respectively; and \(\gamma\), \(k_{n}\) are material constants which control the magnitude of the non-coaxial plastic strain. The term within the Macaulay brackets is introduced to model the decreasing degree of non-coaxiality as the deviatoric stress increases and the approximately coaxiality between stress and strain increment at critical state, as reported for clay [20, 51, 62]. It should be noted that Eq. (14) implies that the same plastic multiplier is used for both the coaxial and the non-coaxial plastic strain rate. This model decision is made as both kinds of irrecoverable deformations are driven by a common plasticity process, and they only differ regarding directions. Moreover, it should be emphasized that while a common multiplier is used, it does not mean that the non-coaxial and coaxial flows will have the same intensity. The inclusion of the parameters \(k_{n}\) and \(\gamma\) will control the magnitudes of non-coaxial irrecoverable deformations relative to the coaxial parts. Lastly, it should be noted that the non-coaxial stress rate \(n_{ij}^{non}\) and its corresponding generation of non-coaxiality agree with the non-coaxial yield theory by Qian et al. [32], which is also called ‘vertex’ yield theory as early proposed by Rudnicki and Rice [35]. Qian et al. [32] revised Rudnicki and Rice’s ‘vertex’ theory into three-dimensional space. Keeping in mind, the previous non-coaxial theory is related to stress-induced anisotropy under non-proportional loading, while this work is intended to revise previous theories to describe non-coaxiality under monotonic shear loading. By combining the coaxial [i.e., Eq. (2)] and the non-coaxial [i.e., Eq. (14)] plastic strain rate, the total plastic flow rule can be expressed as follows:

$$\dot{\varepsilon }_{ij}^{p} = \dot{\Lambda }\left[ {\frac{\partial Q}{{\partial \sigma_{ij} }} + \left\langle{1 - \frac{\eta }{M}} \right\rangle^{\gamma } k_{n} n_{ij}^{non} } \right]$$
(15)

3 Model description

To represent the non-coaxial plastic responses of clays under rotation of principal stress directions, the non-coaxial flow rule described in Sect. 2 is incorporated into a critical state-based elastoplastic model. In the following presentation, all the stress variables are regarded as effective stresses and a compression positive convention is used for both stress and strain measures.

3.1 Elastic behavior

The proposed model adopts a hypoelastic model commonly used in Cam-clay-type models [8, 9, 29, 53, 60]. The bulk modulus K is assumed to depend on the current mean effective stress p′ = σkk/3 as follows:

$$K = \frac{{\left( {1 + e_{0} } \right)p^{\prime } }}{\kappa }$$
(16)

where \(\kappa\) is the slope of the swelling line in e-lnp′ plane. The second independent elastic constant is chosen to be a constant Poisson’s ratio \(\nu\). Accordingly, the shear modulus G can be related to K:

$$G = \frac{3(1 - 2\nu )}{{2(1 + \nu )}}K$$
(17)

The model of Eqs. (16)–(17) represents a simple and convenient way to model the elastic response of clay and, in combination of the isotropic hardening rule introduced in the following, reproduces the normal compression behavior of clay.

The corresponding elastic incremental constitutive relation is given by

$$\dot{\sigma }_{ij} = D_{ijkl}^{e} \dot{\varepsilon }_{kl}^{e}$$
(18)

where \(D_{ijkl}^{e}\) is the elastic stiffness moduli, being a function of K and G as follows:

$$D_{ijkl}^{e} = \left( {K - \frac{2}{3}G} \right)\delta_{ij} \delta_{kl} + G\left( {\delta_{ik} \delta_{jl} + \delta_{il} \delta_{jk} } \right)$$
(19)

3.2 Plastic behavior

The plastic behavior of the model is developed within the framework of the critical state theory. The formulation of the proposed model is given in detail as follows.

For simplicity, we adopt the yield surface employed by Huang et al. [16] and Ling et al. [24] but ignoring its original dependence on the fabric tensor. Such yield function in triaxial stress space can be expressed as:

$$F = \left( {p^{\prime } - p_{c} } \right)\left( {p^{\prime } + \frac{R - 2}{R}p_{c} } \right) + \frac{{\left( {R - 1} \right)^{2} }}{{M^{2} }}q^{2} = 0$$
(20)

The model constant \(R\) controls the ratio of the two major axes of the yield surface, and when \(R\) = 2, Eq. (20) recovers the yield surface employed in the classical modified Cam-clay model, and \(M\) is the slope of the critical state line, which is a function of the Lode angle \(\theta\) in three-dimensional stress space:

$$M = M_{{\text{c}}} \left[ {\frac{{2m^{4} }}{{\left( {1 + m} \right)^{4} - \left( {1 - m} \right)^{4} \sin 3\theta }}} \right]^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-\nulldelimiterspace} 4}}}$$
(21)

In Eq. (21), the variable \(m\) is defined as \(m = {{M_{{\text{e}}} } \mathord{\left/ {\vphantom {{M_{{\text{e}}} } {M_{{\text{c}}} }}} \right. \kern-\nulldelimiterspace} {M_{{\text{c}}} }}\) in which \(M_{{\text{c}}}\) and \(M_{{\text{e}}}\) are the critical state stress ratio for triaxial compression and triaxial extension, respectively. According to Sheng et al. [39], the yield surface is convex provided \(m \ge 0.6\), and it coincides with the Mohr–Coulomb hexagon at all vertices in the deviatoric plane, if \(M_{{\text{c}}}\) and \(M_{{\text{e}}}\) are computed according to the Mohr–Coulomb criteria using the same friction angle. For discussions on the employed yield surface in greater depths, we refer the readers to existing literature (e.g., [3, 7, 16, 24]).

The isotropic hardening rule is used to control the size of the yield surface through the internal variable \(p_{{\text{c}}}\). In line with the Cam-clay model, a volumetric hardening rule [37] is adopted:

$$\dot{p}_{{\text{c}}} = {{p_{{\text{c}}} \dot{\varepsilon }_{{\text{v}}}^{p} \left( {1 + {\text{e}}_{0} } \right)} \mathord{\left/ {\vphantom {{p_{{\text{c}}} \dot{\varepsilon }_{{\text{v}}}^{p} \left( {1 + {\text{e}}_{0} } \right)} {(\lambda - \kappa )}}} \right. \kern-\nulldelimiterspace} {(\lambda - \kappa )}}$$
(22)

where \(\dot{\varepsilon }_{{\text{v}}}^{p}\) is the plastic volumetric strain rate; \(\lambda\) is the slope of the normal compression line in the e − lnp′ space.

Experimental evidence for Shanghai soft clay [16] and Perno clay [18] suggests that the associated flow rule is a reasonable approximation for natural clay. Thus, the yield function of Eq. (20) also serves as the plastic potential in this work. By considering the non-coaxial flow rule described in Sect. 2, the total plastic strain rate finally can be expressed as Eq. (15). Besides, substituting Eqs. (1), (2), (14) and (18) into the consistency condition of the yield surface, the plastic scalar factor can be determined by

$$\dot{\Lambda } = \frac{{\frac{\partial F}{{\partial \sigma_{{{\text{st}}}} }}D_{{{\text{stkl}}}}^{e} \dot{\varepsilon }_{{{\text{kl}}}} }}{{H_{{\text{P}}} + \frac{\partial F}{{\partial \sigma_{{{\text{st}}}} }}D_{{{\text{stkl}}}}^{e} \left[ {\frac{\partial Q}{{\partial \sigma_{{{\text{kl}}}} }} + \left\langle {1 - \frac{\eta }{M}} \right\rangle^{\gamma } k_{n} n_{{{\text{kl}}}}^{non} } \right]}}$$
(23)

where \(H_{{\text{P}}}\) denotes the plastic hardening modulus.

3.3 Model parameters

The calibration of the proposed model requires constraining 8 parameters and knowing the initial void ratio. These parameters can be categorized into three groups: (1) critical state soil mechanics (\(\lambda\), \(\kappa\), \(M_{{\text{c}}}\), \(M_{{\text{e}}}\), \(\nu\)), (2) shape of yield surface (\(R\)) and (3) the evolution of non-coaxiality (\(\gamma\), \(k_{n}\)). All of these parameters can be obtained directly from laboratory tests.

The classical Cam-clay-type parameters \(\lambda\) and \(\kappa\) are, respectively, the slope of the normal compression line and the swelling line in e-lnp′ space obtained from isotropic consolidation tests. They may also be obtained from the compression index \(C_{{\text{c}}}\) and swelling index \(C_{{\text{s}}}\) evaluated from oedometer tests, where \(\lambda = {{C_{{\text{c}}} } \mathord{\left/ {\vphantom {{C_{{\text{c}}} } {2.303}}} \right. \kern-\nulldelimiterspace} {2.303}}\) and \(\kappa = {{C_{{\text{s}}} } \mathord{\left/ {\vphantom {{C_{{\text{s}}} } {2.303}}} \right. \kern-\nulldelimiterspace} {2.303}}\). The critical state stress ratio \(M_{{\text{c}}}\) and \(M_{{\text{e}}}\) can be determined from the effective stress paths of triaxial compression and extension tests or indirectly deduced from the angle of internal friction \(\phi\). The Poisson’s ratio \(\nu\) may be specified as a constant and determined by empirical methods such as the one proposed by Lade [19] that correlates Poisson’s ratio with the plasticity index (PI) of clay.

The shape parameter \(R\) [16, 24, 60] controls the extent of the accessible tensile stress region in the stress space diagonal for \(R\) ≥ 2.0 and also changes the shape of the yield function. Larger values of \(R\) imply a flatter yield surface. In the e-lnp′ space, the shape parameter \(R\) is defined as follows [24, 60]:

$$R = \frac{{p_{x} }}{{p_{{\text{f}}} }}$$
(24)

where \(p_{x}\) and \(p_{{\text{f}}}\) denote the initial consolidation pressure of current yield surface and corresponding critical state mean normal effective stresses. According to this definition, the shape parameter \(R\) can be obtained when knowing parameters \(\lambda\), \(\kappa\) and \(p_{{\text{f}}}\). As \(\lambda\) and \(\kappa\) have been obtained from isotropic consolidation tests, effective stress path of undrained triaxial shearing on normally consolidated clays can be used to obtain the value of shape parameter \(R\) as shown by Ling et al. [24]. The parameter \(R\) = 2.0 is a typical value and recovers the yield surface of the modified Cam-clay model.

The parameter \(\gamma\) controls the diminishing rate of the non-coaxial plastic flow as the current stress ratio approaches the critical state one, while the non-coaxial parameter \(k_{n}\) governs the magnitude of the non-coaxiality. These two parameters can be calibrated from monotonic shear tests with fixed principal stress directions of \(\alpha_{\sigma }\) (i.e., the angle between the soil deposition direction and the major principal stress direction, as depicted in Fig. 1) neither equaling to 0° nor 90°. Otherwise, non-coaxial flow will not occur according to the employed flow rule. According to the definition of the non-coaxial flow rule [i.e., Eq. (14)], \(\varepsilon_{z\theta }^{p}\) is supposed to denote the non-coaxial plastic strains in hollow cylinder torsional shear tests. Hence, one can approximately have

$$\gamma = {{\ln \left( {\frac{{{\text{d}}\varepsilon_{z\theta }^{p1} }}{{{\text{d}}\varepsilon_{z\theta }^{p2} }}} \right)} \mathord{\left/ {\vphantom {{\ln \left( {\frac{{{\text{d}}\varepsilon_{z\theta }^{p1} }}{{{\text{d}}\varepsilon_{z\theta }^{p2} }}} \right)} {\ln \left( {\frac{{1 - {{\eta_{1} } \mathord{\left/ {\vphantom {{\eta_{1} } M}} \right. \kern-\nulldelimiterspace} M}}}{{1 - {{\eta_{2} } \mathord{\left/ {\vphantom {{\eta_{2} } M}} \right. \kern-\nulldelimiterspace} M}}}} \right)}}} \right. \kern-\nulldelimiterspace} {\ln \left( {\frac{{1 - {{\eta_{1} } \mathord{\left/ {\vphantom {{\eta_{1} } M}} \right. \kern-\nulldelimiterspace} M}}}{{1 - {{\eta_{2} } \mathord{\left/ {\vphantom {{\eta_{2} } M}} \right. \kern-\nulldelimiterspace} M}}}} \right)}}$$
(25)

where (\({\text{d}}\varepsilon_{z\theta }^{p1}\),\(\eta_{1}\)) and (\({\text{d}}\varepsilon_{z\theta }^{p2}\),\(\eta_{2}\)) are two different data points from the \({\text{d}}\varepsilon_{z\theta }^{p} - \eta\) curve obtained from the torsional shear tests described above (note that \(\varepsilon_{z\theta }^{p}\) is plastic shear strain within the \(z\theta\) plane depicted in Fig. 1; \(\eta\) is the stress ratio). After the parameter \(\gamma\) is determined, the value of the constant \(k_{n}\) can be determined by fitting the \({\text{d}}\varepsilon_{z\theta }^{p} - \eta\) curve directly. Figure 2 shows the simulated evolution of the strain direction angle \(\alpha_{{{\text{d}}\varepsilon }}\) (i.e., the angle between the deposition direction and the principal strain increment direction) within undrained monotonic shear test with fixed principal stress directions. In this example, the initial consolidation pressure p′ = 150 kPa, the intermediate principal stress ratio b = 0.5 and the major principal stress inclination \(\alpha_{\sigma }\) = 30°. Figure 2a shows that the change of the angle \(\alpha_{{{\text{d}}\varepsilon }}\) due to an increasing stress ratio is relatively small when \(\gamma\) = 0 (i.e., the influence of the current stress ratio on the non-coaxial flow is neglected). When a non-zero \(\gamma\) is employed, the angle \(\alpha_{{{\text{d}}\varepsilon }}\) approaches gradually to the stress direction angle \(\alpha_{\sigma }\) (i.e., a diminishing non-coaxial effect) as the stress ratio advances toward the failure. Figure 2b shows that \(\alpha_{{{\text{d}}\varepsilon }}\) almost coincides with \(\alpha_{\sigma }\) when \(k_{n}\) = 0 (i.e., the non-coaxial plastic strain is not considered), while the non-coaxial angle increases with the increase of the material constant \(k_{n}\).

Fig. 1
figure 1

Stress state of soil element in hollow cylinder torsional shear tests

Full size image
Fig. 2
figure 2

Simulated variation of strain direction angle with the stress ratio under monotonic shearing with fixed principal stress directions: a effect of the parameter γ (kn = 100), b effect of the parameter kn (γ = 0.5)

Full size image

4 Model simulations

The model was calibrated and verified against two different types of clay: Shanghai clay and Wenzhou clay. Undrained hollow cylinder torsional shear tests were performed on undisturbed Shanghai clay specimens. The calibration of Shanghai clay parameters was based on the results of oedometer tests, triaxial tests and monotonic shear tests with fixed principal stress directions using hollow cylinder apparatus. As for Wenzhou clay, testing data reported by Wang et al. [51] were used to verify the proposed model. Parts of model parameters are provided by Wang et al. [51], while the rest is obtained by following the procedures described above. In particular, the parameters \(\lambda\) and \(\kappa\) are determined by using their correlations with the liquid limit wL and plasticity index Ip [27, 37].

4.1 Experiments on Shanghai soft clay

A series of tests on Shanghai soft clay were conducted to assess the proposed model. The test program includes the oedometer test, triaxial test and hollow cylinder torsional shear test. To determine essential critical state parameters for the proposed model, oedometer tests and triaxial tests were performed. The hollow cylinder shear tests are used to obtain non-coaxial parameters and subsequently examine the model capacity to represent the non-coaxial behavior of clays.

In this study, undisturbed samples of Shanghai clay were obtained from a deep excavation site at a depth of 18–20 m. The physical properties of the tested Shanghai soft clay are shown in Table 1. The water table is 0.5–1.0 m below the ground surface, and the vertical effective stress of the subsoil at 18–20 m is around 150 kPa.

Table 1 Physical properties of Shanghai soft clay
Full size table

4.1.1 One-dimensional consolidation characteristics experiments

Figure 3 shows the results of a one-dimensional consolidation test on Shanghai clay conducted in conventional oedometer. Based on the test results, the pre-consolidation pressure σp was determined to be 148.6 kPa using the Casagrande method. The compression index and swelling index (\(C_{{\text{c}}}\) and \(C_{{\text{s}}}\)) for one-dimensional consolidation are 0.484 and 0.092, respectively. The parameters \(\lambda\) and \(\kappa\) for Shanghai clay are estimated from these two indexes (i.e., \(\lambda = {{C_{{\text{c}}} } \mathord{\left/ {\vphantom {{C_{{\text{c}}} } {2.303}}} \right. \kern-\nulldelimiterspace} {2.303}}\) and \(\kappa = {{C_{{\text{s}}} } \mathord{\left/ {\vphantom {{C_{{\text{s}}} } {2.303}}} \right. \kern-\nulldelimiterspace} {2.303}}\)).

Fig. 3
figure 3

Compression curve of undisturbed Shanghai soft clay in e − log σv plane obtained from odometer test

Full size image

4.1.2 Consolidated undrained triaxial tests

Undrained triaxial compression tests were performed after clay specimens were isotropically consolidated to initial confining pressures of p′0 = 150 kPa, 200 kPa and 300 kPa. These consolidation stresses are selected to ensure that the clay samples are normally consolidated before shearing. The Skempton’s pore pressure coefficient B was checked to be greater than 0.98 before consolidation to ensure the triaxial samples were fully saturated. The effective stress paths in p′-q space and the stress–strain response corresponding to the stress state at failure are shown in Fig. 4. The slope of the critical state line, \(M_{{\text{c}}}\), is determined to be 1.32, which corresponds to an effective angle of internal friction \(\phi_{{\text{c}}}\) = 32.8°.

Fig. 4
figure 4

Results of undrained triaxial compression tests on undisturbed Shanghai soft clay: a effective stress paths in p′ − q space, b stress–strain response of εq − q/p′

Full size image

4.1.3 Undrained monotonic shear tests with fixed principal stress directions

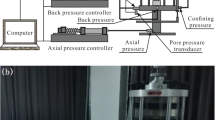
Undrained monotonic shearing with fixed principal stress directions was performed by using the TJ-5 Hz hollow cylinder apparatus (HCA) at Tongji University. The equipment was described in detail by Qian et al. [30, 31]. The hollow cylindrical specimens used have an inner diameter of 60 mm, an outer diameter of 100 mm and a height of 200 mm. As shown in Fig. 1 [14], the four external loads applied to clay samples are the axial load W, torque T, inner cell pressure Pi and outer cell pressure Po. The combination of these external loads results in independent controls over four stress components induced in a tested specimen: the axial stress \(\sigma_{z}\), radial stress \(\sigma_{r}\), circumferential stress \(\sigma_{\theta }\) and shear stress \(\tau_{z\theta }\). They are conveniently converted into an equivalent set of stress parameters, p, q, b and \(\alpha_{\sigma }\), shown in Fig. 1. The equations used to calculate the stress and strain parameters can be found in Qian et al. [30]. After sample preparation, a back pressure of 50 kPa was applied to ensure the saturation of the soils and the Skempton’s pore pressure coefficient B is checked to be greater than 0.96 before proceeding to the next stage. Subsequently, all samples were isotropically consolidated to a mean effective stress of 150 kPa. Then, the monotonic shearing was performed by monotonically increasing the deviatoric stress q, while the other three parameters were maintained constant, as shown in Fig. 5. When q increases to certain values, non-uniform strain occurs, strains increase sharply and q can no longer be controlled. This instance is defined as failure, and throughout this work we only report data before failure. In total, 5 undrained element tests were conducted under different fixed principal stress directions, as listed in Table 2. It should be noted that the orientation relative to the horizontal axis is \(2\alpha_{\sigma }\) in Fig. 5, and it is twice the direction of the major principal stress relative to the vertical.

Fig. 5
figure 5

Stress path in deviatoric stress space for monotonic shearing with fixed principal stress directions

Full size image
Table 2 Test program for Shanghai soft clay
Full size table

In studying the non-coaxiality, the non-coaxial plastic strain rate is related to the deviatoric plastic strain rate. It should be noted that the rate of elastic volumetric strain essentially has no influence to the degree of non-coaxiality. By contrast, the rate of elastic shear strain definitely affects the degree of non-coaxiality. However, compared to the plastic shear strain rate, the elastic shear strain rate can be ignored in dealing with the elastoplastic responses of soil. For example, the original Cam-clay model assumes that the elastic shear strain rate is equal to zero [37]. On the other hand, with an increasing shear stress level up to ultimate failure, the rate of elastic shear strain tends to take a smaller proportion in the rate of total strain where the soil behavior is totally governed by the plastic process. Besides, it is hard to precisely separate the elastic shear strain rate from the total strain rate. So the total strain rate instead of the plastic strain rate is used in the analysis, which is consistent with the conduct of experimental data by Cai et al. [4], Lade and Kirkgard [20], Tong et al. [44] and Wang et al. [51]. The stress path in the \(\tau_{z\theta }\)–\({{\left( {\sigma_{z} - \sigma_{\theta } } \right)} \mathord{\left/ {\vphantom {{\left( {\sigma_{z} - \sigma_{\theta } } \right)} 2}} \right. \kern-\nulldelimiterspace} 2}\) plane and the strain increment vector are shown in Fig. 6. The figure schematically shows the stress paths in the plane of \({{\left( {\sigma_{z} - \sigma_{\theta } } \right)} \mathord{\left/ {\vphantom {{\left( {\sigma_{z} - \sigma_{\theta } } \right)} {\left( {\sigma_{z} + \sigma_{\theta } } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\sigma_{z} + \sigma_{\theta } } \right)}}\) versus \({{2\tau_{z\theta } } \mathord{\left/ {\vphantom {{2\tau_{z\theta } } {\left( {\sigma_{z} { + }\sigma_{\theta } } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\sigma_{z} { + }\sigma_{\theta } } \right)}}\) and the induced strain increments superposed in the stress paths, i.e., \({{\left( {{\text{d}}\varepsilon_{z} - {\text{d}}\varepsilon_{\theta } } \right)} \mathord{\left/ {\vphantom {{\left( {{\text{d}}\varepsilon_{z} - {\text{d}}\varepsilon_{\theta } } \right)} {{\text{d}}s}}} \right. \kern-\nulldelimiterspace} {{\text{d}}s}}\) versus \({{{\text{d}}\gamma_{z\theta } } \mathord{\left/ {\vphantom {{{\text{d}}\gamma_{z\theta } } {{\text{d}}s}}} \right. \kern-\nulldelimiterspace} {{\text{d}}s}}\) where ds is the stress increment, as shown in Eq. (29). \(\alpha_{\sigma }\), \(\alpha_{{{\text{d}}\sigma }}\) and \(\alpha_{{{\text{d}}\varepsilon }}\) denote the angle between the deposition direction and major principal stress direction, major principal stress increment direction and major principal strain increment direction, respectively. The vectors AB (the scalar quantity is ds) denotes the stress increment, and AC is the strain increment per unit stress increment. The latter denotes the deformability under the force which is physically related to the material flexibility [31]. The quantities described above can be related to the control variables of HCA as follows:

$$\alpha_{\sigma } = \frac{1}{2}\arctan \left( {\frac{{2\tau_{z\theta } }}{{\sigma_{z} - \sigma_{\theta } }}} \right)$$
(26)
$$\alpha_{{{\text{d}}\sigma }} = \frac{1}{2}\arctan \left( {\frac{{2{\text{d}}\tau_{z\theta } }}{{{\text{d}}\sigma_{z} - {\text{d}}\sigma_{\theta } }}} \right)$$
(27)
$$\alpha_{{{\text{d}}\varepsilon }} = \frac{1}{2}\arctan \left( {\frac{{{\text{d}}\gamma_{z\theta } }}{{{\text{d}}\varepsilon_{z} - {\text{d}}\varepsilon_{\theta } }}} \right)$$
(28)
$$\left| {{\mathbf{AB}}} \right| = {\text{d}}s = \sqrt {\left[ {{\text{d}}\left( {\frac{{\sigma_{z} - \sigma_{\theta } }}{{\sigma_{z} + \sigma_{\theta } }}} \right)} \right]^{2} + \left[ {{\text{d}}\left( {\frac{{2\tau_{z\theta } }}{{\sigma_{z} + \sigma_{\theta } }}} \right)} \right]^{2} }$$
(29)
$$\left| {{\mathbf{AC}}} \right| = \frac{{\sqrt {\left[ {{\text{d}}\left( {\varepsilon_{z} - \varepsilon_{\theta } } \right)} \right]^{2} + \left[ {{\text{d}}\gamma_{z\theta } } \right]^{2} } }}{{{\text{d}}s}} = \frac{{{\text{d}}\varepsilon_{1} - {\text{d}}\varepsilon_{3} }}{{{\text{d}}s}}$$
(30)
Fig. 6
figure 6

Stress path and non-coaxial behavior between stress direction and strain increment direction

Full size image

Figure 7 shows the effective stress path and stress–strain curves of Shanghai clay subjected to undrained monotonic shear with different fixed principal stress directions. As shown in Fig. 7a, the undrained shear strength is dependent on major principal stress direction. The undrained shear strength decreases when \(\alpha_{\sigma }\) is less than 45° and slightly increases after \(\alpha_{\sigma }\) = 45° with increasing \(\alpha_{\sigma }\), indicating clearly strength anisotropy. Figure 8a presents strain increment vectors of clay specimens under monotonic shearing with fixed principal stress directions in \(\tau_{z\theta }\)–\({{\left( {\sigma_{z} - \sigma_{\theta } } \right)} \mathord{\left/ {\vphantom {{\left( {\sigma_{z} - \sigma_{\theta } } \right)} 2}} \right. \kern-\nulldelimiterspace} 2}\) plane. For a better view of the variation of non-coaxial angle characteristics, the arrow only indicates the direction of strain increment and does not indicate the size of strain increment per unit stress increment. The corresponding variation of the strain increment direction angle with the deviatoric stress is shown in Fig. 9a. These data show that the strain increment direction almost coincides with the stress direction for \(\alpha_{\sigma }\) = 0°, 90° (shearing along the direction of \({{\left( {\sigma_{z} - \sigma_{\theta } } \right)} \mathord{\left/ {\vphantom {{\left( {\sigma_{z} - \sigma_{\theta } } \right)} 2}} \right. \kern-\nulldelimiterspace} 2}\)) and = 45° (shearing along the direction of \(\tau_{z\theta }\)), whereas apparent non-coaxiality exists for \(\alpha_{\sigma }\) = 30° and 60°. Such observation suggests that non-coaxial characteristics of soils may be attributed to the coupling between loading along the directions of \({{\left( {\sigma_{z} - \sigma_{\theta } } \right)} \mathord{\left/ {\vphantom {{\left( {\sigma_{z} - \sigma_{\theta } } \right)} 2}} \right. \kern-\nulldelimiterspace} 2}\) and \(\tau_{z\theta }\). The directional angle of strain increment is greater and less than that of stress for \(\alpha_{\sigma }\) = 30° and \(\alpha_{\sigma }\) = 60°, respectively. The non-coaxial angle decreases gradually with the increase of the deviatoric stress. Moreover, the direction of strain increments almost coincides with that of stress when the failure surface is reached. These observations described above are in agreement with those observed for sand [11, 33, 43] and other types of clay [51, 62] under monotonic shearing with fixed principal stress directions.

Fig. 7
figure 7

Experimental and predicted results of effective stress path and stress–strain relationship εq − q for Shanghai clay: a effective stress path, b stress–strain relationship εq − q

Full size image
Fig. 8
figure 8

Non-coaxiality of strain increment vectors in τzθ − (σz − σθ)/2 plane under monotonic shearing with fixed principal stress directions: a experimental results, b model simulations with non-coaxial flow rule suggested by Qian et al. [32], c model simulations based on the revised non-coaxial flow of this paper

Full size image
Fig. 9
figure 9

Variation of the strain increment direction angle with the deviatoric stress: a experimental results, b model simulations

Full size image

4.2 Model simulations of Shanghai soft clay

The calibration of the proposed model for Shanghai clay is based on the results of one-dimensional consolidation experiments, consolidated undrained triaxial tests and undrained monotonic shear tests with fixed principal stress directions. Table 3 shows the value of model parameters for Shanghai soft clay. These values \(e_{0}\) = 1.060, \(p_{{{\text{c0}}}}\) = 150 kPa have been used in the following simulations. It should be noted that due to the lack of appropriate experimental data, we assume that the Poisson’s ratio for Shanghai clay (also that for Wenzhou clay discussed in the following) is 0.2. This value is consistent with those used in previous studies regarding the same types of soils [16, 59].

Table 3 Model parameters for Shanghai soft clay and Wenzhou soft clay
Full size table

Figure 7 shows the measured and predicted effective stress path and stress–strain relationship εq − q of Shanghai clay subjected to undrained monotonic shear with different fixed principal stress directions. As shown in Fig. 7a, the computed effective stress paths under different stress rotation angles \(\alpha_{\sigma }\) are almost identical, whereas the measured effective stress paths are affected by \(\alpha_{\sigma }\). As shown in Fig. 7b, the predicted stress–strain relationship εq − q at relatively small strains is affected by \(\alpha_{\sigma }\) (note that those for \(\alpha_{\sigma }\) = 0° and 90° are the same, whereas those for \(\alpha_{\sigma }\) = 30° and 60° are the same), but the final value is not affected by the principal stress directions. This may result from that the proposed non-coaxial flow rule employs a fabric-related material axes [i.e., reference stress tensor \(s_{ij}^{p}\) in Eq. (11)] to conduct orthogonal projection of the current stress rate, thus defining the direction of non-coaxial plastic flow. Accordingly, when the directions of principal stresses vary with respect to this material axes, the computed non-coaxial plastic strain rates will be different, thus the growth rate of deviatoric stress with deformations being different. Moreover, as shown in Fig. 7, there are some discrepancies between test data and model simulations of the effective stress path and stress–strain relationship. This might be attributed to the presence of strength anisotropy [1, 2, 54] of the tested nature clay (Fig. 7a). The strength anisotropy might result from a combination of the inherent anisotropy generated during soil depositions and induced anisotropy formed by the anisotropic consolidation stress histories [1, 2, 54]. It should be noted that the Lode angle effect [Eq. (21)] and the plastic volumetric strain [Eq. (22)] have been considered in the modeling. However, the non-coaxial theory in the paper is only related to stress-induced anisotropy to describe non-coaxiality under monotonic shear loading, whereas the anisotropy reflects strength is not considered in the modeling. Such that the model cannot reproduce the development of the effective stress path and stress–strain relationship along different \(\alpha_{\sigma }\).

Figure 8b, c presents the simulated variation of strain increment vector directions using the proposed model with the non-coaxial flow rule suggested by Qian et al. [32] and the one given in this paper. Compared with the non-coaxial flow rule suggested by Qian et al. [32], the one adopted in this work reproduces coaxial plastic flow under principal stress rotation of \(\alpha_{\sigma }\) = 0°, 45° and 90°, whereas predicts non-coaxial flow under the conditions of \(\alpha_{\sigma }\) = 30° and 60°. These phenomena are observed here for Shanghai clay as well as for other types of clays [20, 51, 62]. The new non-coaxial flow rule uses the tensor \(s_{ij}^{p}\) that is related to material axes of natural clay and its fabric as a reference framework, to which an orthogonal projection of the stress rate is conducted, thus defining the direction of non-coaxial flow. Under such flow rule, \(s_{ij}^{p}\) is parallel to stress rate when \(\alpha_{\sigma }\) = 0° or 90°, and the orthogonal projection of the stress rate to \(s_{ij}^{p}\) is zero and so does the non-coaxial plastic strain rate. On the other hand, when the stress direction rotation angles take other values, the orthogonal projection of the stress rate with respect to \(s_{ij}^{p}\) takes finite values and non-coaxial plastic deformations take place. In addition, since the hollow cylinder experiments were performed in a stress-controlled manner, the vertical stress rate \(\dot{\sigma }_{z}\) and circumferential stress rate \(\dot{\sigma }_{\theta }\) are zero and there is only shear stress rate \(\dot{\tau }_{z\theta }\) under \(\alpha_{\sigma }\) = 45°. This result in the predicted \(\dot{\varepsilon }_{z}\) and \(\dot{\varepsilon }_{\theta }\) will be zero. So the predicted \(\alpha_{{{\text{d}}\varepsilon }}\) is always equal to 45° which is coincident with \(\alpha_{\sigma }\). Thus it predicts coaxial plastic flow under principal stress rotation of \(\alpha_{\sigma }\) = 45°. Lastly, it should be mentioned that certain discrepancies between test data and model simulations can also be observed, in particular at relatively high shear stresses.

Figure 9b, c shows the simulated strain increment direction angle using the proposed model with the non-coaxial flow rule suggested by Qian et al. [32] and the one given in this paper, respectively. It can be seen that the model simulations follow the trends observed in the tests, in that it reproduces the coupling between loading along the direction of \({{\left( {\sigma_{z} - \sigma_{\theta } } \right)} \mathord{\left/ {\vphantom {{\left( {\sigma_{z} - \sigma_{\theta } } \right)} 2}} \right. \kern-\nulldelimiterspace} 2}\) and \(\tau_{z\theta }\). Moreover, the model also correctly captures that the directional angle of strain increment is greater than that of stress when \(\alpha_{\sigma }\) = 30°, but it is less than that of stress when \(\alpha_{\sigma }\) = 60°. Nevertheless, the simulated non-coaxial angle at higher shear stress levels tends to be greater than that observed.

The differences between the test data and model simulations, as depicted in Figs. 8 and 9, might be attributed to three resources. The first one is the presence of strength anisotropy of the tested clay as discussed above. For simplicity, the non-coaxial theory in the paper is only related to stress-induced anisotropy to describe non-coaxiality under monotonic shear loading, whereas the anisotropy reflects strength is not considered in the modeling and thus cannot replicate such strength anisotropy. Second, the model assumes a diminishing non-coaxiality as critical state is approached [i.e., see Eq. (14)], as suggested by experimental evidence [20, 51, 62]. On the other hand, the anisotropy of natural clay (in particular, that is related to the preferential deposition direction of soils) might not be fully erased at critical state. Accordingly, the spatial distributions of soil fabrics might not be fully aligned with the principal directions of the current stress states, thus a non-coaxial angle existing between the material axes that are related to soil fabrics and the loading direction. Consequently, non-coaxial plastic flow can still be observed as critical state is approached. The last factor of the mismatches between measured and computed soil response is the potential development of non-uniform stress/strain fields within soil specimens, due to the unequal inner and outer cell pressures in a hollow cylindrical apparatus. This phenomenon becomes increasingly significant as the deviatoric shear stress increases to a higher level, because the difference between inner and outer cell pressures becomes bigger [14, 36].

4.3 Model simulations of Wenzhou soft clay

In addition to the verification program described above, the proposed model is further examined against the published experimental results of Wenzhou soft clay subjected to monotonic shearing with fixed principal stress directions. Wang et al. [51] performed a series of drained hollow cylinder torsional shear tests on Wenzhou clay, where various combinations of principal stress directions and intermediate principal stress values were employed. The loads were applied until the failure of the specimens. The test program is summarized in Table 4, and the selected stress paths are depicted in Fig. 5. Since the parameters \(\lambda\) and \(\kappa\) were not reported, they are estimated from the liquid limit wL and plasticity index Ip [48, 49] according to the empirical relations given by Schofield and Worth [37] and Nakase et al. [27]. Other model parameters including those controls the non-coaxial plastic flow are determined by matching the results of monotonic shearing with the intermediate stress parameter b = 0.5. Accordingly, the computed results for soil tests with b = 0 and 1 are referred to as model prediction. The initial void ratio \(e_{0}\) = 1.570 and the initial consolidation pressure \(p_{{{\text{c0}}}}\) = 150 kPa [51] have been used for the entire simulations.

Table 4 Test program for Wenzhou soft clay
Full size table

Figure 10 compares the computed and measured stress–strain responses of Wenzhou clays under drained shearing with different combinations of b value and the rotations of the principal stresses. Figure 11 shows the observed and predicted axial and shear stress–strain relations for the same series of tests. In both figures, the solid line represents the model prediction, while experimental data are denoted by open symbols. It can be seen that, with a single set of parameters, the proposed model very well predicts the general shearing characteristics of Wenzhou clays subjected to stress paths of varying principal stress directions and intermediate stress ratios. The peak deviatoric stress in the experiment with b = 0 is slightly overestimated by the model due to mild strain localization [15]. Figure 12 shows the experimentally measured and predicted evolution of strain increment direction angle with the deviatoric stress. Unlike the simulations for Shanghai clays, the simulated direction angle here is computed based on the total strain increment. It can be seen that the model reasonably represents the trend of the non-coaxial plastic flow as observed from the experiments, although the agreement between the simulated and experimental non-coaxial angle is less than perfection for ασ = 30°, 60°. The latter might be attributed to the same resources as discussed for the simulations of Shanghai clay.

Fig. 10
figure 10

Experimental and predicted results of the variation of strain components with the equivalent deviatoric stress for Wenzhou soft clay: a b = 0, ασ = 0°, b b = 0, ασ = 30°, c b = 0, ασ = 45°, d b = 1, ασ = 45°, e b = 1, ασ = 60°, f b = 1, ασ = 90°

Full size image
Fig. 11
figure 11

Experimental and predicted results of stress–strain relationship for Wenzhou soft clay: a axial stress–strain curve, b shear stress–strain curve

Full size image
Fig. 12
figure 12

Experimental (a, b) and predicted (c, d) results of the variation of the strain increment direction angle with the equivalent deviatoric stress for Wenzhou soft clay: a, c b = 0, b, d b = 1

Full size image

5 Conclusions

A simple critical state-based constitutive model is developed for describing the non-coaxial plastic deformations of saturated soft clay subjected to monotonic shearing with fixed principal stress directions. Such material behavior has been extensively reported in experimental studies but not adequately addressed by constitutive modeling. For this purpose, this work introduces a revised non-coaxial flow rule, which assumes any plastic strain rate that is not coaxial with the stresses will be colinear with a non-coaxial stress rate orthogonal to a reference deviatoric stress tensor instead of the current deviatoric stress tensor. The latter is often adopted in existing non-coaxial flow rules. By doing so, non-coaxial plastic deformations can be modeled even when the stress rate is coaxial with the current stress state (i.e., during monotonic loading with fixed principal stress directions). Compared with the modified Cam-clay model, the proposed model only requires one more parameter to characterize the yield surface and another two new parameters for controlling the non-coaxial flow behavior. The latter can be straightforwardly calibrated from hollow cylinder torsional shear tests.

Undrained hollow cylinder shear on undisturbed Shanghai clay specimens shows clay can exhibit non-coaxial deformations when stress paths involve coupling between shearing along \({{\left( {\sigma_{z} - \sigma_{\theta } } \right)} \mathord{\left/ {\vphantom {{\left( {\sigma_{z} - \sigma_{\theta } } \right)} 2}} \right. \kern-\nulldelimiterspace} 2}\) and \(\tau_{z\theta }\). The test results for Shanghai clay, combined with a complementary test data reported for Wenzhou clay, are used to validate the proposed model. The comparison shows that the proposed model can reasonably represent non-coaxial plastic flows of clays during monotonic shears characterized by different fixed principal stress directions and various intermediate principal stress levels.

Lastly, it should be noted that to clarify the roles of the new non-coaxial flow rule, we have deliberately to keep the adopted constitutive modeling platform simple. Consequently, factors such as strength anisotropy, which contains inherent anisotropy (i.e., that generated during soil depositions) and induced anisotropy (i.e., that formed by the anisotropic consolidation stress histories and the loading histories), and soil structure that can significantly affect the non-coaxial behavior of clay, are currently not considered. The theoretical work including the strength anisotropy in the modeling should be done in the future. Moreover, the presented model, constructed within conventional elastoplastic framework, is not suitable for exploring the non-coaxial behavior of clay subjected to cyclic loading and the continuous change of principal stress orientation. These represent important steps introducing additional mechanisms and more advanced constitutive platforms that are or will be undertaken to enhance the proposed model.