Influence of linear coupling between volumetric and shear strains on instability and post-peak softening of sand in direct simple shear tests

Abstract

This paper focuses on the influence of volume change boundary condition on the instability and post-peak softening of sand. The laboratory program comprises an extensive series of Direct Simple Shear (DSS) tests with different degrees of linear coupling between volumetric and shear strains. It is observed that progressive loosening of sand associated with the volumetric expansion in a coupled strain path intensifies instability susceptibility, whereas volumetric contractive strains reduce vulnerability to instability and post-peak softening. Analysis of the experimental data using Hill’s second-order work criterion designates a family of state-dependent relational trends for instability lines, normalized peak shear strengths, and maximum pore-water pressure ratios depending on the degree of coupling between the volumetric and shear strain rates. It is found that a simple state-dependent constitutive model can predict relational trends in sand specimens suffering from instability and post-peak softening under different degrees of the linear coupling between the volumetric and shear strains.

1 Introduction

Loose sands sheared under undrained condition are prone to sudden loss of stability and flow liquefaction prior to mobilization of the critical state friction angle [3, 11,12,13, 18, 20, 22, 28, 33,34,35,36, 41,42,43,44,45, 53, 61, 66,67,68, 71, 74]. It is well understood that the mechanical behavior of fully saturated sands under shear depends strongly on the drainage condition. A drained test refers to boundary conditions at which no restriction is imposed on free pore-water inflow/outflow, and accordingly, there is no excess pore-water pressure development. In contrast, undrained loading occurs when soil shears under constant volume condition wherein; both inflow and outflow of the pore-water are prohibited, and thus, the development of excess pore-water pressure is inevitable. Sand liquefaction is usually investigated by means of triaxial and DSS tests under constant volume condition [5, 8, 25, 28, 33, 37, 42,43,44, 50, 53, 64, 69]. However, Chu et al. [11,12,13], Ibraim et al. [26], Nicot et al. [45], Sento et al. [59], Sivathayalan & Logeswaran [60], Vaid & Eliadorani [63], Wanatowski et al. [67], and Yamamoto et al. [73] put forward evidence disapproving conventional presumption that the undrained and drained behaviors define margins of soil behavior in geotechnical engineering practice, and elucidated that controlling volume change leads to a multitude of mechanical responses that are not delimited between the drained and undrained ones. The aforementioned observations are of great interest in practice noticing that analysis of shaking table and centrifuge tests data has indicated that void ratio redistribution and pore-water migration during and soon after earthquake lead to field conditions that depart from the ideal undrained assumption [1, 6, 32, 47, 52, 59]. Accordingly, migration of the pore-water in saturated sand slopes from the higher energy levels to the lower energy regions results in loosening and progressive loss of shear strength in the lower energy regions. Likewise, pore-water flow from saturated sand surrounding a gravel drain results in a behavior for the sand element that is dissimilar to that under the undrained condition [73]. Recently, dynamic centrifuge tests carried out by Adamidis & Madabhushi [1] highlight that the undrained behavior is not always a realistic assumption on the time scale of an earthquake. The pore-water flow from the high energy regions to low energy ones is an inevitable phenomenon in real scale liquefaction events. However, the proximity of boundaries in small-scale single-element undrained laboratory tests reduces the pore-water pressure difference and consequently, pore-water migration becomes practically negligible in such tests. The impact of excess pore-water flow on sands liquefaction susceptibility can be investigated in the laboratory by means of the so-called partially drained tests in which both the volumetric and shear strain rates are varied simultaneously during the tests and restriction on free volume change leads to accumulation of pore-water pressure [11,12,13, 45, 60, 63, 67].

Instability is referred to certain conditions wherein, soil element cannot sustain the prescribed effective stress through satisfying a mathematical criterion [3, 11,12,13,14,15,16, 20, 24, 27, 30, 34,35,36, 40, 67]. Depending on the interaction between imposed effective stress path and volume change boundary condition during shear straining, instability may happen in both loose and dense states. In soil mechanics, strain-softening is a phenomenon wherein the shear strength begins a transient/permanent decrease with further shear strain [11,12,13, 68]. Sand in dense state exhibits post-peak softening under drained condition. Once drainage is fully prohibited, loose sand exhibits post-peak softening which is technically called flow liquefaction instability. Coupling between the expansive volumetric and shear strains may lead to continuous loosening of soil element and thus, the strain-softening behavior becomes inevitable. In such case, sand instability may trigger prior/subsequent to post-peak softening or even without post-peak softening depending on the prescribed pattern of coupling between the volumetric and shear strains. This will be discussed in Sect. 5.3.

Herein, the mechanical behavior of Firoozkuh No. 161 sand specimens sheared under linear coupling between the volumetric and shear strain rates is experimentally investigated using an NGI type DSS apparatus. The current investigation is dissimilar from precursor studies in view of the fact that the testing program covers a wide range of initial states. Accordingly, sand flow behavior over a wide domain of initial states and couplings between the volumetric and shear strains is investigated here. Hill’s second-order work criterion (Hill [24]) is applied to find the certain states for the onset of instability in the tests with constant volume and with coupling between the volumetric and shear strains. For the specimens exhibiting instability and post-peak softening, the influence of the coupling between the volumetric and shear strain rates on the slope of Instability Line (IL), peak shear strength and the maximum pore-water pressure ratios is investigated. For different degrees of linear coupling between the volumetric and shear strains, a simple critical state compatible sand constitutive model is formulated and then employed to reproduce relational trends between stress ratio, peak shear strength, effective normal stress, and maximum pore-water pressure ratio at the onset of instability in one hand, and state parameter and the initial void ratio at the other. A reasonable correspondence between the constitutive model simulations and the laboratory data is achieved.

2 Test sand and experimental device

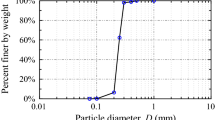
The test soil, i.e., Firoozkuh No. 161, is a crusher run poorly graded fine sand with angular to sub-angular particles (see Fig. 1). Semi-quantitative XRD analysis indicated that Firoozkuh No. 161 comprises of 96.9% Quartz and 3.1% Calcite. The main physical properties of the sand are: G_s = 2.64, d_max = 0.850 mm, d₅₀ = 0.276 mm, C_u = 1.47, C_c = 0.99, e_max = 1.0 and e_min = 0.58. The particle size distribution curve for Firoozkuh No. 161 is demonstrated in Fig. 1.

Fig. 1

Particle size distribution curve and SEM photograph for Firoozkuh No. 161 sand

All tests reported here were carried out using a fully automated NGI Type DSS device capable of performing both the stress and strain-controlled monotonic and cyclic tests on cylindrical specimens 70 mm in diameter and 20 mm in height (see Fig. 2a). ASTM D6528-17 necessitates the height of specimens must be at least 10 times the maximum particle size. The specimen height to d_max ratio in this study was 23.5. Moreover, the height to diameter ratio (= 0.286) was within the range 0.2 to 0.4. Accordingly, a negligible specimen size effect was expected. A pneumatic actuator and a servomotor each of which was outfitted with a 5 kN S-type load cell, were used to impose the vertical and shear forces/displacements independently. The shear and vertical displacements were directly measured using LVDTs with a resolution of 0.01 mm. The maximum shear deformation was limited to 10 mm and ± 5 mm for monotonic and cyclic loadings, respectively. Soil specimens were laterally confined by 10 Teflon coated stacked rings (plus a total of three additional rings around the top and bottom platens) with a width of 9.5 mm and thickness of 2.0 mm for each ring to ensure initial K₀-condition following the vertical compression (see parts “b” and “c” of Fig. 2). Prior to specimen reconstitution, a thin latex membrane was placed in the inner space of the stacked rings to prevent particles from moving between the rings. The specimens were prepared using a moist tamping method (see [28]) in a relatively wide domain of initial densities. An under compaction scheme was applied to ensure the uniform profile of void ratio throughout the height of the specimen. The experimental program consists of a total 47 tests with linear strain paths (i.e., the proportional coupling between the volumetric and shear strain rates), 13 tests with bilinear strain paths (initial linear coupling is followed by a constant volume stress path once a threshold shear strain is attained), and 34 complimentary constant volume tests for determination of the Critical State Line (CSL) [see supplementary material for the complete testing program].

Fig. 2

View of NGI type DSS setup: a general view of the apparatus; b schematic illustration of soil specimen in DSS cell; c a sheared specimen

3 Constant volume behavior and critical state

For three dense (e_in = 0.671), medium (e_in = 0.775), and loose (e_in = 0.861) sand specimens sheared under constant volume condition from $\sigma _{{n0}}^{{\prime }}$  = 300 kPa, the $\tau \;vs.\;\sigma ^{\prime}_{n}$, $\tau \;vs.\;\gamma$, and $\Delta u\;vs.\;\gamma$ curves are, respectively, illustrated in parts “a” to “c” of Fig. 3. Of note, $\Delta u = \sigma ^{\prime}_{{n0}} - \sigma ^{\prime}_{n}$ (i.e., the difference between the initial and current values of normal effective stress) is used here for estimation of equivalent excess pore-water pressure. For the same $\sigma _{{n0}}^{{\prime }}$ of 350 kPa, a decrease in the initial void ratio (e_in) results in a gradual change of the behavior from “flow” type with post-peak softening for the loose specimen to the fully hardening “non-flow” for the dense specimen as shown in Fig. 3. The influence of $\sigma _{{n0}}^{{\prime }}$ on the constant volume behavior of three loose specimens with e_in ranging from 0.875 to 0.887 is studied in Figs. 3d to f wherein, all specimens suffer from flow behavior and the post-peak softening is intensified with $\sigma ^{\prime}_{{n0}}$.

Fig. 3

Behavior of Firoozkuh sand specimens sheared under constant volume condition: a to c three tests on dense (e_in = 0.671), medium (e_in = 0.775), and loose (e_in = 0.861) specimens starting from $\sigma ^{\prime}_{{n0}}$ = 300 kPa; d to f three tests on loose specimens (e_in = 0.875 to 0.887) starting from $\sigma ^{\prime}_{{n0}}$ = 100, 200, and 300 kPa

For the shear strains larger than 40% in Fig. 3, $\tau$ and $\sigma _{n}^{{\prime }}$ of all specimens move toward stabilized asymptotic critical state values corroborating the existence of a unique CSL for Firoozkuh No. 161 sand specimens irrespective of their initial state. Using the data of 34 constant volume DSS tests, the CSL of Firoozkuh No. 161 sand is illustrated in Fig. 4. To represent the CSL in the $\tau$ vs. $\sigma ^{\prime}_{n}$ and e vs. $\sigma ^{\prime}_{n}$ planes, the following equations inspired by Li & Wang [39]:

$$ \tau = M\,\sigma ^{\prime}_{n};\quad e_{{cs}} = \Gamma - \lambda (\sigma ^{\prime}_{n} /p_{{ref}} )^{{\,\xi }} $$

(1)

Fig. 4

CSL for Firoozkuh No. 161 sand in: a $\tau$ vs. $\sigma ^{\prime}_{n}$, and b e vs. $\sigma ^{\prime}_{n}$ planes

where $\text{M}\;( = \tan \upvarphi ^{\prime}_{\text{cs}} )$ is the slope of the CSL in the $\tau$ vs. $\sigma ^{\prime}_{v}$ plane, and $\phi ^{\prime}_{{cs}}$ is the critical state friction angle. $\Gamma$ is the intercept of the CSL at $\sigma ^{\prime}_{n}$ = 0, and $\lambda$ is the slope of the CSL in the e vs. $(\sigma ^{\prime}_{v} /p_{{ref}} )^{{\,\xi }}$ plane. In Eq. (1), p_ref = 101 kPa is a reference normalizing pressure. For Firoozkuh No. 161 sand, M = 0.520 corresponding to $\varphi ^{\prime}_{{cs}} = 27.47^{ \circ }$, $\Gamma$ = 1.012, $\lambda$ = 0.188, and $\xi$ = 0.396 are obtained in Fig. 4.

4 Sand behavior in shear-volume coupled strain paths

4.1 Definition

DSS tests with two patterns of coupling between the volumetric and shear strains, i.e., linear and bilinear, were carried out. In the linear pattern, the volumetric strain rate (i.e., $\delta \varepsilon _{v}$) changes linearly with the shear strain rate (i.e., $\delta \gamma$) through:

$$ \delta \varepsilon _{v} = \zeta \,\delta \gamma $$

(2)

wherein, $\zeta$ defines proportionality. $\zeta < 0$ with $\gamma > 0$ refers to an imposed expansive deformation in which, void ratio increases with shear deformation whereas, $\zeta > 0$ while $\gamma > 0$ corresponds to the imposed contractive deformation with decreasing void ratio. $\zeta = 0$ under $\gamma > 0$ refers to the constant volume loading in which void ratio is kept fixed during shear. Typical strain paths with the linear coupling between the volumetric and shear strain rates under $\zeta$ =  + 0.2, + 0.1, 0.0, and − 0.2 are illustrated in Fig. 5a (see Figs. 6 and 7 for the experimental data).

Fig. 5

Typical strain paths with coupling between the volumetric and shear strains: a linear strain paths with $\zeta$ =  + 0.2, + 0.1, 0.0, − 0.2 (see Figs. 6 and 7 for the tests); b bilinear strain paths with $\zeta$ =  + 0.2, + 0.1, − 0.1 and $\gamma _{{thr}}$≈ 21.0 [%] (see Fig. 8 for the tests); and c bilinear strain paths with $\zeta$ =  + 0.2, + 0.1, 0.0, − 0.1, − 0.2 and $\gamma _{{thr}}$≈18.5 [%] (see Fig. 9 for the tests)

Fig. 6

Behaviors of four loose Firoozkuh sand specimens sheared under linear strain paths with $\zeta$ =  + 0.2, + 0.1, 0.0, and − 0.2 in: a $\tau$ vs. $\sigma _{n}^{{\prime }}$, b $\tau$ vs. $\gamma$, c e vs. $\sigma _{n}^{{\prime }}$, and d $\Delta$u vs. $\gamma$planes

Fig. 7

Behaviors of four medium-dense Firoozkuh sand specimens sheared under linear strain paths with $\zeta$ =  + 0.2, + 0.1, 0.0, and − 0.2 in: a $\tau$ vs. $\sigma _{n}^{{\prime }}$, b $\tau$ vs. $\gamma$ c vs. $\sigma _{n}^{{\prime }}$, and d $\Delta$u vs. $\gamma$planes

In reality, the magnitude of maximum shear strain, field condition for drainage, soil heterogeneity and extent of the liquefied zone may put a physical limit on the maximum volumetric strain. An idealized strain path with limited coupling between the volumetric and shear strain is attained by introducing a limiting shear strain (i.e., $\gamma _{{thr}}$) beyond which, coupling between the volumetric and shear strains becomes nil and shearing continues without any further volume change:

$$ \updelta \upvarepsilon_{v} = \left\{ {\begin{array}{*{20}l} \! \!{\upzeta \,\updelta \upgamma } & \qquad{{\text{if}}\qquad\;\upgamma \le \upgamma _{\text{thr}} } \\ \!\! 0 & \qquad{{\text{if}}\qquad\;\upgamma > \upgamma _{\text{thr}} } \\ \end{array} } \right. $$

(3)

The above configuration gives a limiting volumetric strain $(\varepsilon _{v} )_{{\lim }} = \zeta \;\gamma _{{thr}}$. Bilinear paths under $\zeta$ =  + 0.2, + 0.1, and − 0.1 with $\gamma _{{thr}}$≈21.0 [%] (see Fig. 8 for the experimental data) as well as $\zeta$ =  + 0.2, + 0.1, − 0.1, and -0.2 with $\gamma _{{thr}}$≈18.5 [%] (see Fig. 9 for the experimental data) are, respectively, depicted in Figs. 5b and c.

Fig. 8

Behaviors of three loose Firoozkuh sand specimens sheared under bilinear strain paths with $\zeta$ =  + 0.2, + 0.1, and − 0.1 with $\gamma _{{thr}}$≈21% in: a $\tau$ vs. $\sigma _{n}^{{\prime }}$, b $\tau$ vs. $\gamma$ c e vs. $\sigma _{n}^{{\prime }}$, and d $\Delta$u vs. $\gamma$planes

Fig. 9

Behaviors of three loose Firoozkuh sand specimens sheared under bilinear strain paths with $\zeta$ =  + 0.2, + 0.1, 0.0 and − 0.1 with $\gamma _{{thr}}$≈18.5% in: a $\tau$ vs. $\sigma _{n}^{{\prime }}$, b $\tau$ vs. $\gamma$c e vs. $\sigma _{n}^{{\prime }}$, and (d) Δu vs. $\gamma$ planes

Of note, in real field conditions, the volumetric strain depends on the total amount of pore-water in/out flow as well as soil permeability. Besides, the pore-water flow events usually take place in a given time scale and are limited by the hydraulic conductivity of sand which itself may be affected by the rate of loading. Furthermore, the coupling between the volumetric and shear strains as caused by partial drainage in real field conditions is practically a boundary value problem (not a material-point problem). So, the element tests reported here possess inherent approximations since the loss of homogeneity is likely to happen in the soil mass. However, instability and post-peak softening are usually triggered at relatively low shear strains (less than 2.5%) and thus, the plausible effects of loss of homogeneity are expected to be minimal.

4.2 Behavior of Firoozkuh sand in linear strain paths

The mechanical behavior of four loose (e_in≈0.915, Dr≈20.2[%]) specimens sheared under $\zeta$ =  + 0.2, + 0.1, 0.0, and − 0.2 are illustrated in Fig. 6. The loose specimen sheared under constant volume condition (i.e., test with $\zeta$ = 0.0) exhibits a flow type behavior wherein, $\tau$ = 27.6 kPa is attained at a transient peak shear strength around $\gamma$ = 1.8% beyond which, $\tau$ descends to 10.5 kPa at large shear strains. The test with $\zeta$ =  + 0.1 exhibits limited flow response in which, the transient peak and the minimum post-peak shear strengths of 26.9 kPa and 19.4 kPa are achieved, respectively, at $\gamma$ = 2.2% and 9.5% prior to $\tau$ = 71.5 kPa at the end of the experiment. For the test with $\zeta$  =  + 0.2, hardening is observed throughout the whole strain range studied here and the sand behavior is of non-flow type and $\tau$ = 255.5 kPa is reported at $\gamma$ = 50%. On the other hand, the peak strength of the test with $\zeta$ = − 0.2 is 23.3 kPa which is slightly lower than that of the constant volume test. However, the latter specimen loses its shear strength entirely with further shearing due to excessive loosening caused by the expansive volumetric strains.

Similar comparisons for four medium-dense specimens (e_in = 0.765 to 0.792, Dr≈49.5 to 55.9 [%]) are organized in Fig. 7 wherein the specimen sheared under constant volume condition ($\zeta$ = 0.0) demonstrates a mild strain hardening and $\tau$ = 79.4 kPa is attained at $\gamma$≈50%. Through parts “a” to “d” of Fig. 7, increase in $\zeta$ from 0.0 to + 0.1 and then + 0.2 intensifies the strain hardening and accumulation of negative pore-water pressure. The specimen sheared under $\zeta$  = − 0.2 exhibits permanent post-peak loss of shear strength associated with the excessive loosening as caused by the expansive coupling between the volumetric and shear strains. The laboratory data for the loose and medium-dense sands in Figs. 6 and 7 confirm that the expansive deformation escalates flow behavior susceptibility; whereas, contractive deformation improves specimens compactness and mitigates the flow behavior vulnerability.

4.3 Behavior of Firoozkuh sand in bilinear strain paths

In Fig. 8, three loose specimens consolidated under $\sigma _{{n0}}^{{\prime }}$ = 200 kPa are sheared under $\zeta$ = + 0.2, + 0.1, and − 0.1 until $\gamma_{{thr}}$  = 21% is attained beyond which shearing continues under constant volume condition (see Fig. 5b) for the strain paths. Rapid decrease in the void ratio from 0.874 to 0.794 under 0.2 improves sand compactness, and consequently, a robust strain-hardening with the accumulation of negative pore-water pressure is observed in the behavior of the specimen as long as $\gamma \le \gamma _{{thr}}$. The state of the specimen sheared under $\zeta$ =  + 0.2 in Fig. 8c is located above the CSL once $\gamma = \gamma _{{thr}}$ is attained at $\sigma ^{\prime}_{n}$ = 264.6 kPa and e = 0.794. This manifests sudden strain softening and generation of positive pore-water pressure in the constant volume phase until the CSL is reached in both the $\tau$ vs. $\sigma ^{\prime}_{n}$ and e vs. $\sigma ^{\prime}_{n}$ planes. In Fig. 8, a milder response is observed for the specimen with e_in = 0.917 sheared under $\zeta$ =  + 0.1 that its initial contraction is finished at e = 0.877 ($\sigma ^{\prime}_{n}$ = 64.9 kPa) at the moment the specimen began to dilate a little before. Once $\gamma = \gamma _{{thr}}$ is fulfilled, the state of the specimen with e_in = 0.917 is slightly above the CSL in the e vs. $\sigma ^{\prime}_{n}$ plane, and consequently, a gentle softening occurs in the constant volume regime. The specimen with e_in = 0.914 sheared under $\zeta$ = − 0.1 lost its shear strength completely prior to $\gamma \le \gamma _{{thr}}$; however, a slight improvement of shear strength is observed upon further shearing during the constant volume phase and $\tau$ = 10.8 kPa is attained at the end of the experiment.

Similar experiments for four medium-dense specimens (e_in = 0.789 to 0.801, Dr = 47.3 to 50.0%) subjected to bilinear paths under $\zeta$ =  + 0.2, + 0.1, 0.0, − 0.1, and − 0.2 with $\gamma _{{thr}}$≈18.5% are illustrated in Fig. 9. In the first phase of the loading, the evolution of void ratio associated with the expansive/contractive couplings between the volumetric and shear strains affects mobilization of the shear strength and accumulation of excess pore-water pressure. Nevertheless, the nullification of the volumetric-shear strain coupling for $\gamma \ge \gamma _{{thr}}$ alters the overall behaviors in a way that the specimens sheared under $\zeta > 0$ begin strain-softening and partial loss of the shear strength. In an opposite manner, the specimens sheared initially under $\zeta < 0$ exhibit strain-hardening and accumulation of negative pore-water pressure in the constant volume phase. States of the specimens initially sheared under $\zeta$ =  + 0.1, and + 0.2 in Fig. 9c are located above the CSL at $\gamma$ = $\gamma _{{thr}}$ (see Fig. 9c), and following Been & Jefferies [5], both specimens are vulnerable to flow behavior under constant volume shear. Conversely, states of the specimens firstly sheared under $\zeta$ = − 0.1, and − 0.2 are well located below the CSL at $\gamma$ = $\gamma _{{thr}}$ and therefore, their constant volume behaviors are of non-flow type.

4.4 Sand instability owing to coupling of the volumetric and shear strains

Hill [24] hypothesized that the sign of the second-order work (i.e., d²W) indicates the positive definiteness of the mechanical response of elastoplastic continua {Hill [24] proposed $\int_{\text{V}} {\,\updelta {\text{s}}_{\text{ij}} } \,{\text{d}}\left( {\partial {\text{u}}_{\text{j}} /\partial {\text{x}}_{\text{i}} } \right)\,{\text{dV}} > 0$ as the sufficient condition of stability for elastoplastic continua wherein, V is the volume of the body, s_ij is the transpose of the first Piola-Kirchoff stress tensor, and ${\text{d}}\left( {\partial {\text{u}}_{\text{j}} /\partial {\text{x}}_{\text{i}} } \right)$ is the gradient of velocity. Ignoring geometrical effects under small stain assumption, the Hill’s [24] condition of stability becomes $\int_{\text{V}} {\,{\text{d}}\upsigma _{\text{ij}} \,{\text{d}}\upvarepsilon _{\text{ij}} } \,{\text{dV}} > 0;\quad \forall \;\left\| {{\text{d}}\upvarepsilon } \right\| \ne 0$. Since in the element level $dV > 0$ holds, the latter stability criterion in the element level reads ${\text{d}}^{2} {\text{W}} = {\text{d}}\upsigma _{\text{ij}} \,{\text{d}}\upvarepsilon _{\text{ij}} > 0;\quad \forall \;\left\| {\text{d}\upvarepsilon } \right\| \ne 0$ [51]}:

$$ {\text{d}}^{2} {\text{W}} = \mathop {{\dot{\varvec{\sigma ^{\prime}}}} {\text{:}}\dot{\varvec{\upvarepsilon} }}$$

(4)

wherein, ${\dot{\varvec{\sigma ^{\prime}}}}$ is the rate of the second-rank effective stress tensor, and ${\dot{\varvec{\varepsilon }}}$ is the second-rank strain rate tensor corresponding to ${\dot{\varvec{\sigma ^{\prime}}}}$. An elastoplastic continuum is mechanically stable as long as ${\text{d}}^{2} {\text{W}} > 0$, and unstable when ${\text{d}}^{2} {\text{W}} < 0$. In this context, instability happens once ${\text{d}}^{2} {\text{W}} = 0$ (e.g., [3, 9,10,11,12,13,14, 20, 34,35,36, 40, 45, 67]).

In the NGI-DSS cell, stacked rings (see Fig. 2b and c) prohibit any radial strain and thus, only shear and normal strain rates are applied to specimens and accordingly, Eq. (4) at the onset of the mechanical instability becomes:

$$ d^{2} W = \dot{\sigma ^{\prime}}_{n} \dot{\varepsilon }_{v} + \dot{\tau }\,\dot{\gamma } = 0 $$

(5)

Of note, $\dot{\varepsilon }_{{zz}} = \dot{\varepsilon }_{v}$ holds in NGI type DSS cell wherein, $\dot{\varepsilon }_{{zz}}$ is strain rate normal to the plane of stacked rings. By adopting a linear coupling between the volumetric and shear strain rates (i.e., $\dot{\varepsilon }_{v} = \zeta \,\dot{\gamma }$), Eq. (5) becomes:

$$ d^{2} W = \dot{\gamma }\,[\,\dot{\tau } + \zeta \,\,\dot{\sigma ^{\prime}}_{n} ] = 0 $$

(6)

Since $\dot{\gamma } \ne 0$ holds in the monotonic DSS tests reported here, Eq. (6) necessitates:

$$ \dot{\tau } + \zeta \,\,\dot{\sigma ^{\prime}}_{n} = 0\;{\text{at}}\;{\text{the}}\;{\text{onset}}\;{\text{of}}\;{\text{instability}} $$

(7)

Herein, the generalized effective stress, $\sum$, is defined as:

$$ \Sigma = \tau + \zeta \,\,\sigma ^{\prime}_{n} $$

(8)

Recalling that $\varsigma$ remains unchanged during shear, total differentiation of $\sum$ yields certain state(s) at which $\sum$ becomes an extremum:

$$ \dot{\Sigma } = \frac{{\partial \Sigma }}{{\partial \tau }}\;\dot{\tau } + \frac{{\partial \Sigma }}{{\partial \sigma ^{\prime}_{n} }}\;\dot{\sigma ^{\prime}}_{n} = \dot{\tau } + \zeta \,\,\dot{\sigma ^{\prime}}_{n} = 0 $$

(9)

Considering that $\tau \ge 0$ and $\sigma ^{\prime}_{n} > 0$, Eq. (9) implies that maximizing $\sum$ is mathematically equivalent to the rate-type equation given in Eq. (7). Under the constant volume condition, one has $\zeta$ = 0 and consequently, $\Sigma = \tau$. The latter stipulation indicates that the mechanical instability under constant volume condition happens at the peak $\tau$ prior to the instigation of the strain-softening. The mentioned mathematical provision agrees with the previous findings of Andrade [3], Buscarnera & Whittle [9], Buscarnera et al. [10], Imposimato & Nova [27], Lade [33], Lashkari et al. [34,35,36], and Sadrekarimi [55, 56].

It is well known that the macro-scale (e.g., stress–strain-strength and volume change) response of granular soils stems from the micro-mechanisms taking place at the grain scale (e.g., inter-particle friction, sliding and rolling as well as change in directional characteristic properties such as contact normal-based and particles’ long axes-based fabric tensors). From this perspective, sudden rises and falls observed in the mobilized shear strength and deformation behavior of the granular soils under shear loading can be traced back to generation and buckling-induced elimination of micro-scale force chains transmitting inter-particle forces (e.g., [4, 23, 31, 36, 46, 58, 65, 75,76,77]). Accordingly, sudden fluctuations in the effective stress and strain rates may bring difficulties in demarcating stable and unstable states via direct use of Eqs. (4) (e.g., [20, 30, 36, 45]). However, on the other hand, fluctuations in the effective stress and total strain tensors usually do not affect the $\sum$ drastically and hence, finding the onset of instability in terms of maximizing $\sum$ has a virtue over the direct use of Eqs. (4) and (7).

Stress paths for three loose (e = 0.875 to 0.887; Dr = 26.9 to 29.8%) and one medium-dense (e = 0.775, Dr = 53.6%) specimens sheared under the constant volume condition are depicted in Fig. 10(a). Except for the medium-dense one, the remaining tests exhibit well-defined peaks in shear strength prior to triggering of the instability (of note, the onset of instability in terms of maximizing $\sum$ is marked by “●” in Fig. 10). For four loose specimens with $\zeta$ =  + 0.2, + 0.1, 0.0, and -0.2, stress paths in the $\sum$ vs. $\sigma ^{\prime}_{n}$ and $\tau$ vs. $\sigma ^{\prime}_{n}$ planes are illustrated in Figs. 10b and c, respectively. Figure 10c indicates that the mathematical criterion for the mechanical instability of the specimens with $\zeta < 0$ is fulfilled in the post-peak softening regime; nevertheless, instability of the specimens sheared under $\zeta > 0$ takes place prior to the “phase transformation” where the initial contraction turns into dilation. Nonetheless, once the generalized stress ($\sum$) is used in lieu of $\tau$the onset of instability (if viable) always locates at the peak of $\sum$. Finally, for four medium-dense specimens subjected to bilinear strain paths in Fig. 9, stress paths in the $\sum$ vs. $\sigma ^{\prime}_{n}$ and $\tau$ vs. $\sigma ^{\prime}_{n}$ planes are, respectively, depicted in Fig. 10d and e. The instability of the specimens initially sheared under $\zeta$ = − 0.2, and − 0.1 occurs in the post-peak softening regime; however, for the specimen with $\zeta$ =  + 0.1, the criterion for the onset of instability is fulfilled at the instigation of the constant volume shearing, immediately after the nullification of the coupling between the volumetric and shear strains.

Fig. 10

Onset of the mechanical instability in the $\sum$ vs. $\sigma _{n}^{{\prime }}$ and $\tau$ vs. $\sigma _{n}^{{\prime }}$ planes for: a three constant volume tests; b and c four linear strain paths; d and e four bilinear strain paths

5 Formulation of a state-dependent constitutive model

Airey & Wood [2] reported that DSS is not suitable for constructing Mohr’s circle of stresses during shearing and accordingly, it is not well suited for developing multiaxial constitutive models. However, simpler constitutive models formulated in $\tau$ vs. $\sigma ^{\prime}_{n}$ plane can capture salient aspects of sand behavior under DSS condition.

The critical state compatible elastoplastic model of Li & Dafalias [38] converted to the DSS space is expressed through:

$$ {\dot{\varvec{\upsigma ^{\prime}}}} = {\mathbf{D}}^{\text{ep}} \;{\dot{\varvec{\upvarepsilon }}}\quad {\text{where}}\quad {\mathbf{D}}^{\text{ep}} = {\mathbf{D}}^{\text{e}} - \frac{{{\mathbf{D}}^{\text{e}} \,{\mathbf{R}}\,{\mathbf{n}}^{\text{T}} \,{\mathbf{D}}^{\text{e}} }}{{\text{K}_{\text{p}} + {\mathbf{n}}^{\text{T}} \,{\mathbf{D}}^{\text{e}} \,{\mathbf{R}}}} $$

(10)

wherein, ${\dot{\varvec{\sigma ^{\prime}}}} = \left[ {\begin{array}{*{20}c} {\dot{\tau }} & {\dot{\sigma ^{\prime}}_{n} } \\ \end{array} } \right]^{{\,T}}$ is the effective stress rate vector, ${\dot{\varvec{\varepsilon }}} = \left[ {\begin{array}{*{20}c} {\dot{\gamma }} & {\dot{\varepsilon }_{\text{v}} } \\ \end{array} } \right]^{{\,{\text{T}}}}$ is the strain rate vector corresponding to ${\dot{\varvec{\sigma ^{\prime}}}}$, and D^ep is the elastoplastic stiffness matrix. ${\mathbf{D}}^{e} = \left( {\begin{array}{*{20}c} G & 0 \\ 0 & K \\ \end{array} } \right)$ is the elastic stiffness matrix in which, the elastic shear (G) and bulk (K) moduli are, respectively, calculated from:

$$\begin{aligned} &G = G_{0} \,p_{{ref}} \,\frac{{(e_{g} - e)^{2} }}{{1 + e}}\,\sqrt {\frac{{\sigma ^{\prime}_{n} }}{{p_{{ref}} }}} \\ &K = K_{0} \,p_{{ref}} \,\frac{{(e_{g} - e)^{2} }}{{1 + e}}\,\sqrt {\frac{{\sigma ^{\prime}_{n} }}{{p_{{ref}} }}} \end{aligned} $$

(11)

wherein, G₀ and K₀ are dimensionless constants and e_g = 2.97 is a reasonable assumption for sands with angular and sub-angular particles [38].

The laboratory investigations and DEM simulations have indicated that the $\tau /\sigma ^{\prime}_{n}$ ratio in the DSS tests evolves through (e.g., Oda & Konishi [48], Wood et al. [70], Budhu [7], Jiang et al. [29]):

$$ \frac{\tau }{{\sigma ^{\prime}_{n} }} = \kappa \;\tan \alpha $$

(12)

wherein $\alpha$ is the angle between the major principal effective stress from normal to the bedding plane and $\kappa \approx \tan \varphi ^{\prime}_{{cs}} ( = M)$. Under monotonic shear, the term $H = \kappa \;\tan \alpha$ in Eq. (12) acts like a hardening variable and grows continuously from zero at $\tau$ = 0 to an ultimate asymptotic value of $\kappa = M$ at the critical state where $\alpha = 45^{ \circ }$. A yield function for the monotonic DSS tests is:

$$ {\text{f}}({\varvec{\upsigma ^{\prime}}},\;{\text{H}}) = \uptau - {\text{H}}{{\upsigma ^{\prime}_{\text{n}}}} = 0 $$

(13)

Accordingly, normal to the yield function becomes ${\mathbf{n}} = \left[ {\begin{array}{*{20}c} {\partial {\text{f}}({\varvec{\upsigma ^{\prime}}},\;{\text{H}})/\partial \uptau } & {\partial {\text{f}}({\varvec{\upsigma ^{\prime}}},\;{\text{H}})/\partial \upsigma ^{\prime}_{\text{n}} } \\ \end{array} } \right]^{{\,{\text{T}}}} = \left[ {\begin{array}{*{20}c} 1 & { - {\text{H}}} \\ \end{array} } \right]^{{\;{\text{T}}}}.$ In Eq. (10), the plastic hardening modulus (i.e., K_p) is:

$$ K_{p} = h\,G\;\,\left( {\frac{{M\exp ( - n\psi )}}{H} - 1} \right) $$

(14)

where h and n are soil parameters.

Been & Jefferies [5] introduced “state parameter”, $\psi$, as a scalar measure of sand state expressed through the difference between the current void ratio (i.e., e), and the critical state void ratio [i.e., e_cs in Eq. (1)_b]. For DSS tests, $\psi$ is defined through (e.g., [55, 72]):

$$ \psi = e - e_{{cs}} = e - [\;\overbrace {{\Gamma - \lambda (\sigma ^{\prime}_{n} /p_{{ref}} )^{{\,\xi }} }}^{{e_{{cs}} }}\;] $$

(15)

${\mathbf{R}} = \left[ {\begin{array}{*{20}c} 1 & d \\ \end{array} } \right]^{{\,T}}$ in Eq. (10) is the plastic strain rate direction vector in which, d is:

$$ d = d_{0} \,\left[ {M\exp (m\psi ) - H} \right] $$

(16)

d₀ in Eq. (16) is a soil parameter. Using Eqs. (10) to (16) and provided that $\frac{1}{{\text{K}_{\text{p}} }}{\mathbf{n}}^{\text{T}} \, \dot{{\varvec{:\upsigma ^{\prime}}}} > 0$ (i.e., the existence of positive plastic multiplier), D^ep becomes:

$$ {\mathbf{D}}^{{ep}} = \left( {\begin{array}{*{20}c} {D_{{11}}^{{ep}} } & {D_{{12}}^{{ep}} } \\ {D_{{21}}^{{ep}} } & {D_{{22}}^{{ep}} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} G & 0 \\ 0 & K \\ \end{array} } \right) - \frac{1}{{K_{p} + G - H\,K\,d}}\;\left( {\begin{array}{*{20}c} {G^{2} } & { - H\,K\,G} \\ {d\,K\,G} & { - H\,d\,K^{2} } \\ \end{array} } \right) $$

(17)

5.1 Criterion for onset of instability under coupling of the shear and volumetric strains

Using Eqs. (10) and (17), the stress and strain rates are interrelated through:

$$ \dot{\tau } = D_{{11}}^{{ep}} \,\dot{\gamma } + D_{{12}}^{{ep}} \,\dot{\varepsilon }_{v} \quad ;\quad \dot{\sigma ^{\prime}}_{n} = D_{{21}}^{{ep}} \,\dot{\gamma } + D_{{22}}^{{ep}} \,\dot{\varepsilon }_{v} $$

(18)

Now, the substitution of Eqs. (18) into Eq. (7) yields:

$$ D_{{11}}^{{ep}} \, + (D_{{12}}^{{ep}} \, + D_{{21}}^{{ep}} \,)\;\zeta + D_{{22}}^{{ep}} \;\zeta ^{2} = 0 $$

(19)

Implementation of $D_{{11}}^{{ep}} \,,\;D_{{12}}^{{ep}} ,\;D_{{21}}^{{ep}}$ and $D_{{22}}^{{ep}}$ from Eq. (17) in Eq. (19) results in the following normalized critical plastic hardening modulus of the constitutive model of this study at the onset of instability:

$$ \left( {\frac{{K_{p} }}{G}} \right)_{{cr}} = \frac{{H\,d + (H - d)\,\zeta - \zeta ^{2} }}{{(G_{0} /K_{0} ) + \zeta ^{2} }} $$

(20)

Thus, once $(K_{p} /G) - (K_{p} /G)_{{cr}} = 0$ is fulfilled, instability is triggered. Under the constant volume condition (say $\zeta$ = 0), Eq. (20) is simplified into $\left( {K_{p} /G} \right)_{{cr}} = (K_{0} /G_{0} )Hd$. Of note, maximizing generalized stress [see Eq. (8)] may be interpreted as an integral form for the second-order work criterion. In Sect. 5.3, it will be shown that maximizing the generalized stress and the critical plastic hardening modulus [i.e., Eq. (20)] yield identical states for the onset of the mechanical instability.

Buscarnera et al. [10], Buscarnera & Whittle [9], Daouadji et al. [20], Imposimato & Nova [27], and Mihalache & Buscarnera [40] put forward the theory of loss of controllability to study the onset of instability in the elastoplastic continua. In this context, the mechanical stability of a continuum is investigated thorough ${\dot{\varvec{\Phi }}} = {\mathbf{X}}\,{\dot{\varvec{\Psi }}}$ in which, ${\dot{\varvec{\Phi }}} = \left\{ {\begin{array}{*{20}c} {\,{\dot{\varvec{\sigma ^{\prime}}}}_{\theta } } & {{\dot{\varvec{\varepsilon }}}_{\varpi } } \\ \end{array} } \right\}^{{\,\text{T}}}$ and ${\dot{\varvec{\Psi }}} = \left\{ {\begin{array}{*{20}c} {\,{\dot{\varvec{\varepsilon }}}_{\theta } } & {{\dot{\varvec{\sigma ^{\prime}}}}_{\varpi } } \\ \end{array} } \right\}^{{\,\text{T}}}$ are, respectively, the control and response vectors [${\dot{\varvec{\sigma ^{\prime}}}}_{\theta } ,\;{\dot{\varvec{\varepsilon }}}_{\varpi } ,{\dot{\varvec{\sigma }^{\prime}}}_{\varpi }$ and ${\dot{\varvec{\varepsilon }}}_{\theta }$ are control and response effective stress rate and strain rate variables], and X is the control matrix. The mechanical instability occurs at the loss of controllability once $\det {\mathbf{X}}\, = 0$. Buscarnera & Whittle [9] demonstrated that ${\dot{\varvec{\Phi }}}$ and ${\dot{\varvec{\Psi }}}$ must be work conjugate and thus ${\text{d}}^{2} {\text{W}} = {\dot{\varvec{\upsigma}} ^{\varvec{\prime}}{\mathbf{:}}\dot{\varvec{\upvarepsilon} }} = {\dot{\mathbf{\Phi }}}^{\text{T}} \,{\dot{\mathbf{\Psi }}}$. Accordingly, Hill’s second-order work criterion and loss of controllability are mathematically equivalent.

5.2 Calibration of the constitutive model

The model has a total of nine parameters. G₀ and K₀ are obtained from the resonant column tests performed at extremely small shear strains. Alternatively, G₀ can be estimated from the initial slopes of the $\tau \;vs.\;\gamma$ curves in the constant volume and drained tests (see Fig. 11a). K₀ can be estimated from the initial parts of the $\varepsilon _{v} \;vs.\;\gamma$ curves in drained tests. M is the slope of CSL in the $\tau \;vs.\;\sigma ^{\prime}_{n}$ plane. $\Gamma$ is the intercept of CSL in the $e\;vs.\;\sigma ^{\prime}_{n}$ plane. $\ln \lambda$ and $\xi$ are the intercept, and slope of CSL in the $\ln (\Gamma - e_{{cs}} )\;vs.\;\ln (\sigma ^{\prime}_{n} /p_{{ref}} )$ plane, respectively. For the test sand, the CSL parameters were obtained in Fig. 4 and the best fitted CSL was drawn against the laboratory data. Having data of the phase transformation in the constant volume tests, $m = \frac{1}{\psi }\ln \left[ {\frac{{\tau /\sigma ^{\prime}_{n} }}{M}} \right]$ wherein, $\tau /\sigma ^{\prime}_{n}$ and $\psi$ are measured at the phase transformation (see Fig. 11b). In drained tests on dense specimens, plastic hardening modulus becomes zero temporarily at the peak shear strength and accordingly, $n = - \frac{1}{\psi }\ln \left[ {\frac{{\tau /\sigma ^{\prime}_{n} }}{M}} \right]$ in which, $\tau /\sigma ^{\prime}_{n}$ and $\psi$ are, measured at the peak shear strength. For semi-angular and angular sand specimens prepared through the wet tamping method, n = 1.0 to 1.5 is a reasonable assumption (e.g., Li & Dafalias [38]). Ignoring the small contribution of the elastic shear strains, d₀ and h can be estimated from data of the constant volume DSS tests through $d_{0} \approx - \frac{1}{{K\;[M\exp (m\psi ) - H]}} \cdot \frac{{\delta \sigma ^{\prime}_{n} }}{{\delta \gamma }}$ and $h \approx G\;\left[ {\frac{{M\exp ( - n\psi )}}{H} - 1} \right] \cdot \frac{{\delta \sigma ^{\prime}_{n} }}{{\delta \gamma }}$ (see Figs. 11c to f for sensitivity of the constitutive model predictions to changes in d₀ and h).

Fig. 11

Graphical representation of sand constitutive model calibration/sensitivity analysis for: a G under $\sigma _{{n0}}^{{\prime }}$ = 100, 200, and 300 kPa using G₀ = 85 [see Table 1] vs. laboratory CV data; b m; c and d d₀; and e and f h

5.3 The constitutive model function in prediction of instability

Large shear strains (e.g., 40%) may lead to strain localization in sand specimens in DSS tests. Even though the simple constitutive model is not able to predict strain localization properly, flow instability and post-peak softening were triggered at shear strains lower than 2.5% in the DSS tests reported here. Accordingly, any probable impact of localization on the constitutive model predictions for the onset of instability and post-peak softening is expected to be minimal. Using the data of a total of 13 constant volume DSS tests on Firoozkuh No. 161 sand specimens covering a relatively wide domain of consolidation void ratios from 0.671 to 0.917 with $\sigma _{{n0}}^{{\prime }}$ = 100, 200, and 300 kPa, the constitutive model parameters as listed in Table 1 were determined. For three medium-dense (e_in = 0.711, Dr≈69), medium (e_in = 0.775, Dr≈53), and loose (e_in = 0.852, Dr≈35) specimens sheared from $\sigma ^{\prime}_{n} =$ 300 kPa, the constitutive model predictions are depicted against the laboratory data in Fig. 12a and b. The medium-dense specimen demonstrates a non-flow response throughout the entire range of shear strain studied here. On the other hand, the increase in e_in (= e since the tests in Fig. 12a and b were performed under the constant volume condition) leads to flow behavior of the loose specimen. Without changing the parameters, the model predictions for the behavior of four specimens (e_in≈0.79) sheared under $\zeta$ =  + 0.2, + 0.1, 0.0, and − 0.2 are illustrated against the corresponding laboratory data in Fig. 12c and d. For four specimens subjected to bilinear strain paths in Fig. 5c, the model simulations are demonstrated against the corresponding experimental data in parts “e” and “f” of Fig. 12. It is observed that the simulated forceful strain-hardening under $\zeta$ =  + 0.2 and + 0.1 were abruptly turned into softening once ($\gamma _{{thr}}$= 18.5%) is passed. On the contrary, post-peak softening in the test with $\zeta$ = − 0.1 turned into a mild hardening for the shear strains larger than $\gamma _{{thr}}$. A reasonable conformity between the state-dependent model predictions and the DSS data can be observed in Fig. 12 and the constitutive model succeeded to predict the escalating strain-hardening and dilation with increasing $\zeta$ in Fig. 12c and d as well as the sudden transition from dilation to contraction and vice versa in Fig. 12e and f in bilinear strain paths.

Table 1 Parameters used in simulation of DSS tests on Firoozkuh No. 161 sand

Fig. 12

The state$\zeta$dependent constitutive model predictions vs. results of DSS tests on Firoozkuh No. 161 sand specimens: a and b three constant volume tests ($\sigma ^{\prime}_{{n0}} = 300\,kPa$ in all simulations); c and d four tests with linear coupling between the volumetric and shear strains; e and f four tests with bilinear coupling between the volumetric and shear strains (e_in = 0.79 and $\gamma _{{thr}}$ = 18% are assumed in all simulations)

The model predictions in terms of $(K_{p} /G) - (K_{p} /G)_{{cr}} \;vs.\;\gamma$, $\tau \;vs.\;\sigma ^{\prime}_{n}$, and $\tau \;vs.\;\gamma$ for nine loose specimens (e_in = 0.808, Dr = 28.5%) sheared from $\sigma _{{n0}}^{{\prime }}$ = 100, 200, and 300 kPa under linear coupling between the volumetric and shear strains ($\zeta$ = -0.1, 0.0, and + 0.1) are illustrated in Fig. 13. Superimposed symbols “○” on curves in Fig. 13 indicate the onset of the mechanical instability where Eq. (20) [or equally, Eq. 9] is fulfilled. Curves for $(K_{p} /G) - (K_{p} /G)_{{cr}} \;vs.\;\gamma$ in Fig. 13a and b indicate that for the six numerical tests under $\zeta = - 0.1$ and 0.0, $(K_{p} /G) - (K_{p} /G)_{{cr}} = 0$ is fulfilled where $\gamma$ in the range 1.03% to 1.41%; however, only two samples with $\sigma _{{n0}}^{{\prime }}$ = 200 and 300 kPa are prone to the mechanical instability under $\zeta = + 0.1$ in Fig. 13(c). A search for transient maximums of generalized stress in the $\Sigma \;vs.\;\sigma ^{\prime}_{n}$ plane (see Fig. 13d and f) suggests that all the specimens subjected to the linear coupling with $\zeta$ = − 0.10 and 0.0 are prone to flow instability. However, only two specimens sheared from $\sigma _{{n0}}^{{\prime }}$ = 200 and 300 are susceptible to limited flow instability under $\zeta$ =  + 0.10. Certain states for the onset of instability from the critical plastic hardening modulus [i.e., Eq. (20)] and transient maximums of the generalized stress [i.e., Eq. (9)] superimposed on the specimens’ response in the $\tau \;vs.\;\sigma ^{\prime}_{n}$ and $\tau \;vs.\;\gamma$ planes imply that the mechanical instability occurs in the post-peak regime of the behavior when $\zeta < 0$ (see Fig. 13g and j), peak shear strength when $\zeta$ = 0 (see Fig. 13h and k), and prior to the phase transformation when $\zeta > 0$ (see Fig. 13i and l). Of note, Eqs. (9) and (20) yielded identical states for the onset of instability in Fig. 13g to l. The instability lines in Fig. 13a to c become steeper with decreasing $\sigma _{{n0}}^{{\prime }}$. Throughout Fig. 13g to i, the predicted behaviors become excessively dilative with the increase in $\zeta$ and the initial normal effective stress predominantly affects the early response of the specimens; hence, for each series of $\zeta$, the $\tau \;vs.\;\gamma$ curves in Fig. 13g to i are almost the same in large shear strains.

Fig. 13

The constitutive model predictions for three tests with e_in = 0.88 and $\sigma _{{n0}}^{{\prime }}$ = 100, 200, and 300 kPa under $\zeta$ =  + 0.1, 0.0, − 0.1: a to c normalized plastic hardening modulus difference [i.e., $(K_{p} /G) - (K_{p} /G)_{{cr}}$] vs. shear strain; d to f generalized stress vs. effective normal stress; g to i effective stress paths; and j to l mobilization of shear strength with shear strain

Jrad et al. [30] and Nicot et al. [45] applied the theory of loss of controllability (see Sect. 5.1) to triaxial compression tests with linear coupling between the volumetric and axial strain rates. They demonstrated that instability occurs once $\sigma ^{\prime}_{1} - (1 - \theta )\,\sigma ^{\prime}_{3}$ reaches a transient maximum in the $\sigma ^{\prime}_{1} - (1 - \theta )\,\sigma ^{\prime}_{3} \;vs.\;\varepsilon _{1}$ plane wherein, $\sigma ^{\prime}_{1}$ and $\sigma ^{\prime}_{3}$ are, respectively, the axial and radial effective stresses acting on the cylindrical specimen in the conventional triaxial tests, and $\theta = \frac{{\dot{\varepsilon }_{v} }}{{\dot{\varepsilon }_{1} }}$ defines linear coupling between the volumetric (i.e., $\dot{\varepsilon }_{v}$) and axial (i.e., $\dot{\varepsilon }_{1}$) strain rates. In this context, $\sigma ^{\prime}_{1} - (1 - \theta )\,\sigma ^{\prime}_{3}$ plays the role of a generalized stress whose maximum indicates the onset of instability in the triaxial compression tests with the linear coupling between $\dot{\varepsilon }_{v}$ and $\dot{\varepsilon }_{1}$. Jrad et al. [30], Nicot et al. [45], and Lashkari & Yaghtin [35] showed that flow instability in the triaxial compression tests may trigger next to the peak shear strength under $\theta < 0$ (i.e., expansive coupling) condition, and at the peak shear strength under $\theta = 0$ (i.e., constant volume) condition. Progressive densification of sand under $\theta > 0$ (i.e., contractive coupling) may cause flow instability prior to phase transformation. Sivathayalan & Logeswaran [60] pointed out that in the triaxial compression tests with linear coupling between the volumetric and strain rates, $\frac{{S_{{peak}} }}{{\sigma ^{\prime}_{{3c}} }}$ and $\frac{{\Delta u_{{\max }} }}{{\sigma ^{\prime}_{{3c}} }}$ increase with $\theta$ (of note, $\sigma ^{\prime}_{{3c}}$ is confining stress prior to the instigation of shear deviator stress). Compared to the previous researches with a handful of laboratory data, results of a large number of experiments reported here make it possible systematic investigations on the impact of $\zeta$, e_in, and $\sigma _{{n0}}^{{\prime }}$ on stress ratio at the onset of flow instability, normalized peak shear strength for sand specimens suffering from flow instability, maximum pore-pressure ratio, and stress state at the phase transformation in the following sections.

5.4 Post-peak softening in initially dense specimens under expansive coupling

A particular type of post-peak softening (i.e., strain-hardening → limited flow → transient strain-hardening → flow → complete loss of shear strength) which may happen when medium-dense and dense specimens are subjected to persistent expansive volumetric strains is studied here. For this reason, the behavior of a specimen sheared under $\zeta = - 0.10$ is simulated by the constitutive model and the results are directly compared with the corresponding experimental data in parts “a” to “d” of Fig. 14. The curve for the evolution of $(K_{p} /G) - (K_{p} /G)_{{cr}}$ with $\gamma$ in Fig. 14a and the $\Sigma \;vs.\;\sigma ^{\prime}_{n}$ curve in Fig. 14b indicate that the specimen is mechanically stable [because $(K_{p} /G) - (K_{p} /G)_{{cr}} > 0$ and $\dot{\Sigma } > 0$] from the initial state (i.e., A) up to B [where $(K_{p} /G) - (K_{p} /G)_{{cr}} = 0$ and $\dot{\Sigma } = 0$] which is located to some extent beyond the peak shear strength (see Fig. 14c and d). Thereafter, the specimen experiences a transient instability [$(K_{p} /G) - (K_{p} /G)_{{cr}} < 0$ and $\dot{\Sigma } < 0$] as its state reallocates from B to C. A short-term strain-hardening which instigates at C makes the sand behavior transitionally stable [say $(K_{p} /G) - (K_{p} /G)_{{cr}} > 0$ and $\dot{\Sigma } > 0$] until D wherein, progressive loosening of sand as caused by the expansive volumetric strains results in the second triggering of flow behavior and in due course, complete loss of shear strength in large shear strains.

Fig. 14

The constitutive model predictions vs. results of a DSS test on a medium-dense sand specimen sheared under $\zeta$ = − 0.10: a $(K_{p} /G) - (K_{p} /G)_{{cr}}$ vs. shear strain; b generalized stress vs. effective normal stress, c effective stress path; and d shear stress vs. shear strain [of note, d in the legend stands for the rate of $\Sigma$]

5.5 Slope of instability line

For a total of 38 DSS tests under $\zeta$ = − 0.20, − 0.10, − 0.05, 0.0, + 0.05, and + 0.10, data of the slope of the stability line ($\eta _{{IL}}$) are drawn against the state parameter at the onset of instability ($\psi$_i), and initial void ratio (e_in) in Fig. 15a and b, respectively. The $\eta _{{IL}} \;vs.\;\psi _{i}$ and $\eta _{{IL}} \;vs.\;e_{{in}}$ curves predicted through the implementation of the parameters listed in Table 1 in the state-dependent constitutive model are also superimposed on Fig. 15 wherein, non-unique curves for $\eta _{{IL}}$ descend with $\psi$_i and e_in depending on the applied $\varsigma$ values. In Fig. 15, specimens with $e_{{in}} \ge 0.82$ ($\psi _{i} \ge 0$) are prone to instability under the constant volume ($\zeta$ = 0) condition. However, sand densification under $\zeta > 0$ causes only specimens with $e_{{in}} \ge 0.88$ to be prone to instability under $\zeta = + 0.10$. In opposition, progressive loosening of soil under $\zeta < 0$ widens domain of initial void ratios of the specimens susceptible to instability and consequently, all specimens with $e_{{in}} \ge 0.65$ exhibit signs of instability under $\zeta = - 0.20$.

Fig. 15

Constitutive model predictions and the corresponding laboratory data for the relationship between the slope of instability line in linear strain paths with: a state parameter; and b initial (after consolidation) void ratio prior to shear

5.6 Peak shear strength ratio

The peak shear strength (i.e., S) and the maximum excess pore-water pressure (i.e., $\Delta$u_max) in specimens suffering from flow behavior are key factors in the design and risk assessment of large and high-risk earth structures such as mine tailing dams as well as saturated sand slopes [21, 49, 54,55,56,57, 62]. For a total of 38 specimens suffering from flow behavior, the laboratory data and predicted curves for the variations of $S/\sigma ^{\prime}_{{n0}}$ with $\psi$_i and e_in are, respectively, illustrated in Fig. 16a and 15b. In parts “a” and “b” of Fig. 16, $S/\sigma ^{\prime}_{{n0}}$ descends almost linearly with $\psi$_i and e_in and increase in $\zeta$ from -0.20 to + 0.1 leads to upward relocation of $(S/\sigma ^{\prime}_{{n0}} )\;vs.\;\psi _{i}$ and $(S/\sigma ^{\prime}_{{n0}} )\;vs.\;e_{{in}}$ curves. The latter observation indicates that the transition of the volumetric strains from contractive to dilative leads to a drop in $S/\sigma ^{\prime}_{{n0}}$ ratio.

Fig. 16

Constitutive model predictions and the corresponding laboratory data for the relationship between: a peak shear strength ratio (i.e., $S/\sigma ^{\prime}_{{n0}}$) and $\psi$_i; b $S/\sigma ^{\prime}_{{n0}}$ and e_in; and c $\sigma ^{\prime}_{n}$ at peak shear strength (i.e., $\sigma ^{\prime}_{n} (\tau = S)/\sigma ^{\prime}_{{n0}}$) and $\psi$_i

For six sands different in terms of mineralogy, gradation, fines content, and particle morphology, Lashkari et al. [37] reported that the normal effective stress ratio at the peak shear strength [i.e., $\sigma ^{\prime}_{n} (\tau = S)/\sigma ^{\prime}_{{n0}}$] in the constant volume DSS tests varies in a range from 0.55 to 0.70. For the specimens sheared under $\zeta$ = − 0.20, − 0.10, − 0.05, 0.0, + 0.05, and + 0.10, the laboratory data and state-dependent model predictions for the relationship between $\sigma ^{\prime}_{n} (\tau = S)/\sigma ^{\prime}_{{n0}}$ and $\psi$_i are depicted in Fig. 16c wherein, $\sigma ^{\prime}_{n} (\tau = S)/\sigma ^{\prime}_{{n0}}$ ranges from 0.48 to 0.70. The constitutive model simulations, as well as the laboratory data, also signify that $\sigma ^{\prime}_{n} (\tau = S)/\sigma ^{\prime}_{{n0}}$ increases slightly with $\psi$_i.

5.7 Stress variables at phase transformation

For a total of 48 DSS tests with $\sigma _{{n0}}^{{\prime }}$ = 200 kPa carried out under $\zeta$ = − 0.10, − 0.05, 0.0, + 0.05, + 0.10 and + 0.20, the experimental data and predicted curves for the normal effective stress and shear strength at phase transformation are depicted in Figs. 17a and 16b, respectively. In part “a” of Fig. 17, increasing e_in causes the normal effective stress at phase transformation to decrease; however, increase in $\varsigma$slows down the rate of decrease in $\sigma ^{\prime}_{n}$ with e_in. In Fig. 17b, $\tau$ generally tend to decrease with e_in; however, $\tau \;vs.\;e_{{in}}$ curves possess a transient peak in the tests with $\zeta > 0$ which is attributed to the conical nature of the phase transformation (say dilatancy) surface in the multiaxial stress space [9, 19].

Fig. 17

Constitutive model predictions and the corresponding laboratory data for: a normal effective stress ratio at phase transformation vs. e_in; and b normalized shear strength ratio at phase transformation vs. e_in

5.8 Maximum excess pore-water pressure ratio

The maximum positive excess pore-water ratio [i.e., $(r_{u} )_{{\max }} = \Delta u_{{\max }} /\sigma ^{\prime}_{{n0}}$] for a total of 48 DSS tests are drawn in Fig. 18. The corresponding model predictions are also drawn in Fig. 18 to portray the relationship between (r_u)_max and e_in for the selected $\zeta$ values wherein, (r_u)_max increases with the initial void ratio. For instance, increase in e_in from 0.70 to 0.90 causes an increase in (r_u)_max from 0.22 to 0.87 under constant volume ($\zeta$ = 0) condition. The progressive loosening of sand owing to the expansive deformations accelerates the accumulation of the excess pore-water pressure and accordingly, the $(r_{u} )_{{\max }} vs.\;e_{{in}}$ curves move upward with decreasing $\varsigma$. On the other hand, sand densification due to contractive volume change postpones the accumulation of positive pore-water pressure and thus, the $(r_{u} )_{{\max }} vs.\;e_{{in}}$ curves move downward with growing $\varsigma$.

Fig. 18

Constitutive model predictions and the corresponding laboratory data for the variation of the maximum pore-water pressure ratio with e_in

5.9 Asymptotic stress ratio

For a total of 34 DSS tests under $\zeta$ = − 0.20, − 0.10, − 0.05, 0.0, + 0.05, + 0.10 and + 0.20, the asymptotic stress ratios at the end of the experiments (i.e., $\mu$) are illustrated against the corresponding $\zeta$ values in Fig. 19. Using the parameters given in Table 1, the predicted curve for variation of the asymptotic stress ratio with $\varsigma$ is superimposed on the laboratory data. Figure 19 signifies that the asymptotic stress ratio decreases with the increasing $\varsigma$.

Fig. 19

Constitutive model predictions and the corresponding laboratory data for the variation of the asymptotic stress ratio with $\varsigma$

6 Conclusions

Recent centrifuge testing and field evidences have confirmed that the constant volume laboratory single-element tests may not closely replicate the actual sand resistance against flow behavior during and soon after earthquakes, and some volume change due to pore-water inflow/outflow is inevitable. It has been suggested that considering coupling between the volumetric and shear strains in single-element tests can explain the outcome of volume change on sand flow behavior vulnerability. In this treatment, the behavior of Firoozkuh No. 161 sand specimens sheared with different degrees of linear coupling between the volumetric and shear strains in NGI type DSS apparatus was investigated. The main conclusions drawn are as follows:

• (a) The progressive loosening of sand as caused by volumetric expansion during coupled strain paths intensifies flow behavior vulnerability, whereas contractive volumetric strains improve sand compactness and reduces post-peak softening susceptibility.

• (b) Coupling between the volumetric and shear strain prevents the soil state from approaching CSL even at large shear strains; nevertheless, the soil state moves rapidly toward the CSL once the coupling is nullified and shearing continues under constant volume condition.

• (c) Analysis of the experimental data has indicated that the instability line is non-unique and its slope in the $\eta _{{IL}} \;vs.\;\psi _{i}$ and $\eta _{{IL}} \;vs.\;e_{{in}}$ planes depends on $\zeta$.

• (d) For each $\zeta$ value, the peak shear strength ratio decreases uniquely with $\psi$_i and e_in.

• (e) The asymptotic stress ratio in the $\tau$ vs. $\sigma ^{\prime}_{n}$ plane decreases with $\zeta$.

• (f) It was shown that a simple state-dependent constitutive model can capture the essential elements of sand behavior under the coupling of the volumetric and shear strains.

Appendix

As mentioned earlier, the transient coupling between the volumetric and shear strains is more relevant to real field condition. Such a scenario can be represented mathematically by the following nonlinear differential equation:

$$ \frac{{\dot{\varepsilon }_{v} }}{{\dot{\gamma }}} = \zeta \,\;\left[ {1 - \left( {\frac{{\varepsilon _{v} }}{{(\varepsilon _{v} )_{{\lim }} }}} \right)^{{\,\beta }} } \right]\; $$

(21)

where β, ζ and $(\varepsilon _{v} )_{{\lim }}$ depend on heterogeneity and characteristic properties of soil, and drainage boundary condition. For extremely small volumetric strains (say $\varepsilon _{v} \to 0$), Eq. (21) implies that $\varepsilon _{v}$ evolves almost linearly with $\gamma$ while $\zeta$ defines proportionality. However, $\dot{\varepsilon }_{v} /\dot{\gamma }$ descends gradually towards zero as $\varepsilon _{v}$ asymptotically approaches the limiting volumetric strain [i.e., $(\varepsilon _{v} )_{{\lim }}$] at extremely large shear strains. Typical curves of nonlinear coupling between the volumetric and shear strains for $(\varepsilon _{\text{v}})_{\text{lim}}$ = − 1.0, − 0.65, − 0.35, 0, + 0.35, + 0.65, and + 1.0% under $\zeta$ =  + 0.1 and $\beta$ = 1.0 are illustrated in Fig. 

Fig. 20

Nonlinear coupling between the volumetric and shear strain rates: a predicted strain paths for (ε_v)_lim = − 1.0, − 0.65, − 0.35, 0, + 0.35, + 0.65, and + 1.0 under $\zeta$ =  + 0.1 and $\beta$ = 1.0; b predicted strain paths for $\beta _{{vl}}$ = 0.5, 1, 2, and 5 under $\zeta$ =  + 0.1; c geometry of a bilinear strain path corresponding to a nonlinear strain path

20a. For all strain paths in Fig. 20a, volumetric-shear coupling nullifies gradually and turns into constant volume response as $\varepsilon _{v} \to (\varepsilon _{v} )_{{\lim }}$. Figure 20b indicates that an increase in $\beta$ accelerates the accumulation of $\varepsilon _{v}$ with $\gamma$.

Having the initial slope [i.e., $\varsigma$] and limiting volumetric strain [i.e., ($\varepsilon _{v}$)_lim] of a nonlinear strain path, a bilinear strain path with the initial slope of $\varsigma$ while $\gamma \le \gamma _{{thr}} = \frac{{(\varepsilon _{v} )_{{\lim }} }}{\zeta }$, and $\dot{\varepsilon }_{v} = 0$ for $\gamma > \gamma _{{thr}}$ [see Eq. (3)] can be fitted to the bilinear strain paths [see Fig. 20(c)].