Particle breakage of granular soils: changing critical state line and constitutive modelling

Abstract

When soil particles break, the particle size distribution (PSD) becomes a variable in the same way as other variables like void ratio, soil structure and anisotropy, etc. To consider particle breakage in a constitutive model, we need three key components: (i) quantification of PSD in a realistically simple manner, (ii) evolution of PSD during particle breakage, and (iii) influences of PSD on other soil properties like strength and stiffness. This paper firstly summarizes the latest advances in the first two components, discusses new ways of quantifying PSD effects, and finally presents a new critical state model where the PSD is treated as a variable. In discussing the PSD effects, we focus on the movement of the critical state line (CSL) due to particle breakage. We introduce a new state parameter and a new evolution law of the CSL. We assume that the CSL shifts downwards in the v—lnp space with increasing particle breakage under relatively low stresses, but all the CSLs for different PSDs converge to a steady state at high stresses where particle breakage eventually stops and is no longer the main mechanism for soil deformation. The proposed model is compared with other constitutive model in the literature and validated against experimental data, which demonstrates its satisfactory performance.

1 Introduction

Particle breakage occurs in many geotechnical applications, for example, foundations built on carbonate sands, rail ballast under repeated loads, gravels produced from weak rocks like claystone and siltstone. When particles break, the particle size distribution (PSD) of the soil becomes a variable in the same way as other soil variables like pore size characteristics, soil structure and anisotropy. In classical soil mechanics, the pore size characteristics of a soil is usually quantified by the void ratio, which evolves under stress and affects other soil properties. Similarly, we need to establish the following three key principles to tackle the problem of particle breakage: a parameter or a model that quanitifies soil PSD, a evolution law that describes how PSD evolves with external factors like stress, strain or energy, and constitutive relations that describe the influences of PSD on the other soil properties.

At present, numerous attempts have been made to address the first two issues by proposing a breakage index, which is generally based on the PSDs before and after tests, and correlating the proposed breakage index to the mechanical parameters. As for the last issue, it is of great interest to start from those first-order factors, for example, PSD has a significant influence on the critical state parameters; while its effect on the other soil properties, such as the friction angle is probably less obvious according to many studies [7, 32]. It is therefore not surprising that particle brerakage with a progressive change of PSD significantly affects the position of the critical state line (CSL), but shows very limited influence on the critical state friction angle of granular soils based on many experimental and numerical studies in the literature [1, 6, 7, 18, 37, 52, 57]. In general, to understand the influence of particle breakage on the CSL is of great importance for further developing a constitutive model of granular soils with consideration of particle breakage.

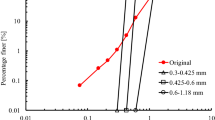
The effect of particle breakage on the location of CSL, however, is complicated and controversial because of the difficulty in determing the evolving CSLs during particle breakage. Nevertheless, a conclusion still can be made that particle breakage will lead to a change of intercept of CSL in the e—ln(p) space revealed by most of the studies. Among which, the framework proposed by Muir Wood and Maeda [32] provides a practical approach for considering the breakage-induced shift of CSL as shown in Fig. 1(a). As indicated by Fig. 1(a), the CSL was assumed to be parallel shifting with increasing degree of particle breakage (i.e., defined as I_G). Such an assumption has also been adopted in modelling particle breakage of limestone fragments [14], rockfill material [49, 56], and carbonate sands [45]. It should be noted that the hypothesis of parallel shifting of CSL is not fully justified, especially when the sample is subjected to high stresses. For example, Bandini and Coop [1] conducted triaxial tests with two different shearing stages, the first stage is to produce different degrees of particle breakage of the original sample, and the second stage is to explore whether such a change in PSD during the first stage will change the CSL. Figure 1(b) shows the different CSLs with different degrees of particle breakage, where CSPs indicates the ctirical state points, and Br is the breakage index proposed by Hardin [13]. It is interesting to note that an obvious convergence of the CSLs with development of particle breakage is observed at high stresses, where the steady-state of particle breakage will be reached [7, 28, 31, 40]. To date, it still remains a challenge to develop a simple mathematical description of changing CSL as particle breakage progresses.

Fig. 1

Changing of CSL due to particle breakage: a parallel shifting of CSL (modified after Muir Wood and Maeda [32]; b CSLs of carbonate sands with different degrees of particle breakage (modified after Bandini and Coop [1]

Furthermore, the breakage-induced evolution of PSD also has a great influence on the calculation of state parameter proposed by Been and Jefferies [2]. The state parameter measures the distance between the current state and the corresponding critical state, and is able to well capture the state-dependent behavior of granular soils. More recently, Ciantia and O’Sullivan [5] reported that it is necessary to consider the shifting of CSL due to particle breakage when calculating the state parameter for crushable soils. Furthermore, some studies found that the CSL is not suitable as a reference line for defining the state parameter because of the different PSDs between the current state and the reference state [12, 15]. It is therefore important to define a more reasonable state parameter to describe the state-depdendent constitutive behavior of granular soils.

The aim of this paper is to propose a constitutive model that can capture the main features of granular soils, i.e., the nonlinear CSL and isotropic compression lines (ICLs) in the e—ln(p) space, the state-dependent behavior, and the influence of particle breakage. This paper firstly summarizes some basic observations on particle breakage in terms of the first two issues. After that, a double logarithmic approach proposed by Sheng et al. [38] is then adopted for modelling the nonlinear CSL and ICLs in the e—ln(p) space, followed by a new and simple evolution law of CSL with the progress of particle breakage. The state-dependent behavior is developed by using the modified state parameter where a new reference compression line (RCL) is employed. The particle breakage effect is also incorporated with consideration of the evolution of the CSL in the e—ln(p) space. Finally, the proposed model is compared with other existing constitutive model and is validated against experimental triaxial test data in the literature.

2 Some observations on particle breakage

2.1 The ultimate PSD

It has been widely reported that the PSD of granular soils will eventually evolve toward an ultimate steady-state even though the applied stress/strain is extremely large [7, 31, 41]. An ultimate PSD implies that particles with different sizes will not break further as a result of the dynamic balance between the particle size effect and the coordination number effect [28, 42]. The ultimate PSD, however is not necessary but commonly assumed to be fractal-graded for most practical cases, which can be expressed as

$$P\left( {d_{i} } \right) = \left( {\frac{{d_{i} }}{{d_{\max } }}} \right)^{{3 - D_{u} }}$$

(1)

where P(d_i) is the mass percentage finer than d_i-sized particles, d_max is the maximum particle size, D_u is defined as the ultimate fractal dimension. Many experimental studies have shown that D_u is highly depdendent on many factors, such as the component minerals, initial state, and stress level applied to the soils [7, 53], which makes it problematic to determine the values of D_u for given granular soils [50]. For example, it was found by Coop et al. [7] that carbonate sands subjected to different vertical stresses may evolve towards to different ultimate PSDs during ring shear tests. For the sake of simplicity, D_u is taken as 2.5–2.6 for sands and 2.7 for gravel materials in several studies [7, 48, 49, 56].

2.2 Quantification of particle breakage

An appropriate constitutive model of granular soils needs to consider the evolution of PSD during stress path, which means the PSD should be treated as a variable in a constitutive model [10, 32, 58]. In that case, it is necessary to adopt a simple variable that can represent the PSD and measure the degree of particle breakage of a sample, preferably within the range of 0 to 1. Inspired by the work of Einav [10], a new breakage index B_λ is proposed in this paper, given by

$$B_{\lambda } = \frac{{\lambda_{pi} - \lambda_{pc} }}{{\lambda_{pi} - \lambda_{pu} }}$$

(2)

with

$$\lambda_{p} = \frac{{d_{63.2} }}{{d_{\max } - d_{63.2} }}$$

(3)

where d_63.2 is the characteristic particle diameter at which 63.2% of the sample by mass is smaller, λ_p is a scale parameter controlling the extent of breakage as proposed by Zhang et al. [58] and Tong et al. [41]. It was also verified by Tong et al. [43], who carried out a series of ring shear and compression tests on dry and saturated carbonate sands and found a good linear relationship between λ_p and Einav’s breakage index B_r^* [10], which is widely adopted for descripting the extent of particle breakage in the literature. As shown in Eq. (2), λ_pi, λ_pu, λ_pc are the initial, ultimate, and current values of λ_p, respectively. All the values of λ_p can be calculated by using Eq. (3) when knowing the corresponding value of d_63.2, as shown in Fig. 2.

Fig. 2

Definition of the breakage index B_λ in terms of d_63.2

The value of B_λ ranges from 0 (no breakage) to 1 (full breakage) as the PSD evolves from the initial state to the ultimate state. The ultimate PSD, is considered to be fractal-graded in this paper as expressed in Eq. (1). It should be noted that different ultimate PSDs will lead to different values of the newly proposed breakage index B_λ, which might affect the relationship between B_λ and plastic work as shown in Eq. (5) and also induce different critical state lines as expressed in Eq. (10). However, such a change in the breakage index will most likely affect the values of parameters a and b in Eqs. (5) and (10), and is outside the scope of this study.

2.3 Evolution of particle breakage

The evolution of particle breakage has been extensively studied, such as from mathematical modelling aspect [4, 34, 42, 58], and from constitutive modelling aspect [9, 10, 13, 14, 19]. The former can describe the evolution of the whole PSD more accurately, while the latter is more constitutive-modelling friendly.

A large number of tests have indicated that particle breakage is affected by both stress and strain [7, 43]. Breakage indices are often correlated to energy quantities which are combinations of stress and strain. There is not much difference when using total input work and plastic work because the amount of elastic work is often several orders of magnitude smaller than that of plastic work in many cases, such as in ring shear test [43], impact test [48], triaxial test with considerable particle breakage [19]. However, the accumulation of particle breakage during cyclic loading cannot be predicted when using total input work. In general, correlating plastic work with particle breakage indices provides a unified and flexible approach when considering particle breakage in constitutive models subjected to both monotonic and cyclic loading [9, 14, 46]. The plastic work $W^{p}$ in a conventional triaxial test can be expressed as suggested by Hu et al. [14]

$$W^{p} = \int {\left\langle {\sigma_{ij} d\varepsilon_{{_{ij} }}^{p} } \right\rangle } = \int {\left\langle {pd\varepsilon_{v}^{p} + qd\varepsilon_{s}^{p} } \right\rangle }$$

(4)

where the symbol is the Macaulay’s brackets (i.e., $\left\langle x \right\rangle = x$, if x ≥ 0; $\left\langle x \right\rangle = 0$, if x < 0). The relationship between the plastic work and breakage index can be described by a unified hyperbolic function, regardless of the initial density or stress path. For example, Hu et al. [14] showed that both B_r^* and B_u (defined as relative uniformity) could be hyperbolically related to the plastic work by extensive experimental results of different granular soils. Similarly, the relationship between B_λ and $W^{p}$ can be given as

$$B_{\lambda } = \frac{{W^{p} }}{{b \times p_{r} + W^{p} }}$$

(5)

where b is a parameter controlling the evolution rate of PSD, p_r is the unit pressure (= 1 kPa) for ensuring the dimensionally consistency. Again, B_λ ranges from 0 (no plastic work) to 1 (infinite plastic work).

3 Changing CSL due to particle breakage

3.1 Nolinear CSL and ICLs

Strictly speaking, the ICL of a granular soil is not unique, and highly depends on its initial void ratio. Those ICLs will eventually converge into a unique line referred to as the Limit Compression Line (LCL) [35], which can be expressed as a perfect straight line in the space of logarithm of void ratio versus logarithm of mean effective stress

$$\ln (e_{LCL} ) = \ln (N) - \lambda \ln (p/p_{r} )$$

(6)

where $e_{{{\text{LCL}}}}$ is the void ratio on the LCL, N is the void ratio on the LCL when p = 1 kPa, λ is the slope of LCL in the ln(e)—ln(p) space. To model the nonlinear CSL and ICLs as observed by many laboratory studies [44, 52, 57], and to avoid the negative void ratio at high stresses, a family of the Isotropic Compression Lines (ICLs) can be given by adding one parameter in the Eq. (6) as proposed by Sheng et al. [38]

$$\ln (e_{ICL} ) = \ln (N) - \lambda \ln \left[ {\left( {p + p_{ICL} } \right)/p_{r} } \right]$$

(7)

where $e_{{{\text{ICL}}}}$ is the void ratio on the ICLs, $p_{{{\text{ICL}}}}$ is defined as a shifting stress controlling the curvature of the ICL, which depends on the initial void ratio of sample, i.e., a smaller initial void ratio leads to a larger $p_{{{\text{ICL}}}}$ value (as indicated by the balck dots in Fig. 3). It is also found that the ICLs are considered to be parallel to the CSL at high stresses [8, 38]. A similar form of CSL with Eq. (7) is also defined by Sheng et al. [38], which takes the form

$$\ln (e_{CSL} ) = \ln (\Gamma ) - \lambda \ln \left[ {\left( {p + p_{CSL} } \right)/p_{r} } \right]$$

(8)

where $e_{{{\text{CSL}}}}$ is the void ratio on the CSL, Г is the void ratio on the CSL when p + $p_{{{\text{CSL}}}}$ = 1 kPa, $p_{{{\text{CSL}}}}$ is defined as a shifting stress controlling the curvature of the CSL.

Fig. 3

Illustration of ICLs, CSL, and LCL with parameters of N = 5, λ = 0.25, Г = 4, e_CSL = 0.9 at p = 10 kPa

3.2 Evolution of CSL due to particle breakage

The CSL in the p—q space can be represented by a straight line and is assumed to be independent of particle breakage in this paper, which is consistent with most studies as discussed previously

$$M = \frac{{q_{{{\text{CS}}}} }}{{p_{{{\text{CS}}}} }} = \frac{{6\sin \phi_{{{\text{CS}}}} }}{{3 - \sin \phi_{{{\text{CS}}}} }}$$

(9)

where M is the critical state stress ratio, and $\phi_{{{\text{CS}}}}$ is the critical state friction angle.

The CSL in the e—ln(p) space, however, will be significantly affected by particle breakage in a complicated way. The constitutive framework developed based on the assumption of parallel shifting of CSL in the e—ln(p) space is considered as an effective approach for modelling particle breakage of granular soils [32]. However, such an approach suffers from limitation at a high stress level as introduced before.

Typical experimental and numerical results show that the CSL shifts downwards with increasing degree of particle breakage under a relatively low stress level [1, 12, 33, 57]. It should be noted that it is not possible to explore the effect of PSD on the CSL at a high stress level because of the evolving PSD at such high stresses. Realising that experimental results tend to show a steady-ultimate state of particle breakage, a new evolution law of CSL will be adopted in this paper according to the assumption that the CSLs of samples with various degrees of particle breakage will eventually converge to steady-state at a high stress level where particle breakage completes and is no longer the main mechanism for soil deformation as indicated by Fig. 4, which is supported by the experimental observations as shown in Fig. 1(b). As shown in Fig. 4, the proposed evolution of CSL moves downwards with decreasing slope of CSL at the same mean effective stress (not high stress level) as particle breakage progresses. This assumption is reasonable and in consistent with the experimental results by Bandini and Coop [1] and Xiao et al. [47], who found that particle breakage will not only result in a downward shift, but also a rotation of the CSL in the e—ln(p) space.

Fig. 4

Evolution of CSL for granular soils with parameters of N = 5, λ = 0.25, Г = 4, $e_{{\text{CS,ref}}} = e_{{{\text{CSL}}}}$ = 0.9 at p = 10 kPa, and a = 0.3

To quantify the evolution of the CSL, we propose the following simple relation between the intercept of CSL (value of $e_{{{\text{CS0}}}}$ at p = 0) and the newly proposed breakage index B_λ

$$e_{{{\text{CS0}}}} = e_{{\text{CS,ref}}} \exp \left( { - aB_{\uplambda } } \right)$$

(10)

where $e_{{\text{CS,ref}}}$ is the intercept of the CSL without particle breakage (B_λ = 0), a is a parameter that controls the rate of the CSL movement caused by particle breakage.

The LCL as shown in Fig. 4 will not change as it is an asymptotic line of the ICLs at high stresses, which is similar with the observations by McDowell, who found the compression index (C_c = (-∆e)/∆log (σ´_´v)) is independent of the initial PSD [29] and the slope of LCL in the log (e)-log (p) space depends on the ultimate fractal dimension, but is independent of the initial PSD [30]. In this case, the parameter N and λ of the LCL as shown in the Eq. (6) are then independent of breakage index B_λ.

4 Effect of particle breakage on the state-dependent behavior

4.1 Limitation of the state parameter

The commonly-used state parameter proposed by Been and Jefferies [2] provides a normalised description of granular soils at various mean effective stresses and densities, and has been successfully used in modelling the state-dependent behaviour of many granunlar soils in the literature, such as sand [11, 16, 17, 21, 27], ballast [3, 39], and rockfill materials [24,25,26, 49, 56]. However, such a state parameter is not able to capture the effect of particle breakage. For example, assuming that a soil sample is initially consolidated to point A (as shown in Fig. 5) with the mean effective stress less than that of the maximum curvature point of the ICL (point D as shown in Fig. 5), which means only limited particle breakage occurs at this stage. After that, the sample is sheared under undrained condition to point B where the flow liquefaction is observed because it is in the instable liquefaction zone. In that case, the sample reaches the liquefied state with almost no change in PSD. However, according to the definition of state parameter, the corresponding reference point at the CSL (point C as shown in Fig. 5) corresponds to a certain amount of breakage. Therefore, point C is not suitable for a reference point for point A when calculating the state parameter, because of the different PSDs. Such a limitation had also been stated by Ghafghazi et al. [12], and Javanmardi et al. [15].

Fig. 5

Illustration of the limitation of state parameter under undrained shearing

4.2 A new reference compression line

To describe the state-dependent behavior of the crushable soils, some new reference lines have been proposed to define the state parameter instead of the traditional CSL, such as the anisotropic compression line defined by Yao et al. [54, 55] and the reference line proposed by Javanmardi et al. [15]. Similarly, a Reference Compression Line (RCL) that intersects with the CSL at point of p = 0, $e = e_{{{\text{CS0}}}}$ and converges to the LCL at high stresses is adopted to further modify the state parameter in this paper. Substituting the point of p = 0, $e = e_{{{\text{CS0}}}}$ into Eq. (7) gives

$$p_{ICL} = \left( {\frac{N}{{e_{CS0} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}} p_{r}$$

(11)

The new RCL can be obtained by substituting Eq. (11) into Eq. (7), which is expressed as

$$\ln (e_{{{\text{RCL}}}} ) = \ln (N) - \lambda \ln \left[ {p + \left( {\tfrac{N}{{e_{{{\text{CS0}}}} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}} } \right]$$

(12)

where $e_{{{\text{RCL}}}}$ is the void ratio on the RCL.

According to Eq. (12), the new RCL needs three parameters: the void ratio on the LCL at p = 1 kPa, the slope of LCL in the ln(e)-ln(p) space, and the void ratio on the CSL at p = 0. It should be noted that the third parameter can be adopted as the void ratio on the CSL at a low mean effective stress if the critical state void ratio at p = 0 is not available. For example, as indicated in Fig. 6, the RCL obtained from Eq. (12) with $e_{{{\text{CS0}}}} = e_{{{\text{CSL}}}}$ at p = 10 kPa almost coincides with the CSL, with only some minor differences at low stresses.

Fig. 6

Definition of the new RCL

4.3 A modified state parameter considering particle breakage

The modified state parameter Ψ is then defined as the difference between the current void ratio and the void ratio on the RCL at the same mean effective stress, which can be written as

$$\Psi = e - e_{{{\text{RCL}}}} = e - \frac{N}{{\left[ {p + \left( {\tfrac{N}{{e_{{{\text{CS0}}}} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}} } \right]^{\lambda } }}$$

(13)

Since the RCL and CSL intersects at a very low mean effective stress (ideally at p = 0), the RCL of a soil sample will shift downwards subsequently at a low stress level with development of particle breakage. Again, all the RCLs of samples with various degrees of particle breakage will eventually converge to the LCL at a high stress level, as shown in Fig. 7.

Fig. 7

Evolution of RCL for granular soils with parameters of N = 5, λ = 0.25, Г = 4, $e_{{\text{CS,ref}}} = e_{{{\text{CSL}}}}$ = 0.9 at p = 10 kPa, and a = 0.3

5 Constitutive modelling

The total strain increment is calculated as the sum of the elastic strain increment and the plastic strain increment

$$d\varepsilon_{ij} = d\varepsilon_{ij}^{e} + d\varepsilon_{ij}^{p}$$

(14)

where the superscripts e and p represent the elastic and plastic, respectively.

5.1 Elastic strain increment

The elastic volumetric strain increment and the elastic deviatoric strain increment can be calculated as

$$\left\{ \begin{gathered} d\varepsilon_{v}^{e} = \frac{dp}{K} \hfill \\ d\varepsilon_{s}^{e} = \frac{dq}{{3G}} \hfill \\ \end{gathered} \right.$$

(15)

where the subscripts v and s represent volumetric and deviatoric component, respectively; K and G are the elastic bulk modulus and the elastic shear modulus, respectively, and are dependent on mean effective stress and void ratio. The nonlinear hypoelastic relation proposed by Richart et al. [36] is adopted for calculating the elastic shear modulus

$$G = G_{0} \frac{{\left( {2.97 - e} \right)^{2} }}{{\left( {1 + e} \right)}}\sqrt {p \times p_{r} }$$

(16)

where G₀ is a material constant. The elastic bulk modulus K can be determined by the Poisson's ratio µ

$$K = \frac{{2\left( {1 + \mu } \right)}}{3(1 - 2\mu )}G$$

(17)

5.2 Plastic strain increment

Since the main focus of this paper is on the evolution of CSL with increasing particle breakage, a simple yield surface that plastic deformation occurs whenever there is a change in stress ratio η (= q/p) proposed by Li and Dafalias [21] for the triaxial compression is therefore adopted. It is clear that the proposed model can be easily improved with a more appropriate yield surface, such as those used in modified Cam-Clay model [51, 54]. The yield surface is expressed as

$$f = q - \eta p = 0$$

(18)

The vector of the loading direction (n_fv, n_fs) is defined as

$$\left\{ \begin{gathered} n_{fv} = \frac{ - \eta }{{\sqrt {1 + \eta^{2} } }} \hfill \\ n_{fs} = \frac{1}{{\sqrt {1 + \eta^{2} } }} \hfill \\ \end{gathered} \right.$$

(19)

The plastic flow direction (n_gv, n_gs) is defined as

$$\left\{ \begin{gathered} n_{gv} = \frac{{d_{g} }}{{\sqrt {1 + d_{g}^{2} } }} \hfill \\ n_{gs} = \frac{1}{{\sqrt {1 + d_{g}^{2} } }} \hfill \\ \end{gathered} \right.$$

(20)

where d_g is the state-dependent dilatancy equation, which is written as

$$d_{g} = {{\frac{\partial g}{{\partial p}}} \mathord{\left/ {\vphantom {{\frac{\partial g}{{\partial p}}} {\frac{\partial g}{{\partial q}}}}} \right. \kern-\nulldelimiterspace} {\frac{\partial g}{{\partial q}}}} = d_{0} \left( {\exp (m\psi ) - \frac{\eta }{M}} \right)$$

(21)

in which g is the plastic potential function, d₀ and m are two positive material constants. Therefore, the non-associated flow rule is adopted in this paper. The plastic strain increment can be written as

$$\left\{ \begin{gathered} d\varepsilon_{v}^{p} = \frac{{n_{fv} n_{gv} }}{{H_{p} }}dp + \frac{{n_{fs} n_{gv} }}{{H_{p} }}dq \hfill \\ d\varepsilon_{s}^{p} = \frac{{n_{fv} n_{gs} }}{{H_{p} }}dp + \frac{{n_{fs} n_{gs} }}{{H_{p} }}dq \hfill \\ \end{gathered} \right.$$

(22)

where H_p is the plastic modulus. The expression of H_p should satisfy the three conditions as suggested by Li and Dafalias [21], i.e., (1) H_p =  + ∞ at η = 0, (2) H_p = 0 at the critical state, and (3) H_p = 0 at the drained peak stress ratio. A new form of H_p is therefore adopted in this paper, which is written as

$$H_{p} = H_{0} G\frac{{M_{p}^{2} - \eta^{2} }}{\eta }\left( {\left| {M - \eta } \right|} \right)^{0.1}$$

(23)

where H₀ is a model constant; M_p is the virtual peak stress ratio, which is given as

$$M_{p} = Me^{{\left[ {n\left\langle { - \Psi } \right\rangle } \right]}}$$

(24)

where n is a material constant. As indicated by Eq. (24), when the sample is at a loose state (-Ψ < 0), we have M_p = M (i.e., hardening); when the sample is at a dense state (-Ψ > 0), we have M_p > M (i.e., softening).

5.3 Stress–strain relationship

As can be obtained from Eq. (15) and Eq. (22), the stress–strain relations in the p-q space can be finally written as

$$\left( {\begin{array}{*{20}c} {d\varepsilon_{v} } \\ {d\varepsilon_{s} } \\ \end{array} } \right) = \left[ {\begin{array}{*{20}c} {\frac{1}{K} + \frac{{n_{fv} n_{gv} }}{{H_{p} }}} & {\frac{{n_{fs} n_{gv} }}{{H_{p} }}} \\ {\frac{{n_{fv} n_{gs} }}{{H_{p} }}} & {\frac{1}{3G} + \frac{{n_{fs} n_{gs} }}{{H_{p} }}} \\ \end{array} } \right]\left( {\begin{array}{*{20}c} {dp} \\ {dq} \\ \end{array} } \right)$$

(25)

6 Model calibration and validation

6.1 Model calibration

The proposed model has 12 model parameters, which can be obtained as described in the following section:

(1) Four CSL, ICLs &LCL related parameters: M, N, λ, and $e_{{\text{CS,ref}}}$.

These four parameters can be obtained by best fitting of the proposed equations of CSL, ICLs, and LCL with knowing experimental data of isotropic compression and triaxial tests. The critical state void ratio M can be measured as the slope of CSL in the p-q space by Eq. (9), and parameter λ and $e_{{\text{CS,ref}}}$ can be determined by Eq. (8). The parameter N can be obtained by conducting one isotropic compression test at any initial void ratio via Eq. (7).

(2) Two elastic parameters: G₀, and µ.

G₀ can be calculated from Eqs. (15)-(16) with ε_s—q plot, which can be rewritten as

$$G_{0} = \frac{dq}{{3d\varepsilon_{s}^{e} }}\frac{{\left( {1 + e_{0} } \right)}}{{\left( {2.97 - e_{0} } \right)^{2} \sqrt {p \times p_{r} } }}$$

(26)

where e₀ is the initial void ratio of sample, $\frac{dq}{{d\varepsilon_{s}^{e} }}$ can be estimated by the slope of ε_s—q plot at small shear strain of approximately 1%. The Poisson's ratio µ can be obtained based on Eqs. (15)-(17) from ε_s—q plot and ε_v—p plot at initial stage

$$\mu = \frac{{9\frac{dp}{{d\varepsilon_{v}^{e} }} - 2\frac{dq}{{d\varepsilon_{s}^{e} }}}}{{18\frac{dp}{{d\varepsilon_{v}^{e} }} + 2\frac{dq}{{d\varepsilon_{s}^{e} }}}}$$

(27)

with $\frac{dp}{{d\varepsilon_{v}^{e} }}$ estimated by the slope of ε_v—p plot at small volumetric strain of approximately 1%.

(3) Two particle breakage related parameters: a, and b.

The determination of the dynamic movement of CSL in the e—ln (p) space is problematic. As proposed before, the critical state void ratio at low stress level $e_{{{\text{CS0}}}}$ will change with various degree of particle breakage with evolution law by Eq. (10). Thus, value of $e_{{{\text{CS0}}}}$ of a given B_λ will be obtained by triaxial tests with low confining pressure, at which particle breakage is ignorable. The parameter b can be obtained by conducting a series of triaxial tests with different initial confining pressures. The input plastic work can be calculated by Eq. (5), and the PSD at the end of each test can be determined by sieving analysis tests.

(4) Two dilatancy parameters: d₀, and m.

The parameter m can be determined when the sample is at phase transformation state where the dilatancy equation equals to zero. By setting d_g = 0 in Eq. (21), parameter m can be expressed as

$$m = \frac{{\ln \left( {\frac{{\eta_{PTS} }}{M}} \right)}}{{\Psi_{PTS} }}$$

(28)

where η_PTS and ψ_PTS are the stress ratio and modified state parameter at the phase transformation state. The parameter d₀ can be estimated by Eq. (21) and ε_s—ε_v plot, where dilatancy equation d_g can be rewritten as

$$d_{g} = d_{0} \left( {\exp \left( {m\psi } \right) - \frac{\eta }{M}} \right) = \frac{{d\varepsilon_{v}^{p} }}{{d\varepsilon_{s}^{p} }} \approx \frac{{d\varepsilon_{v} }}{{d\varepsilon_{s} }}$$

(29)

The parameter d₀ is determined by the slope of $\left( {\exp (m\Psi ) - \frac{\eta }{M}} \right) - \frac{{d\varepsilon_{v} }}{{d\varepsilon_{s} }}$ plot when the value of m is given.

(5) Two hardening parameters: H₀, and n.

The parameter n can be determined when the sample is at peak state by using Eq. (24)

$$n = \frac{{\ln \left( {\frac{{\eta_{PS} }}{M}} \right)}}{{\left\langle {\Psi_{PS} } \right\rangle }}$$

(30)

where $\eta_{PS}$ and $\Psi_{PS}$ are the stress ratio and modified state parameter at the peak state. The parameter H₀ can be determined by the drained triaxial test result based on Eqs. (16), and (19)-(24) with stress path of dq = 3dp, which can be expressed as

$$H_{0} = \frac{{\frac{dq}{{d\varepsilon_{s}^{p} }}\left( {3 - \eta } \right)\eta^{2} }}{{3\sqrt {1 + \eta^{2} } \sqrt {1 + d_{g}^{2} } G\left( {M_{p}^{2} - \eta^{2} } \right)\left( {M - \eta } \right)\left( {\left| {M - \eta } \right|} \right)^{0.1} }}$$

(31)

with $\frac{dq}{{d\varepsilon_{s}^{p} }} \approx \frac{dq}{{d\varepsilon_{s} }}$ by ignoring the small elastic deformations.

In summary, a set of drained and undrained triaxial tests with different initial conditions (enough for modelling CSL), sieving analysis tests after triaxial tests, and one isotropic compression test are needed for determining the abovementioned parameters of the proposed model in this paper.

6.2 Model validation

To validate the proposed model, two sets of experimental data of drained and undrained triaxial tests on granular soils in the literature were adopted, i.e., Cambria sand [20, 52], and Changhe rockfill [22, 23]. Furthermore, a constitutive model named as LB model [21, 32] is adopted in this paper for comparing with the proposed model. The main difference between the proposed model and LB model is the evolution of CSL with the development of particle breakage, where a parallel shifting of CSL is adopted in the LB model as proposed in the literature [14, 32]. In that case, a set of traxial tests with both drained and undrained triaxial stress path together with the sieving analysis tests are needed for obtaining the parameters for the LB model. All model parameters are calibrated as discussed above and list in Table 1, and the computational steps for integration along imposed stress path for drained and undrained triaxial conditions are given in Appendix 1 and 2, respectively.

Table 1 Model parameters of the three granular soils

6.2.1 Cambria sand

A series of drained and undrained triaxial tests on Cambria sand were conducted by Lade and Yamamuro [20, 52]. The sand tested, which was composed of two main mineral constituents (i.e., 54% quartz, and 39% lithic) was uniformly graded with particle sizes between 0.83 and 2 mm. All the samples were prepared with an initial void ratio of 0.52 before isotropic compression. The predicted CSL and ICL using Eqs. (7)-(8) are compared with the measured CSL and ICL as shown in Fig. 8. The RCL is then obtained by Eq. (12) with knowing the values of N, λ, and $e_{{\text{CS,ref}}}$($e_{{{\text{CS0}}}}$ at B_λ = 0). It is shown from Fig. 8 that the proposed functions for CSL and ICL fit well with the measured results. Figure 9 shows the calibration of breakage parameters for the Cambria sand. The ultimate fractal dimension of Cambria sand for calculating the relative PSD index B_λ is adopted as 2.6. A good agreement is obtained by using Eq. (5) with material constant b = 5408 and Eq. (10) with material constant a = 1.30. That the values of $e_{{{\text{CS0}}}}$ at various degrees of particle breakage are adopted from the back analysis conducted by Hu et al. [14].

Fig. 8

Measured and predicted CSL, ICL and proposed RCL of Cambria sand. The square points represent the initial states of sample before undrained shearing (or, after isotropic compression), the diamond points represent the initial states before drained shearing

Fig. 9

Calibration of breakage parameters: a relative PSD index B_λ versus plastic work, b $e_{{{\text{CS0}}}}$ versus relative PSD index B_λ

Figure 10 show the comparison between the measured and the predicted results of drained shearing tests with confining pressure varying between 15.0 MPa and 52.0 MPa, wherein the solid lines represent the predicted results by the proposed model, the dotted lines the predicted results by the LB model, and the dots the experimental results. The initial void ratios after isotropic compression at different confining pressures can be determined by the ICL (shown as the diamond points in Fig. 8). The volumetric strain, however, decreases with increasing confining pressure when it is larger than 17.2 MPa, as shown in the experimental data in Fig. 10. Such behavior is expected for crushable materials because more input work for the samples will be obtained after isotropic compression at larger confining pressure, which will lead to a larger breakage index (as indicated by Eq. (5)) for the sample before the shearing stage. As proposed before, a larger breakage index will also lead to a lower initial position of CSL and RCL in the e—ln(p) space, which means samples after isotropic compression at large confining pressure might be in a ‘loose’ state, while samples after isotropic compression at low confining pressure might be in a ‘dense’ state. The present model can describe such behavior as shown in Fig. 10 that less volumetric contraction during shearing for the sample after isotropic compression at 52 MPa is observed than that of 40 MPa. However, the LB model fails to capture such behavior as indicated in Fig. 10. It is clear that the proposed model performs significantly better than that of LB model in describing the main response of drained tests within a wide range of confining pressures.

Fig. 10

Measured and predicted drained shearing results of Cambria sand with confining pressure varying between 15.0 MPa and 52.0 MPa: a deviatoric stress; and b volumetric strain relations

Figure 11 shows the comparison between the measured and the predicted results of undrained shearing tests with confining pressure varying between 6.4 MPa and 68.9 MPa. Again, the initial void ratios after isotropic compression at different confining pressure can be determined by the ICL (shown as the square points in Fig. 8). As shown in Fig. 11, the proposed model can predict the stress–strain relations and the pore water pressure relations of Cambria sand during undrained shearing with satisfactory accuracy, although is less successful than that of LB model, especially when the major principal strain is less than 10% and the confining pressure is larger than 16.7 MPa.

Fig. 11

Measured and predicted undrained shearing results of Cambria sand with confining pressure varying between 6.4 MPa and 68.9 MPa: a deviatoric stress; and b pore water pressure relations

6.2.2 Changhe rockfill

Liu et al. [22, 23] conducted a series of drained and undrained triaxial compression tests on a rockfill material from Changhe dam with confining pressure ranging from 400 to 4000 kPa. The grains tested were hard diorite with maximum particle size of 60 mm. In Fig. 12, Eq. (7) is used to model the ICL and Eq. (8) is used to model the CSL of Changhe rockfill. The RCL is then determined with knowing parameters N, λ, and $e_{{\text{CS,ref}}}$($e_{{{\text{CS0}}}}$ at B_λ = 0) by using Eq. (12). The agreement between the measured and the predicted results of ICL and CSL is relatively good. The ultimate fractal dimension of Changhe rockfill is adopted as 2.7 when calculating the breakage index B_λ. The breakage parameter b = 1055 is adopted by using Eq. (5) as presented in Fig. (9). Another breakage parameter a, however, cannot be determined directly because of the insufficient experimental data. It can be obtained by best fitting of the stress and strain response under drained and undrained compression.

Fig. 12

Measured and predicted CSL, ICL and proposed RCL of Changhe rockfill

Figure 13 and Fig. 14 show the comparison between the measured and the predicted results of drained and undrained triaxial compression with confining pressure varying between 400 and 4000 kPa, respectively. It is observed from Fig. 13 that the proposed model performs better under low confining pressure; while the LB model performs better under high confining pressure. In general, the proposed model can well capture the stress and strain response of Changhe rockfill subjected to drained shearing, i.e., the strain softening and dilatant behavior are observed at a low confining pressure, while the strain hardening and volumetric contraction behavior become more obvious as the confining pressure increases.

Fig. 13

Measured and predicted drained shearing results of Changhe rockfill with confining pressure varying between 400 and 4000 kPa: a deviatoric stress; and b volumetric strain relations

Fig. 14

Measured and predicted undrained shearing results of Changhe rockfill with confining pressure varying between 400 and 4000 kPa: a deviatoric stress; and b pore water pressure relations

Figure 14 shows the comparison between the measured and the predicted stress–strain and pore-pressure behavior of Changhe rockfill during undrained shearing. The proposed model predicts obviously better values of deviatoric stress than that of the LB model at high confining pressure. The prediction of pore water pressure as shown in Fig. 14(b) is better matched with the experimental results when the confining pressure is low. The pore water pressure is underestimated when the confining pressure is high, especially when the axial strain is less than 5%, and it can be better captured as the axial strain increases for both the proposed model and LB model. In general, the proposed model performs much better than the LB model in modelling the undrained shearing behavior of rockfill material.

Overall, the proposed model seems to be able to capture the main features in granular soils behavior during isotropic compression and drained and undrained shearing processes within a wide range of confining pressures. The LB model, which is developed based on the assumption of parallel shifting of CSL induced by particle breakage, is less successful than the proposed model, especially for the drained shearing for the Cambria sand and undrained shearing for Changhe rockfill.

7 Conclusion marks

Particle breakage will greatly change the PSD of granular soils, and thus significantly affect their stress–strain behaviour. To tackle the problem of particle breakage, it is of great interest to quantify the PSD in a simple manner, to establish the correlation between the PSD quantification and the mechanical parameters, and finally to capture the effects of PSD on the soil mechanical properties. In this study, a simple constitutive model with consideration of the main properties of granular soils is developed within the framework of Li and Dafalias [21]. The proposed constitutive model highlights the influence of particle breakage on the critical state parameters (i.e., CSL) and the calculation of the well-known state parameter [2].

A typical approach for considering particle breakage is primarily based on the assumption that the CSL experiences parallel shifts as particle breakage progresses, which, however is not supported by experimental and numerical tests. To describe the effect of particle breakage on the location of the CSL, a simple yet reasonable evolution law is proposed that the initial position of CSL in the e—ln(p) space moves downwards with increasing particle breakage, but all the CSLs with various degrees of particle breakage will eventually converge at high stresses because of the steady-state of particle breakage.

A modified state parameter is defined as the difference between the current void ratio and void ratio on the RCL at the same mean effective stress. The RCL, which intersects with the CSL at p = 0, therefore evolves similarly with that of the CSL, i.e., shifts downwards from the initial position and converges eventually as particle breakage stops, while the LCL is independent of particle breakage.

The proposed model was compared with the LB model, which is developed based on the parallel shifting of CSL, and validated against experimental results of drained and undrained triaxial tests on Cambria sand and Changhe rockfill. It has been shown that the proposed model is superior to the LB model for most cases in capturing the nonlinearity of CSL, and state-dependent behaviour of granular soils.

Appendix A

1.1 Computational steps for integration under drained shearing

Step 1: The plastic work $W_{0}^{p}$ before shearing (or, after isotropic compression) can be calculated as

$$W_{0}^{p} = \int_{0}^{{\varepsilon_{v}^{p} }} {pd\varepsilon_{v}^{p} } \approx \int_{{e_{0} }}^{{e_{s0} }} {\frac{p(e)}{{1 + e_{0} }}de}$$

(32)

where e₀ is the void ratio before isotropic compression, e_s0 is the void ratio before shearing. For simplicity, the elastic volumetric strain is ignored since it is several orders of magnitude smaller than the plastic volumetric strain if the unloading stress path is not available.

Step 2: Setting the initial value of p = p_init, q_init = 0, η_init = (q_init/ p_init) = 0, calculating G_init, K_init, B_λinit, Ψ_init based on Eqs. (16), (17), (5) & (A1), and (13), respectively. Since H_p =  + ∞, when η = 0, a large value of H_pinit is adopted. Setting the increment of the axial strain Δε₁.

Step 3: The increment of radial strain Δε₃, and the increment of mean effective stress Δp can be determined by Eqs. (25) with the stress path in drained condition, i.e., Δq = 3Δp

$$\left\{ {\begin{array}{*{20}l} {\Delta \varepsilon _{3} = \frac{{2A + 6B - 3C - 9D}}{{2A + 6B + 6C + 18D}}\Delta \varepsilon _{1} } \hfill \\ {\Delta p = \frac{3}{{A + 3B + 3C + 9D}}\Delta \varepsilon _{1} } \hfill \\ \end{array} } \right.$$

(33)

with

$$\left\{ {\begin{array}{*{20}l} {A = \frac{1}{K} + \frac{{n_{{fv}} n_{{gv}} }}{{H_{p} }},B = \frac{{n_{{fs}} n_{{gv}} }}{{H_{p} }}} \hfill \\ {C = \frac{{n_{{fv}} n_{{gs}} }}{{H_{p} }},D = \frac{1}{{3G}} + \frac{{n_{{fs}} n_{{gs}} }}{{H_{p} }}} \hfill \\ \end{array} } \right.$$

(34)

Step 4: Updating the state variables, stress and strain qualities: p_i+1 = p_i + Δp_i, q_i+1 = q_i + 3Δp_i, η_i+1 = q_i+1 / p_i+1, $\varepsilon_{v,i + 1} = \varepsilon_{v,i} + \Delta \varepsilon_{1} + 2\Delta \varepsilon_{3,i} ,\varepsilon_{s,i + 1} = \varepsilon_{s,i} + {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}\left( {\Delta \varepsilon_{1} - 2\varepsilon_{3,i} } \right)$,$W_{i + 1}^{p} = W_{i}^{p} + \left\langle {\Delta W_{i}^{p} } \right\rangle$, $B_{{\lambda ,i + 1}} = f\left( {W_{{i + 1}}^{p} } \right),\Psi _{{i + 1}} = f\left( {p_{{i + 1}} ,B_{{\lambda ,i + 1}} } \right)$, $\Delta p_{i + 1} /\Delta \varepsilon_{3,i + 1} = f\left( {K_{i + 1} ,G_{i + 1} ,\eta_{i + 1} ,\Psi_{i + 1} } \right)\Delta \varepsilon_{1}$.

Step 5: Starting a new step with constant Δε₁.

1.2 Computational steps for integration under undrained shearing

Step 1: Calculating plastic work $W_{0}^{p}$ before shearing from Equation (A1).

Step 2: Setting the initial values with the same procedure with Step 2 in the drained stress path.

Step 3: Calculating the increment of radial strain Δε₃, and the increment of mean effective stress Δp, the increment of mean effective stress Δq from Eqs. (25) with the stress path in undrained condition, i.e., Δε_v = 0

$$\left\{ {\begin{array}{*{20}l} {\Delta \varepsilon _{3} = - \frac{1}{2}\Delta \varepsilon _{1} } \hfill \\ {\Delta p = - \frac{B}{{AD - BC}}\Delta \varepsilon _{1} } \hfill \\ {\Delta q = \frac{A}{{AD - BC}}\Delta \varepsilon _{1} .} \hfill \\ \end{array} } \right.$$

(35)

Step 4: Updating the state variables, stress and strain qualities: p_i+1 = p_i + Δp_i, q_i+1 = q_i + Δq_i, η_i+1 = q_i+1 / p_i+1, $W_{i + 1}^{p} = W_{i}^{p} + \left\langle {\Delta W_{i}^{p} } \right\rangle$, $B_{{\lambda ,i + 1}} = f\left( {W_{{i + 1}}^{p} } \right),\Psi _{{i + 1}} = f\left( {p_{{i + 1}} ,B_{{\lambda ,i + 1}} } \right)$, $\Delta p_{i + 1} /\Delta \varepsilon_{3,i + 1} =$$f\left( {K_{i + 1} ,G_{i + 1} ,\eta_{i + 1} ,\Psi_{i + 1} } \right)\Delta \varepsilon_{1}$, $p_{u,i + 1} = p_{0} + \frac{1}{3}q_{i + 1} - p_{i + 1}$ (where, p_u is the pore water pressure).

Step 5: Starting a new step with constant Δε₁.