Interpretation of cone penetration test in clay with smoothed particle finite element method

Abstract

Cone penetration test (CPT) is widely used to explore the in situ soil mechanical properties and the stratigraphy. The numerical simulation of CPT can help understand its mechanical process and link the testing data to soil properties. However, this task is challenging due to multiple (i.e., geometric, material and contact) nonlinearity of the problem. This study extends a large deformation numerical framework, smoothed particle finite element method (SPFEM), to address this problem. A finite element formulation for multibody frictional contact problems is incorporated to deal with the interaction between the steel cone and soil. An explicit stress point integration scheme with substepping is adopted to solve the elastoplastic constitutive equation of soil. The details of the novel numerical procedure are demonstrated. Using the developed approach, parametric studies are conducted for both undrained Tresca soil and fully drained modified Cam-Clay. The correctness and robustness of the proposed approach are validated. For the undrained Tresca soil, a linear relationship between the cone factor $N_{kt}$ and the natural logarithm of rigidity index $\mathrm {ln}(I_{r})$ is confirmed, and then, a new equation for the interpretation of soil undrained shear strength is proposed. For fully drained modified Cam-Clay, the effects of some model parameters and earth pressure coefficient at-rest $K_0$ on the drained cone factor are elucidated. Direct numerical simulation of CPT with SPFEM can provide an effective approach to determine some key parameters of the soil constitutive model and therefore improve the accuracy of numerical simulation for engineering applications.

1 Introduction

The cone penetration test (CPT) is a field-testing method used to explore in situ soil properties as well as the stratigraphy, which is essential in the design and construction of a wide range of geotechnical projects, such as foundation pits, slopes, tunnels, dams, roads and so on. In the CPT, cone penetrometer is pushed from the ground surface vertically downward at a constant speed, while the resistive forces are continuously measured and recorded. Due to the low cost, fast test process and continuous profiling data of the ground, CPT has become one of the most popular in situ testing methods.

Unlike laboratory tests in which the soil properties can be generally directly measured (e.g., [30, 31, 56, 57]), data from CPTs are usually indirect and require interpretation to obtain soil properties. In order to link the measured testing data from CPTs to soil properties, theoretical understandings of the mechanics of the cone penetration process are essential. Analytical approaches have been commonly adopted to address the problem with various assumptions and simplifications, such as limit equilibrium and slip-line analysis methods [10, 11, 18, 21, 23], cavity expansion theory [3, 9, 14, 15, 22, 39, 40, 45], strain path method [1, 2, 17, 19, 44, 47,48,49, 59]. However, rigorous analytical analyses of the CPT problem are extremely difficult because it is a complex mechanical process involving large deformation as the soil below the cone tip is pushed away by the cone during its advancement [25].

An alternative approach is resorting to numerical methods, which aims at simulating the real cone penetration process numerically. The numerical approaches can be further classified into two categories: indirect and direct models [37]. The former simulates cylindrical or spherical cavity expansion and then converts the limit cavity-expansion pressures to cone tip resistances using semi-empirical or mechanics-based analytical relationships (e.g., [45, 53]). The incorporation of these relationships increases the complexity and decreases the rigor. In contrast, direct models try to simulate the real cone penetration process in a direct way. However, it is numerically challenging due to large deformation around the cone. To date, direct simulation of CPT has been carried out based on some large deformation numerical frameworks, e.g., the remeshing and interpolation technique combined with small strain (RITSS) [28, 32, 33], the arbitrary Lagrangian Eulerian (ALE) algorithm [27, 37, 41, 52], the coupled Eulerian–Lagrangian (CEL) algorithm [38, 16] and the material point method (MPM) [5,6,7, 13]. The key underlying feature is the large deformation algorithm to deal with the mesh distortion encountered in the traditional FEM. Among these algorithms, the arbitrary Lagrangian Eulerian (ALE) might be the most popular [37].

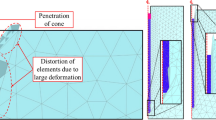
Particle finite element method (PFEM) [35, 61, 63–67] is another numerical frameworks to solve large deformation problems in geomechanics, which combines the arbitrary changes in geometry of the particle-based methods and the solid mathematical foundation of the traditional FEM. In PFEM, the nodes in FEM are treated as particles that carry all the field variables of the continuum medium and move freely in a Lagrangian way. The mesh distortion problem during large deformation is overcome by remeshing with the Delaunay triangulation technique. Recently, the PFEM has been successfully applied to the direct numerical simulation of CPT (e.g., [35, 64]).

In the original version of the PFEM [20], since all the field variables are carried by the particles (i.e., nodes) while the state variables (e.g., stresses, strains, etc.) are calculated at Gauss points as in the traditional FEM, it is necessary to transfer the information of these variables between particles and Gauss points frequently during the calculation, which inevitably introduces error and considerable complexity. In view of this, the authors proposed an improved version, termed as the smoothed particle finite element method (SPFEM) [62, 68, 69], in which a strain smoothing technique for nodal integration is incorporated into the PFEM. As all the field variables are calculated at particles in the SPFEM, frequent information transfer between particles and Gauss points can be avoided, which makes the PFEM more like a particle-based method. Meanwhile, due to the special strain smoothing technique, linear elements (i.e., 3-node triangular element) can be used directly without suffering from the volumetric locking, which greatly enhances the computational efficiency. Moreover, it has been found that severely distorted elements can be used with the strain smoothing technique [8, 26]. The insensitivity to element distortion is of especial significance for large deformation analysis.

In terms of the study of CPT based on direct numerical simulation, many large deformation numerical frameworks have been utilized (i.e., RITSS [30,31,, 32, 33], ALE [27, 37, 41, 52], CEL [38, 16], MPM [5,6,7, 13]). In comparison with these numerical frameworks, a distinct advantage of SPFEM is that all the field variables are calculated at particles and the mapping of field variables is avoided, which makes SPFEM attractive for the direct numerical simulation of CPT.

Aiming at carrying out a systematic direct numerical study on the CPT problem based on SPFEM, this study first extends it to axisymmetric cases. A finite element formulation for multibody frictional contact problems is incorporated to deal with the interaction between the steel cone and soil. An explicit stress integration scheme with substepping is adopted to solve the elastoplastic constitutive equation of soil, including the undrained Tresca soil and fully drained modified Cam-Clay. The details of the novel numerical procedure are demonstrated. The second aim of this study is to numerically investigate the cone penetration test in clay, through a detailed parametric study with the newly developed approach. After the performance of the proposed approach being validated by comparing with the results from physical tests and numerical methods in literature, the CPTs in undrained Tresca soil and fully drained modified Cam-Clay are investigated numerically. For the CPT in undrained Tresca soil, it is confirmed that there is a linear relationship between the cone factor $N_{kt}$ and the natural logarithm of rigidity index $\text {ln}(I_{r}$). Correspondingly, a new equation for the interpretation of soil undrained shear strength is proposed. For the CPT in fully drained modified Cam-Clay, the relationship between drained cone factor $N^{\prime }_{kt}$ and the modified Cam model parameters is studied as well.

2 Outline of smoothed particle finite element method

The basic idea of PFEM is that the continuum medium is described as a cloud of particles, and the mechanical equilibrium equation is solved with a standard FEM approach. All the information of the continuum medium (material properties, displacements, strains, stresses, internal variables, etc.) are carried by the particles, and they can move freely in an updated Lagrangian (UL) fashion. The particles correspond to the nodes in traditional FEM. In order to solve the equilibrium equation with a standard FEM approach, the Delaunay triangulation technique is firstly utilized to obtain a FEM mesh. In brief, the PFEM is actually a UL approach with frequent remeshing based on the Delaunay triangulation technique to overcome the mesh distortion problem.

For a typical calculation step, the primary procedures of PFEM are as follows [20]:

• 1. On the basis of a cloud of particles, the Delaunay triangulation technique is used to build the FEM mesh.

• 2. The alpha-shape approach [12, 20] is used to identify the entire problem domain.

• 3. Map the state variables (strain, stress, internal variables, etc.) from particles to Gauss points.

• 4. Solve the governing equations via a standard incremental FEM.

• 5. Map the state variables from the Gauss points to the particles.

• 6. Modify the positions of particles and transfer all the field information of particles to form a new cloud of particles.

• 7. Go back to Step 1 and repeat until the problem-dependent stop condition.

In the SPFEM developed by the authors, the main distinction lies in Step 4, the governing equations are solved by a FEM approach with a strain smoothing technique for nodal integration. The general advantages of incorporating this technique have been demonstrated by [8] and [26]. For the special case of SPFEM, another benefit is that due to the utilization of nodal integration, the mechanical equilibrium equations are solved on the nodes/particles, and thus, all the field variables are calculated directly on the particles. This benefit removes the need for Step 3 and Step 5 in the original PFEM. That is to say, frequent information transfer between Gauss points and nodes/particles, which inevitably introduces error and considerable complexity to the solution procedure, is avoided. In the SPFEM, a particle has a strain smoothing cell associated with it. When solving the governing equation, the mechanical equilibrium is actually achieved in these smoothing cells associated with particles. Therefore, the SPFEM seems more like a particle-based method in comparison with the original PFEM. Consequently, the primary procedures of SPFEM for a typical calculation step are summarized as follows (Fig. 1) [62, 68]:

• 1. On the basis of a cloud of particles, the Delaunay triangulation technique is used to build the FEM mesh.

• 2. The alpha-shape approach is used to identify the entire problem domain.

• 3. Solve the governing equations via an incremental FEM with a strain smoothing technique for nodal integration.

• 4. Modify the positions of particles and transfer all the field information of particles to form a new cloud of particles.

• 5. Go back to Step 1 and repeat until the problem-dependent stop condition.

Fig. 1

Typical step of SPFEM

Note that Step 3 and Step 5 in the original PFEM vanish, since the information transfer between Gauss points and nodes/particles is not required. Meanwhile, severely distorted elements can be used with the strain smoothing technique [26] which makes the SPFEM more adaptable for large deformation analysis.

The key procedure is Step 3, in which the whole problem domain is divided into finite smoothing cells associated with particles and a smoothing technique for nodal integration, is incorporated in the incremental FEM approach to solve the governing equations. As shown in Fig. 2, based on the Delaunay triangles, the smoothing cells are constructed by connecting sequentially the mid-edge points to the central points of the surrounding triangular elements of particles. The typical smoothing cells associated with a corner particle i, an edge particle j and an internal particle k are shown in Fig. 2a. The smoothing cell associated with particle k is enlarged and shown in Fig. 2b. By using a standard Galerkin procedure, the mechanical equilibrium equation can be discretized in space and the following equilibrium equation in matrix form can be obtained,

$$\begin{aligned} (\mathbf {K}_{\mathrm {ep}} + \mathbf {K}_{\mathrm {g}}) \Delta \mathbf {u} = \mathbf {F}^{\mathrm {ext}} \end{aligned}$$

(1)

where $\Delta \mathbf{u}$ is the incremental displacement vector, and $\mathbf{K} _{\text {ep}}$, $\mathbf{K} _{\text {g}}$ and $\mathbf{F} ^{\text {ext}}$ are, respectively, elastoplastic stiffness matrix, geometric stiffness matrix and external load vector.

Fig. 2

a Strain smoothing cells associated with particles and b strain smoothing cell with particle k

In this study, the SPFEM is first extended to the axisymmetric case to adapt it to the CPT problem. With the smoothing technique for nodal integration, the global elastoplastic stiffness matrix in Equation (1) is assembled by the following expression:

$$\begin{aligned} \mathbf {K}_{\mathrm {ep}} = \sum ^{N_{n}}_{k=1} \tilde{\mathbf {B}}^{(k)T}_{L} \mathbf {D}^{(k)}_{\mathrm {ep}} \tilde{\mathbf {B}}^{(k)}_{L} A^{(k)} r^{(k)} \end{aligned}$$

(2)

where $\tilde{\mathbf{B }}^{(k)}_{L}$ is the smoothed strain-displacement operator matrix, $\mathbf{D} ^{(k)}_{\mathrm {ep}}$ is the elastoplastic stress-strain matrix of particle k, $A^{(k)}$ is the area of the smoothing cell $\Omega ^{(k)}$ associated with particle k, $r^{(k)}$ is the radial coordinate value of particle k, and $N_{n}$ is the total number of nodes/particles in the problem domain. Note that unlike the traditional FEM, the global stiffness matrix is assembled node by node, which is a typical nodal integration approach.

The smoothed strain-displacement operator matrix $\tilde{\mathbf{B }}^{(k)}_{L}$ of particle k related to particle I is calculated by

$$\begin{aligned} \tilde{\mathbf {B}}^{(k)}_{L} = \left[ \begin{array}{cc} \tilde{b}_{Ir} &{} 0 \\ 0 &{} \tilde{b}_{Iz} \\ \tilde{b}_{Iz} &{} \tilde{b}_{Ir} \\ \frac{N_{I}}{r} &{} 0 \\ \end{array} \right] \end{aligned}$$

(3)

where $\tilde{b}_{Ir}$ and $\tilde{b}_{Iz}$ are, respectively, the smooth derivatives of shape function at r and z directions, and $N_{I}$ is the shape function related to particle I.

As the 3-node triangular element is adopted, the smoothed derivatives of shape function in matrix $\tilde{\mathbf{B }}^{(k)}_{L}$ can be calculated by

$$\begin{aligned} \tilde{b}_{Ih} = \frac{1}{A^{(k)}} \sum ^{N^{(k)}_{e}}_{j=1} \frac{1}{3} A^{j}_{e} N^{j}_{I,h} \end{aligned}$$

(4)

where $N^{(k)}_{e}$ is the number of elements around particle k, $A^{j}_{e}$ and $N^{j}_{I,h}$ are the area and derivative of shape function for the jth triangular element around particle k, h denotes the r and z directions, and $A^{(k)}$ is calculated by

$$\begin{aligned} A^{(k)} = \int _{\Omega ^{(k)}} d \Omega = \frac{1}{3} \sum ^{N^{(k)}_{e}}_{j=1} A^{j}_{e} \end{aligned}$$

(5)

From Equations (4), it can be seen that for the special case of a 3-node triangular element, the smoothed strain-displacement operator matrix $\tilde{\mathbf{B }}^{(k)}_{L}$ is the average of the strain-displacement operator matrix of the triangular elements around the particle weighted by area. The above computation procedure is relatively concise and efficient. Note that in the original PFEM, high-order elements (i.e., 6-node triangular elements) [65,66,67] or numerical stabilization methods [35, 36] are utilized to avoid volumetric locking and to obtain a reasonable solution.

In order to consider the material nonlinearity, the equilibrium equations are solved by the Newton–Raphson method to obtain particle incremental solutions for the current incremental loading step. Readers are suggested referring to [68] for more details about the SPFEM. Attention should be paid that the formulations in this study are slightly different from those in [68] because the axisymmetric case is considered here for the CPT problem.

3 Modeling CPT with SPFEM

3.1 Material constitutive models

In the numerical model, the cone is treated as an elastic material with Young’s modulus of 200 GPa and Poisson’s ratio of 0.3, while the soil is treated as an elastoplastic material. As only one phase is considered in the present study, two classes of problems can be analyzed. One is the fully undrained case in which the soil constitutive model is expressed in terms of total stress parameters, and the soil is saturated with no volume change. The other is the fully drained case in which the soil constitutive model is expressed in terms of effective stress parameters. As there is no change in pore fluid pressure, changes in effective and total stress are identical to each other.

In the fully undrained case, soil behavior is idealized by the Tresca model characterized by three parameters: Young’s modulus (E), Poisson’s ratio ($\nu$) and undrained shear strength ($s_{u}$). The Tresca model, originally developed for metal plasticity, assumes strength as a constant and stress-independent. Although it only offers a very simplified description of soil constitutive behavior, it can be applied for normally consolidated clay under undrained conditions since the undrained shear strength of soil remains almost constant throughout the loading process. Meanwhile, when the undrained condition is considered, the undrained Poisson’s ratio should equal to 0.5 to maintain zero volume change. In FEM simulation, the undrained Poisson’s ratio is generally set to be slightly less than 0.5 (e.g., 0.499) to maintain numerical stability. The Tresca model has been widely applied in the existing analytical and numerical studies of CPT (e.g., [2, 32, 33, 41, 47, 49, 59]), whose yield function is written as

$$\begin{aligned} {\sigma }_{1} - {\sigma }_{3} = 2{s}_{u} \end{aligned}$$

(6)

where $\sigma _{1}$ and $\sigma _{3}$ are respectively the first and third principal stress, and $s_{u}$ is the undrained shear strength of soil.

As the real shear strength of soil is not always a constant, a better and more popular constitutive model is the modified Cam-Clay (MCC) model. It can give a more reasonable description of soil constitutive behavior, especially for normally consolidated clay. The MCC yield function is written as

$$\begin{aligned} \frac{q^{2}}{p^{\prime 2}} + M^{2}(1-\frac{p^{\prime }_{0}}{p^{\prime }}) = 0 \end{aligned}$$

(7)

where q is the shear stress invariant, $p^{\prime }$ is the mean effective stress, M is the slope of the critical state line, and $p^{\prime }_{0}$ is the preconsolidation stress.

For modified Cam-Clay soils, the bulk modulus K is not a constant. It depends on mean stress $p^{\prime }$, specific volume v, and the slope of the unloading-reloading line $\kappa$, and it is calculated by

$$\begin{aligned} K = \frac{vp^{\prime }}{\kappa } \end{aligned}$$

(8)

In the fully drained case, the penetration velocity of CPT is assumed to be slow enough to fulfill the fully drained condition (i.e., the pore fluid pressure remains unchanged). A more realistic modeling should be coupled with stress and pore-pressure analysis, which can consider the effect of the penetration velocity. However, it is beyond the scope of the present study.

The material constitutive models are implemented in an incremental form for each particle. Additionally, the explicit integration algorithm with substepping [42, 43] is adopted.

3.2 Interaction between soil and cone

In order to model the interaction between soil and cone, a contact algorithm is required. In the SPFEM, as the solution strategy of the governing equations is similar to the FEM, the contact algorithm in FEM can be easily incorporated. The soil is generally treated as the slave body while the cone is treated as the master body, and both of them are flexible bodies in order not to lose generality. Correspondingly, a simple node to segment contact algorithm is employed.

As shown in Fig. 3, the interaction between soil and cone is considered via a type of contact constraint:

$$\begin{aligned} \begin{aligned} g_{n} \ge 0, \sigma _n \ge 0, \sigma _n g_{n}=0 \\ |\sigma _t|-\mu _{f} \sigma _n \le 0 \end{aligned} \end{aligned}$$

(9)

where $g_{n}$ is the gap between soil and cone, $\sigma _n$ is the contact pressure which is positive corresponding to compression, $\sigma _t$ is the tangential stress, and $\mu _{f}$ is the friction coefficient between soil and cone. If a fully rough condition is considered, the second equation of Equation (9) is neglected and a stick condition with zero-slip displacement is utilized.

Fig. 3

The contact between a deformable body and a rigid surface

The penalty regularization method in the traditional FEM is utilized to satisfy the frictional contact constraint. During the Newton–Raphson iteration process, when a contact pair between a soil particle and a cone segment is detected, the incremental discretization formulation of Equation (1) is modified as follows:

$$\begin{aligned} (\mathbf {K}_{\mathrm {ep}} + \mathbf {K}_{\mathrm {g}} + \mathbf {K}_{\mathrm {c}}) \Delta \mathbf {u}=\mathbf {F}^{\mathrm {ext}} + \mathbf {F}_{\mathrm {c}} \end{aligned}$$

(10)

where $\mathbf{K} _{\text {c}}$ is the penalty stiffness matrix and $\mathbf{F} _{\text {c}}$ is the contact force.

3.3 Set-up of numerical model

As the CPT is an essential axisymmetric problem, a 2D formulation is adopted. In CPTs, a standard cone with a cone angle of $60^{\circ }$ and a shaft cross section area of 10 $cm^{2}$ is generally used. A typical particle distribution and mesh used in this study is shown in Fig. 4. The model extends 20 cone radii to the radial boundary and 40 cone radii below the cone shoulder. These dimensions are proven to be sufficient to avoid boundary effect. The cone tip is initially embedded into the soil with a depth of 2 radii to maintain numerical stability.

Fig. 4

Particle distribution and initial mesh: a global view, b enlarged view near cone tip

A total of 1000 load steps are used to simulate the whole cone penetration process. The cone resistance is computed from the vertical reaction force along the tip surface divided by the cross section area of the shaft step by step, so that a curve of cone resistance versus the penetration depth can be obtained. The computed cone resistance achieves a steady-state value at a depth of approximately 10 cone radii for weightless soil. Hence, the total penetration depth is taken to be 20 cone radii in the simulations to get a steady-state cone resistance.

The computed cone resistance is affected by the size of the mesh, but converges to a specific value as the mesh is continuously refined. To determine a sufficiently refined mesh, seven meshes with different numbers of particles are used to simulate the cone penetration in undrained Tresca soil with Young’s modulus of E=1000 kPa, Poisson’s ratio of $\nu$=0.499 and undrained shear strength of $s_{u}$=10 kPa. The cone is assumed to be smooth. The overburden pressure on the soil surface $\sigma _{v0}$ and the in situ horizontal stress $\sigma _{h0}$ of soil are both set to be zero. The obtained cone resistances with different particle numbers are shown in Fig. 5. It can be seen that when 16341 particles are used, the result tends to converge. The steady-state cone resistance is only approximately 0.5$\%$ lower than the value when more particles are used (i.e., 25045 particles). Therefore, the mesh with 16341 particles is used in the following study.

Fig. 5

Cone factors versus number of particles

4 CPT in undrained Tresca soil

4.1 Justification of the use of cone factor

In undrained penetration, the cone resistance $q_{c}$ is commonly related to the undrained shear strength by way of a relation of the form [29, 60]

$$\begin{aligned} q_{c}=N_{kt}s_{u}+\sigma _{v0} \end{aligned}$$

(11)

where $\sigma _{v0}$ is the overburden pressure, $s_{u}$ is the undrained shear strength, and $N_{kt}$ is termed as cone factor. The cone factor $N_{kt}$ is usually assumed to be a function of the rigidity index $I_{r}$, the cone roughness $\alpha _c$ and the initial stress anisotropy $\Delta$ [28, 47, 49]. The rigidity index $I_{r}$ is calculated by $I_{r} = G/s_{u}$ where G is the soil shear modulus. The cone roughness $\alpha _c=0$ for fully smoothed cone and $\alpha _c=1$ for fully rough cone. The initial stress anisotropy $\Delta$ is calculated by $\Delta =(\sigma _{v0}-\sigma _{h0})/2s_u$.

Without considering the cone roughness and the initial stress anisotropy, the validity of Equation (11) implies that: (1) for the same soil (with the same $s_{u}$ and G), the net cone resistance ($q_{c}$-$\sigma _{v0}$) is constant and independent of the overburden pressure $\sigma _{v0}$; (2) when the shear modulus G and undrained shear strength $s_{u}$ change proportionally, the cone factor is constant because it is a function of the rigidity index $I_{r}$. A reliable numerical approach should reproduce the preceding implications [41].

Using the proposed approach, a series of CPTs in undrained Tresca soil are simulated. The cone is assumed to be fully smooth, and the initial stress is assumed to be isotropic (i.e., $\sigma _{v0}=\sigma _{h0}$). Figure 6 plots the cone factor variation with the penetration depth for different $\sigma _{v0}$. The obtained curves are almost identical to each other, indicating a constant value of cone factor. Figure 7 plots the cone factor variation for different undrained shear strengths $s_{u}$ with a constant rigidity index $I_{r}$.The obtained curves are again almost identical to each other. For all the curves, the cone factor converges to a value between 10.5 and 10.8. The outcomes from the above results are twofold. Firstly, the obtained values of cone factor agree well with the existing numerical results which are generally in the range of 10.2$\sim$11.5 [4, 38, 50, 51]. The proposed approach can thus be verified. Secondly, the validity of adopting the cone factor in Equation (11) can be confirmed by varying overburden pressure $\sigma _{v0}$ and undrained shear strength $s_{u}$ with a constant rigidity index $I_{r}$. Note that in the figures all the results shown are averaged out over a short period to remove oscillations.

Fig. 6

Cone factors versus overburden pressures

Fig. 7

Cone factors versus undrained shear strengths

4.2 Effect of rigidity index

The effect of rigidity index $I_r$ on cone factor $N_{kt}$ can be derived by conducting multiple numerical simulations of CPT with different soil parameters. For CPT in undrained Tresca soil, as Poisson’s ratio is approximately 0.5; there are only two parameters to characterize the soil behavior, the shear modulus G and undrained shear strength $s_{u}$. Therefore, this study conducts a total of 30 numerical simulations, with the shear modulus G ranging from 166.8 to 18000 kPa and the undrained shear strength $s_{u}$ ranging from 5 to 40 kPa. The cone is assumed to be fully smooth and the initial stress is assumed to be isotropic (i.e., $\sigma _{v0}=\sigma _{h0}$)

The obtained cone factors with different parameters are plotted in Fig. 8a. An obvious linear relationship between the cone factor $N_{kt}$ and the natural logarithm of rigidity index $\text {ln}(I_{r})$ is revealed. Linear regression shows the coefficient of determination $R^2$ is 0.92. The gradient and the intercept are, respectively, 0.91 and 8.01. Note that for different undrained shear strength $s_{u}$, this linear relationship remains almost identical, indicating that the linear relationship is independent of $s_{u}$. Consequently, for the CPT in undrained Tresca soil with fully smoothed cone and isotropic initial stress, a reliable correlation between the cone factor $N_{kt}$ and rigidity index $I_{r}$ can be proposed as

$$\begin{aligned} N_{kt}=0.91 \text {ln}(I_{r})+8.01 \end{aligned}$$

(12)

Fig. 8

Cone factors versus rigidity indices: a fully smooth cone case; b fully rough cone case

4.3 Effect of cone roughness

With the assumption of fully rough cone, the effect of rigidity index $I_r$ on the cone factor $N_{kt}$ is investigated again to consider the inevitable friction between the cone and soil and meanwhile to obtain a possible upper bound value of the cone factor. The other settings are the same with Sect. 4.2. Again, a linear relationship between the rigidity index $I_r$ and the cone factor $N_{kt}$ is found, as plotted in Fig. 8b. The gradient and the intercept are, respectively, 1.48 and 6.90, with a coefficient of determination $R^2$ of 0.95. Therefore, for the CPT in undrained Tresca soil with isotropic initial stress and fully rough cone, a reliable correlation between the cone factor $N_{kt}$ and the rigidity index $I_{r}$ can be proposed as

$$\begin{aligned} N_{kt}=1.48 \text {ln}(I_{r})+6.90 \end{aligned}$$

(13)

Note that the gradient with fully rough cone is higher than with smoothed cone. A similar finding has been reported by Walker and Yu [52].

4.4 Comparison against experimental data and existing solutions

There are generally two types of experimental data of CPT, field testing and laboratory calibration chamber testing. The field testing data are not suitable for the verification of theoretical predictions of cone resistance in clay because of several limitations, e.g., soil inhomogeneity, uncertainties regarding the magnitude of in situ stresses and the stress history of the deposit [24]. Moreover, it is extremely difficult and nearly impossible to obtain truly undisturbed samples from the field for determining reference soil parameters. Therefore, the results from the calibration chamber study carried out by Kurup et al. [24] are taken as references in this study. In their study, a total of 8 chamber tests were conducted on three isotropically consolidated specimens using two miniature cone penetrometers. The chamber size was large enough in comparison to the penetrometer size to avoid the potential size effect. The clay specimens were prepared by mixing kaolinite and fine sand with deionized water. The value of cone factor for each CPT was determined from the measured cone resistance, initial stresses applied on the soil specimen and the undrained shear strength and shear modulus measured by triaxial compression tests.

Comparison of experimental results and the correlation equations between the cone factor and the rigidity index proposed by this study is shown in Fig. 9. Note that in this figure, there are only 6 measured data points because 2 points are repeated in the 8 CPTs. Since many other researchers had studied this correlation equation by using direct large-deformation numerical simulations with different large-deformation numerical frameworks, it is of interest to compare the present result with these results. The comparison is also shown in Fig. 9. Theoretically, the cone factors measured in the laboratory calibration chamber tests should lie between the correlation equation with fully smooth cone assumption and that with fully rough cone assumption, because the miniature cone penetrometers used in the chamber tests are inevitably frictional. However, as can be seen in Fig. 9, the correlation equations obtained by direct numerical simulations are generally lower than the measured values, even for the fully rough cone cases. The underlying reason is difficult to analyze. Nevertheless, the correlation equations proposed in this study generally give larger estimations of cone factor than those equations obtained by other large-deformation numerical frameworks, i.e., the present results are closer to the measured results. The correlation equation obtained by ALE [41] is an exception, which even gives a prediction higher than the measured cone factor when the rigidity index $I_r$ is large. However, the other correlation equations obtained by ALE [27, 52] give predictions lower than the cone factor measured in the chamber tests and that predicted by the present approach.

Fig. 9

Comparison of the present equations against experimental results and other existing results: a fully smooth cone case, b fully rough cone case

Due to the complexity of direct numerical simulations of CPT, it is difficult to analyze the underlying reasons that cause the differences among these results. Nevertheless, a distinct advantage of SPFEM is that all the field variables are calculated at the particles and the mapping of field variables, which introduces both complexity and errors, is avoided. This makes SPFEM attractive in the direct numerical simulation of CPT in comparison with other large-deformation numerical frameworks. Moreover, from the perspective of reproducing experimental results, the correlation equations proposed in this study seem closer to the experimental results.

5 CPT in fully drained modified Cam-Clay

5.1 Justification of the use of cone factor

In drained conditions, the cone resistance $q_{c}$ often related to the effective overburden pressure $\sigma ^{\prime }_{v0}$ by the following equation [7, 58],

$$\begin{aligned} q_{c}=N^{\prime }_{kt}\sigma ^{\prime }_{v0} \end{aligned}$$

(14)

For sands, the cone resistance normally varies from 20 to 100 [29] in drained conditions. For clays, the cone resistance is found to be much lower than that in sands [7]. The validity of Equation (14) implies that for the CPT in a fully drained specific soil, the cone resistance is proportional to the effective overburden pressure $\sigma ^{\prime }_{v0}$.

To validate the use of Equation (14), a series of CPTs in fully drained soil treated by the MCC model are simulated, with the material parameters listed in Table 1. The effective overburden pressure $\sigma ^{\prime }_{v0}$ varies from 50 to 200 kPa. The earth pressure coefficient at-rest $K_0$ is 1.0. Except for the different constitutive models and parameters adopted, other aspects of the setup of numerical simulation are the same as those for CPT in Tresca soil. Figure 10 plots the cone factors variation with the penetration depth at different effective overburden pressure $\sigma ^{\prime }_{v0}$. Similar to the case of CPT in undrained Tresca soil, the obtained curves are almost identical to each other, indicating a constant value of the drained cone factor $N^{\prime }_{kt}$. The use of Equation (14) can thus be further verified. It should be pointed out that normally consolidated MCC soil is assumed throughout the study and the initial stress of soil is assumed to lie on the MCC yield surface.

Fig. 10

Cone factors versus varying effective overburden pressure

Table 1 Material parameters for MCC model

5.2 Validation of the present approach

5.2.1 Comparison against experimental result

In order to verify the capability of the present approach to simulate CPT in fully drained modified Cam-Clay, a centrifuge test of CPT in kaolin clay with detailed parameters is numerically simulated. Mahmoodzadeh and Randolph (2014) performed 23 centrifuge tests of CPT in a single sample, all at an acceleration of 110g [34]. Since some of the tests were repeated tests with good consistency observed, only the results of six tests were reported by them, with different penetration rate to ensure capturing the whole range of consolidation conditions, from undrained to (essentially) fully drained. Since only fully drained condition can be simulated by the present approach, the test with a penetration rate of 0.015 mm/s is simulated here. Although the centrifuge test with a penetration rate of 0.0045 mm/s is closer to the fully drained condition and thus is more suitable, the detailed penetration resistance data with such penetration rate were not reported.

In the centrifuge test, the miniature piezocone had a 10 mm diameter and a 60$^{\circ }$ tip angle. The sample was normally consolidated kaolin clay with detailed parameters, as shown in Table 2. The height of the sample was 230 mm. The resulting profile of effective vertical stress was estimated from unit weights based on the water contents measured at the end of the test, ranging from 0 to 160 kPa. In the numerical simulation, the basic settings are the same as those in the centrifuge test. Note that the depth scale in Ref. [34] is given at a prototype scale and is transferred to the model scale before numerical simulation. Some other settings which were not mentioned in Ref. [34] are as follows. The earth pressure coefficient at-rest $K_0$ is taken to be 0.68 [7]. The frictional coefficient between cone and soil is assumed to be 0.04 through parameter calibration. The numerical result of the variation of penetration resistance during the whole penetration process is compared with that measured in the centrifuge test, as shown in Fig. 11. It is clear that the present approach can basically reproduce the resistance during the penetration process. It should be pointed out that the discrepancy for the upper 80 mm penetration is due to the fact that in the centrifuge test the penetration rate in this range is higher than normal (i.e., 0.015 mm/s) to minimize the overall time cost [34], which may lead to higher excess pore pressure and the penetration resistance decreases as a result. Nevertheless, as soon as the penetration rate becomes normal, the variation of penetration resistance can be well captured by the present approach.

Fig. 11

Comparison between experimental result and numerical result obtained by SPFEM

Table 2 Material parameters used in the numerical simulation of the centrifuge test of CPT

5.2.2 Comparison against other numerical result

Ceccato et al. (2016) [7] simulated the CPT in kaolin clay with the material point method (MPM). The MCC model was adopted, and the parameters are listed in Table 1. The overburden pressure $\sigma ^{\prime }_{v0}$ was 50 kPa, and the earth pressure coefficient at-rest $K_0$ was 0.68. Since the two-phase analysis was conducted in their study, the results with the slowest penetration velocity, which corresponds to the fully-drained case, are used here as a benchmark to further verify the present approach.

Figure 12 gives the comparative results obtained by the MPM and the proposed approach. It is clear that the results obtained by the proposed approach are generally coincident with the results obtained by the MPM. After an increasing stage, the cone resistance achieved a stable stage when the penetration depth exceeds about 7 cone radii. The average cone resistance of the stable stage is about 196 kPa, which is close to 208 kPa obtained by the MPM. The cone resistance obtained by SPFEM is about 5.8% lower than that obtained by MPM. This may be due to the upper bound property of SPFEM [26, 68], i.e., the strain energy is always bigger than the exact solution and converges to it with the increase of nodes. Accordingly, the SPFEM models possess a softer stiffness than the exact solution, which would cause the reaction force obtained by the SPFEM is slightly lower than the exact solution. In contrast, traditional FEM as well as MPM possesses lower bound property. The mild discrepancy between the result obtained by SPFEM and that obtained by MPM can thus be explained.

Fig. 12

Comparison between results obtained by SPFEM and MPM

5.3 Effect of MCC model parameters on the cone factor

To study the effect of MCC model parameters on the cone factor, a series of CPTs are simulated with the present approach. Specifically, the slope of critical state line M, the slope of unloading-reloading line $\kappa$ and the slope of normal compression line $\lambda$ are investigated, respectively. The basic material parameters are listed in Table 1. The effective overburden pressure $\sigma ^{\prime }_{v0}$ is taken to be 100 kPa. The earth pressure coefficient at-rest $K_0$ is 1.0.

Figure 13 shows the variation of cone factor $N^{\prime }_{kt}$ against the slope of critical state line M. As expected, the cone factor $N^{\prime }_{kt}$ increases with the increase of M, and an obvious linear relationship between them is also found in both smooth and rough cases. For the smooth cone cases, linear regression shows the coefficient of determination $R^{2}$ is 0.998 for the curve of $N^{\prime }_{kt}$ against M; whereas linear regression shows the coefficient of determination $R^{2}$ is 0.997 in fully rough cone cases. It is clear that the cone factor for CPT in fully drained modified Cam-Clay increases linearly with M.

Fig. 13

Cone factors versus M

To evaluate the effect of $\kappa$ and $\lambda$ on the cone factor $N^{\prime }_{kt}$, either $\kappa$ or $\lambda$ is kept constant and the other is changed. As shown in Fig. 14, when $\kappa /\lambda$ varies from 0.1 to 0.3 with $\lambda$ = 0.205, the cone factor $N^{\prime }_{kt}$ varies from 4.33 to 3.71 for the smooth cone and ranges from 4.75 to 4.55 for the rough cone. The cone factor $N^{\prime }_{kt}$ generally decreases with the increase of $\kappa /\lambda$, indicating that a larger cone resistance is accompanied by a stiffer soil, which is consistent with that in the undrained case of Tresca soil. Meanwhile, when $\kappa /\lambda$ varies from 0.125 to 0.5 with $\kappa$ = 0.04, the cone factor $N^{\prime }_{kt}$ varies from 3.40 to 6.59 for the smooth cone and varies from 3.96 to 8.25 for the rough cone. The cone factor $N^{\prime }_{kt}$ increases with the increase of $\kappa /\lambda$. In the MCC model, higher $\lambda$ corresponds to lower plastic hardening rate. This may explain why lower $\kappa /\lambda$ corresponds to lower cone factor $N^{\prime }_{kt}$.

Fig. 14

Cone factors versus $\kappa /\lambda$

5.4 Effect of earth pressure coefficient at-rest on the cone factor

It is of interest to numerically investigate the effect of earth pressure coefficient at-rest, $K_{0}$, on the cone factor using the newly developed approach. In the parametric study, the earth pressure coefficient at-rest is taken to be 0.5, 0.75, 1.0, 1.25 and 1.5, respectively.

The numerical results are plotted in Fig. 15. Unlike the monotonic linear relationship of $\kappa$ and M, the relationship between $N^{\prime }_{kt}$ and $K_{0}$ shows a concave trend. When $K_{0}$ is set to be 0.75, the cone factor reaches a minimum. It may be interpreted from the viewpoint of the size of the initial plastic yield surface. Because normally consolidated MCC soil is assumed, the initial mean effective $p'_0$ and deviatoric stress $q_0$ lie on the initial yield surface. As the increase of $K_0$ from zero, the mean effective stress $p^{\prime }$ increases. Meanwhile, the shear stress invariant q decreases first and then increases as soon as $K_{0} >$ 1. Correspondingly, the size of initial plastic yield surface decreases first and then increases. Actually, for the specific case in this study, the size of initial plastic yield surface is the smallest for $K_0$=0.75, which helps explain the concave trend of the relationship between $N^{\prime }_{kt}$ and $K_0$. Similar findings on the effect of earth pressure coefficient at-rest on the cone factor have been reported by Ceccato et al. [5].

Fig. 15

Cone factors versus $K_{0}$

6 Conclusions

CPT is one of the most popular in situ test methods to explore soil properties as well as the stratigraphy. Direct large deformation numerical simulation of CPT can effectively help the interpretation of the test results. This paper extends the SPFEM, a large deformation numerical framework proposed by the authors, to solve the CPT problem numerically. Although the problem is strongly nonlinear, including material nonlinearity, geometric nonlinearity and contact nonlinearity, the proposed approach is validated to be precise and robust enough.

After careful verification of the proposed method, the CPT in undrained Tresca soil is investigated numerically using different parameters. The use of the cone factor expressed in terms of the rigidity index is further confirmed. New equations are proposed to quantitatively describe the relationship between the cone factor and the rigidity index for fully smoothed cone and fully rough cone. The equation is useful to determine the soil’s undrained shear strength in engineering scenarios.

Furthermore, the proposed method is validated to be applicable to more complex soil models (in particular, the MCC model). A series of numerical simulations of CPT in fully drained modified Cam-Clay are conducted to study the effect of model parameters on the fully drained cone factor. It is found that the cone factor for CPT in fully drained modified Cam-Cay increases linearly with M. The effect of the earth pressure coefficient at-rest $K_{0}$ is also investigated. With the increase of $K_{0}$ from 0.5 to 1.5, the cone factor first decreases and then increases.

Due to the complexity of the mechanical behavior of actual soil in engineering practice, the interpretation of CPT data with a simple theoretical or empirical equation seems a difficult task. Direct numerical simulation of CPT with a specific constitutive model (e.g., [46, 54, 55]) can deal with this difficult task effectively. With some key constitutive parameters of soil determined by direct numerical simulation of CPT, more reliable numerical simulation for engineering applications would be expected.