1 Introduction

During the design stage of a geotechnical structure, it is often of importance to predict the deformations caused by the construction processes, e.g. foundation settlements or horizontal displacements caused by a nearby excavation. Excessive deformations (e.g. differential settlements) have to be avoided in order to guarantee the serviceability of the existing structures. In case of complicated boundary conditions, as encountered at intra-urban sites with settlement-sensitive historical buildings or non-trivial soil profiles or ground water conditions, such prediction is frequently made by the finite element (FE) method. A reliable FE prediction demands, however, a realistic constitutive description of the soil, covering amongst others the increased stiffness at small strains and its strong degradation with increasing deformation [1, 7, 8, 20, 28, 29, 33, 34, 38, 41, 44,45,46,47, 50, 58, 60, 61, 65, 66, 71, 76, 77]. Numerical simulations usually require a good prediction for various ranges of strain. Therefore, the constitutive model must describe the strain-dependent stiffness very accurately.

The current study concentrates on the stiffness of sand at small strains (\(\varepsilon \le 2 \times 10^{-4}\)). The elastic stiffness at small strains is an essential component of each sound elastoplastic or hypoplastic constitutive model. In isothermal elastic models strain \(\varepsilon _{ij}\) is the only independent state variable, i.e. it dictates the internal energy. The energy change \(\Delta W = \int \sigma _{ij} \mathrm{d}\varepsilon _{ij}\) should be path independent, i.e. \(\Delta W\) must be a function of \(\Delta \varepsilon _{ij}\). Only the initial \(\varepsilon _{ij}(t_0)\) and the final strain \(\varepsilon _{ij}(t_1)\) are energetically of importance. The choice of the path \(\varepsilon _{ij}(t )\) between the end-points does not affect \(\Delta W\). Otherwise one could input less energy on one path \(1\rightarrow 2\) than it is recovered on another path \(2\rightarrow 1\). The gain of energy without change of state violates the 2nd law (perpetuum mobile of the second kind). The function \(W(\varepsilon _{ij})\) has the total differential \(\mathrm{d}W = ( {\partial W}/{\partial \varepsilon _{ij}} ) \mathrm{d}\varepsilon _{ij}\) for any \(\mathrm{d}\varepsilon _{ij}\). From the comparison with \(\mathrm{d}W = \sigma _{ij} \mathrm{d}\varepsilon _{ij}\) follows \(\sigma _{ij} = {\partial W}/{\partial \varepsilon _{ij}}\). Hence, stress \(\sigma _{ij}\) must also be a function of strain. The stiffness \(E_{ijkl} = {\partial \sigma _{ij}}/{\partial \varepsilon _{kl}}\) must be symmetric, \(E_{klij} = E_{ijkl}= {\partial \sigma _{ij}}/{\partial \varepsilon _{kl}} = {\partial ^2 W }/{\partial \varepsilon _{ij} \partial \varepsilon _{kl}}\). Note, however, that the symmetry \(E_{klij} = E_{ijkl}\) is only a necessary condition for a thermodynamically sound elastic law. Let \(E_{klij}( \varepsilon _{mn} )\) be given as a primary symmetric function, \(E_{klij} = E_{ijkl}\). This symmetry does not suffice for the existence of \(W(\varepsilon _{mn})\) because it has still to be shown that there exists a stress function \(\sigma _{ij}(\varepsilon _{ij})\). The integrability \(\int E_{ijkl} \mathrm{d}\varepsilon _{kl} = \sigma _{ij}\) to a function \(\sigma _{ij} (\varepsilon _{kl})\) requires additionally \({\partial E_{ijkl}}/{\partial \varepsilon _{rs}} = {\partial E_{ijrs}}/{\partial \varepsilon _{kl}}\). For example \(E_{ijkl} = -\varepsilon _{nn} (\lambda \delta _{ij} \delta _{kl} + 2 \mu I_{ijkl} )\) is symmetric but not hyperelastic.

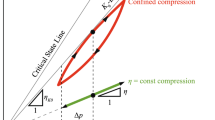
In order to derive and calibrate the elastic stiffness in a constitutive model, high-quality experimental data regarding the stress–strain relationship at small strains are indispensable. The present paper describes the experimental determination of the small-strain stiffness of fine sand. This stiffness can be represented in the form of so-called response envelopes. The polar presentation of stiffness by means of response envelopes [26, 43] is a well-established graphical tool in constitutive modelling. The concept is illustrated in Fig. 1. At a certain state of stress, strain increments of same length are applied in different directions. The resulting stress increments are plotted, constituting the stress response envelope. The isometric strain and stress invariants \(\varepsilon _P = \varepsilon _v/\sqrt{3}\), \(\varepsilon _Q = \sqrt{3/2} \varepsilon _q\) and \(P = \sqrt{3} p\), \(Q = \sqrt{2/3} q\) used on the axes in Fig. 1 are directly related to Roscoe’s invariants, i.e. volumetric strain \(\varepsilon _v = \varepsilon _1 + 2 \varepsilon _3\), deviatoric strain \(\varepsilon _q = 2/3 (\varepsilon _1 - \varepsilon _3)\), effective mean pressure \(p = (\sigma _1 + 2 \sigma _3)/3\) and deviatoric stress \(q = \sigma _1 - \sigma _3\). The isometric space is advantageous because distances and angles from the principal stress or strain coordinate system are preserved.

Fig. 1
figure 1

Concept of stress response envelopes

Full size image

Experimental studies on stress or strain response envelopes are rare in the literature, probably due to the large effort. Cohesive soils were tested by Lewin and Burland [43] (remoulded, saturated, powdered slate dust), Smith et al. [62] (undisturbed samples of Bothkennar clay), Constanzo et al. [9] (reconstituted, normally consolidated silty clay) and Finno and Cho [22] (undisturbed samples of Chicago glacial clays), while test results for granular soils were reported by Royis and Doanh [59] (dense Hostun sand) and Danne and Hettler [11, 12] (Karlsruhe fine sand). In most of these test series, each stress probe was applied to a fresh sample and the strain response envelopes were analysed. However, the measured deformations often contain plastic portions. The experimental stress or strain response envelopes then comprise both elastic and plastic components. In contrast, determining stress response envelopes for a purely elastic response of sand was the aim of the study presented in this paper. Examples for the inspection of the stiffness of various constitutive models by means of response envelopes can be found in [10, 14, 25, 27, 49, 53, 73].

Tests with strain amplitudes \(\varepsilon ^{\mathrm{ampl}}\le 2 \times 10^{-4}\) are technically not feasible in a standard triaxial device. The stiffness derived from such tests would be too strongly blurred by inaccuracies of the test device. At large strain amplitudes, however, various nonlinear effects as accumulation, hysteretic phenomena, pressure-dependence, etc., impede the calibration of small-strain models. Therefore, the current study uses local strain measurements at the triaxial samples, cycles with strain amplitudes \(\varepsilon ^{\mathrm{ampl}}\approx 2 \times 10^{-4}\) and a special analysis procedure to filter the stiffness for smaller strain probes (e.g. \(\Delta \varepsilon = 10^{-4}\)) from the experimental data.

2 Triaxial test device, local displacement transducers and sample preparation procedure

A scheme of the cyclic triaxial device used in the present study is shown in Fig. 2. Figure 3 presents a zoom of the upper part of this scheme, showing the test device prior to the mounting of the pressure cell, while a respective photograph is provided in Fig. 4.

Fig. 2
figure 2

Schematic drawing of the triaxial test device used for the current study

Full size image
Fig. 3
figure 3

Schematic drawing of the triaxial test sample equipped with LDTs

Full size image
Fig. 4
figure 4

Photograph of a sample equipped with LDTs

Full size image

Cube-shaped samples with dimensions \(90 \times 90 \times 180\) mm (width \(\times\) width \(\times\) height) have been tested. The local strain measurements have been realized by means of local displacement transducers (LDTs, strips of stainless steel equipped with strain gauges, similar to [24, 30]). Two lateral faces of the sample were each equipped with four LDTs (length 72 mm, width 8 mm, thickness 0.2 mm) for horizontal strain measurements, while two LDTs (length 124 mm, width 8 mm, thickness 0.2 mm) for axial strain measurements were placed on each of the remaining sides.

The use of cube-shaped samples is common in tests with LDTs [2, 3, 24, 30,31,32, 42], since the interpretation of the horizontal strains is much more straightforward than in case of cylindrical samples. For the measurement in the vertical direction cube-shaped and cylindrical samples are of course equivalent. A comparison of cube-shaped and cylindrical samples in another series of drained triaxial tests with vertical cyclic loading did not reveal significant differences in the results [67].

In the present test series the average and cyclic components of the axial loading were applied by means of a pneumatic cylinder located below the pressure cell (Fig. 2). The samples were tested in the dry condition, and the cell pressure was applied pneumatically without water in the cell, in order to guarantee the long-term stability of the LDT measurements. The cycles of lateral effective stress were applied by a sinusoidal oscillation of pore air pressure, while the cell pressure was kept constant in order to prevent temperature effects on the LDT measurements. A falsification of the measured LDT data by an oscillation of temperature in the cell had been observed in preliminary tests with a cyclic variation of cell pressure, due to the alternating compression and decompression of the air inside the cell (\(\Delta T \approx 6\) K measured with a temperature probe for cycles with load period 100 s, \(\Delta T \approx 2\) K for 1000 s, \(\Delta T \approx 0.1\) K with the new pore pressure control). Of course the tests have been performed in a laboratory with temperature control.

Beside the local strain measurements, a global measurement of axial deformation was also performed, using a displacement transducer attached to the load piston (Fig. 2). The system compliance was determined in preliminary tests on a steel dummy and subtracted from the measured values. The axial load was measured inside the pressure cell, at a load cell incorporated into the load piston and thus located directly below the bottom of the sample. Two pressure transducers were applied for monitoring cell and pore pressure. All measured data were recorded at a data acquisition system connected to a PC.

The self-made LDTs show an accuracy and resolution of < 0.01 mm and a negligible hysteresis. The laborious calibration is done by means a digital calliper (Fig. 5). In that calibration a controlled bending of the LDT is applied by means of a horizontal displacement of one end of the LDT. A typical relationship between the distance \(L_p\) of both ends of the LDT prescribed by the digital calliper and the electrical output voltage \(U_O\) related to the supply voltage \(U_S\) obtained from a calibration is shown in Fig. 6a. For the analysis of the test data these relationships between \(U_O/U_S\) and \(L_p\) have been approximated by a cosine function

$$\begin{aligned} L_m= & \, b \cos {\left[ a \left( U_O/U_S\right) + c\right] } + d \end{aligned}$$
(1)

with four constants a, b, c and d. The index \(\sqcup _m\) stands for “measured”. The quality of this approximation has been checked by evaluating the difference between the \(L_m\) value calculated from Eq. (1) with the measured \(U_O/U_S\) and the prescribed distance \(L_p\). The good fitting of Eq. (1) to the calibration data in Fig. 6a is confirmed by the very small hysteresis in the \(L_m - L_p\) data in Fig. 6b. Using Eq. (1), changes \(\Delta L_m\) of the distance and thus the strain occurring in the sand sample between both support points of the LDT can be derived from the changes in the electrical output voltage \(\Delta U_O\), while the supply voltage \(U_S = 2.5\,{\text {V}}\) is kept constant.

Fig. 5
figure 5

Calibration of an LDT by controlled application of a bending induced by horizontal displacement of one end of the LDT

Full size image
Fig. 6
figure 6

Typical result of a calibration of an LDT used for the local measurement of vertical strain: a measured and approximated relationship between the distance between both ends of the LDT and the ratio \(U_O/U_S\) of output and supply voltage (sequence 123 mm \(\rightarrow\) 119 mm \(\rightarrow\) 123 mm in steps of 0.1 mm); b difference between \(L_m\) obtained from Eq. (1) with the measured \(U_O/U_S\) and the prescribed distance \(L_p\) fulfills \(|L_m - L_p| < 0.01\,{\text {mm}}\)

Full size image

The uniform “Karlsruhe fine sand” (mean grain size \(d_{50} = 0.14\,{\text {mm}}\), uniformity coefficient \(C_u = d_{60}/d_{10} = 1.5\), minimum void ratio \(e_{\min } = 0.677\), maximum void ratio \(e_{\max }= 1.054\), grain density \(\varrho _{s} = 2.65\,{\text {g/cm}}^3\), subangular grain shape) has been used in the experiments. The preparation of the samples by means of dry air pluviation out of a funnel is shown in the photographs in Fig. 7. It requires a special mould consisting of several separate plates and special latex membranes with a circular cross section at the ends (for proper sealing using O-rings) and a square one in the middle (advantageous for the LDT measurements). In order to reduce end frictional effects each end plate was equipped with a layer of grease and a rubber disc. After the sample has been stabilized by means of a suction of 50 kPa, the mould can be removed and the hinges carrying the LDTs are glued to the membrane using a special positioning device (see fourth photograph in Fig. 7). The pressure cell is mounted after all LDTs have been placed in the corresponding hinges.

Fig. 7
figure 7

Sample preparation procedure. From left to right: Mounting of membrane; assembling of mould; pluviation of sand; mounting of hinges for LDTs; after mounting of pressure cell

Full size image

3 Testing program, procedure and results

Three samples with different initial relative densities \(I_{D0} = (e_{\max } - e)/(e_{\max } - e_{\min }) = 0.16\), 0.62 and 0.91 (measured at \(p = 50\,{\text {kPa}}\) and \(\eta = 0\)) have been tested, covering a range from very loose to very dense sand. On each sample the cyclic loading has been applied at several average stresses in succession. An average stress is described by its mean pressure \(p^{\mathrm{av}}\) and its deviatoric stress \(q^{\mathrm{av}}\) or by their ratio \(\eta ^{{\mathrm{av}}} = q^{{\mathrm{av}}}/p^{{\mathrm{av}}}\), respectively. After a loading or unloading of the sample to a certain average stress, the cyclic loading was directly started. During cyclic loading the stress components oscillate around the average values. Seven different average stress ratios \(\eta ^{{\mathrm{av}}}\) between 1.00 (triaxial compression) and \(- 0.40\) (triaxial extension) have been tested at each of the three different average mean pressures \(p^{{\mathrm{av}}} = 100\), 200 and 300 kPa, resulting in 21 combinations (\(p^{\mathrm{av}},\eta ^{\mathrm{av}}\)) as illustrated in Fig. 8. The loose sample was tested at four stress ratios only, i.e. the highest and the lowest stress ratios \(\eta ^{{\mathrm{av}}} = 1.00\) und − 0.40 were leaved out. The sequence of the tests is indicated by the black numbers in Fig. 8.

After preparation the sample stood under an isotropic state of stress with \(p = 50\,{\text {kPa}}\) and \(q = 0\). In a next step the deviatoric stress was increased to \(q = 50\,{\text {kPa}}\), keeping p constant. A stress ratio of \(\eta = q/p = 1.0\) was reached in that way. Finally, p and q were simultaneously increased along a path with \(\eta = 1.0\) until the first average stress \(p^{\mathrm{av}}= q^{\mathrm{av}}= 300\,{\text {kPa}}\) of the test was attained (point No. 1 in Fig. 8).

Fig. 8
figure 8

Tested average stresses illustrated in the p-q plane. The stress cycles applied in six different directions are exemplary shown at \(p^{\mathrm{av}}= 300\,{\text {kPa}}\) and \(\eta ^{\mathrm{av}}= 0.5\). CSL \(=\) critical state line (color figure online)

Full size image

Starting from a certain average stress (\(p^{\mathrm{av}}\),\(\eta ^{\mathrm{av}}\)), stress cycles were applied in six different directions (so-called polarizations P1–P6, see point 7 at \(p^{\mathrm{av}}= 300\,{\text {kPa}}\) and \(\eta ^{\mathrm{av}}= 0.5\) in Fig. 8), by choosing different amplitudes and phase shifts (\(0^\circ\) or \(180^\circ\)) of the sinusoidal signals of the effective axial and lateral stress. In the isometric P-Q plane the angles between the tested polarizations and the horizontal (parallel to P-axis) amounted \(\alpha _{PQ} = 0^\circ\) (purely isotropic stress cycles), \(30^\circ\), \(60^\circ\), \(90^\circ\) (purely deviatoric stress cycles), \(120^\circ\) and \(150^\circ\). Different stress amplitudes were necessary for the various \(\alpha _{PQ}\) to obtain almost similar strain amplitudes \(\varepsilon ^{\mathrm{ampl}}\) in each direction (see scheme in Fig. 9), with the total strain defined as \(\varepsilon =\sqrt{\left( \varepsilon _P\right) ^2 + \left( \varepsilon _Q\right) ^2}\).

Fig. 9
figure 9

Intended strain paths at a certain average stress

Full size image

In order to adequately chose the stress amplitudes in the individual directions, a preliminary test on a medium dense sample with an average stress of \(p^{\mathrm{av}}= 200\,{\text {kPa}}\) and \(\eta ^{\mathrm{av}}= 0.75\) has been performed. In that test different stress amplitudes have been applied in all six directions. Based on the results of this test the stress amplitudes leading to strain amplitudes \(\varepsilon ^{\mathrm{ampl}}\approx 3.0 \times 10^{-4}\) or \(2.0 \times 10^{-4}\), respectively, have been determined. For the average stresses with \(p^{\mathrm{av}}= 100\) kPa and \(p^{\mathrm{av}}= 300\,{\text {kPa}}\), these stress amplitudes were scaled according to the pressure-dependence of stiffness. No adjustment was undertaken, however, to consider the influence of density or stress ratio. This results in strain amplitudes deviating from \(3 \times 10^{-4}\) and \(2 \times 10^{-4}\), respectively, in case of looser and denser samples and in particular for stress ratios \(\eta ^{\mathrm{av}}\ne\) 0.75 (Figs. 10, 11).

Fig. 10
figure 10

Strain paths measured on the dense sample (\(I_{D0} = 0.91\)) during the 10 larger preconditioning cycles (period \(T = 100\,{\text {s}}\)) applied in 6 different directions at \(p^{\mathrm{av}}= 300\,{\text {kPa}}\) and a\(\eta ^{\mathrm{av}}= - 0.40\), b\(\eta ^{\mathrm{av}}= 0\) and c\(\eta ^{\mathrm{av}}= 1.00\)

Full size image
Fig. 11
figure 11

Strain paths measured on the dense sample (\(I_{D0} = 0.91\)) during the 5 smaller cycles (period \(T = 1000\,{\text {s}}\)) applied in 6 different directions at \(p^{\mathrm{av}}= 300\,{\text {kPa}}\) and a\(\eta ^{\mathrm{av}}= - 0.40\), b\(\eta ^{\mathrm{av}}= 0\) and c\(\eta ^{\mathrm{av}}= 1.00\)

Full size image

At each average stress first ten preconditioning cycles were applied in all six directions, with a loading period of \(T = 100\,{\text {s}}\) and an intended strain amplitude of \(\varepsilon ^{\mathrm{ampl}}= 3.0 \times 10^{-4}\). Figure 10 shows examples of the strain paths resulting from these preconditioning cycles for the dense sample, an average mean pressure of \(p^{\mathrm{av}}= 300\,{\text {kPa}}\) and three different average stress ratios (\(\eta ^{\mathrm{av}}= - 0.40\), 0 and 1.00). The accumulation of strain, in particular in case of the polarizations 1 and 2, is evident in those diagrams. In the diagrams in Fig. 10, the strain was set back to \(\varepsilon _P = \varepsilon _Q = 0\) at the start of the 10 cycles applied with a certain polarization.

After the completion of the preconditioning cycles five smaller cycles were applied in all six directions, with a loading period of \(T = 1000\,{\text {s}}\) and an intended strain amplitude of \(\varepsilon ^{\mathrm{ampl}}\approx 2.0 \times 10^{-4}\). The data from these smaller cycles have been used for the further analysis of the elastic stiffness at a given average stress. The purpose of the preconditioning cycles was to lead to a shakedown, i.e. to prevent an accumulation of strain during the subsequent smaller cycles. The examples of the strain paths from the smaller cycles in Fig. 11 actually do not show any accumulation of strain and the hysteretic effects are negligible, i.e. the material response is almost purely elastic. Also in Fig. 11, the strain path for the five cycles applied with a certain polarization starts from \(\varepsilon _P = \varepsilon _Q = 0\). Considering the loading sequence shown in Fig. 8 and the larger amplitudes in the preconditioning cycles, all subsequent smaller cycles are applied in an overconsolidated state, which helps preventing an accumulation of strain. Due to the reasons explained above the strain paths in Fig. 11 for \(\eta ^{\mathrm{av}}\ne\) 0.75 show some deviations from the intended strain amplitude \(\varepsilon ^{\mathrm{ampl}}\approx 2.0 \times 10^{-4}\). This does not impose any problems, however, for the analysis procedure explained in Sect. 4. A dependence of the direction of the strain cycles on average stress ratio \(\eta ^{\mathrm{av}}\) becomes obvious from a comparison of the three diagrams in Fig. 11.

For both phases of cyclic loading applied at a certain average stress, the isotropic stress cycles (polarization P1) have been applied first, followed by the cycles with \(\alpha _{PQ} = 30^\circ\) (P2), \(60^\circ\) (P3), etc. In a preliminary test the sequence of the polarizations has been varied at a given average stress. The accumulation of strain during the preconditioning cycles has been found somewhat affected by this sequence, but the material response during the subsequent smaller cycles did not show such dependence. Since only the data from the smaller cycles are further used in the present study, an influence of the sequence of the polarizations has not to be considered.

The behaviour of sand under drained or undrained cyclic loading is known to be almost independent of the loading frequency [19, 35, 64, 68, 75]. In the present investigation the preconditioning cycles were applied with a larger frequency (\(T = 100\,{\text {s}}\)), because the data from these cycles were irrelevant for the analysis of the elastic stiffness. The relevant smaller cycles following the preconditioning cycles were applied slower (\(T = 1000\,{\text {s}}\)), to record more data per cycle.

In drained cyclic triaxial tests on sand, after the application of the average stress on a virgin sample, one usually observes some creep deformation prior to the start of the cycles (cf. investigations on viscous effects in sand in [4, 5, 13, 36, 37, 39, 40, 51, 52, 63, 74]). After the application of some cycles, if the sample is brought to rest at the average stress again, no further creep occurs. This is due to the fact that the sample is now in an overconsolidated state (the maximum stress during the cycles was larger). In the present test series the preconsolidation cycles were started directly after having reached the average stress. After the application of the \(6 \times 10\) preconsolidation cycles at the first average stress (\(p^{\mathrm{av}}= 300\,{\text {kPa}}\), \(\eta ^{\mathrm{av}}= 1\)) viscous effects were absent. This applies also for all further average stresses tested in the sequence shown in Fig. 8. It can be assumed that due to the overconsolidated state, despite the long periods of the loading cycles, the measured elastic stiffness is not influenced by viscous effects.

4 Determination of incremental elastic stiffness tensor

The elastic stiffness at small strains can be derived in different ways. A secant stiffness is obtained as the ratio of the stress and the strain amplitude. Alternatively, the small-strain stiffness can be determined from the initial phase (\(\varepsilon \le 10^{-5}\)) of a stress–strain curve measured during the loading of a virgin sample. Analogously, it can be obtained from the stress–strain relationship recorded directly after a load reversal. The procedure applied in the present paper utilizes the latter method.

As an example, the stress and strain paths measured on the dense sample (\(I_{D0} = 0.91\)) at an average stress with \(p^{\mathrm{av}}= 300\,{\text {kPa}}\) and \(\eta ^{\mathrm{av}}= 1.00\) are shown in Fig. 12. A procedure proposed by Loges and Niemunis [48] has been used in order to obtain the incremental elastic stiffness tensor for a given average stress. For that purpose all 60 reversal points (6 polarizations \(\times\) 5 cycles \(\times\) 2 reversals) of the strain (\(\varepsilon _P\), \(\varepsilon _Q\)) and stress (P, Q) paths are identified and memorized. They are shown as blue points in the example in Fig. 12. Next, the points on the strain paths lying in a chosen distance \(\Delta \varepsilon = \sqrt{(\Delta \varepsilon _P)^2 + (\Delta \varepsilon _Q)^2}\) to the reversal points are selected. These states of strain are marked by the green points in Fig. 12b. The corresponding stress states are highlighted by green points in Fig. 12a as well. They lie in a distance \(\Delta \sigma = \sqrt{(\Delta P)^2 + (\Delta Q)^2}\) to the reversal points of the stress path. \(\Delta \varepsilon\) and \(\Delta \sigma\) are termed strain span and stress span in the following. In the example in Fig. 12 a strain span of \(\Delta \varepsilon = 10^{-4}\) has been selected for the analysis.

Fig. 12
figure 12

Determination of characteristic points of the measured a stress and b strain paths. The reversal points are formatted blue, the points lying in a distance \(\Delta \varepsilon = 1 \times 10^{-4}\) from the reversal points are given in green colour. The example shows data for the dense sample (\(I_{D0} = 0.91\)) and an average stress with \(p^{\mathrm{av}}= 300\,{\text {kPa}}\) and \(\eta ^{\mathrm{av}}= 1.00\) (color figure online)

Full size image

Figure 13 shows the data of Fig. 12 in terms of stress–strain relationships. Figure 13a contains a P-\(\varepsilon _P\) diagram with the data of the five cycles applied along polarization 1 (purely isotropic), while the Q-\(\varepsilon _Q\) diagram in Fig. 13b presents the results for the five cycles applied along polarization 4 (purely deviatoric). While the P-\(\varepsilon _P\) relationship is essentially linear, some very small hysteresis is observed in the Q-\(\varepsilon _Q\) data. The diagrams in Fig. 13 again confirm the purely elastic material response during the second test phase comprising the smaller cycles.

Fig. 13
figure 13

a\(\varepsilon _P\)-P diagram for five cycles applied along polarization 1 (purely isotropic), b\(\varepsilon _Q\)-Q diagram for five cycles applied along polarization 4 (purely deviatoric). Data for \(I_{D0} = 0.91\), \(p^{\mathrm{av}}= 300\,{\text {kPa}}\) and \(\eta ^{\mathrm{av}}= 1.00\)

Full size image

From the 60 pairs (reversal point, point at distance \(\Delta \varepsilon\)) of stress and strain states and the corresponding stress and strain spans \(\Delta P\), \(\Delta Q\), \(\Delta \varepsilon _P\) and \(\Delta \varepsilon _Q\), the stiffness \({\mathsf{E}}= \{E_{PP}, E_{PQ}, E_{QP}, E_{QQ}\}\) is quantified, following the procedure described in [48]:

$$\begin{aligned} \left[ \begin{array}{cc} \Delta P \\ \Delta Q \end{array} \right] = \left[ \begin{array}{cc} E_{PP} &{} E_{PQ} \\ E_{QP} &{} E_{QQ} \end{array} \right] \left[ \begin{array}{c} \Delta \varepsilon _P \\ \Delta \varepsilon _Q \end{array} \right] \end{aligned}$$
(2)

It should be stressed that the stiffness is not calculated as a secant value separately for each of the \(2 \times 6\) directions, but that the data from all spans are used at once to obtain the components of the incremental stiffness tensor for the average stress, using an error minimization technique described in [48]. The examples of the strain paths in Figs.  11 and 12 show the raw data. In contrast to [48] no further smoothing (in order to reduce the random noise) has been applied prior to the evaluation of the stiffness. The 60 stress spans \(\Delta \sigma\) to be analysed lie in a stellar pattern at some distance to the average stress (Fig. 12a). In order to derive a stiffness \({\mathsf{E}}\) for the average stress (\(p^{\mathrm{av}}\), \(q^{\mathrm{av}}\)), a correction of the data of the individual spans considering the pressure-dependence of stiffness \(E \sim p^n\) has been applied [48]. An exponent of the pressure-dependence of \(n = 0.6\) was used for that purpose. Other corrections described in [48] have not been applied in the present study: A possible influence of the different values of deviatoric stress of the individual stress spans has not been considered. Since the experimental data shows virtually no hysteretic effect, a correction based on the paraelastic model [55,56,57] was not necessary. The same applies to a purifying of the data from cumulative effects, due to the absence of strain accumulation (Fig. 11).

Table 1 summarizes some of the components of the incremental stiffness tensor derived for the dense sample, a strain span of \(\Delta \varepsilon = 1 \times 10^{-4}\) and different average stresses. As already mentioned in the introduction the incremental stiffness tensor must be symmetric, i.e. the condition \(E_{PQ} = E_{QP}\) has to be fulfilled. This condition has not been enforced in the fitting, however, and the discrepancy could be quantified by

$$\begin{aligned} \left| \frac{E_{PQ}-E_{QP}}{\frac{1}{2} (E_{PQ}+E_{QP})}\right| \cdot 100\quad [\%] \end{aligned}$$
(3)

which was always less than 10% (see Table 1). Hence, irrespective of some natural amount of scatter, the \(E_{PQ}\) and \(E_{QP}\) values derived from the experiments satisfied the symmetry condition.

Table 1 Components of the incremental elastic stiffness tensor for a strain span of \(\Delta \varepsilon = 10 ^{-4}\) derived from the test on the dense sample (\(I_{D0} = 0.91\)) and selected average stresses
Full size table

5 Graphical presentation of elastic stiffness by response envelopes

The components of the incremental elastic stiffness tensor derived for a certain average stress were used for a graphical presentation of the stiffness by a stress response envelope. Figure 14 presents the response envelopes plotted for a strain span of \(\Delta \varepsilon = 10^{-4}\) for different densities and average stresses in the P-Q plane. The relative densities of the samples at the beginning of the small cycles are given beside each response envelope. The change of the relative density during the multi-stage test, caused by the change of the average stress and the strain accumulation during the preconditioning cycles, decreases with increasing initial density (\(\Delta I_{D0} = 0.08\) for the loose, \(\Delta I_{D0} = 0.07\) for the medium dense and \(\Delta I_{D0} = 0.01\) for the dense sample, whereby the smaller range of stress ratios \(\eta ^{\mathrm{av}}\) tested on the loose sample has to be considered). The centre point of a response envelope coincides with the average stress in the test. The points on the response envelopes corresponding to purely deviatoric or purely volumetric strain cycles are marked by the blue or red points, respectively. The response envelopes grow with pressure and density, of course. Furthermore, the inclination of the response envelopes towards the horizontal increases with growing stress ratio \(|\eta ^{\mathrm{av}}|\).

Fig. 14
figure 14

Response envelopes for a strain span \(\Delta \varepsilon = 10^{-4}\) at different average stresses and for different densities (color figure online)

Full size image

Considering the accuracy and resolution of the LDTs and the resulting scatter of data visible in Figs. 11 and 12, the analysis of stiffness is restricted to a strain span of \(\Delta \varepsilon = 10^{-4}\) in the present study. From resonant column tests on sands having a similar uniformity coefficient \(C_u\) of the grain size distribution curve as the fine sand tested in the present study, it is known that the secant stiffness G at \(\gamma ^{\mathrm{ampl}}= 10^{-4}\) amounts between 75% (\(p = 100\,{\text {kPa}}\)) and 85% (\(p = 300\,{\text {kPa}}\)) of the value \(G_{\max }\) at very small strain amplitudes (\(\gamma ^{\mathrm{ampl}}\le 10^{-5}\)), considering the range of pressures tested in the present study [70, 71]. Although the stress response envelopes presented in this paper do not correspond to very small strain amplitudes (\(\varepsilon ^{\mathrm{ampl}}\le 10^{-5}\)), i.e. to the maximum stiffness \({\mathsf{E}}_{\max }\), they are useful for a comparison with the stress response envelopes representing the stiffness of constitutive models as well, since they deliver an information about the shape and the orientation of the envelopes.

6 Effects of loading history

It is well known that the soil response can strongly depend on the loading history. The effect seems to be most pronounced in case of very loose sand samples prepared by moist tamping [6, 15,16,17,18, 21, 23]. The cumulative strains in cyclic triaxial tests on sand are also significantly affected by a monotonic or cyclic preloading [69, 72].

In order to examine effects of loading history, i.e. the sequence of the average stresses, an additional test on a medium dense sample (\(I_{D0} = 0.57\)) has been performed. The cycles have been applied at average stresses in the extension regime of the p-q plane and on the isotropic axis only. Compared to the tests presented in Fig. 14, an opposite sequence of the average stresses has been chosen, starting at \(p^{\mathrm{av}}= 300\,{\text {kPa}}\) and \(\eta ^{\mathrm{av}}= - 0.40\) and ending on the isotropic axis at \(p^{\mathrm{av}}= 100\,{\text {kPa}}\) (see red arrows and numbers in Fig. 15). The response envelopes derived from the data of both tests for \(\Delta \varepsilon = 10^{-4}\) are compared in Fig. 15. Evidently, the sequence effects are relatively small at \(\eta ^{\mathrm{av}}= - 0.40\) and − 0.25, where the response envelopes almost coincide. The deviations are somewhat larger on the p axis, where the response envelopes from the additional test show a slight rotation towards the extensional side of the p-q plane, while the sequence illustrated in Fig. 8 lead to envelopes almost aligned with the isotropic axis. The data in Fig. 15 give hints that the elastic stiffness is not significantly influenced by the loading history, at least not in the case of the stress states and paths tested herein. This can presumably be mainly attributed to the preconditioning cycles, which may eliminate effects of the previous loading path.

Fig. 15
figure 15

Response envelopes for a strain span \(\Delta \varepsilon = 10^{-4}\) and medium dense sand, derived from two tests with a different sequence of the average stresses. Blue response envelopes = test from Fig. 14 with the sequence illustrated in Fig. 8, red response envelopes = additional test with a sequence defined by the red numbers, starting at \(\eta ^{\mathrm{av}}= - 0.40\) (color figure online)

Full size image

In most of the experimental studies on response envelopes in the literature each stress probe at a certain average stress has been applied to a virgin sample. Of course this is mandatory if one wants to obtain the response envelopes describing total strain or stress, comprising plastic and elastic portions. The data in Fig. 15 give hints, however, that testing numerous virgin samples is not necessary in the present investigation concentrating on the elastic stiffness. The additional test starts at an average stress of \(p^{\mathrm{av}}= 300\,{\text {kPa}}\) and \(\eta ^{\mathrm{av}}= -0.4\) (point 1 in Fig. 15). The response envelope obtained from this test is shown at this average stress as the red ellipse in Fig. 15, corresponding to a virgin sample. In contrast, the blue ellipse drawn in the same point is obtained from the test with the loading sequence shown in Fig. 8. In that test 18 other stress states have been tested previously. Despite that, the blue and the red ellipse in Fig. 8 show only small differences. Therefore, it is assumed that very similar response envelopes as presented in Fig. 14 were obtained if each average stress was tested on a virgin sample. The effect of the loading history on the response envelopes will be further studied in future. Other preloading paths deviating from those tested in the present study, e.g. involving a large prestraining with several per cent of strain, may have a stronger effect on the elastic stiffness.

7 Comparison with a response envelope evaluated conventionally

Based on the data presented in Fig. 12 a stress response envelope has been also determined conventionally, in order to compare it with the corresponding response envelope from Fig. 14. For each of the six polarizations the initial phase of the first cycle was analysed. Starting from the origin of the \(\varepsilon _P\)-\(\varepsilon _Q\) diagram the stress points (\(P^{\mathrm{av}}\), \(Q^{\mathrm{av}}\)) corresponding to a strain span \(\Delta \varepsilon = 10^{-4}\) were determined. These stress points are given as the black points in Fig. 16. A mirroring of these stress points at the point of average stress (green point in Fig. 16) along the respective lines of polarization results in the grey points in Fig. 16. The 12 points marked by the black or grey symbols were linearly connected to a polygon representing the response envelope determined conventionally. The corresponding elliptical response envelope from Fig. 14 has been superposed in Fig. 16. It is slightly larger in size than the polygon determined conventionally, because the tangent stiffness derived from the 60 stress and strain spans in the vicinity of the reversal points exceeds the secant stiffness determined from the initial phase of the first cycles.

Fig. 16
figure 16

Comparison of the response envelope derived conventionally from the data in Fig. 12 (polygon connecting black and grey symbols) with the corresponding elliptical response envelope from Fig. 14 (color figure online)

Full size image

8 Calibration of hyperelasticity in a hypoplastic model

The response envelopes in Fig. 14 have been used to calibrate the hyperelasticity incorporated into a new hypoplastic model proposed by Niemunis et al. [54]. The proposed hyperelasticity can be derived from the complementary potential \(\psi = c P^\alpha R^{2-n-\alpha }\) with \(R = \sqrt{P^2 + Q^2}\) and \(E_{ijkl} = \left[ \frac{\partial ^2 \psi }{\partial \sigma _{ij} \partial \sigma _{kl}}\right] ^{-1}\). Based on the presented test data, the optimum constants have been determined as \(n = 0.6\), \(\alpha = 0.1\) and \(c = 1.5 \times 10^{-4}\). Fig. 17 demonstrates the good agreement between the experimental and numerical response envelopes. In a similar manner, the experimental data presented in this paper can be applied to check or calibrate the elastic stiffness in any other hypoplastic or elastoplastic constitutive model.

Fig. 17
figure 17

Comparison of the response envelopes derived from the experimental data for the medium dense sand sample (\(I_{D0} = 0.62\)) with those generated numerically based on the hyperelasticity incorporated into the new hypoplastic model proposed by Niemunis et al. [54]

Full size image

9 Summary, conclusions and outlook

Cyclic triaxial tests on cube-shaped samples of fine sand have been performed. Local strain measurements were taken using LDTs, i.e. strips of stainless steel equipped with strain gauges. Three samples with different densities between very loose and very dense were prepared by air pluviation and tested in the dry state. On each sample the cycles were applied at different average stresses in succession, comprising three different average mean pressures in the range 100 kPa \(\le p^{\mathrm{av}}\le 300\) kPa and seven different average stress ratios (\(-0.4 \le \eta ^{\mathrm{av}}= q^{\mathrm{av}}/p^{\mathrm{av}}\le 1.0\)).

At each average stress uniaxial cycles in six different directions (polarizations) were applied, corresponding to angles \(\alpha _{PQ} = 0^\circ\) (purely isotropic cycles), \(30^\circ\), \(60^\circ\), \(90^\circ\) (purely deviatoric), \(120^\circ\) and \(150^\circ\) towards the horizontal in the isometric P-Q plane. Different polarizations were achieved by a simultaneous oscillation of the axial and the lateral effective stress, choosing different amplitudes and phase shifts. In order to investigate a purely elastic response of the sand, ten preconditioning cycles with a larger amplitude (\(\varepsilon ^{\mathrm{ampl}}\approx 3 \times 10^{-4}\)) have been applied along all six polarizations in order to induce a shakedown. They were followed by five smaller cycles (\(\varepsilon ^{\mathrm{ampl}}\approx 2 \times 10^{-4}\)) per polarization whose data was further used for the analysis of the elastic stiffness. While an accumulation of strain usually occurred during the larger amplitudes, it was virtually absent during the smaller ones.

A special procedure has been applied to analyse the small-strain stiffness. From the measured strain and stress paths characteristic points have been identified and memorized, i.e. the reversal points and the points lying in a certain distance \(\Delta \varepsilon\) (e.g. \(10^{-4}\)) from the reversal points. The corresponding strain and stress increments were used to evaluate the incremental elastic stiffness tensor \({\mathsf{E}}= \{E_{PP}, E_{PQ}, E_{QP}, E_{QQ}\}\) for a given average stress and a certain strain span \(\Delta \varepsilon\). A graphical presentation of the incremental stiffness tensor in form of response envelopes is provided. As expected the response envelopes grow with increasing values of pressure and density. Furthermore, the response envelopes rotate with stress ratio, showing a larger inclination at higher \(|\eta ^{\mathrm{av}}|\). Effects of the loading history, i.e. the sequence of the average stresses were found almost negligible. The response envelopes derived from the experimental data have been used to calibrate the hyperelasticity incorporated into a new hypoplastic model. Likewise, they can be used to inspect or calibrate the elastic stiffness of any other sound hypoplastic or elastoplastic constitutive model.