1 Introduction

Numerical simulation of shear band propagation near or after failure which is a progressive phenomenon is a demanding task from numerical and mathematical perspectives. Rudnicki and Rice [33] recommended bifurcation analysis for these problems, while Simo and co-workers [37] showed that the onset of localization coincides with the instability of the equilibrium condition associated with the singularity of the acoustic tensor.

Modeling shear band propagation in saturated porous media is affected by the fluid phase for both shear band initiation and direction. The formulation of the localization condition in terms of effective stress allows to evidence the role of the pore pressure in fully coupled systems [4]. As far as the angle of shear band propagation is concerned, there are several suggestions: a formulation based on the friction and dilation angle has been reported in [36]; on the other hand, in [34] and [43] it has been shown that the angle of shear band depends on strain rates and permeability.

The ill-posedness of boundary value problem during the post-localization has to be considered to circumvent mesh dependency present in conventional models. Well posedness is guaranteed with enhanced constitutive models. For this matter, several regularization techniques exist to enhance the classical methods, such as non-local [11], high-order [21], gradient-dependent [42], viscous [12] and strong discontinuity methods [38].

XFEM is utilized for many problems like modeling localization within Cosserat materials [16], growth of crack in saturated porous media subject to large deformation [14], 3D non-planar crack propagation [1] and bimaterials with new tip enrichment functions [40]. On the other hand, strong discontinuities have been adopted successfully for simulation of strain localization in dry materials in [2, 3, 28]. Combined with XFEM, they have been used for the same problem in [6, 22] and for crack propagation in dry materials in [23, 29, 39, 41]. Strong discontinuities have also been applied in [26] for the fracturing process in saturated materials. Upon mesh refinement stepwise crack advancement was obtained with small time steps, whereas a monotonic crack growth was obtained with a large time steps. To our best knowledge, strong discontinuities together with XFEM have not yet been applied for strain localization problems in saturated geomaterials.

In this paper, we combine hence strong discontinuities with XFEM to investigate strain localization in saturated porous media. Following [37] we make use of instability of the equilibrium condition associated with the singularity of the acoustic tensor. To check whether we actually capture the material instability with the proposed combination of strong discontinuities and XFEM, we invoke the second-order work criterion based on Hill’s sufficient condition of stability [13]. For this purpose we compute and check the sign of the second-order work in the domain. The second-order work criterion has been proved mathematically to be the first bifurcation criterion to be reached along a loading path [17] with respect to failure by divergence instabilities. It has been applied successfully in [15] to capture both developing shear bands and diffuse failure of slopes.

The paper is structured as follows. Section 2 describes the governing equations of the saturated porous medium, the elastoplastic criterion used, the concept of strong discontinuity in the framework of strain localization in dilatant porous materials, the XFEM formulation adopted and the second-order work theory. In Sect. 3, applications of the extended finite element formulation for a fully coupled saturated porous medium are presented. The numerical simulations are discussed in detail in the concluding remarks.

2 Mathematical model

2.1 Governing equation for saturated porous media

We present here briefly the macroscopic setup of the governing equations obtained with averaging approaches in [19]. Small strain theory is used as in most papers dealing with shear band formation in saturated porous media, e.g., [4, 12, 34, 36, 42, 43]. The encountered strains in the examples justify this assumption. For quasi-static condition, the linear momentum balance equation is given by

$$\nabla .{\varvec{\upsigma}} + \rho {\mathbf{b}} = 0$$
(1)

where \(\nabla .\) is the divergence operator, \({\mathbf{b}}\) is the associated body force vector, and \(\rho\) is the total density defined for saturated porous media as

$$\rho = (1 - n)\rho_{\text{s}} + n\rho_{\text{f}}$$
(2)

with \(\rho_{\text{s}}\) and \(\rho_{\text{f}}\) density of solid and fluid phases, respectively, and n the porosity of the medium. The total stress \({\varvec{\upsigma}}\) is set in terms of effective stress \({\varvec{\upsigma}}'\) and fluid pore pressure p with the assumption of stresses being tension positive for the solid phase and pore pressure compressive positive for the fluid

$${\varvec{\upsigma}} = {\varvec{\upsigma}}' - \alpha p{\mathbf{I}}$$
(3)

where \(\alpha\) is the Biot constant, (\(\alpha = 1 - {\frac{{K_{T} }}{{K_{\text{s}} }}}\)), expressed in terms of the bulk moduli of porous matrix \(K_{T}\) and solid grains \(K_{\text{s}}\), and \({\mathbf{I}}\) is the unit tensor.

According to the \(u - p\) formulation, with \(u\) being the displacement, the fluid mass balance equation reads

$$\left[ {\frac{\alpha - n}{{K_{\text{s}} }} + {\frac{n}{{K_{\text{f}} }}}} \right]\dot{p} + \alpha \nabla .{\dot{\mathbf{u}}} + v = 0$$
(4)

where \(v\) is the Darcy velocity given as

$$v = \nabla .\left[ {\frac{{\mathbf{k}}}{{\mu_{f} }}\left( { - \nabla p + \rho {\mathbf{b}}} \right)} \right]$$
(5)

with \({\mathbf{k}}\) the permeability tensor and \(\mu_{f}\) the dynamic viscosity. Equations (1) and (4), after incorporation of Eq. (5) have to be solved in a coupled manner.

2.2 Material nonlinearity and shear band formation

The part relating to the solid phase has been published in [22]. It is repeated here for sake of completeness.

The elastoplastic constitutive model of bulk, considered as pressure dependent, can be defined as [10]

$$\Pi ({\varvec{\upsigma}}',c) \le 0,{\text{ d}}{\varvec{\upsigma}}' = {\mathbf{C}}:({\text{d}}{\varvec{\upvarepsilon}} - {\text{d}}{\varvec{\upvarepsilon}}^{{\mathbf{p}}} ),{\text{ d}}{\varvec{\upvarepsilon}}^{{\mathbf{p}}} = {\text{d}}\lambda \,{\frac{{\partial\Pi }}{{\partial {\varvec{\upsigma}}'}}}$$
(6)

where \(\Pi\) is the yield function, \(c\) is cohesion stress, \({\mathbf{C}}\) is the elastic constitutive tensor, \({\varvec{\upvarepsilon}}\) is total strain tensor, \({\varvec{\upvarepsilon}}^{{\mathbf{p}}}\) is the plastic strain tensor, and \({\text{d}}\lambda\) is plastic consistency multiplier.

The Drucker–Prager model is chosen for describing the elastoplastic behavior of the solid phase,

$$\Pi ({\varvec{\upsigma}}',c) = \sqrt {\frac{1}{2}{\mathbf{s}}:{\mathbf{s}}} + \frac{3\tan \varphi }{{\sqrt {9 + 12\tan^{2} \varphi } }}\bar{p} - {\frac{3}{{\sqrt {9 + 12\tan^{2} \varphi }} }}\,{\text{c }}$$
(7)

where \({\mathbf{s}}\) is the deviatoric stress tensor, \(\bar{p}\) is the hydrostatic stress, and \(\varphi\) represents the friction angle.

The non-associated plasticity model accounts for dilatancy during plastic flow. The direction of plastic strain is obtained from the potential function

$$ \Lambda = \sqrt{\frac{1}{2}}{\mathbf{s}}:{\mathbf{s}} + \frac{3\tan \varPsi }{{\sqrt {9 + 12\tan^{2} \varPsi }} }\bar{p} $$
(8)

where \(\Lambda\) is the potential function and \(\varPsi\) is the dilation angle. By inserting the effective stress \({\text{d}}{\varvec{\upsigma}}' = {\mathbf{C}}:({\text{d}}{\varvec{\upvarepsilon}} - {\text{d}}{\varvec{\upvarepsilon}}^{{\mathbf{p}}} )\) into the yield function and using the plastic strain increment \({\text{ d}}{\varvec{\upvarepsilon}}^{{\mathbf{p}}} = {\text{d}}\lambda {\frac{{\partial\Pi }}{{\partial {\varvec{\upsigma}}'}}}\), the plastic consistency parameter for non-associated case is derived

$${\text{d}}\lambda = \frac{{\partial_{{{\varvec{\upsigma}}'}}\Pi :{\mathbf{C}}:{\text{d}}{\varvec{\upvarepsilon}}}}{{\partial_{{{\varvec{\upsigma}}'}}\Pi :{\mathbf{C}}:\partial_{{{\varvec{\upsigma}}'}}\Lambda + H(\partial_{{{\varvec{\upsigma}}'}}\Pi )(\partial_{{{\varvec{\upsigma}}'}}\Lambda )}}$$
(9)

where H is the hardening modulus. The corresponding elastoplastic tangent modulus is

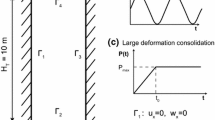
$${\mathbf{C}}^{{{\mathbf{ep}}}} = {\mathbf{C}} - \frac{{{\mathbf{C}}:\partial_{{{\varvec{\upsigma}}'}}\Xi \otimes \partial_{{{\varvec{\upsigma}}'}}\Theta :{\mathbf{C}}}}{{\partial_{{{\varvec{\upsigma}}'}}\Theta :{\mathbf{C}}:\partial_{{{\varvec{\upsigma}}'}}\Xi + H(\partial_{{{\varvec{\upsigma}}'}}\Theta )(\partial_{{{\varvec{\upsigma}}'}}\Xi )}}$$
(10)

The localization of plastic deformations along a zero thickness shear band is here modeled as a displacement jump termed strong discontinuity. Across the shear band surface, the traction must satisfy equilibrium [32]. For a body \(\Omega\) as shown in Fig. 1, this condition is written as

$${\mathbf{n}}.\left[\kern-0.15em\left[ {{\dot{\mathbf{\sigma }}}'} \right]\kern-0.15em\right] = 0, \, {\mathbf{n}} = \left\{ \begin{aligned} \cos \eta \hfill \\ \sin \eta \hfill \\ \end{aligned} \right\}$$
(11)

where \({\mathbf{n}}\) is the unit vector normal to the shear band surface and \(\eta\) represents the angle between the unit vector \({\mathbf{n}}\) and axis \({\mathbf{x}}\) (see Fig. 1). Expressing the effective stress rate by means of the effective strain rate yields

$${\mathbf{n}}.{\mathbf{C}}^{{{\mathbf{ep}}}} .\left[\kern-0.15em\left[ {{\dot{\mathbf{\varepsilon }}}} \right]\kern-0.15em\right] = 0$$
(12)
Fig. 1
figure 1

Body \(\Omega\) containing a shear band and associated boundary conditions

Full size image

The symbol \([\kern-0.15em[ {\,} ]\kern-0.15em]\) indicates the jump of the corresponding field across the discontinuity. The associated displacement field after shear band initiation may be written as

$${\dot{\mathbf{u}}} = {\dot{\hat{\mathbf{u}}}} + \left[\kern-0.15em\left[ {{\dot{\mathbf{u}}}} \right]\kern-0.15em\right]H_{\text{s}}$$
(13)

where the \({\dot{\hat{\mathbf{u}}}}\) and \(\left[\kern-0.15em\left[ {{\dot{\mathbf{u}}}} \right]\kern-0.15em\right]\) are the continuous and jump components of the displacement field. \(H_{\text{s}}\) is the Heaviside step function, centered at the discontinuity, and is defined as

$$H_{\text{s}} (x) = \left\{ {\begin{array}{*{20}c} 1 & {x \in\Omega ^{ + } } \\ 0 & {x \in\Omega ^{ - } } \\ \end{array} } \right.$$
(14)

The strain rate during strain localization can then be obtained from

$${\dot{\mathbf{\varepsilon}}} = {\dot{\hat{\varvec{\upvarepsilon}}}} + \left( {\left[\kern-0.15em\left[ {{\dot{\mathbf{u}}}} \right]\kern-0.15em\right] \otimes {\mathbf{n}}} \right)\delta$$
(15)

where \({\dot{\hat{\varvec{\upvarepsilon}}}}\) is the continuous component of strain field and \(\delta\) is the Dirac Delta function.

Equation (12) can be rewritten in terms of the displacement jump

$${\mathbf{n}}.{\mathbf{C}}^{{{\mathbf{ep}}}} .\left( {\left[\kern-0.15em\left[ {{\dot{\mathbf{u}}}} \right]\kern-0.15em\right] \otimes {\mathbf{n}}} \right)\delta = 0$$
(16)

and consequently

$${\mathbf{n}}.{\mathbf{C}}^{{{\mathbf{ep}}}} .{\mathbf{n}}\left[\kern-0.15em\left[ {{\dot{\mathbf{u}}}} \right]\kern-0.15em\right] = 0$$
(17)

The first part of Eq. (17) is known as the acoustic tensor [37]

$${\mathbf{A}} = {\mathbf{n}}.{\mathbf{C}}^{{{\mathbf{ep}}}} .{\mathbf{n}}$$
(18)

The singularity of the acoustic tensor determines the localization condition and consequently the components of vector \({\mathbf{n}}\).

Finally, the condition of localization in terms of singularity of the acoustic tensor and unit localization vector must be satisfied:

$${\mathbf{A}}{\mathbf{.m}} = 0$$
(19)

The localization vector \({\mathbf{m}}\) consists of relative shear band normal displacements across discontinuous interface,

$${\mathbf{m}} = \left\{ \begin{aligned} \, \cos \omega \hfill \\ - \sin \omega \hfill \\ \end{aligned} \right\}$$
(20)

where \(\omega\) is the angle of vector \({\mathbf{m}}\) with axis \({\mathbf{x}}\).

For a body undergoing shear banding with nonzero discontinuity value, matrix A must be singular. According to Eq. (17), the initiation of localization occurs when \(\left[\kern-0.15em\left[ {{\dot{\mathbf{u}}}} \right]\kern-0.15em\right] \ne 0\), consequently;

$$\det {\mathbf{A}} = \left[ \begin{aligned} A_{11} \hfill \\ A_{21} \hfill \\ \end{aligned} \right. \, \left. \begin{aligned} A_{21} \hfill \\ A_{22} \hfill \\ \end{aligned} \right] = 0$$
(21)

\(\left[\kern-0.15em\left[ {{\dot{\mathbf{u}}}} \right]\kern-0.15em\right]\) is rewritten in the form of its magnitude (\(\left| {\left[\kern-0.15em\left[ {{\dot{\mathbf{u}}}} \right]\kern-0.15em\right]} \right|\)) multiplied by its unit vector (m = \(\left\{ \begin{aligned} \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{1} \hfill \\ \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{2} \hfill \\ \end{aligned} \right\}\))

$$({\mathbf{n}} \cdot {\mathbf{D}}^{{\text{ep}}} \cdot {\mathbf{n}})\left| {\left[\kern-0.15em\left[ {{\dot{\mathbf{u}}}} \right]\kern-0.15em\right]} \right|\left\{ \begin{aligned} \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{1} \hfill \\ \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{2} \hfill \\ \end{aligned} \right\} = 0, \, \left| {\left\{ \begin{aligned} \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{1} \hfill \\ \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{2} \hfill \\ \end{aligned} \right\}} \right| = 1$$
(22)

Thus,

$$({\mathbf{n}} \cdot {\mathbf{D}}^{{\text{ep}}} \cdot {\mathbf{n}})\left\{ \begin{aligned} \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{1} \hfill \\ \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{2} \hfill \\ \end{aligned} \right\} = {\mathbf{0}}$$
(23)

where \(\left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{1}\) and \(\left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{2}\) are the components of the unit discontinuity vector

$${\mathbf{Q}}_{{{\mathbf{ij}}}} \left\{ \begin{aligned} \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{1} \hfill \\ \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{2} \hfill \\ \end{aligned} \right\} = 0$$
(24)

To have a non-trivial answer, the determinant of matrix \({\mathbf{Q}}_{{{\mathbf{ij}}}}\), the acoustic tensor, must be equal to zero,

$$\det \left( {{\mathbf{Q}}_{{{\mathbf{ij}}}} } \right) = 0$$
(25)

After obtaining the vector \({\mathbf{n}}\) from Eq. (25), and introducing it into \({\mathbf{Q}}_{{{\mathbf{ij}}}}\), its components are derived. Since

$$Q_{11} Q_{22} - Q_{12} Q_{21} = 0$$
(26)
$$Q_{11} = \frac{{Q_{12} Q_{21} }}{{Q_{22} }}, \, Q_{21} = \frac{{Q_{11} Q_{22} }}{{Q_{12} }}$$
(27)

The first equation obtained from the system of Eqs. (24) is written as

$$Q_{11} \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{1} + Q_{12} \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{2} = 0$$
(28)

By substituting \(Q_{11}\) in Eq. (28)

$$\frac{{Q_{12} Q_{21} }}{{Q_{22} }}\left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{1} + Q_{12} \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{2} = 0$$
(29)

The second equation obtained from Eq. (24) results in

$$Q_{21} \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{1} + Q_{22} \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{2} = 0$$
(30)

Substituting \(Q_{21}\) in Eq. (30) yields

$$\frac{{Q_{11} Q_{22} }}{{Q_{12} }}\left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{1} + Q_{22} \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{2} = 0;$$
(31)

therefore,

$$\frac{{\left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{2} }}{{\left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{1} }} = - \frac{{Q_{21} }}{{Q_{22} }} = - \frac{{Q_{11} }}{{Q_{12} }}$$
(32)

Accounting for the components of vector \({\mathbf{m}}\), \(\left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{1}\) and \(\left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{2}\)

$$\left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{2} = \sin \gamma , \, \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{1} = - \cos \gamma$$
(33)

we obtain

$$\frac{{\left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{2} }}{{\left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{1} }} = \frac{ - \sin \gamma }{\cos \gamma } = - \frac{{Q_{21} }}{{Q_{22} }} = - \frac{{Q_{11} }}{{Q_{12} }}\;{\text{or}}\;\gamma = \arctan \left( {\frac{{Q_{21} }}{{Q_{22} }}} \right) = \arctan \left( {\frac{{Q_{11} }}{{Q_{12} }}} \right)$$
(34)

Finally, the components of vector \({\mathbf{m}}\) in terms of the components of the acoustic tensor are obtained as

$$\frac{{\left[\kern-0.15em\left[ {{\dot{\mathbf{u}}}} \right]\kern-0.15em\right]}}{{\left| {\left[\kern-0.15em\left[ {{\dot{\mathbf{u}}}} \right]\kern-0.15em\right]} \right|}} = {\mathbf{m}} = \left\{ \begin{aligned} \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{1} \hfill \\ \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right]_{2} \hfill \\ \end{aligned} \right\} = \left\{ \begin{aligned} \cos \left( {\arctan \left( {\frac{{Q_{21} }}{{Q_{22} }}} \right)} \right) \hfill \\ - \sin \left( {\arctan \left( {\frac{{Q_{21} }}{{Q_{22} }}} \right)} \right) \hfill \\ \end{aligned} \right\} = \left\{ \begin{aligned} \cos \left( {\arctan \left( {\frac{{Q_{11} }}{{Q_{12} }}} \right)} \right) \hfill \\ - \sin \left( {\arctan \left( {\frac{{Q_{11} }}{{Q_{12} }}} \right)} \right) \hfill \\ \end{aligned} \right\}$$
(35)

The magnitude of dilation in terms of the vertical and horizontal components of the unit discontinuity displacement increment with respect to the local coordinates n–t is [22]

$$\vartheta = \frac{{{\text{d}}m_{\text{v}} }}{{{\text{d}}m_{\text{h}} }}$$
(36)

where \({\text{d}}m_{\text{v}}\) and \({\text{d}}m_{\text{h}}\) are, respectively, the vertical and horizontal components of the localization vector (\({\text{d}}{\mathbf{m}}\)) with respect to the local coordinate x and t axes. The strong discontinuity approach belongs to the regularization techniques adopted to lessen the mesh dependency during softening. For elements containing shear band, the internal force is dependent upon the dissipated energy which is calculated by the cohesive law. According to the cohesive law, the cohesive traction across discontinuous interface is a function of the relative displacement of discontinuous surfaces. In this work, a mixed-mode cohesive model is implemented and the stress updates for the Drucker–Prager plastic model in Eq. (1) are performed using the modified cohesive traction in the shear band elements, i.e., on Gauss points of the element edges on the shear band interface.

$$\Theta ({\varvec{\upsigma}}',c_{x} ) = \sqrt {\frac{1}{2}{\mathbf{s}}:{\mathbf{s}}} + \frac{3\tan \varphi }{{\sqrt {9 + 12\tan^{2} \varphi } }}p - \frac{3}{{\sqrt {9 + 12\tan^{2} \varphi } }}c_{x} \,$$
(37)

where the extended cohesion is defined

$$c_{x} = c_{0} + H\bar{\varepsilon }^{p} + \bar{H}S_{x} , \, S_{x} = 2|u|$$
(38)

and \(S_{x}\) is the relative displacement of the surfaces limiting the shear band, \(\bar{H}\) is the softening modulus, and \(|{\mathbf{u}}|\) is the magnitude of the discontinuity in displacement field.

The cohesive law or in other words traction-slip law yields the relation between the stress tensor and the relative discontinuity displacement

$${\varvec{\uptau}}_{{\mathbf{c}}} = {\varvec{\uptau}}_{{\mathbf{c}}} (\left[\kern-0.15em\left[ {\mathbf{u}} \right]\kern-0.15em\right])$$
(39)

where \({\varvec{\uptau}}_{{\mathbf{c}}}\) is the cohesive traction vector and \(\left[\kern-0.15em\left[ {\mathbf{u}} \right]\kern-0.15em\right]\) is the relative displacement vector in the direction of the discontinuity as shown in Fig. 2. The normal and tangential components of cohesive force along the discontinuity are

$${\varvec{\uptau}}_{c} .\left[\kern-0.15em\left[ {\mathbf{u}} \right]\kern-0.15em\right] = \left[ \begin{aligned} \tau_{{\text{c}_{\text{t}} }} \hfill \\ \tau_{{\text{c}_{\text{n}} }} \hfill \\ \end{aligned} \right.\left. \begin{aligned} \tau_{{\text{c}_{\text{t}} }} \hfill \\ \tau_{{\text{c}_{\text{n}} }} \hfill \\ \end{aligned} \right]\left| {\left[\kern-0.15em\left[ {\mathbf{u}} \right]\kern-0.15em\right]} \right|\left\{ \begin{aligned} \left[\kern-0.15em\left[ \text{u} \right]\kern-0.15em\right]_{1} \hfill \\ \left[\kern-0.15em\left[ \text{u} \right]\kern-0.15em\right]_{2} \hfill \\ \end{aligned} \right\} = \left| {\left[\kern-0.15em\left[ {\mathbf{u}} \right]\kern-0.15em\right]} \right|\left\{ \begin{aligned} \tau_{{\text{c}_{\text{t}} }} (\left[\kern-0.15em\left[ \text{u} \right]\kern-0.15em\right]_{1} + \left[\kern-0.15em\left[ \text{u} \right]\kern-0.15em\right]_{2} ) \hfill \\ \tau_{{\text{c}_{\text{n}} }} (\left[\kern-0.15em\left[ \text{u} \right]\kern-0.15em\right]_{1} + \left[\kern-0.15em\left[ \text{u} \right]\kern-0.15em\right]_{2} ) \hfill \\ \end{aligned} \right\}$$
(40)
Fig. 2
figure 2

The schematic geometry of shear band zone and flux exchange

Full size image

2.3 Weak form and fluid flow contribution

Integrating the governing Eqs. (1) and (4) after incorporating (5), over the whole domain \(\Omega\), their weak form for the continuum part is written as

$$\int\limits_{\varOmega } {\delta {\mathbf{u}}(\nabla .{\varvec{\upsigma}} + \rho {\mathbf{b}}){\text{d}}\Omega = 0}$$
(41)
$$\int\limits_{\varOmega } {\delta p} \left[ {\left( {\frac{\alpha - n}{{K_{\text{s}} }} + \frac{n}{{K_{\text{f}} }}} \right)\dot{p} + \alpha \left( {\nabla .{\dot{\mathbf{u}}}} \right) + \nabla .\left( {\frac{{\mathbf{k}}}{{\mu_{f} }}\left( { - \nabla p + \rho {\mathbf{b}}} \right)} \right)} \right]{\text{d}}\Omega$$
(42)

where \(\delta {\mathbf{u}}\) and \(\delta p\) are test functions.

The essential and natural boundary conditions as depicted in Fig. 1 are

$$\begin{aligned} {\mathbf{u}} = {\mathbf{u^{\prime}}}{\text{ on }}\Gamma _{u} \hfill \\ {\mathbf{p}} = {\mathbf{p^{\prime}}}{\text{ on }}\Gamma _{w} \hfill \\ \end{aligned}$$
(43)
$$\begin{aligned} {\varvec{\upsigma}}'{\mathbf{.n}}_{\Gamma } = {\mathbf{t^{\prime}}}{\text{ on }}\Gamma _{t} \hfill \\ {\mathbf{q}}{\mathbf{.n}}_{\Gamma } = {\mathbf{q^{\prime}}}{\text{ on }}\Gamma _{q} \hfill \\ \end{aligned}$$
(44)

where \({\mathbf{t^{\prime}}}\) is the external traction across the external boundary \(\Gamma _{t}\), \({\mathbf{n}}_{\Gamma }\) is a unit normal vector to the boundary \(\Gamma _{t}\), and \({\mathbf{q^{\prime}}}\) is the external flux across the external boundary \(\Gamma _{q}\). The behavior of the fluid in the shear band region is now investigated in more detail with the following internal boundary conditions, see Fig. 2. Fluid localization occurs due to the dilation across discontinuity.

$$\begin{aligned} {\varvec{\upsigma}}'{\mathbf{.m}}_{{n_{{\Gamma _{c} }} }} = {\varvec{\uptau}}_{n} {\text{ on }}\Gamma _{\text{c}} \hfill \\ {\varvec{\upsigma}}'{\mathbf{.m}}_{{t_{{\Gamma _{c} }} }} = {\varvec{\uptau}}_{t} {\text{ on }}\Gamma _{\text{c}} \hfill \\ {\mathbf{q}}{\mathbf{.n}}_{\Gamma } = {\mathbf{q^{\prime}}}{\text{ on }}\Gamma _{\text{c}} \hfill \\ \end{aligned}$$
(45)

where \({\mathbf{m}}_{{n_{{\Gamma _{c} }} }}\) is the normal component and \({\mathbf{m}}_{{t_{{\Gamma _{c} }} }}\) is the tangential component of unit discontinuity (localization) vector across the discontinuity \(\Gamma _{\text{c}}\). Accordingly, \({\varvec{\uptau}}_{n}\) and \({\varvec{\uptau}}_{t}\) are the normal and tangential components of the cohesive traction \({\varvec{\uptau}}_{\text{c}}\) across the discontinuity \(\Gamma _{\text{c}}\). And \({\mathbf{q^{\prime}}}\) is the fluid flow normal to the \(\Gamma _{\text{c}}\).

By using the divergence theorem, we can investigate the equilibrium for \(\Omega\) and flow in the shear band area

$$\int\limits_{{\Omega _{ \circ } }} {\text{divE}} {\text{d}}\Omega = \int\limits_{{\Gamma _{\text{c}} }} {E.{\mathbf{n}}_{\Gamma } {\text{d}}\Gamma - \int\limits_{{\Gamma _{\text{c}} }} {\left[\kern-0.15em\left[ E \right]\kern-0.15em\right]} } .{\mathbf{n}}_{\Gamma } {\text{d}}\Gamma$$
(46)

The final weak form of equilibrium Eq. (41) with shear band discontinuity and corresponding boundary conditions, using divergence theory, becomes

$$\begin{aligned} & \int\limits_{\Omega } {\delta ({\mathbf{L}}_{s} {\mathbf{u}}):{\varvec{\upsigma}}{\text{d}}\Omega + \int\limits_{{\Gamma _{\text{c}} }} {\left[\kern-0.15em\left[ {\delta {\mathbf{u}}} \right]\kern-0.15em\right]} .{\varvec{\uptau}}_{c} {\text{d}}\Gamma - \int\limits_{\Omega } {\delta {\mathbf{u}}\rho {\mathbf{b}}{\text{d}}\Omega } } \\ & \quad - \int\limits_{{\Gamma _{t} }} {\delta {\mathbf{u}}} .{\mathbf{t^{\prime}}}_{t} {\text{d}}\Gamma = 0 \\ \end{aligned}$$
(47)

where \({\mathbf{L}}_{s}\) is a differential operator. According to the flow continuity, we have in direction n, shown in Fig. 2,

$$\begin{aligned} & \int\limits_{{\Omega _{ \circ } }} {\delta p\left( {\frac{\alpha - n}{{K_{\text{s}} }} + \frac{n}{{K_{\text{f}} }}} \right)\dot{p}{\text{d}}\Omega - \int\limits_{{\Gamma _{\text{c}} }} {\delta p\left[\kern-0.15em\left[ {\mathbf{v}} \right]\kern-0.15em\right]} .n_{{\Gamma _{\text{c}} }} {\text{d}}\Gamma + \int\limits_{{\Omega _{ \circ } }} {\delta p\alpha \left( {\nabla .{\dot{\mathbf{u}}}} \right)} {\text{d}}\Omega } \\ & \quad + \int\limits_{{\Omega _{ \circ } }} {\nabla \delta p\frac{{\mathbf{k}}}{{\mu_{f} }}\left( { - \nabla p + \rho {\mathbf{b}}} \right){\text{d}}\Omega = 0} \\ \end{aligned}$$
(48)

The mass transfer across the localization zone along vector n is then

$$\begin{aligned} & \int\limits_{{\Gamma _{\text{c}} }} {\delta p\left[\kern-0.15em\left[ {\mathbf{v}} \right]\kern-0.15em\right]} .{\mathbf{n}}_{{\Gamma _{\text{c}} }} {\text{d}}\Gamma = \int\limits_{{\Omega _{ \circ } }} {\delta p\left( {\frac{\alpha - n}{{K_{\text{s}} }} + \frac{n}{{K_{\text{f}} }}} \right)\dot{p}{\text{d}}\Omega + \int\limits_{{\Omega _{ \circ } }} {\delta p\alpha \left( {\nabla .{\dot{\mathbf{u}}}} \right)} {\text{d}}\Omega } \\ & \quad + \int\limits_{{\Omega _{ \circ } }} {\nabla \delta p\frac{{\mathbf{k}}}{{\mu_{f} }}\left( { - \nabla p + \rho {\mathbf{b}}} \right){\text{d}}\Omega } \\ \end{aligned}$$
(49)
$$\begin{aligned} \int\limits_{{\Gamma _{\text{c}} }} {\delta p\left[\kern-0.15em\left[ {\mathbf{v}} \right]\kern-0.15em\right]} .{\mathbf{n}}_{{\Gamma _{\text{c}} }} {\text{d}}\Gamma & = \int\limits_{{\Gamma _{\text{c}} }} {\delta pq^{\prime}} {\text{d}}\Gamma = \int\limits_{{\Gamma _{\text{c}} }} {\delta p\left( {\frac{\alpha - n}{{K_{\text{s}} }} + \frac{n}{{K_{\text{f}} }}} \right)\dot{p}2\vartheta {\text{d}}\Gamma } \\ & \quad + \int\limits_{{\Gamma _{\text{c}} }} {\delta p\alpha 2\vartheta \left( {\frac{{\partial {\dot{\mathbf{u}}}_{x} }}{{\partial x^{\prime}}}} \right){\text{d}}\Gamma } + \int\limits_{{\Gamma _{c} }} {\delta p\alpha \left[\kern-0.15em\left[ {{\dot{\mathbf{u}}}_{{y^{\prime}}} } \right]\kern-0.15em\right]{\text{d}}\Gamma } \\ & \quad - \int\limits_{{\Gamma _{\text{c}} }} {\frac{{\mathbf{k}}}{{\mu_{f} }}2\vartheta \left( {\frac{\partial \delta p}{{\partial x^{\prime}}}\frac{\partial p}{{\partial x^{\prime}}}} \right)} {\text{d}}\Gamma \\ & \quad + \int\limits_{{\Gamma _{\text{c}} }} {\left( {\frac{{\mathbf{k}}}{{\mu_{f} }}2\vartheta \left( {\frac{\partial \delta p}{{\partial x^{\prime}}}} \right)\rho_{f} {\mathbf{b}}} \right)} {\text{d}}\Gamma \\ \end{aligned}$$
(50)

According to the literature of strong discontinuity regularization method for shear band modeling, the dilation occurs by the separation of discontinuity surfaces and this is the dominating factor. Therefore, updating hydraulic parameters is negligible, particularly in infinitesimal deformations range [5]. There is hence no need to update the permeability in the shear band once it is formed because its effect would be negligible. In fact, in [35] both combinations of cubic law in the fracture and Darcy outside and Darcy everywhere with same parameters gave no appreciable difference in the results. Note that in hydraulic fracturing flow issues are more pronounced than in our case.

2.4 Second-order work theory

Different criteria are available for the failure analysis of soil. In the context of strain localization, the most used one is the acoustic tensor analysis, while the use of second-order work criterion is less common. It has been observed in practice that failure can occur well before the Mohr–Coulomb criterion is met. This is due to the non-associated behavior (the yield surface does not coincide with the plastic potential, which leads to a non-symmetric constitutive tensor) of cohesive and/or frictional materials, such as soils. According to [8, 17] in case of such materials, one can find an unstable domain strictly inside the plastic limit envelope. Interestingly, material instabilities can lead to diffuse modes of failure inside the plastic limit condition, which are characterized by the lack of localization patterns, and for this reason, it cannot be detected neither by a plastic limit criterion nor by a localization criterion [9, 27]. The concept of the second-order work was proposed by Hill [13] who connected the notion of stability with the sign of the second-order work. At the material point level, it is described as follows: a mechanical stress–strain state is considered as stable if the second-order work is strictly positive for any couple \(({\text{d}}{\varvec{\upsigma}}',{\text{d}}{\varvec{\upvarepsilon}})\) linked by the rate-independent constitutive relation

$$\forall ({\text{d}}{\varvec{\upsigma}}',{\text{d}}{\varvec{\upvarepsilon}}) \in R^{2n} \backslash \{ 0\} {\text{ with d}}{\varvec{\upvarepsilon}} = {\mathbf{C}}:{\text{d}}{\varvec{\upsigma}}'{ , }W_{2} = {\text{d}}{\varvec{\upsigma}}':{\text{d}}{\varvec{\upvarepsilon}}$$
(51)

where n is the dimension of the stress (or strain \({\varvec{\upvarepsilon}}\)) space and \({\mathbf{C}}\) is the stiffness tensor. The vanishing of the value of the second-order work indicates potential instability. It can then be considered as a generalized criterion because, in case of non-associated materials, the second-order work \(W_{2}\) (which first vanishes together with the determinant of the symmetric part of the stiffness tensor \({\mathbf{C}}\), [20]) becomes zero before the vanishing of the determinant of the constitutive tensor \({\mathbf{C}}\) and of the determinant of the acoustic tensor [7, 17, 20]. There is still the question regarding the type of stress that should be used in Eq. (51) when studying the stability of a multiphase porous body. The possible choices are discussed in [15]. Consistently with what used for the evaluation of the acoustic tensor, we write the second-order work in terms of effective stresses. For evaluating Eq. (51), the differential operator \(d()\) is substituted by its discrete counterpart

$$\Delta ( \, ) = ( \, )_{n + 1} - ( \, )_{n}$$
(52)

where \(n + 1\) is the present time step and \(n\) is the previous time step. In this paper the efficiency of second-order work criteria within the framework of XFEM is investigated for stability analysis of strong discontinuity shear bands. To our best knowledge, it is the first application in case of XFEM. As will be shown, the tool seems quite robust and can be extended to 3-D shear band problems.

2.5 XFEM formulation

For solving the fluid–structure interaction, both displacement and pressure fields have to be discretized in the whole domain. The discontinuous components of the displacement and pressure field are approximated by XFEM [23, 24]

$${\mathbf{u}}(\varvec{x}) = \sum\limits_{i \in j} {N_{\text{s}} (\varvec{x}){\mathbf{u}} + \sum\limits_{i \in k} {N_{\text{s}} (\varvec{x})\chi_{i} {\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{u} }}} }$$
(53)
$$p(\varvec{x}) = \sum\limits_{i \in j} {N_{\text{f}} (\varvec{x})p + \sum\limits_{i \in g} {N_{\text{f}} (\varvec{x}){\rm M}_{i} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{p} } } \,$$
(54)

where \(N_{\text{s}}\) and \(N_{\text{f}}\) are the standard displacement and pressure shape functions, respectively, \(j\) is the number of element nodes, \(k\) represents the number of nodes with displacement enrichment terms, and \(g\) is the number of nodes with pressure enrichment functions. \({\mathbf{u}}\) and \({\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{u} }}\) also \(p\) and \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{p}\) are, respectively, the standard and enriched degrees of freedom. Further,

$$\chi_{i} = \left[ {H_{\text{s}} ({\mathbf{x}}) - H_{\text{s}} ({\mathbf{x}}_{i} )} \right]{\mathbf{m}},\quad H_{\text{s}} (x) = \left\{ {\begin{array}{*{20}c} 1 & {x \in\Omega ^{ + } } \\ { - 1} & {x \in\Omega ^{ - } } \\ \end{array} } \right. \,$$
(55)

where \(H_{\text{s}} (x)\) is the Heaviside step function and \({\mathbf{m}}\) is the unit localization vector across the discontinuous interface. The enrichment function is correlated with two degrees of freedom across the normal and tangential directions of the discontinuity in the n–t local coordinate system in Eq. (19). It is emphasized that the discontinuity in the displacement field includes the two normal and tangential components. The node enrichment selection for elements containing a shear band is shown in Fig. 3. Further

$${\rm M}_{i} = \left[ {\varUpsilon ({\mathbf{x}}) - \varUpsilon_{i} ({\mathbf{x}})} \right],$$
(56)
$$\varUpsilon ({\mathbf{x}}) = \sum\limits_{{i \in n_{ \circ } }} {N_{fi} ({\mathbf{x}})\left| {\zeta_{i} } \right| - \left| {\sum\limits_{{i \in n_{ \circ } }} {N_{fi} ({\mathbf{x}})\zeta_{i} } } \right|}$$
(57)

where \(\varUpsilon\) is the modified level set function and \(\zeta\) is the value of level set function in nodes across the discontinuous interface. This function is continuous although its normal gradient is discontinuous. And as result, it implies water flow normal to the shear band surface discontinuity.

Fig. 3
figure 3

Selection of enriched nodes for elements containing a shear band

Full size image

For the solid phase, the corresponding strain field is accordingly derived as

$${\varvec{\upvarepsilon}}(\varvec{x}) = {\mathbf{B}}_{s}^{\text{std}} (\varvec{x}){\mathbf{u}} + {\mathbf{B}}_{s}^{\text{enr}} (\varvec{x}){\tilde{\mathbf{u}}}$$
(58)

where \({\mathbf{B}}_{s}^{\text{std}}\) and \({\mathbf{B}}_{s}^{\text{enr}}\) are the matrices of derivatives of the standard and enrichment shape functions, respectively,

$${\mathbf{B}}_{s}^{\text{std}} (\varvec{x}) = {\mathbf{L}}_{s} N_{\text{s}}^{\text{std}} (\varvec{x})$$
(59)
$${\mathbf{B}}_{s}^{\text{enr}} (\varvec{x}) = {\mathbf{L}}_{s} N_{\text{s}}^{\text{enr}} (\varvec{x})$$
(60)
$${\mathbf{B}}_{s} = \left[ {{\mathbf{B}}_{s}^{\text{std}} \, {\mathbf{B}}_{s}^{\text{enr}} } \right]$$
(61)

and \({\mathbf{L}}_{s}\) is the differential operator for the plane problem

$${\mathbf{L}}_{s} = \left[ \begin{aligned} \frac{\partial }{{\partial \varvec{x}}} \hfill \\ \hfill \\ 0 \hfill \\ \frac{\partial }{{\partial \varvec{y}}} \hfill \\ \end{aligned} \right. \, \left. \begin{aligned} 0 \hfill \\ \hfill \\ \frac{\partial }{{\partial \varvec{y}}} \hfill \\ \frac{\partial }{{\partial \varvec{x}}} \hfill \\ \end{aligned} \right]$$
(62)

The virtual displacement field \(\varvec{\xi}\) and its associated gradient \({\mathbf{L}}_{s}\varvec{\xi}\) are defined by

$$\varvec{\xi}= \sum\limits_{i \in j} {N_{\text{s}}^{\text{std}} \delta {\mathbf{u}} + \sum\limits_{i \in k} {N_{\text{s}}^{\text{std}} \left( {H_{\text{s}} - H_{{{\text{s}}_{i} }} } \right){\mathbf{m}}_{i} \delta {\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{u} }}} } { , }N_{\text{s}} = \left[ {N_{\text{s}}^{\text{std}} \, N_{\text{s}}^{\text{enr}} } \right]$$
(63)
$${\mathbf{L}}_{s}\varvec{\xi}= \sum\limits_{i \in j} {{\mathbf{B}}_{s}^{\text{std}} \delta {\mathbf{u}} + \sum\limits_{i \in k} {{\mathbf{B}}_{s}^{\text{enr}} \delta } } {\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{u} }}{ , }{\mathbf{B}}_{s} = [{\mathbf{B}}_{s}^{\text{std}} \, {\mathbf{B}}_{s}^{\text{enr}} ]$$
(64)

For the fluid phase, the virtual pressure and its gradient are defined as,

$$\varvec{\xi^{\prime}} = \sum\limits_{i \in j} {N_{\text{f}}^{\text{std}} \delta p + \sum\limits_{i \in k} {N_{\text{f}}^{\text{std}} \left( {\varUpsilon - \varUpsilon_{i} } \right)\delta \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{p} } } { , }N_{\text{f}} = \left[ {N_{\text{f}}^{\text{std}} \, N_{\text{f}}^{\text{enr}} } \right]$$
(65)
$${\mathbf{L}}_{\text{f}} \varvec{\xi^{\prime}} = \sum\limits_{i \in j} {{\mathbf{B}}_{f}^{\text{std}} \delta p + \sum\limits_{i \in k} {{\mathbf{B}}_{f}^{\text{enr}} \delta } } \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{{\text{p} , }}{\mathbf{B}}_{f} = \left[ {{\mathbf{B}}_{f}^{\text{std}} \, {\mathbf{B}}_{f}^{\text{enr}} } \right] \,$$
(66)

where \({\mathbf{L}}_{\text{f}}\) is differential operator for fluid pressure,

$${\mathbf{L}}_{\text{f}} = \left[ \begin{aligned} \frac{\partial }{{\partial \varvec{x}}} \hfill \\ 0 \hfill \\ \end{aligned} \right. \, \left. \begin{aligned} 0 \hfill \\ \frac{\partial }{{\partial \varvec{y}}} \hfill \\ \end{aligned} \right]$$
(67)

Eventually, the discretized form of Eqs. (1) and (4) can be rewritten as

$${\mathbf{F}}_{s}^{{\text{int} ,n + 1}} + {\mathbf{F}}_{s}^{{\text{coh,}n\text{ + 1}}} - {\mathbf{C}}_{sf}^{n + 1} {\mathbf{P}}^{n + 1} = {\mathbf{F}}_{s}^{{\text{ext,}n\text{ + 1}}}$$
(68)
$${\mathbf{C}}_{fs}^{n + 1} {\dot{\mathbf{U}}}^{n + 1} + {\mathbf{P}}_{ff}^{n + 1} {\dot{\mathbf{P}}}^{n + 1} + {\mathbf{H}}_{ff}^{n + 1} {\mathbf{P}}^{n + 1} + {\mathbf{Q}}_{\text{int}}^{n + 1} = {\mathbf{F}}_{f}^{{\text{ext,}n\text{ + 1}}}$$
(69)

and the internal forces for standard and enriched components are

$$\begin{aligned} {\mathbf{F}}_{s}^{{\text{int} ,n + 1}} = \int_{\Omega } {{\mathbf{B}}_{s} \cdot {\varvec{\upsigma}}{\text{d}}\Omega } = \int_{\Omega } {{\mathbf{B}}_{s} .{\mathbf{C}}^{{{\mathbf{ep}}}} .{\mathbf{B}}_{s} {\text{d}}\Omega } {\mathbf{U}}^{n + 1} = {\mathbf{KU}}^{n + 1} \hfill \\ \hfill \\ \end{aligned}$$
(70)
$${\mathbf{F}}_{s}^{{\text{coh}}} = \int_{{\Gamma _{\text{c}} }} {\left[\kern-0.15em\left[ {N_{\text{s}} H_{\text{s}} } \right]\kern-0.15em\right]} {\varvec{\uptau}}_{c} {\text{d}}\Gamma _{c} = \int_{{\Gamma _{\text{c}} }} {N_{\text{s}} \left( {1 - H_{\text{s}} } \right)} {\varvec{\uptau}}_{c} {\mathbf{m}}{\text{d}}\Gamma _{c} - \int_{{\Gamma _{\text{c}} }} {N_{\text{s}} \left( { - 1 - H_{\text{s}} } \right)} {\mathbf{m\tau }}_{c} {\text{d}}\Gamma _{\text{c}} = 2\int_{{\Gamma _{c} }} {N_{\text{s}} {\mathbf{m}}} {\varvec{\uptau}}_{c} {\text{d}}\Gamma _{\text{c}}$$
(71)
$${\mathbf{C}}_{sf} = \int_{\Omega } {{\mathbf{B}}_{s}^{T} \alpha mN_{\text{f}} {\text{d}}\Omega }$$
(72)
$${\mathbf{P}}_{ff} = \int_{\Omega } {N_{\text{f}}^{T} \left( {\frac{1}{{Q_{f} }}} \right)N_{\text{f}} {\text{d}}\Omega }$$
(73)
$${\mathbf{H}}_{ff} = \int_{\Omega } {\left( {{\mathbf{L}}_{f} N_{\text{f}} } \right)^{\text{T}} \left( {\frac{{\mathbf{k}}}{{\mu_{f} }}} \right)\left( {{\mathbf{L}}_{f} N_{\text{f}} } \right){\text{d}}\Omega }$$
(74)
$$\begin{aligned} Q_{\text{int}} & = \int\limits_{{\Gamma _{\text{c}} }} {{\mathbf{N}}_{\text{f}}^{T} q^{\prime}{\text{d}}\Gamma _{\text{c}} = \int\limits_{{\Gamma _{\text{c}} }} {N_{\text{f}}^{T} \left( {\frac{\alpha - n}{{K_{\text{s}} }} + \frac{n}{{K_{\text{f}} }}} \right)\dot{p}2\vartheta {\text{d}}\Gamma _{\text{c}} } } \\ & \quad + \int\limits_{{\Gamma _{\text{c}} }} {N_{\text{f}}^{T} \alpha 2\vartheta \left( {\nabla {\dot{\mathbf{u}}}} \right){\text{d}}\Gamma _{\text{c}} } + \int\limits_{{\Gamma _{\text{c}} }} {N_{\text{f}}^{T} \alpha \left[\kern-0.15em\left[ {{\dot{\mathbf{u}}}} \right]\kern-0.15em\right]{\text{d}}\Gamma _{\text{c}} } \\ & \quad - \int\limits_{{\Gamma _{\text{c}} }} {\frac{{\mathbf{k}}}{{\mu_{f} }}2\vartheta \left( {{\mathbf{L}}_{f} N_{\text{f}}^{T} } \right)\nabla p} {\text{d}}\Gamma _{\text{c}} + \int\limits_{{\Gamma _{\text{c}} }} {\left( {\frac{{\mathbf{k}}}{{\mu_{f} }}2\vartheta \left( {{\mathbf{L}}_{f} N_{\text{f}}^{T} } \right)\rho_{f} {\mathbf{b}}} \right)} {\text{d}}\Gamma _{\text{c}} \\ \end{aligned}$$
(75)

\({\mathbf{C}}_{sf}\) is the coupling matrix, \({\mathbf{P}}_{ff}\) is the compressibility matrix, \({\mathbf{H}}_{ff}\) is the permeability matrix, and \(Q_{\text{int}}\) is the fluid mass exchange from the continuum to the strain localized zone. The external forces for standard and enriched components are

$${\mathbf{F}}_{s}^{\text{ext}} = \int_{\Omega } {N_{\text{s}} {\mathbf{b}}{\text{d}}\Omega + } \int_{{\Gamma _{t} }} {N_{\text{s}} } {\mathbf{T}}{\text{d}}\Gamma$$
(76)
$${\mathbf{F}}_{f}^{{\text{ext}}} = \int_{\Omega } {N_{\text{f}} {\mathbf{b}}{\text{d}}\Omega + } \int_{{\Gamma _{\text{f}} }} {N_{\text{f}} } \text{q}{\text{d}}\Gamma _{f}$$
(77)

Finally, the nonlinear, coupled discretized Eqs. (68) and (69) must be discretized in time domain [44] and then solved incrementally by the Newton–Raphson method until required convergence is obtained at each increment.

$${\mathbf{F}}_{s}^{{\text{int} ,n + 1}} + {\mathbf{F}}_{s}^{{\text{coh,}n\text{ + 1}}} - {\mathbf{C}}_{sf}^{n + 1} {\mathbf{P}}^{n + 1} = {\mathbf{F}}_{s}^{{\text{ext,}n\text{ + 1}}}$$
(78)
$${\mathbf{C}}_{fs}^{n + 1} {\dot{\mathbf{U}}}^{n + 1} + {\mathbf{P}}_{ff}^{n + 1} {\dot{\mathbf{P}}}^{n + 1} + {\mathbf{H}}_{ff}^{n + 1} {\mathbf{P}}^{n + 1} + {\mathbf{Q}}_{\text{int}}^{n + 1} = {\mathbf{F}}_{f}^{{\text{ext,}n\text{ + 1}}}$$
(79)

With the following terms, an implicit integration results

$${\dot{\mathbf{U}}}^{n + 1} = \frac{{{\mathbf{U}}^{n + 1} - {\mathbf{U}}^{n} }}{\Delta t}, \, {\dot{\mathbf{P}}}^{n + 1} = \frac{{{\mathbf{P}}^{n + 1} - {\mathbf{P}}^{n} }}{\Delta t}$$
(80)

and the residual of the equilibrium and mass conservation discretized equations are

$${\mathbf{R}}_{s}^{i,n + 1} = {\mathbf{F}}_{s}^{{\text{int} ,n + 1}} + {\mathbf{F}}_{s}^{{\text{coh,}n\text{ + 1}}} - {\mathbf{C}}_{sf}^{n + 1} {\mathbf{P}}_{f}^{i,n + 1} - {\mathbf{F}}_{s}^{{\text{ext,}n\text{ + 1}}}$$
(81)
$${\mathbf{R}}_{f}^{i,n + 1} = {\mathbf{C}}_{fs}^{n + 1} \left( {\frac{{{\mathbf{U}}^{n + 1} - {\mathbf{U}}^{n} }}{\Delta t}} \right) + {\mathbf{P}}_{ff}^{n + 1} \left( {\frac{{{\mathbf{P}}^{n + 1} - {\mathbf{P}}^{n} }}{\Delta t}} \right) + {\mathbf{H}}_{ff}^{n + 1} {\mathbf{P}}^{n + 1} + {\mathbf{Q}}_{\text{int}}^{n + 1} - {\mathbf{F}}_{f}^{{\text{ext,}n\text{ + 1}}}$$
(82)

\({\mathbf{U}}^{i,n + 1}\) and \({\mathbf{P}}^{i,n + 1}\) are the unknown vectors and \({\mathbf{R}}_{s}^{i,n + 1}\) and \({\mathbf{R}}_{f}^{i,n + 1}\) are residual vectors.

At each iteration, the unknown vectors are obtained from

$$\left\{ \begin{aligned} {\mathbf{R}}_{s}^{i + 1,n + 1} \hfill \\ {\mathbf{R}}_{f}^{i + 1,n + 1} \hfill \\ \end{aligned} \right\} = \left\{ \begin{aligned} {\mathbf{R}}_{s}^{i,n + 1} \hfill \\ {\mathbf{R}}_{f}^{i,n + 1} \hfill \\ \end{aligned} \right\} + {\mathbf{J}}\left\{ \begin{aligned} {\text{d}}{\mathbf{U}}^{i + 1,n + 1} \hfill \\ {\text{d}}{\mathbf{P}}^{i + 1,n + 1} \hfill \\ \end{aligned} \right\} = 0$$
(83)

with the \({\mathbf{J}}\) Jacobian matrix

$${\mathbf{J}} = \left\{ \begin{aligned} {\mathbf{K}} + \frac{{\partial {\mathbf{F}}_{\text{coh}} }}{{\partial {\mathbf{u}}}} \hfill \\ {\mathbf{C}}_{fs} + \frac{{\partial {\mathbf{Q}}_{\text{int}} }}{\partial p} \hfill \\ \end{aligned} \right. \, \left. \begin{aligned} \, {\mathbf{C}}_{sf} + \frac{{\partial {\mathbf{F}}_{\text{coh}} }}{{\partial {\mathbf{u}}}} \hfill \\ \frac{{{\mathbf{P}}_{ff} }}{\Delta t} + {\mathbf{H}}_{ff} + \frac{{\partial {\mathbf{Q}}_{\text{int}} }}{\partial p} \hfill \\ \end{aligned} \right\}$$
(84)

Consequently, the unknown vector is calculated as,

$$\left\{ \begin{aligned} {\text{d}}{\mathbf{U}}^{i + 1,n + 1} \hfill \\ {\text{d}}{\mathbf{P}}^{i + 1,n + 1} \hfill \\ \end{aligned} \right\} = - {\mathbf{J}}^{ - 1} \left\{ \begin{aligned} {\mathbf{R}}_{s}^{i,n + 1} \hfill \\ {\mathbf{R}}_{f}^{i,n + 1} \hfill \\ \end{aligned} \right\}$$
(85)

According to the theory of second-order work, the incremental Eq. (51) must be checked at each time step n + 1 in which the components of stress and strain at Gauss points of each element are calculated. This procedure is challenging when shear band discontinuity crosses a continuous element (and divides it into two parts), due to the new configuration of the added Gauss points used for integration in the discontinuous element. For discontinuous elements, we use an integration method other than the conventional one, dividing the element into sub-triangles, as shown in Fig. 4a. In this procedure, each side of discontinuity is divided into sub-triangles in which the integration of each sub-triangle is done by conventional Gauss integration method [6]. To circumvent the difficulty of computing Eq. (51) when the shear band has just crossed the continuous element (Fig. 4b), an averaging procedure is adopted to extrapolate the magnitudes of new Gauss points to the conventional Gauss points.

Fig. 4
figure 4

a Subdivision of shear banded element including sub-triangles with new Gauss points. b Continuous element with conventional Gauss points

Full size image

3 Numerical simulations

We present now numerical examples based on the above outlined approach, investigating also the propagation of shear band in saturated porous media where applicable. Two problems are presented: a plane strain compression test of a strip and a foundation with two rates of imposed displacements. The second example evidences that an apriori unknown localization path can be captured with the method.

3.1 Plane strain compression simulation

For this case, we consider two mesh configurations with higher and lower mesh density which allows to shed light on the sensitivity of the proposed numerical method. The related material properties are listed in Table 1.

Table 1 Material properties for plane strain compression test
Full size table

The strip and associated boundary conditions for the solid are depicted in Fig. 5; a geometry imperfection is applied to the top right corner point of the sample to initiate the shear band by means of an ensuing stress concentration. Along all the boundaries of the sample drainage of the fluid is allowed, as in [18] where the problem was solved with an element embedded band approach and a cohesive isotropic hardening/softening law. At the upper face a velocity of \(0.1\frac{{\hbox{mm}}}{{\hbox{s}}}\) is prescribed.

Fig. 5
figure 5

Geometry of sample and related boundary conditions

Full size image

The two meshes used are shown in Fig. 6. Figure 7 displays the shear band and its inclination angle for the two meshes and for two rates of loading, \(\dot{\delta }_{1} = 0.1\frac{{\hbox{mm}}}{{\hbox{s}}}\) and \(\dot{\delta }_{2} = 0.5\frac{{\hbox{mm}}}{{\hbox{s}}}\). Path A is for mesh type 1, D is for mesh type 2, C is the solution of [18], and B relates to mesh type 1 with loading rate type 2. The modes of localization evolution for two meshes are similar, and there are little changes as the rate of loading increases 5 times (rate type-2); this is due to the easy drainage of the excess pore water pressure. This example evidences the mesh independency of numerical method. In this example there is no real advancement of the shear band as it develops almost instantaneously once the required conditions are met.

Fig. 6
figure 6

Different mesh types for plane strain strip. a Mesh type-1. b Mesh type-2

Full size image
Fig. 7
figure 7

The angle and path of formed shear bands for different mesh types and rates of loading

Full size image

Figure 8 shows the global response of the sample under prescribed rates of displacement. The peak load and the corresponding displacement of the top surface are the same as in [18]. As expected, the responses differ for different loading rates which evidence the time dependency of the numerical solution due to the presence of a pore fluid. This can be seen in Fig. 9 where the variation of the fluid pressure at the midpoint of the sample is drawn against the vertical displacement; this point falls within the shear band. According to this figure, the formation of the shear band affects the pressure field. Some suction develops as the shear band forms and a discontinuity of the pressure gradient appears as will be shown below.

Fig. 8
figure 8

Force–displacement curve for different loadings

Full size image
Fig. 9
figure 9

Pressure–displacement curve for different loadings for point A

Full size image

The shear band is localized in highly plastic deformed zones as shown in Fig. 10.

Fig. 10
figure 10

Evolution of plastic straining during the stages of loading; δ indicates the maximum displacement imposed

Full size image

Drained or undrained conditions would not only affect the flow pattern but also the solid deformation within and outside the shear band. This is evidenced in Fig. 11 where for only drainage from the top surface the plastic strains are shown for two loading stages. It appears that the localization of plastic strains in shear bands decreases as the draining condition changes to relatively undrained state. In fact, in globally undrained conditions and dilatant materials, localization can start only when the cavitation pressure is reached, as shown by Mokni [25].

Fig. 11
figure 11

Evolution of plastic straining for relative undrained condition during the stages of loading

Full size image

Because of the boundary conditions for the flow field and the high permeability, there is no real pressure localization in the shear band as evidenced for instance in [43]. However, suction develops in the process and the pressure field is slightly tilted in the direction of the shear band once it is fully developed as shown in the last picture of Fig. 12. The corresponding pressure gradients are drawn in Fig. 13. No pressures are shown in [18]; hence, a comparison is not possible.

Fig. 12
figure 12

Pressure fields for different steps of loading

Full size image
Fig. 13
figure 13

Pressure gradient field (Pa/m) for different stages of loading

Full size image

Finally, Fig. 14 shows the distribution of the three stress components in the sample for the last stage of formation of the shear band. The discontinuity of the stresses between the two sides of the shear band is remarkable.

Fig. 14
figure 14

Distribution of stresses for last time step. a \(\sigma_{xx}\), b \(\sigma_{xy}\), c \(\sigma_{yy}\)

Full size image

Initiation of softening behavior and its successive development are a precursor to the instability of the structure. The proposed second-order work criterion for saturated porous media determines the material point stability state and gives us a new insight in the structure overall condition. As shown in Fig. 15, the computed second-order work for the strip is positive when delta is \(0.72\delta\), while with the nucleation of the shear band, instability localizes in a banded zone. At this instance the region outside remains still stable. In the loading step \(0.85\delta\), the second-order work of the whole area is negative, indicating that the entire domain is unstable. This confirms what could be seen from Fig. 8.

Fig. 15
figure 15

Second-order work for strip at various loading steps

Full size image

3.2 Foundation

A more common situation for shear band formation can be found under foundations due to excessive loading which may eventually lead to failure of the structure. We model hence such a problem, depicted in Fig. 16 together with the boundary conditions for the solid phase. The material properties are taken from [4]: Young’s modulus \(30\,{\text{MPa}}\), Poisson ratio \(0.2\), Drucker–Prager friction constant \(24^{ \circ }\) and dilatancy parameter \(5^{ \circ }\), Poisson ration \(0.25\), initial cohesive stress \(63.41\,{\text{KPa}}\), bulk modulus of solid \(3.3 \times 10^{9} \,{\text{Pa}}\), bulk modulus of fluid \(3.3 \times 10^{19} \,{\text{Pa}}\), Biot’s constant 1 with softening modulus of \(100\,{\text{KPa}}\). For the fluid it is assumed that the left and above edges are open to flow. Vertical velocities \(\dot{\delta }_{1} = 5 \times 10^{ - 7} \frac{{\hbox{mm}}}{{\hbox{s}}}\) and \(\dot{\delta }_{2} = 1 \times 10^{ - 7} \frac{{\hbox{mm}}}{{\hbox{s}}}\) are imposed to the rigid permeable foundation. Two mesh configurations with 800 and 400 irregular triangular element are selected as shown in Fig. 17 to check mesh dependence of the solution.

Fig. 16
figure 16

Geometry of foundation with associated boundary conditions

Full size image
Fig. 17
figure 17

Types of mesh. a Mesh type 1 and b mesh type 2

Full size image

The load–deflection curves are compared in Fig. 18 for the two mesh types and Ref. [4]. As is shown, the load bearing capacity increases with the rate of loading. In fact due to the coupling effects, high rates of loading increase the pore pressure and consequently the related bearing capacity of the foundation. In case of single-phase media of [31] and [30], where only tangential sliding of the shear band is considered together with a von Mises yield criterion, the shear band formation is accompanied by brittle behavior, severe softening and failure. In our fully saturated case the behavior is rather ductile, see Fig. 18. Also the plastic deformation is distributed throughout a large part of the section as can be seen in Fig. 25 from the distribution of the second-order work: differently from the relevant cases of [31] and [30], only part of the energy is dissipated in the shear band. As in [4] where a continuous pressure and discontinuous gradient of pressure field across shear band is assumed, the slight softening behavior of the model is reproduced and a good agreement of the results is observed.

Fig. 18
figure 18

Load–displacement curve

Full size image

Figure 19 compares the path of shear band propagation for two mesh types with Ref. [4]. We obtain a curved form of the shear band which is common in such situations, see, e.g., [18]. The solution of [4] in Fig. 19 is an idealized representation because those authors obtain a mesh dependent wavy form of the shear band in the lower part which does not seem realistic.

Fig. 19
figure 19

Shear band path

Full size image

Figure 20 depicts the plastic deformation during the evolution of the shear band for four stages. As the shear band initiates, the plastic deformations localize into shear band surfaces and continue until the full formation of the shear band and consequent failure of the structure. The propagation of the shear band is here well captured.

Fig. 20
figure 20

Effective plastic deformation distribution

Full size image

The variation of fluid pressure during loading is for point A of Fig. 16 (x = 2.5 m, y = 10.8 m) which is shown in Fig. 21. Again the comparison with [4] is quite good, given the difference of the respective models. Prior to the appearance of the shear band the pressure increases, while from the onset of the band on it decreases. This drop is a consequence of the dilation of the solid phase in the shear band resulting in a pressure gradient toward the shear band.

Fig. 21
figure 21

Pressure–displacement curve

Full size image

The fluid pressure contours and gradient are presented in Figs. 22 and 23, respectively, for successive stages of loading. Some localization of the pressures can be observed. The flow toward shear band is captured by the gradients of the pressure field in Fig. 23 which was enriched with weak discontinuous functions Eq. (57).

Fig. 22
figure 22

Fluid pressure contours

Full size image
Fig. 23
figure 23

Pressure gradient field (Pa/m) contours

Full size image

Figure 24 presents the distribution of stresses at the last stage of the analysis. Again the discontinuity of the stresses across shear band is well represented.

Fig. 24
figure 24

Components of stresses for last time step of fully developed shear band

Full size image

For problems with moderate softening behavior, investigation of the global instability is very important for evaluating the global response of the structure under external loading. As depicted in Fig. 25, the instability is not so severe in contrast to the plastic strain localization in shear band region (Fig. 20). The value of the second-order work obtained by integration on the whole physical domain could give measure for the stability of the entire soil mass [15].

Fig. 25
figure 25

Second-order work distribution during the shear band development

Full size image

4 Conclusions

We have combined a strong discontinuity approach with XFEM analysis to investigate with a Drucker–Prager model within non-associated plasticity shear banding in fully saturated porous media. This combination works well and is able to represent properly the evolution of the shear band and the pore pressures and yields mesh independent result. This has been shown on two examples where the results compare well with those found in the literature. Further, the results have been confirmed by the application of the second-order work criterion. As pointed out in [15], this criterion not only indicates the development of the local instability but if integrated over the whole soil mass could give useful information about the instability of the global  value. If this global domain is negative, the entire domain is unstable. The global value plays the role of a safety factor. When local negative values are obtained with a positive global value, the criterion indicates that the whole domain is still globally stable, possibly approaching to a properly unstable state. The procedure outlined in this paper will now be extended to partially saturated cases.