Effects of the micro-structure and micro-parameters on the mechanical behaviour of transversely isotropic rock in Brazilian tests

Abstract

Based on the Brazilian test results of 23 kinds of transversely isotropic rocks, five trends are obtained for the variation of normalized failure strength (NFS) as a function of the weak plane-loading angles. For each angle, three kinds of fracture patterns are obtained. Furthermore, a new numerical approach based on the particle discrete element method is put forward to systematically investigate the influence of the micro-structure of rock matrix and strength of weak plane on NFS and fracture patterns. The results reveal that the trend of NFS and fracture patterns are slightly influenced by coordination number of rock particles and tensile strength of weak plane, but greatly influenced by percentage of pre-existing cracks and shear strength of weak plane. Micro-parameters of the numerical approach are calibrated to reproduce behaviours of transversely isotropic rocks with different trends, and the simulation results are well matched with experimental results in terms of NFS and fracture patterns. Finally, the numerical approach is applied to study the failure process of layered surrounding rock after tunnel excavation. The simulation results also agree well with observation results of engineering projects.

1 Introduction

The transverse isotropy inherent in rocks (bedding planes, stratification, layering or weak plane) often determines their physical and mechanical behaviour [8, 23]. Among these behaviour, the tensile strength, which is considerably lower than the compressive strength, is vulnerable to transverse isotropy and thus plays an important role in in situ stress measurement [1, 18], the formation and evolution of excavation damaged zone (EDZ) during tunnel excavation [14, 27], rock-cutting efficiency in mechanized tunnelling [17, 36], drilling direction control in oil and gas fields [7] and the pathway of hydraulic fractures [26, 29, 47, 51].

The Brazilian test is more widely used to measure tensile strength than the direct test method [25]. In 1973, the Brazilian test began to be used to determine the tensile strength of transversely isotropic rocks. Then, Barla and Innaurato [4] discussed its feasibility. Subsequent studies presented experimental results obtained from tests on sandstone [8, 16, 40, 43], slate [11, 28], shale [9, 20, 48], schist [9], gneiss [9, 11, 35], and granite [14]. These results revealed that the relationship between the fracture patterns or tensile strength and the weak plane-loading angle (the angle between the loading direction and the weak plane, β) is complex due to the influence of several important factors, including the strength ratio between weak planes and the rock matrix and the micro-structure of the rock matrix (percentage of pre-existing cracks and coordination number of rock particles). However, it is difficult to figure out the ways in which these factors can affect variation of strength and fractures in detail through experiments.

As a supplement to laboratory experiments, numerical simulation provides another method to study the problem discussed above. As a means of characterizing weak planes, numerical methods can be divided into continuous medium methods (CMMs) and discrete element methods (DEMs). CMMs can be further divided into the diffusion element method and finite discrete element method (FDEM). In the diffusion element method, the effect of weak planes is dispersed into each rock matrix unit [11]. In the FDEM, the elastic properties of rock are described by a transversely isotropic elastic model, whereas the fracture process of rock is described using a nonlinear fracture mechanics criterion [27]. The DEM can be a block [12, 39] or particle DEM [13, 34] based on the shape of the elements. In the DEM, weak planes can be embodied intuitively, and the initiation and propagation of cracks can be obtained explicitly without applying complex constitutive laws.

The continuum techniques could be easily adopted to large-scale engineering problems, while complex constitutive models are needed to fully capture the main features of the progressive breakdown of transversely isotropic rocks [38, 41, 42]. As for DEM methods, although the large computational demand tends to limit their applicability to small-scale problems, it may offer unique advantages when simulating the fracture mechanism and process of transversely isotropic rocks.

It is crucial to figure out the meso-mechanism of rock isotropy when adopting DEM methods to characterize transversely isotropic rocks. With the advent of new testing techniques [5, 37], numerous test results have made the meso-mechanical analysis of rock isotropy more reliable, providing a basis for numerical simulation. Based on nanoscale structure of shale revealed by Hornby et al. [19], Zhang [50] proposed a numerical model to simulate rock anisotropy at nanoscale scale. In their numerical model, a composite structure is used to reproduce the skeleton of shale and weak fillings are simulated by particles; Kim et al. [24] obtained the 3D pore structure of Berea sandstone based on X-ray CT test and established an DEM model which can describe its pore structure; Chong et al. [10] put forward a DEM model which is capable of considering the composition of particles; Park and Min [31] found that the bonded-particle DEM model with embedded smooth joint can behave as an equivalent transversely isotropic continuum; Wang et al. [44] built a DEM model of stratified granulite based on its microscopic observation result of thin section, the simulation result revealed that both the rock matrix and weak planes are characterized by bonded-particle model can also characterize the transverse isotropy of rock well.

In this article, a more realistic numerical approach employing the DEM is proposed to represent transversely isotropic rocks. Firstly, the influence of the strength of weak plane and the micro-structure of rock matrix on the failure strength and fracture patterns of transversely isotropic rocks in Brazilian tests is discussed in detail. Then, the micro-parameters of the numerical model are calibrated to reproduce the behaviour of transversely isotropic rocks with different trends for the variation of the failure strength as a function of the weak plane-loading angles. Finally, the numerical approach is applied to simulate the fracture process of the layered surrounding rock after tunnel excavation.

2 Database of the Brazilian tests

The formula for indirect tensile strength is

$$\sigma_{\text{t}} = \frac{2F}{\pi Dt}$$

(1)

where σ_t is the tensile strength, F is the peak pressure, and D and t are the diameter and thickness of the specimen, respectively. This formula is applicable to homogeneous isotropic rocks under the condition that tensile fracture initiates from the centre of the disc specimen. However, the fracture pattern of transverse isotropic rocks under the Brazilian test is complex, and it is not a pure tensile pattern in most cases. Therefore, the formula is adopted in this article to normalize the load to the diameter and thickness. Furthermore, the term ‘failure strength’, corresponding to formula 1, will be used instead of ‘tensile strength’.

Vervoort et al. [43] obtained four trends for the variation of the failure strength as a function of β based on Brazilian test results for nine different rocks. To validate this classification, the number of rocks is increased to 23, as shown in Table 1. The statistical analysis shows that Vervoort’s classification has general applicability, and a new trend is found in addition to the four original trends.

Table 1 Results of Brazilian tests

The normalized failure strength (NFS) of rock is defined as

$$\alpha { = }\frac{{\sigma_{\beta } }}{{\sigma_{\rm max}}}$$

(2)

where α is the NFS, σ_β is the failure strength when the angle is β, and σ_max is the maximum failure strength among various angles.

The following five different trends are shown in Fig. 1.

Fig. 1

Relationship between the normalized failure strength and foliation-loading angle. a trend I, b trend II, c trend III, d trend IV, e trend V

• 1. Trend I: The NFS fluctuates within a small range over the entire interval.

• 2. Trend II: The NFS systematically increases over the entire interval.

• 3. Trend III: The NFS exhibits a constant value between 0° and 30°–60° and then increases linearly.

• 4. Trend IV: The NFS increases from 0° to 45°–70° and then remains unchanged.

• 5. Trend V: The NFS exhibits a U-shaped distribution.

The fracture patterns are shown in Fig. 2. Only the features of the main cracks are depicted in this figure; the secondary cracks are not shown. The fracture patterns can be classified into three types:

Fig. 2

Fracture patterns of disc specimens (the thick solid lines represent primary cracks. From left to right, β is 0°, 15°, 30°, 45°, 60°, 75° and 90°, respectively). a NLA failure, b LA failure, c mixed failure

• 1. Layer activation (LA) failure: failure occurs along weak planes.

• 2. Non-layer activation (NLA) failure: failure occurs across weak planes.

• 3. Mixed failure (MF): failure occurs along and across weak planes.

The three fracture patterns can be found in each angle, but NLA is not observed for β = 0°.

3 Numerical approach

The DEM has been used successfully to simulate the crack initiation, propagation and coalescence of rocks under various stress conditions [33]. In this study, a new DEM approach adopting a smooth joint model (SJM) and flat joint model (FJM) provided by PFC2D code is proposed to investigate the transverse isotropy of tensile behaviour of rocks. A brief introduction to this numerical approach is provided below.

3.1 Flat joint model

Before the FJM was established, the bonded-particle model (BPM) [33] was widely used to represent the inherent properties of rocks. Numerous simulation results have shown that the BPM has the following disadvantages: (1) spherical particles cannot provide a sufficiently large self-locking force; (2) the parallel contact cannot reproduce rotational resistance among particles when it is broken; and (3) pre-existing cracks are not considered in grain–grain contacts. Therefore, Potyondy [32] proposed a new contact model, the FJM, to address these problems. In the FJM, the micro-parameters, including the size distribution of particles, the strength of bonds (normal strength $\bar{\sigma }_{\text{c}}$ and shear strength $\bar{\tau }_{\text{c}}$), the stiffness of particles ($k^{\text{n}}$ and $k^{\text{s}}$), the stiffness of bonds ($\bar{k}^{\text{n}}$ and $\bar{k}^{\text{s}}$), the friction coefficient between particles (μ_c), the installation gap ratio (g_ratio) and the slit element fraction (φ_S), are calibrated until the emerging macro-properties match those obtained from sample experiments or in situ tests. Among these micro-parameters, g_ratio and φ_S have the largest impact on the micro-structure of the rock matrix [45].

In the FJM, the coordination number (CN) of particles is adjusted by setting the threshold of distance between the two particles. The magnitude of this threshold is g = g_ratio * min (R_A, R_B), where g is the distance threshold and R_A, R_B are the radii of two adjacent particles. A flat joint contact forms when the distance between two particles is less than g. As illustrated in Fig. 3, there are four particles around particle 1 (Fig. 3a). Particle 5 is tangent to particle 1, particle 3 intersects particle 1, and particles 2 and 4 are separated from particle 1. The radius of particle 1 is r₁, and the radius of particles 2, 3, 4, and 5 is r₂ (r₁ > r₂). The distances between the centres of particle 1 and particles 2, 3, 4, and 5 are d₁, d₂, d₃, and d₄, respectively. Furthermore, d₁ > d₃ > d₄ > d₂. There are four contact states between these particles as the result of different g_ratio values:

Fig. 3

Schematic diagram of the installation of flat joint contacts. a Particles, b state I, c state II, d state III, e state IV

• 1. State I: g_ratio * r₂ < d₄ − (r₁ + r₂), the contacts between particles 3 and 1 are installed as a flat joint contact (Fig. 3b).

• 2. State II: d₄ − (r₁ + r₂) < g_ratio * r₂ < d₃ − (r₁ + r₂), the contacts between particles 3 and 5 and particle 1 are installed as a flat joint contact (Fig. 3c).

• 3. State III: d₃ − (r₁ + r₂) < g_ratio * r₂ < d₁ − (r₁ + r₂), the contacts between particles 3, 4, and 5 and particle 1 are installed as a flat joint contact (Fig. 3d).

• 4. State IV: g_ratio * r₂ > d₁ − (r₁ + r₂), the contacts between particles 2, 3, 4, and 5 and particle 1 are installed as a flat joint contact (Fig. 3e).

Therefore, a larger value of g_ratio causes a larger value of CN, which generates more contacts around particles and increases the grain interlocking.

There are three types of flat joint contacts (Fig. 4). Type B (bonded contact) is a contact and bonded state among particles. Type G (gapped contact) is an un-contact and un-bonded state, and Type S (silt contact) represents a contact and un-bonded state. Therefore, type S can be regarded as pre-existing cracks in rock, and type G can be used to characterize open pore space in rock. The proportion of each contact type is adjusted by changing the value of φ_S. Thus, a lower φ_S can form a more intact rock.

Fig. 4

Three types of flat-joint contacts

3.2 Smooth joint model

The SJM has been adopted successfully in simulating the mechanical behaviour of rock joints [2, 3, 49]. A typical example is illustrated in Fig. 5. In this model, contacts are assigned as smooth joint contacts between particles lying on opposite sides of a joint plane, and the pre-existing bonds (if they exist) are removed at the corresponding positions. Thus, these particles intersected by a smooth joint can slide along the joint plane rather than move around one another (Fig. 5c).

Fig. 5

Smooth joint model. a Original contacts, b smooth joint contacts, c sliding along weak plane (after [22])

The micro-parameters of the SJM include the normal stiffness, shear stiffness, normal strength and cohesion of the contacts ($\bar{k}_{\text{n}}$, $\bar{k}_{\text{s}}$, $\sigma_{\text{c}}$ and $c_{\text{b}}$), the radius multiplier ($\bar{\lambda }$), friction coefficient and friction angle (μ and $\varphi_{\text{b}}$).

3.3 Sample generation

Transversely isotropic specimens are generated as follows:

• a. Generating an isotropic Brazilian disc. The smallest diameter of a particle is 0.2 mm, and the ratio of the maximum diameter to the minimum diameter is 1.66. The number of pre-existing cracks accounts for 10% of the total number of contacts. All contacts between particles are assigned as flat joint contacts.

• b. Applying smooth joint contacts into the isotropic Brazilian disc. The distance between joint planes is 5 mm. This value can ensure the specimens have a sufficient number of weak planes to represent the transverse isotropy of rocks at the macroscopic level (Fig. 6). The simulation cases are displayed in Table 3. The parameters of the FJM are shown in Table 2.

  Fig. 6

  

  Generation of the transversely isotropic specimens

  Table 2 Parameters of the FJM contacts

4 Simulation results

4.1 Effect of g _ratio

The effect of g_ratio was investigated by considering values of 0, 0.1, 0.3, and 0.5, and other parameters are shown in Table 3.

Table 3 Numerical simulation cases

As shown in Fig. 7a, the NFS curves all follow trend III regardless of the value of g_ratio. (NFS remains nearly unchanged at low angles (0°–45°) and increases when β > 45°.) For specimens with the same angle, g_ratio has a slight influence on the NFS when β < 45°, whereas the NFS increases with increases in g_ratio for β > 45°. However, further increases in this factor do not increase the NFS further when g_ratio reaches a certain value (0.3 in this case).

Fig. 7

Effect of g_ratio: a variation of NFS, b percentage of micro-cracks, c fracture patterns, g_ratio = 0, 0.1, 0.3, 0.5 (black segments: tensile failure of smooth joint contacts; dark blue segments: shear failure of smooth joint contacts; red segments: tensile failure of flat joint contacts; light cyan segments: shear failure of flat joint contacts. These colourful segments have the same meanings in following figures) (color figure online)

In the DEM, micro-cracks account for the shear and tensile failure of flat joint contacts and smooth joint contacts. In this study, the percentage of cracks developed on flat joint contacts are displayed through normalization by the total number of micro-cracks (Fig. 7b). For each g_ratio, the percentage of cracks developed on flat joint contacts increases from low angles to high angles, indicating that the facture patterns change from layer activation to non-layer activation. As shown in Fig. 7c, the fracture pattern is LA when β < 45°, MF when β is 45°–60°, and NLA when β is 75°–90°.

Another phenomenon is that for specimens with the same β, the percentage of cracks developed on flat joint contacts decreases with an increase in g_ratio when β < 45°; the relationship between the percentage of cracks developed on flat joint contacts and g_ratio is not clear when β is 45°–60°, and when β is 75°–90°, the percentage of cracks developed on flat joint contacts increases with an increase in g_ratio (Fig. 7b). This phenomenon can be attributed to the enhancement effect of a larger g_ratio on the micro-structure of rock matrix. Failure is more prone to occur along the weak plane for a denser rock matrix (corresponding to a larger g_ratio) when the failure pattern is LA. Therefore, micro-cracks developed on flat joint contacts become less for larger g_ratio when β < 45°. In contrast, a denser rock matrix bears more loading on the condition that the failure pattern is NLA, causing more micro-cracks to be inherited from breakage of the flat joint contacts when β is 75°–90°. However, the interaction between the weak plane and rock matrix is more complex when the fracture pattern is MF.

4.2 Effect of φ _S

The effect of φ_S was investigated by considering values of 0, 0.1, 0.2, 0.3, and 0.4, and other parameters are shown in Table 3.

The value of φ_S has a considerable influence on the trends of the NFS curves. The variation of the NFS changes from trend III (φ_S = 0.1) to trend V (φ_S = 0.3), and then to trend I (φ_S = 0.4). As shown in Fig. 8b, c, when φ_S is 0 or 0.3, the fracture pattern is LA (β is 0°–60°) or MF (β is 75°–90°). When φ_S is 0.4, the fracture pattern is LA (β is 0°–45°) or NLA (β is 60°–90°).

Fig. 8

Effect of φ_S. a Variation of NFS, b percentage of micro-cracks, c fracture patterns, φ_S = 0.1, 0.3, 0.4

In the DEM, a larger φ_S indicates that there are more pre-existing cracks in the specimen, while it has no effect on the micro-structure of the weak plane. Thus, the influence of φ_S on NFS and the fracture patterns of specimens is not clear when the rock fracture occurs along weak plane. However, when the rock fracture is determined mainly by the rock matrix, the NFS decreases with an increase in φ_S for same angle. When the factor reaches a certain threshold (0.4 in this case), the NFS remains constant over the entire interval, indicating that in this special condition, the generation of micro-cracks exhibits nearly the same resistance when propagating along or cross weak plane.

4.3 Effect of the smooth joint strength

The effect of the smooth joint strength was investigated through the following three cases:

• 1. case 3: σ_c = c_b, $\sigma_{\text{c}} /\bar{\sigma }_{\text{c}}$ = 0.1, 0.2, 0.4, 0.5, 1.

• 2. case 4: c_b = 20 MPa, σ_c/c_b = 0.5, 0.75, 1, 1.25, 2.5.

• 3. case 5: σ_c = 20 MPa, c_b/σ_c = 0.5, 0.75, 1, 1.25, 2.5.

Other parameters are shown in Table 3. The simulation result for case 3 is shown in Fig. 9. The strength of the smooth joint has a significant influence on the NFS and fracture patterns. When the strength of the smooth joint is equal to the strength of the rock matrix, the NFS remains constant over the entire interval, similar to trend I. The fracture pattern is NLA, with the percentage of cracks generated on flat joint contacts accounting for more than 80% of the total number of cracks. With a decrease in the strength of the smooth joint, the variation of the NFS exhibits the features of trend II ($\sigma_{\text{c}} /\bar{\sigma }_{\text{c}}$ = 0.4 or 0.5) or trend III ($\sigma_{\text{c}} /\bar{\sigma }_{\text{c}}$ = 0.2 or 0.1).

Fig. 9

Effect of the smooth joint strength. a Variation of NFS, b percentage of micro-cracks, c fracture patterns, $\sigma_{\text{c}} /\bar{\sigma }_{\text{c}}$ = 0.1, 0.4, 1

When the strength of the smooth joint is reduced by a factor of 0.4, the fracture pattern is LA (β is 0°–60°) or MF (β is 75°–90°), and the percentage of cracks generated on flat joint contacts increases with an increase in β. When the reduction factor reaches 0.1, the fracture pattern is LA on the condition of β < 75°, and only cracks generated on smooth joint contacts appear within a certain range of angles (15°–60°). At high angles, the fracture pattern is MF, and the percentage of cracks generated on flat joint contacts increases from 47% (β = 75°) to 60% (β = 90°).

The simulation result of case 4 is shown in Fig. 10. The tensile strength of the smooth joint contacts has only a slight influence on the NFS and fracture patterns because fractures at low angles (β = 0°–60°) mainly occur as shear failure of the weak plane, whereas fractures at high angles (β = 75°–90°) form mainly as tensile failure of the rock matrix. However, the tensile strength of the smooth joint contacts does affect the microscopic failure mechanism of specimens. Firstly, increasing the tensile strength of smooth joint contacts suppresses the emergence of tensile cracks developed on flat joint contacts. As shown in Fig. 10c, the number of micro-cracks generated from the tensile breakage of the smooth joint contacts decreases with increases in the tensile strength of the weak plane for each angle. Secondly, increasing the tensile strength of smooth joint contacts can cause the load to be transferred from the weak plane to the rock matrix. Figure 10b shows that when β is 15°–60°, the percentage of cracks generated on flat joint contacts increases with increases in the tensile strength of the weak plane for each angle.

Fig. 10

Effect of the tensile strength of smooth joint contacts. a Variation of NFS, b percentage of micro-cracks, c fracture patterns, σ_c/c_b = 0.5, 1.25, 2.5

The simulation result of case 5 is displayed in Fig. 11. The shear strength of the smooth joint contacts has a significant influence on NFS and the fracture patterns. Figure 11a clearly shows that increasing the shear strength of the smooth joint contacts significantly increases the NFS at low angles (β = 0°–60°) because fractures mainly occur as shear failure along the weak plane in these cases. When the angle exceeds 60°, this effect becomes minor because loading is carried mainly by the rock matrix. The variation of the NFS follows trend IV (c_b/σ_c = 2.5) or trend III (other values). The fracture pattern is LA (β = 0°–15°) or MF (β = 30°–45°) or NLA (60°–90°) for c_b/σ_c = 2.5, whereas it is LA (β < 75°) or MF (75°–90°) under other conditions. The percentage of cracks generated on the flat joint contacts increases with increases in c_b/σ_c, indicating that increasing the shear strength of the smooth joint can improve the integrity of the rock and transfer more load to the rock matrix.

Fig. 11

Effect of the shear strength of smooth joint contacts. a Variation of NFS, b percentage of micro-cracks, c fracture patterns, c_b/σ_c = 0.5, 1.25, 2.5

5 Calibration results

The simulation results from Sect. 4 indicate that the micro-parameters of the DEM have a considerable influence on the macro-mechanical behaviour of rocks. Thus, the following calibration procedures are adopted to determine the micro-parameters:

Determining the deformation parameters of the DEM through uniaxial compression tests

When β = 0°, the stiffness of the smooth joint contacts has the smallest influence on the Young’s modulus of the specimen. Thus, the stiffness of the FJM ($k^{\text{n}}$, $k^{\text{s}}$, $\bar{k}^{\text{n}}$, $\bar{k}^{\text{s}}$) is calibrated to match the E₀ (Young’s modulus for β = 0°) obtained from laboratory tests.

The stiffness of the SJM ($\bar{k}_{\text{n}}$, $\bar{k}_{\text{s}}$) is calibrated to match the E₉₀ (Young’s modulus for β = 90°) obtained from the laboratory tests. $\bar{k}_{\text{n}}$ and $\bar{k}_{\text{s}}$ are set equal for simplicity.

Determining the strength parameters of the DEM through Brazilian tests

When β = 90°, the strength of the smooth joint contacts has the smallest influence on the strength of the specimen. Therefore, the strength of the FJM ($\bar{\sigma }_{\text{c}}$, $\bar{\tau }_{\text{c}}$) is calibrated to reproduce the σ₉₀ obtained from laboratory tests.

The strength parameters of the SJM ($\sigma_{\text{c}}$, $c_{\text{b}}$, $\varphi_{\text{b}}$) are calibrated based on the trends of the NFS.

The flowchart for the calibration procedure discussed above is shown in Fig. 12. Following this procedure, the DEMs are calibrated to reproduce the behaviour of five typical rocks with different trends, namely trend I (poster sandstone), trend II (Leubsdorfer gneiss), trend III (phyllite), trend IV (Boryeong shale) and trend V (slate). The Young’s modulus obtained from uniaxial compression tests is shown in Table 4. The micro-parameters calibrated based on experiments are provided in Table 5. Good agreement can be found between the numerical and experimental results in terms of the NFS and fracture patterns when comparing Figs. 13 and 14. Only numerical results are displayed for Poster sandstone because information on its fracture pattern is not available in the literature. The only exception is slate at β = 15°. In this case, the fracture pattern of the specimen is NLA and LA for the numerical and experimental results, respectively, which leads to a difference in the NFS.

Fig. 12

Flowchart of calibration

Table 4 Young’s modulus obtained from uniaxial compression tests

Table 5 Micro-parameters of different types of rocks

Fig. 13

Comparison of BTS between numerical and experimental results. a Poster sandstone, b Leubsdorfer gneiss, c phyllite, d Boryeong shale, e slate

Fig. 14

Comparison of fracture patterns between numerical and experimental results. a Poster sandstone, b Leubsdorfer gneiss, c phyllite, d Boryeong shale, e slate. The pictures of experimental results are after [9, 11, 28, 46]

6 Application in engineering

As Fig. 15 shows, the transverse isotropy has a considerable influence on the fracture pattern of the layered surrounding rock during tunnel excavation. Therefore, the DEM is adopted to investigate this engineering problem.

Fig. 15

Fracture patterns of surrounding rocks after excavation (the dash line represents bedding planes). a Stratified Lias limestone in Lötschberg tunnel (after [15]), b micro-tunnel (after [30]), c horseshoe-shaped access drift (after [6])

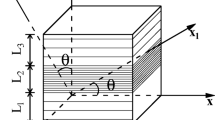
The numerical model is illustrated in Fig. 16. The size of the model is 80 m × 80 m. To increase the computational efficiency, the inner part with a size of 40 m × 40 m is simulated using discrete particles, whereas the external part is simulated with finite difference grids. The algorithm of data transmission between particles and grids is based on Buddhima et al. [21]. In this model, L (the spacing of the layers) is 0.6 m and θ (the angle between the layers and horizontal plane) is 0°–90° with an interval of 15°. λ (geostress ratio) is 0.5, 1, and 2. When λ = 0.5, σ_x = 15 MPa, and σ_y = 30 MPa. When λ = 1, σ_x = σ_y = 20 MPa. When λ = 2, σ_x = 30 MPa and σ_y = 15 MPa.

Fig. 16

Numerical model

The parameters of phyllite displayed in Table 4 are chosen as the micro-parameters of the particles. The minimum diameter of the particles is 5.8 cm, and the total number of particles is 60,285. The transversely isotropic elastic model is adopted in the finite difference grids, and its parameters are listed in Table 6.

Table 6 Parameters of finite difference grids

6.1 Failure process of the surrounding rocks

The failure processes of homogeneous rock and layered rock (case: λ = 1, θ = 45°) after tunnel excavation are shown in Fig. 17. For homogeneous rock, a large number of tensile micro-cracks occur near the tunnel section as the result of stress redistribution, which forms a clear shear slip area around the waist of the tunnel. For layered rock, primary stress redistribution causes sliding and opening failure along layers after the tunnel excavation. Comparing step 100 and step 0 in Fig. 17b, the contact force of the smooth joint contacts in area I is zero for step 100, which means that layers are open in this position. Then, as shown in step 2000, further stress redistribution initiated by the failure of layers causes tensile fracture of the intact rock mass between layers. With repetition of the above process, the final fracture pattern is displayed in step 25,000, and fractured rock is concentrated in two regions perpendicular to the layers.

Fig. 17

Fracture processes of surrounding rock. a Isotropic rock, b transversely isotropic rock. From left to right: step = 0, 100, 2000, 5000, 2500 (red lines: tensile failure of flat joint contacts; light cyan lines: shear failure of flat joint contacts; blue line: contact force of smooth joint contacts) (color figure online)

6.2 Effect of the bedding direction

When the stress field is isotropic (λ = 1), the angle θ plays a dominant role in determining the fracture pattern of the surrounding rock. The damaged zones are concentrated in certain regions which extend from the tunnel in the direction normal to the layers for each angle, as illustrated in Fig. 18.

Fig. 18

Fracture patterns of surrounding rocks with different θ: a θ = 0°, b θ = 15°, c θ = 30°, d θ = 45°, e θ = 60°, f θ = 75°, g θ = 90°

6.3 Effect of the geostress field

The effect of the geostress field on fracture patterns is shown in Fig. 19. For homogeneous rock, the damaged zone propagates along the direction of the minimum principal stress. For layered rock, there is a certain angle between the direction of the evolution of the damaged zone and the minor principal stress, and the direction of the evolution of the damaged zone is not normal to the layers. Therefore, the fracture pattern of the layered rock is determined by both the layer direction and geostress field, which is different from the trend for homogeneous rock.

Fig. 19

Fracture patterns of surrounding rock for different geostress fields. a Homogeneous rock, b transversely isotropic rock. From left to right, λ is 0.5, 1, 2, respectively

7 Discussion

To further discuss the effect of the micro-structure of the rock matrix on the failure process, the relationship between stress and strain in the Brazilian disc test and the evolution of micro-cracks and contact force for the specimens with β = 15° or 75° are displayed in Figs. 20 and 21 (φ_S = 0.15, g_ratio = 0.3), respectively.

Fig. 20

Fracture process of specimen for β = 15°. a Contact force, b failure strength versus strain and increment of micro-cracks formation, c fracture pattern

Fig. 21

Fracture process of specimen for β = 75°. a Contact force, b failure strength versus strain and increment of micro-cracks formation, c fracture pattern

Figure 20 shows that nearly no micro-cracks formed before loading point a, with the compressive and tensile stress fields evenly distributed in the middle part of the specimen. When the specimen was loaded to point b, shear micro-cracks on flat joint contacts appeared along weak plane (Crack ①), and concentrated tensile stress occurred near the tip of crack ①. When the specimen was loaded from point b to point c, due to the influence of the concentrated tension stress area, the propagation direction of the cracks shifted, and new micro-cracks were produced as a result of the tensile breakage of the type S contact (pre-existing cracks), forming crack ②. Meanwhile, tensile stress was released near the tip of crack ①, and the newly developed crack tip served as a new tensile stress concentration region, as could be inferred from the increased area of the red-coloured segments at the newly developed crack tip of crack ②. Numerous micro-cracks appeared when the axial stress was loaded after the peak strength. Crack ② continued to propagate through pre-existing cracks in the rock matrix, and the tensile stress concentration region was transferred to the new crack tip of crack ② simultaneously. A new crack ③ initiated from the tip of crack ① during this loading period. The formation of micro-cracks can be divided into two stages. From the initial loading stage to point b, micro-cracks were mainly produced from shear breakage of the smooth joint contacts. From point b to the final stage, micro-cracks that initiated from the tensile breakage of pre-existing cracks dominated during the loading process.

As shown in Fig. 21, there were a small number of shear micro-cracks along the weak plane and in the rock matrix at the initial loading stage before point a. When the specimen underwent the deformation stage from point a to point b, numerous micro-cracks propagated towards the middle part of the specimen by penetrating through pre-existing cracks, and the stress attenuation region appeared on opposite sides of the cracks. During the post-peak loading stage, cracks on the top and bottom sides of the disc specimen coalesced to a macro-crack after passing through pre-existing cracks, and the tensile stress in the macro-crack area was clearly attenuated. In this case, the damage of the rock is determined by shear and tensile breakage of pre-existing cracks in the rock matrix, and tensile cracks are dominant throughout the loading process.

8 Conclusions

The results obtained from Brazilian tests on 23 types of transversely isotropic rock yielded five trends for the variation of the NFS as a function of the weak plane-loading angle. The NFS ranges from fluctuating with a small difference (trend I) to systematic increasing (trend II) over the entire interval. Trend III is characterized by a constant value between 0° and 30°–60°, followed by a linear increase. Trend IV corresponds to an increase from 0° to 45°–70°, after which the NFS remains unchanged. Trend V is a U-shaped distribution. Three types of fracture patterns were obtained for each weak plane-loading angle: LA, NLA and MF.

A new numerical approach was proposed based on the DEM. In this model, the FJM and SJM are adopted to simulate the rock matrix and weak plane, respectively. A series of numerical samples (β = 0°, 15°, 30°, 45°, 60°, 75°, and 90°) were established to investigate the influence of the micro-structure of the rock matrix and the strength of weak plane on the NFS and fracture patterns. The results reveal that the trends in the NFS and fracture patterns are slightly influenced by the coordination number of the rock particles and the tensile strength of the weak plane but greatly influenced by the percentage of pre-existing cracks and the shear strength of the weak plane.

A calibration procedure for determining the micro-parameters of the DEM was proposed. Based on the results of uniaxial compression tests and Brazilian tests, the DEM models were calibrated to reproduce the behaviour of five typical rocks with different trends. Good agreement was obtained between the numerical and experimental results in terms of the NFS trends and fracture patterns.

Finally, the DEM was applied to study the fracture patterns of layered rock after tunnel excavation. The results indicated that for the layered rock mass, the geostress ratio and the angle between the layers and tunnel axis play an important role in determining the fracture patterns. For an isotropic stress field, the damaged zone is concentrated in two regions that extend from the tunnel in a direction normal to the layers. For a non-isotropic stress field, there is a certain angle between the direction of evolution of the damaged zone and the minor principal stress, and the direction of evolution of the damaged zone is not normal to the layers either.