Contact angle mechanical influence in wet granular soils

Abstract

We investigate the macroscopic mechanical influence of the local liquid–solid contact angle that governs the fluid distribution in granular soils under unsaturated conditions. To this end, a discrete element method (DEM)-based implementation that accommodates for any contact angle is proposed and applied to an idealized granular material in the pendular regime. The DEM model includes resultant capillary forces as well as a comprehensive description of the capillary bridges (volume, surface, orientation tensor) by solving the Laplace–Young equation in a general case, instead of using any unnecessary phenomenological relation. Macroscale mechanical simulations for different constant contact angle values reveal that granular assemblies are less sensitive to unsaturated conditions for higher contact angles, which is in line with the contact angle influence at the microscopic capillary bridge scale. The contribution of the fluid mixture to the total stresses of the wet soil, the so-called capillary stresses, indeed decreases according to the contact angle. Thus, the increase in apparent shear strength due to unsaturated conditions is reduced for higher contact angles. As such, the classical assumption of perfect wetting (zero contact angle) appears to be non-conservative.

1 Introduction

Granular soils encountered in geotechnical engineering often encompass several immiscible fluids within their pore network such as in situations related to oil and gas production, non-aqueous pollutant transport in groundwater, frozen soils, or simply, classical unsaturated soil mechanics dealing with a mixture of air and water. The presence of such fluid mixture is an important issue since it greatly influences the soil’s mechanical behaviour, as illustrated by the classical example of sandcastles that require wet sand to hold. Restricting ourselves to ternary mixtures with one granular solid phase and two-fluid phases, one key parameter that controls the various fluid distributions is the contact (or wetting) angle $\theta$ describing the contact between the solid phase and the wetting fluid phase along the so-called contact lines where the three phases intersect. The contact angle value is highly dependent on the particular case of interest. For spherical particles, wet samples of glass beads may show low contact angle values ($\leqslant 10^{\circ }$) [30, 32], while the contact angle between steel balls and water is around $50^{\circ }$ [34]. As far as real sandy soils are concerned, contact angle values reaching $50^{\circ }$ and more have been reported in [2, 20]. Adding to complexity, the contact angle is also dependent on the hydraulic loading path; its value showing a hysteresis between extreme limits that correspond to receding or advancing contact lines. Such hysteresis has now been shown to affect the fluid phase distribution [25].

Focusing on low degrees of saturation within the so-called pendular regime, the fluid distribution is characterized by isolated capillary bridges, i.e. menisci, consisting of the wetting fluid (considered from now on to be a liquid) and that form between solid particles pairs. Several capillary bridge analyses have been proposed that accommodate for any contact angle value, giving the possibility to investigate the contact angle influence at this microscopic scale [17–19, 27, 34]. From these studies, the contact angle is known to affect the liquid volume–capillary pressure relationship and the capillary force magnitude, for instance. Such microscopic effects necessarily also reflect into the macroscopic behaviour of soil samples. However, a proper macroscopic analysis of the contact angle influence seems to be at best limited in the literature. Straightforward experiments are prevented by the major difficulties measuring contact angle at a soil sample scale, compared with the ideal case of droplets lying on a flat surface [2, 9]. On the other hand, only few macroscopic modelling approaches include a contact angle analysis such as done in [8, 9, 25]. Among these studies, the focus is mostly set on the description of two-phase pore flow within a fixed packing [9, 25]. Finally, the assumption of a zero contact angle is still routinely adopted in most macroscopic-scale numerical modelling of unsaturated soils in a mechanical framework [13, 24, 31, 33, 35, 39]. As such, the objective of the present paper is to assess through careful modelling how contact angle influences the mechanical behaviour of wet granular assemblies, in the pendular regime.

We herein consider an idealized granular material with solid particles being spherical in shape. Such assumption eases the menisci computation from the Laplace–Young equation. Both the solid and liquid phases show in the pendular regime a discrete microstructure, with distinct solid grains and liquid bridges. In connection with this discrete microstructure, it is convenient to choose the discrete element method (DEM) as a modelling approach, as done in [13, 24, 31, 33, 35, 39]. The DEM describes any internal force using interaction forces between the discrete elements that correspond to spherical solid particles. As such, the wetting and non-wetting (from now on, a gas) fluids are indirectly incorporated in the model through the resultant capillary forces that act on the particle pairs bonded by a capillary bridge.

Because the capillary force depends on the liquid bridge geometry, we begin with Sect. 2 that gives details of a liquid bridge determination for various contact angles that is inspired from previous works on monosized particles pairs [17, 19]. Next, the results of Sect. 2 are implemented in the open source DEM code Yade [36] in line with Scholtès et al. [33] who restricted the computations to zero contact angles. The DEM implementation leads to a macroscopic analysis of the contact angle influence in Sect. 3. Finally, Sect. 4 analyses in depth the results of Sect. 3, focusing on the capillary stresses that encompass the mechanical actions existing in a wet assembly due to the fluid mixture.

2 Liquid bridge determination

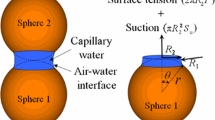
Considering a polydispersed idealized granular material, capillary bridges form in between two dissimilar spherical particles of radii $R_1$, $R_2$ with radius ratio $r = R_2 / R_1 \geqslant 1$. Three-dimensional axisymmetric conditions hold when neglecting gravity g, i.e. for low Bond numbers $B = (\rho _l - \rho _g)\, g \, {R_2}^2 / \gamma$ with $\rho _l$, $\rho _g$ being, respectively, the liquid and gas densities, g the gravity and $\gamma$ the liquid–gas surface tension. It is thus convenient to use 3D cylindrical coordinates $(\rho ,\phi ,z)$ with z as the axis of rotational symmetry defined by angle $\phi$, such that a function $\zeta (z)$ defines the liquid bridge surface $\{\rho = \zeta (z);\phi \in [0;2\pi ];z\in [0;z_f]\}$ where $z_f$ is the distance between the two three-phase contact lines. Figure 1 illustrates such a liquid bridge between two spherical particles: $\delta _1$ and $\delta _2$ refer to the half-filling angles, and $\theta$ is the contact (wetting) angle.

Fig. 1

Liquid bridge geometry

It is convenient to normalize all lengths through division by the largest radius $R_2$ which serves as a length scale so that normalized quantities are $z^*=z / R_2$, $\rho ^*=\rho / R_2$ and $\zeta ^*(z^*) = \zeta (R_2\, z^*) / R_2$. Thus, the liquid bridge surface is described in the dimensionless space as $\{\rho ^* = \zeta ^*(z^*);\phi \in [0;2\pi ];z^* \in [0;z^*_f]\}$.

Generally speaking, liquid–gas interfaces always obey the Laplace–Young equation given as:

$$\begin{aligned} u_g - u_l = u_{\rm c} = \gamma \, {{\rm{div}}}\,{\mathbf {n}} \end{aligned}$$

(1)

with the normal ${\mathbf {n}}$ oriented towards the liquid, $u_g$ and $u_l$ as the gas and liquid pressure, respectively, and $u_{\mathrm{c}}$ the capillary pressure. Since adsorbed liquid layers are negligible for granular soils, the capillary pressure $u_{\mathrm{c}}$ also corresponds to the matric suction.

The Laplace–Young equation serves as a partial differential equation describing the liquid bridge configuration. In order to obtain the latter, Eq. (1) is classically rewritten in the following dimensionless form accounting for the 3D axisymmetric situation, and denoting $\zeta ^{*\prime }$ and $\zeta ^{*\prime \prime }$ as the first and second derivatives of $\zeta ^*(z^*)$, i.e.

$$\begin{aligned} \dfrac{u_{\mathrm{c}}\,R_2}{\gamma } = u_{\mathrm{c}}^* = \dfrac{\zeta ^{*\prime \prime }}{\left( 1+{\zeta ^{*\prime }}^2 \right) ^{3/2}} - \dfrac{1}{\zeta ^* \left( 1+{\zeta ^{*\prime }}^2 \right) ^{1/2}} \end{aligned}$$

(2)

which introduces a dimensionless capillary pressure $u^*_{\mathrm{c}}$.

Equation (2) might be approximately solved using a toroidal expression for $\zeta ^*$ from two constant principal radii with the meridian liquid profile being simply a circular arc [11, 16]. However, this approximation leads to a non-constant surface curvature locally as defined by ${{\mathrm{div\,}}}{\mathbf {n}}$, which, strictly speaking, contradicts the Laplace–Young equation (1) [17, 19].

2.1 Numerical procedure

Similar to [19] which dealt with only monosized spherical particles, the current numerical procedure to solve Eq. (2) considers a particular half-filling angle $\delta _1$ on the smallest particle and the dimensionless capillary pressure $u_{\mathrm{c}}^*$. Starting from the smaller particle on the left with boundary condition $\zeta ^*_0 = \sin (\delta _1) / r$, the liquid bridge profile $\zeta ^*(z^*)$ is incrementally computed using a second-order Taylor series expansion:

$$\begin{aligned} \zeta ^*\big (z^* = (i+1) \, \Delta z^*\big ) &=\,\zeta ^*_{i+1} = \zeta ^*_i + \Delta z^* \, \zeta ^{*\prime }_i \nonumber \\& \quad + \dfrac{1}{2} \Delta z^{*2} \, \zeta ^{*\prime \prime }_i \end{aligned}$$

(3)

The first derivative $\zeta ^{*\prime }_i$ is computed using a second-order finite difference approximation, Eq. (4), that is suited to describe the evolving profile slope, contrary to the always positive expression presented in [19]. The initial value $\zeta ^{*\prime }_0$ is a distinct case and is obtained from the wetting of the smallest solid particle along the left contact line:

$$\begin{aligned} \zeta ^{*\prime }_i = \left\{ \begin{array}{ll} \dfrac{-1}{\tan (\delta _1 + \theta )} &{} { \hbox {for} }\; i=0 \\ \dfrac{\zeta ^*_i - \zeta ^*_{i-1}}{\Delta z^*} + \dfrac{1}{2} \Delta z^* \, \zeta ^{*\prime \prime }_{i-1} &{} { \hbox {else}} \end{array} \right. \end{aligned}$$

(4)

Appearing in Eqs. (3) and (4), the second derivative $\zeta ^{*\prime \prime }$ is expressed in terms of $\zeta ^*$ and $\zeta ^{*\prime }$ from Laplace–Young Eq. (2), i.e.

$$\begin{aligned} \zeta ^{*\prime \prime }_i = \dfrac{1+{\zeta ^{*\prime }_i}^2}{\zeta ^*_i} + u_{\mathrm{c}}^* \, \left( 1+{\zeta ^{*\prime }_i}^2 \right) ^{3/2} \end{aligned}$$

(5)

As such, the liquid bridge profile is obtained by applying successively Eqs. (4), (5), and (3) until the right contact line, defined by $\zeta ^*_f = \sin (\delta _2)$, is reached for $z^*=z^*_f$. Prior to that the filling angle $\delta _2$ on the largest particle is deduced by expressing Eq. (6) at both contact lines and solving numerically for $\delta _2$:

$$\begin{aligned} \dfrac{\zeta ^*}{\left( 1+{\zeta ^{*\prime }}^2 \right) ^{1/2}} + \dfrac{u_{\mathrm{c}}^*}{2} {\zeta ^*}^2= C = \hbox {cst} \end{aligned}$$

(6)

The l.h.s. of Eq. (6) is the dimensionless expression of the capillary force resulting from capillary pressure and surface tension actions along any meniscus cross section, in particular the left or right wetted particles surfaces. Obtained from making a variable substitution in the Laplace–Young equation as given in [19], Eq. (6) basically expresses meniscus force equilibrium.

Also, an increment $\Delta z^*$ is chosen to be small enough ($2\times 10^{-6}$ typically) so as not to have any influence on the numerical results. In particular, this ensures both stability and accuracy of the explicit scheme related to Eqs. (3)–(5).

Determining the liquid bridge profile $\zeta ^*(z^*),\ z^*\in [0;z^*_f]$, following the above numerical procedure ultimately leads to a comprehensive geometrical description of the liquid bridge and other characteristics. For instance, the dimensionless interparticle distance $d^* = d/R_2$ and liquid volume $V^* = V_l / {R_2}^3$ are readily computed excluding the solid volumes:

$$\begin{aligned} d^* = z^*_{\mathrm{f}} - \dfrac{1}{r} \, (1-\cos \delta _1) - (1-\cos \delta _2) \end{aligned}$$

(7)

and

$$\begin{aligned} V^*= & {} \sum \limits _{i=1}^f \pi \, {\zeta _i^*}^2 \, \Delta z^* - \dfrac{\pi }{3 \, r^3} \, (\cos ^3\delta _1 - 3 \cos \delta _1 +2)\nonumber \\&- \dfrac{\pi }{3} \, (\cos ^3\delta _2 - 3 \cos \delta _2 +2) \end{aligned}$$

(8)

Furthermore, the dimensionless capillary force is directly obtained by satisfying Eq. (6) along either contact line of the liquid bridge:

$$\begin{aligned} F^* = \dfrac{F^{\hbox {cap}}}{2\, \pi \,\gamma \, R_2} = C \end{aligned}$$

(9)

Finally, the liquid bridge description is completed by the calculation of the dimensionless meniscus orientation tensor ${\mathsf {\varvec{\pi ^*}}}$:

$$\begin{aligned} {\mathsf {\varvec{\pi ^*}}} = \dfrac{1}{{R_2}^2} \int _{S_m} {\mathbf {n}} \otimes {\mathbf {n}} \ \hbox {d}S \end{aligned}$$

(10)

that is obtained from the normal ${\mathbf {n}}$, the local orientation tensor ${\mathbf {n}} \otimes {\mathbf {n}}$, and a numerical integration along the liquid bridge external surface $S_m$, see Appendix 1. Such meniscus orientation tensor enters into the description of the internal surface tension forces within the liquid bridge surface [6, 7, 15] and represents a pertinent tensorial quantity that was not provided by previous analyses [19, 33]. In particular, the inclusion of ${\mathsf {\varvec{\pi ^*}}}$ facilitates the stress analysis in Sect. 4 without using any assumption on the meniscus orientation. It is worth noting that the expression of ${\mathsf {\varvec{\pi ^*}}}$ in the local (meniscus) basis $(\mathbf {e_\rho },\mathbf {e_\phi },\mathbf {e_z})$ is diagonal and axisymmetric with $\pi ^*_{\rho \rho } = \pi ^*_{\phi \phi } \ne \pi ^*_{zz}$ because of the meniscus shape. Further insight is gained by considering the trace of ${\mathsf {\varvec{\pi ^*}}}$ which turns out to be the dimensionless meniscus surface $S_m^*$:

$$\begin{aligned} {{{\mathrm{tr}}}}({\mathsf {\varvec{\pi ^*}}}) = 2\,\pi ^*_{\rho \rho } + \pi ^*_{zz} = \dfrac{1}{{R_2}^2} \int _{S_m} ||{\mathbf {n}}||^2 \, \hbox {d}S = \dfrac{S_m}{{R_2}^2} = S_m^* \end{aligned}$$

(11)

In the end, the numerical procedures described in the above lead to a schema in which, for given values of normalized suction $u_{\mathrm{c}}^*$, contact angle $\theta$, and radius ratio r, the complete set of liquid bridge configurational parameters $\{d^* , V^*, F^*, \delta _1 , \delta _2,\pi ^*_{\rho \rho },\pi ^*_{zz}\}$ is obtained by sweeping through various filling angles $\delta _1 \in [0^\circ ;90^\circ - \theta ]$. Values of $\delta _1$ greater than $(90^\circ - \theta )$ are not considered since they would correspond to concave liquid bridges (negative suctions). Also, numerical computations may give configurations that present negative volume and/or particles distance. Such non-physical solutions correspond to impossible liquid bridges and are thus disregarded.

2.2 Liquid bridge stability

When analysing granular assemblies, a key variable that provides insights into the nature of the liquid bridge solution is the inter-particle distance. As such, liquid bridge configurations obtained in the previous Sect. 2.1 are depicted according to $d^*$ in Fig. 2, which shows two possible bridge configurations for the same distance and same $\{r ;\theta ;u_{\mathrm{c}}^*\}$ parameters. These two solutions both obey the force equilibrium condition expressed by Laplace–Young equation and correspond to stable or unstable distinct equilibrium states [19, 22, 28]. Several free energy expressions have been proposed to assess the stability of these different configurations [5, 19]. However, these expressions rely on a constant liquid volume assumption, whereas constant pressure conditions prevail herein. As this disparity in state description affects stability properties [22], we consider here the following more suitable dimensionless free energy $E^*$ whose derivation is given in Appendix 2:

$$\begin{aligned} E^*= & {} \dfrac{E}{\gamma \, {R_2}^2} = u_{\mathrm{c}}^*\, V^* + 2 \, \pi \Bigg [ \sum \limits _{i=1}^f \zeta ^*_i \sqrt{1+ {\zeta ^{*\prime }_i}^2} \Delta z^* \nonumber \\&- \cos \theta \left( \dfrac{1-\cos \delta _1}{r^2} + 1 - \cos \delta _2 \right) \Bigg ] \end{aligned}$$

(12)

The highlights of the dimensionless free energy expressed in Eq. (12) include surface energies for liquid-gas as well as liquid-solid and solid-gas interfaces, considering constant solid surfaces for the particles. Specific volume fluid energies are included, assuming that the global volume $(V_l + V_g + V_s)$ is kept constant.

Fig. 2

Possible liquid bridge configurations according to the particles distance; for $r=2$, $\theta = 20^\circ$ and different suctions. a Filling angles, b meniscus surface and volume, c capillary force

It is through the finding of the minimum values of $E^*$ for a given distance, see Fig. 3, that we can retain among the two solutions the configuration with the largest liquid volume as the stable one, i.e. the “upper” branches of the curves previously depicted in Fig. 2. As such, the unstable configurations showing the smallest liquid volumes are from now on disregarded.

Fig. 3

Free energy of the different liquid bridge configurations of Fig. 2 ($r=2;\theta = 20^\circ$ and different suctions)

2.3 Contact angle influence at the liquid bridge scale

The determination of capillary bridge configurations for different contact angles offers first micromechanical insights in the contact angle influence on wet granular packings. At the microscopic scale, and for given dimensionless suction, interparticle distance, and relative radii parameters, an increasing contact angle decreases the wetted surfaces, the meniscus volume and surface, and the capillary force, see Fig. 4. Such decreases in liquid volume and capillary forces with the contact angle have also been described in [18, 27].

Fig. 4

Contact angle influence at the liquid bridge scale. For $r=3$ and $u_{\mathrm{c}}^* = 200$. a Mean filling angle, b meniscus surface and volume, c capillary force

2.4 Comparison with empirical relations

As an alternative to systematically solve Laplace–Young equation, several empirical relations for the capillary force have been proposed in the literature [7, 31, 41]. These are now compared with the results of the presented numerical procedure.

Pitois et al. [7] derived the following Eq. (13) for the capillary force in the case of a monosized particle pair and assuming a cylindrical (flat) liquid bridge profile. The following relation has been experimentally verified for $\theta = 10^\circ$, i.e.

$$\begin{aligned} F^* = \cos \theta \left( 1 - \dfrac{1}{ \sqrt{1+\dfrac{2\, V^*}{\pi \, {d^*}^2} } } \right) \end{aligned}$$

(13)

For such a monosized particle pair, a fairly good agreement is found between our solution and Eq. (13) for a wide range of contact angles as illustrated in Fig. 5a, b. Consistent with other experimental comparisons presented in [7], the agreement between the solution of Laplace–Young equation and Eq. (13) is most satisfactory for small liquid volumes (Fig. 5a) for which the flat profile assumption is the most relevant. However, Fig. 5c illustrates the obvious inadequacy of Eq. (13) in the polydisperse case for which the flat profile assumption never holds.

Fig. 5

Comparison with Eq. 13, from [7]. a $r = 1 ; V^* = 10^{-4}$, b $r = 1 ; V^* = 10^{-2}$, c $r = 3 ; V^* = 10^{-4}$

In order to account for polydispersity, Richefeu et al. [31] proposed Eq. (14) for macroscopic DEM simulations purposes, i.e.

$$\begin{aligned} F^* = \dfrac{\cos \theta }{\sqrt{r}}\, \exp { \left( -\dfrac{r}{0.9 \sqrt{V^* (1+r) / 2}} \,d^*\right) } \end{aligned}$$

(14)

However, for the cases herein considered, the comparison between Eq. (14) and our numerical solutions shows a poorer agreement for the polydisperse cases than for the monodisperse ones, see Fig. 6.

Fig. 6

Comparison with Equ. 14, from [31]. a $r = 1 ; V^* = 10^{-4}$, b $r = 3 ; V^* = 10^{-4}$, c $r = 3 ; V^* = 2\, 10^{-3}$

A last comparison is made with the relation proposed by Willett et al. [41], detailed in Appendix 3 due to its complexity, that has been used for DEM simulations in [24]. Among the cases here tested, there is a very good agreement for only contacting particles, irrespective of the volume and radius ratio. Then, deviations increase according to the interparticle distance, see Fig. 7.

Fig. 7

Comparison with Willett’s equation [41]. a $r = 1 ; V^* = 10^{-4}$. b $r = 3 ; V^* = 10^{-4}$, c $r = 3 ; V^* = 2\, 10^{-3}$

In summary, this brief review and comparison exercise discussed in the above are intended to show the difficulties in obtaining empirical relations that are valid in any configuration, and thus the need of an efficient numerical solution of Laplace–Young equation. Moreover, it is noted that the numerical solution not only gives the capillary force, but also furnishes other pertinent liquid phase information such as liquid bridge volume and surface, filling angles and orientation tensor.

3 Contact angle influence at the macroscale

3.1 DEM model description

To pass from pairwise particle interaction to a network of particles at the macroscale and appreciate the implications of contact angle on the mechanical strength of a polydispersed assembly of wet granular material, DEM modelling is pursued by invoking the liquid bridge computations expounded in Sect. 2 within a numerical framework similar to the one used in [33] for zero contact angles.

First, a comprehensive data set of liquid bridge configurations is built for a wide set of contact angles $\theta$, radius ratios r, and dimensionless capillary pressures $u_{\mathrm{c}}^*$ values. For a given numerical sample, eight r values are considered between 1 and the $D_{{\mathrm{max}}} / D_{{\mathrm{min}}}$ ratio. Regarding the capillary pressure, values of $u_{\mathrm{c}}^*$ are chosen between 0 and an arbitrary maximum value ${u_{\mathrm{c}}^*}_{{\mathrm{max}}}$ using 350 equal intervals. This maximum suction value ${u_{\mathrm{c}}^*}_{\mathrm{max}}$ is defined as the one leading to a mean filling angle lower than $1^\circ$ for contacting particles. Such suction cut-off disregards liquid bridges that would show negligible liquid volume and capillary forces. Thus, approximating unsaturated conditions beyond ${u_{\mathrm{c}}^*}_{\mathrm{max}}$ with dry conditions introduces a negligible error in the DEM model.

Simulations of suction-controlled loading paths are thereafter carried out by interpolating during the DEM workflow from the above generated data set to determine all possible liquid bridges between the individual particles according to the ratio of their radius and separation distance, given the constant suction and contact angle values. The suction-controlled nature of the loading paths is consistent with drained conditions, while the prescribed suction at the macroscale translates into constant capillary pressure conditions at the micro-scale where liquid bridges are computed from Sect. 2. Thus, the corresponding liquid distribution conforms with uniform capillary pressure conditions that are specific to thermodynamic equilibrium and also considered by [33, 39]. On the other hand, contrary to [13, 26], the model does not include any pore flow computations. Thus, some phenomena known to affect the fluid distribution in unsaturated conditions, such as the ink-bottle effect, are not included in the model. Also, the consideration of a constant uniform contact angle value for each simulation disregards the possibility for contact angle hysteresis that is also known to impact the fluid distribution [25]. However, the liquid phase distribution that results from such numerical modelling paradigm has been favourably compared with experiments in terms of soil–water characteristic curves in a previous paper [37]. Capillary bridges, with their associated capillary forces, are thus defined for all contacting and separated particles for which a solution of the Laplace–Young equation can be found. As such, contrary to many other DEM studies [24, 26, 31, 35], the capillary force is not obtained from any phenomenological relations such as the ones discussed in Sect. 2.4.

The standard DEM calculations then carry on with classical frictional contact forces being applied between contacting particles in addition to the above-mentioned capillary forces. In other words, along the normal direction, repulsive contact forces evolve with a fictitious overlap according to linear elasticity. It is to be understood that the numerical overlap corresponds in reality to slight changes in shape when the contact force increases between two actual spherical particles. By design, such deformations in DEM calculations are restricted to small values, and these are thus not accounted for during capillary force determination in the contact regime. In addition to the normal component of the contact force, a tangential component is expressed from the tangential relative displacements using a linear elastic–plastic relation. As usual, the contact law only requires three parameters: Y and P that govern the normal and tangential stiffnesses, and a contact friction angle $\varphi$. However, the particle size distribution of the sample (Fig. 8) becomes another parameter in the model since capillary force computations are size-dependent, and hence a characteristic length scale is introduced. All parameter values are given in Table 1, and we refer to a previous work [37] for more details concerning Y, P, $\varphi$. The considered surface tension is the one developing between air and water at ambient temperature. Note finally that there are a total number of 20,000 particles making up the numerical sample, which is high enough to have no influence on the results.

Fig. 8

Particle size distribution of the DEM sample

Table 1 Model parameters

3.2 Contact angle influence on SWCC

The computation of all liquid bridge volumes in the DEM calculations provides the possibility of obtaining the macroscale soil–water characteristic curves (SWCCs) for uniform suction conditions. Being dependent on the chosen particle size distribution, the SWCCs are generated for different contact angles under an isotropic stress of $p = 10$ kPa—this value has little influence on the final result—and imposing different suction values to the numerical sample. For each contact angle, two distinct SWCCs are determined by computing menisci either between contacting particles only, or between both contacting and separated particles. As water vapour condensates into liquid primarily over contacting solid surfaces, the consideration of menisci at contacts only may be related to a pseudo-primary wetting path. On the other hand, considering menisci for admissible particle distances, i.e. as long as a solution to the Laplace–Young equation can be found, is presented as a pseudo-primary drying path. However, it is reminded that there is no simulation of the pore flow of the two fluids, which leads the model to neglect some mechanisms such as the ink-bottle effect that are responsible for hysteresis during physical hydraulic paths. As such, a limited hysteresis is obtained between the pseudo-wetting and pseudo-drying SWCCs, see Fig. 9.

Fig. 9

Pseudo-wetting and pseudo-drying SWCCs for different contact angles

It is noted that the contact angle inevitably influences the SWCC since it is directly connected to the volumetric-suction $V^*(u_{\mathrm{c}}^*)$ relationship at the liquid bridge scale. As seen in Fig. 9, there is a significant difference in SWCC for contact angles greater than $\theta = 20^\circ$. Indeed, an increasing contact angle reduces the suction for a given degree of saturation with the two being interchangeable. This result further suggests that soils are less sensitive to unsaturated conditions for higher contact angles, as the next sections will demonstrate in detail.

3.3 Contact angle influence on strength

The association between the contact angle value and the mechanical consequences of unsaturated conditions is investigated into more details considering the apparent shear strength of wet samples. For each contact angle value, and different applied suctions, two triaxial, i.e. axisymmetric compressions, with 10 and 20 kPa confining pressure, are carried out in order to determine the corresponding apparent shear strength as interpreted using a Mohr–Coulomb criterion. As has been observed experimentally [29, 30], the macroscopic friction angle $\phi$ is unaffected by unsaturated conditions and corresponds to the friction angle developed in dry conditions: all $\phi$ values are equal to $30.1\pm 0.3^\circ$. The correspondence between $\phi$ that has been measured for dry conditions in previous works [10, 37], with the local friction angle between two discrete elements, $\varphi$, is purely coincidental. Disregarding the constant friction angle, the shear strength is then quantified through the apparent cohesion c (Fig. 10). We recall first that the cohesion values depend on the chosen particle size distribution: greater cohesions would be obtained for another distribution involving smaller particles.

Also, in line with the differences in the SWCCs previously shown in Fig. 9, the apparent cohesion of the unsaturated samples significantly decreases with the contact angle, independent of the suction or degree of saturation as depicted in Fig. 10. Such a decrease in the apparent cohesion is attributed to the lower attractive capillary forces that were observed for higher contact angles back in Sect. 2.3 (Fig. 4).

Fig. 10

Apparent cohesion for different contact angles

We notice that the strength as expressed in terms of the apparent cohesion globally increases with the degree of saturation, i.e. decreasing suction, for a given contact angle. This trend is typical of granular materials with low degrees of saturation, as has been observed experimentally [29, 30]. The explanation resides in the underlying microscopic mechanism where the capillary force associated with a liquid bridge decreases in the range of high capillary pressures, see Fig. 11. This is equivalent to increases in capillary forces with water content at the low end of water contents within the pendular regime.

Fig. 11

Dimensionless capillary force according to dimensionless suction for different distances and $r=2.5 ; \theta = 20^\circ$. See also [27] for $r=1$

The case of a liquid bridge between two contacting particles is nonetheless different, displaying a monotonic increase in the capillary force with decreased liquid saturation, i.e. an increase in suction. It turns out that this difference in mechanical behaviour confers a significant role to liquid bridges between distant particles that have been previously argued to not contribute to the stress transmission inside an unsaturated granular soil [30], and thereafter neglected in DEM models similar to the one here considered [38].

In the present paper, it is chosen to simulate mechanical loadings from an initial state including menisci at contacts only, and thereafter consider menisci even if contact is lost, but ensuring Laplace–Young equation can be solved. This includes the instance when initially contacting spheres start separating, while new menisci also form at new contacts. For the purpose of emphasizing the role of stretched menisci between separated particles, apparent cohesions are also measured with a simplified version of the model that discards menisci and capillary forces as soon as initially contacting spheres separate. As expected, lower cohesions are measured with the simplified model due to a lower number of liquid bridges and attractive forces inside the sample, see Fig. 12. More importantly, the cohesion trends with water content are also affected with the simplified model showing a monotonic decrease with water content that contradicts experimental evidence [29, 30] or other numerical models [26]. Figure 12 considers the case of $\theta = 0^\circ$, but the exact same trends have been measured for other contact angle values. It is for the above reason that we conclude stretched menisci should not be disregarded in the DEM modelling as long as they are admissible, i.e. a solution of Laplace–Young equation.

Fig. 12

Apparent cohesion for $\theta = 0^\circ$ accounting for menisci between distant particles (“cont. + dist.” data set), or not (“cont. only” data set)

3.4 Contact angle influence on constitutive behaviour

Finally, we examine the constitutive behaviour during suction-controlled triaxial loading paths under 20 kPa confining pressure and 20 or 300 kPa suction, for different contact angles. Table 2 gives the corresponding initial degrees of saturation.

Table 2 Initial degree of saturation (%) of considered triaxial loadings (with 20 kPa confining pressure)

Apart from the previously discussed strength changes, the contact angle has negligible influence on the overall constitutive behaviour, see Figs. 13 and 14. It is clear that virtually the same residual states and strain behaviour are observed for a given suction, irrespective of the contact angle. Initial stiffnesses are also found to be unaffected.

Fig. 13

Contact angle influence during triaxial loadings with 20 kPa suction

Fig. 14

Contact angle influence during triaxial loadings with 300 kPa suction

4 Micromechanical interpretation from capillary stresses

In order to get further insights in the role played by the contact angle in wet conditions, e.g. on the apparent shear strength, attention is now focused on the nature of the stress state of an unsaturated soil.

4.1 Stress state of wet soils

As a starting point, the various stress contributions to the total stress $\varvec{\sigma }$ in an unsaturated soil are briefly presented. Alluding to the various internal forces that exist within a wet granular material, these contributions necessarily implicate contact forces between solid particles as well as fluid pressures and surface tension forces.

The contact stress tensor ${\mathsf {\varvec{\sigma }^{\hbox {cont}}}}$ accounting for the contact forces is given by the celebrated Love–Weber formula [21, 40]:

$$\begin{aligned} {\mathsf {\varvec{\sigma }^{\hbox {cont}}}} = \dfrac{1}{V} \sum \limits _{c.\ 1,2} \mathbf {f_2} \otimes \mathbf {l_{12}} \end{aligned}$$

(15)

Eq. (15) considers all contacting particles pairs 1-2 in the REV V, with $\mathbf {f_2}$ the contact force as sustained by 2, and $\mathbf {l_{12}}$ the branch vector connecting the centre of 1 to that of 2.

Whereas the contact stress tensor equals to the total net stresses in dry conditions, a capillary stress tensor ${\mathsf {\varvec{\sigma }^{\hbox {cap}}}}$ arises in unsaturated conditions, accounting for the stress contributions from the fluid phases and the existing interactions between the various phases:

$$\begin{aligned} {\mathsf {\varvec{\sigma }^{\hbox {cap}}}} = \varvec{\sigma }- u_g \, \varvec{\delta } -{\mathsf {\varvec{\sigma }^{\hbox {cont}}}} \end{aligned}$$

(16)

Note that the capillary stress terminology, used also by Scholtès et al. [33], corresponds to the suction stress as coined by Lu & Likos [23]. From micromechanics, and under quasi-static conditions, the expression for ${\mathsf {\varvec{\sigma }^{\hbox {cap}}}}$ is obtained from the different mechanical actions related to fluid pressures and surface tension forces [6, 7]:

$$\begin{aligned} {\mathsf {\varvec{\sigma }^{\hbox {cap}}}}&= - u_{\mathrm{c}} \, {\mathsf {\varvec{\chi }}} - \gamma \, {\mathsf {\varvec{\xi }}} \nonumber \\ {\mathsf {\varvec{\chi }}}&= \dfrac{1}{V} \left( V_l \, \varvec{\delta } + \sum \limits _p \, R_p \int _{S_p^l} {{\mathbf {n}}} \otimes {{\mathbf {n}}}\ \hbox {d}S\right) \nonumber \\ {\mathsf {\varvec{\xi }}}&= \dfrac{1}{V} \left( \int _{S_{lg}} ({\mathsf {\varvec{\delta }}} - {{\mathbf {n}}} \otimes {{\mathbf {n}}}) \, \hbox {d}S + \sum \limits _p R_p \int _{\varGamma _p} {\mathbf{ e}} \otimes {{\mathbf {n}}} \, {{\hbox{d}}l} \right) \end{aligned}$$

(17)

Fig. 15

Liquid bridge characteristics associated with Eq. (17)

Figure 15 shows the various characteristics of a liquid bridge between two particles that appear in the capillary stress expression (17). The latter encompasses all internal forces within the fluid volumes in terms of an isotropic capillary pressure term $- u_{\mathrm{c}} \, V_l / V\, \varvec{\delta }$, as well as the internal forces within the so-called contractile skin [12] formed of all liquid-gas interfaces $S_{lg} = \sum S_m$ in terms of surface tension forces oriented along the surface projection tensor $({\mathsf {\varvec{\delta }}} - {{\mathbf {n}}} \otimes {{\mathbf {n}}})$ [6, 7, 15]. Eq. (17) also includes interactions terms between the different phases: first, the non-isotropic fluids action on the solid through the capillary pressure $u_{\mathrm{c}}$ acting along the wetted surfaces $S_p^l$ of the solid particles p showing radii $R_p$; and second, surface tension forces $\gamma \, \mathbf {e} \, \hbox {d}l$ as sustained by solid particles along the contact lines $\varGamma _p$ from the contractile skin. The vector ${{\mathbf {n}}}$ is the outward external normal to the solid particles in the last term of (17).

Previous DEM modelling approaches customarily use an alternate expression for ${\mathsf {\varvec{\sigma }^{\hbox {cap}}}}$ that is based on resultant capillary forces only [30, 33, 35, 39]. Interestingly, the comprehensive description of the solid and fluid microstructure by the DEM model enables one to compute the capillary stresses from Eq. (17) as well. Because the internal forces within an actual wet granular material differ in nature from point forces, the choice is made here to only consider Eq. (17) that reflects the distributed nature of, e.g. liquid pressure, instead of relying on resultant point forces. The discussion here is not trivial because internal stresses and resultant forces are not interchangeable, as any medium sustaining stresses, while in equilibrium—under zero resultant force—illustrates it. However, this issue is outside the scope of this paper and other publications by the authors present further details and explanations [37].

From the capillary stresses expression (17), it is noteworthy that the capillary stresses systematically include in the general case a deviatoric part depending on the distribution of fluids implicating $S_p^l$, $S_{lg}$, $\varGamma _p$ and interface orientations, which extends the classical Bishop’s theory [4]. Such deviatoric stress contribution from the fluids has previously been investigated for a zero contact angle, e.g. by the authors using a slightly different expression for ${\mathsf {\varvec{\sigma }^{\hbox {cap}}}}$ [10, 37, 38]. Because the contact angle governs the whole fluid distribution—for instance the contact line orientation and the $\int _{\varGamma _p} \mathbf {e} \otimes {{\mathbf {n}}}\, \hbox {d}l$ term—it is natural to expect that the contact angle affects the capillary stresses.

4.2 Capillary stresses during hydraulic loading

Capillary stresses are first measured along a pseudo-primary drying path simulated under constant isotropic (total) stresses $p = 10$ kPa. At this stage, the sample is isotropic, and the liquid distribution including menisci between contacting and separated particles is also isotropic. As such, ${\mathsf {\varvec{\sigma }^{\hbox {cap}}}}$ is spherical and is completely characterized by its mean pressure $p_{\hbox {cap}}$. We have namely:

$$\begin{aligned} p_{\hbox {cap}}= & {} \dfrac{ {{{\mathrm{tr}}}}({\mathsf {\varvec{\sigma }^{\hbox {cap}}}})}{3} = p_\chi + p_\gamma \nonumber \\ p_\chi= & {} - \dfrac{u_{\mathrm{c}}}{3\, V} \left( 3\, V_l + \sum \limits _p R_p \, S^l_p \right) \nonumber \\ p_\gamma= & {} - \dfrac{ \gamma }{3\, V} \left( 2 \, S_{lg} + \sum \limits _p\, R_p \,\varGamma _p\, \sin \theta \right) \end{aligned}$$

(18)

Fig. 16

Capillary stresses during the hydraulic loading of an isotropic sample ($S_r = 0$ as well as $p_\chi = 0$ are both never reached limits). a $p_{\hbox {cap}} = p_\chi + p_\gamma = {{{\mathrm{tr}}}}({\mathsf {\varvec{\sigma }^{\hbox {cap}}}}) /3$. b $p_\chi$. c $p_\gamma$

Irrespective of the degree of saturation, an increasing contact angle leads to a decrease (in absolute value) of the capillary stress $p_{\hbox {cap}}$ due to the two-fluid mixture, see Fig. 16. The decline in $p_{\hbox {cap}}$ with $\theta$ follows a decreasing (in absolute value) $p_\chi$ that is not counterbalanced by an increasing $p_\gamma$. As for $p_\chi$, higher contact angles induce lower suctions for a given water content (Fig. 9), then lower $p_\chi$. As for $p_\gamma$, its direct dependence on the contact angle with $\sin \theta$ appearing Eq. (18) leads $p_\gamma$ to increase with $\theta$.

For a given contact angle, changing the degree of saturation, i.e. suction, has a minor influence on the capillary stress $p_{\hbox {cap}}$ because of the opposite trends of $p_\chi (S_r)$ and $p_\gamma (S_r)$. Note finally that apart from very low water contents, with negligible interface surfaces and wetted contours, a significant amount of the capillary stresses is due to $p_\gamma$ that accounts for surface tension forces.

4.3 Capillary stresses during mechanical loading

Capillary stresses are next computed during the triaxial loading paths presented back in Sect. 3.4 (Table 2). Contrary to the previous isotropic example, induced anisotropy here takes place in the initially isotropic sample upon the deviatoric mechanical loading. As menisci form along new contacts following induced anisotropy in the granular packing, an anisotropic liquid bridge distribution develops which gives way to deviatoric capillary stresses $q_{\hbox {cap}}$ [10, 37, 38].

Fig. 17

Capillary stresses during triaxial loadings with 20 kPa suction. a Mean stress $p_{\hbox {cap}}$, b deviatoric stress $q_{\hbox {cap}}$, c deviatoric nature

Fig. 18

Capillary stresses during triaxial loadings with 300 kPa suction. a Mean stress $p_{\hbox {cap}}$, b deviatoric stress $q_{\hbox {cap}}$. c Deviatoric nature

Turning to the influence of contact angle, it is found that higher values of $\theta$ decrease the intensity of capillary stresses with regards to both $p_{\hbox {cap}}$ and $q_{\hbox {cap}}$ for all suction values, see Figs. 17 and 18. Also, the deviatoric nature of ${\mathsf {\varvec{\sigma }^{\hbox {cap}}}}$—as measured by $\eta _{\hbox {cap}} = |q_{\hbox {cap}} / p_{\hbox {cap}}|$—slightly increases with the contact angle for low suctions, Fig. 17c. On the other hand, for high suction, the deviatoric nature of ${\mathsf {\varvec{\sigma }^{\hbox {cap}}}}$ does not depend anymore on the contact angle, as evidenced in Fig. 18c. Such high suction prevents menisci to exist between separated particles, and there is in this case equivalence between the liquid bridge and the contact distributions, hence between the deviatoric nature of ${\mathsf {\varvec{\sigma }^{\hbox {cap}}}}$ and the contact anisotropy. Contrary to the stress state, the straining of the packing can be considered as insensitive to the contact angle, as suggested previously in Figs. 13 and 14. This explains why $\eta _{\hbox {cap}}$ does not depend on the contact angle for $u_{\mathrm{c}} = 300$ kPa. Note that the apparent ultimate value for $\eta _{\hbox {cap}}$ is related to an existing critical state for the contact anisotropy [3, 42].

4.4 Failure description from capillary stresses

The distinct limit stress states as a function on wettability that we alluded to back in Sect. 3.3 are directly related to the corresponding capillary stresses observed in Sect. 4.3. However, a unified failure description is still possible, irrespective of the contact angle values. Such unified failure description is only obtained when the stress limit states (maxima of $\eta = q/p$) are expressed in terms of the contact stress tensor ${\mathsf {\varvec{\sigma }^{\hbox {cont}}}} = {\mathsf {\varvec{\sigma }}} - {\mathsf {\varvec{\sigma }^{\hbox {cap}}}}$ (neglecting $u_g$), instead of the total stresses ${\mathsf {\varvec{\sigma }}}$ that are necessarily affected by the fluid mixture and the contact angle. Shear strength data from triaxial compressions under 10 and 20 kPa confining pressures and several degrees of saturation in $[0.01 \%;10 \%]$ illustrate clearly that the consideration of ${\mathsf {\varvec{\sigma }^{\hbox {cont}}}}$ leads to a unique plastic limit criterion, for all contact angles and degrees of saturation, see Fig. 19.

Fig. 19

Failure description during triaxial compressions. a Using total stresses ${\mathsf {\varvec{\sigma }}}$. b Using contact stresses ${\mathsf {\varvec{\sigma }^{\hbox {cont}}}} = {\mathsf {\varvec{\sigma }}} - {\mathsf {\varvec{\sigma }^{\hbox {cap}}}}$

This interesting result illustrates the validity of the single effective stress concept to describe the failure of granular materials in both dry and unsaturated conditions as discussed, e.g. by Alonso et al. [1]. However, we do not address here the more complex issue of a comprehensive stress-strain behaviour. Also, this study confirms previous numerical results pertaining to the pendular regime with $\theta = 0^\circ$ [10, 33, 37], as well as experimental works [1, 23].

5 Conclusion

The contact angle $\theta$ affects the mixture of fluids in multiphasic granular soils, which, in turn, impacts on the mechanical behaviour of the soil. In order to assess this contact angle mechanical influence, we proposed a DEM model allowing a macroscopic mechanical analysis for any $\theta$ value. The DEM model relies on a systematic numerical solution of Laplace–Young equation, so that capillary bridges are precisely described in terms of capillary force, volume, surface, and orientation tensor.

In line with the microscopic contact angle influence at the capillary bridge scale, macroscale mechanical simulations performed with the DEM model show that the stress state of macroscopic soil samples is less sensitive to unsaturated conditions for higher contact angles. As a matter of fact, higher $\theta$ values reduce the suction, i.e. capillary pressure as well as the apparent shear strength increase classically associated with unsaturated conditions. Such contact angle influence arises from a decrease in the capillary stresses according to $\theta$. As such, the classical zero contact angle assumption is shown to be non-conservative for the mechanical analysis of wet granular soils.

Appendices

Appendix 1: Liquid bridge orientation tensor

Considering a meniscus-related orientation basis $(\mathbf {e_\rho },\mathbf {e_\phi },\mathbf {e_z})$ (Fig. 1), the liquid bridge external normal ${{\mathbf {n}}}$ and the local orientation tensor ${{\mathbf {n}}} \otimes {{\mathbf {n}}}$ are:

$$\begin{aligned} {{\mathbf {n}}} =&\dfrac{1}{\sqrt{1+{\zeta ^{*\prime }}^2}} \begin{pmatrix} 1 \\ 0 \\ - \zeta ^{*\prime } \end{pmatrix} \end{aligned}$$

(19)

$$\begin{aligned} {{\mathbf {n}}} \otimes {{\mathbf {n}}} =&\dfrac{1}{1+{\zeta ^{*\prime }}^2} \begin{pmatrix} 1 &{} 0 &{} - \zeta ^{*\prime }\\ 0 &{} 0 &{} 0\\ - \zeta ^{*\prime } &{} 0 &{} {\zeta ^{*\prime }}^2 \end{pmatrix} \end{aligned}$$

(20)

From the discrete description of the liquid bride profile $(z^*_i,\zeta _i^*)$ and a numerical integration along the profile—$z^*_i \in [0;z^*_f]$—the dimensionless meniscus orientation tensor $\varvec{\pi ^*}$ is obtained as:

$$\begin{aligned} \varvec{\pi ^*} = \int _{S_m^*} {{\mathbf {n}}} \otimes {{\mathbf {n}}} \ \hbox {d}S^* = \pi \, \Delta z^* \sum \limits _{i=1}^{f} \dfrac{\zeta ^*_i}{\sqrt{1+{\zeta ^{*\prime }_i}^2}} \begin{pmatrix} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 2\,{\zeta ^{*\prime }_i}^2 \end{pmatrix} \end{aligned}$$

(21)

Appendix 2: Free energy of liquid bridge configurations

The capillary bridge depicted in Fig. 1 includes free energy of different types:

• surface free energy $E_{int}$ is present along the interfaces between liquid and gas, liquid and solid, and solid and gas [5, 28]. We denote A, $A_{ls}$ and $A_{sg}$ the respective areas; and $\gamma$, $\gamma _{ls}$ and $\gamma _{sg}$ the respective surface tensions. Using Young’s equation $\gamma \, \cos \theta = \gamma _{sg} - \gamma _{ls}$, and the area decomposition $A_s = A_{ls} + A_{sg}$, it transpires directly that:

  $$\begin{aligned} E_{int} &= \gamma \, A + \gamma _{ls} \, A_{ls} + \gamma _{sg} \, A_{sg}\nonumber \\&= \gamma \, (A - A_{ls} \, \cos \theta ) + \gamma _{sg} \, A_s \end{aligned}$$

  (22)

  The wetted area $A_{ls}$ is:

  $$\begin{aligned} A_{ls} = 2\, \pi \, \left( {R_1}^2 \,(1-\cos \delta _1) + {R_2}^2 \,(1-\cos \delta _2) \right) \end{aligned}$$

  (23)

  Through classical differential geometry, the profile $\zeta ^*(z^*)$ gives the axisymmetric meniscus area:

  $$\begin{aligned} A&= 2\, \pi \, {R_2}^2 \int \limits _0^{z^*_f} \zeta ^*(z^*)\, \sqrt{1 + {\zeta ^{*\prime }(z^*)}^{2}} \, \hbox {d}z^* \nonumber \\&\approx 2\, \pi \, {R_2}^2 \sum \limits _{i=1}^{f} \zeta ^*_i \, \sqrt{1+ {\zeta ^{*\prime }_i}^2} \, \Delta z^* \end{aligned}$$

  (24)

• liquid and gaseous fluid volumes include the free energy $E_f = -u_f \, V_f$ ($f=l,g$). We consider the capillary bridge forming in a constant surrounding volume ${\mathcal {V}} = V_s + V_l + V_g$, such that:

  $$\begin{aligned} E_f = -u_g\, V_g - u_l \, V_l = -u_g\, ({\mathcal {V}}-V_s) + u_{\mathrm{c}} \, V_l \end{aligned}$$

  (25)

• no energy is associated with the rigid spheres. The same assumption leads to consider $A_s$ as constant in Eq. (22).

Omitting the constant terms $\gamma _{sg} \, A_s$ and $u_g\, ({\mathcal {V}}-V_s)$, the expression of $E_{int} + E_f$ in a dimensionless form—$E^* = (E_{int} + E_f) / (\gamma \, {R_2}^2)$—gives Eq. (12).

Appendix 3: Comparison with Willett’s model

With respect to our notations, the capillary force expression proposed by Willett [41] applies to a dimensionless force equal to $F^*\, (1+r)/2$. In [41], the relation is expressed according to a dimensionless distance $S^+$ that corresponds, here, to $d^* \sqrt{2/(V^* (1+r))}$. Namely, the equation proposed by Willett finally reads:

$$\begin{aligned} F^* = \dfrac{2}{1+r}\exp \left( f_1 - f_2 \exp \left( f_3 \ln S^+ + f_4 \ln ^2 S^+\right) \right) \end{aligned}$$

(26)

The coefficients $f_i$ depend on the contact angle and a dimensionless volume that corresponds here, with respect to our notations, to $V^* (1+r)^3 / 8$. Their exact expressions can be found in the Appendices of [41] or [14].