Stagnation proofness in n-agent bargaining problems

Abstract

Some bargaining solutions may remain unchanged under any extension of a bargaining set which does not affect the utopia point, despite the fact that there is room to improve the utility of at least one agent. We call this phenomenon the stagnation effect. A bargaining solution satisfies stagnation proofness if it does not suffer from the stagnation effect. We show that stagnation proofness is compatible with the restricted version of strong monotonicity (Thomson and Myerson in Int J Game Theory 9(1):37–49, 1980), weak Pareto optimality, and scale invariance. The four axioms together characterize the family of the bargaining solutions generated by strictly-increasing paths ending at the utopia point (SIPUP-solutions).

1 Introduction

When the feasible set of a bargaining problem (Nash 1950) is expanded leaving the utopia point unaffected, some bargaining solutions are not responsive to potential improvements, whereas some other solutions can translate the expanded possibilities into better payoff of at least one agent. We call this lack of responsiveness the stagnation effect.

This phenomenon is not an issue for 2-agent bargaining problems, since the axiom of strong Pareto optimality¹ implies the avoidance of the stagnation effect. However, our concern is that the vast majority of bargaining solutions do not satisfy this axiom when there are 3 or more agents. In addition, with 3 or more agents, strong Pareto optimality is not compatible even with restricted versions of monotonicity (García-Segarra and Ginés-Vilar 2015). In contrast, most of the well-known bargaining solutions satisfy weak Pareto optimality for the case of n agents. Weak Pareto optimality does not guarantee the avoidance of the stagnation effect since some of the solutions satisfying it remain stagnant under all possible expansions of the bargaining set that keeps the utopia point unchanged.

In view of the stagnation effect, we introduce a new axiom, stagnation proofness. Whenever a bargaining solution satisfies this property such bargaining solution does not suffer from the stagnation effect.

Many bargaining solutions are defined by means of monotone paths, for instance, the egalitarian solution and the solution characterized by Kalai and Smorodinsky (1975) (hereinafter KS).² Two interesting results about families of solutions generated by monotone paths deserve especial attention. The first one is a characterization of a family of solutions generated by strictly increasing paths that holds for n-agent problems (Thomson and Myerson 1980). This result focuses on the environment of solutions where there is interpersonal comparability of utility across agents. The egalitarian solution, for instance, belongs to this family. The second one is a family that generalizes a particular weighted version of the KS solution (Alós-Ferrer et al. 2017), i.e., solutions generated by increasing paths ending at the utopic point (which is the point that reflects the maximum aspirations of each agent given a bargaining problem.) There are two characterizations of this family. One of them holds for 2-agent problems (Peters and Tijs 1985), while the other one holds for the case of three or more agents (Peters and Tijs 1984). Both characterizations refer to the environment of solutions in which there is no interpersonal comparability of utility. Obviously, the KS solution belongs to this environment.

The solutions characterized in Thomson and Myerson (1980) do suffer from the stagnation effect. In contrast, the family of solutions characterized in Peters and Tijs (1984, 1985) satisfy the axiom of strong Pareto optimality, therefore they do not suffer from the stagnation effect. However, in order to provide a characterization for n-agent problems, a restriction on the bargaining domain is required (Peters and Tijs 1984).

Relying on the axiom of stagnation proofness, we provide a characterization of the family of solutions generated by strictly increasing paths (as the ones in Thomson and Myerson 1980) ending at the utopia point (as the ones in Peters and Tijs 1984, 1985) that holds for n agents and for the whole class of canonical bargaining problems.

The paper is organized in four sections. Section 1 contains definitions and notation. In Sect. 2, we introduce the stagnation effect and the concept of stagnation proofness. In Sect. 3, we state and prove our main result. Section 4 concludes.

2 Definitions and notation

An n-agent bargaining problem consists of a set of agents $N=\{1,...,n\}$ with $n\ge 2$, a vector of utilities $d=(d_{1},...,d_{n}) \in \mathbb {R}^n$, and a compact, convex subset $S\subset \mathbb {R}^{n}$ of utility vectors containing d and at least one element x with $x>d$.³ In addition, we ask for the fulfillment of d-comprehensiveness, i.e., for every $x \in S$ and every $y \in \mathbb {R}^{n}$ with $d\le y \le x$, it follows that $y \in S$. The interpretation is that the set S is the set of feasible expected utility payoffs to the players. Those can be achieved by unanimous agreement, but if an agreement is not reached, the disagreement vector d ensues. Let $\Sigma$ be the class of such pairs (S, d).⁴

A bargaining solution is a function f defined on the class of bargaining problems $\Sigma$ which provides a feasible outcome for every pair, i.e., $f: \Sigma \mapsto \mathbb {R}^{n}$ such that $f(S,d)\in S$ for every $(S,d)\in \Sigma$. The point f(S, d) is the solution of the bargaining problem represented by the pair (S, d). Following Kalai and Smorodinsky (1975) and Kalai (1977), we only consider solutions such that $f(S,d) \ge d$, i.e., that satisfy individual rationality.

For a given bargaining problem (S, d), the utopia point, m(S, d) is a point defined by the maximum outcome reachable by each agent i on the individually rational part of the set S. Formally, for each i,

$$\begin{aligned} m_i(S,d)\equiv \max \{x_{i} \left| x \ge d, x\in S\right. \}. \end{aligned}$$

For simplicity we fix $d= (0,...,0) \equiv \mathbf{0}$ and we will refer to a bargaining problem $(S,\mathbf{0})$ as S. We remark that this is without loss of generality if we consider solutions satisfying translation invariance, i.e. the property that $f(S+t, d+t) = f(S, d) + t$ for all $t \in \mathbb {R}^n$.

Fig. 1

The stagnation effect

The strong and weak Pareto frontiers of a bargaining set S are the sets $SPO(S) \equiv \{x\in S \mid \ \not \exists \ y \in S\ \text{ with }\ y \ge x\}$ and $WPO(S) \equiv \{x\in S \mid \ \not \exists \ y \in S\ \text{ with }\ y > x\}$, respectively.

3 The stagnation effect

Some bargaining solutions may remain unchanged under any extension of a bargaining set which does not affect the utopia point, despite the fact that there is room to improve the utility of at least one agent. We call this phenomenon the stagnation effect. Bargaining solutions such as the weighted KS solution (Thomson 1994), the egalitarian solution, the family of solutions generated by strictly monotone paths (Thomson and Myerson 1980), and the proportional solutions (Kalai 1977) are affected by this stagnation effect. When a bargaining solution satisfies SPO this implies that the solution does not suffer from the stagnation effect.

For 2-agent problems, it would be possible to find solutions failing SPO (but still fulfilling WPO) that do not suffer from stagnation effect, however these solutions would not be among the ones typically studied in the literature. The picture is different if we focus on problems with 3 or more agents, since then we can observe some well-known WPO-solutions suffering from stagnation effect and some others that do not. This is why we illustrate the stagnation effect using a 3-agent problem. In Fig. 1, we have two WPO-solutions generated by monotone paths. However, they behave differently when the bargaining set is expanded without affecting the utopia point. The path connecting the disagreement point ($d=A$) with the utopia point ($m(S)=D$), i.e., the segment AD, recommends the outcome at point C. Hence, an eventual expansion in the bargaining set without affecting the utopia point may improve the outcome of at least one agent. In contrast, the solution generated by the path connecting AB recommends an outcome that remains stagnant at point B irrespectively of any expansion of the bargaining set. We provide a formal definition of the stagnation effect.

Definition 1

A solution suffers from the stagnation effect if and only if there is a set $S \in \Sigma$, with $m(S) \notin S$, such that for each $S' \supsetneq S$ with $m(S') = m(S)$, $f(S')=f(S)$.

We define the axiom of stagnation proofness as the logical negation of the stagnation effect.

Stagnation proofness For each $S\in \Sigma$, with $m(S)\notin S$, there is at least one $S^{\prime }\supsetneq S$ with $m(S^{\prime })=m(S)$ and one agent $j\in N,$ such that $f_{j}(S^{\prime })>f_{j}(S)$.

Stagnation proofness says that for each bargaining set S such that utopia point m(S) is not feasible there is at least one superset $S^{\prime }$ with the same utopia point $m(S^{\prime })=m(S)$ such that, for at least one agent j, the solution of the superset $S^{\prime }$ is greater than the solution of the bargaining set S. In other words, this axiom requires the logical negation of the stagnation effect, therefore says that given a bargaining set, a solution can improve the payoff of at least one agent for at least one expansion of the bargaining set that keeps the utopia point unchanged.

There are many solutions satisfying stagnation proofness. Examples include the individually-monotonic solutions (Peters and Tijs 1984, 1985), the Nash solution (Nash 1950), the utilitarian solution, the KS solution, and many other solution concepts (Dubra 2001; Imai 1983; Chun and Peters 1989; Salonen 1987; Herrero and Marco 1993; Herrero 1998; Driesen 2016).

4 Main result

We present here several axioms used in the literature to characterize bargaining solutions (for a discussion, see Thomson 1994). The first two axioms capture the economic idea of efficiency.

Strong Pareto optimality: For every $S \in \Sigma$, $f(S) \in SPO(S)$.

Weak Pareto optimality: For every $S\in \Sigma$, $f(S)\in WPO(S)$.

Strong Pareto optimality says that all gains from cooperation should be exhausted, while weak Pareto optimality states that no opportunity that benefits all agents should be ignored. Obviously, the former implies the latter since $SPO(S)\subseteq WPO(S)$. Paretian axioms are standard requirements in the characterization of bargaining solutions.

The next axiom reflects the idea of monotonicity. Monotonicity is a desirable property in interpersonal bargaining, since human decision makers usually associate this property with fairness concerns.

Restricted strong monotonicity For each pair $S,T \in \Sigma$, if $S \supseteq T$ and $m(S) = m(T)$, then $f(S) > f(T)$ or $f(S) = f(T)$.

This axiom says that, if there is an expansion of the feasible set leaving unaffected its utopia point, all agents should benefit from the new opportunities. It can be interpreted as full solidarity, in the sense that the agents only benefit from an expansion whenever all agents improve their utility, otherwise no one benefits from such expansion. Restricted strong monotonicity is a straightforward version of the strong monotonicity axiom introduced by Thomson and Myerson (1980). The only difference between these axioms is that the restricted version requires the utopia point of the bargaining set to be unaffected. It is also a strengthening of restricted monotonicity proposed by Rosenthal (1976), which allows for an improvement of some agents leaving the rest unaffected. Therefore, if a solution satisfies restricted strong monotonicity, then also satisfies restricted monotonicity. To the best of our knowledge nobody introduced this axiom before as we formally defined in this paper.

Scale invariance is an axiom that deals with the possibility of normalizing the bargaining set by means of a positive transformation. Let $\mathbb {R}_{+}^{n} \equiv \left\{ x \in \mathbb {R}^{n}\;\left| \; \; x \ge 0\right. \right\}$. For every $\lambda \in \mathbb {R}_{+}^{n}$, let $\lambda S\equiv \{(\lambda _{1}s_{1}, ..., \lambda _{n} s_{n})\mid s \in S \}$, and $\lambda f(S)\equiv (\lambda _{1}f_{1}(S), ..., \lambda _{n}f_{n}(S))$. Formally, this axiom is stated as follows:

Scale invariance: For each $S\in \Sigma$, $\lambda f(S)=f(\lambda S)$.

When a solution satisfies scale invariance, a bargaining set can be normalized and transformed into another set with utopia point $m(S)=(1,...,1)\equiv \mathbf{1}$. Therefore, the scale of units in which agents measure their utility does not matter.

Fig. 2

The paths that generate SIPUP-solutions

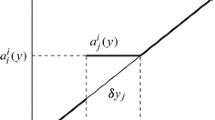
We now turn to our characterization result. Our aim is to identify the family of solutions fulfilling stagnation proofness, plus the natural axioms introduced above. For this purpose, we define a family of solutions through a small change in the definition of Peters and Tijs (1984). This change allows us to focus on solutions generated by strictly increasing paths ending at the utopia point (SIPUP). Specifically, given a path $\gamma :[1,n]\mapsto \mathbb {R}_{+}^{n}$ such that $\gamma _{1}(p)+\cdots +\gamma _{n}(p)=p$ for every $p \in [1,n]$ (this means that the sum of the coordinates of $\gamma$ equals to p), we say that $\gamma$ is a strictly-increasing path ending at the utopic point if for each $p,q \in \mathbb {R}$ with $1 \le p, q \le n$, $p < q$ implies $\gamma (p) < \gamma (q)$. Let us denote these paths by $\Gamma$. See Fig. 2 for an illustration of the paths that generate the SIPUP-solutions.

Definition 2

The family of the SIPUP-solutions for n-agent bargaining problems is given by all solutions $g^\gamma$ with $\gamma$ a strictly increasing path ending at the utopia point, where

$$\begin{aligned} g^\gamma (S) = \max \{\gamma (p) \in S| p \in [1, n] \} \end{aligned}$$

(1)

for each $S \in \Sigma$ with $m(S)= \mathbf{1}$.

By definition, S is a set bounded from above and $\gamma$ is a continuous strictly-increasing path ending at the utopic point. Therefore, $g^{\gamma }(S)$ is well defined.

Analogously to Peters and Tijs (1984), if $m(S)\ne \mathbf{1}$, by scale invariance we can normalize the set S, hence, we apply the solution $g^\gamma$ to the new normalized set and we rescale back the solution to the original set S.

The following result characterizes the SIPUP-solutions for n-agent problems and for the whole class of canonical bargaining problems.

Theorem 1

A solution f satisfies weak Pareto optimality, scale invariance, restricted strong monotonicity, and stagnation proofness if and only if there is a $\gamma \in \Gamma$ such that $f = g^\gamma$.

Proof

Part 1, “if”. The SIPUP-solutions are defined as bargaining solutions generated by strictly-increasing paths that connect the disagreement with the utopia point of each bargaining set. Thus, by construction, $g^\gamma$ satisfies weak Pareto optimality, scale invariance, and restricted strong monotonicity. To see the latter, note that if $S \subseteq T$ with $m(S) = m(T)$, and $g^\gamma$ is a SIPUP-solution, then there are $p \le q$ such that $g^\gamma (S) = \gamma (p)$ and $g^\gamma (T) = \gamma (q)$. Two possibilities arise, since $\gamma$ is a strictly increasing function, if $p=q$ then $g^\gamma (S) = g^\gamma (T)$, if $p<q$ then $g^\gamma (S) < g^\gamma (T)$. Therefore the SIPUP-solutions satisfy restricted strong monotonicity.

We have to show that $g^\gamma$ also satisfies stagnation proofness. Let $S \in \Sigma$ be a bargaining set with $m(S) = \mathbf{1}$ and $m(S) \notin S$. If $m(S) \ne \mathbf{1}$, by scale invariance we normalize the set. We define $\mathrm {comp}(1,0)\equiv \{x \in \mathbb {R}^n | \mathbf{0} \le x \le \mathbf{1} \} \supsetneq S$. By restricted strong monotonicity, either $g^\gamma (S) = g^\gamma (\mathrm {comp}(1,0))$ or $g^\gamma (S) < g^\gamma (\mathrm {comp}(1,0))$. Since $g^\gamma (\mathrm {comp}(1,0)) = \mathbf{1} \notin S$, we conclude that $g^\gamma (\mathrm {comp}(1,0))> g^\gamma (S)$. Therefore there is at least one expansion of S keeping m(S) unchanged that provides an improvement for at least one agent.

Part 2, “only if”. Let f be a solution that satisfies the axioms of Theorem 1. For each $t\in [1,n]$, we define $V_{t}\equiv \{x \in \mathrm {comp}(1,0) | \sum _{i=1}^{n} x_{i} \le t \}$. Note that $V_t$ is a compact and convex subset of $\mathrm {comp}(1,0)$ for each t with $V_n=\mathrm {comp}(1,0)$ and $V_s\subseteq V_t$ whenever $s,t\in [1,n]$ with $s\le t$.

We show that the bargaining solution f defines a strictly increasing path ending at the utopia point, $\hat{\gamma }$. For each $t\in [1,n]$, define $\hat{\gamma }(t) = f(V_t)$. First, we show that $\hat{\gamma }$ is well defined in two steps.

Step 1. We have to show that for each $t \in [1,n]$, $\sum _{i \in N} \hat{\gamma }_i (t) = t$.

Suppose that there are $t'$ and $p \in [1, n]$ such that $p = \sum _{i \in N} \hat{\gamma }_i (t') = \sum _{i \in N} f_i (V_{t'}) < t'$. It follows that $f(V_{t'}) \in V_p$. By weak Pareto optimality of $f(V_{t'})$, there is $j \in N$ such that $f_j(V_{t'})= 1$. By stagnation proofness, there is $S \supsetneq V_{t'}$ with $m(S)=m(V_{t'})= \mathbf{1}$ and there is a $k \in N$ such that $f_k(S) > f_k(V_{t'})$. By restricted strong monotonicity, $f(S)=f(V_{t'})$ or $f(S)>f(V_{t'})$. Since k is such that $f_k(S) > f_k(V_{t'})$, then $f(S)>f(V_{t'})$. This contradicts the fact that $f_j(V_{t'}) = 1$.

Step 2. We have to show that for each $t,t' \in [1, n]$ with $t < t'$, we have that $\hat{\gamma } (t) < \hat{\gamma } (t')$.

Since $V_{t'} \supseteq V_t$, by restricted strong monotonicity we have that either $f(V_{t'})= f(V_t)$ or $f(V_{t'})> f(V_t)$. By step 1, $f(V_{t'})> f(V_t)$. It follows that, $\hat{\gamma } (t') = f(V_{t'}) > f(V_t)= \hat{\gamma } (t)$ as desired. Therefore, $\hat{\gamma }$ is well defined.

Finally, we prove that $f=g^{ \hat{\gamma }}$. Let S be a bargaining set. If $m(S)\ne \mathbf{1}$, by scale invariance we can normalize the set into another set with $m(S) = \mathbf{1}$. Suppose by contradiction that $f(S) \ne g^{\hat{\gamma }} (S)$. Let $q \in [1,n]$ such that $q= \sum _{i\in N} f_i(S)$. By definition of $V_q$, $f(S) \in V_q$. It follows that $f (S) \in S \cap V_q$. We know that $S \supseteq S \cap V_q$, by restricted strong monotonicity, $f(S) = f(S \cap V_q)$ or $f(S) > f(S \cap V_q)$. Suppose $f(S) > f(S \cap V_q)$, by weak Pareto optimality of $f(S \cap V_q)$, $f(S) \notin S \cap V_q$ which is a contradiction. Therefore, $f(S) = f(S \cap V_q)$ and $\sum _{i \in N} f_i(S \cap V_q) = q$.

Analogously, $V_q \supseteq S \cap V_q$. By restricted strong monotonicity, $f(V_q) = f(S \cap V_q)$ or $f(V_q) > f(S \cap V_q)$. Suppose $f(V_q) > f(S \cap V_q)$, this contradicts the fact that $\sum _{i \in N} f_i(S \cap V_q) = q = \sum _{i \in N} f_i( V_q)$. Hence, $f(V_q) =f(S \cap V_q)$. Therefore, we conclude that $f(S) =f(S \cap V_q) = f(V_q)= \hat{\gamma } (q)$.

By definition of $g^{\hat{\gamma }}$, there is a $p \in [1,n]$ with $p \ge q$ such that $g^{\hat{\gamma }} (S)= \hat{\gamma } (p)$. If $p > q$, since $\hat{\gamma }$ is an strictly increasing function in every component, $g^{\hat{\gamma }} (S) = \hat{\gamma } (p) > \hat{\gamma } (q) = f(S)$. This is a contraction of weak Pareto optimality of f. Therefore, we conclude that $p=q$ and $f(S) =g^{\hat{\gamma }} (S)$ as desired. $\square$

We now show that the axioms of Theorem 1 are independent. First recall that the KS solution is given by: Let $\lambda (S) = \max \left\{ \lambda \in [0,1]\;\left| \; \; \lambda m(S) \in S\right. \right\}$,

$$\begin{aligned} KS(S)= \lambda (S) m(S) \end{aligned}$$

• 1. Dropping weak Pareto optimality. We define a solution G that satisfies the rest of axioms in Theorem 1. For each $S \in \Sigma$, define

  $$\begin{aligned} G(S)= {\left\{ \begin{array}{ll} \mathbf{0} &{}\quad \text {if } \sum \nolimits _{i=1}^{n} \frac{s_{i}}{m_i(S)} \le 1 \text { for all } s\in S \\ KS(S) &{}\quad \text {otherwise.} \end{array}\right. } \end{aligned}$$

  For the sets with $G(S)=\mathbf{0}$ there is a violation of weak Pareto optimality.

• 2. Dropping restricted strong monotonicity, the Nash bargaining solution (Nash 1950) becomes admissible.

• 3. Dropping scale invariance. We define a bargaining solution H that satisfies the rest of axioms in Theorem 1. For each $S \in \Sigma$ and $\gamma ^{1} \in \Gamma$ with $g^{\gamma ^{1}} (S) \ne KS(S)$, let

  $$\begin{aligned}H(S)= \left\{ \begin{array}{ll} g^{\gamma ^{1}} (S) &{}\quad \ \ if \ \ m(S) = \mathbf{1} \\ KS(S) &{}\quad \ \ otherwise. \\ \end{array} \right. \end{aligned}$$

  Clearly, for each $S \in \Sigma$ with $m(S) \ne \mathbf{1}$, if $\lambda = \left( \frac{1}{m_1(S)}, \ldots , \frac{1}{m_n(S)} \right)$, then $m(\lambda S)= \mathbf{1}$. Hence, $H(\lambda S) = g^{\gamma ^{1}} (S) \ne \lambda KS(S) = \lambda H (S)$. Therefore, the bargaining solution H fails scale invariance.

• 4. Dropping stagnation proofness, the weighted Kalai–Smorodinsky solutions (Thomson 1994) satisfy the remaining axioms of Theorem 1.

Our main result can be compared with other characterizations of solutions generated by monotone paths as the ones mentioned above. For instance, the solutions in Peters and Tijs (1984, 1985) are characterized by strong Pareto optimality, scale invariance, and restricted monotonicity. Our characterization also relies on scale invariance, but the rest of axioms are different. For instance, we use a stronger version of monotonicity, which is however a restricted version of strong monotonicity used by Thomson and Myerson (1980) to characterize a family of solutions generated by strictly increasing paths that do not satisfy scale invariance. Finally, we relax strong Pareto optimality asking for weak Pareto optimality and stagnation proofness (note that SPO implies the latter two). Regarding the characterization of Peters and Tijs (1984) for n-agent problems, by the impossibility result of García-Segarra and Ginés-Vilar (2015) a restriction on the bargaining domain has to be imposed, otherwise there is no solution satisfying strong Pareto optimality and restricted monotonicity for the whole class of canonical bargaining problems.

5 Concluding remarks

We have shown that some bargaining solutions remain stagnant under every possible expansion of a bargaining set that do not affect the utopia point. We call this phenomenon the stagnation effect. Whenever a solution satisfies SPO, such solution does not suffer from this effect. However, there are many solutions that fail to satisfy this axiom for 3 or more agents. For instance, the KS solution satisfies SPO when there are 2 agents but only satisfies WPO for problems with 3 or more agents. Some other solutions fail to satisfy SPO even for 2-agent problems, e.g., the proportional solutions (Kalai 1977). In this paper we introduce the axiom of stagnation proofness, which is the logical negation of the stagnation effect. Therefore, solutions satisfying this axiom do not remain stagnant to every possible expansion of a bargaining set that keeps the utopia point unaffected.

This axiom is satisfied by many well-behaved solutions and we use it to characterize the family of SIPUP-solutions. The SIPUP-solutions are those solutions generated by strictly increasing paths (in all components) that connect the disagreement point of each bargaining problem with its utopia. Although we characterize a narrower family of solutions than Peters and Tijs (1984), our result holds for n agents and for the whole class of canonical bargaining problems.